A Coupled Global Registration and Segmentation Framework With Application to Magnetic Resonance Prostate Imagery

Abstract

Extracting the prostate from magnetic resonance (MR) imagery is a challenging and important task for medical image analysis and surgical planning. We present in this work a unified shape-based framework to extract the prostate from MR prostate imagery. In many cases, shape-based segmentation is a two-part problem. First, one must properly align a set of training shapes such that any variation in shape is not due to pose. Then segmentation can be performed under the constraint of the learnt shape. However, the general registration task of prostate shapes becomes increasingly difficult due to the large variations in pose and shape in the training sets, and is not readily handled through existing techniques. Thus, the contributions of this paper are twofold. We first explicitly address the registration problem by representing the shapes of a training set as point clouds. In doing so, we are able to exploit the more global aspects of registration via a certain particle filtering based scheme. In addition, once the shapes have been registered, a cost functional is designed to incorporate both the local image statistics as well as the learnt shape prior. We provide experimental results, which include several challenging clinical data sets, to highlight the algorithm’s capability of robustly handling supine/prone prostate registration and the overall segmentation task.

I. Introduction

Prostate cancer ranks among one of the most widespread of all cancers for the U.S. male population [21]. In diagnosing prostate cancer, transrectal ultrasound (TRUS) guided biopsies have become the gold standard. However, the accuracy of the TRUS guided biopsy relies on and is limited by the fidelity. Magnetic resonance (MR) imaging is an attractive alternative for guiding and monitoring such interventions because it provides superior visualization of not only the prostate, but also its substructure and the surrounding tissues [14], [33], [49]. Such advancements provide a greater opportunity for successfully extracting the geometry of the prostate from the image, which is closely related to the prostate cancer assessment, and the need for therapy planning [56]. In this work, we present a shape-based framework to extract the prostate from MR imagery. Under this framework, a global image registration scheme is first proposed to align the training shapes. Once the shapes have been registered, a certain cost functional is then designed to incorporate both the local image statistics as well as the learnt shape prior in order to drive the curve in a variational manner toward the prostate surface. However, before presenting our method in detail, we first recall some of the results and specifics of both the segmentation and registration fields.

Segmentation entails separating an object from the background in an image. Although a complete review of image segmentation is beyond the scope of this paper, we briefly review some of the relevant work for the case of the prostate. Since ultrasound has been the dominant image modality for prostate diagnosis, most image segmentation techniques were tuned to this modality, and those for MR imagery have been more limited. We, therefore, review some of the relevant literature of both modalities. We begin with ultrasound. In [40], Pathak et al. propose an edge based method to delineate the prostate boundary for human editing. Similarly, Knoll et al. [26] propose an edge based scheme in which they employ a wavelet decomposition to give multiresolution prior information for the shape of a prostate contour. However, both of these edge based methodologies may be susceptible to noise problems as well as initialization. To address this issue, Betrouni et al. [4] adopt a filtering scheme to better handle image artifacts. That is, their method first combines an adaptive morphological and median filtering step, and then an active contour is deformed toward the desired edge. One should also note that texture information can be utilized for increased robustness [4], [44]. More recently, work has been done to extend the prostate segmentation to 3-D [64]. For example, the authors of [19] provide a 3-D deformable model to extract the surface of the prostate with six manually provided points as initialization, whereas in [15], a few slices with contours are required.

Regarding MR imagery, Zwiggelaar et al. proposed a semiautomatic method to extract prostate from the MR images [67]. In their work, the polar transformation is employed for the elliptical shape of the prostate. Furthermore, line detection is carried out to extract the prostate boundary. Likewise, Vikal et al. in [55] also detect the contour in each slice and then refine them to form a 3-D surface. However, one particular difficulty of MR prostate image segmentation is that the information from the target image alone is usually insufficient to constrain the shape of the final segmentation. Along this direction, Zhu et al. used a hybrid model to combine 2-D active shape model and 3-D optimization in order to obtain a better delineation of the prostate boundary in MR images [65], [66], which nicely handles both spatially isotropic and anisotropic images. Besides prostate, coupled-shape models are used to segment other related organs such as the bladder and rectum [39], [53]. More recently, Toth et al. combines the spectral clustering and active shape models to perform a segmentation utilizing the MR imagery and MR spectroscopy [52]. Moreover, Klein et al. construct an atlas from the nonlinear registered training shapes. The image is then segmented by atlas matching under the local mutual information criteria [25].

In order to restrict the contour evolution in an acceptable fashion during segmentation, one needs to learn the shape prior in advance [8], [29], [54], [64]. Before doing so, the training shapes need to be well-aligned so that any variation in training shapes is not due to pose, which is clearly an image registration problem. In general, registration can be usually categorized by either the similarity functional that is employed for comparison of two or more images, or by the transformation group. The former includes image feature correspondence [13], [29], [45], [58], [60], L^P norm or cross-correlation [43], [51], [54], mutual information [31], [57], [61], and the gradient of the intensity [16]. In the latter category, the transformation groups may range over rigid transformations [12], [29], [31], similarity transformations [22], [54], affine transformations [32], free form deformations represented by B-splines [46], thin plate splines [5], NURBS [59], or vector field representations [18], [50]. Further, for prostate registration, the authors of [2] and [37] combine the biomechanical property of the prostate and image information to obtain a registration preoperatively and during the surgical procedure.

It is important to note that almost all of the above schemes only handle the local registration task. Indeed, the global image registration problem is only briefly addressed in [1] and [22]. On the other hand, this notion of “global” registration is usually performed using a point-set framework.

Indeed, in contrast with image registration, point-set registration usually requires an extra step of explicitly finding the correspondences between points in the two sets. Then the transformation parameters can be estimated. This is the main theme of the well-known iterative closest point (ICP) algorithm introduced in [3]. However, the basic ICP approach is widely known to have issues with local minima. To address this issue, Fitzgibbon [11] introduced a robust variant by optimizing the cost functional via the Levenberg–Marquardt algorithm. Moreover, Chui and Rangarajan employed an annealing scheme to broaden the convergence range and reduce the influence of outlier [7]. However the temperature in the annealing scheme needs to be carefully chosen to balance the convergence range and algorithm stability. In addition, point-set registration can be alternatively be viewed as a parameter estimation task, whereby the transformation parameters are considered to be random variables. To this end, the authors of [30], [36], [48] employ filtering techniques to estimate the distribution of rigid transformation parameters.

A. Related Work

Our shape-based segmentation framework, where we unify registration and segmentation for the specific task of extracting the prostate from MR imagery, is strongly motivated by [54]. In their work, the training shapes are registered under a mean square error type of a cost functional defined over the group of similarity transformations. Then, with the shapes being represented by the signed distance function (SDF), shape priors are constructed via principle component analysis (PCA). The shape weights are then evolved along with the pose parameters to optimize a cost functional that is dependent upon global region based statistics.

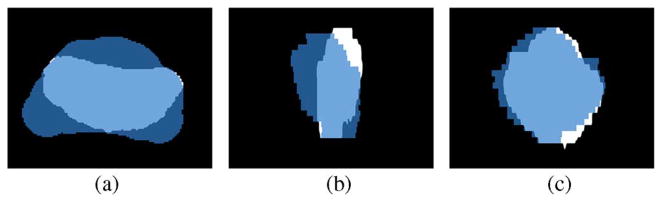
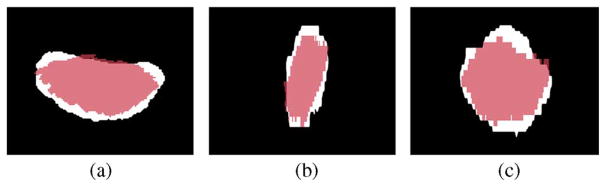
However, this scheme is not suitable for many kinds of prostate MR data. This is due to the fact that the training sets typically contain mixed supine/prone prostate shapes which inherently have very large pose variations. This can be seen in Fig. 4. In many (but not all) image data files, there may exist a tag indicating the subject’s position, from which the supine or prone can be inferred. However, this is not a given assumption in general. Moreover, even when all the training shapes are of the same position (supine or prone), the pose differences especially the angle differences are usually too large for the local optimization based registration procedures to capture. Hence, to register shapes of this kind, instead of relying on the orientation information in the image headers, we need to approach the problem with a global registration scheme. Secondly, the large values remote to the zero level set in the SDF representation may strongly interfere with the learning process. As a result, large SDF values may produce a wrong shape prior. Lastly, in many MR prostate images, the global statistics inside and outside the prostate are not descriptive enough to separate the prostate gland from the background.

Fig. 4.

Supine/prone prostates, before registration. Subplots show the (a) axial, (b) sagittal, and (c) coronal views.

To address the global registration problem, we employed an approach strongly related to [48], in which the authors proposed a particle filtering based scheme. However, the method only focuses on rigid point set registration and it cannot be readily applied to the prostate image registration task at hand.

Considering the segmentation problem, our work is also highly influenced by that of [28] where a scheme was proposed in which the evolution of each point on the curve depends on the local statistics within a ball centered at that point. Although this ameliorates the problem of the interference of image content far from the contour, it is computationally intensive because of the necessity of constructing a ball around each of the points under consideration.

B. Our Contributions

The contributions of the present work are threefold. First, we propose a global nonrigid (affine) registration method. In doing so, we present a way to represent images as point-sets. This bridges the areas of image and point-set registration, and enables us to solve the problem under a particle filtering framework in order to achieve a global optimality condition. Secondly, inspired by [28], our cost functional uses the image statistics localized in a banded region around the contour. It shares the local/global advantage of [28] for segmentation, but does not add extra computation when compared to purely global schemes. Lastly, the above two aspects are unified in a shape-based segmentation framework to extract the prostate from the MR imagery.

The remainder of the paper is organized as follows. In Section II, we demonstrate how to represent images as point-sets, and register images in the point-set framework under a particle filtering framework. After that, the shape prior is constructed in Section III. Next, in Section IV, the shape prior is combined with the local image statistics to perform the segmentation. We note that experiments and results will be given as each method is presented. Future and ongoing work is discussed in Section V.

II. Prostate Shape Registration

The way we represent images is crucial and so we summarize here some of the more common representations. We define an (intensity) image to be a nonnegative function f : Ω → ℝ⁺, where Ω is some compact domain in ℝ^d. In this work d = 2 or 3. Numerically, a given image may be represented as a discrete function defined on a uniform grid, where a value is associated with each spatial sampling location, namely the image intensity. We will refer to this as the discrete function representation (DFR). Using the probability density function (PDF), below we will define another representation called the point-set representation (PSR) for images. The central idea is to represent the image as a set of random samples rather than as a discrete function. We will show that such a representation is fully equivalent to DFR, and so no information is lost. However, PSR handles some of the difficult registration issues that are normally associated when the images are represented using DFR.

A. Point-Set Representations of Images

We now assume that our image is represented by a continuous function f on the compact image domain Ω. Set ||f||₁ := ∫_Ω f(x)dx and f̃(x) := f(x)/||f||₁, we then have

$$\{\begin{array}{l}\stackrel{\sim }{f}(\mathit{x})\ge 0,\forall \mathit{x}\in \mathrm{\Omega }\hfill \\ {\int }_{\mathrm{\Omega }}f(\mathit{x})d\mathit{x}=1\hfill \end{array}.$$ (1) (2)

This simple normalization allows us to treat f̃ as a PDF defined on Ω. In doing so, we can then represent the image f by drawing samples from this distribution. Indeed, we adopt the rejection sampling algorithm of [9] in order to obtain M samples from the above distribution, giving the set of points $\mathcal{P}=\{{\mathit{p}}_1,\dots ,{\mathit{p}}_M:{\mathit{p}}_i=(p_i^x,p_i^y,p_i^z)\in \mathrm{\Omega }\}$.

Unlike DFR, where a real (or integer) number is associated with each spatial position, the image is now purely represented by 2-D or 3-D points. Consequently, the higher intensity regions in the image are now represented as the denser points in the corresponding point set.

It is easy to show that the DFR representation can be easily obtained, modulo a normalization factor, from the PSR. Indeed, this is actually the PDF estimation problem [10]. Given the PSR $\mathcal{P}=\{{\mathit{p}}_1,\dots ,{\mathit{p}}_M:{\mathit{p}}_i=(p_i^x,p_i^y,p_i^z)\in \mathrm{\Omega }\}$, the DFR can be approximated as

$${\stackrel{\sim }{f}}_M(\mathit{x}):=\frac{1}{M}\sum _i^M{K}_{\sigma }(\mathit{x}-{\mathit{p}}_i)$$ (3)

where K_σ(x) is a kernel function and σ is its bandwidth. As M → ∞ and σ → 0, we have f̃_M(x) → f̃(x) [10].

B. Affine Image Registration Under PSR

Given the images f, g : Ω → ℝ⁺ we can obtain the corresponding PSR’s as described in the previous section. We denote the point-set for g as $\mathcal{Q}=\{{\mathit{q}}_1,\dots ,{\mathit{q}}_N:{\mathit{q}}_i=(q_i^x,q_i^y,q_i^z)\in \mathrm{\Omega }\}$. Then, we register the two images f and g by aligning their corresponding point-sets 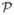and 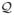using the following:

$$E(\mathit{A},\mathit{t}):=\frac{1}{N}\sum _{i=1}^N\left|\right|{\mathit{Aq}}_i+\mathit{t}-Cl({\mathit{Aq}}_i+\mathit{t})\left|\right|+\frac{\lambda }{{det}^2(\mathit{A})}$$ (4)

where A ∈ ℝ^3×3, det(A) ≠ 0 is the affine transformation matrix, t ∈ ℝ³ is the translation vector, and CI : ℝ³ → 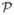maps a point in ℝ³ to its closest point in 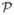. Note that the second term in (4) with weighting λ > 0, penalizes det(A) from getting close to zero. Indeed, this is because the optimization process wants to register the two point sets by minimizing the cost E with respect to A and t. However, without the second term, one cheap but incorrect way to minimize E is to set A to be the zero matrix. Then the moving point set, after multiplied by A, will degenerate to a single point (0, 0, 0), and one can then set t to the coordinate of any point in the fixed point set for a “perfect match.” In such a scenario, the cost function E will be 0, but apparently it is a false result. Hence, to prevent such a degeneration, we penalize the trend of the determinant of A going to 0 in E with the second term. In this case, if the determinant A becomes close to zero, this term will increase to prevent such situation.

Concerning numerical details, a KD-tree data structure may be utilized to achieve a fast (O(log M)) search [24]. The minimization of the registration cost functional E in (4) is a 12-D nonlinear unconstrained optimization problem (six dimensions for each 2-D image). The gradient of E with respect to the affine matrix A and translation t are computed. Then the BFGS algorithm, one of the most popular quasi-Newton methods [38], is employed to obtain a fast (super-linear) convergence. The resulting (locally) optimal affine transformation parameters are applied to the image g.

One of the advantages of using PSR is that it naturally handles the case of large translations between the two given images. Specifically, many registration schemes under the DFR align the images by minimizing certain cost functionals. However, the cost functional usually takes an integral or summation form evaluated on the domain of overlap of the two images. Hence, a small cost functional value may be due to the effect of the overlapping domain being small, rather than the two images being well registered. This situation is often observed when two images differ by a large translation. In addition, under such a configuration the fastest way to reduce the cost functional is to further shrink the overlapping domain area by increasing the translation. However, this will only degrade the registration result. This is a fundamental drawback of using DFR. In contrast, without the concept of the fixed image domain, the registration in PSR naturally handles the above difficulty. In particular, when the translation is large, the gradient always tends to reduce this distance. This will be demonstrated in the experimental section.

Another commonly known problem with DFR is the long computation time. Under DFR, traversing of the domain grids may be quite time consuming. In contrast, PSR sparsely represents the image by far fewer points (comparing to the number of the grids in DFR). Hence, the solution time is significantly reduced by more than two orders of magnitude (see Table I below).

TABLE I.

Running Times Comparison. Image Size is 256 × 256 × 26. MSE and MI Registration Codes are Implemented as in [20]. 5000 Points are Used for PSR

Image	MSE	MI	Proposed Method
3D prostate	433.5 sec	610.0 sec	2.5 sec

C. Prostate Shape Registration via Particle Filtering

Though PSR has certain advantages, it is still a local optimization procedure. Specifically, although large translations are effectively handled, large rotations are not. Unfortunately, a large rotation is common in prostate registration where the supine and prone views of the prostate need to be registered. However, in such supine/prone registration cases, we have the prior knowledge that the optimal rotation would be either close to 0° or 180°. Ideally, we would like to naturally incorporate this a priori information in a global registration setting. Thus, we treat the registration problem as system parameter estimation task where the 12 transformation parameters constitute the state variables of a dynamic system. Such estimation can be solved under the particle filtering framework. Moreover, using particle filtering, the a priori information can be easily combined.

1) General Formulation of Particle Filtering

Particle filtering is a sequential Monte Carlo method [47]. It provides a sequential estimate of the distribution of the state variable of a dynamical system. Denote the state variable at time t as x_t and the observation as y_t. The objective then is to estimate the distribution of x_t based on all the observations made until time t, y_{1, 2, …, t}(=: y_1:t), namely p(x_t|y_1:t). With this goal, the process and observation models are given as

$$\{\begin{array}{l}{\mathit{x}}_{t+1}=f({\mathit{x}}_t,u_t)\hfill \\ {\mathit{y}}_t=g({\mathit{x}}_t,v_t)\hfill \end{array}$$ (5) (6)

where f and g may be nonlinear functions while u_t and v_t are the process and observation noises, respectively. We assume u_t and v_t are independent and are both independent in time. Further, we assume the distribution of the initial state p(x₀) is known.

The recursive estimation of p(x_t|y_1:t) consists of two steps, namely the prediction and update steps. Assuming p(x_t−1|y_1:t−1) is available, the prediction step gives the prior PDF of x_t at time t as

$$p({\mathit{x}}_t\mid {\mathit{y}}_{1:t-1})=\int p({\mathit{x}}_t\mid {\mathit{x}}_{t-1})p({\mathit{x}}_{t-1}\mid {\mathit{y}}_{1:t-1})d{\mathit{x}}_{t-1}$$ (7)

where

$$p({\mathit{x}}_t\mid {\mathit{x}}_{t-1})=\int \delta ({\mathit{x}}_t-f({\mathit{x}}_{t-1},u))p(u)du.$$ (8)

Here δ denotes the Dirac function.

At time t after the observation y_t is available, it can then be used to update the estimation to obtain the posterior PDF

$$p({\mathit{x}}_t\mid {\mathit{y}}_{1:t})=\frac{p({\mathit{y}}_t\mid {\mathit{x}}_t)p({\mathit{x}}_t\mid {\mathit{y}}_{1:t-1})}{p({\mathit{y}}_t\mid {\mathit{y}}_{1:t-1})}$$ (9)

where

$$p({\mathit{y}}_t\mid {\mathit{x}}_t)=\int \delta ({\mathit{y}}_t-h({\mathit{x}}_t,v))p(v)dv.$$ (10)

In cases where f and g are nonlinear, the analytical result of p(x_t|y_1:t) is rarely available. Therefore, one can expect a numerical approximation of the PDF. To this end, particle filter employs the Bayesian recursion under the Monte Carlo framework.

Firstly, samples (particles) are obtained from the initial prior distribution p(x₀) and they are denoted as {x₀(i) : i = 1, …, N}. Secondly, we assume the particles {x_t−1(i) : i = 1, …, N} approximating the density p(x_t−1|y_1:t−1) are available, then the prior distribution of p(x_t|y_1:t−1) is computed. Specifically, the particles { ${\mathit{x}}_t^{\ast }(i):i=1,\dots ,N$} approximating the prior density p(x_t|y_1:t−1) are computed as ${\mathit{x}}_t^{\ast }(i)=f({\mathit{x}}_{t-1}(i),u(i))$ where u(i) are realizations of the process noise. Thirdly, with the arrival of y_t, the likelihood of each ${\mathit{x}}_t^{\ast }$ is computed as

$$q_i=\frac{p({\mathit{y}}_t\mid {\mathit{x}}_t^{\ast }(i))}{{\sum }_{j=1}^{N}p({\mathit{y}}_t\mid {\mathit{x}}_t^{\ast }(j))}$$ (11)

for i = 1, …, N and q₀ = 0. Lastly, the posterior particles {x_t(i) : i = 1, …, N} are obtained by sampling from { ${\mathit{x}}_t^{\ast }(i):i=1,\dots ,N$} such that $P({\mathit{x}}_t(j)={\mathit{x}}_t^{\ast }(i))=q_i$, ∀j. This is achieved by generating N uniform distributed (on (0, 1]) random variables w_i’s and assigning ${\mathit{x}}_t(i)=x_t^{\ast }(M)$ where M satisfies

$$\sum _{j=0}^{M-1}{q}_j<w_j\le \sum _{j=0}^M{q}_j.$$ (12)

2) Affine Image Registration by Particle Filtering

We formulate the affine registration as a parameter estimation task, and solve it using particle filters.

In affine registration, the state space 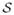is 12-D where the first nine dimensions are for the affine matrix and the last 3 dimensions are for translation. Denoting the state vector as x ∈ 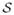, the process model takes the form

$${\mathit{x}}_{t+1}=\mathcal{R}({\mathit{x}}_t+\mathit{u})$$ (13)

where the operator 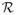: 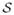→ 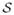takes x_t as the initial configuration, proceeds with a few steps of the deterministic affine registration described in Section II-B, and returns the resulting parameter estimated as x_t+1.

The observation model is

$${\mathit{y}}_t=\mathcal{E}({\mathit{x}}_t)+\mathit{v}$$ (14)

where the operator 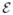: 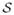→ ℝ⁺ gives the cost function under the state x_t. The process and observation noises are u and v, respectively. It can be seen from above that both the process and the observation models are highly nonlinear.

In addition to the process and observation models, the prior distribution p(x₀) is required. Usually, without a priori information of the solution, p(x₀) is assumed to be Gaussian or uniformly distributed. However, in cases such as supine/prone prostate registration, the a priori knowledge of the rotation can be incorporated through a careful design of p(x₀). This will be shown in the experimental Section II-E3. Altogether, the complete algorithm can be described as follows.

Algorithm 1.

Affine Registration by Particle Filtering

1:	Sample from p(x0) to get {x0(i) : i = 1, …, N}
2:	for i = 1, 2, …, t do
3:	Obtain the prior samples { ${\mathit{x}}_t^{\ast }(i)$} by the process model.
4:	Evaluate the likelihood qi’s using (11)
5:	Resample to get posterior {xt(i)} using (12)
6:	end for

D. Justification of Particle Filtering Under PSR

In Section II-A two salient properties of using PSR in registration were discussed. It is further argued there that such advantages enable one to use particle filtering to achieve global registration under PSR. Firstly, to pursue global optimization, essentially all methods (e.g., simulated annealing, genetic algorithms, and even particle filtering) contain the idea of stochastically exploring a large part of the state space. However, under DFR those states corresponding to long translations will result in small or even zero cost functional values and therefore will be erroneously accepted. This fundamentally excludes the applicability of particle filtering to DFR-based (local) registration schemes. Contrastingly, the cost functional (4) behaves consistently, and can be nicely fitted to the particle filtering framework. Secondly, the global scheme is computationally more costly. Thus, the local step in the more global scheme should be computationally efficient. Here again, PSR fits well with this requirement.

E. Registration Experiments and Results

We provide experiments to demonstrate 1) the behavior of different registration cost functionals, 2) robustness of the proposed method to initialization, 3) supine/prone prostate registration, and 4) computational efficiency. It has been noticed that the number of the points in the set, which is derived via PSR, is a parameter for the proposed method. However, in all of the experiments performed, we use 500 points to represent a moderate size 2-D image and 5000 points for a 3-D image. Nevertheless, we have observed that the algorithm is fairly robust to the choice of number of points.

1) Cost Functional Behavior

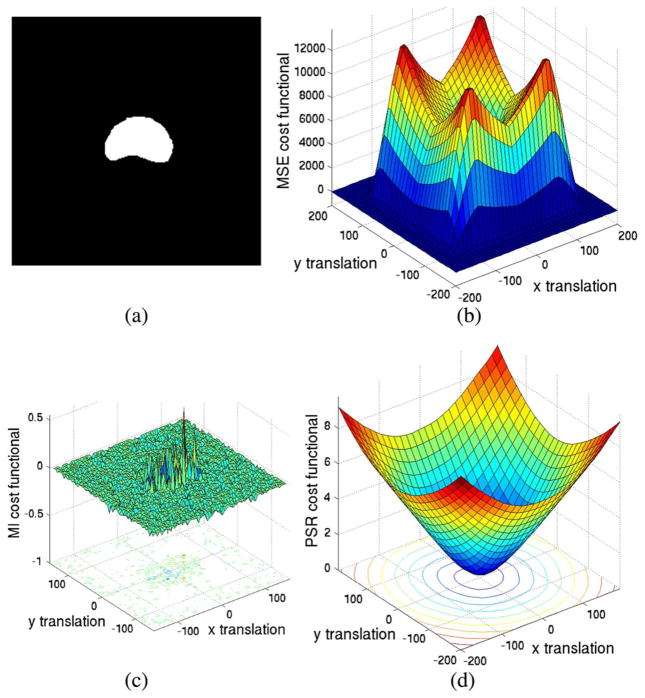
In the first set of experiments, we compare the region of convergence for several widely used cost functionals to that of our proposed method. These include mean square error (MSE) in [54] as well as the scheme based upon mutual information (MI) [57], [61]. This is achieved by first translating a 2-D image, as seen in Fig. 1(a), in the x-y plane. Then, one can interpret the energy as a function of x-y displacement [Fig. 1(b)–(d)].

Fig. 1.

Plot of different cost functional values with respect to various 2-D translations. (a) Testing prostate binary image. (b) MSE. (c) MI. (d) PSR.

Ideally, the cost functional should have a minimum at (0, 0) and smoothly increase as the translations increase. Fig. 1(b) is the plot of the MSE with respect to various translations. The valley in the middle can be regarded as the “region of convergence.” That is, if the initial translation parameter is within this region, the MSE registration algorithm will gradually drive the parameter to converge to the ground truth. Not only is the region of convergence small (relative to that of PSR), more importantly, the cost functional values drop to zero when the transitions are large. As described in Section II-D, such a phenomenon makes MSE an inadequate cost functional for “stochastic probing” based global image registration.

Fig. 1(c) is obtained in a similar fashion except that (negative) mutual information (MI) cost functional is now employed. Moreover, to mitigate the error resulting from the implementation, we opt to use the MI registration scheme found in the In-sight Toolkit [20].¹ Apart from being noisy, the cost functional is flat for most of the regions. Such behaviors of the cost functionals make the registration process very sensitive to the initialization and the optimization step size.

As can be seen in Fig. 1(d), the minimum of the proposed cost functional is located at the correct position and smoothly grows monotonically outward as translation increases. This result can be mainly attributed to the representation provided under PSR, whereas MSE and MI registration approaches suffer the inherent drawback of representing an image on a fixed grid. Hence, no matter how large the translation is, the registration process is able to drive it to the correct place.

2) Robustness to Initialization

Previous section gives more of a visual demonstration of the behavior of the various cost functionals. It provides the intuition but has certain limitations: Due to the dimensionality, the image is restricted to 2-D and the transformation is restricted to 2-D translation. However the real optimization is in 6-D affine transformation space for 2-D image, and 12D affine transformation space for 3-D images, which are difficult to display. To evaluate the robustness in there, in this section we perform real test for 2-D images. Specifically, two identical images are registered by starting from a random position in the registration parameter space. Therefore, the ground truth for the registration is the identity matrix and the zero translation vector. Again, three types of registration are compared, namely affine image registration using both MSE and MI as well as our proposed method. All three methods are run until convergence. Furthermore, to evaluate the performance of the registration, the affine matrix and the translation vector are concatenated together to form a 6-D state space vector. The registration result is then compared with the ground truth by the vector I² metric, denoted as the “recovery error.” We note that the initial affine matrix and the translation vector are perturbed separately. This is because usually the perturbation for translation is one or two degrees of magnitude larger than that of the affine matrix. So if they are perturbed together, the recovery error will be dominated by its translation components.

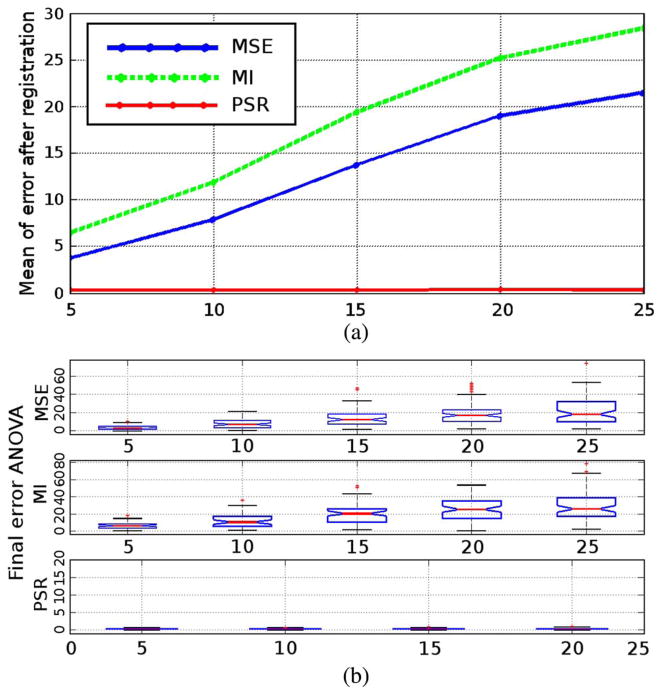
Thus, the robustness to the initial translation is tested first. The initial translation vector is set to a Gauss random variable with the standard deviation (STD) ranging in {5, 10, …, 25}. For each STD, 100 realizations are generated as the initial translation, and the initial affine matrix is set to the identity matrix. After the registration converges, 100 recovery errors are recorded for one type of registration. Fig. 2(a) shows the means of the recovery errors at different STD levels. The horizontal axis shows the STD of the initial translations vector, while the vertical axis is the mean of the recovery error. It can be observed that when the initial perturbation becomes larger, the MSE and MI registration recovery errors grow larger. At the same time, the PSR always register the two images. Such a result is consistent with the cost functional analysis in the previous section. In addition to the means, Fig. 2(b) shows the spread in the recovery errors. Specifically, the notches indicate the medians of each set of 100 recovery errors while the box encloses those recovery errors within one quartile. This plot further demonstrates that when using MSE- or MI-based approaches, the median performance is not only poor, but the stability is also unsatisfactory.

Fig. 2.

Recovery error analysis for initial translation perturbation. Details given in text.

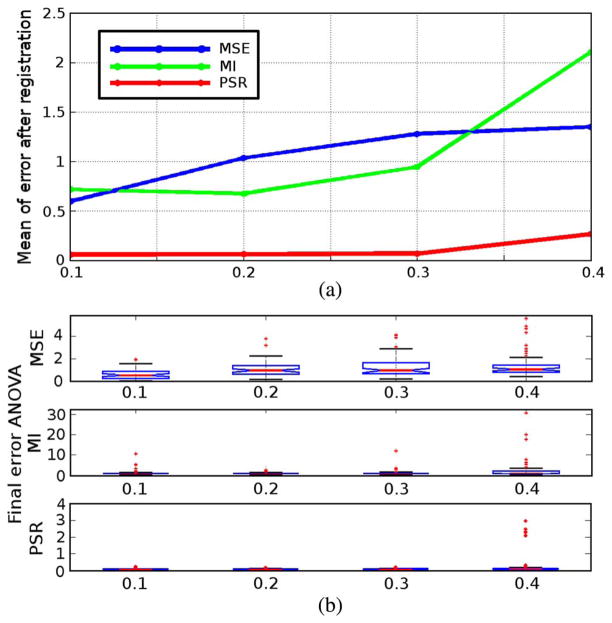
The experiment is conducted similarly for the initial affine matrix. The initial translation vector is now set to zero while the affine matrix is a perturbed identity matrix. Specifically, each element of the identity matrix is added with a Gauss random variable with the STD ranging in {0.1, 0.2, 0.3, 0.4}. Similarly, 100 tests are performed for each STD for all three types of registration schemes and the recovery errors are recorded. Fig. 3 shows that as the perturbation on the initial state gets larger, the mean recovery errors of all the three registration schemes grow. Interestingly, not only does the mean recovery errors of the PSR scheme grow the least, but their variances are also the smallest.

Fig. 3.

Recovery error analysis for initial affine matrix perturbation. Details given in text.

3) Supine-Prone Prostate Registration

One challenging problem in prostate registration is to register the supine and prone prostates. Fig. 4 shows one case of the supine/prone prostates in the axial, sagittal and coronal views. The moving prostate 3-D image (blue) is overlaid on the fixed image (white).

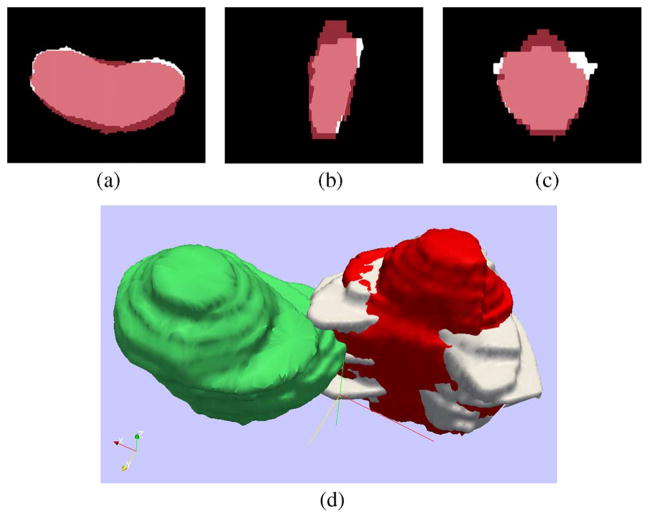
First, MSE image affine registration is used to register the two images and the result is shown in Fig. 5. The moving image (red) is stretched to align with the fixed image. However, the local registration scheme could not detect the global optimal configuration 180° away. Therefore, it provides an erroneous result where different sides of prostates are aligned.

Fig. 5.

Supine/prone prostates registration using image affine registration with respect to MSE cost function. Subplots show the (a) axial, (b) sagittal, and (c) coronal views.

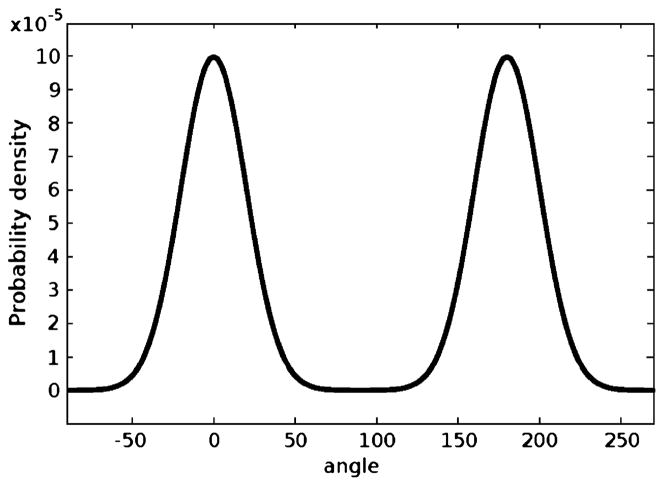
The registration using the proposed global affine registration scheme under PSR is then conducted. Under the particle filtering framework, the prior knowledge can be incorporated into the construction of the prior distribution p(x₀) to reflect the fact that the two images may (or may not) differ by 180° around the z-axis. In other words, under the probability framework this can be interpreted by the fact that the optimal rotation around the z-axis, θ, has a higher probability of taking the values near 0° and 180°. Thus, its prior distribution is defined to be

$$p({\theta }_0)=\frac{1}{2\sqrt{2\pi }\sigma }\left(e^{-\frac{{\theta }^2}{2{\sigma }^2}}+e^{-\frac{{(\theta -\pi )}^2}{2{\sigma }^2}}\right)$$ (15)

whose plot is shown in Fig. 6. In cases where such prior knowledge is not available, a uniform distribution is a common choice.

Fig. 6.

Prior for rotation.

The results generated by the proposed algorithm are shown in Fig. 7. The registered moving image is denoted by the red color and it can be observed that the large rotation is correctly recovered. We can better appreciate the global registration results using the 3-D view as seen in Fig. 7(d). The fixed prostate is again in white, the moving image (before registration) is in green, and its registered version is in red.

Fig. 7.

Supine/prone prostates registration using PSR affine registration and particle filtering. Subplots show the (a) axial, (b) sagittal, (c) coronal, and (d) 3-D views.

Furthermore, it is noted that although particle filtering is a general state estimation framework and theoretically registration using MSE/MI also seems to fit in such framework. However, for our purposes, it may not be the best choice. This is mainly due to two reasons. First, as plotted in Fig. 1, MSE and MI cost functionals depend on the overlapping of the image sample grids. Hence, to explore the optimal solution, particle filtering samples at those regions corresponding to (false) low cost functional values, such as the large remote areas in Fig. 1(b) and (c). Secondly, the computation time of using MSE/MI with particle filtering is very long especially for 3-D case. This further prohibits the combination of MSE/MI with particle filtering.

In addition to a typical case for demonstration here, the global registration scheme has been applied to 112 data sets² to test the robustness of the supine/prone prostate registration. For this purpose, we arbitrarily pick one image as the template and align all the other 111 images with the template. As seen in Fig. 8, the variation in pose and shape among the 112 images are very large before registration.

Fig. 8.

Overlay all the prostate shapes before registration. Subplots show the (a) axial, (b) sagittal, and (c) coronal views.

After the proposed supine/prone prostate registration method is run to convergence in all of the 111 tests, the registered images are summed and we arrive at the results presented in Fig. 9. It can be seen that the pose and shape variations are drastically reduced.

Fig. 9.

Overlay all the prostate shapes after registration. Subplots show the (a) axial, (b) sagittal, and (c) coronal views.

4) Increased Efficiency

Registering image via point-sets is much more efficient, especially in 3-D. The mean times of registering the 112 prostates using different methods are shown in Table I. The efficiency is due to the sparsity of the PSR. For instance, in the prostate case shown in Fig. 7, 5000 points are used to represent the image, whereas 1703936 image voxels are contained in the whole image. Hence, the computation is very significantly reduced. All the methodologies are implemented in C++ with a Pentium 3.20 GHz CPU with 4 G RAM.

III. Shape Prior Construction

With the training shapes registered, the shape prior is constructed for the subsequent segmentation. Before learning, an appropriate shape representation is important. Interestingly, although binary/label maps are widely used in literature, they violate the usual Gaussian assumption in the PCA framework. This can attributed to the fact that the intensities of the binary/label map can only be 0 or 1, which are not likely to constitute a Gaussian distribution. The signed distance function (SDF) is also commonly used. However, the SDF representation generally has large values far from the zero level set. Therefore, during the learning step, the variations may overwhelm those around the zero contour causing inconsistencies in shape learning.

A. Shape Representation Using Hyperbolic Tangent

In this work, we modify the SDF via a transformation of the form s(x) = 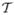(SDF(x)) to provide a better representation for shapes. More precisely, we want to choose the mapping 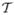that preserves the zero level set of the SDF and eliminates the large values/variances far from the zero level set.

Sigmoid functions are good candidates for this purpose. Thus, a natural choice is to apply the hyperbolic tangent to the SDF to represent shapes

$$s(\mathit{x})=tanh(\text{SDF}(\mathit{x}))=\frac{e^{2\text{SDF}(\mathit{x})}-1}{e^{2\text{SDF}(\mathit{x})}+1}.$$ (16)

Note that tanh(0) = 0 and $\underset{t\to \pm \infty }{lim}tanh(t)=\pm 1$ so we preserve the zero level set as the object boundary, but eliminate the variance far from the boundary. This will benefit the learning phase. Moreover, since tanh′(x)|_x=0 = 1, we have that tanh(x) ≈ x when x ≈ 0. Hence, around the zero level set, s(x) is close to the SDF. This representation of shape will be referred to as the T − SDF (T for tanh) in what follows.

Denote the N manually segmented training images, which have been previously aligned by the method described above, as I_i : Ω → {0, 1} where Ω ⊂ ℝ³. The T-SDF representations of the registered images are then computed as s_i = tanh(SDF(I)) : i = 1, …, N.

B. Shape Learning

The standard PCA is adopted to learn the shapes. The mean shape is obtained as

$$\overline{s}(\mathit{x})=\frac{1}{N}\sum _{i=1}^N{s}_i(\mathit{x}).$$ (17)

Then, the mean shape is subtracted from each shape, i.e., s̃_i = s_i − s̄. Since each s̃_i is a 3-D volume, we can concatenate the rows to form a long vector η_i. Then the covariance matrix is formed as

$$C=\frac{1}{N}({\eta }_1,\dots ,{\eta }_N){({\eta }_1,\dots ,{\eta }_N)}^T$$ (18)

and the singular value decomposition gives

$$C=G\mathrm{\Lambda }{G}^T$$ (19)

where Λ is a diagonal matrix containing the eigenvalues and the columns of G store the eigenvectors. Note that these are reshaped to the original image size and are denoted as g_i(x). Usually, only the eigenshapes corresponding to the first L eigenvalues are kept while the others (with smaller eigenvalues) are ignored. Hence, the shape prior is a space spanned by {g_i : 1, …, L}. In the subsequent segmentation, the shape is constrained to lie within this space.

We note that besides the shapes of the prostate, the mean and the variance of the image intensity within the prostate could also be learned if the training shapes and their corresponding original images are both available.

IV. Shape-Based Prostate Segmentation

In this section, we describe our segmentation strategy for MR prostate data. Briefly, given the image to be segmented, it is pre-processed under a Bayesian framework to highlight the region of interest. Then a variational scheme based on local regional information is used to extract the prostate from the posterior image. We now give the details.

A. Bayesian Preprocessing

Given an image J(x), the likelihood l_J(x) is computed as

$$l_J(\mathbf{x}):=\frac{1}{\sqrt{2\pi }\sigma }exp\left(-\frac{{(J(\mathbf{x})-\mu )}^2}{2{\sigma }^2}\right)$$ (20)

where the μ and σ are the mean and standard deviation of the object intensity, respectively. Both μ and σ may either be provided by the user or learned during the learning process. To compute the posterior we still need the prior term. While uniform priors are often used in previous works [17], [62] where the posterior is in fact the (normalized) likelihood, we show in this work that with a careful construction of the prior, the posterior is more convincing and makes the segmentation easier.

To this end, we propose to use the image content based directional distance in the prior. This means that both the image content and the distance to the object center are considered when calculating the distance. Specifically, given the image J(x), we first construct the metric [34], [41], [42] d : Ω × A → ℝ⁺ by

$$d(\mathbf{x},\phi )=\mid J(\mathbf{x}-J(\mathbf{x}+\phi ))\mid$$ (21)

where φ ∈ A = {(0, 0, ±1), (0, ± 1, 0), (±1, 0, 0)}. Denote the estimated center of the object by p_c. Similarly to μ above, p_c may be learned or assigned. This enables us to compute a directional distance map (DDM) ψ by solving the Hamilton–Jacobi–Bellman equation

$$\{\begin{array}{l}0=\underset{\phi \in A}{inf}\{d(\mathbf{x},\phi )+\langle \phi ,\nabla \psi (\mathbf{x})\rangle \}\hfill \\ \psi ({\mathbf{p}}_c)=0.\hfill \end{array}$$ (22)

Equation (22) may be solved efficiently by using the the fast sweeping method proposed by Kao et al. [23]. Thus, with ψ obtained in this manner, we can define the prior by prior := exp(−ψ), and compute the posterior by the Bayesian rule.

Fig. 10 shows the comparison of the posteriors computed using different priors. The images shown are one slice taken from the given 3-D prostate volume. In both images, the red contour shows the target object. In Fig. 10(a), a uniform prior is used to compute the posterior. Since the average intensity within the prostate is similar to that of the surrounding tissue, both prostate and surrounding tissue have high posterior (bright), poorly differentiate the object from the background. On the other hand, in Fig. 10(b), the prior was constructed from the DDM. Here the prostate is almost the only bright region in the posterior image. From the posterior image alone we can already differentiate the prostate fairly well. Though the bright region below the prostate is difficult to exclude at this stage, the subsequent shape-based segmentation recognizes it as background.

Fig. 10.

Posterior image of a slice: (a) using uniform prior, (b) using DDM as prior.

B. Segmentation in the Posterior Image

We propose a local regional information based segmentation scheme, in which the segmentation curve is driven to maximize the difference between the average posterior within a banded region inside and outside of the curve. More specifically, given the current segmentation curve, which is represented by the zero level set of the T-SDF, it is driven to enclose the desired object in the posterior image K(x) by minimizing the following cost functional:

$$\begin{array}{l}E:=-\frac{1}{2}{(u-v)}^2\\ =-\frac{1}{2}{\left(\frac{{\int }_{\mathrm{\Omega }}{\mathcal{H}}_B(h(\mathit{x}))K(\mathit{x})d\mathit{x}}{{\int }_{\mathrm{\Omega }}{\mathcal{H}}_B(h(\mathit{x}))d\mathit{x}}-\frac{{\int }_{\mathrm{\Omega }}{\mathcal{H}}_B(-h(\mathit{x}))K(\mathit{x})d\mathit{x}}{{\int }_{\mathrm{\Omega }}{\mathcal{H}}_B(-h(\mathit{x}))d\mathit{x}}\right)}^2\end{array}$$ (23)

where h(x) is the T-SDF representation of the curve and is defined as

$$h(\mathit{x})=\overline{s}(A\mathit{x}+T)+\sum _i^L{\omega }_i{g}_i(A\mathit{x}+T).$$ (24)

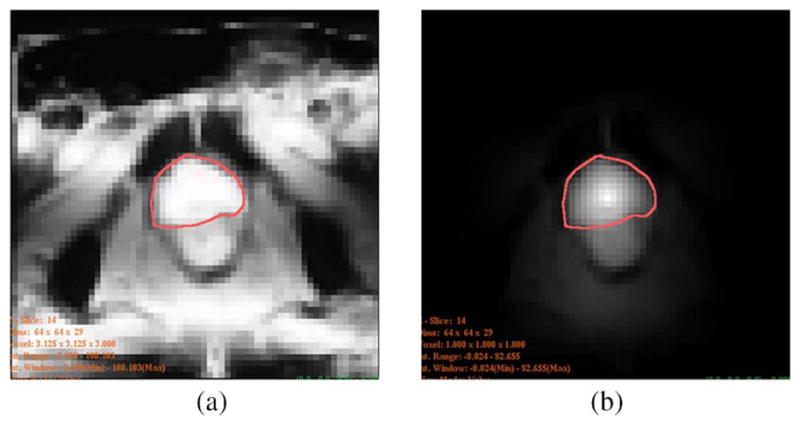
Here, A and T denote the affine matrix and translation vector, respectively. Moreover, in (23), the : ℝ → ℝ is the “banded Heaviside function” defined as

$${\mathcal{H}}_B(t)=\frac{1}{\pi }\left(arctan\left(\frac{t}{\epsilon }\right)-arctan\left(\frac{t-B}{\epsilon }\right)\right).$$ (25)

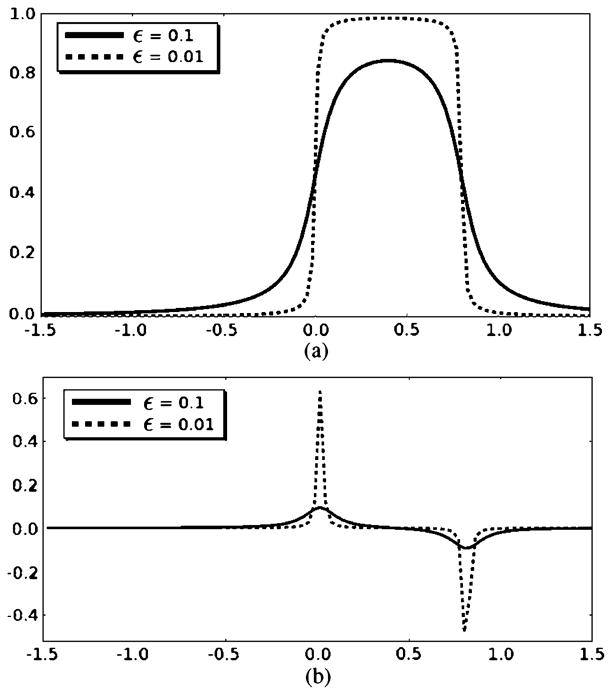
The banded Heaviside function and its derivative are plotted in Fig. 11.

Fig. 11.

(a) Banded Heaviside function and (b) its derivative with different ε coefficient values.

The banded Heaviside function realizes the localized property of the cost functional. Therefore, u is the mean of posterior in a banded region inside the object. The width of the band is determined by B ∈ (0, 1]. (B = 0.8 is a choice that worked well for all our tests.) Similarly, v is the mean of posterior in a banded region outside the object. Comparing to [6], [63], this cost functional is more robust to the influence remote to the curve. Moreover, because the value range of the T-SDF representation is (−1, 1), as B → 1, E in (23) converges to the global cost functional as in [6], [63].

By minimizing the segmentation cost functional with respect to T, A and the ω_i’s, the optimal contour and transformation are found. To achieve this, the gradient of E is calculated and this finite dimensional (12 + L dimensions in 3-D) nonlinear optimization problem is solved using the BFGS method for fast convergence [38].

C. Segmentation Results

In this section, we provide prostate segmentation results for two data sets, one of which is publicly available. In particular, we provide not only qualitative results, but also give quantitative results in the form of the Dice coefficient and Hausdorff distance (HD) to illustrate the viability of the proposed algorithm in the context of prostate segmentation. Lastly, either because code was not readily available or the corresponding data sets on which various algorithms were run, it should be emphasized that we do not claim the proposed method is superior to any number of existing techniques, but provides a promising new alternative approach to an important medical imaging task. For example, the method of Klein et al. [25], achieves excellent results; however, a direct comparison of the proposed algorithm would be unfair since the data sets differ (e.g., seminal vesicles are excluded in our data set whereas they are included in [25]). Thus, the experiments were performed to highlight the (dis)advantages of the proposed approach for prostate segmentation.

1) Experiments on NCI Data

The first group of experiments employed 33 MRI prostate data sets, collected at the NIH National Cancer Institute (NCI) from different prostate cancer patients on a 3.0T Philips machine and provided to us by Queen’s University, Kingston, ON, Canada [27] The patient ages ranged from 57 to 73 with a mean of 65.2. The image volume grid size was 256 × 256 × 27 with 0.51 mm in-plane resolution and 3 mm slice thickness. The boundaries were manually traced out by a clinical expert at NCI, and 20 cases were utilized for learning while the other 13 for testing. In order to demonstrate the capability of the proposed method in dealing with multiple modalities, the 13 test cases are a mixture of T1/T2 images (9 T1 and 4 T2). Furthermore, for comparison, we also trained and tested the algorithm proposed in [54] with the same set of training data and testing data, respectively. Specifically, among the three choices for the segmentation energy in [54], the Chan–Vese model was chosen.

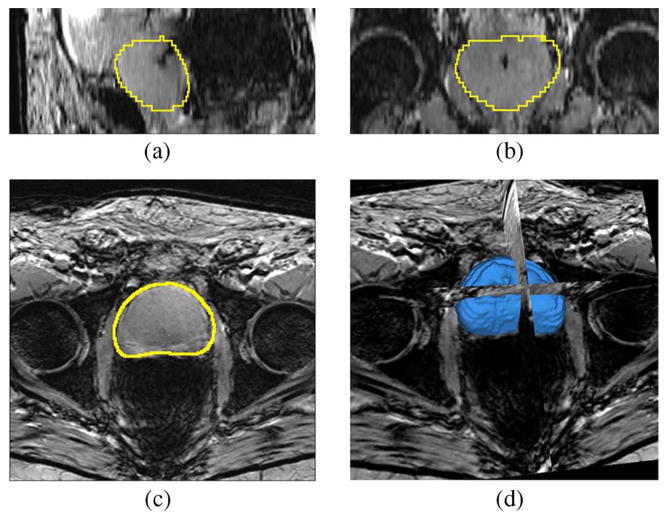
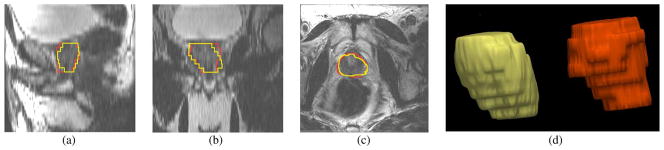
Fig. 12 shows the segmentation result for one patient in the testing data set. The image is T1 weighted with the gradient echo sequence (GRE), and the SENSE-cardiac coil is used. Note that we have chosen the number of principle modes to be L = 6. The center of the target object, i.e., the p_c in (22), is given by a click in the prostate region. The mean and standard deviation for (20) are 300 and 100, respectively.

Fig. 12.

Segmentation results for Patient 1. This is a T1 weighted image. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

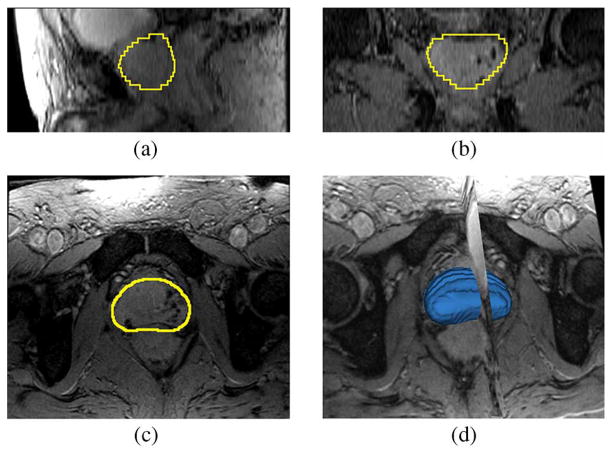
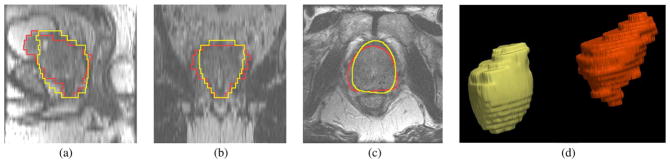
Fig. 13 shows the segmentation result for a second patient in the testing data set. Like that of the previous image, the current image is T1 weighted using the GRE sequence and the SENSE-cardiac coil. In the experiment, all the parameters are the same as the previous case except the mean and the standard deviation are 150 and 50 (units in image intensity, the same in what follows), respectively.³

Fig. 13.

Segmentation results for Patient 2. This is a T1 weighted image. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

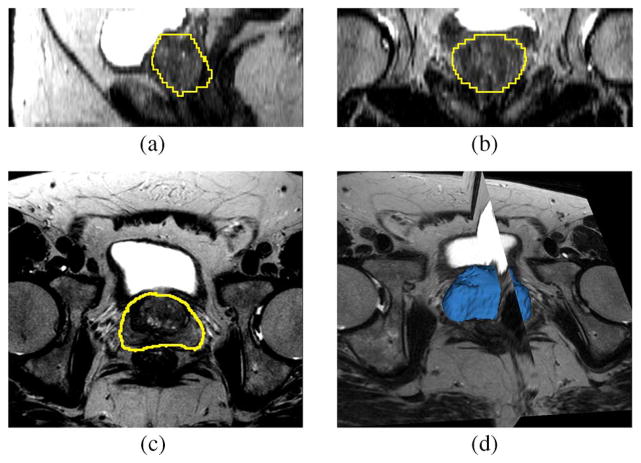
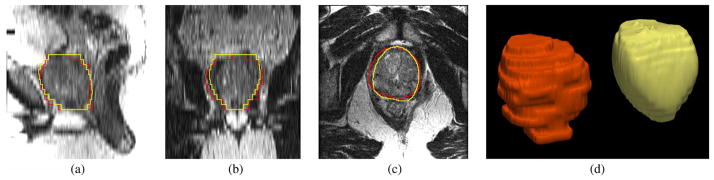
In the experiment of Fig. 14, the mean and the standard deviation are 500 and 200, respectively. Although the image is T2 weighted using the turbo spin echo (TSE) sequence (SENSE-cardiac coil) and the bladder in the image is extremely bright, the proposed method correctly captured the position and the shape of the prostate.

Fig. 14.

Segmentation results for Patient 3. This is a T2 weighted image. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

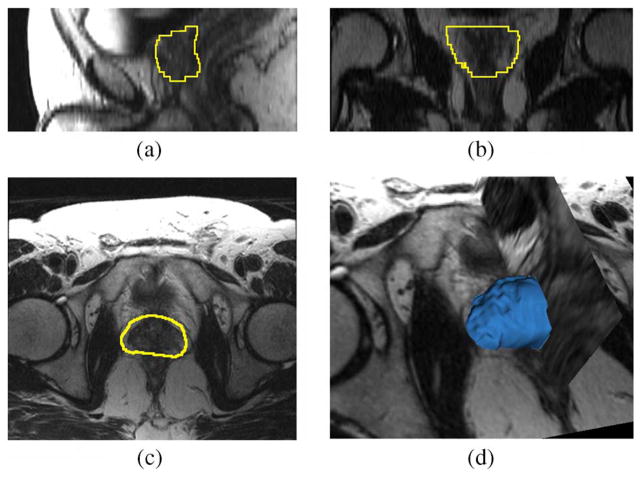
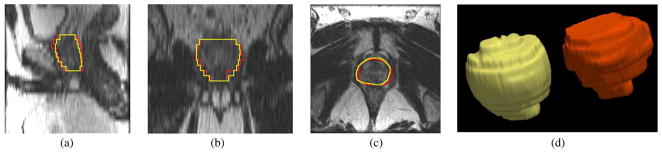
Fig. 15 shows another example where the prostate shape differs from the previous learnt shapes. In particular, the prostate can be seen to be more spherical. Still the method yields a visually excellent segmentation and this indicates that the learned shape prior does have the capacity to represent different shapes. Note, the mean and the standard deviation in this case are 200 and 100, respectively. We also note that the image is again T1 weighted using GRE sequence (SENSE-cardiac coil).

Fig. 15.

Segmentation results for Patient 4. This is a T1 weighted image. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

Furthermore, we computed the Dice coefficient that quantitatively compares each segmentation result (by the proposed method as well as the method given in [54]) with the corresponding manual drawing. The two sets of coefficients are plotted in Table II. It can be seen that the proposed method provides satisfying results overall. Note that the key reason that the method of [54] produces low Dice coefficients for data sets #3, #11, #12, and #1 is because it employs the Chan-Vese model which assumes the image to be bi-modal. However, those four images are T2 weighted image in which the bladder region is the brightest. Therefore, it extracts the brightest region and misses the prostate region. On the other hand, the method proposed in the present work only looks at the locally prominent features, and hence is more robust to the influence in the remote regions.

TABLE II.

Dice Coefficients and 95% Hausdorff Distance of the Proposed Method and the Method in [54]. Third, Eleventh, Twelve, and Thirteenth Testing Images are T2 Images Where the Bladder is Very Bright. Hence the Chan-Vese Model Used in [54] Extracts the Bladder Region Instead of Prostate. In Computing the Mean/Standard Deviation, Those Cases are Not Counted

Patient ID	1	2	3	4	5	6	7	8	9	10	11	12	13	Mean	STD
Dice Coef, proposed method	0.88	0.84	0.85	0.85	0.87	0.85	0.80	0.86	0.81	0.88	0.79	0.82	0.78	0.84	0.03
95% HD, proposed method	7.02	7.55	7.92	9.37	6.87	6.96	7.35	7.84	10.10	11.02	7.01	8.52	7.74	8.10	1.50
Dice Coef, [54]	0.75	0.80	-	0.77	0.81	0.73	0.77	0.81	0.72	0.75	-	-	-	0.76	0.03
95% HD, [54]	10.27	8.60	-	11.68	6.93	8.87	7.91	7.80	11.21	9.77	-	-	-	9.23	1.62

2) Experiments on Publicly Available Data Set

The next set of segmentation experiments concerns the testing of the proposed algorithm on the publicly available data online.⁴ This website consists of 30 data sets from 15 patients, each containing both T1 and T2 MR prostate images from a 1.5T MR scanner. However, given that only the expert segmentations for T2 images are provided, we opted to segment these 15 T2 images. The ages of the patients range from 50 to 80 with a mean at 63.7.

Although the shape space is learnt in the experiment above, the mean and eigen-shape modes are used directly in the segmentation task of this experiment. That is, we have not adapted or altered our training set of prostate shapes in order to accomplish the segmentation for the public data set shown in this section. From a practical viewpoint, this is essential since in general it is difficult for one to make a a priori decision on a training set before the segmentation process (e.g., that prior knowledge of the data is rarely known).

Applying the proposed method, we obtained segmentation results for all the 15 T2 images. Furthermore, the Dice coefficients and the Hausdorff distances with respect to the expert segmentation results given on the web site are provided in Table III. Moreover, two cases corresponding to the lowest Dice coefficients (#45 and #73), and the two cases corresponding to the highest Dice coefficients (#64 and #69) are picked out for visual inspection.

TABLE III.

Dice Coefficients and the 95% Hausdorff Distances for the T2 Images in the Publicly Available Date Set. It is Noted That the Patient IDs are Taken From the Clinical Study and They are Not Contiguous

Patient ID	#29	#35	#36	#41	#45	#49	#54	#55	#56	#60	#64	#69	#73	#85	#88	Mean	STD
Dice Coef	0.81	0.85	0.79	0.80	0.69	0.85	0.80	0.85	0.85	0.83	0.89	0.86	0.76	0.86	0.82	0.82	0.05
95% HD	9.54	8.55	8.17	17.33	20.35	7.23	8.65	10.27	8.55	10.14	5.7	8.65	14.47	7.11	8.46	10.22	4.03

Fig. 16 shows the segmentation result for patient #45. Similar to the experiments previously described, the number of principle modes was chosen to be L = 6, and the center of the target object, p_c, is given by a click in the prostate region. The mean and standard deviation for (20) are 60 and 30, respectively. The orange contour is the expert result whereas the yellow contour is generated by the algorithm. It can be observed that in the apex and base regions, the method does not provide perfect results. In fact, the intensity contrast in those regions are so low that it is difficult to define the boundary even for a clinical expert.

Fig. 16.

Segmentation results for Patient #45. The orange contour is the expert result whereas the yellow contour is generated by the algorithm. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

Fig. 17 shows the segmentation result for patient #73. The settings are the same as those for patient #45, and the mean and standard deviation for (20) are again set to 60 and 30, respectively. Similar to the above case, the algorithm did not agree with the ground truth contour well at the apex and base regions. Besides the low image contrast at these locations, the prostate shape in this image is significantly more deformed than in any other case (including the ones used for training). Hence, such features are not captured by the learning process, and the corresponding segmentations suffer accordingly.

Fig. 17.

Segmentation results for Patient #73. The orange contour is the expert result whereas the yellow contour is generated by the algorithm. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

Fig. 18 shows the segmentation result for patient #69. The settings are the same as those for patient #45 except that the mean and standard deviation for (20) are set to 120 and 100, respectively.

Fig. 18.

Segmentation results for Patient #69. The orange contour is the expert result whereas the yellow contour is generated by the algorithm. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

Fig. 19 shows the segmentation result for patient #64, which received the highest Dice coefficient. The mean and standard deviation for (20) are 100 and 50, respectively. Not only is the Dice coefficient is high, the visual inspection also shows high degree of matching between the algorithm result and the expert result.

Fig. 19.

Segmentation results for Patient #64. The orange contour is the expert result whereas the yellow contour is generated by the algorithm. Subplots show the (a) sagittal, (b) coronal, (c) axial, and (d) 3-D views.

Lastly, we should mention that currently the number of eigen-shape modes (six in all the experiments) is chosen to balance the computation load and the accuracy. Sometimes, increasing the eigen-shape may improve the segmentation result for certain cases. However, in general we find 1/3 to 1/2 of the number of training shapes are good choices for the number of eigen-shapes in the given segmentation task.

V. Conclusion and Discussion

In the present work, we described a unified shape-based frame-work to extract the prostate from MR prostate imagery. Firstly, we proposed a discrete representation for the image using point-sets. By representing the image as a set of points, we are able to take advantage of well-developed methodologies in order to handle some challenging image registration problems. In particular, the sparsity of the representation gives a much faster registration procedure. Moreover, our proposed cost functional behaves better, especially when the translation is large between the two images. Lastly, by treating the registration problem as a parameter estimation task, we achieve global registration of the images under the particle filtering framework.

Next, in the stage of statistical learning of the shapes, a representation of a training shape-based on the SDF, was proposed. By using the hyperbolic tangent of the SDF, the variances in the remote region are effectively reduced, which aids in better learning. Finally, in the segmentation step, the regional statistical based segmentation is localized around the evolving contour. It focuses on the image information near the segmenting curve and effectively reduces the influence from image content far away.

Future work includes investigating the number of points needed for representing a given image to achieve optimal registration efficiency as well as accuracy. In the segmentation step, a user-provided input (mouse click) is needed to locate the center of the prostate, since simply using the mean of the centers in the training shapes is not adaptive enough for all the testing images. To this end, we plan to further automatize this step by better utilizing the learnt centers of the training shapes. In addition to that, the mean and standard deviation for (20) are currently set by user. This is mainly due to the facts that the estimation from the single click (which user makes for the prostate center) is not reliable enough, and the standard deviation in the prostate region over all the training images are too large because there are multimodality training images involved. Moreover, the current segmentation cost functional relies only on the first order statistics. We plan to test an algorithm which utilizes all of the statistical information based on the Bhattacharyya coefficient [35] to better separate the prostate from the background.