A Dual-Process Discrete-Time Survival Analysis Model: Application to the Gateway Drug Hypothesis

Abstract

The gateway drug model is a popular conceptualization of a progression most substance-users are hypothesized to follow as they try different legal and illegal drugs. Most forms of the gateway hypothesis are that “softer” drugs lead to “harder,” illicit drugs. However, the gateway hypothesis has been notably difficult to directly test – i.e., to test as competing hypotheses in a single model that licit drug use might lead to illicit drug use or the reverse. This article presents a novel statistical technique, dual-process discrete-time survival analysis, which enables this comparison. This method uses mixture-modeling software to estimate two concurrent time-to-event processes and their effects on each other. Using this method, support for the gateway hypothesis in the National Longitudinal Survey of Youth 1997 was weak. However, this paper was not designed as a strong test of causal direction but more as a technical demonstration, and suffered from certain technological limitations. Both these limitations and future directions are discussed.

The gateway drug hypothesis posits that the use of a given drug increases the chances of the subsequent use of other drugs (Kandel, 1975). Most forms of the gateway hypothesis are that “softer” less serious drugs lead to “harder” illicit drugs (Hamburg, Kraemer, & Jahnke, 1975; Kandel & Faust, 1975). Although there is some debate as to which drugs should be considered gateway drugs, the most commonly researched among adolescents are cigarettes, alcohol, and marijuana (e.g., Chen et al., 2002; Golub & Johnson, 2001; Kandel, 2003). Research has indicated that prior tobacco and alcohol use precede marijuana use which may lead to subsequent involvement in other, “harder,” illicit drugs such as cocaine or heroin (Lee & Abdel-Ghany, 2004; Wagner & Anthony, 2002). However, none argue that all substance-using adolescents follow this path.

One alternative gateway path that has recently received considerable attention is the progression from marijuana use to cigarette smoking (Patton, Coffey, Carlin, Sawyer, & Lynsky, 2005; Ream, Benoit, Johnson, & Dunlap, 2008; Timberlake et al., 2007). For example, Vaughn, Wallace, Perron, Copeland, and Howard(2008) found that African-American adolescents were significantly more likely than other ethnic groups to use marijuana before cigarettes, suggesting that the gateway theory may not apply equally across ethnicities. This result supports previous findings (e.g., Macksey-Amiti, Fendrich, & Goldstein,, 1997) that unconventional drug use progressions are more common among minorities and disadvantaged groups.

In the current study, we illustrate the use of a novel statistical approach, referred to herein as dual-process discrete-time survival analysis (DPDTSA), with potential to further investigate the gateway hypothesis among adolescents. Numerous studies provide evidence for the gateway drug phenomenon; however, many of the research designs are cross-sectional and retrospective in nature and take temporal order only loosely into account in the study design (Kandel, 2002). Other strategies including two-wave studies also fall short in successfully evaluating the gateway drug theory among adolescents. Kandel, Yamaguchi, and Klein(2006) suggest that researchers must document association, sequencing, and causation before the gateway hypotheses can truly be tested. There is a clear need for prospective multi-wave studies in this area which employ sound methodological approaches and sophisticated statistical methods.

We argue that the gateway hypothesis is at heart a question of survival modeling, or time-to-event modeling. The core elements of the hypothesis can be stated in terms of “initiation” as follows:

1. In adolescents who ultimately use both licit (i.e., alcohol and/or tobacco) and illicit drugs, initiation of licit drug use tends to temporally precede initiation of illicit drug use by the same individuals (sequencing);

2. Initiation of licit drug use increases the likelihood of subsequent initiation of illicit drug use in individuals who had previously used neither (association); and, crucially,

3. Initiation of illicit drug use does not increase the likelihood of subsequent initiation of licit drug use in individuals who had previously used no drugs (association’s reverse).

All three elements invoke the construct of initiation, which is a question of survival analysis. These can be formally stated in terms of hazard probabilities, where A is probability of licit drug use and B is probability of illicit drug use:

1. P (A | ~A, ~B) > P (B | ~A, ~B);

2. P (B | A, ~B) > P (B | ~A, ~B); and

3. P (A | ~A, B) <= P (A | ~A, ~B).

Stated in these absolute terms, the hypotheses to be tested are clear. However, the equality in point 3 presents a problem: that of endorsing the null hypothesis. We propose that points 2 and 3 can be re-stated as follows, with minimal change in meaning:

• 2a. (P (B | A, ~B) − P (B | ~A, ~B)) > (P (A | ~A, B) − P (A | ~A, ~B)).

In natural language, the increase in probability of B (initiation of illicit drug use) given A (licit drug use) is greater than the increase in probability of A given B – use of licit drugs increases the likelihood of illicit drug use to a greater extent than the reverse. There is a small slippage in meaning from the original hypothesis, in that illicit drug use may increase the likelihood of licit drug use while still satisfying 2a (or, considerably less likely in this example, both differences could be negative). We contend that this is a reasonable re-statement of the gateway hypothesis, and, conveniently, one that lends itself to significance testing in a model in which the two differences can be estimated simultaneously.

Dual-Process Discrete-Time Survival Analysis

The statistical methods used in this study are a novel application of associative latent transition analyses (ALTA; Bray, Lanza, & Collins, in press), dual-process discrete-time survival analysis. To elaborate, we discuss this rather unwieldy term in parts. In most usage, survival analysis (aka hazard modeling or time-to-event modeling) is an umbrella term for models of the timing of a non-repeatable event – in this case, first use of a type of drug; in other instances, perhaps death or first marriage. Survival analysis was originally developed in the context of continuous time in which the timing of the event could be reasonably precisely measured (e.g., days of a laboratory rodent’s life-span) and there were few “ties” in the timing across subjects (Elandt-Johnson & Johnson, 1980). Measurements of adolescent substance use seldom approximate continuous-time in any but the smallest samples, and so we turn to the alternative. Discrete-time survival analysis, then, is survival modeling where ties are common: i.e., there are many fewer measurement occasions than “failures” to survive (Muthén & Masyn, 2005).

Finally, DPDTSA is an approach in which two discrete-time time-to-event processes are modeled concurrently and linked to each other in a fashion similar to a cross-lagged panel design. To our knowledge, no methodological nor substantive work to date has incorporated multiple discrete-time survival processes in a single statistical model, though it should be noted that the recently developed ALTA model (Bray et al, in press) approach provides a relevant general framework. However, using a single model is necessary to test the constraint 2a described above and thus the gateway hypothesis as construed.

In our strategy, each outcome variable at each measurement occasion is modeled as a “latent” class variable with known class membership, modulo missing data. While the class membership is known and by definition not latent, the latent class/latent transition framework in the latent variable modeling software Mplus (L. K. Muthén & Muthén, 2009) provides the facility for handling the case of “not applicable” for outcomes, when initiation has occurred at a prior time.

To continue with the substance use problem, at the first occasion, each latent class variable comprises two classes: any lifetime use vs. no lifetime use. At subsequent occasions, each variable comprises three classes: first-time use (failure to survive), no lifetime use (survival), and past use (previously failed). Onset of each substance type at each occasion can be predicted by onset of the other type at preceding occasions.

A schematic of the model is presented in Figure 1. The latent transition matrix within substance is highly constrained. If a respondent has never used a (for example) licit drug at time T, then they can remain in the never-use class or transition to the first-time-use class at time T+1, but could not transition directly to the past-use class. Alternatively, a respondent who uses the licit drug for the first time at time T automatically transitions to the past-use class at time T+1. Finally, a respondent in the past-use class at any time remains in the past-use class at all subsequent times. This within-substance portion of the model is entirely descriptive, directly reflecting the empirical onset data for each group of drugs, and is replicated for licit and illicit drugs.

Figure 1.

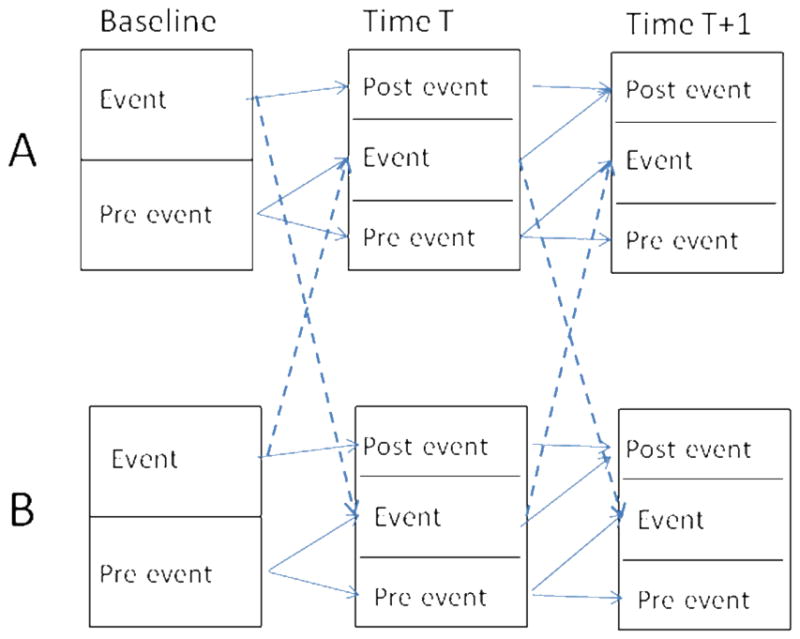
Schematic of Dual-Process Discrete-Time Survival Analysis model as a latent transition model. Solid lines depict possible transition pathways within event. Dashed lines depict possible effects of one event on the other.

The novel element of the DPDTSA is in the cross-links between the two processes. Specifically, first use of either type of drug (i.e., membership in the first-time-use class) at time T is modeled as predicting first use of the other type of drug (transition from the never-use class to the first-time-use class) at time T+1, and could in concept predict first use at T+2 and subsequent as easily. It should be noted that the model as constructed is entirely symmetric – neither process (licit or illicit drug use) is specified a priori as a leading indicator of the other.

Returning to our summation above of the gateway hypothesis, terms 1 and 2a can be cast in this framework as follows. Again, A is initiation of licit drug use and B is initiation of illicit drug use. The subscript trans indicates a shift to transition probabilities versus probabilities of use. This removes the need for the subtraction term in the earlier presentation of 2a.

1. P_trans (A_T+1 | ~A_T, ~B_T) > P_trans (B_T+1 | ~A_T, ~B_T); and

   2a. P_trans (B_T+1 | A_T, ~B_T) > P_trans (A_T+1 | ~A_T, B_T).

In natural language, given no past substance use, the probability of initiation of licit drug use is greater than the probability of initiation of illicit drug use at any given time, and the probability of initiation of illicit drug use given past licit use is greater than the reverse – matching our restatement of the gateway hypothesis, above.

Current Study

The current work illustrates DPDTSA as a potential new tool in the arsenal of methods to study questions of related onset such as the gateway hypothesis. Using data from the 1984 birth cohort of the National Longitudinal Survey of Youth 1997 (NLSY97) -- a large, nationally representative dataset with extensive annual measures of substance use -- we set out to show the utility of the DPDTSA and make a preliminary assessment of the simplest form of the gateway hypothesis, that licit substances (i.e., alcohol and/or tobacco use) serve as gateways for illicit substance use (e.g., marijuana, crack, cocaine). Further, we demonstrate the incorporation of covariates and potential moderators (e.g., socioeconomic status [SES] , gender, and ethnicity). We argue that this methodology uniquely captures the relation between onset of one substance type and another in such a way as to facilitate testing of the gateway model in terms of association and sequencing. Documenting causality is, of course, a much more difficult proposition which we do not attempt here, but to a discussion of which we will return.

Methods

This study used data collected as part of the National Longitudinal Survey Series (Ohio State University, 1997). The NLSY97 was created by the United States Department of Labor Bureau of Labor Statistics to investigate a representative sample of United States residents who were born between the years of 1980 and 1984, inclusive. Respondents were first surveyed in 1997 and then attempts were made to survey each respondent in each calendar year since then. The present investigation focused on behavior variables related to licit and illicit drug use.

Participants

During the first wave of data collection, all residents between 12 and 16 years old were eligible to be interviewed from the randomly selected houses for NLSY97. Parents of youth living in the home were asked to participate, as well. The youth sample includes 8,984 respondents from 6,819 unique households, including an oversample of Black and Hispanic youth. The current study utilizes data from the 1984 birth cohort, following annual surveys from 1997 through 2000 (ages 12–15 at the beginning of the study years).

In round 1 (1997), the age 12 sample (N = 1,231) comprised 52% males (n = 634); 22% (n = 268) Hispanic respondents; 25% (n = 312) non-Hispanic Black respondents; 1% (n = 12) “mixed” race respondents; and 52% (n = 639) non-Hispanic White and other-race youth. As a measure of attrition, we examined response to the substance use portion of the survey in Round 4 (2000), the last year’s data used in the current study. Ninety-three percent (93%) of the 1984 birth cohort responded to these measures, including 94% of males, 93% of females, 93% of Hispanic youth, 94% of non-Hispanic Black youth, 100% of mixed-race youth, and 93% of non-Hispanic, non-Black respondents. Given the low attrition, and our primarily illustrative purpose here, we elected to use listwise deletion in cases of attrition, resulting in an analysis sample size of 974. Although this is not necessary for the technique, it facilitates verifying the results of the method against the original data. For all subsequent analyses, the twelve mixed-race youth were included in the non-Hispanic, non-Black respondent group for simplicity.

Procedures

Face-to-face interviews were conducted with a majority of respondents on an annual basis. However, the time period between wave 1 and wave 2 was approximately 18 months. The NLSY97 used a computer-assisted personal interviewing (CAPI) system; between 3% (round 1) and 9% (round 4) of interviews were conducted over the phone, rather than face-to-face. Audio computer-assisted self-interview technology was used to assess sensitive areas, including substance use.

Measures

Questions related to alcohol, tobacco, marijuana, crack, cocaine, heroin, and other non-prescribed drugs (“hard drugs”) were asked of all respondents. The questions were asked in every year, except where indicated otherwise. Beginning in round 1 (1997) for alcohol, tobacco, and marijuana, and round 2 (1998) for hard drugs, respondents were asked about whether they had ever used these substances (rounds 1–4). Starting in round 2, respondents were asked if they had used the substance since the date of the last interview. For alcohol-related questions, a drink was defined by “a can or bottle of beer, a glass of wine, a mixed drink, or a shot of liquor,” and respondents were instructed to “not include childhood sips that you might have had from an older person's drink.” Other aspects of substance use were measured, but our focus in this study was strictly on onset and so only responses to the lifetime and since-last-interview questions were used.¹ As we only modeled licit versus illicit substance use initation, alcohol and tobacco use were combined as “licit” and marijuana and all other substances measured as “illicit” for all purposes. The variables for analysis were dichotomous indicators of licit and illicit use at each of the four ages. The indicators were set to missing in years after initiation.

SES at baseline (1997) was indicated in this study by a “poverty ratio” variable, the result of an algorithm programmed by the Bureau of Labor Statistics and incorporated into the public-release dataset. This variable is the ratio of the total household income to the federal poverty line for a household of a specific composition. Valid data existed for this variable for 931 (76%) respondents in the 1984 cohort, 16 (2%) of whom reported zero household income. The indicator was coded as missing for households with zero income and as the natural logarithm of the poverty ratio for the 915 respondents from households with income.

Sampling Weights

Due to the complexity of construction of this sample, cross-sectional weights were created by NLSY97 staff for each survey round. We applied the Round 1 Sampling Weight (variable “R12361.00” in the public use dataset) for all analyses to recapture parameters reflecting a nationally representative sample.

Results

Sample Statistics

Table 1 presents both the proportions of youth experiencing onset at a given round among those not yet having used (the actual data used in survival analysis) as well as the cumulative proportion experiencing onset at or before that round (a more intuitive presentation). The entry for age 12 also includes any initiation before age 12.

Table 1.

Onset and Cumulative Use of Licit and Illicit Substances

Age	Licit Substances		Illicit Substances
	Onset	Cumulative Use	Onset	Cumulative use
<=12	.31	.31	.05	.05
13	.26	.49	.11	.15
14	.24	.62	.10	.23
15	.21	.69	.13	.34

Note: N = 974; tabled values are proportions. Licit substances include alcohol and tobacco. Illicit substances include marijuana, cocaine, and other illegal drugs.

Initial Model

For the initial model, we estimated a DPDTSA for two processes (use of the “licit” substances, tobacco and alcohol, and use of the “illicit” substances, marijuana, inhalants, and other drugs) each with four (coincident) measurement occasions. Longer measurement chains presented technical difficulties; these are discussed with other limitations below. Each variable at each occasion was modeled as a latent class variable with known class membership. At the first occasion, age 12, each latent class variable comprised two classes: any lifetime use (including earlier initiation) vs. no lifetime use. At subsequent occasions, through age 15, each variable comprised three classes: first-time use (failure to survive), no lifetime use (survival), and past use (previously failed). Onset of each substance type at each occasion was predicted by onset of the other type at the immediately preceding occasion, relative to no lifetime use, and by all covariates (race/ethnicity [effect-coded], sex, and SES). We did not assume proportional hazards – that is, the effects of the predictors on onset of each outcome were allowed to vary with age of potential onset.

The model followed the schematic presented in Figure 1, using the highly constrained transition matrix described in the introduction to the method. Further, we included respondent race/ethnicity (effect codes of the combined variable indicated in the Methods section), respondent sex, and log-poverty-ratio as covariates, predicting onset at all occasions. The software implementation for this model is not obvious; documented Mplus syntax for the initial model is available from the first author’s website, http://people.cas.sc.edu/malonep/Malone_et_al_DPDTSA_code.rtf. Note that version 5.21 of Mplus can only estimate this model using Monte Carlo numeric integration. We used the default number of integration points, which varied for different analyses by dimensions of integration. It should also be noted that, because there was no uncertainty in class membership, this analysis was not sensitive to starting values; an analysis with missing data could be so.

Absolute model fit is not readily evaluated in mixture models, and the software does not report absolute fit even with known class membership. However, recent versions of Mplus do report local model fit for the categorical indicators – i.e., the substance use indicators. By this measure, the model reproduced the original frequencies well, Likelihood Ratio χ² (201, N = 974) = 29.5, ns. The key parameter estimates for the model, transformed into odds ratios with 95% confidence intervals are presented in Table 2. As shown, onset odds of illicit drug use at ages 13 and 15 were significantly, positively predicted by the previous year’s onset of licit drug use, with odds ratios of 4.95 and 2.05, respectively. For the converse, only one of the three relations (age 15 licit use predicted from age 14 illicit use) was significant, with an odds ratio of 17.67. The very large confidence intervals in prediction from illicit drug use should be noted, presumably due to the rarity of illicit drug use in the early ages.

Table 2.

Predictions of Onset of Licit and Illicit Substance Use

Outcome		Predictor
	Age	Licit Age 12	Licit Age 13	Licit Age 14	Illicit Age 12	Illicit Age 13	Illicit Age 14	Male (vs. mean)	Black (vs. mean)	Hispanic	Income (log pov Ratio)
Licit Drugs
	12	--	--	--	--	--	--	1.46 (1.07, 1.99)	1.07 (0.82, 1.40)	0.63 (0.46, 0.87)	0.74 (0.59, 0.92)
	13	--	--	--	1.02 (0.07 15.79)	--	--	0.99 (0.67 1.45)	0.68 (0.48, 0.98)	1.19 (0.83 1.71)	0.77 (0.59 1.00)
	14	--	--	--	--	0.83 (0.08, 8.98)	--	1.07 (0.68, 1.69)	0.78 (0.52, 1.18)	1.07 (0.69, 1.65)	1.39 (1.00, 1.91)
	15	--	--	--	--	--	17.67 (2.19, 142.50)	1.05 (0.58, 1.88)	0.69 (0.43, 1.11)	0.86 (0.50, 1.48.)	0.67 (0.43, 1.05)
Illicit Drugs
	12	--	--	--	--	--	--	1.74 (0.89, 3.39)	1.50 (0.84, 2.68)	0.47 (0.22 1.04)	0.90 (0.61 1.34)
	13	4.95 (3.07, 7.98)	--	--	--	--	--	0.89 (0.55, 1.43)	0.79 (0.52, 1.21)	1.10 (0.70, 1.73)	0.81 (0.61, 1.08)
	14	--	1.70 (0.94, 3.08)	--	--	--	--	1.09 (0.65, 1.81)	1.17 (0.75, 1.81)	0.72 (0.43, 1.20)	0.97 (0.72, 1.31)
	15	--	--	2.05 (1.13, 3.71)	--	--	--	1.89 (1.16, 3.07)	0.71 (0.45, 1.11)	0.94 (0.58, 1.52)	0.73 (0.55, 0.97)

N = 974. Tabled values are odds ratios and 95% confidence intervals for each predictor (column) predicting initiation of substance at the indicated age by row. Significant odds ratios greater than 1.0 indicate positive relations. ‘--‘ indicates a prediction path excluded from the model. Significant effects, p < .05, in bold type.

Test of Sequencing

The simplest (and strictest) test of the sequencing hypothesis is that the initiation of licit substance use is more likely than initiation of illicit use at each possible time of onset. Inspection of the logistic regression intercepts for new use of licit drugs revealed that the point estimates were greater (indicating more probable initiation) than those for contemporaneous illicit drug initiation at all four waves. The test of the simultaneous constraints that the intercepts were equal over time was significant, Wald χ² (4, N = 974) = 375.1, p < .001. The intercepts and their standard errors are shown in Table 3.

Table 3.

Logistic Regression Intercepts for Drug Use Onset

	Licit Drugs	Illicit Drugs
Age 12	−0.75 (.08)	−3.04 (.17)
Age 13	−0.99 (.10)	−2.75 (.18)
Age 14	−1.09 (.12)	−2.34 (.15)
Age 15	−1.45 (.15)	−2.01 (.14)

N = 974. Tabled values are logistic regression intercepts and standard errors for initiation of each type of substance at the indicated age by row. Higher (less negative) values indicate greater likelihood if initiation.

Tests of Association

A simultaneous test of the three licit-to-illicit paths showed significant overall prediction, Wald χ² (3, N = 974) = 50.0, p < .001. The comparable simultaneous test for the three illicit-to-licit paths (irrespective of direction) did not meet standard significance criteria, Wald χ² (3) = 7.30, p = .063. However, a specific contrast between the three licit-to-illicit links and the contemporaneous illicit-to-licit paths showed no significant difference, Wald χ² (3) = 5.38, p = .146. This test indicates that the paths leading from initiation of licit drug use to the next year’s initiation of illicit drug use were not significantly stronger than the opposite links, contrary to predictions of the gateway hypothesis.

Moderation of the Gateway Model

We next explored the feasibility of incorporating moderating effects into the DPDTSA model. We tested a categorical moderator of the gateway links (respondent sex) and a continuous moderator (income) in separate models.

We created the categorical moderator by first mean-centering the dummy-coded sex variable and then creating product terms between the sex variable and the dichotomous drug use variables. The mean-centering does not affect hypothesis testing, but retains the meaning of the main effects within drug use as being estimated across gender, rather than within the reference group. Each product term (sex X [licit/illicit] use at time T) was entered into the model as a predictor of [illicit/licit] use at time T+1. The product terms for both directions of prediction were entered simultaneously. (This parameterization is equivalent to that presented in example 8.13, “LTA with a Covariate and an Interaction,” in the Mplus User’s Guide, Muthén & Muthén, 2009; however, the product-term formulation is likely to be more familiar.) The overall predictive model was significantly moderated by sex, Wald χ² (6, N = 974) = 27.2, p < .001. Decomposing the interaction, we found that the interaction predicting illicit substance use from licit substance use by sex did not meet the p < .05 level, Wald χ² (3) = 7.02, p = .071. The prediction of licit substance use from illicit substance use, however, was significantly moderated by sex, Wald χ² (3) = 19.7, p = .002. On inspection of the individual moderator terms, we found an unexpected pattern. The interaction term of sex with age 12 illicit substance use in predicting age 13 licit substance use was positive (with “male” coded high) and not significant, b = 2.24, SE = 2.86, Est./SE < 1, and the interaction term with age 14 illicit use predicting age 15 licit use was negative and not significant, b = −1.71, SE = 2.17, Est./SE < 1, but the interaction coefficient for age-13 illicit use to age-14 licit use was extremely large, with a correspondingly large standard error, b = −61.40, SE = 23.42, Est./SE = 2.62, p = .009. In order to probe this pattern, we tested the constraint that the three coefficients – the interaction terms between sex and illicit substance use at each age – were equal across age. The intent of this test was to indicate whether this constraint could stabilize the coefficients without harming fit. Results indicated that this constraint did harm fit, Wald χ² (2) = 17.2, p < .001.

The continuous moderator was handled in a similar fashion. In this case, the overall test for moderation by income (logged poverty ratio) did not show significant differences, Wald χ² (6, n = 974) = 6.14, p = .408.

Discussion

In a recent edited volume (Kandel, 2002), four chapters (Bentler, Newcomb, & Zimmerman, 2002; Collins, 2002; Yamaguchi, 2002; Yamaguchi & Kandel, 2002) deal specifically with methodology for assessing the gateway hypothesis, each with a different method in a different context. A consistent theme in these chapters is the need to document not only sequencing but also association between steps in the gateway, and even then to interpret results with caution. With these caveats, we now turn to our results.

Our analyses centered on early adolescence (ages 12–15) and the simple gateway association between any licit substance use (i.e., drugs for which use is a status offense for minors, but possession of which is not criminal for adults) and any illicit substance use. The significant prediction of initiation of illicit drug use from prior-year onset of licit drug use was clear evidence of association. However, the evidence of sequencing was weakened by the near-significant and, more importantly, not significantly different prediction in the opposite direction. That is, the licit-to-illicit progression was not significantly stronger than the illicit-to-licit progression, violating one of the key implications of the gateway hypothesis (Yamaguchi & Kandel, 2002). This conclusion should be read lightly, given the relatively large confidence intervals for the illicit-to-licit paths (presumably due to the low incidence of early illicit drug use in the sample). However, our findings are certainly no more than ambiguous support for the gateway hypothesis.

We also attempted to demonstrate the use of DPDTSA in moderator analyses. We did find significant moderation of the gateway progression by youth sex; however, the pattern of coefficients moderating the prediction of licit drug use initiation from illicit was suspect. We believe this was most probably due to the low base rates of illicit substance use in this age group; future directions planned include simulation studies examining the sample size requirements of DPDTSA under varying conditions.

The above discussion of hypothesis testing highlights the difficulty of drawing causal inferences in gateway drug models. Clearly, controlled experimentation is impossible for this question (at least as applied to normative development, in the absence of intervention), so the standard difficulties with inferring causality from observational data are present. The NLSY97 uses a prospective longitudinal design which addresses some of the alternate explanations (such as recall bias), but cannot wholly address the question of spurious relations due to third-variable causation. In our analyses, we did not attempt to address this. We could have included a host of covariates and possible confounds, but a conclusive test of the gateway hypothesis was not our purpose – and indeed was blocked by technological limitations which we discuss below. Those limitations notwithstanding, the third-variable causation possibility cannot be comprehensively ruled out in an observational study. A further limitation of the NLSY97 for our purposes is the issue of left-censoring – i.e., a substantial degree of initiation of alcohol and tobacco use likely occurred before age 12. Thus, our age 12 to 13 paths are biased by the “age 12” initiation not necessarily occurring within that year.

The reader by this time will likely have questioned the limited time frame and limited number of substances tested in our gateway sequence. To both of these, we have a simple answer: Current commercial software and readily available computing hardware are not adequate to the task. Because the DPDTSA is modeled as an elaborate latent transition model, the complexity of estimation increases exponentially with the number of measurement occasions. Indeed, with four times of measurement, we had (2 x 2 x 3 x 3 x 3 x 3 x 3 x 3 = ) 2,916 cells in the crosstabulation; adding one more time would have multiplied that by 9 for 26,244 cells. In preliminary tests, we have successfully modeled five measurement occasions, but the Mplus output file was measured in gigabytes and in the tens of millions of lines; adding moderators expanded that further still. Even though the vast majority of those cells were structural zeroes (i.e., impossible to be populated due to the model constraints), the software output was infeasibly long to read or edit. Thus, we addressed only four time-points. Similarly, we attempted in preliminary analyses to include a third substance, with potential gateway paths linking all three, but encountered like difficulties. We have brought this problem to the attention of the Mplus developers, in hopes of future availability of options to suppress some of the output, but currently we are at the limits of our technological capacity.

Alternative Strategies

An alternative approach to the dual-process problem could be extrapolated from Singer and Willett’s (1993) presentation of discrete-time survival analysis via logistic regression. In that approach, the survival analysis dataset is transformed into a person-period dataset which is then amenable to logistic regression. For a dual-process model, the parameterization would be similar to a bivariate logistic growth model. In a case with no interval censoring – i.e., no missing data before either the event or the end of the study – this may be a simpler approach. However, interval censoring is all too common in longitudinal substance use research as respondents leave and return to the study. In such a case, the missing-data problem for the categorical observed variables would be unwieldy, and potentially intractable for problems any larger than the current example. Although we used listwise deletion in the example problem, previous analyses with interval censoring were accommodated with no changes other than adding a random starting-value search to reduce the possibility of reaching a solution at a local maximum.

A second approach worth mentioning here is the ALTA model (Bray et al., in press). This is a general framework for dual-process discrete-time models with categorical indicators. It would be fair to say that, rather than an alternative approach, the DPDTSA is a special case of the ALTA model with specific constraints and predictions.

Conclusions

We believe that, (temporary) technical difficulties notwithstanding, dual-process discrete-time survival analysis is a powerful new tool for researchers studying time-to-event processes in which one event does not preclude the other. While it seems particularly well-suited to tests of the gateway drug hypothesis, other possible research questions for DPDTSA might include the links between illicit drug use and high school dropout (e.g., Malone, Masyn, Lamis, & Northrup, 2008, June); which of two or more alternative opportunistic infections first manifests in immunodeficient individuals; or many other purposes – ironically exclusive of survival analysis’ original purpose of modeling time-to-death (as the reciprocal relations would not be possible). We chose to highlight in this paper the capabilities of DPDTSA in the gateway drug hypothesis, including its flexibility for moderator analyses. Further, this is, to our knowledge, the first method of evaluating the gateway hypothesis that allows null hypothesis significance testing (in the form of the Wald test) of competing directional paths. We also hope to explore in future work the potential for lagged prediction – the effect of initation of one substance on another may not be timed at the convenience of data collection waves. Another future direction is its potential for facilitating mediation tests, where timing of one variable (e.g., high school dropout) may mediate the prediction of another time-to-event process (e.g., drug use) from a prior variable (e.g., poor parental monitoring). The DPDTSA is a special-purpose tool, but one which we argue is a significant advance in time-to-event modeling.