Complex cell receptive fields: evidence for a hierarchical mechanism

Abstract

Simple cells in the primary visual cortex have segregated ON and OFF subregions in their receptive fields, while complex cells have overlapping ON and OFF subregions. These two cell types form the extremes at each end of a continuum of receptive field types. Hubel and Wiesel in 1962 suggested a hierarchical scheme of processing whereby spatially offset simple cells drive complex cells. Simple and complex cells are often classified by their responses to moving sine wave gratings: simple cells have oscillatory responses while complex cells produce unmodulated responses. Here, using moving gratings as stimuli, we show that a significant number of cells that display low levels of response modulation at high contrasts demonstrate high levels of response modulation at low contrasts. Most often a drifting low contrast grating generates a large phasic response at the fundamental frequency of the grating (F₁) and a smaller but significant phasic response that is approximately 180 deg out-of-phase with the F₁ component. We present several models capable of capturing the effects of stimulus contrast on complex cell responses. The model that best reproduces our experimental results is a variation of the classical hierarchical model. In our model several spatially offset simple cells provide input to a complex cell, with each simple cell exhibiting a different contrast response function. At low contrasts only one of these simple cells is sufficiently excited to reveal its receptive field properties. As contrast is increased additional spatially offset simple cells with higher contrast thresholds add their responses to the overall spiking activity.

Introduction

Understanding the receptive field organization of neurons in the primary visual cortex is critical because they provide the basic building blocks that lead to all further cortical processing of the visual environment (Carandini et al. 2005). The receptive field structure of neurons in visual cortex systematically changes, depending on cortical layer. A high proportion of cells in layer 4 and upper layer 6 receive direct input from the thalamic relay neurons and have segregated ON and OFF subregions in their receptive fields; they are termed simple cells (Gilbert, 1977; Martinez et al. 2005). Far fewer cells in layers 2/3, 5 and lower-6 have segregated ON and OFF subregions in their receptive fields; the great majority have overlapping ON and OFF subregions and are termed complex cells. The transformation in receptive field structure between simple and complex cells represents a fundamental computation being made in visual cortex. Understanding how this transformation occurs is essential in determining how the cerebral cortex processes information.

There has been much controversy over the classification of cells into simple and complex types and the most appropriate models to explain their response properties. Some classification systems divide the population distinctly into simple and complex types (Skottun et al. 1991), while others suggest a continuum of receptive fields (Dean & Tolhurst, 1983; Mechler & Ringach, 2002). Our emphasis here is on the models that might generate simple and complex receptive fields, rather than any particular classification system. When Hubel & Wiesel (1962) first described simple and complex cells they also presented a hierarchical model to account for complex cell responses. As an example, the spatial characteristics of the receptive field of a theoretical simple cell are presented in Fig. 1A. It has segregated ON (white) and OFF (black) zones such that when stimulated by a drifting sine wave grating of the appropriate orientation and spatial frequency the cell's membrane potential (V_m) oscillates at the fundamental temporal frequency of the grating as it moves in and out of phase with the cell's receptive field. The membrane potential V_m is transformed into a firing rate code by half-wave rectification (black oscillating response, Fig. 1A). This non-linear transformation exaggerates the oscillation such that the in-phase excitations produce narrow peaks with intervening null zones (Tolhurst & Dean, 1990). Using Fourier analysis it is possible to extract the mean response (F₀) and the amplitude of the response at the fundamental frequency (F₁) (Movshon et al. 1978a). Simple cells have been defined in several species as cells with an F₁/F₀ ratio >1, while complex cells have F₁/F₀ ratios <1 (Movshon et al. 1978a; Skottun et al. 1991; Ibbotson et al. 2005). The modulation of responses to moving gratings has been shown to have a close relationship to classification based on direct measures of spatial summation (Tolhurst & Dean, 1987; Skottun et al. 1991). The theoretical cell in Fig. 1A has an F₁/F₀ ratio of 1.2. For comparison, the spiking response of a real simple cell is shown in Fig. 1D.

Figure 1. Schematic representations of a simple cell (A) and complex cell (B and C), along with their predicted responses (D–F) to moving sine wave gratings.

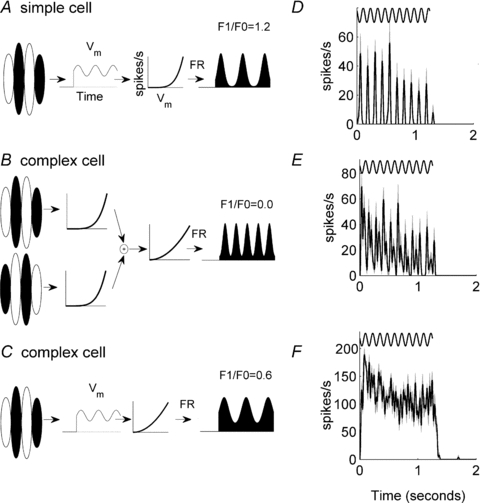
The responses of three example cortical cells are shown: simple cell (D), an oscillatory complex cell (E) and a complex cell with no oscillations in its response to a moving grating (F). In D–F the sinusoids above the responses show the temporal frequency of the grating stimulus. The grey shaded area shows the standard error of the mean. The model simple cell in A includes a linear spatiotemporal filter which determines the membrane potential. The membrane potential is then converted to a firing rate (FR) through half-wave rectification and power transformations (( )^p). The shape of the power function is shown by the graphs that plot spikes s⁻¹ against V_m (membrane potential). The spiking response in A is a classical simple cell response. The hierarchical model of a complex cell in B takes inputs from two simple cells whose linear filters are 180 deg out of phase. Note that for brevity the membrane potential V_m is not illustrated in B. The simple cell outputs are combined and further transformed by half-wave rectification and power transformations. The spiking response oscillates at twice the frequency of the stimulus grating. From the definition of the Fourier transform it follows that F₁ = 0. An alternative model complex cell is shown in C. This model is identical to that for the simple cell in A except that the power transformation emphasizes the offset rather than the oscillatory component.

Hubel & Wiesel (1962) proposed that the output of two (or more) spatially offset simple cells might provide the input to a complex cell (Fig. 1B). For example, the spiking output from two simple cells whose receptive fields are 180 deg out-of-phase might be summed by the complex cell producing, after rectification, a complex-like response oscillation (Fig. 1B). In the example shown, the amplitude of the F₁ component of the response is zero (F₁/F₀ ratio = 0) and the cell is classically defined as complex. It is common to find complex cells with non-zero F₁ components and relatively large oscillating responses at twice the frequency of the input (F₂) (Fig. 1E), but in many cases no obvious response oscillations are apparent (Fig. 1F). The latter response can be modelled in an analogous fashion by adding more spatially offset simple-like inputs to the complex cell model.

While Hubel and Wiesel's model provides a possible explanation for the formation of complex cells, Mechler & Ringach (2002) have shown that a basic simple cell receptive field can also produce complex-like responses (Fig. 1C). In this model the basic receptive field is identical to that shown in Fig. 1A, but the transformation between V_m and the firing rate is different, leading to a cell with an F₁/F₀ ratio <1 (black response in Fig. 1C). There is evidence that this formulation is appropriate in many cortical cells (Priebe et al. 2004). Another model attributes complex cell activity to lateral recurrent connections between cortical neurons rather than interactions between the thalamic inputs (Chance et al. 1999; Tao et al. 2004).

If complex cell receptive fields arise by combining the inputs from several simple cells it should be possible to uncover the structure of these subunits. Indeed, a number of different techniques have been employed to uncover the structure of the input to complex cells (e.g. Movshon et al. 1978a; Szulborski & Palmer, 1990; Anzai et al. 1999; Martinez & Alonso, 2001). These studies suggest that complex cell inputs may resemble simple cells but no technique has unequivocally uncovered a simple cell receptive field as a subunit within a complex cell receptive field. White noise stimuli and associated spike-triggered covariance analysis has revealed that complex cells are made up of multiple linear subunits, but it is not possible to describe the exact number or configuration of subunits, as many possibilities lead to the same observed response (Rust et al. 2005; Touryan et al. 2005).

In this paper we explore the mechanisms underlying complex cell receptive fields using a spatiotemporal frequency analysis wherein moving sine wave gratings covering a range of spatial and temporal frequencies were used to analyse the receptive fields at both high and low contrasts. Among complex cells we reveal that there is a significant shift towards higher levels of response modulation (indicative of simple cell behaviour) at low contrast. This suggests that cells have overlapping ON and OFF subregions at high contrast, but spatially segregated ON and OFF subregions at low contrast.

Methods

Anaesthesia and surgical procedures

Single-unit recordings were made from area 17 in four anaesthetized and neuromuscularly blocked cats. All procedures were approved by the Animal Experimentation Ethics Committee of the Australian National University and followed the National Health and Medical Research Council's Australian Code of Practice for the Care and Use of Animals for Scientific Purposes.

Animals were prepared as described previously (Crowder et al. 2006; Hietanen et al. 2007). Specifically, anaesthesia was induced by intramuscular injection of a ketamine/xylazine mixture (ketamine HCl, 20 mg kg⁻¹; xylazine, 1 mg kg⁻¹). An adequate level of ketamine anaesthesia prior to and during surgery was confirmed by the absence of corneal and toe withdrawal reflexes. Animals were intubated to ensure adequate respiration and the right cephalic vein was cannulated. Anaesthesia was then maintained for the duration of the experiment (4–5 days) by inhalation of gaseous halothane (1–2% during surgery, 0.5% during unit recordings) in a 2:1 mixture of N₂O and O₂. Animals were instrumented to facilitate continuous monitoring of the electrocardiogram (principally heart rate) and end-tidal CO₂ concentration to ensure an adequate level of anaesthesia was maintained at all times. For fluid replacement, animals received a continuous intravenous infusion (2.5 ml kg⁻¹ h⁻¹) containing Hartmann's (lactated Ringer) solution (25% by volume), 5% glucose–0.9% NaCl solution (25% by volume) and an amino acid solution (50% by volume). Body temperature was maintained at 37.7°C by way of an electric heating blanket under feedback control.

The head was held in a stereotaxic frame using ear bars, a bite bar and head bolt positioned on the skull at the midline approximately 30 mm anterior to interaural zero. To allow access to primary visual cortex (area 17), the scalp was reflected and a craniotomy was performed 0–8 mm posterior to interaural zero and 2–8 mm lateral to the midline. To prevent eye movements during unit recordings, animals were subject to neuromuscular blockade by continuous intravenous infusion of gallamine triethiodide (10 mg kg⁻¹ h⁻¹). During neuromuscular blockade animals were mechanically ventilated to maintain end-tidal CO₂ between 3.5 and 4%. Neutral power rigid gas-permeable contact lenses were fitted to the eyes to ensure corneal perfusion, and drops (1% atropine; 10% phenylephrine) were administered daily to cause pupillary dilatation and to retract the nictitating membrane. Refractive errors were assessed by reverse ophthalmoscopy and corrected as required using spherical lenses placed in front of the eyes to focus the stimulus (presented on a screen placed 57 cm in front of the animal) on the retina. Artificial pupils (3 mm in diameter) were placed in front of the eyes to reduce spherical aberrations. Animals were given daily injections to reduce salivation (atropine, 0.2 mg kg⁻¹; s.c.), cerebral oedema (dexamethasone phosphate, 1.5 mg kg⁻¹; i.m.) and the risk of infection (Clavulox, a broad spectrum antibiotic, 0.5 ml kg⁻¹; i.m.). The locations of the optic disc and area centralis of each eye were plotted daily by reverse ophthalmoscopy.

At the conclusion of the experiment animals were killed by intravenous injection of an overdose of barbiturate (sodium pentobarbitone, 150 mg kg⁻¹) and immediately perfused with 0.9% saline followed by 10% formol saline. The brain was then extracted for histological reconstruction of recording track locations (for details see Crowder et al. 2006).

Extracellular recordings and visual stimuli

Extracellular recordings were made with epoxy-coated tungsten microelectrodes (FHC, Bowdoinham, ME, USA) driven by a piezoelectric drive (Burleigh inchworm and 6000 controller, Burleigh Instruments, Victor, NY, USA). All recording tracks were reconstructed and recording sites were verified as being in Area 17. Extracellular signals from individual units were isolated, amplified, filtered and then sampled at 40 kHz using a CED1401 interface and Spike2 software (Cambridge Electronic Design Ltd, Cambridge, UK).

The dominant eye and receptive field location of each recorded neuron were first determined using a hand held ophthalmoscope to project bright spots or bars on a white screen placed in front of the animal. The non-dominant eye was then covered and further characterization and testing were performed using the dominant eye only. Visual stimuli were produced by a ViSaGe stimulus generator (Cambridge Research Systems, Cambridge, UK) and presented on a calibrated monitor (Eizo T662-T, 100 Hz refresh, 1024 × 768 pixels) at a viewing distance of 57 cm. Moving sine wave gratings were presented in a circular aperture surrounded by a grey background of mean luminance (Lum; 56 cd m⁻²). Sine wave (Michelson) contrast is defined as C = (L_max−L_min)/(L_max+L_min) where L_max and L_min are the maximum and minimum luminance of the grating. For all cells, the preferred orientation/direction, spatial frequency (SF) and temporal frequency (TF) were determined by calculating on-line tuning functions using 100% contrast gratings. The size of the classical receptive field was determined using a 100% contrast moving sine wave grating of optimal orientation/direction, spatial and temporal frequency, presented within a circular aperture centred on the middle of the receptive field. The size of the aperture was systematically expanded and the size at which the spiking response saturated/peaked was identified and then used for all subsequent tests. Extensive prior experiments had shown that expanding the size of the stimulus region as contrast was reduced (to match the expanding receptive field size) had minimal effects on the F₁/F₀ ratios of the cells (Crowder et al. 2007). Contrast response functions were obtained by presenting moving sine wave gratings (optimal size, orientation, SF and TF as determined at 100% contrast) at contrasts in the range 0.04 ≤C≤ 1.0. Stimuli were each presented 10 times in random order. Each presentation lasted 1 s, interleaved with 4 s of mean luminance. The resulting contrast response functions were used to ascertain an appropriate low contrast sufficient to produce a response around 10% of the size of the response at 100% contrast. The low contrast value so determined was then used in the full spatiotemporal analysis described below.

Spatiotemporal analysis

The traditional quantitative method of assessing if a cortical cell is simple or complex is to calculate a modulation index (F₁/F₀) based on its response to a moving sine wave grating (Movshon et al. 1978a; Skottun et al. 1991). The spatial and temporal frequencies of the sine wave grating, as well as its size are typically chosen so as to optimize the cell's response amplitude. Here we compare the F₁/F₀ ratio from cells tested with different stimulus contrasts. It is established that the properties of a cell's response to moving gratings vary with stimulus contrast (Sceniak et al. 1999; Crowder et al. 2007; Nauhaus et al. 2009). It is also known that changes in contrast can alter the spatial and temporal frequency tuning of a given cell such that a stimulus which was optimal at 100% contrast is no longer optimal at lower contrasts (Shapley & Victor, 1981; Nolt et al. 2004). Therefore, we carefully measured full spatiotemporal response profiles of all recorded neurons at both high and low stimulus contrasts to determine the appropriate spatiotemporal location at which to assess the F₁/F₀ ratio (e.g. Ibbotson & Price, 2001; Priebe et al. 2006).

Full spatiotemporal response profiles at both high and low contrasts were obtained by presenting moving sine wave gratings drawn from a pool of 49 spatial and temporal frequency combinations (7 different TFs for each of 7 different SFs). Stimuli were each presented 12 times in random order. Each presentation lasted 1 s plus the time period of the grating so that at least one complete cycle of the stimulus was shown. Grating stimuli were separated by 2 s periods of mean luminance. These periods were used to determine the spontaneous spiking rate (F_spont) of the recorded cell. Full spatiotemporal response profiles are presented in the form of contour plots (e.g. Ibbotson et al. 1994; Ibbotson & Price, 2001). Spikes were sampled throughout the entire stimulus cycle including the onset transient. In a previous study it was found that including the onset transient does not systematically alter F₁/F₀ ratios (Crowder et al. 2007).

Data analysis

Spike arrival times were determined off-line through action potential template matching (Spike2; Cambridge Electronic Design). Neuronal responses were then represented as spike density functions (SDFs) with 1 kHz resolution generated by convolution of a Gaussian kernel of unit area and σ = 10 ms with a train of Dirac delta functions, one delta function corresponding to the arrival time of each spike. Mean SDFs were then calculated by trial averaging responses to individual stimulus presentations for each condition.

Fourier analysis was performed on a section of the mean responses (averaged across trials) that was an integer multiple of the stimulus period. F₀ values were calculated as the increase in the mean firing rate above the spontaneous baseline (F_spont). F₁ and F₂ values were obtained using the first and second Fourier coefficients of the mean response respectively, produced using the FFT function in Matlab (The Mathworks Inc., Natick, MA, USA).

Modelling

The firing rate (r(t)) of a simple or complex cell in response to a moving sine wave grating with temporal frequency ω is given by (modified from Chance et al. 1999):

(1)

where | |⁺ represents half-wave rectification, ϕ is the phase of the response and V₁ and V₀ are respectively the amplitudes of the intracellular response modulation and mean. V₁ and V₀ are sigmoidally related to contrast. The power function ( )^p represents the non-linear relationship between membrane potential (V_m) and spiking response (from Abbott & Chance, 2002; Priebe et al. 2004). We have also assumed that the threshold voltage is zero. Thus, an ideal simple cell has V₀ = 0 whereas complex cells have a significant V₀ value compared to V₁. If p = 1, for example, then the condition for a cell to be complex is that V₁ > V₀.

Another model of a complex cell was based on the classic hierarchical architecture (Hubel & Wiesel, 1962; Pollen & Ronner, 1983) and more recent studies (Chance et al. 1999; Tao et al. 2004). The input layer is modelled as two simple cells defined by eqn (1) with V₀ = 0 and with phases differing by 180 deg. The firing rate r(t) of this complex cell is the sum of the response of these two simple cells.

Results

Responses of simple and complex cells to moving gratings

Recordings were made from 93 cortical neurons. When tested at high contrast, 16 cells were classed as simple (F₁/F₀ ratio >1) and 77 as complex (F₁/F₀ ratio <1). To provide the reader with a baseline for comparison, we first present full spatiotemporal response profiles for typical simple and complex cells measured at both high and low stimulus contrasts (Fig. 2). The F₁/F₀ ratios for the cells shown do not change at different stimulus contrasts. The top row shows the mean elevation in firing rate (F₀) calculated over an integer number of stimulus cycles at each of the spatiotemporal frequency combinations used. The middle and bottom rows show the amplitudes of the first (F₁) and second (F₂) Fourier components, respectively. It is evident that the simple cell exhibits very prominent F₁ (Fig. 2A, second row) and F₂ response components (Fig. 2A, bottom row). The F₁ response component is the signature of a simple cell while the F₂ component results from the half-wave rectification process: Fourier analysis of a perfectly half-wave rectified sine wave reveals a strong F₁ component (F₁/F₀ ratio = 1.57: Movshon et al. 1978a) and a smaller F₂ component (F₂/F₀ ratio = 0.66). For the simple cell shown in Fig. 2A, the F₁ response combined with the mean elevation in spiking (F₀) gives an F₁/F₀ ratio of 1.41 at the optimum spatiotemporal frequency combination. The F₂/F₀ ratio for the simple cell shown in Fig. 2A is 0.59. By comparison, the complex cell response profiles (Fig. 2B) exhibit very little modulation at the fundamental or second harmonic frequencies (F₁/F₀ ratio = 0.13, F₂/F₀ ratio = 0.04).

Figure 2. The spatiotemporal tuning for a simple cell (A) and complex cell (B) to a moving grating at high contrast (left) and low contrast (right).

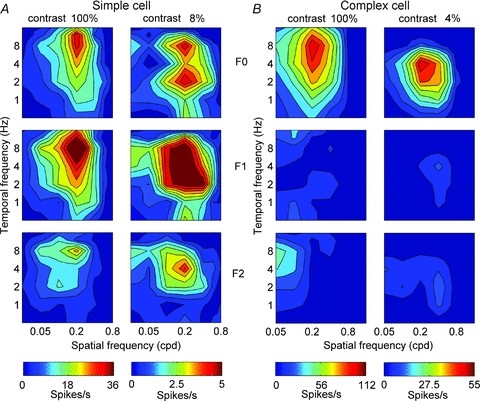
The mean amplitude F₀ is shown in the top panels, the amplitude of the response at the input temporal frequency of the grating (F₁) is plotted in the middle panels and the amplitude of the response at twice the input temporal frequency (F₂) is plotted in the bottom panels. Note that for both the simple and complex cells the relative amplitudes of the F₀, F₁ and F₂ components are similar at high and low contrasts. There is a tendency for cells to be tuned to lower temporal frequencies at low contrasts (see Fig. 3).

The peak amplitude of the F₀, F₁ and F₂ components for many cells shifted to lower temporal frequencies as contrast was reduced. Figure 3A plots, for each cell in our population, the fitted optimum temporal frequency at low contrast (TF_low) against the optimum temporal frequency at high contrast (TF_100%). For complex cells (crosses, n = 77) the optimum values were defined as those producing the peak F₀ component amplitude, while for simple cells (triangles, n = 16) the optimum values were defined as those producing the peak F₁ component amplitude. Most cells fall below the line of equality of the two metrics, demonstrating that optimum temporal frequency tuning shifts to lower values as contrast is reduced. The downward shift in optimum temporal frequency tuning is significant for complex cells (paired t test, P < 4 × 10⁻⁸, n = 77) and simple cells (paired t test, P < 0.01, n = 16). Figure 3B plots, for each cell, the fitted optimum spatial frequency at low contrast (SF_low) against the optimum spatial frequency at high contrast (SF_100%). Although for many cells there is a difference between the two metrics, there is no consistent shift towards either higher or lower spatial frequency tuning (paired t test; complex cells, n = 77, P > 0.28; simple cells, n = 16, P > 0.29). These data emphasizes the importance of using spatial and temporal frequencies that are optimized at each contrast for determining the peak F₁/F₀ ratios. Using the same spatial and temporal frequencies at different contrasts is not appropriate when the peak tuning frequencies change.

Figure 3. Scatter plots of the population data.

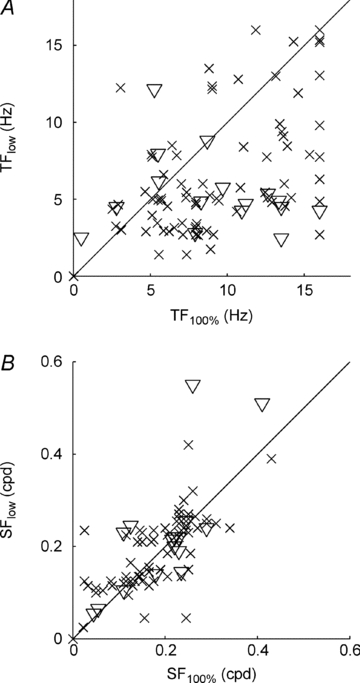
A, the optimum temporal frequency at low contrast (TF_low) plotted against the optimum temporal frequency at high contrast (TF_100%). B, the optimum spatial frequency at low contrast (SF_low) plotted against the optimum spatial frequency at high contrast (SF_100%). In each case, triangles denote simple cells (n = 16) and crosses denote complex cells (n = 77), as defined at high contrast.

Contrast-dependent F₁/F₀ ratios

Figure 4A shows the distribution of F₁/F₀ ratios, measured at low and high contrasts, for all 93 cells in this study. There were 16 classically defined simple cells at high contrast (indicated by triangles in Fig. 4). Eight had similar or higher F₁/F₀ ratios when tested at low contrast and eight showed a reduction in F₁/F₀ ratio. This pattern is similar to that reported by Tolhurst & Dean (1990). Based on six reported cells, they showed that some simple cells show slight increases in F₁/F₀ ratio and some show dramatic reductions in F₁/F₀ ratio at very low contrast. There was no significant shift in F₁/F₀ ratio for our simple cell population when tested at low contrasts (t test, P = 0.33). We recorded from 77 complex cells (indicated by crosses in Fig. 4). This population of complex cells showed a significant shift towards higher F₁/F₀ ratios when tested at low contrasts (t test, P = 0.001).

Figure 4. Scatter plots showing the effect of stimulus contrast on response modulation for each cell.

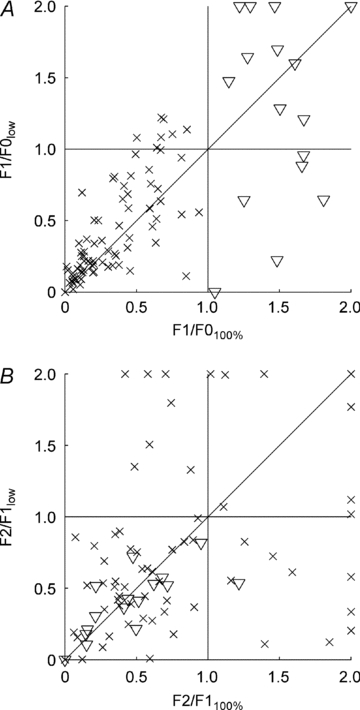
A, the F₁/F₀ ratio when tested at low contrast plotted against the F₁/F₀ ratio when tested at high contrast. Classically defined simple cells (shown as triangles) show no consistent change in their F₁/F₀ ratios at low contrast compared to those at high contrast. Complex cells (shown as crosses) exhibit a significant shift towards higher F₁/F₀ ratios at low contrast compared to those observed at high contrast (t test, P = 0.001). B, the F₂/F₁ ratio when tested at low contrast plotted against the F₂/F₁ ratio when tested at high contrast. Comparing the F₂/F₁ ratios for high and low stimulus contrast, it is evident that classically defined simple cells (triangles) exhibit no consistent change in F₂/F₁ ratio as contrast is reduced (t test, P > 0.05). However, classically defined complex cells (crosses) exhibit a number of interesting effects. Most exhibit similar F₂/F₁ ratios at high and low stimulus contrasts. However, 14 cells exhibit a pronounced increase in their F₂/F₁ ratio when tested at low contrast compared to that observed at high contrast. These cells exhibit responses at low contrast characterized by a small but significant out-of-phase response modulation (an example of which is shown in Fig. 5B).

The size of the F₂ component of cell responses was also investigated (Fig. 4B). For classically defined simple cells there was virtually no change in the ratio between the F₂ and F₁ components when stimulus contrast was reduced (triangles, Fig. 4B). Statistically, the shift was not significant (t test, P > 0.05). While this was also true of the classically defined complex cells (crosses, Fig. 4B), closer inspection revealed interesting results. Most complex cells had similar F₂/F₁ ratios at high and low contrast. Several complex cells showed reductions in F₂/F₁ ratios (bottom right corner of Fig. 4B) but, following visual inspection of the responses, this was always due to the very low spiking rates, which reduced both the F₁ and F₂ components to such low levels that Fourier analysis became problematic. Conversely, 14 cells showed distinct increases in F₂/F₁ ratios at low contrasts (top left corner of Fig. 4B). Visual inspections of these response profiles revealed clear and distinct F₁ components, along with smaller response modulations that were out-of-phase with the F₁ component by 180 deg (an example of which is shown in Fig. 5B).

Figure 5. Representative responses of two cells presented with high contrast (100% contrast, left column) and low contrast (16% contrast, right column) moving gratings, together with their F₁/F₀ ratios.

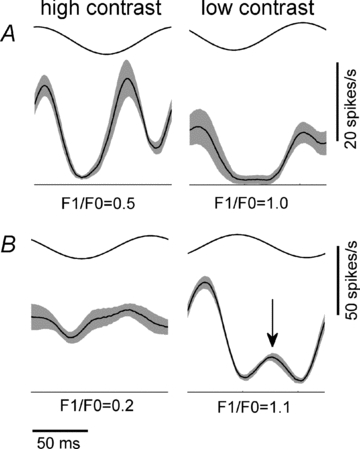
Both cells have low F₁/F₀ ratios (i.e. both cells are complex) when tested at high contrast. The cell in A exhibits a frequency doubled response at high contrast but a classical simple-like oscillatory response at low contrast. The cell in B shows very little modulation in its response at high contrast. However, at low contrast it displays a strong oscillation at the frequency of the input (F₁) together with a small (but significant) out-of-phase response (arrow).

Figure 5 shows mean spiking responses over one cycle of a moving sine wave grating from two representative cells in which the F₁ response modulation increased at low contrasts. Based on the accepted classification system both cells are complex (F₁/F₀ < 1) when tested at high contrast but both cells have simple-like characteristics at low contrast (i.e. F₁/F₀ ratio > 1). At high contrast, the first cell shows a clear response modulation at twice the input frequency (left column, Fig. 5A), while at low contrast the modulation occurs at the same frequency as the input (right column, Fig. 5A). Only two cells from the 77 complex cells tested showed this clear trend, i.e. a response waveform indicative of a single linear simple cell was evident when tested at low contrast. The cell in Fig. 5B demonstrates the more common finding. It shows relatively little modulation when tested at high contrast (F₁/F₀ ratio = 0.2). However, at low contrast the cell exhibits clearly modulated responses (F₁/F₀ ratio = 1.1). While the F₁ modulation is dominant at low contrast, there is a small but highly reliable out-of-phase modulation (right column, Fig. 5B, arrow). As suggested by the existence of an increased F₂ response component in several cells at low contrast (Fig. 4B), we were able to identify a small out-of-phase modulation in 14 complex cells when tested at low contrasts.

Figure 6 shows complete spatiotemporal response profiles for a cell that increases its F₁/F₀ ratio at low contrasts. For this cell the F₀ component is dominant at high contrast, but there are F₁ and F₂ components (F₁/F₀ ratio = 0.79). At low contrast the F₁ component is relatively larger in amplitude than the F₀ component (F₁/F₀ = 1.1). The F₂ component also increases in relative amplitude when tested at low contrast. In this cell the spatiotemporal tuning at high and low contrasts was similar for all the Fourier components however, as noted in Fig. 3 this was not always the case.

Figure 6. Spatiotemporal tuning, as inFig. 2, for a single cell presented with high contrast (100% contrast, left column) and low contrast (16% contrast, right column) moving gratings.

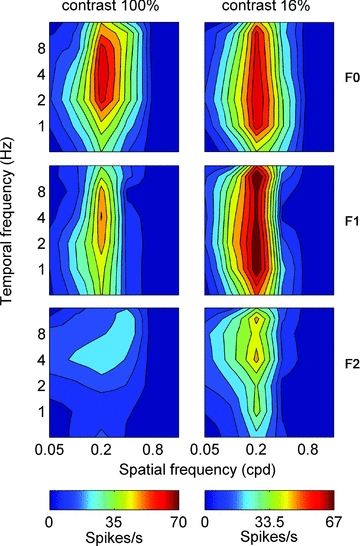
At high contrast the cell exhibits classical complex cell behaviour: large F₀ response component and smaller F₁ and F₂ components. Conversely, at low contrast the cell exhibits a relatively small F₀ response component together with very large F₁ and F₂ components.

Modelling receptive field properties

We have shown that there is a significant shift in the complex cell population towards higher F₁/F₀ ratios when tested at low contrasts. In some cases the complex cell responses to low contrast moving gratings become so phasic that they can be re-classified from complex to simple cells (Fig. 4). To simulate the effects we observe we have developed three models of complex cells based on those presented in Fig. 1B and C. Before we describe these models we first describe a model of a classical simple cell (illustrated in Fig. 7A and B) which forms the basis of our complex cell models. In brief, the model simple cell has ON and OFF zones in its receptive field such that stimulation with a moving grating of optimal orientation and spatial frequency produces an oscillating membrane potential (V_m). The spiking response of the cell is derived from a linear filter with a gain (V₁) that is sigmoidally dependent on contrast. The output of the linear filter (V_m) is converted to a firing rate (FR) via half-wave rectification and an instantaneous non-linearity in the form of a power function ( )² (Fig. 7A). Although the gain of this model simple cell decreases with reduced contrast the relatively large F₁ component is maintained (Fig. 7B).

Figure 7. Modelling the effects of contrast on a simple cell.

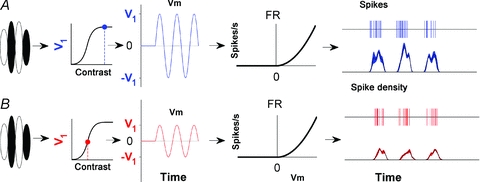
A and B show a classical model simple cell and its response to high and low contrast moving gratings (shown in blue and red respectively). In both panels the output of the linear filter that defines the cell's receptive field produces a sinusoidal oscillation in the membrane potential in response to a sinusoidal grating. The amplitude of this sinusoid (V₁) is a sigmoidal function of contrast. The membrane potential is rectified and transformed into an instantaneous firing rate via a power-law non-linearity. The form of the power function is illustrated by the graphs that plot the firing rate (FR) in spikes s⁻¹ against the membrane potential (V_m). Spikes are produced through a random Poisson process where the rate depends on the output from the non-linear stage. The phasic nature of the response of this cell is maintained at low contrasts even though the gain is decreased.

We now present three candidate models for complex cells. The first is shown in Fig. 8A. This model is similar in form to the classical simple cell model just described. However, V_m contains not only a sinusoidal oscillation with amplitude V₁ but also contains an offset with amplitude V₀. This offset provides the constant component of the cell's response making it complex (Fig. 8A, shown in blue). While both V₀ and V₁ are sigmoidally dependent on contrast, V₀ has a contrast response function that is shifted to the right. Consequently, as shown in red (Fig. 8A), at lower contrast the value of V₀ will be reduced relative to V₁ and the cell becomes simple.

Figure 8. Three candidate models of complex cell responses to moving gratings.

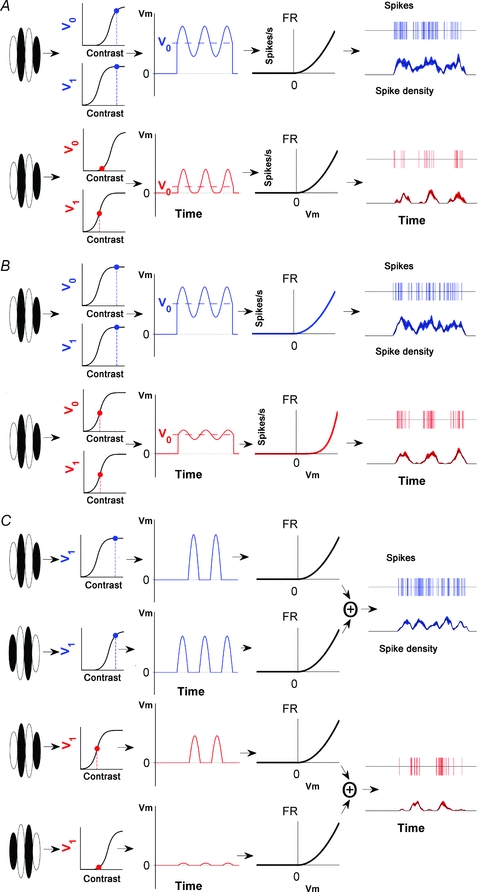
In all cases, responses are complex-like at high contrast (shown in blue) and simple-like at low contrast (shown in red). A, a model based on the same basic structure as the simple cell in Fig. 7 but where there is an offset in the membrane potential response (V₀). Like V₁, V₀ is sigmoidally dependent on contrast but this relationship is shifted to the right compared to that for V₁. As contrast is reduced, V₀ is reduced compared to V₁ leading to a relative increase in the amplitude of the phasic component of the spiking response (F₁) compared with its mean (F₀). B, similar to the model in A, this model has V₀ and V₁ components with matching contrast response functions but there is a change in the power function, p, at low stimulus contrasts such that the oscillatory component of the membrane potential is emphasized. This is the source of the phasic modulation seen in the spiking output of this model at low contrast (shown in red). C, a hierarchical model formed from the combination of two simple cells with offset contrast response functions. At high contrast, the outputs from the two simple cells are summed to produce the instantaneous firing rate shown in blue. At low contrasts one of the simple cell inputs exhibits reduced gain and the combined response becomes more phasic (shown in red).

In the second model the power function (( )^p), which, along with half-wave rectification, transforms the membrane potential to a firing rate, is dependent on stimulus contrast. This is a modification of the model by Mechler & Ringach (2002). They suggested that different cells in cortex have different power functions. Further to this, we suggest that the power function for a given cell could change depending on the contrast of the stimulus. This model produces spiking outputs at high contrasts that resemble complex cells (p = 2), while at low contrast the output exhibits a clearly dominant F₁ component (p = 5). The models in Fig. 8A and B can adequately explain the data in Fig. 5A in which responses at low contrast resemble those of a simple cell. However, these models cannot explain the finding that some cells exhibit small responses that are out-of-phase with the dominant oscillatory response (e.g. Fig. 5B).

The conspicuous out-of-phase responses, as seen in Fig. 5B, are suggestive of input from multiple subunits. Such a model, based on the hierarchical model of complex cell processing first proposed by Hubel and Wiesel, is illustrated in Fig. 8C. The outputs of two simple cells with complementary receptive fields are combined, producing a spiking output in response to a moving grating that is clearly complex-like. In our model, the contrast sensitivities of the two simple cells are different. One cell is less responsive at low contrast because it has a contrast response function that is shifted to the right relative to the other simple cell. When stimulated at low contrast, the combined responses of the two simple cells are dominated by just one of the simple cells. The consequence of this differential response gain is that the response to the low contrast stimulus has a large F₁ component but also exhibits a smaller out-of-phase response as seen in Fig. 5B. In Fig. 5B the F₂/F₀ ratio for the low contrast response was 1.3. The conspicuous F₂ component is not expected from a linear simple cell, which would be predicted to have a much lower F₂/F₀ ratio of 0.66. This latter observation suggests input from more than one simple cell.

Discussion

Tolhurst & Dean (1990) showed that the F₁/F₀ ratios of simple cells remained well above unity at all contrasts, usually showing little contrast dependence. In some cases F₁/F₀ ratios increased at very low contrasts (<5%). In other cells where response modulations relative to spontaneous rates were low, F₁/F₀ ratios were reduced at low contrasts. The latter effect can be explained by saturation phenomena associated with the relatively high spontaneous rates. These results are generally similar to those reported in the present paper. The essential finding reported here is that unlike simple cells, complex cells show a significant trend towards higher modulation amplitudes (F₁/F₀ ratios) at low contrasts with some cells exhibiting F₁/F₀ ratios that actually rise above unity (indicative of simple cells). Here we consider five possible mechanisms by which the change in receptive field properties with contrast come about in complex cells.

First, it is plausible that some of the responses reflect the convergence of X and Y cells from the dLGN (Bullier & Henry, 1979; Stone et al. 1979; Martin & Whitteridge, 1984). X cells have linear receptive fields, such that stimulation with a drifting sine wave gratings leads to responses that oscillate at the same frequency as the input (the F₁ response) (Enroth-Cugell & Robson, 1966; Victor et al. 1977; Victor, 1987). Conversely, Y cells respond in a non-linear fashion, full-wave rectifying their input such that a given input frequency produces a response oscillation at twice that frequency (an F₂ response). The addition of a frequency doubling input, as might come from a Y cell, could account for the small out-of-phase response (leading to a larger F₂ component) seen in some complex cells at low contrasts (e.g. Fig. 5B). The addition of Y cell inputs has been discussed previously as the mechanism underlying complex cell responses (Movshon et al. 1978b; Ferster & Jagadeesh, 1991). Both X and Y cells appear to provide input to the primary visual cortex of the cat (areas 17 and 18), although far fewer X cells project to area 18 (Stone & Dreher, 1973). All cells in the present study were anatomically located in area 17, where it has been suggested that complex cells are most likely driven by X cells from the lateral geniculate nucleus, or from X cells via simple cells (Movshon et al. 1978b). For the F₂ components to arise from Y cell inputs, and to appear only at low contrasts, suggests that the Y cells are more sensitive than most X cells at low contrasts. In fact, at low contrasts the F₁ components of the cortical responses were very large, suggesting that any contrast-dependent change in the relative contribution from X and Y subunits is minimal. The contrast sensitivities of X and Y cells are in fact similar (Enroth-Cugell & Robson, 1966), so it is unlikely that X cells would selectively drop out at low contrasts. While we cannot completely discount the idea that Y cells are contributing to the out-of-phase responses we observed in complex cells, it is unlikely to explain the majority of the data.

The second possible mechanism underlying the shift towards higher F₁/F₀ ratios at low contrasts attributes differences in spatiotemporal response profiles to different levels of phase-invariant recurrent amplification. It has been suggested that both simple and complex cells share the same basic cortical circuitry, but have low and high levels of phase-invariant recurrent amplification, respectively (Chance et al. 1999; Tao et al. 2004). It is plausible that a contrast-dependent change in the level of recurrent amplification could account for the changes in spatiotemporal response profiles which we observe in some cells. Specifically, this would require a reduction in the level of recurrent amplification at low stimulus contrasts. However, Nauhaus et al. (2009) suggest recurrent connectivity is larger at lower contrasts, a result consistent with other data that suggests spatial summation also increases at lower contrasts (although this need not be entirely a cortical phenomenon, see Nolt et al. 2004). It is therefore unlikely that the recurrent model can explain the behaviour of those complex cells that shift their F₁/F₀ ratios to higher values at low contrasts because the increased recurrent connectivity at low contrast would be expected to lead to more, not less, phase averaging.

The third possible mechanism underlying the observed complex cell responses was proposed here (illustrated in Fig. 8B) and is a modification of the theory proposed by Mechler & Ringach (2002). Here, a reduction in contrast changes the spike threshold and associated non-linearity (the power law) which transforms the membrane potential into the observed spiking output. Our results reveal that two complex cells (from 77) fit well with this model: at low contrast we were able to isolate a perfect simple-like receptive field as the core feature of the cells behaviour, even though they were classed as complex cells when tested at high contrast (e.g. Fig. 5A). This experimental finding was rare, suggesting that the explanation, while valid, is not common in cortex. Using intracellular recordings Priebe et al. (2004) showed that all complex cells have V₁/V₀ ratios <1. This ratio is the intracellular equivalent of the F₁/F₀ ratio, with V₁ representing the amplitude of the membrane potential oscillation at the fundamental frequency, while V₀ is the mean change in membrane potential during stimulation. This important observation shows that all complex cells have relatively low oscillatory responses in their membrane potential prior to conversion into spike trains. In stark contrast, most simple cells have large V₁/V₀ ratios (65% are > 0.6). It therefore seems likely that a degree of phase averaging has occurred in most complex cells prior to the generation of spikes. This is inconsistent with the model shown in Fig. 8B. Moreover, this model cannot account for the out-of-phase responses observed in some complex cells at low contrasts, suggesting that this model is unlikely to be in operation in a high proportion of cells. Furthermore, Finn et al. (2007) showed that it is not the power function that changes with contrast in simple cells of cat cortex, but rather the scale factor of the transformation from membrane potential to spikes. A change in scale factor will not produce the change in F₁/F₀ ratios that we observe.

A fourth mechanism that could underlie the increase in F₁/F₀ ratio with decreasing contrast is based on the increase in the V₁/V₀ ratio with contrast. This model is consistent with the measurements of V₀ and V₁ in contrast adapted simple cells (Carandini & Ferster, 1997) although it is not clear the extent to which these results can be extended to complex cells. Furthermore, the cells recorded from here are not given an adapting contrast between tests and are therefore unlikely to be in an adapted state. Although the responses predicted by this model are consistent with some cells, like the third mechanism described above, it fails to account for the significant out-of-phase response seen at low contrasts in some of our complex cells.

The fifth mechanism we consider is based on the hierarchical model first proposed by Hubel & Wiesel (1962) (Fig. 8C). It is proposed that simple cells receive input from dLGN neurons and converge onto complex cells. This theory suggests that simple cells should reside only in thalamo-recipient areas. Work using intracellular recording and anatomical reconstruction suggests that this may indeed be the case, with cells that have clearly distinct ON and OFF zones in their receptive fields, being found exclusively in the thalamo-recipient layers of cortex (layer 4 and upper-layer 6) (Martinez et al. 2005). Simple cells defined using their F₁/F₀ ratios are also over-represented in thalamo-recipient areas (Crowder et al. 2007). Physiological data in support of the hierarchical scheme comes from the combination of white noise stimulation and subsequent spike-triggered covariance analysis, which has revealed that cortical cell receptive fields are made up of multiple linear subunits (Rust et al. 2005). However, the subunits that make up a given complex cell's receptive field have not been easy to isolate. Most of the cells that shifted their F₁/F₀ ratios to higher values at low contrasts exhibited at least two phase-shifted response components when presented with moving gratings at low contrasts (e.g. Fig. 5B). This finding strongly suggests that the receptive fields of these neurons are made up of converged inputs from multiple spatially offset simple-like subunits. However, conventional formulations of the hierarchical model cannot account for the observed contrast-dependent change in spatiotemporal response profiles. We have therefore suggested a modification to the basic hierarchical model, whereby receptive field subunits (i.e. simple cells) are afforded different contrast sensitivities. For example, the gain of one subunit might be reduced at low contrast, as would occur if it had a contrast response function that was shifted to the right relative to the other subunit (as depicted in Fig. 8C). At high stimulus contrasts, both subunits contribute similarly to the cells spiking output, resulting in complex-like response profiles. However, at low stimulus contrasts, the cell receives greatly reduced input from one subunit resulting in simple-like response profiles reflecting the neural activity of its remaining simple cell input.

We have shown that complex cells exhibit a significant increase in their level of response modulation as stimulus contrast is reduced. Highly modulated responses to periodic stimuli such as the moving gratings employed here are a defining characteristic of simple cells. In effect, as stimulus contrast is reduced, complex cells become simple. Moreover, we have shown that at low stimulus contrasts some complex cells exhibit pronounced out-of-phase response components not evident at higher stimulus contrasts. This is a key observation since only a hierarchical model such as we describe can adequately account for such out-of-phase responses. Our results therefore argue strongly for a hierarchical mechanism underlying the response properties of these complex cells. However, it is also evident that not all complex cells require such a hierarchical model to explain their properties. Together, these observations suggest a degree of diversity in mechanisms underlying complex cell responses.

Author contributions

All experiments were performed at the Australian National University. J.P.v.K. conceived and designed the experiments, and collected and analysed the data. S.L.C. helped design experiments and collected and analysed data. M.R.I. conceived the experiments and collected and interpreted data. All authors participated in drafting the manuscript and approved the final version as submitted.