Broker Genes in Human Disease

Abstract

Genes that underlie human disease are important subjects of systems biology research. In the present study, we demonstrate that Mendelian and complex disease genes have distinct and consistent protein–protein interaction (PPI) properties. We show that five different network properties can be reduced to two independent metrics when applied to the human PPI network. These two metrics largely coincide with the degree (number of connections) and the clustering coefficient (the number of connections among the neighbors of a particular protein). We demonstrate that disease genes have simultaneously unusually high degree and unusually low clustering coefficient. Such genes can be described as brokers in that they connect many proteins that would not be connected otherwise. We show that these results are robust to the effect of gene age and inspection bias variation. Notably, genes identified in genome-wide association study (GWAS) have network patterns that are almost indistinguishable from the network patterns of nondisease genes and significantly different from the network patterns of complex disease genes identified through non-GWAS means. This suggests either that GWAS focused on a distinct set of diseases associated with an unusual set of genes or that mapping of GWAS-identified single nucleotide polymorphisms onto the causally affected neighboring genes is error prone.

Introduction

Protein interaction data are commonly drawn as networks with nodes representing proteins and edges representing the detected protein interactions. Individual proteins (or nodes) can then be characterized with a variety of topological measures, such as degree, betweenness centrality, and clustering coefficient. These measures turn out to relate to functional properties of genes such as, for example, the closer the two proteins are located to each other in protein–protein networks the more similar they are in functional annotations (Sharan et al. 2007). Network properties also appear to be somewhat predictive of protein function with, for instance, highly connected and globally centered genes in protein networks tending to be physiologically more “important” and less dispensable (Jeong et al. 2001; Hahn and Kern 2005; Wuchty and Almaas 2005).

Network properties of genes underlying human inherited diseases have been investigated (Goh et al. 2007; Feldman et al. 2008; Jiang et al. 2008). Although different studies focused on substantially different disease gene sets, they reached some similar conclusions. Specifically, they found that disease genes encode non-hub proteins and tend to have an intermediate levels of degree in the protein–protein interaction (PPI) networks (Goh et al. 2007; Feldman et al. 2008). This allowed network properties of disease genes to be used for the purpose of disease gene prioritization (e.g., Kohler et al. 2008; Wu et al. 2008).

The current understanding of network properties of disease genes is limited for a number of reasons. The first problem is that the widely used network property measures are strongly correlated with each other, which makes it difficult to relate different studies using different measures to each other. The second problem is that many studies pooled Mendelian and complex disease genes, as well as complex disease genes detected in pedigree- or candidate gene–based studies with those detected in genome-wide association studies (GWASs). Third, previous studies have not taken into account the fact that Mendelian disease genes tend to be evolutionarily old and complex disease genes tend to be of an intermediate age (Domazet-Loso and Tautz 2008; Cai et al. 2009). Given that several network properties are correlated with gene age, such as, for example, older genes tending to have more protein–protein connections, we think this feature of disease genes must be considered. Finally, it is possible that disease genes have been better studied than other genes and thus might have artifactually high numbers of discovered PPIs.

In the present study, we use high-quality data sets of human disease genes in conjunction with a comprehensive human PPI network and a validated measure of evolutionary age to investigate the relationships among five network topology metrics. We define two principal components (PCs) that capture most of the network properties and address several key questions concerning disease genes, including: 1) Are disease genes exceptionally well connected and globally centered in the protein network? 2) Can we identify characteristic network properties that distinguish disease from nondisease genes? 3) Are properties of disease genes more homogeneous than those of randomly sampled genes? and 4) To what extent do genes identified in GWAS exhibit network properties similar to those of other disease genes?

Materials and Methods

Integrated PPI Network

We obtained the integrated human PPI network (between 10,299 human proteins) from Bossi and Lehner (2009). The network contains 80,922 interactions compiled from a total of 21 different human PPI databases (see table 1 of Bossi and Lehner 2009 for details). All interactions included are supported by at least one piece of direct experimental evidence demonstrating physical interaction between two human proteins (Bossi and Lehner 2009). Several network metrics we computed (see below) require a connected graph; therefore, we extracted the largest connected component (including 10,042 genes and 80,543 connections), and all data analyses were conducted with this connected component (supplementary fig. S1, Supplementary Material online).

Table 1.

Mean and Variance of Network Measures of Genes

The network measures include degree centrality (k), betweenness centrality (Btw), current information flow (Cif), bridging centrality (Bdg), and clustering coefficient (Clu). All measures, except of Clu, were log10-transformed before computation of mean and variance (inside parentheses). Student's t-tests were conducted to compare the mean between disease and nondisease genes (significance levels: ^nsnot significant; ^*P < 1 × 10⁻³; ^**P < 1 × 10⁻⁵; ^***P < 1 × 10⁻¹⁰). F-tests were conducted to compare the variance between disease and nondisease genes (significance levels: ^nsnot significant; ^#P < 1 × 10⁻⁵; ^##P < 1 × 10⁻¹⁰). Note that Mann–Whitney U test and Levene's test, which are less sensitive to nonnormal distributions, were also used to test equality of means and variances, respectively; similar results were produced (data not shown).

Network Centrality and Topological Measures

The interaction network was represented as an undirected graph with proteins as nodes and interactions as undirected edges. We considered five measures to capture the distinct features of network centrality and topology of each node:

1. Degree centrality (k) of a given node is simply the number of links that a node has with other nodes in the network (Nieminen 1974; Dorogovtsev and Mendes 2003).

2. Betweenness centrality (C^Btw) is the fraction of shortest paths passing through node i:

   

   where g_jk(i) is the number of shortest paths from j to k through i and g_jk is the total number of shortest paths between j and k. C^Btw measures the global importance of a protein in communicating between pairs of proteins from the viewpoint of shortest paths (Freeman 1977).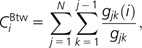

3. Current information flow (C^Cif) is computed using a method modeling a PPI network as an electrical circuit, where interactions are modeled as resistors and proteins as interconnecting junctions (Missiuro et al. 2009). Computation of C^Cif takes into account the relative contribution of all possible paths. Proteins central to the transmission of biological information throughout the network have higher C^Cif. It has been shown that C^Cif provides more consistent results than C^Btw when noisy data is added to a PPI network (Missiuro et al. 2009).

4. Bridging centrality (C^Bdg) measures the extent to which a node or an edge is located between well-connected regions (Hwang et al. 2006). It is defined as

   

   where $C_i^{Btw}$is the betweenness centrality of node i, and BC_i is the bridging coefficient that assesses the local bridging characteristics in the neighborhood of node i, which is defined as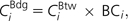

   

   where d(i) is the degree of node i and N(i) is the set of neighbors of node i. C^Bdg can help to identify bridging nodes, that is, nodes with high information flow that are located between highly connected modules.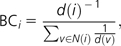
5. Clustering coefficient (C^Clu) is defined as

   

   where n denotes the number of direct links connecting the K_i nearest neighbors of node i. C^Clu ranges from zero (for a node that is part of a loosely connected group) to one (for a node at the center of a fully connected cluster). C^Clu measures the degree of interconnectivity in the neighborhood of a node (Watts and Strogatz 1998).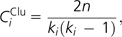

A Matlab toolbox called SBEToolbox (Systems Biology and Evolution Toolbox, http://www.bioinformatics.org/sbetoolbox/) was developed to calculate all these network metrics.

Human Disease Genes

First, we obtained 952 Mendelian disease genes from the nonredundant version of the Mendelian Inheritance in Man (OMIM) called hOMIM (Blekhman et al. 2008), which is hand-curated and free of complex phenotypic entries. We mapped about 68% (647) of them onto the network. Second, we retrieved 1,656 complex disease genes from genetic association database (GAD) (Becker et al. 2004). We excluded genes that are also Mendelian disease genes from the GAD gene set. We mapped 67% (1,110) of them onto the network. Third, we obtained GWAS genes (i.e., genes reported in GWA studies) from the online catalog of published genome-wide association studies (http://www.genome.gov/gwastudies; Hindorff et al. 2009). As of date of access (18 October 2009), the catalog contained 1,293 GWAS genes associated with 269 distinct traits reported in 419 publications. We removed 592 GWAS genes associated with nondisease traits (such as, height, weight, skin pigmentation, and “select biomarker”). We mapped 59% (412) of the remaining 701 genes onto the network. Finally, we used the comprehensive collection of 21,528 human protein-coding genes from the Ensembl build 50 (Flicek et al. 2008) as a representative set of all well-characterized human genes. Genes that do not appear in any of the three disease gene sets are regarded as nondisease genes.

Evolutionary Age of Genes

Domazet-Loso and Tautz (2008) studied the evolutionary origin of human protein-coding genes using a well-supported phylogeny of 19 species that were carefully chosen based on the availability of complete annotated genomes, the reliability of phylogenetic relationships, and the importance of evolutionary transitions (supplementary fig. S2, Supplementary Material online). The internodes at different phylogenetic levels form a phylostratigraphic scheme of metazoan evolution (Domazet-Loso et al. 2007). To place all human genes into these phylostrata, they used Blast analysis with an E value cutoff of 0.001 to compare human proteins against the National Center for Biotechnology Information nonredundant database. They then mapped human genes according to the evolutionary origin of their founder genes on the phylogeny.

Adopting the Dollo parsimony principle (i.e., assuming that genes can be lost but cannot reevolve independently in different lineages [Le Quesne 1974; Farris 1977] or be horizontally transferred), we used the phylostratum of each gene to approximate its evolutionary age (reversing the order of the various phylostrata to obtain an estimate of the gene age). Genes at the highest phylostratum (19) were assigned into the youngest age group 1, the lowest phylostratum 1 were assigned into the oldest age group 19, and so on and so forth. To increase statistical power, we further pooled the genes in the 19 age groups into six combined age classes: Mammalia/Primates, Chordata/Vertebrate, Eumetazoa/Deuterostomia, Metazoan, Eukaryota, and cellular organisms (see supplementary fig. S2, Supplementary Material online for the pooling schema and the numbers of genes in six age groups after combination). The nonsynonymous substitution rate (d_N) and synonymous substitution rate (d_S) for human–Macaque orthologs were downloaded from BioMart (http://www.biomart.org).

Results

We used an integrated network data set that contains nearly half of all human proteins (Bossi and Lehner 2009). The Mendelian and complex disease genes were retrieved from hOMIM (Blekhman et al. 2008) and GAD (Becker et al. 2004), respectively. These two types of disease genes were investigated separately because they show distinct properties in many respects (Blekhman et al. 2008; Cai et al. 2009). In addition, we obtained genes identified in GWAS of human disease (Hindorff et al. 2009). In total, 647 hOMIM, 1,110 GAD, and 412 GWAS genes can be mapped on the PPI network (Materials and Methods). However, the three sets are not mutually exclusive. For instance, 331 genes are shared between hOMIM and GAD, whereas 109 genes are shared between GAD and GWAS (supplementary fig. S3, Supplementary Material online). In order to study each type of disease genes independently, we removed hOMIM genes from GAD gene set and removed both hOMIM and GAD genes from GWAS gene set. No genes were removed from hOMIM as all of them were manually curated and are free of associations with complex phenotypes (Blekhman et al. 2008). The results reported in this paper were based on data analysis with three nonoverlapping sets of 647 Mendelian disease genes, 779 complex disease genes, and 287 GWAS genes.

Characteristic Network Properties of Mendelian and Complex Disease Genes

We calculated degree (k), betweenness centrality (C^Btw), current information flow (C^Cif), bridging centrality (C^Bdg), and clustering coefficient (C^Clu) for each applicable protein in the complete interaction network (Materials and Methods). Table 1 provides the results of comparisons of the mean and variance of these metrics between disease genes and nondisease genes. Average degree (k) of Mendelian disease genes is not different from that of nondisease genes, and of complex disease genes is only marginally significantly higher than that of nondisease genes. This result suggests that Mendelian and complex disease genes are not hub genes, which is consistent with results of previous studies (Goh et al. 2007; Feldman et al. 2008). Mendelian and complex disease genes have significantly higher C^Btw and C^Cif, suggesting that these disease genes tend to occupy network positions that are of global importance in communications between protein pairs. At the same time, they have significantly lower C^Clu suggesting that the number of connections among the neighboring proteins of disease genes is unusually low. Interestingly, the variance of k, C^Bdg, and C^Clu of Mendelian and complex disease genes is also unusually small, suggesting consistency in network properties of disease genes. Finally, GWAS genes do not show any statistically significant differences from nondisease genes. Note that this might be partially due to the small sample size of GWAS genes. We will return to this question later in the paper.

It seems that Mendelian and complex disease genes (but not GWAS genes) have distinct and consistent network properties; however, this is difficult to interpret for three reasons. First, the network metrics are strongly correlated with each other (table 2) and thus it is not entirely clear which network properties tend to be truly distinct for disease genes. Second, evolutionary ages of Mendelian and complex disease genes differ from those of nondisease genes (Domazet-Loso and Tautz 2008; Cai et al. 2009) and genes of different ages tend to have different network properties (see below). Thus, disease genes might have distinct network properties simply due to their different age. Finally, it is possible that disease genes have been studied more thoroughly compared with other genes and thus might have a disproportionately high number of detected PPIs. Below we 1) reduce the dimensionality of the network metrics using principal component analysis (PCA), 2) show that the network properties of disease genes are distinct over and above what is expected of genes of their age, and 3) provide evidence that the inspection bias cannot account for the observed results.

Table 2.

Correlation Coefficients between Variables: Degree (k), Betweenness Centrality (Btw), Current Information flow (Cif), Bridging Centrality (Bdg), Clustering Coefficient (Clu), Nonsynonymous Substitution Rate (d_N), Synonymous Substitution Rate (d_S), the Nonsynonymous-to-Synonymous Substitution Ratio (d_N/d_S), and Evolutionary age (age)

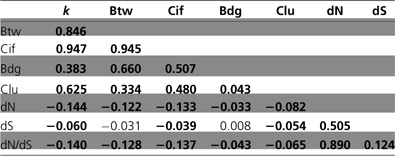Significant coefficients (P < 0.001, Spearman correlation test) are indicated in bold.

Defining Two Key PCs for Network Properties of Disease Genes

To understand the relationships among the five network measures, we conducted PCA. All variables that show deviation from normality (i.e., all except C^Clu) were log transformed and then scaled to zero mean and unit variance. The result of PCA shows that the first two PCs explain 73.4% of the total variation (40.7% and 32.7% for the first and second PC, respectively).

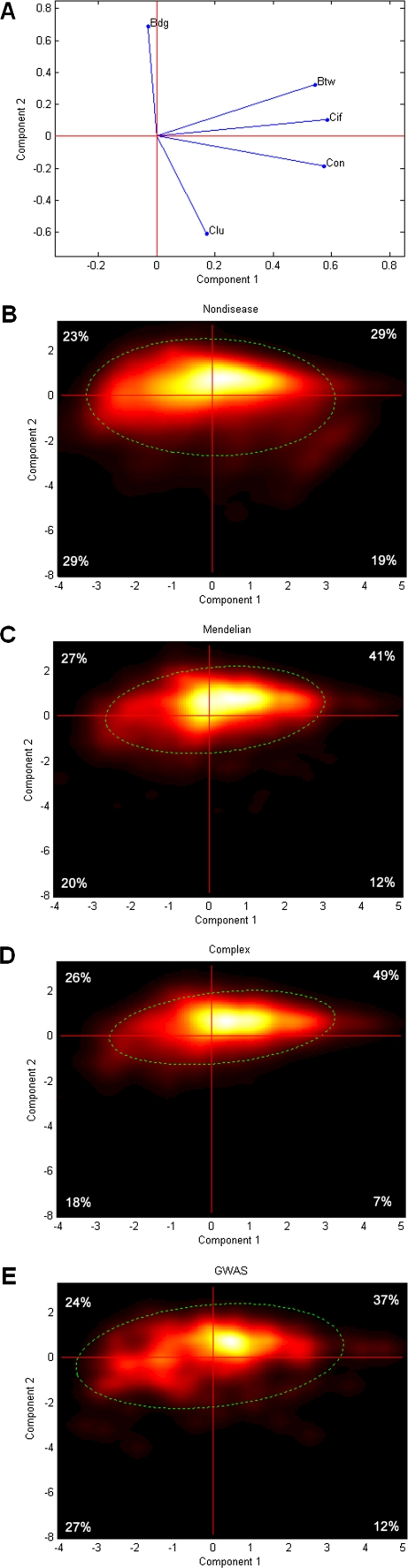
The magnitude and sign of each variable's contribution to the first two PCs are shown in a PC biplot (fig. 1A). Each variable is represented by a line from the origin to a point with coordinates (c1, c2). The coordinates c1 and c2 are the correlations between the variable and the first and second axis, respectively. Longer lines indicate stronger correlations between a PC (biplot axis and everything related to that) and the corresponding variable. The first PC (PC 1) correlates most strongly with three variables, k, C^Btw, and C^Cif; the second PC (PC 2) correlates strongly with the other two variables, C^Bdg and C^Clu.

FIG. 1.—

PCA of network properties of human genes. (A) Biplot showing five variables (represented by arrows): degree (k), betweenness centrality (Btw), current information flow (Cif), bridging centrality (Bdg), and clustering coefficient (Clu). (B,C,D,E) Heat maps show density and distribution of nondisease, Mendelian, complex, and GWAS genes, on the PC space. Numbers at the four corners of each heat map is the percentages of genes located inside the corresponding quadrants. The dished line indicates 90% confidence ellipse for the probability that the corresponding genes will fall within the area.

PCA was conducted with all (disease and nondisease) genes. Nondisease and disease genes were highlighted separately in heat maps to show their density and distribution in the PC 1–2 space (fig. 1B,C,D,E). Compared with nondisease genes, Mendelian, and complex disease genes occupy a much narrower region. Distributions of Mendelian and complex disease genes are more biased (41%, 27%, 20%, and 12% in I–IV quadrants for Mendelian disease genes, fig. 1C; 49%, 26%, 18%, and 7% for complex disease genes, fig. 1D) than nondisease genes, which are more evenly distributed in the four quadrants (29%, 23%, 29%, and 19%, fig. 1B). The centers of distributions are shifted toward the first quadrant with proportionally more Mendelian and complex disease genes having positive PC 1 and PC 2 (G-test, P < 0.001 for the comparison of Mendelian and complex disease genes with nondisease genes). Note that complex disease genes have a more biased distribution toward the first quadrant than the Mendelian genes (G-test, P < 0.001). Because PC 1 correlates strongly and positively with degree (k) and PC 2 correlates strongly and negatively with clustering (C^Clu), the above results can be stated differently: Mendelian or complex disease genes tend to be highly connected (high k) to genes that are themselves are not very well connected (low clustering C^Clu). This property can be thought of as “brokering” value of a protein such that a protein with a high brokering value connects many other proteins that would not be connected otherwise. For an example of the connection patterns for two broker genes (SUMO4 and PRKCZ) and two examples of nonbroker genes with similar values of k (PCBP1 and BMS1), see supplementary fig. S4 (Supplementary Material online).

Distribution of GWAS genes in the four quadrants is less biased (37%, 24%, 27%, and 12%, fig. 1E) than that of other disease genes and is only marginally enriched in the direction of the first quadrant (P = 0.016) compared with nondisease genes. Their distribution is also not different from that of Mendelian genes (P = 0.32), however, it is significantly different from that of complex disease genes (P < 0.01). This indicates that the different network propertied of GWAS genes compared with complex disease genes is not merely a result of the small number of GWAS genes and lack of power.

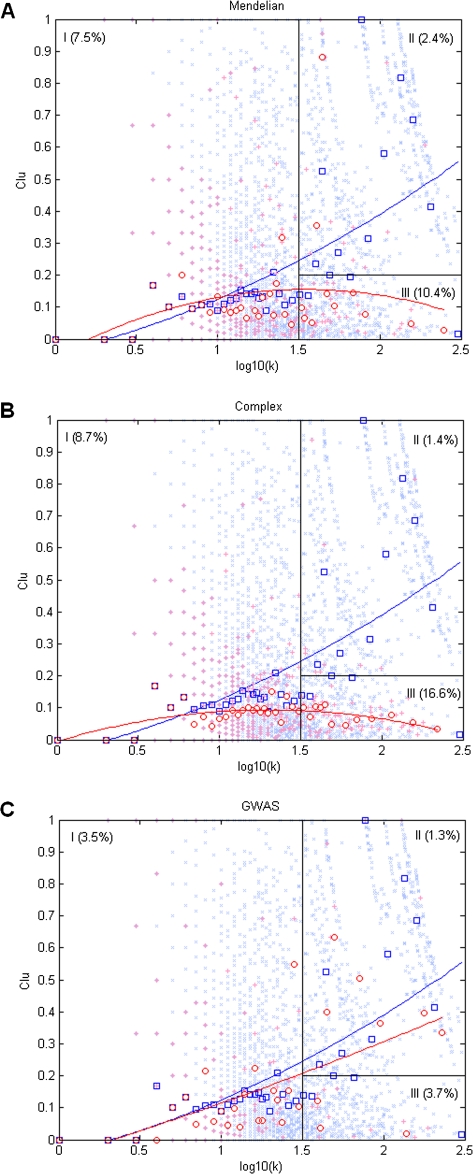
We further placed disease and nondisease genes on the scatter plot of k and C^Clu (fig. 2). It is clear that most of the highly connected Mendelian (fig. 2A) and complex (fig. 2B) disease genes (with log10(k) ≥ 1.5) have a low C^Clu (≤0.2), which is not the case for the nondisease genes with similar values of k. GWAS genes do not show this distinct feature (fig. 2C). We split the scatter plot area ad hoc (based on visual inspection) into three regions defined by log10(k) = 1.5 (or k = 31) and C^Clu = 0.2 (fig. 2). Region I contains genes with relatively low k, whereas regions II and III contain genes with high k. The difference between regions II and III is that region III contains genes with lower C^Clu. Region III represents a characteristic “high brokering value” zone, in which both Mendelian and complex disease genes are present much more often. For instance, only 2.4% and 1.3% of all genes in region II are Mendelian and complex genes, while this number goes up to 10.4% and 16.6% in region III, respectively (P < 0.001 for all comparisons, G-test). Again the pattern is much less pronounced albeit marginally significant for GWAS genes (III [3.7%] vs. II [1.3%], P = 0.008, G-test).

FIG. 2.—

Characteristic changes of clustering coefficient (Clu) as a function of degree (k) for disease genes. Red crosses are data points of disease genes, (A) Mendelian, (B) complex, and (C) GWAS. Red circles are means of Clu for data points in the bins with unequal widths (so that each bin contains same number of disease genes). Blue crosses and blue squares are for nondisease genes for comparison. The solid line shows the quadratic fit of a linear model with first-order and second-order predictors of log10(k). The red and blue lines are for disease and nondisease genes, respectively. Rectangles represent three empirically defined regions (I, II, and III). Percentages of genes that are disease genes in each region are given in parentheses. The results of χ² tests for the percentage of region III against those of regions I and II are III versus II, P = 7.4 × 10⁻⁹ and III versus I, P = 0.02 for Mendelian disease genes; III versus II, P = 0 and III versus I, P = 8.9 × 10⁻⁹ for complex disease genes; III versus II, P = 0.008 and III versus I, P = 0.8 for GWAS genes.

Network Properties as a Function of Gene Age

To investigate whether genes of different ages tend to have different network properties and whether this can explain differences in network properties of disease genes, we grouped all genes into different age groups. Gene age was estimated based on the concept of phylostrata (Domazet-Loso and Tautz 2008), assuming Dollo parsimony (Le Quesne 1974; Farris 1977). Six age groups were defined (labeled 1–6, where group 1 includes the youngest genes and group 6 the oldest genes) and each protein was assigned to one of these age groups (Materials and Methods). Disease and nondisease genes are not distributed equally in different age groups. Mendelian disease genes are overrepresented in the old group, whereas complex disease genes are overrepresented in the middle age groups (Domazet-Loso and Tautz 2008; Cai et al. 2009).

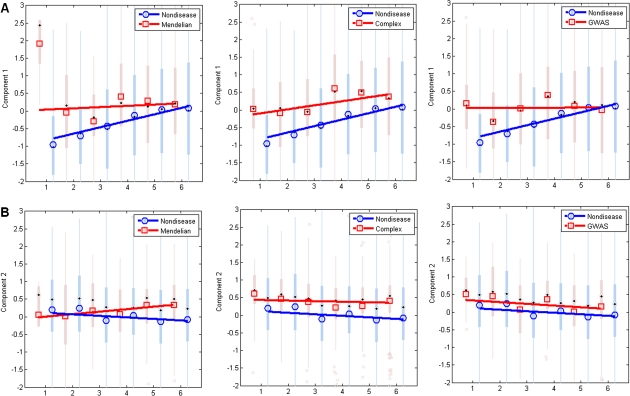
Figure 3 illustrates the changes of PCs as a function of the evolutionary age of the gene. For nondisease genes, average PC 1 increases monotonically with gene age (Spearman's ρ = 0.104, P = 4.44 × 10⁻¹⁶), indicating that older nondisease genes have higher levels of k, C^Btw, and C^Cif. This is not unexpected because proteins of older genes had more time to acquire interactions with other proteins. In contrast, Mendelian and GWAS genes show no correlation between PC 1 and evolutionary age (both P > 0.001). For complex disease genes, the correlation is positive and marginally significant (Spearman's ρ = 0.113, P = 5.61 × 10⁻⁴, table 3; fig. 3A). All disease genes have relatively high level of PC 1 compared with nondisease genes of the same age (fig. 3A). PC 2 shows no correlation with gene age for all the genes (table 3, fig. 3B). We also show the changes of individual network metrics as a function of gene age in the supplementary Information (supplementary fig. S5–S7, Supplementary Material online).

FIG. 3.—

PCs as a function of gene age. (A) PC 1, nondisease versus disease genes; (B) PC 2, nondisease versus disease genes. Types of disease genes include Mendelian, complex, and GWAS genes, at left, middle, and right panels, respectively. Box plots of PCs for nondisease genes (shaded blue) and disease genes (shaded red) are superimposed by average PCs for nondisease genes (blue circles) and disease genes (red squares). Regression lines are depicted for nondisease genes (blue) and disease genes (red).

Table 3.

Correlations between Evolutionary Age of Genes (age) and Variable x: the First PC (PC 1), Degree (k), Betweenness Centrality (Btw), Current Information Flow (Cif), the Second PC (PC 2), Bridging Centrality (Bdg), and Clustering Coefficient (Clu)

Significant coefficients (P < 0.001, Spearman correlation test) are indicated in bold.

The lack of correlation between PC 1 and gene age is one of the characteristic patterns for all three types of disease genes. Given that the numbers of disease genes (especially those in the young age groups) are small, it is possible that the lack of correlation between PC 1 and gene age in disease genes is a product of the small sample size. To rule out this possibility, we randomly sampled nondisease genes in each age bin such that the number of genes in the sampled subset was equal to the number of Mendelian, complex, or GWAS genes in the corresponding age bin, respectively. We repeated this subsampling process to create 10,000 replicates of nondisease gene sets and computed the Spearman's correlation coefficients between PC 1 and the age of the gene for these subsets. The observed correlation coefficients obtained for disease genes falls at the very end of the lower tail of the resampled ρ distribution (empirical P < 0.0001, 6.67 × 10⁻⁴, and 3.33 × 10⁻⁴ for Mendelian, complex, and GWAS genes, respectively). Thus, the lack of correlation between PC 1 and gene age cannot be attributed to the small sample size of disease gene sets.

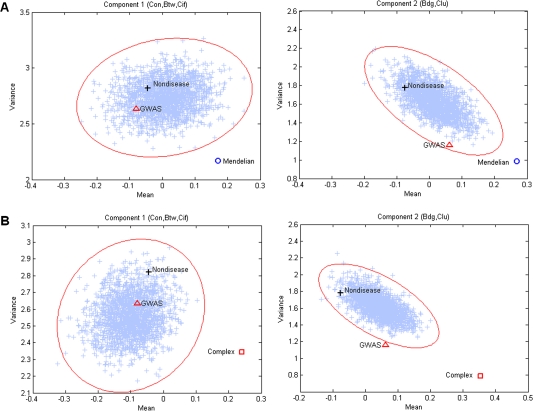
Because Mendelian and complex disease genes have distinct age distributions (Domazet-Loso and Tautz 2008; Cai et al. 2009, supplementary fig. S8, Supplementary Material online), it is possible that their distinct network properties are simply a function of their age. To rule out this possibility, we randomly sampled a subset of nondisease genes to the same size and age distribution of corresponding diseases genes (fig. 4). The procedure allowed us to control for different size and age distribution of gene groups. Figure 4A,B shows the results derived from using Mendelian and complex disease genes as subsampling targets, respectively. Means and variances of PC 1 and PC 2 for subsampled gene subsets are shown as scatter crosses. The subsampling procedure was repeated 10,000 times to get the 99.9% confidence ellipses. Observed data points for nondisease genes are within the confidence ellipses. The variance of PC 1 for Mendelian disease genes is lower, and the mean of PC 1 for complex disease genes is higher than expected by chance. Mendelian and complex disease genes have significantly higher mean and lower variance of PC 2. As expected based on the above results, the GWAS genes do not deviate significantly from the subsampled nondisease genes (fig. 4). Note that the GWAS genes have the same age distribution as the nondisease genes (supplementary fig. S4, Supplementary Material online) and thus figure 4 shows comparison of the GWAS genes with nondisease genes without any subsampling.

FIG. 4.—

Variance and mean of PCs of disease genes. The open circle and square indicate observed data points of variance against mean of the two PCs for Mendelian and complex disease genes, respectively. The crosses are data points of mean and variance for 10,000 randomly sampled subsets of nondisease genes, with the same size and age distribution as (A) Mendelian and (B) complex disease genes. The contour denotes the 99.9% confidence ellipse.

Impact of the Inspection Bias

Last, we address the problem of inspection bias—the impact of more intense investigation of known, especially disease genes on the number of detected PPIs. The inspection bias alone should not dramatically affect the signals we have detected because Mendelian and complex disease genes do not have a higher average degree than nondisease genes (table 1), which is opposite to the expectation of inspection bias. Nevertheless, we conducted additional tests to control for other less obvious potential effects of this bias.

First, we applied a simple assay to show that disease genes have indeed been studied more intensively than other genes. We separated human genes into named and unnamed genes according to whether they have HGNC-(HUGO Gene Nomenclature Committee)-approved names. Genes under intensive experimental studies tend to have unique and meaningful names; genes that have undergone fewer studies may not have such names. In our gene set, there are 447 unnamed genes, including 419 nondisease genes, 6 Mendelian disease genes, 19 complex disease genes, and 3 GWAS genes (supplementary table S1, Supplementary Material online). Proportionally disease genes are more likely to be named than nondisease genes (P < 0.0003 for all three types of disease genes, G-test).

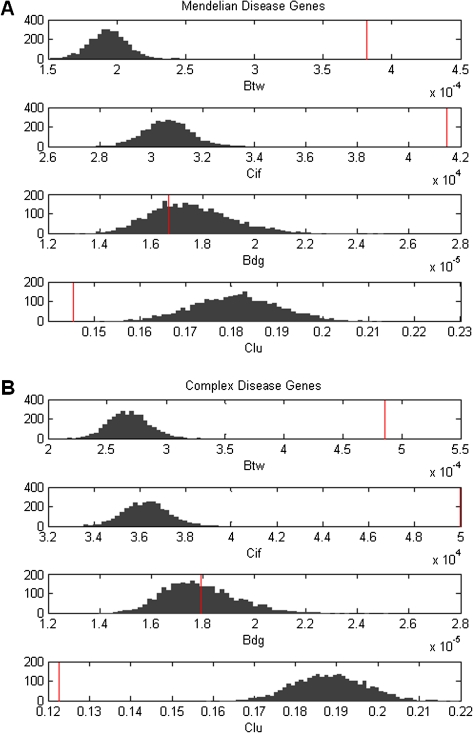
We then filtered out all unnamed genes and repeated data analysis with only named genes. In this way, we decreased the impact of inspection bias due to nondisease genes being disproportionately poorly studied. We found that all results in above sections hold without any qualitative changes (data not shown). Second, we randomly sampled nondisease genes to generate multiple gene sets with the same number of genes and the same distribution of k as that in the corresponding disease gene set. For each type of disease genes, we constructed 10,000 such replicates and obtained the distribution of C^Btw, C^Cif, C^Bdg, and C^Clu. We found that, except for C^Bdg, the three other network measures for Mendelian and complex disease genes fall far away from the center of distribution of the measures, with significantly higher C^Btw and C^Cif and significantly lower C^Clu (fig. 5). Thus controlling for k does not affect the detection of characteristic network properties of disease genes. This confirms that genes with the same level of k still differ in other aspects depending on whether they are disease genes or not.

FIG. 5.—

Distributions of network metrics for subsampled nondisease genes. Network metrics include betweenness centrality (Btw), current information flow (Cif), bridging centrality (Bdg), and clustering coefficient (Clu). Values of network metrics for (A) Mendelian and (B) complex disease genes are shown as vertical red bars. For each distribution, 10,000 replicates of nondisease genes with same number and degree of genes as disease genes were constructed.

Discussion

Given the functional importance of PPI networks, network properties of genes underlying human diseases might reveal important clues about the origin and etiology of disease. It is not surprising that these properties have been a subject of many studies (Goh et al. 2007; Feldman et al. 2008; Jiang et al. 2008). Here, we have tried to improve upon these studies in a number of ways. First, we used well-curated nonredundant disease gene sets separated into three categories: Mendelian disease genes, complex disease genes discovered in pedigree studies, and genes discovered through GWAS. Second, we considered correlations among various network metrics and reduced them to two independent PCs using PCA. Third, we incorporated into our analysis the evolutionary age of genes, which has not been controlled for by the studies of network properties of disease genes and rarely in the studies of protein–protein networks in general (with some notable exceptions, e.g., Kunin et al. 2004; Wuchty and Almaas 2005; Kim et al. 2007). PPI networks are not static in evolution. Rather they change constantly through the rewiring of interactions as well as through the gain and loss of genes. Older genes are likely to differ in the number and type of PPIs and we know that disease genes do have biased age distributions (Domazet-Loso and Tautz 2008; Cai et al. 2009). We therefore believe that incorporating information about the evolutionary age of each gene into the network analysis is essential for revealing characteristic network properties of genes. Finally, we tested whether our results could be explained by the artifact of the inspection bias: the increase in the number of PPIs produced through more careful studies of well-known genes.

We demonstrated that five network metrics (degree, betweenness centrality, information flow, bridging centrality, and clustering coefficient) can be mapped onto two PCs without losing much ability to explain the overall variation in the data. The first PC correlates strongly with degree, betweenness centrality, and current information flow, whereas the second PC correlates strongly and positively with bridging centrality and strongly and negatively with the clustering coefficient. We discovered that Mendelian and complex disease genes have unusually high values of both PC 1 and PC 2. In other words, disease genes tend to be highly connected (large values of PC 1 and thus degree) but often they are connected to genes that are not connected well among themselves (high values of PC 2 and thus low values of clustering). In this way, disease genes appear to serve as “brokers.” Just as human brokers connect strangers who otherwise would not know each other, broker proteins connect “stranger” proteins that do not interact with each other. It is possible that in this way, disease genes find themselves in particularly fragile positions in PPI networks and this is why their disruption leads to identifiable disease phenotypes.

The network properties of Mendelian and complex disease genes appear both distinct and remarkably consistent. Indeed, the value of degree for disease genes does not only have an elevated mean value but it also has very low variance. Similarly, both the mean and the variance of clustering coefficient for disease genes are significantly reduced compared with those of nondisease genes. This consistency can be seen also in that the network properties of disease genes do not vary with age. This is in contrast to nondisease genes that become connected to more genes with age (i.e., PC 1 and degree correlate strongly and positively with gene age). Importantly, we also showed that the distinct age distributions of disease genes could not account for the observed network properties. Note that the strong positive correlation between gene age and degree for nondisease genes emphasizes the importance of studying PPI networks as evolving entities.

It is important to consider the possibility that disease genes show distinct network properties because they are better studied. We tested this possibility in several ways. First, we did find some evidence for the inspection bias in that the disease genes were more often named than nondisease genes and that the named genes had a higher degree. The reason for the observation that named genes have a higher degree is not clear given that it is both possible that known genes are indeed better studied and thus have an artificially high degree or that more highly connected genes are mutable to more obvious phenotypes and thus become detected in genetic studies more often and then named. Importantly, our study is not affected by this possible bias because we can show that the observed patterns are still detectable when we focus exclusively on only named genes in both disease and nondisease sets. In addition, when we subsampled nondisease genes to the same level of degree as the disease genes, disease genes still showed significantly lower clustering coefficients compared with nondisease genes.

We found that genes that have been detected in GWAS studies of disease but have not been previously identified as disease genes (Mendelian or complex disease) deviate very slightly from nondisease genes in their network properties in the direction of other disease genes. The weakness of this signal is intriguing. First and foremost this might be due to the small sample size of GWAS genes. This can explain some but not all the weakness of the signal because GWAS genes do have significantly weaker signal than complex disease genes. If the weakness of the signal is not a mere question of statistical power one can think of a number of reasons for this pattern. First, it is possible that GWAS genes relate to a distinct set of diseases that show distinct etiology and that the genes that underlie these diseases behave in a distinct manner. Second, it is possible that GWAS genes are related to more polygenic diseases on average. However, this second possibility does not seem very likely as the complex disease genes show the most strikingly different network patterns that are even stronger than those of Mendelian genes. The third possibility is that the identification of genes associated with specific GWAS-identified SNPs has some error. This does seem likely especially given that regulatory regions in the human genome are often located many tens or even hundreds of base pairs away from the coding regions they affect (Wellcome Trust Case Control Consortium 2007; Eeles et al. 2008; Loos et al. 2008; Zeggini et al. 2008) and it is not the most straightforward task to predict which gene(s) are associated with an identified intergenic polymorphism. In the future, disease prioritization studies such as this could help us predict which genes located in the neighborhood of GWAS-associated SNPs are directly and causally associated with the studied diseases.

Taken together, we demonstrate that Mendelian and complex disease genes have distinct and consistent properties in the PPI network. Disease genes occupy topologically critical positions of the network as brokers that interact with many neighboring proteins that are less connected themselves. It will be important to study whether such broker genes indeed specify particularly fragile points in the network. Finally, our results provide new insights for developing powerful and discriminating approaches for prioritizing and identifying causal genes related to human disease.

Supplementary Material

Supplementary figs. S1–S8 and table S1 are available at Genome Biology and Evolution online (http://www.oxfordjournals.org/our_journals/gbe/).