Selective-diffusion regularization for enhancement of microcalcifications in digital breast tomosynthesis reconstruction

Abstract

Purpose: Digital breast tomosynthesis (DBT) has been shown to improve mass detection. Detection of microcalcifications is more challenging because of the large breast volume to be searched for subtle signals. The simultaneous algebraic reconstruction technique (SART) was found to provide good image quality for DBT, but the image noise is amplified with an increasing number of iterations. In this study, the authors developed a selective-diffusion (SD) method for noise regularization with SART to improve the contrast-to-noise ratio (CNR) of microcalcifications in the DBT slices for human or machine detection.

Methods: The SD method regularizes SART reconstruction during updating with each projection view. Potential microcalcifications are differentiated from the noisy background by estimating the local gradient information. Different degrees of regularization are applied to the signal or noise classes, such that the microcalcifications will be enhanced while the noise is suppressed. The new SD method was compared to several current methods, including the quadratic Laplacian (QL) method, the total variation (TV) method, and the nonconvex total p-variation (TpV) method for noise regularization with SART. A GE GEN2 prototype DBT system with a stationary digital detector was used for the acquisition of DBT scans at 21 angles in 3° increments over a ±30° range. The reconstruction image quality without regularization and that with the different regularization methods were compared using the DBT scans of an American College of Radiology phantom and a human subject. The CNR and the full width at half maximum (FWHM) of the line profiles of microcalcifications within the in-focus DBT slices were used as image quality measures.

Results: For the comparison of large microcalcifications in the DBT data of the subject, the SD method resulted in comparable CNR to the nonconvex TpV method. Both of them performed better than the other two methods. For subtle microcalcifications, the SD method was superior to other methods in terms of CNR. In both the subject and phantom DBT data, for large microcalcifications, the FWHM of the SD method was comparable to that without regularization, which was wider than that of the TV type methods. For subtle microcalcifications, the SD method had comparable FWHM values to the TV type methods. All three regularization methods were superior to the QL method in terms of FWHM.

Conclusions: The SART regularized by the selective-diffusion method enhanced the CNR and preserved the sharpness of microcalcifications. In comparison with three existing regularization methods, the selective-diffusion regularization was superior to the other methods for subtle microcalcifications.

INTRODUCTION

Digital breast tomosynthesis (DBT) is an emerging imaging modality that can provide quasi-three-dimensional (3D) structural information of the breast. Low-dose x-ray projections of the breast are acquired at a small number of angles over a limited angular range.^{1, 2} The total radiation dose of a DBT scan can be set to be comparable to that of a single mammogram. A set of tomosynthesized slices is reconstructed from the limited-angle projections. The reconstructed images (slices) provide 3D information of anatomical structures.

DBT reconstruction can be modeled as a limited-angle cone-beam tomographic problem. Most existing reconstruction problems fall into four categories: Back-projection (BP) algorithms,³ transform algorithms,^{4, 5} algebraic reconstruction techniques (ART),^{6, 7} and statistical reconstruction algorithms.⁸ We previously showed that the BP method provided very smooth reconstructed images with low background noise, while the simultaneous algebraic reconstruction technique (SART) and the maximum likelihood method with the convex algorithm (ML-convex) can enhance the contrast and edges of the high-contrast features but simultaneously amplify the image noise.⁶

Tomosynthesis reconstruction is an ill-posed problem. The ill-posedness of the tomosynthesis reconstruction arises from two issues: The incomplete acquisition of projection data and the ill-posedness of the projection operator.⁹ Because of the missing projection data, the tomosynthesis reconstruction is often modeled as solving an underdetermined system of linear equations. For the resultant underdetermined linear system, if there is a solution, there will be infinitely many solutions. On the other hand, because the related projection operator is ill-posed, the reconstruction does not continuously depend on the projection data and thus, a small inevitable measurement noise in the projection data may cause a large perturbation in the reconstructed images.

Because of the low dose used at each angle in DBT imaging, the obtained projection views (PVs) are much noisier than mammograms. The noise in the PVs is propagated to the reconstructed images via the ill-posed linear system. In iterative reconstruction, the image noise is amplified as the number of iterations increases. Image noise will reduce the detectability of abnormalities on the reconstructed images. For example, subtle microcalcifications could become inconspicuous among the amplified noise after several SART iterations.

Regularization may alleviate the ill-posedness problem in tomosynthesis reconstruction. The regularization method chooses a reconstruction with certain regularity to approximate the true data, where the regularity of the data is measured via proper regularization functions that represent the desired geometric features of the data. A number of regularization functions have been employed in tomographic reconstruction in the past three decades. A quadratic regularization function¹⁰ results in low background noise but smooths out important edge information. For the purpose of edge preservation, some nonquadratic regularization functions have been developed.^{11, 12} A systematic comparison between quadratic and nonquadratic methods can be found in the literature.¹³ After it was introduced for image denoising,¹⁴ the total variation (TV) method has been successfully applied to tomographic reconstruction.^{15, 16, 17} The TV method can provide a stable reconstruction that preserves geometric features. Different variations of the TV method have been developed adaptive to different tomography models.^{18, 19}

The regularity of the approximate reconstruction is related to the physical features of the data. For example, the contrast of calcifications and the sharpness of their boundaries are important to the detection of microcalcifications. For this purpose, we need to enhance the contrast of calcifications and to preserve the sharpness of the calcification boundaries. The TV-type method has been proven to be an efficient method to preserve the edges of relatively high-contrast signals in tomosynthesis reconstruction.^{19, 20} Sidky et al.^{19, 20} proposed to incorporate TV-type regularization in the framework of iterative reconstruction for DBT. Each iteration in the iterative algorithm is split into two steps: Reconstruction step to reduce data error and denoising step to constrain image regularity. ART is used for reducing data error and the total p-variation (TpV) method is used for denoising purpose. This framework is natural for balancing between data error and desirable image regularity.

Our laboratory and several other groups^{6, 21, 22} have chosen SART for DBT reconstruction. Our previous study showed that SART can achieve high image quality in DBT with a few iterations.⁶ In the SART method, the linear coefficients are updated at each projection view rather than after all views have been processed. Therefore, we propose to incorporate regularization into the reconstruction formula. In this way, the noise from each PV can be suppressed sequentially and regularization is applied during each linear coefficient update instead of applying regularization after all views have been processed.

The aim of this study is to develop a regularized reconstruction method to improve the contrast-to-noise ratio (CNR) of microcalcifications in the DBT slices for human or machine detection. For DBT reconstruction, subtle microcalcifications that have relatively low contrast can occur anywhere within the breast. Most existing gradient-based regularization methods use local gradient to guide the regularization. Subtle calcifications might be treated as noise and smoothened by a gradient-based regularization method because of their small gradients. In order to enhance the CNR for microcalcification reconstruction, we proposed a selective-diffusion (SD) regularization method, which classifies voxels into signal category and noise category by using local gradient information around the voxels and applies regularization to noise voxels while excluding signal voxels. We compared our SD regularization to the quadratic Laplacian (QL) method and the TpV method used by Sidky et al.¹⁹ for microcalcification reconstruction.

MATERIALS AND METHODS

Breast tomosynthesis system

A GE GEN2 DBT system at the University of Michigan was used to acquire DBT scans of an American College of Radiology (ACR) mammography phantom and the breast of human subjects with biopsy-proven calcifications. Patient imaging was performed with IRB approval and informed consent. The DBT of a subject with a malignant cluster containing microcalcifications of various sizes and contrasts was chosen as an example in this study. The DBT was acquired in CC view and the thickness of the compressed breast was measured by the DBT system as 5.7 cm. The breast density was categorized by an experienced breast radiologist to be heterogeneously dense (BI-RADS 3).

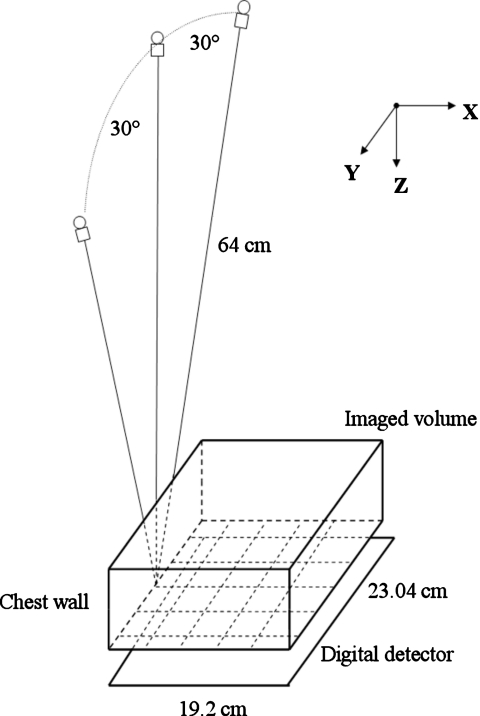
The imaging geometry of this DBT system is illustrated in Fig. 1. The distance from the x-ray focal spot to the center of the rotation is 64 cm and the x-ray source rotation plane is parallel to the chest wall. The system has a CsI phosphor∕a:Si active matrix flat panel digital detector with a matrix size of 1920×2304 pixels and a pixel pitch of 0.1 mm×0.1 mm. The digital detector is stationary during image acquisition. The distance from the breast support plate, where the center of the x-ray source rotation is located, to the detector plane is 2 cm. The system uses a step-and-shoot design and acquires PV images from a total of 21 angles in 3° increments over a ±30° range in less than 8 s. The DBT system uses a Rh-target∕Rh-filter x-ray source for all breast thicknesses. For both the ACR phantom and the breast of the selected subject, the images were acquired with an exposure technique of 29 kV and a total of 95.6 mA s for 21 PVs. The mean glandular dose of the ACR phantom was estimated to be 2.5 mGy. The phantom imaging was repeated six times under the same imaging conditions. The phantom was repositioned and recompressed to a similar force for each repeated scan.

Figure 1.

Geometry of the GE prototype GEN2 digital breast tomosynthesis system used in this study.

In our reconstruction algorithm, the voxel resolutions of the imaged volume in the x- and y-directions were both chosen to be 0.1 mm, the same as the pixel pitch of the detector. The slice spacing in the z-direction was chosen to be 1 mm. In our study, a ray-tracing algorithm similar to the Siddon algorithm is employed for calculating the contribution of each voxel to the forward projection.²³ Logarithmic transformation is applied to the raw pixel intensities of the detected image before reconstruction. The projection model assumes a monoenergetic x-ray source and ignores the effects of scattering and beam hardening, similar to the approach by Wu et al.^{2, 4}

SART

SART was used for DBT reconstruction in this study. SART is an iterative algorithm which provides successive estimates of the physical objects and has fast convergence speed. The linear attenuation coefficient of each voxel is updated after all the rays in one projection view have been processed once. The number of updates in one SART iteration is equal to the number of PVs. SART is applicable to any imaging geometry and adaptive to different physical models. Theoretically, the SART method can be represented as a weighted least square method and it will converge to a weighted least square solution.²⁴ Compared to ART which converges to a least square solution, SART is less noisy for limited-angle tomosynthesis reconstruction. The details of our implementation of the SART method were described in the literature.⁶

Let the image volume be subdivided into J voxels and the linear attenuation coefficient for the jth voxel be denoted by x_j, 1≤j≤J; the digital area detector contains I pixels and the ith ray, 1≤i≤I, is defined as a line from the point x-ray source to the ith detector pixel. Assuming one ray is traced for each pixel, the number of rays is equal to the number of pixels. The path length of the ith ray passing through the jth voxel in the nth projection view is denoted by A_ij,n. The projection model can then be expressed as

$${\mathit{A}}_n\mathit{x}={\mathit{y}}_n,$$ (1)

where A_n is the projection matrix for the nth PV with A_ij,n as its (i,j)th element; y_n is the vector of the PV data. The ith projection value y_i,n is proportional to the logarithmic transform of the ratio of the incident x-ray intensity I_o,n and the transmitted intensity I_i,n of the ith ray

$$y_{i,n}=k\text{\hspace{0.17em}ln}\frac{I_{0,n}}{I_{i,n}},$$

which can be derived from the pixel values of the nth PV, 1≤n≤N, where N is the total number of PVs. The linear system model for breast tomosynthesis reconstruction is summarized as

$$\left[\begin{array}{c}{\mathit{A}}_{\mathbf{2}}\\ ⋮\\ {\mathit{A}}_{\mathit{N}}\end{array}\right]\mathit{x=}\left[\begin{array}{c}{\mathit{y}}_1\\ ⋮\\ {\mathit{y}}_{\mathit{N}}\end{array}\right]\to \mathit{Ax}=\mathit{y}.$$ (2)

For the nth PV, we define the row sums and column sums of the projection matrix A_n as

$${\mathit{A}}_{\mathit{i}+,\mathit{n}}=\sum _{\mathit{j}=1}^{\mathit{J}}{\mathit{A}}_{\mathit{ij},\mathit{n}}\text{and}{\mathit{A}}_{+\mathit{j},\mathit{n}}=\sum _{\mathit{i}=1}^{\mathit{I}}{\mathit{A}}_{\mathit{ij},\mathit{n}}.$$

In each SART iteration, the jth voxel will be updated as follows when the information from the nth PV is used for the updating:

$${\mathit{x}}_{\mathit{j}}^{\left(\mathit{n}\right)}={\mathit{x}}_{\mathit{j}}^{\left(\mathit{n}-1\right)}+\frac{\mathbf{\lambda }}{{\mathit{A}}_{+\mathit{j},\mathit{n}}}\sum _{\mathit{i}=1}^{\mathit{I}}\frac{{\mathit{A}}_{\mathit{ij},\mathit{n}}}{{\mathit{A}}_{\mathit{i}+,\mathit{n}}}\left({\mathit{y}}_{\mathit{i},\mathit{n}}-{\left({\mathit{A}}_{\mathit{n}}{\mathit{x}}^{\left(\mathit{n}-1\right)}\right)}_{\mathit{i}}\right)$$ (3)

for 1≤n≤N and 1≤j≤J, where λ is the relaxation parameter controlling the convergence of SART. For simplicity, the index for the iteration number is not explicitly included in Eq. 3. For a given iteration, x⁽⁰⁾ is the output from the previous iteration or, for the first iteration, a value obtained from an initialization method. Equation 3 can be written in the following form:

$${\mathit{x}}^{\left(\mathit{n}\right)}={\mathit{x}}^{\left(\mathit{n}-1\right)}+\mathbf{\lambda }{\mathit{V}}_{\mathit{n}}{\mathit{A}}_{\mathit{n}}^{\mathit{T}}{\mathit{W}}_{\mathit{n}}\left({\mathit{y}}_{\mathit{n}}-{\mathit{A}}_{\mathit{n}}{\mathit{x}}^{\left(\mathit{n}-1\right)}\right),$$ (4)

where W_n is the diagonal matrix with diagonal entries as 1∕A_i+,n, 1≤i≤I; V_n is the diagonal matrix with diagonal entries as 1∕A_+j,n, 1≤j≤J; and ${\mathit{A}}_{\mathit{n}}^{\mathit{T}}$ is the transpose of the projection matrix A_n. For the linear equation Ax=y, consider the following weighted least square functional defined by:²⁴

$$\frac{1}{2}{\parallel \mathit{y}-\mathit{Ax}\parallel }_{\mathit{W}}^2≔\sum _{\mathit{i}=1}^{\mathit{I}}\frac{1}{{\mathit{A}}_{\mathit{i}+}}{\left({\mathit{y}}_{\mathit{i}}-{\left(\mathit{Ax}\right)}_{\mathit{i}}\right)}^2,\mathit{x}∊{\mathit{R}}^{\mathit{J}},$$

where A_i+ and A,W are similar to the definitions above. It can be proven that the iterated solution of Eq. 4 converges to a weighted least square solution of Ax=y,²⁴ which is equivalent to solving the following optimization problem:

$$\underset{\mathit{x}∊{\mathit{R}}^{\mathit{J}}}{\text{min}}\frac{1}{2}{\parallel \mathit{y}-\mathit{Ax}\parallel }_{\mathit{W}}^2.$$ (5)

Regularization methods

The weighted least square solution of the ill-posed linear system Eq. 2 is not stable and is sensitive to noise. With an increasing number of iterations, the image noise will be amplified significantly. Regularization has been proven to be an efficient method to overcome the difficulty caused by the ill-posedness of the system. In the following, we first introduce the TpV regularization by Sidky et al.^{19, 20} within the context of SART. Then we discuss the relationship between the framework of TpV regularization and diffusion regularization. Based on this relationship, we propose the selective-diffusion regularization method and compare it to some existing regularization methods.

TpV regularization method

Sidky et al.^{17, 19, 20} used ART for iterative reconstruction of DBT. They defined an image regularity penalty, a functional R(x), and proposed a regularization method by solving the following optimization problem:

$${\mathit{x}}^{\ast }=\text{arg}\text{\hspace{0.17em}min}\mathit{R}\left(\mathit{x}\right),$$ (6)

subject to the constraint

$${\left|\mathit{Ax}-\mathit{y}\right|}^2\le {\rho }^2,$$ (7)

where ρ is a constant. A practical image reconstruction algorithm was implemented using the adaptive steepest descent-projection onto convex sets (ASD-POCS) framework.¹⁹

In the context of SART, constraint 7 would be

$$\frac{1}{2}{\parallel \mathit{y}-\mathit{Ax}\parallel }_{\mathit{W}}^2\le {\rho }^2.$$ (8)

If R(x) is in a discrete form, the Euler–Lagrange equation of optimization problem 6 with constraint 8 is

$$\nabla \mathit{R}\left(\mathit{x}\right)+\mu \left({\mathit{A}}^{\mathit{T}}\mathit{W}\left(\mathit{y}-\mathit{Ax}\right)\right)=0,$$ (9)

where ∇ is the gradient operator and μ is the Lagrange multiplier. For simplicity, we use the same symbol to denote a gradient operator in either discrete or continuous formulation. In the discrete formulation, the partial derivatives in the gradient operator are defined as the directional finite difference operators. From Eq. 9 we have a regularized SART algorithm as follows:

$${\mathit{x}}^{\left(\mathit{n}\right)}={\mathit{x}}^{\left(\mathit{n}-1\right)}+\mathbf{\lambda }{\mathit{V}}_{\mathit{n}}\left({\mathit{A}}_{\mathit{n}}^{\mathit{T}}{\mathit{W}}_{\mathit{n}}\left({\mathit{y}}_{\mathit{n}}-{\mathit{A}}_{\mathit{n}}{\mathit{x}}^{\left(\mathit{n}-1\right)}\right)+\mathbf{\omega }\nabla \mathit{R}\left({\mathit{x}}^{\left(\mathit{n}-1\right)}\right)\right),$$

where ω=1∕μ. For each entry of the vector x⁽ⁿ⁾, the value is updated with

$${\mathit{x}}_{\mathit{j}}^{\left(\mathit{n}\right)}={\mathit{x}}_{\mathit{j}}^{\left(\mathit{n}-1\right)}+\frac{\mathbf{\lambda }}{{\mathit{A}}_{+\mathit{j},\mathit{n}}}\left(\sum _{\mathit{i}=1}^{\mathit{I}}\frac{{\mathit{A}}_{\mathit{ij},\mathit{n}}}{{\mathit{A}}_{\mathit{i}+,\mathit{n}}}\left({\mathit{y}}_{\mathit{i},\mathit{n}}-{\left({\mathit{A}}_{\mathit{n}}{\mathit{x}}^{\left(\mathit{n}-1\right)}\right)}_{\mathit{i}}\right)+\mathbf{\omega }{\left(\nabla \mathit{R}\left({\mathit{x}}^{\left(\mathit{n}-1\right)}\right)\right)}_{\mathit{j}}\right),$$ (10)

where ω is the regularization parameter balancing between the data fidelity term and the regularization term.

Sidky et al.^{19, 20} chose the total p-variation norm as the image regularity metric. We denote by x_k,l,m the voxel values on a 3D grid of the image volume. The TpV norm is defined by

$${\parallel \mathit{x}\parallel }_{\mathit{TpV}}=\sum _{\mathit{k},\mathit{l},\mathit{m}}{\mathbf{\Lambda }}_{\mathit{k},\mathit{l},\mathit{m}}^{\mathit{p}},$$ (11)

where

$${\mathbf{\Lambda }}_{\mathit{k},\mathit{l},\mathit{m}}=\sqrt{{\left({\mathit{x}}_{\mathit{k},\mathit{l},\mathit{m}}-{\mathit{x}}_{\mathit{k}-1,\mathit{l},\mathit{m}}\right)}^2+{\left({\mathit{x}}_{\mathit{k},\mathit{l},\mathit{m}}-{\mathit{x}}_{\mathit{k},\mathit{l}-1,\mathit{m}}\right)}^2+{\left({\mathit{x}}_{\mathit{k},\mathit{l},\mathit{m}}-{\mathit{x}}_{\mathit{k},\mathit{l},\mathit{m}-1}\right)}^2+\mathit{s}}.$$

s is a small positive number introduced to make the TpV norm differentiable with respect to the voxel values. The TpV regularization reduces to the TV regularization when p=1 and to the quadratic Laplacian regularization when p=2. An interesting choice of p is 0<p<1. In this case, optimization problem 6 with constraint 8 is a nonconvex problem and experiments showed that edges of signals can be well enhanced if the iteration is stopped properly.

The continuous counterpart of the TpV norm 11 is ∫_Ω|∇x|^p and the optimization problem 6 with TpV regularization can be naturally linked to an unconstrained problem

$$\underset{\mathit{x}}{\text{min}}{\int }_{\mathbf{\Omega }}{\left|\nabla \mathit{x}\right|}^{\mathit{p}}+\frac{\mu }{2}{\parallel \mathit{y}-\mathit{Kx}\parallel }^2,$$ (12)

where Ω is a continuous domain of images and K is the continuous operator related to A. The corresponding Euler–Lagrange equation of problem 12 is

$$\mathit{p}\nabla \cdot \left(\nabla \mathit{x}{\left|\nabla \mathit{x}\right|}^{\mathit{p}-2}\right)+\mu \left({\mathit{K}}^{\ast }\left(\mathit{y}-\mathit{Kx}\right)\right)=0,$$ (13)

where K^* is the adjoint operator of K. Note that the regularization term of Eq. 13p∇⋅(∇x|∇x|^p−2) can be treated as a diffusion function ∇⋅(c(u,v)∇x) with the conduction coefficient function

$$\mathit{c}\left(\mathit{u},\mathit{v}\right)=\mathit{p}{\left|\nabla \mathit{x}\left(\mathit{u},\mathit{v}\right)\right|}^{\mathit{p}-\mathbf{2}},$$

where u is the space variable and v is the time variable. Therefore, the TpV regularization can be related to the diffusion regularization in a general form as

$$\nabla \cdot \left(\mathit{c}\left(\mathit{u},\mathit{v}\right)\nabla \mathit{x}\right)+\mathbf{\mu }\left({\mathit{K}}^{\ast }\left(\mathit{y}-\mathit{Kx}\right)\right)=\mathbf{0}.$$ (14)

In Sec. 2C2, we will discuss how to employ the diffusion regularization for reconstruction in DBT with a goal to enhance microcalcifications.

Selective-diffusion regularization method

Clinical data have various types of signals with different contrast levels. The different geometric features of various types of signals favor different types of diffusion in local area, which are dominated by the conduction coefficient function. Specifically, the diffusion defined in Eq. 14 is guided by the constant p that defines the regularity metric. In DBT, it is important to improve the detectability of microcalcifications. For small, subtle microcalcifications, a regularization method may smooth them out as noise. We are proposing a selective-diffusion regularization that adjusts the regularity metric according to the features of signals.

Motivated by optimization problem 12, we formulate a modified optimization problem as

$$\underset{\mathit{x}}{\text{min}}{\int }_{\mathbf{\Omega }}{\left|\nabla \mathit{x}\right|}^{\mathit{p}\left({\left|\nabla \mathit{x}\right|}^2\right)}+\frac{\mu }{2}{\parallel \mathit{y}-\mathit{Kx}\parallel }^2,$$ (15)

where p is a smooth function of local gradient of images, referred to as the regularity function, in place of the constant p in Eq. 12. In this way, we link the regularity metric to the local gradient measurement of images. The related Euler–Lagrange equation of the above optimization problem is derived as

$$2\nabla \cdot \left({\left|\nabla \mathit{x}\right|}^{\mathit{p}\left({\left|\nabla \mathit{x}\right|}^2\right)}{\mathit{p}}^{\prime }\left({\left|\nabla \mathit{x}\right|}^2\right)\text{ln}\left(\left|\nabla \mathit{x}\right|\right)\nabla \mathit{x}\right)+\nabla \cdot \left(\mathit{p}\left({\left|\nabla \mathit{x}\right|}^2\right){\left|\nabla \mathit{x}\right|}^{\mathit{p}\left({\left|\nabla \mathit{x}\right|}^2\right)}\frac{\nabla \mathit{x}}{{\left|\nabla \mathit{x}\right|}^2}\right)+\mu \left({\mathit{K}}^{\ast }\left(\mathit{y}-\mathit{Kx}\right)\right)=0,$$ (16)

where p^′(t) is the first order derivative of the function p(t) with respect to a variable t. The existence, uniqueness, and long-term behavior of the modified optimization problem 15 when function p(t) ranges in the interval [1,2] have been established.²⁵

Note that the first term in the above formula need higher computation cost in comparison with the other two terms because of the first order derivative involved. To overcome this difficulty, we propose a regularity function as follows:

$$\mathit{p}\left(\mathit{t}\right)=\{\begin{array}{ll}\mathit{a}\hfill & \mathit{t}>\mathbf{\eta }+\mathbf{\epsilon }\hfill \\ \mathit{q}\left(\mathit{t}\right)\hfill & \mathbf{\eta }-\mathbf{\epsilon }\le \mathit{t}\le \mathbf{\eta }+\mathbf{\epsilon }\hfill \\ \mathit{b}\hfill & \mathit{t}<\mathbf{\eta }-\mathbf{\epsilon }\hfill \end{array}\phantom{\}},$$

where η, ε, a, and b are constants and q(t) is a function to make p(t) smooth. When ε is close to zero, p^′ vanishes almost everywhere but at the point η. Eq. 16 can therefore be approximated by

$$\nabla \cdot \left(\mathit{p}\left({\left|\nabla \mathit{x}\right|}^2\right){\left|\nabla \mathit{x}\right|}^{\mathit{p}\left({\left|\nabla \mathit{x}\right|}^2\right)}\frac{\nabla \mathit{x}}{{\left|\nabla \mathit{x}\right|}^2}\right)+\mu \left({\mathit{K}}^{\ast }\left(\mathit{y}-\mathit{Kx}\right)\right)=0.$$ (17)

In the discrete form, if we choose ε=0 and $\delta =\sqrt{\eta }$, when SART is applied, for each voxel of the image vector x⁽ⁿ⁾, the voxel value is updated with an approximate formula

$${\mathit{x}}_{\mathit{j}}^{\left(\mathit{n}\right)}=\{\begin{array}{cc}{\mathit{x}}_{\mathit{j}}^{\left(\mathit{n}-1\right)}+\frac{\mathbf{\lambda }}{{\mathit{A}}_{+\mathit{j},\mathit{n}}}\left(\sum _{\mathit{i}=1}^{\mathit{I}}\frac{{\mathit{A}}_{\mathit{ij},\mathit{n}}}{{\mathit{A}}_{\mathit{i}+,\mathit{n}}}\left({\mathit{y}}_{\mathit{i},\mathit{n}}-{\left({\mathit{A}}_{\mathit{n}}{\mathit{x}}^{\left(\mathit{n}-1\right)}\right)}_{\mathit{i}}\right)+\mathit{a}\mathbf{\omega }{\left(\nabla \cdot \left({\left|\nabla {\mathit{x}}^{\left(\mathit{n}-1\right)}\right|}^{\mathit{a}}\frac{\nabla {\mathit{x}}^{\left(\mathit{n}-1\right)}}{{\left|\nabla {\mathit{x}}^{\left(\mathit{n}-1\right)}\right|}^2}\right)\right)}_{\mathit{j}}\right),& \left|\nabla \mathit{x}\right|\ge \delta \\ {\mathit{x}}_{\mathit{j}}^{\left(\mathit{n}-1\right)}+\frac{\mathbf{\lambda }}{{\mathit{A}}_{+\mathit{j},\mathit{n}}}\left(\sum _{\mathit{i}=1}^{\mathit{I}}\frac{{\mathit{A}}_{\mathit{ij},\mathit{n}}}{{\mathit{A}}_{\mathit{i}+,\mathit{n}}}\left({\mathit{y}}_{\mathit{i},\mathit{n}}-{\left({\mathit{A}}_{\mathit{n}}{\mathit{x}}^{\left(\mathit{n}-1\right)}\right)}_{\mathit{i}}\right)+\mathit{b}\mathbf{\omega }{\left(\nabla \cdot \left({\left|\nabla {\mathit{x}}^{\left(\mathit{n}-1\right)}\right|}^{\mathit{b}}\frac{\nabla {\mathit{x}}^{\left(\mathit{n}-1\right)}}{{\left|\nabla {\mathit{x}}^{\left(\mathit{n}-1\right)}\right|}^2}\right)\right)}_{\mathit{j}}\right),& \left|\nabla \mathit{x}\right|<\delta \end{array}\phantom{\}}.$$ (18)

Here, δ is a threshold to distinguish signals from noise. Equation 18 is the general formulation of our proposed regularization method, referred to as SD regularization, which is designed to selectively treat signal and noise. The parameters a, b, ω, and δ can be chosen to fit specific applications.

Figures of merit

Two image quality measures that characterize the contrast and sharpness of microcalcifications were analyzed to quantitatively compare the image quality of SART reconstruction using different regularization methods.

The gray-level line profile and its full width at half maxi-mum (FWHM) in the focal plane of a calcification were used to measure the in-plane signal sharpness. Two gray-level line profiles across the center of each signal, one in the x-direction (vertical to the chest wall) and the other in the y-direction (parallel to the chest wall), were analyzed. The baseline of each line profile was calculated from the average of the background voxels in the neighborhood of the object of interest and subtracted from the line profile.

A Gaussian function was fitted to the background-corrected linear profile and the FWHM of the line profile was computed as

$$\text{FWHM}\mathit{=}\left(2\sqrt{2\text{\hspace{0.17em}ln}2}\right)\sigma ,$$ (19)

where σ is the standard deviation of the fitted Gaussian function.

The CNR was used to measure the contrast relative to the background noise of the object of interest. The CNR value is defined by

$$\text{CNR}\left(\mathit{z}\right)=\frac{\overline{\mathit{I}}\mathit{c}\left(\mathit{z}\right)-{\overline{\mathit{I}}}_{\text{BG}}\left(\mathit{z}\right)}{{\sigma }_{\text{BG}}\left(\mathit{z}\right)},$$ (20)

where $\overline{\mathit{I}}\mathit{c}\left(\mathit{z}\right)$ is the mean voxel value in a selected region centered on the center of the calcification at a depth z, ${\overline{\mathit{I}}}_{\text{BG}}\left(\mathit{z}\right)$ is the mean voxel value in a region of interest (ROI) in a neighboring background region at the same depth, and σ_BG(z) is the standard deviation of voxel values in the background ROI. The depth z was chosen to be the in-focus plane of the calcification, determined visually as the slice where the calcification appeared to be the sharpest. Once the center location and the background ROI were chosen for a given calcification from the SART reconstructed slices without regularization, their values were fixed and used for the calculation of the CNR and FWHM measures of the calcification for all regularization methods. This would make the comparison of a given signal consistent among the different methods, although the selection of the center and ROI was subjective. For the ACR phantom data, all measurements were obtained by averaging the results from six repeated DBT scans of the same phantom under the same imaging conditions.

Study conditions

DBT images of an ACR phantom and a patient breast were reconstructed with SART using four different regularization methods: (1) The SD regularization method, (2) the nonconvex TpV regularization method (p=0.8), (3) the TV regularization method (TpV method with p=1.0), and (4) the QL regularization method. The TV and TpV methods were implemented following the pseudocode and the parameters described by Sidky et al.¹⁹ The QL method was implemented using Eq. 10 with ∇R(x)= Δx, where Δ is the Laplace operator (a second order differential operator). The SD regularization method was implemented using Eq. 18. Five iterations of SART were employed and the images after each iteration were analyzed to evaluate the dependence of the image quality measures on iterations for each method in comparison with those without regularization (NR).

In Eqs. 10, 18, the relaxation parameter λ was chosen to be 0.5 which was studied and selected from our previous study. For the SD method, the two constants a and b were chosen to be 0 and 2, respectively, for microcalcifications. In this way, no regularization was applied to the category of signals and stronger regularization (quadratic regularization) than TV regularization was applied to the category of noise. The choice of applying no regularization to the category of signals was made to preserve subtle microcalcifications, but it might lead to some noise fluctuations at a small number of isolated voxels due to misidentification of some random noise as signals, which we denote as short noise in the following discussion. To avoid the influence of the short noise, median filtering with a 3×3 kernel was applied to the images at the end of the second iteration. The optimal regularization parameter ω was selected experimentally within a local interval, as shown below. In our implementation of the SD method, signal voxels are assumed to have a gradient greater than the threshold δ=0.01, which was chosen by analyzing the local signal and background noise properties of our previous DBT reconstructions. The threshold was estimated by assuming that the background noise follows a Gaussian distribution and that the threshold of the local signal gradient norm of the signals of interest was greater than three times that of the standard deviation of the background noise.

RESULTS

Phantom calcifications

We analyzed three clusters of simulated microcalcifications from the reconstructed ACR phantom images for the quantitative analysis. The nominal diameters of the aluminum oxide specks are 0.54, 0.32, and 0.24 mm, respectively, which are smaller than the reconstruction slice interval of 1 mm used in this study. One speck was selected from each group with relatively high-contrast microcalcifications (0.54 and 0.32 mm) and two specks from the group with subtle microcalcifications (0.24 mm) (see Fig. 2).

Figure 2.

Regions of interest from a DBT slice of the ACR phantom reconstructed without regularization showing the largest, the third, and the fourth speck groups. The signals 1, 2, 3, and 4, with nominal sizes of 0.54, 0.32, 0.24, and 0.24 mm, respectively, were selected for analysis in this study.

The dependence of the CNR of the microcalcifications in the reconstructed images on the regularization parameter ω of the SD method is shown in Fig. 3 and the “optimal” regularization parameter for the SD regularization was estimated from the results. Figures 3a, 3b show that for the higher contrast signals 1 and 2, the CNR values increased with the increase of the regularization parameter. However, for subtle microcalcifications such as signals 3 and 4, Figs. 3c, 3d show that although the CNR increased with increasing ω for ω below about 0.003, it leveled off and then decreased when ω further increased. Because of the uncertainties in estimating the CNR for subtle signals, the standard deviations of the measurement were large. To preserve subtle microcalcifications in DBT, the regularization parameter for the SD method was selected to be 0.003 for both the phantom and breast reconstructions. This regularization parameter was also used for the QL method for comparison of the selective and nonselective-diffusion regularization methods.

Figure 3.

Dependence of CNR values on regularization parameter for (a) signal 1, (b) signal 2, (c) signal 3, and (d) signal 4 from an ACR phantom. All CNR values were obtained by averaging six repeated measurements and the error bars indicated one standard deviation of the measurements.

The dependence of the CNR values of the signals in phantom DBT on the number of iterations was plotted in Fig. 4. Figures 4a, 4b show that for large microcalcifications (signals 1 and 2), the TV method was superior to other methods. The TV method provided 10%–50% higher CNR than the SD method, whereas the SD method provided up to 50% higher CNR than the TpV method and 10%–100% higher CNR than the QL method and NR. Figures 4c, 4d show that for subtle microcalcifications in the phantom (signals 3 and 4), the SD method provided the highest CNR among the four methods, with about 50%–100% higher CNR than the TpV method and the TV method and 0%–100% higher CNR than the QL method and NR. The difference in the CNR among the different methods depended on the number of iterations.

Figure 4.

Dependence of CNR values on the number of iterations in SART for (a) signal 1, (b) signal 2, (c) signal 3, and (d) signal 4 from an ACR phantom. Four regularization methods, SD, nonconvex TpV, TV, QL, and NR, are compared. All values were obtained by averaging six repeated measurements and the error bars indicated one standard deviation of the measurements.

The FWHM of the selected gray-level line profiles in phantom DBT were plotted in Fig. 5. It can be seen that the trend of FWHM values are consistent between the x- and y-directions. For large microcalcifications (signals 1 and 2), the TV and TpV methods had smaller FWHM values than the other three methods. The SD method was comparable to NR, indicating that the SD method could preserve the shape of signals. The QL method had the largest FWHM value and was mostly blurred. For small microcalcifications (signals 3 and 4), the standard deviations of the measurements were large and the four methods were comparable within the measurement error although the trend that the QL method was more blurred was still apparent.

Figure 5.

Comparison of FWHM values for the four regularization methods and without regularization in the (a) x-direction and the (b) y-direction. FWHM values were measured for the four simulated microcalcifications selected from the ACR phantom. All values were obtained by averaging six repeated measurements and the error bars indicated one standard deviation of the measurements.

Microcalcifications in breast

A CC view DBT of a subject containing a cluster of microcalcifications with a range of sizes was chosen for analysis. In Fig. 6a, the cluster of microcalcifications is shown at a slice reconstructed by SART without regularization 3.1 cm above the breast support plate. Four calcifications of different sizes that had their best focused plane on this slice were selected and numbered as shown. Calcification 1 was large and high contrast. Calcification 2 was slightly larger and higher contrast than calcification 3. Calcification 4 was the smallest and the lowest in contrast. The estimated CNRs of the calcifications at the focal slice reconstructed by SART without regularization and with five iterations are 9.4, 5.9, 5.2, and 3.0, respectively (Fig. 7). The FWHMs averaged over the x- and y-directions of the calcifications are 0.36, 0.33, 0.25, and 0.17 mm, respectively (Fig. 8).

Figure 6.

(a) A cluster of microcalcifications of various sizes from a DBT of a human subject reconstructed without regularization. The in-focus DBT slice for the four selected calcifications is shown. The four selected signals were numbered in approximately decreasing size and contrast. The reconstructed clusters using four regularization methods (b) SD, (c) nonconvex TpV, (d) TV, and (e) QL are compared. All images were displayed with the same window and level settings.

Figure 7.

Dependence of CNR values on the number of iterations in SART for (a) signal 1, (b) signal 2, (c) signal 3, and (d) signal 4 from DBT of a human subject. Four regularization methods and without regularization are compared.

Figure 8.

Comparison of FWHM values for the four regularization methods and without regularization in the (a) x-direction and the (b) y-direction. FWHM values were measured for the four microcalcifications selected from the DBT of a human subject.

A comparison of the CNR values of the selected microcalcifications for the five methods and up to five iterations were plotted in Fig. 7. For large microcalcifications (signals 1 and 2) in Figs. 7a, 7b, respectively, the TpV method and the SD method were comparable. Both methods achieved 10%–40% higher CNR than the TV method for signal 1 and 50%–200% higher CNR than the TV method for signal 2. Both methods were similar to the QL method at the first iteration for signals 1 and 2. For signal 1, both methods reached about 100% higher CNR than the QL method and NR at five iterations. For signal 2, both methods achieved 10%–120% higher CNR than the QL method from two to five iterations and 10%–60% higher CNR than NR from three to five iterations, but lower CNR than NR in the first two iterations. For subtle microcalcifications (signals 3 and 4) shown in Figs. 7c, 7d, respectively, the SD method provided the highest CNR among the four regularization methods, with about 40%–200% higher CNR than the TpV method, 20%–120% higher CNR than the QL method from three to five iterations, and 20%–50% higher CNR than NR from three to five iterations. The CNR of the QL method was consistently lower than that of NR for all signals and iterations studied. The TV method was very ineffective for subtle signals such as calcifications 3 and 4; the CNR was very low and was consistently lower than that of NR and the QL method for all iterations studied.

The in-plane signal sharpness in terms of the FWHM in the x- and y-directions was plotted in Figs. 8a, 8b, respectively. The trend of the FWHM values was reasonably consistent between the x- and y-directions except for the NR measurement for signal 1. For the high-contrast calcification (signal 1), the FWHMs of the SD, TV, and TpV methods were comparable. For signal 2, the FWHMs of the SD and TV methods were similar but that of the TpV method was substantially smaller. For both signals 1 and 2, the blurring by the QL method was very noticeable. For signal 3, the FWHMs of the SD and TV methods were still comparable while the signal sharpening by the TpV method and the blurring by the QL method became less obvious. For signal 4, which had the lowest contrast, the SD method preserved the FWHM of the signal much better than the other three methods which were comparably large.

DISCUSSION

In this study, we proposed a selective-diffusion regularization method and compared it to three existing regularization methods. Preliminary results show that SART with the SD, TV, and TpV methods can reconstruct microcalcifications satisfactorily within a few iterations. SART has no ability to control noise. Without regularization, the noise is amplified with increased number of iterations. All four regularization methods can remove noise efficiently. However, the QL method would blur small features. From the CNR analysis, the QL method failed to increase the CNR values with increasing number of iterations. The other three regularization methods are efficient in enhancing the CNR of microcalcifications. Among these CNR-enhancing regularization methods, the TV method performs best for relatively high-contrast signals in uniform background noise. For complex structured noise, the TV type method could oversmooth the structure and create the staircasing effect.²⁶ For small, subtle signals, the TV method was the worst in terms of CNR for both phantom and real calcifications. At p<1, the TpV method is nonconvex and can enhance even some low-contrast features. However, we observe that the TpV method also enhanced some noise. This is the reason that the TpV method performed worse than the TV method for signals embedded in uniform background noise. Both the SD and the nonconvex TpV method could reduce the staircasing effect from the TV method. For large microcalcifications in the breast, these two methods performed similarly. For the phantom data, the SD method removed the background noise efficiently and enhanced the contrast of signals at the same time. The SD method achieved higher CNR than the TpV method for both obvious and subtle signals.

The main advantage of the SD method is enhancing the CNR of subtle microcalcifications. When the contrast of microcalcifications is too small, both the TV and TpV methods may treat the microcalcifications as noise and smooth them out. By using the estimated local gradient and background noise, the SD method attempts to classify voxels into signal and noise and treats the two classes with different degrees of regularization. In this way, we can preserve or enhance very subtle microcalcifications. Some noise could be preserved because the noise can be classified into the signal class by chance. To overcome this difficulty, we apply median filtering at an early iteration which can remove the short noise efficiently to prevent the short noise from being amplified in subsequent iterations. Further investigation will be conducted to compare the effectiveness of using different methods for the classification of signal and noise in the local region.

From both FWHM analysis and visual comparison, the SD method preserved the shape of the signals relatively well in comparison with that of NR. The TV and TpV methods were more variable such that they showed a trend to sharpen high-contrast large calcifications but to blur small, subtle calcifications.

Equation 18 is the general formulation of the selective-diffusion regularization method. In this preliminary implementation, we chose the two constants a and b to be 0 and 2 that yield relatively simple forms of the regularization terms in Eq. 18. For the class of potential signals, a is set to be 0 so that the regularization term vanishes. For the class of background, b is set to be 2; the regularization term is reduced to a discrete Laplacian filter applied to the image. These choices significantly reduce the computational cost of the regularization terms. Other choices of a and b are eligible for the implementation of the SD method if the computation cost is not a consideration. We will investigate different choices of a and b and fast algorithms related to the regularization strategy in the future.

The order of the PV updating can affect the reconstruction image quality.²⁷ However, it is still unknown whether there exists one order that is superior to the others for all types of signals at different locations of the imaged volume. The current study used the order of PV updating that was designed to reduce the truncated projection artifacts in the reconstruction.²⁸ Since the determination of whether a pixel is signal or noise during SD regularized reconstruction depends on the local gradient, the order of PV updating may be relevant especially at the early stage when the signal gradient has not been strongly localized. The interaction between the order of PV updating with regularized reconstruction will have to be investigated in future studies.

The selective-diffusion regularization depends on the choice of gradient threshold δ. We used a fixed gradient threshold in our current implementation. The gradient threshold is relatively large compared to the image gradient field at the initial stage of the reconstruction so that more noise may be removed when the coarse structures of the volume are reconstructed. With an increase in the number of iterations, the gradients of all structures are increased. However, because of the regularization, the background noise increases only slowly compared to the gradient norm of signals. Therefore, a fixed gradient threshold can differentiate signal and noise effectively even when the noise and signal gradients change with increasing number of iterations. We will investigate adaptive strategies to differentiate signals from background noise such as a normalized gradient threshold or a CNR threshold in future studies.

We incorporate the selective-diffusion regularization into the SART framework. In practice, the ASD-POCS framework can be used for implementing the selective-diffusion regularization method. The computational time of the SD method is about 10% higher than that without regularization in the SART framework. The computational burden of one SART iteration is comparable to the four regularization methods in this study. Most of the computational cost is spent on the calculation of the entries of the forward projection matrix. All four regularization methods can be implemented as parallel computational algorithms.

As demonstrated by the results of our study, the size (e.g., FWHM in the x- and y-directions) and the contrast (e.g., CNR) of individual microcalcifications vary over a wide range, even within a single cluster in one human subject. The relative performance of the regularization methods depends on the characteristics of the microcalcifications. These trends (Figs. 78) were verified with the analysis of real calcifications in additional human subjects (not shown to avoid redundancy). Since there is no ground truth on the size and contrast of a real calcification, it is difficult, if not impossible, to identify a number of individual microcalcifications that have the same contrast and size in order to estimate the statistics (e.g., average trend and variance) of our results. Because of the radiation risk, it is not possible to image a patient multiple times to obtain repeated measurements of the same calcification for statistical analysis. Our phantom experiments and analysis were performed to alleviate this problem. We used a standard ACR phantom and acquired six repeated DBT scans. We analyzed the simulated microcalcifications in the ACR phantom of three different nominal sizes to cover approximately the range of calcifications of interest in human breasts. The mean values and standard deviations of measurements from the same calcification were estimated from the six repeated DBT scans. The reasonably consistent trends between the real and phantom calcifications (subtle versus subtle, obvious versus obvious, etc.) indicate that the statistics from phantom experiments would provide validation of the trends to a certain degree and some estimates of the confidence intervals of the measurements.

CONCLUSION

In this study, we have developed a framework of the diffusion regularization, which can be approximated by a selective-diffusion regularization method for enhancing the CNR of microcalcifications in DBT reconstruction using SART. This method employed the local gradient information to classify voxels into two categories and apply regularization with different degrees of regularity according to the classification. The effect of regularization on signal quality was evaluated quantitatively using the DBT data of an ACR phantom and a patient breast. The results demonstrated that the SART regularized by the selective-diffusion method enhanced the CNR and preserved the sharpness of microcalcifications. In comparison with three existing regularization methods, the selective-diffusion regularization was superior to the other methods for subtle microcalcifications.