Abstract
Cell responses are commonly heterogeneous, even within a subpopulation. Here we investigate the source of heterogeneity in the Ca2+ response of anterior pituitary lactotrophs to a Ca2+ mobilization agonist, thyrotropin-releasing hormone. This response is characterized by a sharp increase of cytosolic Ca2+ concentration, due to mobilization of Ca2+ from intracellular stores, followed by a decrease to an elevated plateau level that results from Ca2+ influx. We focus on heterogeneity of the evoked Ca2+ spike under extracellular Ca2+ free condition. We introduce a method that uses the information provided by a mathematical model to characterize the source of heterogeneity. This method compares scatter plots of features of the Ca2+ response obtained experimentally to those made from the mathematical model. The model scatter plots reflect random variation of parameters over different ranges, and matching experimental and model scatter plots allows us to predict which parameters are most variable. We find that a large degree of variation in Ca2+ efflux is a likely key contributor to the heterogeneity of Ca2+ responses to TRH in lactotrophs. This technique is applicable to any situation in which the heterogeneous biological response is described by a mathematical model.
Keywords: heterogeneity, calcium, lactotroph, mathematical model, sensitivity analysis
Introduction
Heterogeneity is at the core of biological systems. The presence of heterogeneity might be an important feature (1-3), but from the experimental point of view it makes it harder to understand the system. Within an organism there are many different cell types and within each cell type there is considerable variation (4). In addition, there are multiple sources of heterogeneity, such as stochastic gene expression (5), different cellular stages (6) and variation in channel/receptor modulation/expression (7).
Modelling approaches to heterogeneity have traditionally focused on two main goals. One aims to construct models that can reproduce all behaviors observed in the experimental data (8-9), while the other is concerned with understanding how the observed heterogeneity may contribute to the overall performance of a system (10-11). Our approach is to use mathematical modelling to uncover the source of the heterogeneity.
We look at the responses of anterior pituitary lactotrophs to a Ca2+ mobilizing agonist as a case study. It is widely recognized that these cells are very heterogeneous (12-17). Such variability is expressed in terms of electrical activity (18, 19), Ca2+ signaling (17-18, 20-21), hormone secretion (18, 22), and responsiveness to regulatory hormones (18, 23-25). Specifically, we look at the cytosolic Ca2+ response to thyrotropin-releasing hormone (TRH). This neurohormone mobilizes Ca2+ from the endoplasmic reticulum (ER) via activation of the Gq signalling pathway (26). The intracellular Ca2+ response consists of an initial spike and a subsequent plateau phase (26). The spike phase corresponds to rapid Ca2+ mobilization from the ER, causing a transient increase of Ca2+ in the cytosol that is followed by a decay in the cytosolic Ca2+ concentration. The plateau phase is characterized by Ca2+ influx through voltage-dependent and -independent Ca2+ channels (27). To facilitate the analysis, we focus solely on heterogeneity in the spike phase, by applying TRH in the absence of extracellular Ca2+ to remove the plateau. First we show that the spike response is very heterogeneous across the cell population, but the response of each cell is self-consistent during the course of the experiment. We then use a mathematical model of the spike response combined with sensitivity analysis to examine the source of heterogeneity.
One often uses sensitivity analysis to study the robustness of a model to variation in parameter values. That is, a parameter in the model is varied and the effect on the output is monitored. While very useful in the analysis of the model, this type of manipulation is rarely possible in an experimental context. Instead, we use the heterogeneity in the Ca2+ response to TRH to find relationships between the observables of the response, and then compare these relationships to the ones obtained from a population of model cells with different degrees of variation in each parameter. The comparison between experimental and model data is enhanced by the results of sensitivity analysis, which provides us with a framework to interpret these relationships. This approach can be extended to study other features of cells or cellular networks provided that a mathematical model exists for the system.
Methods
Cell dispersion and lactotroph enrichment
Pituitary cell dispersion was conducted using papain/DNAse enzymatic digestion as previously described (28), pooling pituitary glands from several adult Sprague-Dawley pro-oestrus female rats. Anterior pituitary lactotrophs were enriched using a previously described protocol (29). Briefly, a Percoll- bovine serum albumin (BSA 0.3%) discontinuous density gradient was made by sequentially adding 2 ml layers of Percoll at densities of 70%, 60%, 50% and 35% (from bottom to top) to a 15 ml Falcon tube. Freshly dispersed anterior pituitary cells were placed on top of this gradient. After 30 min of centrifugation at 1500 g at room temperature, the cells at the interface between the 50% and the 35% layers were washed in medium 199 (M199) and centrifuged for 10 min at 600 g, resuspended, counted, plated on 1.5 glass bottom dishes (250K per dish), and cultured for one day in M199 with 10% fetal bovine serum. Viability of cells, determined by trypan blue exclusion, was always ≥ 95 %. All cells in the lactotroph-enriched culture that responded to TRH were considered lactotrophs (28, 30).
Calcium imaging
During each of the experiments (n=12), the field of view contained an average of 20 cells. The cells were rinsed once with HEPES-buffered saline (HBS) and then incubated in HBS containing 2 μM of fura-2-AM (Molecular Probes, Carlsbad, CA) for 45 minutes at room temperature. The cells were then rinsed three times with HBS, placed on the stage of an inverted microscope and continuously perfused with HBS at room temperature. TRH (10-7 M) was bath applied for periods of 1 min. Pairs of images were acquired every 2 seconds with a 12 bit CCD camera set to 8x8 binning, controlled by TI Workbench software developed by T. Inoue. The software also controlled the alternating illumination of the cells with 340- and 380-nm light beams. [Ca2+]i is expressed as the ratio of the intensity of the light emitted by cells after stimulation with 340 and 380 nm light (F340/F380). We assumed that the ratio R = F340/F380 was sufficiently far from the saturation portion of its curve to consider [Ca2+]i to be a linear function of R.
Data analysis
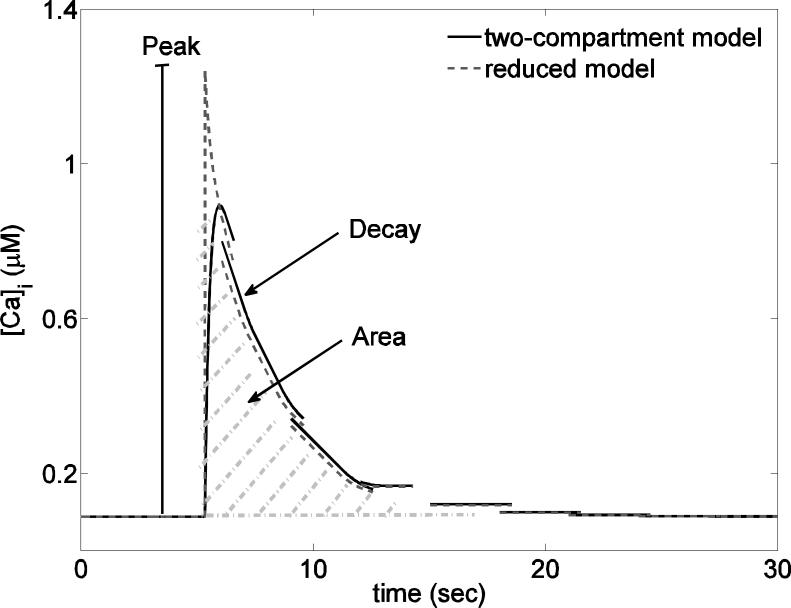
The data consist of time series of Ca2+ fluorescence imaging. For each cell's time series we first subtracted the average Ca2+ level so that each response had a baseline Ca2+ level of zero and then we computed three measures: the peak, the decay rate and the area under the curve (Fig. 2). The decay rate was computed by fitting an exponential decay function to each time series. The analysis was performed in Matlab (The Mathworks, Natick, MA). The code used for the analysis is available on http://www.math.fsu.edu/~bertram/software/pituitary.
Figure 2.
Comparison of the two-compartment (solid line) and the reduced (dashed line) model. The features measured in the model and experimental data (peak, decay rate and area) are also illustrated.
Two-compartment model
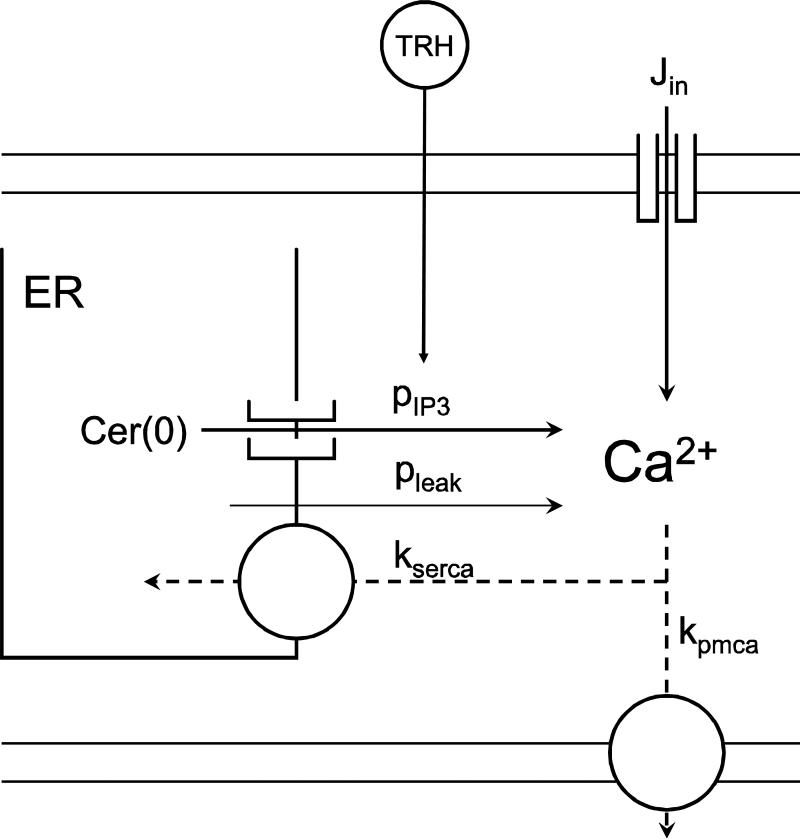
We use a two-compartment model (31) that describes the dynamics of calcium concentration in the cytosol and in the ER (Fig. 1).
Figure 1.
Representation of the simplified model of Ca2+ dynamics. Each Ca2+ flux is represented by an arrow with the corresponding parameter name. Parameter values and definitions are in Table 1.
This model contains the essential elements for Ca2+ dynamics in pituitary cells. The concentration of Ca2+ in the cytosol is a function of Ca2+ flux across the plasma membrane (Jmem) and the ER membrane (Jer). The differential equation for the concentration of free cytosolic Ca2+ (Ca) is:
| (1) |
where fc is the fraction of free cytosolic Ca2+ and
| (2) |
To replicate the experimental conditions we set the rate of Ca2+ influx to zero (i.e. Jin = 0), but we retain Jin temporarily during the development of the reduced model. The Ca2+ efflux (Jout) results from the combined action of plasma membrane Ca2+-ATPase pumps and Na+-Ca2+ exchangers. Previous findings suggest that the exchangers play a minor role (32), so we do not include them in the model. The plasma membrane Ca2+ pump rate is assumed to be linear,
| (3) |
where kpmca is the constant pump rate.
The concentration of Ca2+ in the ER (Cer) is a function of Ca2+ flux through the ER membrane and is described by
| (4) |
where fer is the fraction of free Ca2+ in the ER, and v is the ratio of the cytosolic to the ER volume (vc/ver). We model the flux through the ER membrane as
| (5) |
Here Jserca describes the flux through sarco/endoplasmic reticulum Ca2+-ATPase pumps (SERCA), while Jleak and Jip3 describe the flux from the ER into the cytosol due to leakage and IP3 receptor/channel permeability. These are described by:
| (6) |
| (7) |
| (8) |
where kserca represents the SERCA pumps rate (we assume a linear pump flux), and pleak and pip3 are the flux rates through leakage and IP3 channels respectively. All parameter values are listed in Table 1. The differential equations were solved numerically (in Fig. 2) using the Runge-Kutta 4th order method in XPPAUT (33).
Table 1.
Default parameter values.
| Parameter | Value | Definition | Units |
|---|---|---|---|
| fc | 0.01 | fraction of free cytosolic calcium | |
| fer | 0.01 | fraction of free ER calcium | |
| ν | 30 | ratio of cytosol to ER volume | |
| pleak | 0.0002 | leakage from ER into the cytosol | ms-1 |
| pip3 | 0.004 | rate of IP3 channels flux | ms-1 |
| Cer(0) | 132 | initial concentration of calcium in the ER | μM |
| kpmca | 0.15 | plasma membrane pump rate | ms-1 |
| kserca | 0.3 | SERCA pump rate | ms-1 |
Model reduction
Here we use the rapid equilibrium approximation to simplify the model and obtain formulas for some features of interest. This technique makes use of the fact that if two variables change on very different time scales, the faster one can be approximated by its equilibrium value. In our model this is the case for the cytosolic Ca2+ concentration, which changes much faster than the ER Ca2+ concentration (34). The rapid equilibrium approximation is obtained by setting Eq. (1) to zero and solving for the (quasi-equilibrium) Ca2+ concentration (Caeq):
| (9) |
By substituting Caeq for Ca in equation (4) we obtain
| (10) |
with
| (11) |
Equation (10) is a differential equation that we can solve analytically provided that Jin is constant or piecewise constant, obtaining
| (12) |
where Cer(0) is the initial concentration of Ca2+ in the ER. In our analysis, this would correspond to the point in time when TRH is applied. In addition, λ1 = ferνωJin, and
| (13) |
The reduced model is thus composed of Eqs. (9) and (12). To simulate the TRH response we switch the value of pip3 from zero to a positive value, instantaneously activating the IP3 channels and producing a cytosolic Ca2+ spike that then decays to its baseline concentration. The TRH response is thus reduced to an exponential decay from the peak Ca2+ value (Fig. 2).
Using the reduced model we can derive analytical expressions for the same features that we measure from the experimental data: the peak of the Ca2+ response, the rate of decay and the area under the curve (Fig. 2). The peak of the Ca2+ response is computed from (9), increasing the IP3 channel flux rate from 0 to pip3:
| (14) |
The peak increases with an increase of the IP3 channel flux rate (pip3), the concentration of Ca2+ in the ER at the time of agonist application (Cer(0)), the Ca2+ leakage rate (pleak) and the amount of Ca2+ influx (Jin). The rate of decay λ2 is defined in Eq. (13) and is a function of several parameters. A quick investigation reveals that the decay rate increases with pip3, pleak and the rate of Ca2+ extrusion from the cytosol through the plasma membrane calcium pumps (kpmca). Finally, we compute the area under the response curve, as the integral of equation (9) assuming no Ca2+ influx (Jin = 0), taken from the peak until Ca2+ returns to its baseline concentration, which simplifies to
| (15) |
Equation (15) reveals that the area is actually equal to peak/decay rate, which is proportional to the concentration of [Ca2+]ER at the time of agonist application and inversely proportional to the rate of Ca2+ extrusion via plasma membrane Ca2+ pumps. It is interesting that the area does not depend on the IP3 channel flux, but both the height of the peak and the decay rate do (Eqs. 13 and 14). A larger Jip3 increases the peak and produces a compensatory increase in the decay rate, so that the area is unchanged. The reduced model, Eqs (9) and (12), overestimates the peak response to a simulated application of TRH (Fig. 2). However, it retains the relationships between peak, decay rate, and area that are needed for comparisons with experimental data.
Results
Between-cell variation is larger than within-cell variation
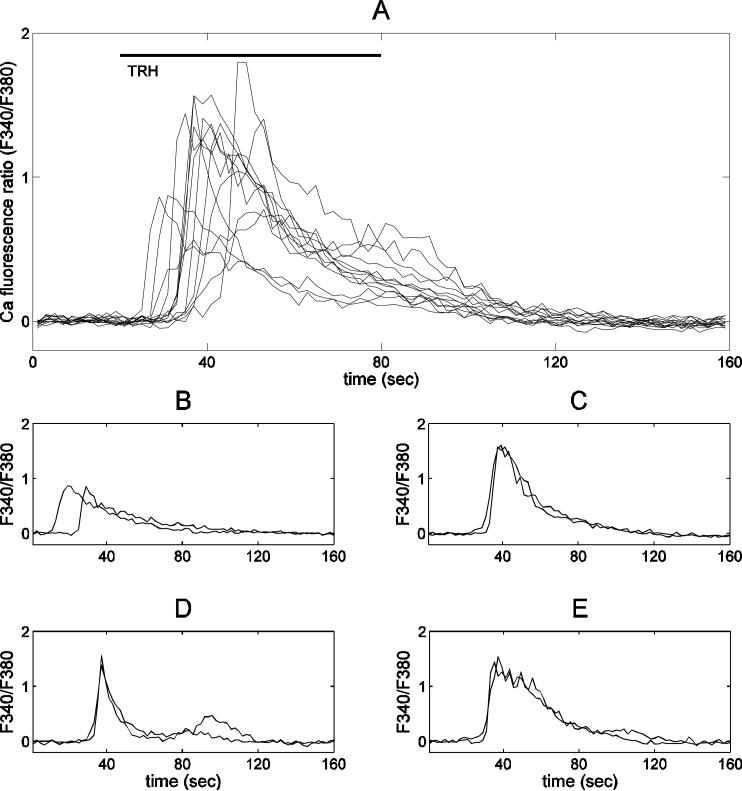
This paper investigates the heterogeneity in the lactotroph response to TRH. First, we show that changes in cellular behavior that emerge during the time course of the experiments do not contribute to heterogeneity. We recorded Ca2+ responses to a 1 minute challenge of TRH (100 nM). Consecutive TRH applications were given 30 minutes apart to allow ER stores to replenish between applications (35). Each challenge of TRH was applied in the absence of extracellular Ca2+ (removed 5 minutes before and added back 5 minutes after TRH treatment), to prevent Ca2+ influx into the cell during the stimulation. This removes one potential factor in the response heterogeneity. Figure 3A shows thirteen Ca2+ traces from individual lactotrophs responding to the same application, exhibiting considerable variability. In contrast, Fig. 3B-E show traces from four different cells subjected to two consecutive TRH applications. In each cell, the response to the second TRH application was very similar to that of the first application. Thus, during the time course of our observations, there is heterogeneity in the TRH response between cells, but uniformity of response within single cells to multiple TRH applications. This also shows that the observed heterogeneity is not due to measurement noise.
Figure 3.
Heterogeneity of the Ca2+ response to TRH in pituitary lactotrophs. In all panels the x-axis shows time in seconds, and the y-axis shows the Ca2+ fluorescence ratio (F340/F380). (A) Thirteen individual Ca2+ traces from the same experiment. Extensive variation exists in the peak, area, latency of response, and decay rate. (B-E) Examples of single cell Ca2+ traces from the same experiment showing very similar responses to two successive challenges of TRH 30 minutes apart.
Single parameter sensitivity analysis
Between any two cells there are many potential differences that could result in the heterogeneity of the Ca2+ response. Our goal is to determine where this variation is more likely to be found. For instance, is variation in the rate of Ca2+ flux through sarco/endoplasmic reticulum Ca2+-ATPase pumps (SERCA) a more likely source of measurable heterogeneity than variation in the flux through plasma membrane pumps or G-protein coupled receptor activities?
Analysis of a mathematical model can help us address this question. The model described in Methods contains several parameters that represent factors such as SERCA or plasma membrane pump rates. One can study how variation in these parameter values affects a simulated response to TRH. This is the goal of sensitivity analysis, which determines how sensitive a model output is to changes in parameter values. Since we derived analytical expressions for the features we want to measure, we would not need to implement sensitivity analysis in the standard way (the formula for each feature could be plotted as a function of each parameter). We do it here to show the procedure that one would use in the more typical case where analytical expressions for the features cannot be obtained. We quantify the effects of parameter changes using the relative change (RC) in model output (y) given a change (Δp) in the parameter value (p):
| (16) |
where Δp is the absolute change (positive or negative) in the default value of p. The relative change in p is then α = Δp/p. For instance if α = 0.1 and RC(p) = 0.5 then a 10% increase in the parameter corresponds to a 50% increase in model output. We simulate the TRH application with the model, and use the free cytosolic Ca2+ concentration (the Ca variable) time course to determine the peak, the decay rate and the area under the curve. Each of these features is used, separately, in Eq. (16) to calculate the sensitivity of the feature to changes in the various model parameters. In our simulations we changed the value of each parameter considered by as much as 70% of its default value.
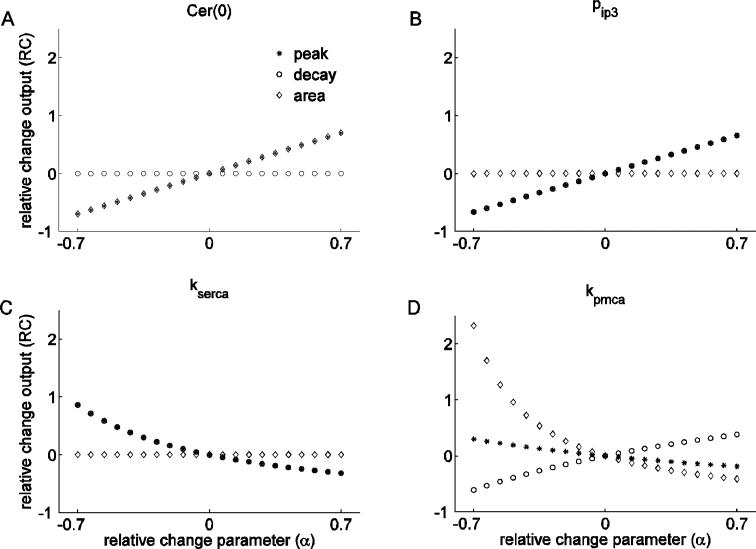
We start by looking at the effects of changing the concentration of Ca2+ in the ER ([Ca2+]ER) at the time of the simulated TRH application, Cer(0) (Fig. 4A). By increasing this parameter, we observe a positive linear effect on the peak and on the area (overlapping symbols), while there is no effect on the decay rate. Thus, increasing the initial [Ca2+]ER results in an increase of the peak and the area of the response. This happens because there is more Ca2+ available for release through the IP3 channels, increasing the peak of the response. Since the decay rate is unchanged, the area is increased due to the increase in the peak.
Figure 4.
Single parameter sensitivity analysis. In all panels the x-axis shows the relative change in the parameter value, and the y-axis shows the corresponding relative change in output. (A) Changes in Cer(0) have identical effect on the peak and the area of the response, but no effect on the decay rate. (B) Changes in pip3 affect peak and decay rate in the same way, but have no effect on the area. (C) Changing kserca affects peak and decay rate in the same way, but has no effect on the area. (D) Changes in kpmca have different effects on all features.
We next examine the effects of changing the parameter that describes the efficacy of the IP3 pathway (pip3), determining the magnitude of the Ca2+ flux through activated IP3 channels following agonist binding to the TRH receptor. Variation in this parameter reflects the multiple events involved in the Gq signaling pathway, from the extent of receptor occupancy and coupling, to the number of IP3 receptors present on the ER membrane. Figure 4B shows that increasing pip3 increases both the peak and the decay rate (overlapping symbols), while there is no effect on the area. Thus, the increase in the peak is exactly compensated by the increased decay rate, keeping the area constant. It is interesting that although an increase in either Cer(0) or pip3 increases the capacity for a robust response to stimulation, their effect on the three features are quite different. This reflects the fact that increasing Cer(0) increases the driving force for the response, while increasing pip3 increases the permeability of the release pathway.
The effects of changing the SERCA pump rate are considered next (kserca, Fig. 4C). Increasing this parameter decreases the peak and the decay rate (overlapping symbols), but it has no effect on the area. We observed the same property with changes in pip3, where variations in the peak and decay rate exactly compensate so that there is no change in the area.
Changes in the rate of cytosolic Ca2+ extrusion are shown in Fig. 4D. A change in this parameter (kpmca) affects all of the features nonlinearly. An increase in kpmca reduces the peak and the area, but increases the decay rate. This happens because by increasing kpmca we increase the rate at which Ca2+ is extruded from the cytosol, which in turn blunts the TRH response and accelerates the return of Ca2+ to the basal level.
It is clear that the different parameters have different effects on each of the features. For instance, kserca and kpmca have opposite effects on the decay rate but similar effects on the peak, while pip3 and kserca have opposite effects on peak and decay rate, but no effects on the area. A summary of the effects of each parameter on the measured features from the model output is presented in Table 2.
Table 2.
Summary of effects of model parameters on the features. A plus (minus) sign means that an increase (decrease) in parameter value results in an increase in the feature, a zero means that changing parameter value has no effect on the feature.
| Parameter | Peak | Decay rate | Area |
|---|---|---|---|
| Cer(0) | + | 0 | + |
| pip3 | + | + | 0 |
| kserca | - | - | 0 |
| kpmca | - | + | - |
Feature scatter plots
Using sensitivity analysis helps us to gain insight into a biological system, but it suffers from an inconvenient caveat: it cannot be directly applied experimentally. That is, we can change a parameter in the model by a desired amount and observe the effect it has on the output, but we can rarely do the same in an actual experiment. We can, however, use the information gained from sensitivity analysis in a different way.
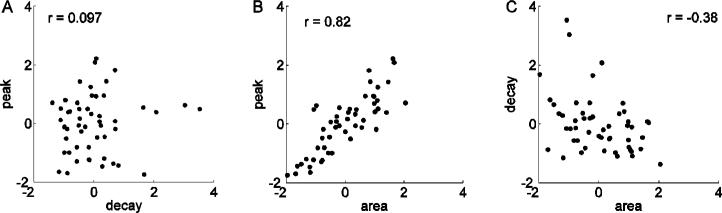
First, we construct scatter plots of the measured features from experimental data. The results from one experiment are shown in Figure 5. One can, for instance, construct a plot of all the peaks against all the decay rates, or all the peaks against all the areas, and so forth. In the example shown there is no correlation between decay rate and peak (Fig. 5A), a strong positive correlation between area and peak (Fig. 5B) and a negative correlation between decay rate and area (Fig. 5C). In these scatter plots we standardize the data, thus for instance a peak of 2 corresponds to a peak which is two standard deviations from the mean of the experiment (i.e. (x - μx) / σx = 2).
Figure 5.
Experimental data scatter plots constructed from one experiment. The data for each feature have been standardized (see text). (A) No correlation exists between peak and decay rate. (B) There is a positive correlation between peak and area. (C) There is a negative correlation between area and decay rate.
Now, using the model, we can construct a plot similar to the scatter plot made with experimental data by varying one or more parameters. We can then compare the plots resulting from the experimental data to those obtained from the simulations to gain insight into which parameter(s) is most likely responsible for the response variability in the cell population.
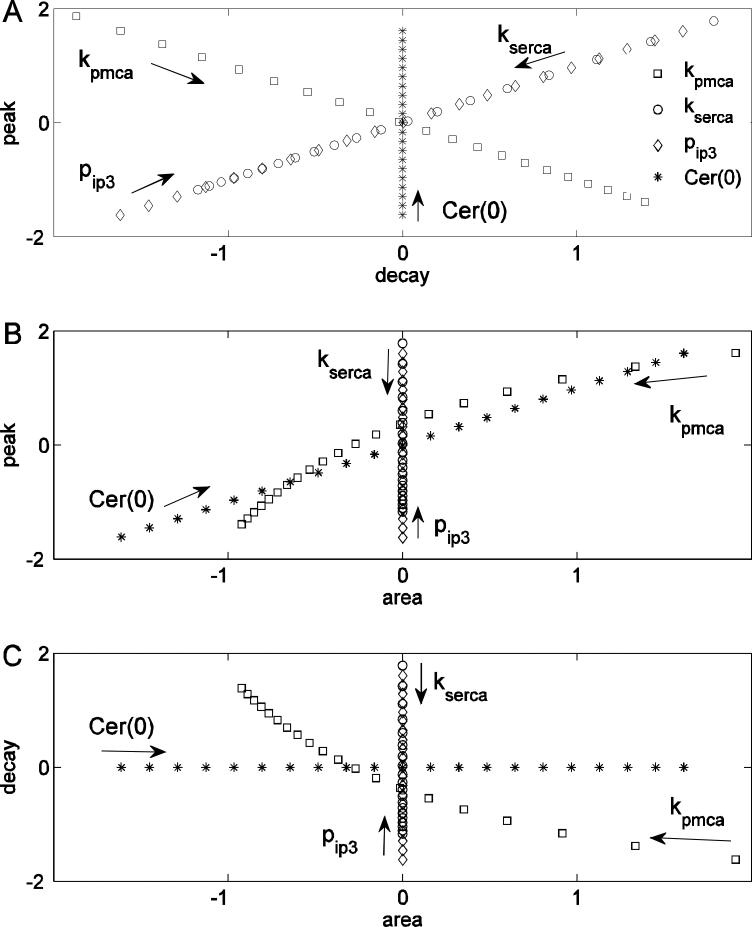
We begin by examining model scatter plots obtained by changing one parameter at a time (Fig. 6, arrows indicate direction of parameter increase). Figure 6 is constructed using the same model results as Fig. 4, but plotted in a different way. Figure 6A shows the scatter plot between the decay rate and the peak. Changes in kserca and pip3 both result in a positive correlation between peak and decay rate. That is, variations (positive or negative) in either parameter produce points on a curve with positive slope in the decay rate-peak plane. This is clear from inspection of the expressions for decay rate (Eq. 13) and peak (Eq. 14). The kserca (or pip3) parameter appears in the same position in each equation, thus changing this parameter will affect these two features in a similar way. Changes in kpmca result in a negative correlation between peak and decay rate. This happens because in the expressions for these two features kpmca appears in the numerator of one (Eq. 13) and in the denominator of the other (Eq. 14), so an increase in one corresponds to a decrease of the other. Changes in Cer(0) have no effect on the decay rate but have a large effect on the peak, because Cer(0) only appears in the numerator of the peak equation (Eq. 14). Taken together, these observations indicate that in the decay rate-peak feature space variations in different parameters produce very different patterns; some patterns have positive slope, some have negative slope, and some are vertical. Importantly, the pattern is a reflection of the parameter that is varied.
Figure 6.
Single parameter feature scatter plots. (A) Variation of different parameters produces different patterns in the peak-decay rate scatter plot. (B) Variation of kpmca and Cer(0) cause a positive correlation between peak and area, while kserca and pip3 have no effect on the area. (C) Variation of Cer(0) has no effect on the decay rate, kserca and pip3 have no effect on the area, and kpmca variation produces a negative correlation between decay rate and area.
Next we examine the scatter plot between peak and area (Fig. 6B). In this case, changing pip3 and kserca affects the value of the peak but not the area (since neither of these parameters appears in Eq. 15). Changes in Cer(0), or in kpmca, result in a positive correlation between area and peak, although with different slopes (both parameters appear in Eqs. 14 and 15). In the area-peak feature space no parameter introduces a negative correlation, so we should always expect either no correlation or a positive correlation between these two features.
The scatter plot between area and decay rate (Fig. 6C) reveals that changes in pip3 and kserca affect the decay rate, but not the area. Conversely, changes in Cer(0) affect the area but not the decay rate. Finally, changing kpmca results in a negative correlation between area and decay rate, because changes in this parameter affect the decay rate more than the peak, resulting in higher peaks having faster decays and consequently smaller areas. As a result, one should expect either no correlation or a negative correlation between these features.
In summary, variations in the different model parameters produce distinct patterns in the different slices (scatter plots) through feature space. The relations (positive, negative or zero) of the scatter plot curves can be determined from the sensitivity analysis (Fig. 4) or, if available, from the analytical expressions for the different features.
Multiple parameter variation
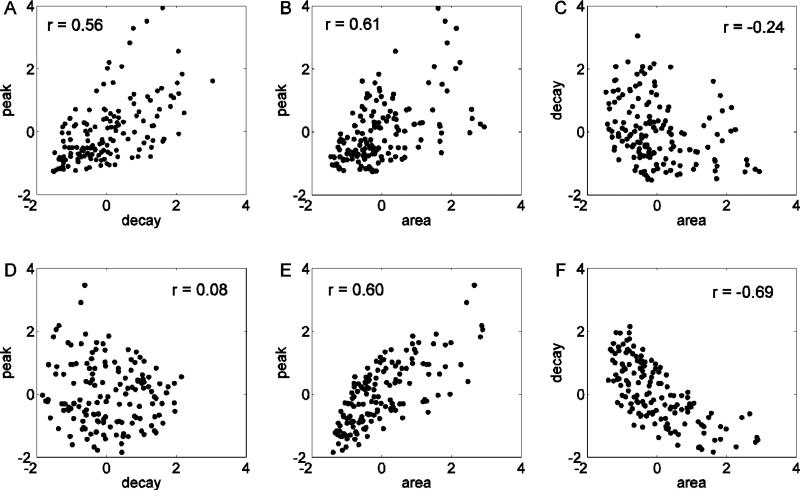
Here we investigate the correlation patterns of the model feature scatter plots obtained by changing multiple parameters simultaneously, using the single parameter scatter plots to aid with the interpretation. We started by using equal variation in all the parameters. For each parameter we selected a random value from a uniform distribution that spans ±50% of its default value. The results show a positive correlation in the decay rate against peak (Fig. 7A), and area against peak feature scatter plots (Fig. 7B). No correlation is found between decay rate and area (Fig. 7C). The single parameter correlation patterns in Fig. 6 help in understanding how these multiple parameters correlations come about. The positive correlation between decay rate and peak (Fig. 7A) arises because changes in both kserca and pip3 give positive correlations, while only variation in kpmca results in a negative correlation (Fig. 6A). The positive correlation between area and peak (Fig. 7B) arises because variation of all parameters gives either a positive correlation or no correlation (Fig. 6B). The absence of a correlation between area and decay rate (Fig. 7C) suggests that the influence of kpmca variation (which would create a negative correlation) is dominated by the influence of variation in the other parameters (which results in no correlation) (Fig. 6C).
Figure 7.
Model scatter plots constructed by randomly drawing multiple parameter values. (A-C) All four model parameters are drawn from a uniform distribution spanning ±50% of the default parameter value. (D-F) Parameter kpmca is drawn from a uniform distribution that spans ±50% of its default value, while all other parameters are drawn from a uniform distribution spanning ±25% of their default parameter values.
The feature scatter plots obtained from the model (Fig. 7-A,B,C), however, are not in good agreement with the corresponding scatter plots obtained from the experimental data (Fig. 5). In both cases there is a positive correlation between peak and area, but the experimental scatter plots show no correlation between decay rate and peak, and a negative correlation between area and decay rate. Analysis of the one parameter scatter plots (Fig. 6) suggests that increasing the variation in kpmca relative to the variation of other parameters should remove the correlation between decay rate and peak, and at the same time, introduce a negative correlation between area and decay rate, as in Figure 5.
Thus, we tested unequal variation in a different set of simulations. Parameters kserca, pip3 and Cer(0) were chosen from a uniform distribution that spans ±25% of the default parameter value. Parameter kpmca was chosen from a wider uniform distribution spanning ±50% of the default parameter value. The results of these simulations (Fig. 7-D,E,F) show a good qualitative agreement with the experimental data. That is in both model and experimental scatter plots there was no correlation in panel D, a positive correlation in panel E, and a negative correlation in panel F.
Is a larger variation in kpmca the only way to reproduce the correlation patterns, or can other combinations of parameters be found to achieve this? To check this we used 10% or 50% variation of each parameter. Since there are four parameters (kpmca, kserca, pip3 and Cer(0)), there are sixteen possible combinations of small/large parameter variations.
In the first two combinations all parameters are drawn from distributions with the same variation. We denote these as HHHH and LLLL, for high and low variation respectively. The next sets of combinations consist of one of the four parameters being drawn from the high variation distribution and all the others from the low variation distribution (HLLL, LHLL, etc.). Next, we draw two parameters from the high distribution and two from the low distribution. Finally, three are drawn from the high distribution and one from the low distribution.
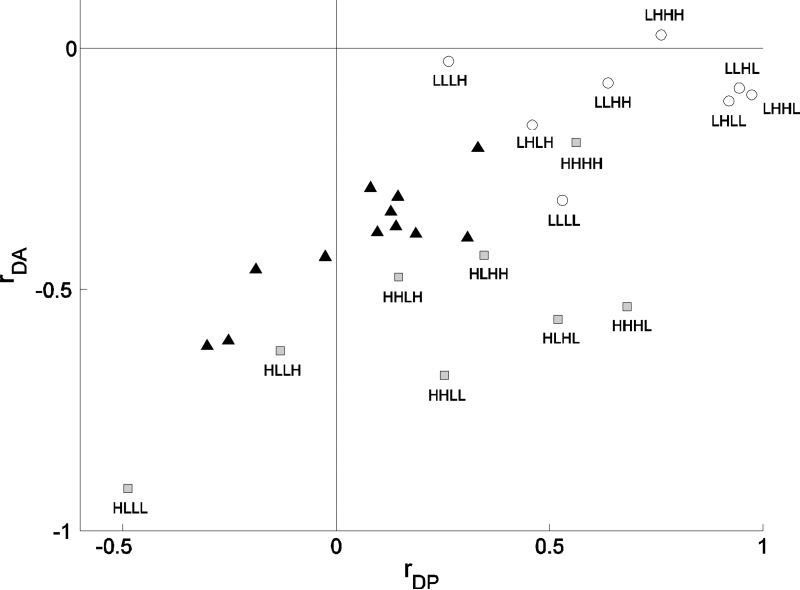
We present the results of these simulations using yet one more scatter plot, this time between two correlation values. We plotted together experimental data (Fig. 8, black triangles) and simulation results (Fig. 8, squares and circles). The value of the correlation between decay rate and peak is on the horizontal axis, while the value of the correlation between area and decay rate is plotted on the vertical axis. Plotted this way, we see that the correlation pairs measured from the data lie almost on a line with positive slope. This line connects positive correlations on the horizontal axis and small negative correlations on the vertical axis with negative correlations on the horizontal axis and larger negative correlations on the vertical axis.
Figure 8.
Comparison between model and experimental results. The x-axis is the value of the correlation between peak and decay rate, the y-axis is the value of the correlation between decays and area. Labels H and L correspond to a parameter value drawn from a high (±50%) and low (±10%) variance distribution, respectively. The order of the parameters is kpmca, kserca, pip3, Cer(0). Model simulations are divided in two categories, the ones in which at least kpmca was chosen from a high distribution (gray filled squares) and all others (open circles). Model correlations are closer to experimental correlations (black filled triangles) when the value of kpmca, Cer(0) and one or no other parameter were drawn from the high variation distribution.
We distinguished between two categories in the simulations. First there are simulations in which at least kpmca was chosen from a high distribution (HLLL, HHLL, HHHL, etc.). These are the gray squares in Fig. 8. The open circles represent all other combinations (LLLL, LLLH, LLHH, etc.).
Comparison of model with experimental correlations shows that the agreement is best when Cer(0), kpmca and another parameter have high variation. The points that most closely match the experimental results correspond to the HLLH, HHLH and HLHH combinations, all of which have a larger variation in kpmca and Cer(0). Thus, the analysis suggests that the most likely highly variable physical quantities in the lactotroph population used in these experiments are the plasma membrane pump rate and the level of Ca2+ concentration in the ER at the time of agonist application.
Discussion
Our goal was to evaluate the likely source of heterogeneity in the cytosolic Ca2+ response to Ca2+ mobilization. We described a method that combines scatter plots from experimental data with those made with a mathematical model. This allows one to predict the primary source of heterogeneity. We illustrated the technique using the cytosolic Ca2+ response of pituitary lactotrophs to TRH challenge as a case study. From each Ca2+ trace we extracted three features: the peak, the decay rate and the area under the curve. We found that kpmca is one parameter that must vary across cells more than other parameters. This suggests that the Ca2+ extrusion pathway varies extensively among cells. Previous findings suggested that TRH may modulate the activity of the plasma membrane Ca2+ ATPase pump (36), which might contribute to the observed kpmca heterogeneity.
We also found that variability in the Ca2+ concentration in the ER is likely a key element of heterogeneity in the response to TRH. This variability of [Ca2+]ER might be explained by the fact that cells that exhibit high degree of spontaneous activity would tend to have a higher ER Ca2+ level due to Ca2+ influx during electrical activity, as opposed to silent cells which may have low ER Ca2+ level. The absence of dopamine inhibition in our in vitro conditions may increase the level of spontaneous activity (12, 19), which would allow the expression of the variability in the ER Ca2+ level.
In previous studies (17, 37), pituitary lactotrophs were challenged over a range of concentrations of TRH, essentially performing a sensitivity analysis. It was found that the peak of the Ca2+ response increases, up to a maximum, while at the same time the spike duration decreases. This relation between peak and spike duration corresponds to a positive correlation between peak and decay rate using the method we describe. While this relationship is present in the single parameter sensitivity analysis of pip3 (Fig. 6A), it does not appear in the peak vs. decay rate scatter plot of the experimental data (Fig. 5A) or in the model scatter plot with non-uniform parameter variation (Fig. 7D). This apparent discrepancy is due to the very large variation in Ca2+ mobilization imposed by the range of TRH concentrations in (17, 37). This would be much larger than the natural variation occurring within a population of cells all exposed to the same dose of TRH. Thus, when looking at the results within a single dose of TRH the positive correlation between peak and decay rate predicted by single parameter sensitivity analysis can be masked by variations in other parameters. This illustrates that even when single parameter sensitivity analysis can be achieved experimentally, its results say little about the intrinsic heterogeneity within the cells.
In the data from different cells, all the parameters are varied at the same time, producing the observed variability. One way that mathematical models are sometimes adapted to such heterogeneous data is to adjust parameters so that the model output matches the mean of the experimental data. Another approach is to use a range of parameter values so that the distribution of model output matches the distribution of the experimental data. We use neither of these approaches; instead we look at the qualitative relationships between features and determined which parameters must vary the most to reproduce these qualitative relations. We did so by drawing parameter values from a uniform distribution. Other distributions could be used, but the basic procedure would be the same. We assumed that the parameters of the model were uncorrelated. That is, the biological components that the parameters represent are independent of each other. This may not be the case. For example, the expression levels of plasma membrane and SERCA pumps could be linked, so that cells would express high or low levels of both. To our knowledge there are no data describing these linkages.
The model we used was simplified in order to derive analytical expressions, improving our understanding of the dynamics involved in the Ca2+ response to TRH. More complete mathematical models could be used, at the expense of more parameters. For instance, one could incorporate a detailed description of all the intracellular events that take place from the binding of TRH to the opening of the IP3 receptors. These events include G-protein subunit dissociation, phospholipase C activation, IP3 formation and binding to receptors, and the gating of IP3 receptor-channels as a function of Ca2+ and IP3 concentrations. However, our results so far suggest that variations in the Gq/IP3 pathway are not the main source of heterogeneity, otherwise the data would exhibit a positive correlation between peak and decay rate. Extensions of the model can be used to allow extracellular Ca2+ flux during agonist application, or consider other features such as the response latency. Extensions of this technique include other experiments and not only a more complex model. As a follow-up to our findings, one could challenge the lactotrophs with other stimulators. For example, one could briefly challenge the cells with potassium chloride. This would depolarise the membrane and open voltage-dependent Ca2+ channels, causing an increase in cytosolic Ca2+ that does not involve mobilization from internal stores. In this way one can produce a similar Ca2+ spike with a decaying phase that depends on a different set of parameters, but still includes kpmca. This would allow one to test the variability results from the TRH application against those from an independent source.
Finally, extensions may be considered to other biological systems. Relevant features (like peak, decay rate and area) that are system specific must be identified first. For example, pituitary gonadotrophs typically produce an oscillatory Ca2+ response to gonadotropin-releasing hormone (38). If the agonist is applied in the absence of extracellular Ca2+ the oscillations die out over time (38). Features that could be examined in this response are the oscillation period and amplitude and, if the experiment is done in the absence of extracellular Ca2+, the number of oscillations produced. Although the features differ from those in the present study, the approach used to investigate likely sources of heterogeneity would be the same.
Acknowledgements
We would like to thank Marc Freeman for the many insightful comments on this manuscript, and Takafumi Inoue for kindly providing the Ca2+ imaging software TI Workbench. This research was supported by NIH grants DA-19356 and DK-43200.
References
- 1.Alvarez-Buylla A, Kohwi M, Nguyen TM, Merkle FT. The heterogeneity of adult neural stem cells and the emerging complexity of their niche. Cold Spring Harb Symp Quant Biol. 2008;73:357–365. doi: 10.1101/sqb.2008.73.019. [DOI] [PubMed] [Google Scholar]
- 2.Salk JJ, Fox EJ, Loeb LA. Mutational heterogeneity in human cancers: origin and consequences. Annu Rev Pathol. 2010;5:51–75. doi: 10.1146/annurev-pathol-121808-102113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cleaver JE, Lam ET, Revet I. Disorders of nucleotide excision repair: the genetic and molecular basis of heterogeneity. Nat Rev Genet. 2009 Nov;10:756–768. doi: 10.1038/nrg2663. [DOI] [PubMed] [Google Scholar]
- 4.McArdle CA, Evans JJ. The circus in the pituitary. Trends Endocrinol Metab. 2001;12:429–430. doi: 10.1016/s1043-2760(01)00520-3. [DOI] [PubMed] [Google Scholar]
- 5.Kærn M, Elston TC, Blake WJ, Collins JJ. Stochasticity in gene expression: from theories to phenotypes. Nat Rev Gen. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 6.Evans JJ. The anterior pituitary gland is mysterious, alluring and useful. Arch Physiol Biochem. 2002;110:3–8. doi: 10.1076/apab.110.1.3.896. [DOI] [PubMed] [Google Scholar]
- 7.Van Goor F, Zivadinovic D, Stojilkovic SS. Differential expression of ionic channels in rat anterior pituitary cells. Mol Endocrinol. 2001;15:1222–1236. doi: 10.1210/mend.15.7.0668. [DOI] [PubMed] [Google Scholar]
- 8.Wilkinson DJ. Stochastic modeling for quantitative description of heterogeneous biological systems. Nat Rev Gen. 2009;10:122–133. doi: 10.1038/nrg2509. [DOI] [PubMed] [Google Scholar]
- 9.Chung JD, Stephanopoulos G. On physiological multiplicity and population heterogeneity of biological systems. Chem Eng Science. 1996;51:1509–1521. [Google Scholar]
- 10.Li X, Zhang J, Small M. Self-organization of a neural network with heterogeneous neurons enhances coherence and stochastic resonance. Chaos. 2009;19:013126. doi: 10.1063/1.3076394. [DOI] [PubMed] [Google Scholar]
- 11.Kitano H. Biological robustness. Nature. 2004;5:826–837. doi: 10.1038/nrg1471. [DOI] [PubMed] [Google Scholar]
- 12.Ho MY, Kao JPY, Gregerson KA. Dopamine withdrawl elicits prolonged calcium rise to support prolactin rebound release. Endocrinology. 1996;137:3513–3521. doi: 10.1210/endo.137.8.8754781. [DOI] [PubMed] [Google Scholar]
- 13.Winiger BP, Schlegel W. Rapid transient elevations of cytosolic calcium triggered by thyrotropin releasing hormone in individual cells of the pituitary line GH3B6. Biochem J. 1988;255:161–167. doi: 10.1042/bj2550161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Winiger BP, Wuarin F, Zahnd GR, Wollheim CB, Schlegel W. Single cell monitoring of cytosolic calcium reveals subtypes of rat lactotrophs with distinct responses to dopamine and thyrotropin-releasing hormone. Endocrinology. 1987;121:2222–2228. doi: 10.1210/endo-121-6-2222. [DOI] [PubMed] [Google Scholar]
- 15.Castaño JP, Kineman RD, Frawley LS. Dynamic monitoring and quantification of gene expression in single, living cells: a molecular basis for secretory cell heterogeneity. Mol Endocrinol. 1996;10:599–605. doi: 10.1210/mend.10.5.8732690. [DOI] [PubMed] [Google Scholar]
- 16.De Paul AL, Pons P, Aoki A, Torres AI. Heterogeneity of pituitary lactotrophs: immunocytochemical identification of functional subtypes. Acta Histochem. 1997;99:277–289. doi: 10.1016/S0065-1281(97)80022-0. [DOI] [PubMed] [Google Scholar]
- 17.Ashworth R, Hinkle PM. Thyrotropin-releasing hormone-induced intracellular calcium responses in individual rat lactotrophs and thyrotrophs. Endocrinology. 1996;12:5205–5212. doi: 10.1210/endo.137.12.8940336. [DOI] [PubMed] [Google Scholar]
- 18.Lledo PM, Guerineau N, Mollard P, Vincent JD, Israel JM. Physiological characterization of two functional states in subpopulations of prolactin cells from lactating rats. J Physiol. 1991;437:477–494. doi: 10.1113/jphysiol.1991.sp018607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Israel JM, Kirk C, Vincent JD. Electrophysiological responses to dopamine of rat hypophysial cells in lactotroph-enriched primary cultures. J Physiol. 1987;390:1–22. doi: 10.1113/jphysiol.1987.sp016682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shorte SL, Faught WJ, Frawley LS. Spontaneous calcium oscillatory patterns in mammotropes display non-random dynamics. Cell Calcium. 2000;28:171–179. doi: 10.1054/ceca.2000.0147. [DOI] [PubMed] [Google Scholar]
- 21.Reid G, Bauer CK, Bunting R, Mason WT, Schwarz JR. Most lactotrophs from lactating rats are able to respond to both thyrotropin-releasing hormone and dopamine. Mol Cell Endocrinol. 1996;124:121–129. doi: 10.1016/s0303-7207(96)03933-0. [DOI] [PubMed] [Google Scholar]
- 22.Zhang J, Chen C, Kukstas LA, Vincent JD, Israel JM. Functional lactotroph heterogeneity in lactating rats and in vitro modification by 17Beta-Estradiol. J Neuroendocrinol. 1990;2:815–823. doi: 10.1111/j.1365-2826.1990.tb00646.x. [DOI] [PubMed] [Google Scholar]
- 23.De Paul A, Pons P, Aoki A, Torres A. Different behavior of lactotroph cell subpopulations in response to angiotensin II and thyrotrophin-releasing hormone. Cell Mol Neurobiol. 1997;17:245–258. doi: 10.1023/a:1026322130243. [DOI] [PubMed] [Google Scholar]
- 24.Velkeniers B, Kazemzadeh M, Vanhaelst L, Hooghe-Peters EL. Functional heterogeneity with respect to oestrogen treatment in prolactin cell subpopulations separated by Percoll gradient centrifugation. J Endocrinol. 1994;141:251–258. doi: 10.1677/joe.0.1410251. [DOI] [PubMed] [Google Scholar]
- 25.Burris TP, Freeman ME. Low concentrations of dopamine increase cytosolic calcium in lactotrophs. Endocrinology. 1993;133:63–68. doi: 10.1210/endo.133.1.8391429. [DOI] [PubMed] [Google Scholar]
- 26.Hinkle PM, Nelson EJ, Ashworth R. Characterization of the calcium response to thyrotropin-releasing hormone in lactotrophs and GH cells. Trends Endocrinol Metab. 1996;10:370–374. doi: 10.1016/s1043-2760(96)00188-9. [DOI] [PubMed] [Google Scholar]
- 27.Albert PR, Tashjian AH. Relationship of thyrotropin-releasing hormone-induced spike and plateau phases in cytosolic free Ca2+ concentrations to hormone secretion. J Biol Chem. 1984;259:15350–15363. [PubMed] [Google Scholar]
- 28.Tabak J, Gonzalez-Iglesias AE, Toporikova N, Bertram R, Freeman ME. Variations in the response of pituitary lactotrophs to oxytocin during the Rat estrous cycle. Endocrinology. 2010;151:1806–1813. doi: 10.1210/en.2009-1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Velkeniers B, Hooghepeters EL, Hooghe R, Belayew A, Smets G, Claeys A, Robberecht P, Vanhaelst L. Prolactin cell subpopulations separated on discontinuous Percoll gradient – An immunocytochemical, biochemical, and physiological characterization. Endocrinology. 1988;123:1619–1630. doi: 10.1210/endo-123-3-1619. [DOI] [PubMed] [Google Scholar]
- 30.Koshimizu T, Tomic M, Wong AOL, Zivadinovic D, Stojilkovic SS. Characterization of purinergic receptors and receptor-channels expressed in anterior pituitary cells. Endocrinology. 2000;141:4091–4099. doi: 10.1210/endo.141.11.7737. [DOI] [PubMed] [Google Scholar]
- 31.Bertram R, Sherman A. Filtering of calcium transients by the endoplasmic reticulum in pancreatic β-cells. Biophys J. 2004;87:3775–3785. doi: 10.1529/biophysj.104.050955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fiekers JF. The contribution of plasma membrane Na+-Ca2+-exchange and the Ca2+-ATPase to the regulation of cytosolic calcium ([Ca2+]i) in a clonal pituitary cell line (AtT-20) of mouse corticotropes. Life Sci. 2001;70:681–698. doi: 10.1016/s0024-3205(01)01443-6. [DOI] [PubMed] [Google Scholar]
- 33.Ermentrout GB. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students. SIAM; Philadelphia: 2002. [Google Scholar]
- 34.Bertram R, Arceo RC., II A mathematical study of the differential effects of two SERCA isoforms on Ca2+ oscillations in pancreatic islets. Bull Math Biol. 2008;70:1251–1271. doi: 10.1007/s11538-008-9298-1. [DOI] [PubMed] [Google Scholar]
- 35.Yu R, Hinkle P. Desensitization of thyrotropin-releasing hormone receptor-mediated response involves multiple steps. J Biol Chem. 1997;272:28301–28307. doi: 10.1074/jbc.272.45.28301. [DOI] [PubMed] [Google Scholar]
- 36.Nelson EJ, Hinkle PM. Thyrotropin-releasing hormone activates Ca2+ efflux. J Biol Chem. 1994;49:30854–30860. [PubMed] [Google Scholar]
- 37.Nelson EJ, Hinkle PM. Characteristics of the Ca2+ spike and oscillations induced by different doses of thyrotropin-releasing hormone (TRH) in individual pituitary cells and nonexcitable cells transfected with TRH receptor complementary deoxyribonucleic acid. Endocrinology. 1994;3:1084–1092. doi: 10.1210/endo.135.3.8070350. [DOI] [PubMed] [Google Scholar]
- 38.Stojilkovic SS, Kukuljan M, Ida T, Rojas E, Catt KJ. Integration of cytoplasmic calcium and membrane potential oscillations maintains calcium signaling in pituitary gonadotrophs. Proc. Natl. Acad. Sci. USA. 1992;89:4081–4085. doi: 10.1073/pnas.89.9.4081. [DOI] [PMC free article] [PubMed] [Google Scholar]