Abstract
Understanding the regulation and control of complex networks of reactions requires analytical tools that take into account the interactions between individual network components controlling global network function. Here, we apply a generalized matrix method of control analysis to calculate flux and concentration control coefficients, as well as response coefficients, in an integrated model of excitation-contraction (EC) coupling and mitochondrial energetics (ECME model) in the cardiac ventricular myocyte. Control and regulation of oxygen consumption (VO2) was first assessed in a mitochondrion model, and then in the integrated cardiac myocyte model under resting and working conditions. The results demonstrate that in the ECME model, control of respiration is distributed among cytoplasmic ATPases and mitochondrial processes. The magnitude of control by cytoplasmic ATPases increases under working conditions. The model prediction that the respiratory chain exerts strong positive control on VO2 (control coefficient 0.89) was corroborated experimentally in cardiac trabeculae utilizing the inhibitor titration method. In the model, mitochondrial respiration displayed the highest response coefficients with respect to the concentration of cytoplasmic ATP. This was due to the high elasticity of ANT flux toward ATP in the cytoplasm. The analysis reveals the complex interdependence of sarcolemmal, cytoplasmic, and mitochondrial processes that contribute to the control of energy supply and demand in the heart. Moreover, by visualizing the structure of control of the metabolic network of the myocyte, we provide support for the emerging concept of control by diffuse loops, in which action on the network (e.g., by a pharmacological agent) may bring about changes in processes without obvious direct mechanistic links between them.
Introduction
Since the chemiosmotic hypothesis was formulated, mechanism(s) involved in the control and regulation of energy supply and demand in the heart have been subject to intense scrutiny and debate. After many years of research, there is currently no consensus about the mechanism(s) and relative importance of the processes involved in matching energy supply with demand in the heart (for a review of the subject see (1,2)).
The complexity of the issue stems from the fact that mitochondrial energetics both modulates and is modulated by the network of mechano-electrical processes existing in the heart. In the past, most studies on this subject have considered only the major processes in isolation (e.g., mitochondrial energetics, electrophysiology, etc.). Consequently, it has been difficult to examine, in an intact system, whether the mechanisms controlling mitochondrial energetics differ depending on whether the muscle is at rest or is under working conditions. A computational model integrating both mitochondrial energetics and excitation-contraction (EC) coupling thus provides an important tool to address basic questions of energy supply and demand matching in the heart. Based on currently available evidence, it is likely that there is more than one mechanistic path implicated in metabolic control. On the one hand, mitochondrial Ca2+ appears to be a main regulator of energy production, presumably through the activation of Ca2+-sensitive dehydrogenases. However, the Frank-Starling relation emphasizes that large changes in work and ATP production can occur in response to varying preload on the ventricle without substantial changes in the cytosolic Ca2+ transient, suggesting a mechanism involving ADP and classical respiratory control that is independent of Ca2+ (1). A combination of both regulatory mechanisms is needed to account for the ability of the heart to maintain NADH balance and ATP production under various conditions (1,2).
To quantitatively assess the mechanism(s) involved in matching energy supply with demand in the heart, mathematical models, applied together with direct experimentation, provide a way to understand the complex interactions of the many processes involved in EC-bioenergetic coupling. Over the past several years, we have developed and validated a computational model of the ventricular cardiomyocyte which integrates excitation-contraction coupling (EC coupling) and mitochondrial energetics, and which can simulate experimentally observed changes in force and oxygen consumption rates in cardiac muscle when challenged by an increase in workload (such as during an increase in stimulation frequency). This model, referred to as the excitation-contraction coupling and mitochondrial energetics (ECME) model, reproduces the steady-state and transient behavior of NADH and Ca2+ in the mitochondrial matrix, clarifying the parallel regulatory role of Ca2+ and ADP in matching energy supply and demand (3,4).
In this work, we apply the stoichiometric matrix method of Reder (5) to analyze the role of sarcolemmal, cytoplasmic, and mitochondrial process in the control of oxidative phosphorylation in the cardiomyocyte. This method generalizes earlier metabolic control analysis tools (6–8). Calculations of the control and response coefficient matrices and changes in steady-state fluxes induced by perturbations of the system permit a deeper understanding of the relationship among the electrophysiological, Ca2+ handling, contractile, and metabolic components of the ECME model.
A glossary of terms used in this article is supplied as Table 1.
Table 1.
Glossary
| ADPm | Mitochondrial ADP |
| ANT | Adenine nucleotide translocator |
| CK | Creatine kinase |
| Co | Flux control coefficient in the absence of inhibitor |
| CrP | Creatine phosphate |
| Dxv | Elasticity matrix |
| EC | Excitation contraction |
| ECME | EC coupling-mitochondrial energetics |
| Eo | Total concentration of enzyme interacting with inhibitor |
| ICab | Background Ca2+ current |
| Idr | Identity matrix of dimension r |
| INaK | Current through the Na+ K+ ATPase |
| INCX | Current through the sarcolemmal Na+ Ca2+ exchanger |
| Ji | Flux in the presence of saturating levels of inhibitor |
| Jo | Flux in the absence of inhibitor |
| KD | Inhibitor dissociation constant |
| L | Link matrix |
| Nr | Reduced stoichiometric matrix |
| SR | Sarcoplasmic reticulum |
| VAM-ATP | Rate of myofibrillar ATPase |
| VANT | Rate of adenine nucleotide translocator |
| VATPsy | Rate of mitochondrial ATP synthase |
| VCauni | Rate of mitochondrial Ca2+ uniporter |
| VHFe | Rate of succinate-driven proton pumping |
| VHNe | Rate of respiratory chain proton pumping |
| VHu | Rate of proton pumping through ATP synthase |
| Vleak | Rate of proton leak |
| VNCE | Rate of mitochondrial Na+ Ca2+ exchanger |
| VO2 | Rate of oxygen consumption |
| VPMCA | Rate of sarcolemmal Ca2+ ATPase |
| VRC | Rate of respiratory electron transport |
| VTCA | Rate of the tricarboxylic acid cycle |
| ΔΨm | Mitochondrial membrane potential |
Computational and Experimental Methods
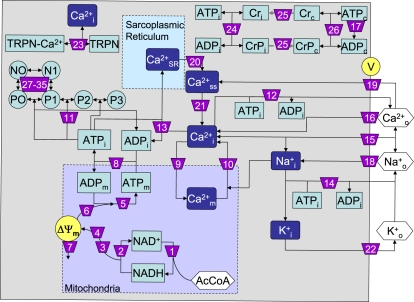
Fig. 1 depicts a general scheme of the ECME model describing EC coupling (in guinea pig ventricular myocytes) (9,10) and mitochondrial energetics (3,11). In this model, EC coupling and energetics are linked through the concentrations of ATP, ADP, creatine, and creatine phosphate as well as mitochondrial and cytoplasmic Ca2+ and Na+. The mitochondrial energetic model considers separately proton (VHNe) and electron transport (VO2) functions of the respiratory chain as well as the fluxes associated with phosphorylation (VATPase) and the proton pumping (VHu) across the mitochondrial F1, F0 ATP synthase (11,12). Despite being tightly coupled, the distinction between, e.g., VO2 and VHNe, has the advantage of enabling the computation of molecular slip or intrinsic uncoupling that accounts for chemical reactions not coupled to proton translocation in oxidative phosphorylation (13,14).
Figure 1.
Scheme of the model ECME subjected to control analysis. The scheme shows mass transformation interactions between the state variables of the ECME model. For simplicity, regulatory interactions were omitted in the scheme (see Computational and Experimental Methods). State variables are indicated in rectangular (ion or metabolites) or circular (myofibril conformations) boxes. Boxes depict a light-blue background when the state variables participate in conservation relationships (ATP/ADP, Cr/CrP, NAD+/NADH, TRPN/TRPN-Ca, and the various conformations of myofibrils). Ionic species are indicated on a dark-blue background. Hexagonal boxes denote inputs (ions or carbon substrate) that correspond to parameters in the model. Arrowheads point to the products of the numbered processes, whereas lines without arrowheads indicate inputs to those processes. In mitochondria, the TCA cycle was considered as a single step in the stoichiometric matrix; however, for the quantitation of the elasticity coefficients of the TCA cycle with respect to the intermediates, the disaggregated individual rate expressions, and their dependence with respect to Ca2+m, NAD+, NADH, ADPm, and ATPm were taken into account. The individual elasticities were then added together to compute the overall elasticity of the TCA cycle with respect to each state variable, such that the stoichiometric matrix and that of elasticity coefficients are dimensionally consistent. The values V and ΔΨm correspond to sarcolemmal and mitochondrial membrane potentials, respectively. See Table 2 for process key. The source code of the ECME model is available for download from http://senselab.med.yale.edu/ModelDB/ShowModel.asp?model=105383.
The electrophysiological module includes the main ion transport processes involved in EC coupling. It accounts for Ca2+, Na+, and K+ currents across the sarcolemma, Ca2+ transport within the sarcoplasmic reticulum (SR) and across the SR membrane, and Ca2+ handling by mitochondria. Five different Ca2+ compartments are defined including the mitochondrial matrix, the dyadic subspace, the junctional and network SR, and the cytoplasmic space.
The mitochondrial module describes the production (F1, FO ATPase) and transport (15) of ATP, Ca2+ transport, and the activation of TCA cycle dehydrogenases by Ca2+. The creatine kinase (CK) reaction occurs near the mitochondria, and the CrP diffuses to the cytoplasmic compartment where another pool of CK catalyzes the regeneration of ATPic to fuel constitutive cytoplasmic ATPases. The main ATP-consuming processes related to EC coupling are the myofibrillar ATPase (AM_ATP), SERCA, the Na+-K+ ATPase (INaK), and the Ca2+ ATPase (PMCA).
Control analysis of the ECME model: theoretical approach
Control analysis
Control analysis was performed by applying the method developed by Reder (5) as adapted to the mitochondrial (11) or the ECME model (3). In the framework of metabolic control analysis, Reder developed a generalized linear algebraic method that provides a way of analyzing the sensitivity of metabolic systems to perturbations triggered by either a change in the internal state of the system or by the environment. Here, we applied this method to a system in which metabolism, ion transport, and mechanical function are coupled. Because the ECME model was constructed in a modular way, the method can be applied with a higher or lower degree of detail or refinement. In this way, and depending on the question to be examined, the extent of control exerted by a module can be applied by zooming in and out.
The departure point of the analysis is the stoichiometric matrix, obtained from the set of differential equations of the model. The stoichiometric matrix defines the structural relationships between the processes and the intermediates participating in the metabolic network under consideration. The information contained in the stoichiometric matrix is independent of both the enzyme kinetics and the parameters that rule the dynamic behavior of the metabolic system.
The second piece of information required to perform control analysis is the elasticity matrix, defined by the dependence of each process in the metabolic network on the intermediates (e.g., ions or metabolites) included in the model. The elasticity matrix is quantified through the derivatives of the rates of individual processes with respect to each possible effector. Each elasticity coefficient reflects the local property of a process; for example, an enzyme activity with respect to its substrate, which is linked to the global behavior of the system through the steady-state levels of metabolites (substrates or effectors) that intervene in the network dynamics.
By applying matrix algebra, the matrices corresponding to control and response coefficients are obtained. Both kinds of matrices quantify the relationships between control and regulation, respectively, in the network of reactions. The regulation exerted by internal or external effectors to a network can be quantified by the response coefficient (16).
The following matrix relationships were used in the computation of flux and metabolite concentration control coefficients,
| (1) |
| (2) |
with C and Γ referring to the flux- and metabolite concentration control coefficients, respectively; Idr, the identity matrix of dimension r, the number of processes in the network under study; Dxv the elasticity matrix; Nr the reduced stoichiometric matrix; and L, the link matrix that relates the reduced- to the full-stoichiometric matrix of the system. (For a more detailed description of Eqs. 1 and 2, see the Appendices.)
The advantages of the matrix method of Reder (5) over similar tools developed by others (7,8) is that: 1) it can be applied to networks of any complexity, including conserved cycles or multiple branches, and hierarchical relationships (17); and 2), it is not based on the compliance of the theorems of metabolic control analysis and the particular conditions under which the analysis is carried out.
Illustratively, the matrices used in the case of the isolated mitochondrial model for calculating the control and response coefficients are presented in the Appendices. The reactions of the TCA cycle, both in the mitochondrial or the ECME model, have been lumped into a single step. However, the regulatory interactions involved in each step of the TCA cycle were explicitly taken into account and the individual elasticities were added for consistency in the dimensions of the network matrices (see also legend of Fig. 1).
Control under resting and working conditions
We simulated the steady-state behavior of the ECME model under resting (i.e., no stimulation) and voltage-clamp (working) conditions. The voltage-clamp condition corresponds to successive 2 Hz cycles during which membrane potential is clamped at +10 mV for 200 ms followed by a voltage clamp at −80 mV for 300 ms. The average value of state variables and fluxes calculated during the last 100 ms at +10 mV were used to perform the control analysis. The (pseudo) steady-state value of the state variables so-determined were used to calculate the elasticity coefficients. In most cases, the elasticity coefficients could be determined analytically (when the rate expression is a direct function of the concentrations or levels of the variables, i.e., sarcolemmal or mitochondrial membrane potential) or numerically (when the rate expression of, e.g., a channel current, is a function of additional variables such as gating probabilities that are not amenable to algebraic computation). Once the elasticity and stoichiometric matrix were calculated, the system was algebraically manipulated with the linear algebra package of Maple 11 (Maplesoft, Waterloo, CA).
Experimental methods
Oxygen consumption determination in rat trabeculae
Rat cardiac trabeculae were excised and mounted in a force transducer, as described previously (3). The muscle was field-stimulated while being perfused with an oxygenated Krebs-Henseleit solution (in mM): 1.0 CaCl2, 120 NaCl, 5.0 KCl, 2.0 MgSO4, 1.2 NaPO4H, 20 NaHCO3, 10 glucose, pH 7.4. All experiments were carried out at 22°C. The rate of oxygen consumption was determined using an oxygen-sensitive fiber-optic sensor (Ocean Optics, Largo, FL). Oxygen consumption was measured with the sensor positioned within 100 μm of the muscle in the absence or presence of the indicated concentration of rotenone, a complex I inhibitor.
The control of mitochondrial respiration was assessed by titrating the respiratory flux with rotenone (concentrations ranging from 30 nM to 2.5 μM). After each increase in rotenone concentration, VO2 was measured as the slope of the O2 decline upon brief cessation of flow of the perfusate. Since the muscle tissue was intact, we could not directly measure the extent of inhibition of complex I by rotenone. Thus, to quantify the control coefficient, we applied the method developed by Gellerich et al. (18), which is based on nonlinear regression analysis of inhibitor titration curves. The expression used to fit the inhibitor titration curve is
| (3) |
where
| (4) |
In Eq. 3, J is the measured flux at a given inhibitor concentration, Jo is maximal flux in the absence of inhibitor, and Ji is flow through the pathway with the enzyme completely inhibited; E is the concentration of free enzyme (variable according to the concentration of inhibitor, I,); Eo and KD are the total concentration of enzyme and the dissociation equilibrium constant between enzyme and inhibitor, respectively; and Co is the flux control coefficient in the absence of inhibitor. The empirical exponent n has been introduced in order not to be constrained by the rather restrictive linearity condition (18).
Results
In this work, the term “control” indicates the extent to which a flux through a pathway, or the concentration of an intermediary metabolite, is altered by changing the activity of one or more steps, and will be quantified by flux and concentration control coefficients, respectively. The term “regulation” refers to how the flux of a pathway or a metabolite level is modified through the effect on the rate of an individual step by cellular factors, which may include intermediary metabolite concentrations, the ionic environment, etc., and will be quantified by the response coefficient. The response coefficient measures the fractional change in flux, e.g., respiration, in response to a fractional change in a parameter P (e.g., an effector such as Ca2+) other than enzyme activity (16). The response of a pathway to an effector depends on two factors (19): 1), the extent of control exerted on the pathway by the enzyme that is the effector's target; and 2), the strength or elasticity of the effect of P on that enzyme. The response coefficient defined in this manner is the product of the control and elasticity coefficients. According to these definitions, metabolites or ions “regulate”, whereas changes in enzyme activity or posttranslational modifications “control”.
Control analysis of the mitochondrial energetics (ME) model
The control of mitochondrial energetics was first analyzed in the isolated mitochondrial model (11) in a similar parametric domain to that described below for the whole-cell integrated model to determine whether the control of energetics differed for isolated mitochondria and those interacting with the other subsystems of the cell.
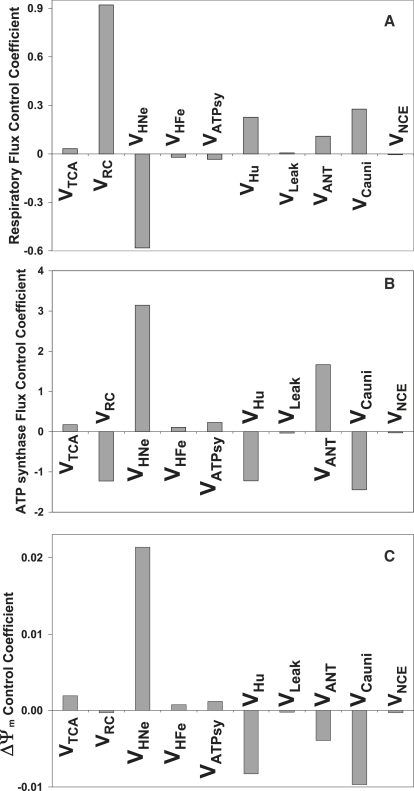
The profile of control of VO2 by the different mitochondrial processes, the F1,FO ATP synthase, and the membrane potential (ΔΨm) are displayed in Fig. 2. VO2 is mainly controlled by the activity of the respiratory chain carriers (VRC), the proton fluxes associated with respiratory electron transport (VHNe), and ATP synthesis (VHu) (Fig. 2 A; see also (11): their Eqs. 26, 27, 31, and 32). By discriminating between VHNe and VHu, we show that mitochondrial respiration is negatively controlled by the buildup of the proton motive force (VHNe), and positively controlled by the flux of H+ associated with ATP synthesis. As a caveat, the opposite pattern of control displayed by VRC and VHNe on VO2 should not be seen as being in conflict with respect to their acting as coupled processes; it only indicates that when the proton motive force is built up by VHNe, it feeds back negatively on respiration. These effects also explain the positive and negative control displayed by VHNe and VHu, respectively, on ΔΨm (Fig. 2 C). Additionally, VO2 is significantly and positively controlled by the Ca2+ uniporter (VCauni) and the adenine nucleotide translocator (VANT) (Fig. 2 A). Minor positive control of respiration is contributed by the TCA cycle (VTCA) and the proton leak (Vleak), and negative control of respiration is contributed by the proton flux associated with succinate-driven respiration (VHFe) and the ATP synthase (VATPsy) (Fig. 2 A).
Figure 2.
Metabolic fluxes and ΔΨm control in the mitochondrial energetics model. VO2 stands for respiratory electron transport (from NADH to O2) whereas VHNe represents the respiratory proton translocation associated to VO2. VHFe represents the rate of proton translocation associated to succinate-driven respiration. (A) Control profile of the respiratory electron transport; (B) control of the ATP synthase; and (C) ΔΨm control coefficients by each of the steps of the ME model (16).
The ATP synthase control profile mirrors that of respiration, with the exception of VANT and the TCA cycle (VTCA). For instance, VRC and VHNe exert negative and positive control, respectively, on VATPsy (Fig. 2, A and B). The positive control displayed by the ANT on VATPsy is due to the transport of ADP, the substrate for ATP synthesis, to mitochondria (Fig. 2 B), whereas in the case of respiration, the ANT exhibits positive control by dissipating ΔΨm, thereby accelerating respiration (Fig. 2 A). Accordingly, VANT displays negative control over ΔΨm (Fig. 2 C). The profile of control of ATP synthesis mirrored that of the respiratory flux, due to ΔΨm acting as the common intermediate. ΔΨm exhibits a similar control profile as the ATP synthesis; both are controlled by the same processes and with the same sign but with different strengths (Fig. 2, B and C).
Ca2+ exerts two main effects in our model of mitochondrial energetics: 1), activation of the TCA cycle dehydrogenase activities that stimulate NADH production and respiration; and 2), dissipation of ΔΨm by the transport processes, i.e., the Ca2+ uniporter (VCauni) and the Na+ Ca2+ exchanger (VNCE). In the case of VCauni-mediated Ca2+ transport, both the TCA cycle stimulation and the ΔΨm dissipation contribute positively to control respiration, whereas VNCE negatively controls respiration even though it dissipates ΔΨm (Fig. 2, A and B) because the impairment of the stimulatory effect of Ca2+ on the TCA cycle dehydrogenases overrides the ΔΨm dissipation by VNCE.
The results presented in this section show that the control of energetics in isolated mitochondria and, more specifically, of the respiratory and ATP synthesis fluxes, is distributed. Control is shared by processes associated with adenine nucleotide production and transport, as well as by Ca2+ dynamics.
Control analysis of mitochondrial energetics integrated with EC coupling
In this section, we examine how the control profile of energetics is modified when mitochondria are integrated with EC coupling. To perform these studies, we quantified the structure of control and regulation of the network of reactions described by the ECME model (Fig. 1).
The calculations are performed under resting and working conditions. The latter condition is assessed by clamping the voltage at +10 mV until a pseudo-steady state is attained (see Control under Resting and Working Conditions, above). A voltage of +10 mV was chosen because it corresponds approximately to the plateau of the action potential. Contractile force is close to its maximum during the plateau phase, and the energy-consuming pumps are nearly at maximal work during the contraction cycle. Although this corresponds to a transient state of the myocyte beating cycle, it was chosen to represent the working state in our calculations.
Control of respiration
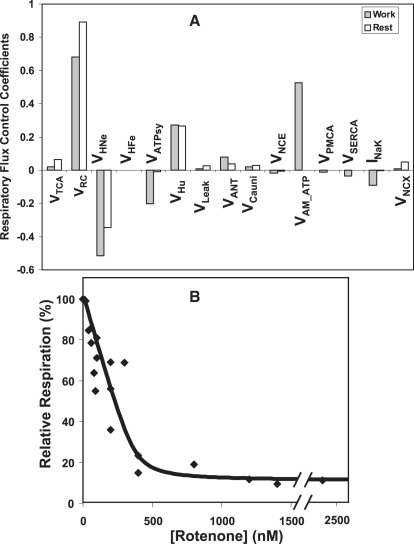
Control by mitochondrial processes. Fig. 3 A shows the distribution of flux control coefficients of VO2 by mitochondrial and cytoplasmic processes under similar parametric conditions as described above. Qualitatively, isolated and integrated mitochondria share the same rate-controlling steps (compare Fig. 2 A and Fig. 3 A). Quantitatively, the control in integrated mitochondria under resting conditions resembles that of the isolated mitochondria in state 4 (low ADP), in keeping with the low energy demand of the system.
Figure 3.
Control analysis of mitochondrial respiration in the ECME model and in rat trabeculae. (A) Control coefficients of mitochondrial and cytoplasmic processes on VO2 under resting or working conditions. The control of the electron transfer from NADH is calculated following the matrix method as indicated in Computational and Experimental Methods. (B) Rat trabeculae O2 consumption flux titrated with the complex I inhibitor, rotenone. The data shown correspond to averages of three independent determinations performed in triplicate for each rotenone concentration. From these data a control coefficient of 0.89 was calculated based on the inhibitor titration method (18) (see Computational and Experimental Methods).
As expected, the interaction between cytoplasmic and mitochondrial processes is quantitatively more important under working conditions. This is revealed by the control over respiration exerted by cytoplasmic ATP hydrolases, such as the myofibrillar ATPase (VAM_ATP), whose contribution to control is only significant during working conditions (Fig. 3 A).
Control of respiration is widely distributed among mitochondrial processes with VRC, VHNe, VATPsy, VHu, and VANT being quantitatively the most conspicuous, under both resting and working conditions. This is due to the control exerted by those processes on ΔΨm, which is a main effector of the respiratory flux (Fig. 3 A). The mitochondrial leak, Vleak, exhibits a larger control under resting than working conditions because its relative importance as a ΔΨm consumer decreases during work. In the resting cell, the major rate-controlling processes of respiration were: VRC > VHNe > VHu > VTCA > VANT > VCauni > Vleak, with a negative control exerted by the VNCE, and insignificant control by VATPsy. During work, the most relevant rate-controlling steps were: VRC > VHNe > VHu > VATPsy > VANT > VTCA > VCauni > VNCE > Vleak (Fig. 3 A).
Control by EC coupling processes. As noted earlier, the control of mitochondrial respiration by cytoplasmic processes is apparent only during work. The only EC coupling process that exerts some control over respiration under resting conditions is the sarcolemmal Na+/Ca2+ exchanger (INCX), which influences Na+ and Ca2+ levels in the cytoplasm, ΔΨm, and Na+ and Ca2+ transport across the mitochondrial membrane.
Under working conditions, the respiratory flux is also controlled by the major cytoplasmic ATPases: VAM-ATP, VSERCA, INaK, and plasmalemmal Ca2+ ATPase (VPMCA) (Fig. 3 A). While VAM-ATPase exerts a positive control on respiration, the others exhibit a negative control: INaK > VSERCA > VPMCA, because of their important effects on Ca2+ dynamics.
Experimental assessment of the control of mitochondrial respiration in intact tissue. This section is intended to illustrate how a particular control coefficient in the network may be subjected to experimental test to compare it with the calculated value. According to the control analysis calculations, the activity of the respiratory chain carriers (VRC) exerts a strong control on VO2. To verify this experimentally, rat heart trabeculae were subjected to 0.5 Hz field stimulation, and rotenone, an inhibitor of complex I of the respiratory chain, was titrated (Fig. 3 B). This inhibitor titration experiment rendered a control coefficient of 0.89 for the control of VO2 by the respiratory chain. This result is in quantitative agreement with the high control exhibited by the respiratory carriers in the control analysis of the ECME model (Fig. 3 A).
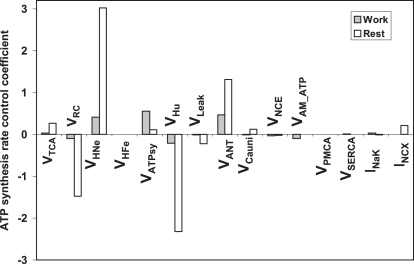
Control of ATP synthesis
Control by mitochondrial processes. When energy demand is low, flux of ATP synthesis can display larger variations than under working conditions when the ATP production is tightly committed to fulfilling the energy demand. This explains why values of the control coefficients for ATP synthesis are larger under resting than working conditions (Fig. 4). Mitochondrial ATP synthesis is positively controlled by the TCA cycle and the ANT, and negatively controlled by the respiratory chain activity (VRC) and proton transport through the ATP synthase (VHu) (Fig. 4). As ΔΨm consumers, the proton leak and NCE display negative control on ATP synthesis, whereas the Ca2+uniporter exhibits a small amount of positive control at rest, but a negligible (slightly negative) effect under working conditions. ATP synthase is the only mitochondrial process that displays a higher degree of control on ATP production under working, rather than resting, conditions (Fig. 4).
Figure 4.
Control of the synthesis of ATP in the ECME model. The control coefficients of the rate of ADP phosphorylation, VATPsy, by each of the mitochondrial and several cytoplasmatic processes are displayed. The control coefficients were calculated by applying the matrix method described in Computational and Experimental Methods and in the Appendices.
Control by EC coupling processes. The AM-ATPase negatively controls the flux of ATP synthesis (Fig. 4). This seemingly counterintuitive result can be explained as control by diffuse loops mediated, in this case, by the decrease in ATPi that an increase in AM-ATPase would bring about, in turn causing a decrease in the activity of the SERCA pump (see Discussion and Table 3, third row). Thus, AM-ATPase has a positive control on the concentration of Ca2+i in the cytoplasm. The increase in Ca2+i concentration resulting from the decrease in SERCA activity will, in turn, produce an increase of VCauni, transporting more Ca2+ into the mitochondria (also reflected by the large positive control of AM-ATPase on VCauni, not shown). The effect of the Ca2+ uniporter to dissipate ΔΨm overrides the small positive control of the ANT brought about by the increase in ADP produced by the AM-ATPase. The net effect is a decrease of flux through the ATP synthase (Fig. 4).
Table 3.
Control of energetic variables through diffuse loops
| Variable controlled | Controlling process | Intermediate variable | Intermediate process |
|---|---|---|---|
| Respiration | VAM_ATP | Ca2+m | VSERCA, VTCA |
| VCauni and VNCE | Ca2+m | VTCA | |
| ATP synthesis (work condition) | VAM_ATP | Ca2+m and ΔΨm | VSERCA and VCauni |
| INaK | Na+ and Ca2+i | INCX, VSERCA, and VCauni | |
| Ca2+m | VTCA, VHNe | ΔΨm | VNCE, VCauni |
| ATPi (work condition) | VSERCA, INaK | Ca2+i | VAM_ATP |
As mentioned above for the AM-ATPase, the cytoplasmic ATPases exert their control on mitochondrial respiration and ATP synthesis by translating the direct effect on ATPi into changes in Ca2+i and Ca2+m levels, which primarily impacts ΔΨm. Another example is the negative effect of an increase in Na+ K+ ATPase on respiration. The increase in Na+ pump activity lowers intracellular Na+, leading to an increased cellular extrusion of Ca2+i via the sarcolemmal Na+/Ca2+ exchanger (NCX). This decrease in Ca2+i lessens the extent of ΔΨm dissipation associated with mitochondrial Ca2+ transport, which results in a higher ΔΨm and a decrease of respiration. The decrease in the flow through the electron transport chain is due to the inverse relationship between VO2 and ΔΨm, i.e., the higher the ΔΨm, the lower the respiratory flux. This is the main mechanism that drives mitochondria between states 3 (high respiration, low ΔΨm, high ADP) and 4 (low respiration, high ΔΨm, high ATP) under physiological conditions.
Regulation of mitochondrial respiration by the effectors Ca2+, ATP, and ADP
The ECME model recapitulates the linearity between cardiac work and respiration in the heart (3) and the rapid time-dependent changes in mitochondrial NADH and Ca2+m in response to abrupt changes in workload (3,11). The model incorporates Ca2+ and ADP as two important messengers that signal changes in cardiac work and modulate mitochondrial energy production. The dynamics is dependent on the balance between ADP-dependent stimulation of mitochondrial oxidative phosphorylation and Ca2+-dependent activation of TCA cycle dehydrogenases. However, from a quantitative standpoint, it is unknown to what extent mitochondrial respiration is regulated by mitochondrial Ca2+ and ADP. To address this question, we calculated the response coefficients of energy fluxes to variations in Ca2+, ATP, and ADP.
As can be seen in Table 4, ATPi is the major regulatory intermediate. Mitochondrial ADP (ADPm; not shown), and Ca2+i contribute response coefficients that are smaller by several orders of magnitude. Interestingly, after ATPi, the regulation conferred by ΔΨm on key mitochondrial processes is the second most important factor, in terms of partial response coefficients (the partial response coefficient is defined in Appendix 1 by Eq. 8). However, in the computation of the total response coefficients (shown in Table 4), the terms corresponding to the respiratory chain and the ATP synthase cancel each other out, rendering very small total response coefficient values (see also Appendix 1).
Table 4.
Response coefficients of respiration and ATP synthase with respect to regulatory intermediates
| Condition Intermediate | Work |
Rest |
||||
|---|---|---|---|---|---|---|
| ATPi | Ca2+i | ΔΨm | ATPi | Ca2+i | ΔΨm | |
| VO2 | −0.04 | −2.10−11 | −1.10−9 | −0.01 | 4.10−10 | −2.10−8 |
| VHNe | −0.05 | 0 | −3.10−9 | −0.03 | 3.10−12 | −3.10−8 |
| VATPsy | −0.19 | −8.10−12 | 2.10−9 | −1 | 3.10−11 | 3.10−7 |
| VHu | −0.17 | −5.10−12 | 5.10−9 | −0.02 | 5.10−12 | −9.10−9 |
The response coefficient of flux Ji with respect to the intermediate x was calculated according to the expression being the flux control coefficient with respect to the activity of process k, and the elasticity of the rate of k with respect to the intermediate x, as defined in Ainscow and Brand (16) (see also Appendices).
Control of ATPi, Ca2+m, and ΔΨm
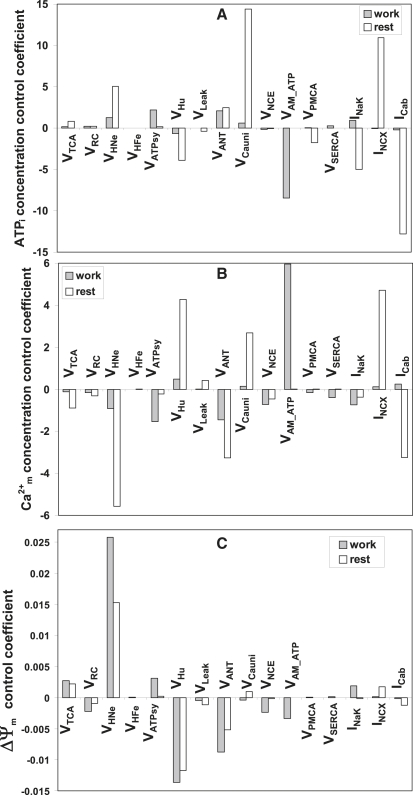
Control by mitochondrial processes. Due to the relevance of ATPi, ΔΨm, and Ca2+m as main regulators of the respiratory flux, we looked closely at the processes controlling their levels.
Under working conditions, the control of ATPi concentration is highly distributed with positive control exerted by VATPsy > VANT > VHNe > VCauni > VRC > VTCA, and negative control by VHU > VNCE (Fig. 5 A). As expected, the control of ATPi by the ATP synthase was much higher under working than resting conditions, likely due to the large ATP demand associated with the contractile activity. However, at rest, the magnitude of control coefficients of most mitochondrial processes are larger than under working conditions, VCauni > 2VHNe > VHu > VTCA > Vleak, except for those of VRC and VANT, which are similar under both conditions (Fig. 5 A). In most cases, the control of ATPi by mitochondrial processes is mediated by ΔΨm or Ca2+m. The VANT represents an exception to this pattern, despite being a ΔΨm consumer, because it provides the substrate for ATP synthesis and transports the newly synthesized ATP to the cytoplasm.
Figure 5.
Control of ATPi, Ca2+i concentrations, and ΔΨm in the ECME model. From the computation, under resting or working conditions of the matrix Γ of metabolite concentration control coefficients, the control coefficients of ATPi (A), Ca2+m (B), and ΔΨm (C), are extracted.
Overall, with the notable exception of the control of Ca2+m by the NCE and the ATP synthase, the magnitude of the control coefficients is larger under resting than under working conditions (Fig. 5 B). At rest, Ca2+m is controlled largely by mitochondrial processes; only NCX and the background Ca2+ current serve to influence Ca2+m in the absence of pacing (Fig. 5 B). Ca2+m is negatively controlled by the TCA cycle, respiration, VNCE, and the ANT, and positively by the leak, VHu, and the Ca2+ uniporter (Fig. 5 B). It may appear counterintuitive that processes that consume ΔΨm result in an increase in Ca2+ accumulation in the mitochondrial matrix. This can be explained through the sensitivity (quantified by the elasticity coefficient) of the Ca2+ uniporter and NCE to ΔΨm; although both processes are dependent on ΔΨm, the stimulation of NCE activity will be larger than VCauni for a similar increase in ΔΨm. Thus, every process that contributes positively to building ΔΨm exerts negative control over Ca2+m, as a consequence of the stimulation of Ca2+ efflux from mitochondria. On the contrary, processes that consume ΔΨm positively control Ca2+m (Fig. 5). As a consequence, the positive/negative control of mitochondrial processes on Ca2+m depends upon an increase/decrease of the net mitochondrial uptake of Ca2+ due to consumption/buildup of ΔΨm, respectively.
The control of ΔΨm by mitochondrial processes followed the expected pattern according to their ability to dissipate or build-up ΔΨm. Notably the magnitude of the control displayed by every process controlling ΔΨm was much larger under working than resting conditions. This result speaks to the important role of ΔΨm as a mediator of mitochondrial energy production.
Control by cytoplasmic processes. In the resting cardiomyocyte, only NCX and the background sarcolemmal Ca2+ current, ICab, exerted some positive and negative control, respectively, on the level of Ca2+m. This control may be explained through the same control pattern for ATPi, which fuels the activity of PMCA, resulting in a decrease of Ca2+m. ATPi is mainly consumed by the Na+K+ ATPase and PMCA under rest. This is a rather complex diffuse loop encompassing the ion transporters NCX, ICab, INaK, and PMCA, Ca2+i, and ATPi as mediators of the effects on mitochondrial Ca2+.
The main ATP consumer during work is the myofibrillar ATPase; thus, the negative control exerted by AM-ATPase on the ATPi concentration can be readily understood. The other ATP-consuming processes such as the Na+K+ ATPase, SERCA, and PMCA display a positive control on ATPi. This control is mediated by the negative control these ATPases exert on Ca2+i that brings about ATP consumption by the myofibrils. The activities leading to a decrease in Ca2+i result in an increase of ATPi, irrespective of their ATP-consuming properties (Fig. 5). The opposite rationale applies to the effect of the NCX that, when studied at +10 mV, is operating in reverse mode, thus contributing to the increase of Ca2+i as well as ICab.
Discussion
The main goal of this work was to investigate in an integrated and quantitative manner the mechanisms of control and regulation of energy supply and demand in cardiomyocytes under resting and working conditions. This is the first time that such an attempt has been performed on a coupled network of enzyme reactions and ion transport processes to elucidate the interplay among energetic, electrical, Ca2+ handling, and contractile processes.
The following findings further illustrate the power and the potential of the approach undertaken: 1), the control of mitochondrial respiration was distributed across several mitochondrial processes in both the isolated and integrated models, with differences in the magnitude of the control coefficients; 2), when linked with EC coupling, mitochondrial respiration was additionally controlled by cytoplasmic ATPases; 3), the control profile was quantitatively different during resting and working conditions; 4), the highest response of mitochondrial respiration was to ATPi, as a consequence of the high elasticity of the ANT toward ATPi; and 5), control in this complex network was exerted through diffuse loops, often leading to counterintuitive conclusions.
The following three main features have emerged from previous analyses of control in metabolic networks (6,20,21); 1), control is distributed, as opposed to being concentrated in rate-limiting steps; 2), control changes both qualitatively (which site or step) and quantitatively (control strength) with the physiological conditions; and 3), there is a difference between control and regulation. All three findings are corroborated by this work, and further extended to show that in complex networks, control operates through diffuse loops.
Control of energy supply and demand in the ECME model
The analyses of Figs. 3 A and 4 are particularly instructive in answering the main question posed by the study. It can be seen clearly that the control of energy supply and demand is highly distributed among mitochondrial and EC coupling processes. As expected, when the demand is higher (work condition) the control of the rate of mitochondrial respiration by cytoplasmic ATPases is also higher, especially the positive control exerted by the myofibrillar ATPase (Fig. 3 A). Moreover, we were able to show experimentally in working muscle that respiration through complex I is one of the main rate-controlling steps of the respiratory chain (Fig. 3 B). However, the model analysis (Figs. 3 A and 4) also revealed that the control of respiration and ATP supply depend on other processes, including some which exert negative control, e.g., the effects of the F1,F0 ATPase, VHNe, and several cytoplasmic ATPases on respiration (Fig. 3 A). Thus, when analyzed as a whole, one cannot rely on one process in the network, not matter how quantitatively important it is.
The control of ATP synthesis is shared by most of the mitochondrial processes analyzed (Fig. 4). A reduction in the magnitude of most of these control coefficients under working conditions suggests that the range of variation of ATP production is more restricted when the energetic demand is large.
Regulation of energy supply and demand in the ECME model
A central finding was that the regulation by cytoplasmic processes of most mitochondrial fluxes, as well as the concentrations of metabolic intermediates, was exerted through ATPi via the ANT, as illustrated by the response coefficients shown in Table 4. Quantitatively, this result is explained by the large elasticity that the ANT displays toward ATPi, consistent with its role as the mediator of ADP/ATP exchange between mitochondria and the cytoplasm (3). Because of the inherent definition of the response coefficients (19), the response of respiration to ATPi depends on two factors: the extent of control exerted on respiration by the ANT; and the elasticity exhibited by the ANT toward ATPi.
Mechanistically, the central role of ATPi in the regulatory dynamics of the ECME is realized through the direct relationship between ATPi production by mitochondria, and ATP consumption by EC coupling processes. This interpretation is supported by results obtained with a preliminary version of the ECME model in which the integration of EC coupling with mitochondrial energetics was effected only through Ca2+ and Na+ without communication between the adenine nucleotide pools. This type of coupling was insufficient to elicit significant cross talk between the two submodels (S. Cortassa, M. Aon, and B. O'Rourke, unpublished data).
ATPi was the major regulator of mitochondrial respiration under working conditions and its regulatory effect is mediated through the control exerted by the ANT on ATP synthase and respiration. Indirectly, ATPi also exerts its regulatory action on mitochondrial functions through the effect on ΔΨm. Even if quantitatively small, the control of ΔΨm is relevant since all processes that contributed to building up ΔΨm had a negative effect on respiration, whereas those that consume ΔΨm exerted positive control over respiration (Fig. 5).
The dependence of respiration on adenine nucleotide levels has been well validated in isolated mitochondria (22), but its assessment in intact tissue has been more difficult to obtain. The problem revolves around the methods typically used to measure bulk ATP and ADP (i.e., chemical extraction or phosphorous NMR). The results obtained with these procedures do not truly reflect the local environment of the enzymes of the mitochondrial inner membrane, such as the ANT or creatine kinase (CK). In intact cells and tissues, the reaction catalyzed by CK both buffers ATPi and transmits changes in the ATP/ADP ratio from the contractile machinery to the mitochondrion. Hence, the increase in ATP turnover at the myofilament is necessarily accompanied by a similar increase in ADP transport across the inner mitochondrial membrane. Dynamic ADP compartmentation models have been developed to address this issue (23) In this model, the shuttling of the ADP signal from the AM-ATPase sites to the mitochondrial membrane is simulated by incorporation of a separate pool of nucleotides, which responds rapidly to EC coupling-mediated changes. Thus, control by energy demand (the “pull” condition described in (11)) is a prominent feature of the ECME model.
Ca2+ activation of the TCA cycle dehydrogenases makes a smaller contribution to the control of global cardiac cell function in the model, but it should be emphasized that this mechanism is important for maintaining the steady-state redox potential during periods of increased work (3). This could have potential implications for adaptive or signaling responses sensitive to the cellular redox status (24,25).
Control and regulation by diffuse loops in complex networks
When the pattern of control shown in, e.g., Fig. 2 A, is analyzed, it reveals that while control exerted by some processes can be readily interpreted, control by other processes may not be evident on first consideration. The detailed analysis of the two following examples illustrates the type of control that arises when a network is examined as a whole. The control of the flux through a process A (e.g., respiration) by a process B (e.g., VCauni) is exerted indirectly through an effector (e.g., Ca2+) resulting in an increase of the flux through process C (e.g., TCA cycle) that in turn controls positively the flux through process A. Thus, when the control of A by B is mediated by C, we will name this mechanism as control by diffuse loops. Control by diffuse loops may be considered to be a transitive property (if A=B and B=C, then A=C). Thus, due to the inherent interconnectedness between all processes, the potential exists that in a complex network of reactions, control by diffuse loops is very frequent.
Table 3 summarizes some diffuse control loops shown in this work. Let us analyze the positive control on mitochondrial respiration exerted by the AM-ATPase that, under working conditions, also controls positively the flux through the TCA cycle, and the concentration of NADH (not shown). This control is ultimately mediated by the increase in Ca2+m as a consequence of larger amounts of cytoplasmic Ca2+, Ca2+i (Table 3, first row). The increase in Ca2+i, in turn, depends on the decrease in SERCA activity, which is negatively controlled by AM-ATPase (not shown). In a nutshell, both the positive control of AM-ATPase on respiration and NADH is mediated by Ca2+m. This control also explains the positive control displayed by AM-ATPase on Ca2+i (not shown).
Another interesting example is given by the control exerted on respiration by the processes participating in mitochondrial Ca2+ transport; under working conditions, VCauni controls positively and VNCE negatively (Fig. 3). Despite the fact that both processes are ΔΨm consumers, the effect appears to be operating more significantly through mitochondrial Ca2+, Ca2+m (Table 3, second row). The following facts should be considered in order to understand this control: 1), the TCA cycle controls positively respiration; 2), VCauni and VNCE control Ca2+m positively and negatively, respectively, both under resting and working conditions; and 3), the TCA cycle dehydrogenases display a positive elasticity coefficient with respect to Ca2+. Thus, VCauni exerts a positive control on respiration because when its activity increases, the subsequent increase in Ca2+m results in a higher flux through the TCA cycle, which then leads to an increase of the electron transport flux through the respiratory chain.
Control and regulation by diffuse loops as applied to the matching between energy supply and demand in the heart
When the network of reactions underlying cardiomyocyte function is assessed as a whole, the concept of control by diffuse loops suggests that the system has evolved with multiple control and regulatory loops. A certain degree of redundancy is expected from such a system, which has to respond robustly over a broad range of physiological stimuli or pathophysiological conditions. Within this framework, a case worth further analyzing is the current controversy concerning the role of Ca2+ or adenine nucleotides upon matching between energy supply and demand. One side of the problem concerns the lack of quantitative agreement between the extents of Ca2+ activation of respiratory flux observed in vitro as compared with in vivo data. Changes in Ca2+ concentration can at maximum, double the respiration (11,26), whereas increases in energy flux of more than an order-of-magnitude higher can be observed in muscle cells in vivo (27). Another facet of the problem relates to the question of matching ATP production and consumption during length-dependent activation of cardiac work without substantial changes in the cytosolic Ca2+ transient (27).
Concerning the problems posed, our calculations show that mitochondrial respiration exhibits the highest response toward ATPi (Table 4). Although the response toward Ca2+ was much lower, as compared to ATPi, diffuse loops dependent on Ca2+ affect the levels of ATPi; in this way, Ca2+ affects, indirectly, the respiration through ATPi. Within this rationale, any process that influences the levels of ATPi at constant Ca2+ will also end up controlling mitochondrial respiration, as exemplified by the Frank-Starling mechanism, where a change in ventricle volume increases respiration at constant amplitude and frequency of Ca2+ transients. Additionally, the calculations showed that ADPi was the second intermediate to which respiration exhibits the highest response coefficient. ATPi level does not exhibit quantitatively important changes with cardiac workload, but this is not the case for ADP, whose low concentration (μM range) in the cytoplasm is difficult to measure and whose mitochondrial matrix concentration cannot be determined in vivo. Although the concentration of ADPi has been considered to be fairly constant based on the assumption of equilibrium of the creatine kinase reaction, this may not be the case for ADPi in the neighborhood of the sites of ATP consumption and ATP production (27).
Taken together, the results presented indicate a direct response of mitochondrial respiration toward ATPi, and an indirect one with respect to Ca2+, exerted through diffuse loops. Both the high response coefficient of respiration toward ADPi and quantitatively important local changes in its concentration can account for the matching of energy supply and demand after muscle length-dependent activation of cardiac work. Overall, the control of respiration resides in multiple nodes of the network while a combined action of adenine nucleotides and Ca2+ accounts for the regulation of mitochondrial respiration observed in vivo.
Limitations of metabolic control analysis
Metabolic control and its analytical tools have been developed to study the steady state of metabolic systems. Indeed, the derivations in Reder's method are valid only in the neighborhood of a steady state. This issue raises concerns about the application of metabolic control to analyze time-dependent behavior, as in this model. The way we have circumvented this limitation has been to clamp the sarcolemmal membrane potential at +10 mV, a membrane potential that roughly corresponds to the voltage at the plateau phase of the cardiac action potential. The system was allowed to evolve during the clamp to a pseudo-steady state and the control variables were calculated from averages during that period. In contrast, during rest, as there is no pacing, the system evolves toward a steady state. Despite this caveat, this assumption is supported by the work of Ingalls and Sauro (28) in which the validity of applying the tools of metabolic control analysis to averages of time-dependent systems such as those undergoing cyclic variations or rhythms was established. These authors showed that the theorems of metabolic control analysis, such as the summation and connectivity theorems, are fulfilled during time-varying behavior.
Comparison with previous control analyses in whole cells or in tissue
Although metabolic control analysis has been extensively applied to isolated mitochondria from different sources (29,30), few studies have been carried out using intact cells. Ventura et al. investigated the metabolic control of oxidative phosphorylation in isolated mitochondria from liver, revealing a large control coefficient for complex I that increases with age (31). This result is in agreement with our experimental results and theoretical predictions (Fig. 3).
In intact heart, Vogt et al. (32) studied the control and regulation of glycolysis during ischemic preconditioning to understand the mechanisms involved in the protection. Based on the co-response coefficients experimentally determined, new regulatory steps and/or new regulatory mechanisms of glycolytic enzymes had to be invoked to understand the biochemical interactions described. With the assistance of a computational model, and the application of the matrix method for its analysis, the experimental co-responses might be attributed to control by diffuse loops, as described in this work.
In vivo studies performed in skeletal muscle analyzed 31P-NMR data describing changes in high-energy phosphates, ATP and ADP, in the working forearm (33). These authors showed that the actomyosin ATPase exerts a strong control over the ATP turnover at stimulus frequencies up to 1.6 Hz. At higher frequencies, control by mitochondrial ATP production became more prominent. Although this work does not analyze the control at different frequencies, the myofibrillar ATPase is shown to exhibit a high degree of control on mitochondrial respiration that, in turn, is limited by the control exerted by the respiratory chain activity under working conditions.
Concluding Remarks
Control and regulation in complex reaction networks
The matrix method presented here illustrates the application of tools of metabolic control analysis to networks of processes involving not only metabolic reactions, but electrical and mechanical processes as well. This method may also provide an invaluable tool to assess the functional impact of the overwhelming datasets produced by high-throughput technologies. In addition, this work highlights the need for a combined experimental and modeling approach to deeply understand the control and regulation of mitochondrial energetics in cardiac muscle.
Table 2.
Processes accounted for by the ECME model, numbered according to the keys in the table
| Number | Abbreviation | Name |
|---|---|---|
| 1 | TCA | Tricarboxylic acid cycle |
| 2 | VRC | Respiratory electron transport |
| 3 | HNe | Respiratory chain proton pumping |
| 4 | HFe | Succinate-driven proton pumping |
| 5 | ATPsy | Mitochondrial ATP synthase |
| 6 | Hu | Proton pumping through ATP synthase |
| 7 | Leak | Proton leak |
| 8 | ANT | Adenine nucleotide translocator |
| 9 | Cauni | Mitochondrial Ca2+ uniporter |
| 10 | VNCE | Mitochondrial Na+ Ca2+ exchanger |
| 11 | AM-ATP | Myofibrillar ATPase |
| 12 | PMCA | Sarcolemmal Ca2+ ATPase |
| 13 | SERCA | Sarcoplasmic reticulum Ca2+ ATPase |
| 14 | INaK | Current through the Na+ K+ ATPase |
| 15 | INCX | Current through the sarcolemmal Na+ Ca2+ exchanger |
| 16 | ICab | Background Ca2+ current |
| 17 | ATPasec | Constitutive cytosolic ATPase |
| 18 | INa | Na+ inward currents |
| 19 | LCC | L type Ca2+ current |
| 20 | JRel | Ca2+ release from RyR |
| 21 | Jxfer | Ca2+ transport from subspace into cytoplasm |
| 22 | IK | Outward potassium currents |
| 23 | — | Ca2+ association-dissociation to troponin |
| 24 | CKi | Mitochondrial creatine kinase |
| 25 | — | Creatine species transport |
| 26 | CrKc | Cytosolic creatine kinase |
| 27–35 | — | Transitions between tropomyosin conformations |
Acknowledgments
This work was supported by National Institutes of Health grant Nos. P01HL081427, R33HL87345, and N01-HV-28180.
Appendix 1: Metabolic Control Analysis—Some Definitions
Given a network of processes of any complexity, the rates of the individual processes constituting such network influence are influenced by the rates of the other constituent processes with which they interact. Metabolic control analysis provides a theoretical and conceptual framework to address questions as to what extent a flux in a network depends on the activity of all other different processes (20,21). To quantify such control, a series of coefficients have been introduced. The most frequently reported value is the flux control coefficient,
| (5) |
with Ji representing the flux of interest, and Ek the activity of process k whose control is quantified by The flux control coefficient measures how much of the flux through a pathway (e.g., oxygen consumption flux, Ji) or a single step (e.g., adenine nucleotide translocase, Ji) would be modified if any activity in the system changes through either modification in enzyme abundance or activity (e.g., changes in the rate of ATP synthase, Ek). An analogous definition applies for the metabolite concentration control coefficient, These two coefficients reflect global properties of the network; both are dependent on the rates of all processes in the system. If the magnitude of the control coefficient is close to 1.0, it indicates that a change in the flux (e.g., O2 consumption rate) will be almost proportional to the change in the activity of the process whose rate has been altered (e.g., electron transport through complex I activity, as in Fig. 3 B).
On the other hand, the elasticity coefficient, quantifies the dependence of the rate of a specific process, k, on the concentration of any intermediate or effector in the network, SJ. The elasticity coefficient, as defined in Eq. 6, computes the magnitude by which an enzyme activity (e.g., ATP synthase, vk) changes upon variation in the level of a substrate or an effector (e.g., ADP, Sj). In contrast to control coefficients, elasticities depend upon local properties of the enzyme, and the concentrations of its substrates and effectors. In practical terms, elasticities correspond to the slope of the plot of the initial rate of an enzyme-catalyzed reaction as a function of its substrate (or an effector),
| (6) |
(For a more in-depth discussion and development of the analytical tools of MCA, the reader is referred to (19).)
To quantify regulatory interactions with respect to internal or external variables operating in a metabolic network, Ainscow and Brand (16) utilized the response coefficients of, e.g., flux Ji with respect to intermediary x, as
| (7) |
where is the flux control coefficient with respect to the activity of process k, and the elasticity of the rate of k with respect to the intermediate x. The quantity accounts for the participation of different factors (e.g., metabolites, x) in the mechanisms of control of a variable, such as a flux Ji. Each of the terms in the summation in Eq. 7 highlights the importance of the individual process, k, in the control of variable Ji, and are called partial response coefficient, as follows:
| (8) |
Appendix 2: Matrix Method of Metabolic Control Analysis as Applied to the Mitochondrial Energetics (ME) Model
In the matrix method developed by Reder (5), the control and regulation of a biochemical network of processes is calculated from the stoichiometry matrix (N) and the matrix of elasticity coefficients (Dxv). In the common case of conservation relationships, the stoichiometric matrix N contains rows that are linear combinations of other ones in the same matrix (singular matrix). This property does not allow performing the matrix inversion operations that are required to compute the control coefficient matrices. Thus, a reduced stoichiometric matrix, Nr, has to be introduced, containing only those rows with variables not related through conservation relationships. The complete stoichiometric matrix, N, and the reduced matrix, Nr, are related through a link matrix, L. In the method, the flux control coefficients and the metabolite concentration control coefficients are calculated according to the following linear algebra operations (see also Computational and Experimental Methods):
| (9) |
| (10) |
Below we show the structure of the matrices, Nr and Dxv, applied to the ME model in which the TCA cycle has been lumped:
| (11) |
| (12) |
Algebraic operations on these two matrices (indicated in Eqs. 9 and 10) allow the computation of the flux and intermediate concentration control coefficients as well as the response coefficients.
Since the ME model is not merely a biochemical system but also involves transport processes, the applicability of the method has respect to the theorems of metabolic control analysis, although the matrix method does not assume fulfillment of those theorems (5). When applied to a steady state, the summation theorems for the flux and intermediate concentration control coefficients should apply. Tables 5–7 demonstrate agreement with the summation theorems for the ME model.
Table 5.
Flux control coefficients of each of the fluxes (rows) by individual processes (columns) of the ME model
| VTCA | VO2 | VHNe | VHFe | VATPsy | VHu | Vleak | VANT | VCaUni | VNCE | Sum | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| VTCA | 0.032 | 0.921 | −0.581 | −0.021 | −0.034 | 0.226 | 0.007 | 0.109 | 0.277 | −0.005 | 0.93 |
| VO2 | 0.032 | 0.921 | −0.582 | −0.021 | −0.034 | 0.226 | 0.007 | 0.109 | 0.277 | −0.005 | 0.93 |
| VHNe | 0.029 | −0.077 | 0.390 | −0.022 | −0.035 | 0.237 | 0.007 | 0.114 | 0.289 | −0.004 | 0.93 |
| VHFe | −0.056 | 0.008 | −0.619 | 0.978 | −0.035 | 0.241 | 0.007 | 0.113 | 0.280 | 0.009 | 0.93 |
| VATPsy | 0.173 | −1.226 | 3.146 | 0.112 | 0.229 | −1.225 | −0.036 | 1.666 | −1.443 | −0.027 | 1.37 |
| VHu | 0.051 | −0.197 | 0.756 | 0.027 | −0.107 | 0.706 | −0.009 | 0.216 | −0.345 | −0.008 | 1.09 |
| Vleak | 0.002 | 0.000 | 0.017 | 0.001 | 0.001 | −0.007 | 1.000 | −0.003 | −0.008 | 0.000 | 1.00 |
| VANT | 0.092 | 0.014 | 0.993 | 0.035 | 0.077 | −0.387 | −0.011 | 0.767 | −0.450 | −0.014 | 1.12 |
| VCaUni | 0.005 | −0.001 | 0.050 | 0.002 | 0.003 | −0.020 | −0.001 | −0.009 | 0.977 | −0.001 | 1.01 |
| VNCE | 0.005 | −0.001 | 0.050 | 0.002 | 0.003 | −0.020 | −0.001 | −0.009 | 0.977 | −0.001 | 1.01 |
Table 6.
Metabolite concentration control coefficients of each state variable (rows) by individual processes (columns) of the ME model
| VTCA | VO2 | VHNe | VHFe | VATPsy | VHu | Vleak | VANT | VCaUni | VNCE | Sum | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NADH | 0.236 | −0.238 | 0.025 | 0.001 | −0.002 | −0.010 | 0.000 | 0.004 | 0.025 | −0.037 | 0.003 |
| ΔΨm | 0.002 | 0.000 | 0.021 | 0.001 | 0.001 | −0.008 | 0.000 | −0.004 | −0.010 | 0.000 | 0.003 |
| ADPm | −0.015 | −0.004 | −0.157 | −0.006 | −0.014 | 0.061 | 0.002 | 0.041 | 0.071 | 0.002 | −0.018 |
| Ca2+m | −0.001 | 0.000 | −0.006 | 0.000 | 0.000 | 0.002 | 0.000 | 0.001 | 0.609 | −0.606 | −0.001 |
| NAD+ | −1.594 | 1.614 | −0.169 | −0.006 | 0.015 | 0.066 | 0.002 | −0.027 | −0.169 | 0.248 | −0.021 |
| ATPm | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
Table 7.
Response coefficients of the state variables (rows) with respect to intermediates in the ME model (columns)
| NADH | ΔΨm | ADPm | Ca2+m | NAD+ | ATPm | |
|---|---|---|---|---|---|---|
| NADH | −0.5 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 |
| ΔΨm | 0.0 | −1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| ADPm | 0.0 | 0.0 | −0.5 | 0.0 | 0.0 | 9.4 |
| Ca2+m | 0.0 | 0.0 | 0.0 | −1.0 | 0.0 | 0.0 |
| NAD+ | 3.4 | 0.0 | 0.0 | 0.0 | −0.5 | 0.0 |
| ATPm | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | −0.5 |
The deviations of the sum from 1.0 (Table 5 or zero (Table 6) are likely due to the accuracy in the calculation of certain variables. In fact, the summations that display the largest deviation from 1 are those corresponding to ATP synthase and ANT. This is due to the large relative error because of the small value of the concentration of ADPm compared to the level of ATPm. (i.e., μM against mM, respectively). Another source of error is given by the lumping of the TCA cycle. ATPsynthase, ANT, and succinate lyase (embedded, in this analysis, in the TCA cycle) are the three processes participating in the equation that rules ADPm concentration. The lumping of the TCA cycle, introduced for simplicity in the calculations, leads to an error in the quantification of elasticities with respect to ADPm. This error translates into the computation of the control coefficients for ATP synthase and ANT, thus explaining the deviations of the order of 10−1 from the summation theorem.
In Table 7, the values in bold in the diagonal indicate that the summation of the response coefficients (−1.0) for metabolites is fulfilled (16). The fact that metabolites corresponding to the pyrimidine and adenine nucleotide pools (NADH, NAD, ADP, ATP) exhibit half of the value is due to them being subjected to conservation relationships.
References
- 1.Saks V., Favier R., Guzun R., Schlattner U., Wallimann T. Molecular system bioenergetics: regulation of substrate supply in response to heart energy demands. J. Physiol. 2006;577:769–777. doi: 10.1113/jphysiol.2006.120584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Balaban R.S. Cardiac energy metabolism homeostasis: role of cytosolic calcium. J. Mol. Cell. Cardiol. 2002;34:1259–1271. doi: 10.1006/jmcc.2002.2082. [DOI] [PubMed] [Google Scholar]
- 3.Cortassa S.C., Aon M.A., O'Rourke B., Jacques R., Tseng H.J. A computational model integrating electrophysiology, contraction and mitochondrial bioenergetics in the ventricular myocyte. Biophys. J. 2006;91:1564–1589. doi: 10.1529/biophysj.105.076174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brandes R., Bers D.M. Simultaneous measurements of mitochondrial NADH and Ca2+ during increased work in intact rat heart trabeculae. Biophys. J. 2002;83:587–604. doi: 10.1016/S0006-3495(02)75194-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Reder C. Metabolic control theory: a structural approach. J. Theor. Biol. 1988;135:175–201. doi: 10.1016/s0022-5193(88)80073-0. [DOI] [PubMed] [Google Scholar]
- 6.Kacser H., Burns J.A. The control of flux. Biochem. Soc. Trans. 1995;23:341–366. doi: 10.1042/bst0230341. [DOI] [PubMed] [Google Scholar]
- 7.Sauro H.M., Small J.R., Fell D.A. Metabolic control and its analysis. Extensions to the theory and matrix method. Eur. J. Biochem. 1987;165:215–221. doi: 10.1111/j.1432-1033.1987.tb11214.x. [DOI] [PubMed] [Google Scholar]
- 8.Westerhoff H.V., Kell D.B. Matrix method for determining steps most rate-limiting to metabolic fluxes in biotechnological processes. Biotechnol. Bioeng. 1987;30:101–107. doi: 10.1002/bit.260300115. [DOI] [PubMed] [Google Scholar]
- 9.Jafri M.S., Rice J.J., Winslow R.L. Cardiac Ca2+ dynamics: the roles of ryanodine receptor adaptation and sarcoplasmic reticulum load. Biophys. J. 1998;74:1149–1168. doi: 10.1016/S0006-3495(98)77832-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rice J.J., Jafri M.S., Winslow R.L. Modeling short-term interval-force relations in cardiac muscle. Am. J. Physiol. Heart Circ. Physiol. 2000;278:H913–H931. doi: 10.1152/ajpheart.2000.278.3.H913. [DOI] [PubMed] [Google Scholar]
- 11.Cortassa S., Aon M.A., Marban E., Winslow R.L., O'Rourke B. An integrated model of cardiac mitochondrial energy metabolism and calcium dynamics. Biophys. J. 2003;84:2734–2755. doi: 10.1016/S0006-3495(03)75079-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Magnus G., Keizer J. Minimal model of β-cell mitochondrial Ca2+ handling. Am. J. Physiol. 1997;273:C717–C733. doi: 10.1152/ajpcell.1997.273.2.C717. [DOI] [PubMed] [Google Scholar]
- 13.Pietrobon D., Zoratti M., Azzone G.F., Caplan S.R. Intrinsic uncoupling of mitochondrial proton pumps. 2. Modeling studies. Biochemistry. 1986;25:767–775. doi: 10.1021/bi00352a005. [DOI] [PubMed] [Google Scholar]
- 14.Zoratti M., Favaron M., Pietrobon D., Azzone G.F. Intrinsic uncoupling of mitochondrial proton pumps. 1. Non-Ohmic conductance cannot account for the nonlinear dependence of static head respiration on δμH. Biochemistry. 1986;25:760–767. doi: 10.1021/bi00352a004. [DOI] [PubMed] [Google Scholar]
- 15.Dos Santos P., Aliev M.K., Diolez P., Duclos F., Besse P. Metabolic control of contractile performance in isolated perfused rat heart. Analysis of experimental data by reaction:diffusion mathematical model. J. Mol. Cell. Cardiol. 2000;32:1703–1734. doi: 10.1006/jmcc.2000.1207. [DOI] [PubMed] [Google Scholar]
- 16.Ainscow E.K., Brand M.D. Internal regulation of ATP turnover, glycolysis and oxidative phosphorylation in rat hepatocytes. Eur. J. Biochem. 1999;266:737–749. doi: 10.1046/j.1432-1327.1999.00856.x. [DOI] [PubMed] [Google Scholar]
- 17.Kahn D., Westerhoff H.V. Control theory of regulatory cascades. J. Theor. Biol. 1991;153:255–285. doi: 10.1016/s0022-5193(05)80426-6. [DOI] [PubMed] [Google Scholar]
- 18.Gellerich F.N., Kunz W.S., Bohnensack R. Estimation of flux control coefficients from inhibitor titrations by non-linear regression. FEBS Lett. 1990;274:167–170. doi: 10.1016/0014-5793(90)81355-r. [DOI] [PubMed] [Google Scholar]
- 19.Fell D.A. Portland Press; London: 1996. Understanding the Control of Metabolism. [Google Scholar]
- 20.Fell D.A. Metabolic control analysis: a survey of its theoretical and experimental development. Biochem. J. 1992;286:313–330. doi: 10.1042/bj2860313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cortassa S., Aon M.A., Iglesias A.A., Lloyd D. World Scientific; Singapore: 2002. An Introduction to Metabolic and Cellular Engineering. [Google Scholar]
- 22.Chance B., Williams G.R. The respiratory chain and oxidative phosphorylation. Adv. Enzymol. Relat. Subj. Biochem. 1956;17:65–134. doi: 10.1002/9780470122624.ch2. [DOI] [PubMed] [Google Scholar]
- 23.Vendelin M., Kongas O., Saks V. Regulation of mitochondrial respiration in heart cells analyzed by reaction-diffusion model of energy transfer. Am. J. Physiol. Cell Physiol. 2000;278:C747–C764. doi: 10.1152/ajpcell.2000.278.4.C747. [DOI] [PubMed] [Google Scholar]
- 24.Aon M.A., Cortassa S., Maack C., O'Rourke B. Sequential opening of mitochondrial ion channels as a function of glutathione redox thiol status. J. Biol. Chem. 2007;282:21889–21900. doi: 10.1074/jbc.M702841200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Maack C., O'Rourke B. Excitation-contraction coupling and mitochondrial energetics. Basic Res. Cardiol. 2007;102:369–392. doi: 10.1007/s00395-007-0666-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Territo P.R., French S.A., Dunleavy M.C., Evans F.J., Balaban R.S. Calcium activation of heart mitochondrial oxidative phosphorylation: rapid kinetics of mVO2, NADH, and light scattering. J. Biol. Chem. 2001;276:2586–2599. doi: 10.1074/jbc.M002923200. [DOI] [PubMed] [Google Scholar]
- 27.Saks V., Dzeja P., Schlattner U., Vendelin M., Terzic A. Cardiac system bioenergetics: metabolic basis of the Frank-Starling law. J. Physiol. 2006;571:253–273. doi: 10.1113/jphysiol.2005.101444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ingalls B.P., Sauro H.M. Sensitivity analysis of stoichiometric networks: an extension of metabolic control analysis to non-steady state trajectories. J. Theor. Biol. 2003;222:23–36. doi: 10.1016/s0022-5193(03)00011-0. [DOI] [PubMed] [Google Scholar]
- 29.Groen A.K., Wanders R.J., Westerhoff H.V., van der Meer R., Tager J.M. Quantification of the contribution of various steps to the control of mitochondrial respiration. J. Biol. Chem. 1982;257:2754–2757. [PubMed] [Google Scholar]
- 30.Rossignol R., Letellier T., Malgat M., Rocher C., Mazat J.P. Tissue variation in the control of oxidative phosphorylation: implication for mitochondrial diseases. Biochem. J. 2000;347:45–53. [PMC free article] [PubMed] [Google Scholar]
- 31.Ventura B., Genova M.L., Bovina C., Formiggini G., Lenaz G. Control of oxidative phosphorylation by Complex I in rat liver mitochondria: implications for aging. Biochim. Biophys. Acta. 2002;1553:249–260. doi: 10.1016/s0005-2728(01)00246-8. [DOI] [PubMed] [Google Scholar]
- 32.Vogt A.M., Poolman M., Ackermann C., Yildiz M., Schoels W. Regulation of glycolytic flux in ischemic preconditioning. A study employing metabolic control analysis. J. Biol. Chem. 2002;277:24411–24419. doi: 10.1074/jbc.M201138200. [DOI] [PubMed] [Google Scholar]
- 33.Jeneson J.A., Westerhoff H.V., Kushmerick M.J. A metabolic control analysis of kinetic controls in ATP free energy metabolism in contracting skeletal muscle. Am. J. Physiol. Cell Physiol. 2000;279:C813–C832. doi: 10.1152/ajpcell.2000.279.3.C813. [DOI] [PubMed] [Google Scholar]