Abstract
Hypothetical scenarios for “tetanic rundown” (“short-term depression”) of synaptic signals evoked by stimulus trains differ in evolution of quantal amplitude (Q) and covariances between signals. With corticothalamic excitatory postsynaptic currents (EPSCs) evoked by 2.5- to 20-Hz trains, we found Q (estimated using various corrections of variance/mean ratios) to be unchanged during rundown and close to the size of stimulus-evoked “miniatures”. Except for covariances, results were compatible with a depletion model, according to which incomplete “refill” after probabilistic quantal release entails release-site “emptying”. For five neurons with 20 train repetitions at each frequency, there was little between-neuron variation of rundown; pool-refill rate increased with stimulus frequency and evolved during rundown. Covariances did not fit the depletion model or theoretical alternatives, being excessively negative for adjacent EPSCs early in trains, absent at equilibrium, and anomalously positive for some nonadjacent EPSCs. The anomalous covariances were unaltered during pharmacological blockade of receptor desensitization and saturation. These findings suggest that pool-refill rate and release probability at each release site are continually modulated by antecedent outputs in its neighborhood, possibly via feedback mechanisms. In all data sets, sampling errors for between-train variances were much less than theoretical, warranting reconsideration of the probabilistic nature of quantal transmitter release.
Introduction
At various synapses, trains of afferent stimuli elicit postsynaptic responses that characteristically grow to a maximum (facilitate), remain fairly constant, or decline from an early peak to a plateau (tetanic rundown or short-term depression). The behavior is developmentally regulated (1) and presumably functions to optimize the transfer of information across the synapse (2,3).
Tetanic rundown, which is prominent at the curarized skeletal neuromuscular junction, has been traditionally explained by a depletion model (4). According to this model, rundown results from incomplete refill between stimuli of a presynaptic store of neurotransmitters from which synaptic responses (outputs) are evoked. Subsequent studies in the 1960s provided strong support for a purely presynaptic mechanism (constant quantal size). The degree of rundown also was graded with Ca2+/Mg2+ (presumably governing fractional release) and stimulation frequency (governing refill), all in good agreement with the depletion model (5–7).
Negative correlation between the amplitudes of the first two responses in trains (5,8) was shown by Vere-Jones (9) to arise from the stochastic nature of release and site “emptying” in the depletion model, which also gives a binomial distribution of outputs. An important implication is that reasonable estimates of quantal amplitude can be obtained from means, variances, and correlations (covariances) of synaptic responses evoked by repetitive trains of stimuli. In addition, because the model makes testable predictions with regard to the evolution of covariances (9,10), it is theoretically possible to determine whether data from a synapse undergoing tetanic rundown indeed fit the model.
The experiments presented were prompted by the report of Scheuss and Neher (11) that appropriate covariances exist at the calyx of Held, allowing correction of variance/mean ratios to obtain putative quantal size at all stimulation numbers in repeated excitatory postsynaptic current (EPSC) trains (12,13). These studies found that (postsynaptic) reduction of quantal size contributes to tetanic rundown. However, others have reported an absence of negative correlation between pairs of synaptic signals, despite clear rundown (14,15), suggesting that the depletion model might not be generally applicable. Consideration of other models/scenarios using Monte Carlo simulations (see Theory) suggested to us that analysis using covariances as well as variances might be achieved for any type of synapse where it is practical to record for more than a few minutes. That is, information from different cells could be pooled, and there was no reason to restrict the methodology to giant synapses that are particularly amenable to recording.
Here, we have used corticothalamic (glutamatergic) synapses where tetanic rundown is known to be prominent (16–18) and similar, in terms of dependence on stimulus frequency, to that seen at two giant synapses (the calyx of Held and the neuromuscular junction). For EPSCs evoked by stimulation at 2.5, 5, 10, and 20 Hz, our data analysis employs some novel methods suggested by theoretical considerations that are described in detail in the Theory section.
Our results differ from those reported for the calyx of Held (12) in that we find no postsynaptic contribution to rundown. That is, putative quantal amplitude was invariant within trains and independent of stimulation frequency. There was a superficial fit to the depletion model in that there were clear negative covariances between the first two signals in trains. However, covariances did not fit the model with regard to magnitude or evolution within trains. Instead, the data consistently gave either overly negative covariances, or positive or zero covariances where negative ones should exist. These conform to none of the theoretical models that we had considered. There was another major anomaly: between-stimulus number variances consistently varied much less than expected with binomial (or Gaussian or Poisson) distribution of outputs. It remains unclear how or whether this low variation can be reconciled with the stochastic/probabilistic nature of quantal release (19) otherwise supported by the correspondence of estimated quantal amplitude and the size of spike-triggered “miniature” events, sampled immediately after the stimulus trains.
Theory
With the fluctuation/quantal analysis using covariances as well as variances and means, introduced by Scheuss and Neher (11), it became possible to obtain estimates of quantal size at each stimulus in iterated trains of EPSCs that showed “tetanic rundown” (“short-term depression”), but on the assumption of equations derived for a simple binomial-depletion model (9–11), which omitted the possibility of postsynaptic contribution to the fall in EPSC amplitude. Here, we amplify and extend the theoretical basis for this approach by considering this and alternative scenarios to obtain expected evolution of means, variances, and covariances of signals, and consequent estimates of quantal amplitude(s). These, and sampling errors, have been found using Monte Carlo simulation (see Appendix), and/or mathematically derived equations. We assume that an experimenter wishes to obtain from data quantal amplitude(s) (Q) and quantal content (m), number of release sites (N), whether Q changes in the train, a characterization of the rundown of signals, and which scenario is most consistent with the data.
Scenarios
Possible mechanisms underlying rundown of synaptic signals during a train can be grouped into two categories: release-dependent, including 1), presynaptic depletion of available quanta, and/or 2), depression of postsynaptic sensitivity (desens) or reduction of the amount of transmitter per quantum; and release-independent, which could occur because of 1), graded reduction of output probability (p) (Pdown) and/or 2), inactivation of release sites (Ndown).
Under release-dependent presynaptic depletion, we include any process by which release sites become temporarily nonfunctional as a consequence of release, since each process yields the same equations, loss of available quanta being a plausible mechanism. In release-dependent desens, we include any process (post- or presynaptic) that produces reduction of postsynaptic response per quantum; a combination of such processes would require more than the one recovery rate used in the equations below.
In Pdown scenarios, output probability falls progressively to its equilibrium value, perhaps reflecting decreased presynaptic Ca2+ current per action potential, and shows kinetics that can mimic depletion. This produces sequences of signals and variances indistinguishable from depletion.
With Ndown scenarios, Monte Carlo simulations show that we must distinguish between at least three possibilities. In Ndown1, release sites become probabilistically and reversibly nonfunctional. This is the same as depletion, except that site inactivation is independent of whether release has occurred. In Ndown2, release sites differ in their probability of becoming inactivated and do not recover until after the train. To account for eventual nonzero equilibrium (final) outputs, we assume that the probability of site elimination diminishes with stimulation number. Ndown3 is the same, except that the sequence of site inactivation is repeated at each train iteration. The above scenarios represent two extremes; a variety of other rules for site loss gave intermediate results.
The computer subroutine in the Appendix, used for simulations, makes explicit all the underlying assumptions for each model.
Means, variances, and covariances
In general, covariances give information regarding the mutual dependence of values in subsets of data. Consider a number of train iterations with EPSC amplitudes S1, S2, etc. If the average (S1 − 〈S1〉)(S2 − 〈S2〉;) is less than zero (i.e., cov(S1,S2) is negative), the implication is that whatever made S1 larger or smaller than average, in a particular train, had (on average) the opposite effect on S2 in that train, unless the negative covariance arose by chance. Generally speaking, with later signals, the interpretation of covariances is inherently ambiguous: covariances can arise from correlations of both signals with antecedents. Note that for signals from voltage-clamped neurons no covariances can arise from feedback via action-potential outputs to interneurons.
With the above scenarios for rundown of S in trains, negative covariances are characteristic of any release-dependent process, depletion and/or desens. In the absence of desens, Pdown and Ndown3 give zero covariances, whereas with Ndown1 and, especially, Ndown2, positive covariances occur that grow within the train, resulting from the “random walk” implicit in each model. Here, cov(S1,S2) is zero, but with desens the net covariances are negative for all these scenarios, except the covariances for late signals with Ndown2.
The evolution of average outputs can be the same for any model. A Pdown model with an appropriate set of output probabilities, or Ndown with an appropriate set of inactivation probabilities, can always mimic a depletion model with a set of pjs (output probabilities if a quantum is “available” for release) and αjs (probabilities of refill between stimuli). The evolution of variances also does not distinguish between models, apart from Ndown3, which produces constant variance to mean ratios if output probability is constant.
Basic assumptions and derived equations
The relevant equations for synaptic signals for some scenarios can be deduced ab initio from basic principles. We begin by assuming that at any single release site only one quantum of transmitter can be released when it is stimulated, and that this occurs probabilistically. This, by definition, implies a binomial distribution of quantal outputs. Counting any response more than zero as 1, whatever its height (h), a record from such a site, consisting in a series of 0s (failures) and 1s (successes), will have a mean quantal content, 〈m〉, the number of successes divided by the number of stimuli, with an expected value of p, the release probability. Since the square of 1 is also 1, the mean-square is also 〈m〉. The variance (mean-square − square of mean) is therefore 〈m〉(1 − 〈m〉) with an expected value p(1 − p). It makes no difference whether p is constant or fluctuating. The formulae are unchanged, although the parameter p can represent an average. If we were to count 0s as responses with h = 0, as might arise with desens, the series of 0s and 1s is then interpreted as 〈m〉 = 1, var(m) = 0, 〈h〉 = fraction of successes, and var(h) = 〈h〉(1 − 〈h〉).
For the depletion model, we postulate that release of a quantum can occur only if the presynaptic state is full (9,10). We also assume full recovery between repetitions of stimulus trains. At any stimulus j, there is a pj (output probability if a site is full) and an fj (probability that a site is full). The mean quantal content, 〈mj〉, has an expected value of pjfj; the net probability of release. The variance is 〈mj〉(1 − 〈mj〉) = 〈mj〉(1 − pjfj). The outputs are binomially distributed with parameters N = 1 and Pj = pjfj, with Pj evolving in the train as fj evolves (see below), even if pj is constant, to equilibrium or final values, indicated by a subscript f. At equilibrium, 〈mf〉 = pf ff and var(mf) = 〈mf〉(1 − pf ff), within trains as well as between trains.
The amplitude of responses at each j must have an average, 〈Qj〉. If amplitude changes with stimulus number (desens), this is more conveniently expressed as 〈Q〉〈hj〉, where 〈hj〉 is the mean fraction of the initial Q value. The mean unit signal (〈uj〉) has the expected value 〈Q〉hj〈mj〉. The coefficients of variation in transmitter per quantum (cvwj) and postsynaptic kindliness (cvhj) contribute to 〈mj〉〈Q2〉〈hj2〉 = 〈mj〉〈Q〉2〈hj〉2(1 + cvw2)(1 + cvh2), in which the j subscript has been dropped, for brevity, from the cvs. We include variation in response per quantum due to stochastic components (appreciable if there are few channels per unit response) in cvw.
Equating means and expected values,
If release of a quantum of transmitter causes an “empty” presynaptic state (depletion), a response at stimulus j in a train implies no response at j + 1 if there is no “refill”; the first covariance (mean product = 0, minus product of means) is cov(uj,uj+1) = −〈uj〉〈uj+1〉. Total desensitization gives the same result, because a zero response to a quantum is indistinguishable from the absence of a response. By the same logic, 〈uj+1〉 and var(uj+1) must also be the same as for the depletion model—hj+1 becomes <1 and cvh becomes >0, because null responses are included in both.
Realistically, there must be some probability (αj) of refill and/or a rate of recovery from desensitization (αH). The only case in which desens produces fairly simple equations is when there is always the same h, call it d1, when the antecedent stimulus elicited release. If desensitization is total, and desensitized receptors produce no response, d1 = αH. Whenever there is a response at j, the probability of a quantum being released at j + 1 is the product of probability of refill and probability of release, i.e., pj+1αj.
Therefore, for depletion and/or desens,
Similarly, cov(uj,uj+2), cov(uj,uj+2), etc., can be found by considering the overall probability of a quantum appearing at j + 2, j + 3, etc… if there is one at j, and its expected amplitude. However, the resulting equations are unwieldy and give little insight.
Average signals
Immediately after release, the average fraction of sites with an available quantum is reduced from fj to fj(1 − pj). A subsequent refill adds αj(1 − fj(1 − pj)). Therefore, one has a recurrent relationship, starting with f1 = 1:
| (1) |
Eventually, p and α go to equilibrium (final) values pf and αf; The final ff = fj = fj+1 is
| (1a) |
If α and p are constant, defining γ ≡ (1 − α)(1 − p), (fj − ff) falls geometrically with parameter γ for each increment in j (9). Average signals parallel fj if there is no desens. Note that a pure depletion model corresponds to d1 = αH = 1, whereas setting all αj equal to 1 gives pure desens with all fj equal to 1.
Two finite summations (nominally of all values), using fj, give relationships that are potentially useful for determining the number of release sites:
| (1b) |
| (1c) |
Signals from N sites
Real signals will generally arise from a set of N sites, each with a 〈Q〉. If all sites are the same with regard to p, α, and αH, then means, variances, and covariances are simply multiplied by N, and wherever 〈Q2〉 occurs in the above equations, with 〈u〉 fully expressed, there is multiplication by (1 + cvb2), where cvb is the between-site coefficient of variation of Q. Extra terms are generated by any nonstationarity between trains, e.g., if 〈Q〉 gradually falls as stimulus trains are repeated. Thus, given a certain homogeneity, and assuming that release of transmitter at different sites is such that their signals add linearly, Eqs. 1a–1c apply, and the above equations for uj become
| (2) |
| (2a) |
| (3) |
| (4) |
Here, δ2 is the square of the coefficient of variation, corresponding to any nonstationarity. For example, if 〈Q〉 falls by a factor of 1.5 over 20 trains, δ2 will be 0.0155, which is not negligible if N = 100. An important point is that for all k, cov(Sj,Sj+k) contains the extra term δ2〈Sj〉〈Sj+k〉, whereas otherwise all covariances decline with k. This makes it possible (with caveats) to find δ2(see below). In contrast, it is in principle not possible to find cvb, cvw, or cvh. Below, we assume δ2 to be negligible, or dealt with, until returning to the problem it presents.
With partial desens, the equations remain valid, but with d1 > αH and a function of j, pj, and αj. It is worth noting that a little algebra shows that the slope of a scatter graph of Sj+1 versus Sj, cov(Sj,Sj+1)/var(Sj), is independent of (1 + cvb2), 〈Q〉, and N. Without desens, and with negligible cvw2 and α1, cov(S1,S2)/var(S1) = −p2.
If all sites do not have the same p, α, and αH, the evolution of fj is different at each site, resulting in mean equilibrium signals (Sf) that are dominated by sites with the highest ff (and/or αH). If these have Q higher or lower than average, estimates of the final Q will reflect these Q values, but it must be borne in mind that in such cases cvb is not negligible. The equations for var and cov also become more complicated (see (10)).
Without desens, d1 = hj = 1. Using 〈Sj+1〉 = N 〈Q〉pj+1fj+1,
and with γj ≡ (1 − pj)(1 − αj), fj+1 is αj+fj γj. Hence,
| (4a) |
Following the same logic, we obtain
etc.
At equilibrium, for any k,
Thus, all covariances are negative. With no desens, constant α and p, and γ ≡ (1 − p)(1 − α), the covariances fall geometrically to the equilibrium with parameter γ for each increment in j (9). Exclusively negative covariances are also produced by desens.
Estimation of p and α assuming constant values
Any train in which signals run down smoothly to an equilibrium can be characterized by a p and α corresponding to a depletion model with no desens and unchanging parameters. Then, every fj = sj = 〈Sj〉/〈S1〉 and, from Eq. 1a, at equilibrium fj is ff = α/(α + p − αp); for any arbitrary p, there is a corresponding α = pff/(1 − ff + pff), and a unique predicted set of sj—there must exist a p/α pair that gives a least-squares best fit to the observed sj series. The apparent p and α (pA and αA, respectively) are of course merely descriptive parameters unless the assumptions are valid and deviations of real sj from theoretical fj may be of interest. However, simulations show that goodness of fit may not be much affected by depletion and/or p and α increasing or decreasing in the train. This arises because changing p and α do not necessarily entail much change in ff. Conversely, poor fits of real sj to theoretical fj do not distinguish between depletion, with changing p and/or α, and alternative scenarios (Pdown or Ndown). Because desens causes exaggeration of the signal fall early in the train, it produces a pA greater than the p, corresponding to decline of quantal contents in the train. Simple depletion with a compound binomial (p varying between sites (10)) yields pA ≅ 〈p〉(1 + cvp2), and poor fits of sj to theoretical fj, for the first few j.
Monte Carlo simulation gives (for 20 trains and 10 equilibrium signals) sampling errors (SE) of ∼9% of (1 − pA) for pA and ∼5% for αA, unless sf is >∼0.6 and/or pA is <∼0.3, which raises the SE. For any set of data, the SE can be estimated by making ∼100 pseudotrains with Sj constructed from true 〈Sj〉 and random Gaussians scaled by the standard deviations at each j and going through the same computer subroutine with each train. As described below, having pA allows estimation of apparent N (NA) and 〈Q〉 (QA) and their SEs can be estimated at the same time.
Correction for nonstationarity: finding δ2
Of course, the best method of dealing with nonstationarity is to minimize δ2 which can be done if there is a slow trend in Q, by calculating var and cov between adjacent trains (11), with little increase in SE.
A value of δ2 (actually δ2 plus terms involving 〈Q〉 and N) can readily be found, since, if 1/N is negligible, it is the sum of all cov between signals divided by the sum of all cross products of signals (〈S1〉〈S2〉, 〈S2〉〈S1〉, 〈S2〉〈S3〉, etc.). Summing all amplitudes in each train, the variance of these sums (varT) is the sum of var (Σvar) plus the sum of all covariance between signals. The square of the mean sum of all S (〈ΣSj〉2) is Σ(Sj)2 plus the sum of all cross products. Thus, ignoring complications,
For true δ2 = 0, this gives zero values when there is zero covariance (Pdown and Ndown3 scenarios), and positive values with true positive covariance (Ndown1 and, especially, Ndown2). With depletion, apparent δ2 is negative, but much smaller than −1/N, (e.g. −0.003 for N = 50, p = 0.4, ff = 0.25), because most covariances are much smaller than −〈Sj,〉〈Sj+1〉/N; for any particular pA and αA given by data, the expected value of δ2 can be calculated. Because desens introduces or exaggerates negative covariance, it shifts the apparent δ2 in the negative direction. The SE of apparent δ2 is very low and its difference from the expected value is by far the most sensitive indicator of desens plus depletion (e.g., –0.0020 ± 0.0006 for 〈Qf〉/〈Q1〉 = 0.65). However, even small nonstationarity erases this measure and true desens also erases much of the distinction between scenarios.
Given putative δ2, all variances and covariances can be corrected by subtracting 〈Sj〉2δ2 from variances and 〈Sj〉〈Sj+1〉δ2 from covariances, and dividing variances by 1 + δ2. This poses a problem. Should one use apparent δ2 even if it is negative, δ2 only if it is positive (correcting for nonstationarity), or use δ2 minus the expected value? The answer is that none of these options is appropriate for all scenarios, but simulations show that the choice makes little difference. Each option gives variances and covariances that are virtually the same as in the absence of nonstationarity (except for a fairly small increase in SE). However, using negative values of δ2 shifts true negative covariances in the positive direction (theoretically visible in cov(Sj,Sj+k), with k > 4 or so) and where there are true positive covariances (Ndown1 and Ndown2), the correction with δ2 reduces or reverses the covariances. In Ndown2 scenarios, where growing positive covariances produce a false positive δ2, the correction produces a large negative cov(S1,S2).
Eliminating covariances arising from mutual correlation with other signals
An alternative method for dealing with nonstationarity is to correlate each Sj in a train with the sum of the others, subtract from each Sj the amount given by this correlation, and calculate the variances of the residuals. For covariances, the correlations are with all points except the two being correlated. By and large, this gives less complete correction for nonstationarity than using apparent δ2. However, with low-level or no nonstationarity, it has the advantage of giving true variances and covariances, with the notable exception of Ndown2, for which the positive covariances are reduced to near 0 and variances are altered to make var(Sj)/〈Sj〉 constant.
Estimates of quantal amplitude
In the absence of nonstationarity (and without correction for putative δ2), derived values that approximate 〈Qj〉 at each j are
| (5) |
and various “corrected” vmjs,
| (6) |
| (6a) |
| (7) |
| (8) |
Note that every vmj and corrected vmj is multiplied by (1 + cvb2) and, correspondingly, N′, Pj′, Ncov, and Nj′ are divided by (1 + cvb2). The diversity of estimators is useful for determining which model best corresponds to the observed data (see below).
We have phrased Eq. 6 in terms of N′, because all methods of finding N use vm that is intrinsically biased by the coefficients of variation that go with 〈Qj〉. The variant cvmj = vmj/(1 − Pj′) merely rephrases the problem of how to find N′ in terms of finding appropriate Pj′ values. Equation 6a circumvents this problem with the assumption that 〈hj〉pA/p1 is 1, and, if this is so, gives Qaj = 〈Qj〉(1 + cvb2)[1 + (1 + cvw2)(1 + cvh2)/(1 − pjfj)]. Continuing with the simplifying assumptions, that pj is constant and equal to pA, the equilibrium value of Qaj (call it QA rather than Qaf), which is vmf/(1 − pAsf) also provides an estimate of N′ (call it NA) as 〈S1〉/pA/QA (which is (〈S1〉/pA − Sf)/vmf), since 〈S1〉 = p〈Q〉N. Using NA for N′ and then averaging equilibrium values of cvmj, or using cvmf = vmf + Sf/NA, gives cvmf the same as QA. For 20 trains and 10 available equilibrium values of 〈SJ〉 (j > 4), the SE of QA came close to ±10%, whereas the SE of NA was ∼±11%, unless sf was made >∼0.6 and/or pA <∼0.25, producing larger SEs. Individual values of cvmj and Qaj had SE ∼ ±30% (for 20 trains). With the single exception of Ndown3, characterized by depletion with constant p and α, or a series of 〈S〉 mimicking depletion, QA and NA were found correctly; the error with Ndown3 arises from vmf not approximating 〈Q〉, etc. With the depletion model, an initially high α, falling to half its final value, produced negligible error in QA but an NA of 135% of the true value, arising from an underestimate of pA. In general, errors in pA arise from a decline of early signals not conforming to the depletion model with constant α and p, or because QA is lower than the initial 〈Q〉 (desens).
Equation 7 is an example of correcting vmj using a constant putative N, Ncov. Note that 1/Ncov may be zero (Pdown, and Ndown, without desens), in which case cvm′ j is the same as vmj. With between-train nonstationarity, 1/Ncov can be negative, but cvm′ j is the same as without nonstationarity.
Equation 8 differs from Eqs. 6 and 7 in that it uses, for putative N, a value Nj′ obtained from cov(Sj,Sj+1)/〈Sj+1〉 at each j, rather than a constant (11,12); positive covariances (Ndown1 and Ndown2) produce Qcj < vmj. Allowing, in effect, negative N, results in Qcj being unaffected by nonstationarity. SEs of Qcj are ∼1.2 times those of cvmj, and equilibrium values are about halfway between cvmj and vmj for the depletion model. A variant of Eq. 8 is to use vmj − cov(Sj,Sj-1)/〈Sj-1〉, but this is nearly the same as Qcj and is unavailable for j = 1, which is of particular interest.
Clearly, for estimates of 〈Qj〉 better than vmj, using Eq. 6 is preferable to using Eq. 8 to obtain Qcj, since each cov(Sj,Sj+1) is prone to sampling error and the resulting 1/Nj′ is also intrinsically subject to bias that is not independent of j. The validity of Eq. 6 also does not depend on covariances fitting the depletion model. However, using NA for N′ is as open to question as are the underlying assumptions. Nevertheless, it turns out that cvm is rather insensitive to error in putative N′ if sj is <∼0.5. Without desens and pj = p1, making fj = sj, if sj = 0.4, a guess of p1 = 0.4 gives cvmj = 1.19 vmj, whereas p1 = 0.6 gives cvmj = 1.32 vmj. The first guess corresponds to an N′ that is 1.66 times the N′ of the second guess. In other words, systematic error in the estimate of N′ as NA, as arises with desens, hardly affects QA.
Note that the (1 + cvh2) in Eqs. 5–8 cannot be omitted, since otherwise one could distinguish, if recording at a single site, between signals of zero amplitude and absence of signals. Monte Carlo simulations show that with pure desens, 〈hj〉(1 + cvh2) tends to remain close to 1 early in trains. That is, desens implies high variance of quantal amplitude after the first signal. As a result, vmj (and notably Qcj) does not parallel 〈hj〉. This effect is mitigated if there is also depletion so that sites with antecedent responses contribute less to signals. At equilibrium, cvh2 becomes relatively low (∼0.1–0.2), but not negligible.
Quantal size from variances within trains
Implicitly cov-corrected estimates of 〈Q〉〈hf〉 are obtainable without using variances or covariances between trains. This arises because when signals have run down to (or near) equilibrium, the expected values of 〈2Sj − Sj−1 − Sj+1〉 is 0, but the expected value of the mean-square of (2Sj − Sj-1 − Sj+1) is
Since the expected values of means and variances are nearly the same for the three signals, and the covariances are nearly the same, one has for each trio of signals in each iterated train an estimate of quantal size (Q3). One can make averages between and/or within trains:
| (9) |
| (9a) |
The calculation is identical to obtaining variance within groups of three with correction for linear regression (cf. (5)), where groups of five were used, producing less appropriate subtraction of covariances). Averaging the squares and then dividing by 6〈Sj〉 or 6Sf or 2(〈Sj〉 + 〈Sj−1〉 + 〈Sj+1〉) makes a negligible difference, and any of these is preferable when quantal contents are so low as to produce failures. Using mean values of Q3 at each j from each train, and then averaging to obtain overall Qt, the SE is ∼1.2 times the SE of Qcf. Simulations show that Qt is indistinguishable from Qcf. The between-train variance of 〈Q3〉 or its regression with sums of signals in trains are both of negligible value in finding between-train nonstationarity.
With Ndown1, because it produces positive covariances, Qt and Qcf are both less than vmf by ∼15−20%; with Ndown2, because the positive covariances are relatively large for equilibrium signals, Qt and Qcf can be as little as half of vmf. These differences from vmf are much reduced if there is also desens.
Alternatives for finding N
Evidently, NA and QA are biased (see above), even if p is pA and ff = sf. From Eq. 5, vmf is actually 〈Q〉(1 + cvb2)(1 + cvw2)(1 − Sf/N/(1 + cvw2)); cvmf (QA) turns out higher than true 〈Q〉 by a factor of a little more than (1 + cvb2)(1 + cvw2), and NA < N by the same factor. With desens, QA approximates 〈Qf〉(1 + cvh2)(1 + cvb2)(1 + cvw2), with various biases tending to cancel, except in the case of Ndown3 (where vmj is constant if pj is constant). With desens or depletion, NA is biased upward and cvm1 < Qa1. Moreover, models in which α is not constant but rises or falls from an initial value show a systematic bias in pA (high with falling α), and since NA is calculated as 〈S1〉/pA/QA, the same bias appears in it. It would therefore be desirable to have an alternative estimate of N or N′. However, it should be recognized that without assumptions as to the evolution (or constancy) of 〈Q〉, p, and α, there is no valid way of obtaining N.
The method of plotting 〈Sj〉s versus their accumulated sum (5) can immediately be ruled out: as with NA, it depends on the assumption of unchanging 〈Q〉 but also completely neglects α; it consistently overestimates N and fails when sf > ∼0.15.
The relationships in Eqs. 1b and 1c give alternatives for finding N, but again with the assumption of constant p = pA, 〈Q〉 = QA, and α = αA. Since each 〈Sj〉 = Np〈Q〉fj, it follows from Eq. 1b that Σ(〈Sj〉 − Sf) = NpA〈QA〉(1 − sf)/(1 − γ), and from Eq. 1c that Σ(〈Sj〉 γj−1) = NpA〈QA〉(1 + γsf)/(1 − γ2). Excluding 〈S1〉 from each summation, the multiplying terms are the same minus (1 − sf) and minus 1, respectively. In simulations, with simple constant p and α, all four options give values for N nearly the same as those for NA with, perhaps surprisingly, much the same SE. Mutual ratios, in particular NC2/NB2, showed high sensitivity to even small deviations from constant p/α behavior, as occurs with desens as well as evolving p and/or α.
Correlation of vmj and 〈Sj〉
In the absence of desens (and nonstationarity), Eq. 5 gives vmj = (1 + cvb2) (〈Q〉(1 + cvw2) − 〈Sj〉/N). Plots of variance/mean versus mean (cf. (7)), (with noise variance subtracted from var) yield a linear regression (y = a + bx) with least-squares best fits for “1/Nx” = putative 1/N (b = −(1 + cvb2)/N) and “Qx” (extrapolated vm at 〈Sj〉 = 0) = 〈Q〉(1 + cvb2)(1 + cvw2). Plots of var(Sj) versus 〈Sj〉 (quadratic) produce identical numbers given appropriate weighting and treatment of noise variance.
Simulations show that Qx has the advantage of being unaffected by nonstationarity, and has an SE only ∼1.1 times the SE for QA. Moreover, the method depends on no assumptions regarding p and α, although the assumption of a depletion model (or mimicking Pdown) with no desens is implicit. At worst, with desens, Qx is close to vmf.
A high SE of 1/Nx—Nx can be approximately infinite—makes Nx scarcely useful as a substitute for NA as “true” N, unless a large number of trains are available, and between-train nonstationarity can be ruled out or eliminated using δ2. Uncorrected nonstationarity, which can produce vm1 > vmf, makes 1/Nx too small, 0, or negative.
Otherwise, 1/Nx is of interest as an indicator of which scenario best fits the data. Without desens the nominal NA/Nx (product of NA and 1/Nx) has a value close to 1, with SE ∼0.6 (again with 20 trains), except in the case of Ndown3 (vm is constant with no nonstationarity or δ2-corrected), where it is 0. Correcting vm using apparent δ2 gives an undetectably small reduction of NA/Nx with depletion (e.g., to 0.8), but a large increase with Ndown2 to 2 or more. In other words, Ndown2 and Ndown3 can be identified in this way. With desens, NA/Nx becomes negative with all scenarios, about −0.3 with depletion, Pdown, and Ndown1, about −1 and −2 for Ndown2 and Ndown3 (with higher SE); the negativity is exaggerated with δ2-corrected vm (except Ndown2). That is, although the distinction between scenarios is largely lost, at least desens can be seen.
Correcting vm for putative mutual covariance with other signals in the train (see above) uniquely changes NA/Nx with Ndown2, to near 0 (except with desens, where values are near −1). It also uniquely leaves positive NA/Nx with desens/depletion (values of ∼0.5, SE ∼ 0.7).
Distinguishing between scenarios and validity of estimates
It is evident that whether any set of real data agrees with one or another model is easily ascertained if there is no desens. In this regard, only depletion produces negative covariances, and positive covariances (except at j = 1) are large with Ndown2 and small but visible (Qcf = Qt < vmf) with Ndown1. Zero covariances occur with both Ndown3 and Pdown, but the former contrasts with the latter in that vmj does not rise as 〈Sj〉 falls, yielding 1/Nx = 0. One also has the differences in NA/Nx produced by the alternative corrections for nonstationarity described in the previous section. A decline in Qa to the equilibrium value, QA, signals desens. However, desens in conjunction with any of the models confuses matters, because the covariances that are the major discriminants between scenarios become negative. Therefore, it is essential to determine whether there is desens before concluding that negative covariances indicate the depletion model. There may also be modification of data and derived values arising from nonlinear summation in signals. The latter must be considered when deciding how data may be used to distinguish between models, and therefore, implicitly, what validity can be attributed to estimates of quantal amplitude.
Nonlinear summation
With excitatory or inhibitory postsynaptic potentials (EPSPs or IPSPs, respectively), all signals are subject to nonlinear summation (20,21), and this also applies to EPSCs or IPSCs if the voltage clamp is imperfect. This is always the case, because synaptic cleft voltage cannot be clamped, but it is especially the case if signals are generated at some distance from the recording point, on dendrites or muscle fibers with spatially distributed release sites (frogs, crustaceans). The functions involved are complex, because current flow causes voltage change, which modifies channel kinetics as well as current flow through channels. However, going through the calculations for various possibilities gives, as a generally useful approximation, measured Sj close to true Sj/(1 + trueSj/c), where c is a maximum possible S, for measurements of either signal height or area, provided that S < ∼c/2. If maximum S < ∼c/4 effects on signal configuration are invisible. True variances and covariances are close to the variances and covariances using measured values divided by (1 − 〈S〉/c)4 (derived by Vere-Jones (22)), whereas true means are close to 〈S〉/(1 − 〈S〉/c). The net result is a major underestimate of vm for the largest signals (S1); e.g., with c = 10〈S1〉, vm1 (and cov(S1,S2)) will be underestimated by ∼27%; with c = 5〈S1〉, the underestimate is ∼50%. However, when signals run down, the errors in vm and covariance become much less, and there is very little error in Sf that is very small. The net result is only a modest underestimate of QA and pA and an overestimate of NA, and signaling of nonlinear summation by Qa1 < QA (cvm1 is less reduced), provided sf < ∼0.4.
The smaller error in smaller signals results in plots of vmj versus 〈Sj〉 yielding down-biased estimates of Nx. Indeed, an infinite N (Poisson release) will look like binomial release with spurious N roughly equal to c/Q. However, the high SE of NA/Nx and up-bias of NA makes this a poor indicator of nonlinear summation.
Given that the net effects on NA and QA are not large, and there is no doubt as to whether covariances are present, there would seem to be little reason to attempt correction for nonlinear summation, except with regard to EPSPs and IPSPs where c can be guessed as the difference between membrane potential and equilibrium potential for the transmitter (20,21). However, there is a basic problem in that the effect of nonlinear summation (Nonlin) is almost exactly the converse of desens, and with both Nonlin and desens, the two effects can effectively cancel. In general, the possibility of nonstationarity in conjunction with desens excludes the unambiguous interpretation of negative covariances as indicating depletion, and with Nonlin, one loses the decline in Qa (or cvm) values that otherwise characterizes desens.
The one case where the coexistence of Nonlin and desens is detectable is when there is no nonstationarity (true δ2 is 0). Then, because covariances and variances are modified to the same extent by Nonlin, the value of varT/Σvar, and therefore of (negative) δ2, is little affected; a value less than expected for simple depletion indicates desens, and the failure of early Qa and cvm to be greater than the final values then indicates Nonlin. To find desens even with small nonstationarity (total range of 〈Q〉 >∼1.2-fold), the best indicators using Qa become the weighted means of the first four Qas ((a) weights = fj − ff); (b) weights = fj/(1 + fj/4) − ff/(1 + ff/4), with f calculated from pA and αA), and SEs are such that ∼200 trains are required to see this, with c = 4〈S1〉.
There remains one indicator of desens that is nearly independent of Nonlin. In principle, if there is desens, it should be greater the more signals run down in trains (i.e., proportional to stimulation frequency), which should be reflected in QA.
Relationship between refill probability (α) and pool-refill rate (rα)
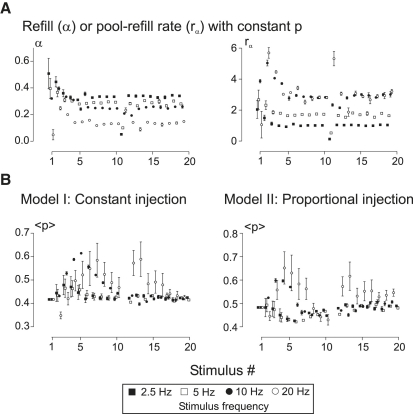
The depletion model for signal rundown in trains was historically phrased in terms of depletion and refill of an “available pool” of quanta (4–6). This pool corresponds to Nfj. With sites being at any moment refilled, in proportion to the deficit, from a back-up pool that remains full, in the time between stimuli, Δt, and designating A(t) as the amount available, as a fraction of 1, we have the differential equation, dA(t)/dt = rα(1 − A(t)), where rα is the pool-refill rate. It follows that the unfilled fraction declines exponentially: 1 − A(Δt) = (1 − A(0)) exp(−rαΔt). However, α is the fraction of unfilled sites that are refilled, i.e., α ≡ (A(0) − A(Δt))/(1 − A(0)), and 1 − α = (1 − A(Δt))/(1 − A(0)). Hence, α = 1 − exp(−rαΔt) and rα= −ln(1 − α)/Δt. Therefore, stimulation at different frequencies allows determination of whether pool-refill rate is dependent on stimulation frequency.
Finding quantal contents
It is evident that the quantal content at stimulus j should be 〈mj〉 = 〈Sj〉/Qj′, where Qj′ is any one of the estimates given by Eqs. 5–7. However, this is close to 〈Sj〉/〈vmj〉 and (from simulation) this value is up-biased because sampling vagaries in 〈Sj〉 and 〈vmj〉 are correlated. If there is no desens, 〈mj〉 = 〈Sj〉/Q′, with Q′ any equilibrium estimator of Q, is to be preferred. However, values of 〈Sj〉/〈S1〉 are then the same as 〈mj〉/〈m1〉. In general, all data regarding m is provided by 〈S1〉, alternatives for Q′, and plots of 〈Sj〉/〈S1〉 and Qj′ /Q′, versus j.
Jumps after an omitted stimulus
These give added information at little cost. If, at equilibrium, with final values pf and αf, a stimulus is omitted (pj+1 = 0), there is extra refill in the next Δt. At j + 1, the system does not “know” the stimulus is to be omitted, and therefore fj+1 = ff. Designating α′ as the α for the next Δt, fj+2 = α′ + ff (1 − α′), with ff = αf/(αf + pf − αfpf) Hence, fj+2/ff = 1 + pf α′ (1/αf − 1), and if p and 〈Q〉〈h〉 are unchanged by the gap, this will also be the ratio of 〈Sj+2〉 to 〈Sj〉. Thus, 〈Sj+2〉/〈Sj〉 ≠ 1 + pf(1 − αf) indicates a change in parameters during the extra recovery time provided by the omitted stimulus. From the simulation, it turns out that the SE of the jump is quite low if one uses the average of four or five 〈Sj〉s before the omission instead of 〈Sj〉, but is very much higher for estimated quantal size. For example, with pf = 0.6, α′ = αf = 0.2 and no desensitization, the simulation gave, for 20 iterations, jump = 1.48 ± 0.1, jump_Qc = 1.01 ± 0.5, and jump_cvm = 1.01 ± 0.34. Averaging estimates of the jump from each train is to be avoided, because it gives a very high SE and an upward bias.
Finding all α and p
Assuming Q (and its variation) to be constant, the equations fj+1 = αj + fj(1 − αj)(1 − pj) and sj ≡ 〈Sj〉/S1 = pjfj/p1 imply a unique set of αj for any assumed set of pj: at each jfj+1 = pj+1sj+1/p1 and the first equation then gives αj. Conversely, any preset array of α yields an array of p that exactly fits the observed sj array. No further information is available from vmj. The sole constraint is that derived α or p must not be negative or >1. Theoretically, with values of cov(Sj,Sj+1)/var(Sj), it is possible to obtain all α and p without assuming a set of α or p—the relevant equations are readily deduced—but it turns out that the derived ps are largely governed by the covariances. If, from sampling error or reality, covariances are excessively negative, p becomes >1, and covariances that are near 0 or positive produce p that is near 0 or negative.
Measurement of signals
This is generally not a trivial problem. All the above equations assume that S accurately represents the sum of signals from N sites. In reality, the signal seen is the sum of signals initiated at different times (23), each being the convolution of an impulse function at its time of generation with the time course of channel opening and the time course of channel closing. The latter have stochastic components that can be ignored only if the number of channels opened by each quantum is not small. In theory, the only correct measure is the area of the signal, but in practice this is prone to error because of baseline uncertainty. Such error is reduced if the signal is made briefer by using the augmented derivative of the record (yi) − zi = (yi − ayi-1)/(1 − a), where a = exp(−1/τ); z(t) is the “deconvoluted” waveform − using for τ the main time constant of signal decay, presumably the τ of channel closing. However, smoothing z(t) with a τ high enough to make its peak later than the time period encompassing the bulk of z(t) will have at this peak (and everywhere after) a value proportional to the area of z(t), and this smoothed waveform may already be available as the original signal. However, there are two more considerations. Measurement should not be made at a time when there is an appreciable but ill-defined tail of an antecedent signal. With decay τ more than one-fourth the time between stimuli, to avoid artifactual covariances it may be better to use areas of deconvoluted signals rather than subtracting from the peaks extrapolated tails of previous signals. Second, a computer program will always find a maximum in the allotted time window, from noise or a spontaneous event, even if there is no true signal. A simple alternative to peak height is to determine the time at which the peak value occurs in the average of signals, and to measure all signals at this time.
Covariance of records with signal heights: maximizing detection of covariance
One method of detecting covariance is to measure the heights of the first signal (S1) in each train and obtain the covariance of S1 with every point (yi) in the records of each train for the first few stimuli. Even if the signals are superimposed on the tails of previous signals, the covariances are visible as bumps at the times of the signals, superimposed on the positive covariances generated by (self) covariance of S1 with the tail of the first signal. Provided other signals can be measured unambiguously (i.e., well separated from residua of previous signals) the same can be done with S2, S3, etc. It can readily be shown that the time course of every bump covariance (including the self-covariance) should have the same time course as the signal itself, with two provisos. The S with which the correlation is made must adequately reflect the area of the signal, and time dispersion of quantal release in each signal must be random rather than reflecting differences in latency of subpopulations of sites. Any noncorrespondence of time course is made much more obvious by doing the correlations with deconvoluted records (zi; see above).
Individual values of covariance between signals at equilibrium have a high sampling error, but a negative average is implied by Qcf and Qt larger than vmf, whereas a positive average is indicated by Qcf and Qt less than vmf.
Nonhomogeneous sites: “compound binomial”
Early in trains, the first fall, 〈S1〉 to 〈S2〉, is more than with homogeneous sites. Final (equilibrium) 〈S〉 and estimated 〈Q〉 arise mainly from sites with relatively high final α and p, because final quantal content at a site is higher with high final α and/or p. This affects estimated 〈Q〉 only if Q is correlated with α and/or p. With desensitization, this effect is modified, since high quantal contents imply lower 〈hj〉.
Branch or whole axon failure of afferent action potentials
If stimulation fails intermittently at groups of sites that constitute a substantial fraction of N, and not at the same stimuli at which trains are iterated, the result is a large increase in vm and correspondingly false estimates of quantal size. The error is readily detectable unless the failure of stimulation of release sites is as likely for early as for late stimuli in the trains.
Sites releasing more than one quantum
If single sites can release more than one quantum at each stimulus, it makes no difference to means, variances, and covariances (except for NA rising in proportion) unless the probability of release of a quantum is altered by whether or not another is released. Any tendency for two or more quanta to be released together produces raised vm and derived values, and reduced apparent N.
Release-modified α and p
Models in which the α for refill after a stimulus is increased by the output (and previous outputs) at a site (or group of sites) can produce sequences of 〈Sj〉 and variances that resemble those generated with a simple model (constant α and p) but add a positive component to the negative covariances produced by depletion—a net positive cov(Sj,Sj+2) is always largest at equilibrium and least for cov(S1,S3). Making α absolutely contingent on output history gives slow drift of 〈Sj〉 either to zero or to 〈S1〉. Modifying p by previous outputs generally produces sets of 〈Sj〉 and, especially, vmj (note that these use between-train variance) that differ substantially from those produced by a simple model.
Sampling errors
SEs of vm (i.e., the between-stimulus-number standard deviation of average between-train variance/mean) and all corrected vm values are independent of N and dominated by the SE of variance, since the SE of means is relatively negligible; with ni representing the number of values over which variance is determined, this is SEv = SE(var)/〈var〉 = 0.1 × (200/ni)0.5, i.e., ±10% for ni = 200 iterations, and ±32% for ni = 20, for Gaussian variables, and (checked with 10,000 randomly generated values). The same applies for binomial variates with p < ∼0.8 – at p > 0.9, where the SE becomes noticeably more. Thus, with 10 estimates of equilibrium vm, each at one stimulus number, the expected SE of vmf is ±10%. If variances are determined in smaller groups the SD of variances (or vm) increases somewhat. Given ni = 20, taking averages of two variances each determined in groups of 10, the SE goes from ±32% to ±32.5%, averages of four variances from groups of five gives ±34.5%, and averages of 10 variances from groups of two gives ±43%, although the average variances do not differ. Thus, SEs of vm are in principle somewhat raised if variances (and covariances, see below) are determined between adjacent pairs of iterated trains (11), to minimize positive covariances and excess variance arising from nonstationarity, instead of using differences in each iteration from overall averages. In the same simulations, SEs of Qt (eliminating any contribution of nonstationarity to variances) came out somewhat higher (±55%) than vm using adjacent pairs.
The above numbers are absolutely stereotyped, and all models invariably produced these values for the SEs of vm, those of QA (or cvm) being lower by the factor (1 − pAsf), ∼0.8–0.9. However, with models modified in various (implausible) ways (e.g., cycling of p) to produce a component of between-train variances that was common to all the stimulus numbers (at equilibrium), the SEs of vmf could be reduced, roughly in proportion to the increase in variances above that arising from the binomial nature of outputs.
The sampling error of cov(Sj,Sk), which was independent of its value, came out between 70% and 90% of SEv multiplied by (var(Sj)var(Sk))0.5. In terms of percentage (given that average values are appreciable), this increases greatly as signals decline. For example, with a simple depletion model, with negligible α and p constant at 0.5, with 20 iterations, the sampling errors of cov(S1,S2), cov(S1,S3), and cov(S2,S3) came to about ±40%, ±60%, and ±100%, respectively. Despite the high sampling errors of covariances, sampling errors of Qc are uniformly ∼1.1–1.2 times SEv. Using any reasonable value of N′, the corrected vmj has the highest SE at j = 1 and progressively less as the correcting term becomes closer to 1. Accordingly, SE of QA (cvmf) were generally lower than those of vmf in proportion to this factor (1 − pAsf), ∼0.8–0.9.
Thus, with 20 iterated trains and 10 S in each at equilibrium, for seeing desens, one has a value of QA ± 9%, and early signals (before desensitization is complete) each with a Qa of ±28%. Consequently, Qa1/QA has a sampling error of ±26%. If 〈Q〉(1 + cvh2) declines by 40%, one needs approximately three repeats (or data from three cells, or at three different stimulation frequencies) to see the reduction with a “t” test with P < 0.05. Using four early Qas, depending on how fast quantal size goes down, the decline should be seen in one or two sets of data.
Methods
Slice preparation
The Animal Care Committee at The University of British Columbia approved these experiments on young adult Sprague-Dawley rats. Rat brain at age P12–15 presents favorable conditions for proper formation of patch-clamp seals, due to a lack of extensive myelination. Animals were decapitated while under deep isoflurane anesthesia. The brain was quickly removed (in ∼1 min) and immersed for 1–2 min in ice-cold (∼0°C) sucrose solution. The sucrose solution contained (in mM) 248 sucrose, 26 NaHCO3, 10 glucose, 2.5 KCl, 2 CaCl2, 2 MgCl2, and 1.25 NaH2PO4. The brain was quickly transferred to artificial cerebrospinal fluid (ACSF), which had the composition (in mM) 124 NaCl, 25 glucose, 3 myoinositol, 2 Na-pyruvate, and 0.4 ascorbic acid (∼320 mOsm). On saturation with 95% O2 and 5% CO2, the ACSF was adjusted to a pH of 7.3–7.4. The brain was trimmed into a cube and, with a Vibroslicer (Campden Instruments, London, United Kingdom), cut into 250-μm sagittal slices for whole-cell recording. The slices were cut in a coronal plane that intersected with a sagittal plane at a 45° angle. The slices included portions of the ventrobasal thalamus and nucleus reticularis thalami (nRT), and importantly preserved fibers of the internal capsule. The slices were incubated for 2–6 h in ACSF until required. For recording (at 22–25°C), the slices were perfused in a submersion type of chamber (∼0.3 mL) on a Nylon mesh with oxygenated ACSF and drugs.
Whole-cell recording
Voltage-clamp recording was performed in the whole cell configuration with microelectrodes (resistances, 5–8 MΩ) and an Axoclamp 2A amplifier (Axon Instruments, Foster City, CA). To minimize capacitance, the volume of the recording bath solution was lowered and the electrode was coated with Sylgard. EPSCs were sampled at 20 kHz and filtered at 1 kHz. pClamp 8.2 software (Axon Instruments) was used for data acquisition, storage, and analysis. The electrode solution contained (in mM) 125 Cs-gluconate, 20 TEA-Cl, 3 QX-314 (the lidocaine derivative), 10 N-2-hydroxyethylpiperazine-N-2-ethanesulfonate (HEPES), 5 Na-phosphocreatine, 4 Mg2+-adenosine 5′-triphosphate salt (MgATP), 0.4 Na+-guanosine 5′-triphosphate (NaGTP), and 10 ethylene glycol-bis-(β-aminoethyl-ether)-N,N,N′,N′-tetraacetic acid (EGTA). MgATP, EGTA, NaGTP, HEPES, QX-314, CsCl, and the inorganic chloride salts were obtained from Sigma (St. Louis, MO). The electrode solution had an adjusted pH of ∼7.3 and an osmolarity of 295–300 mOsm.
Passive membrane properties
With QX-314 and Cs-gluconate applied intracellularly to block, respectively, Na+ and K+ channels, the input resistance (Ri) increased by ∼81% (380 ± 25 MΩ, n = 10, P < 0.05) compared to values obtained using solutions containing K+-gluconate and no QX-314 (210 ± 15 MΩ, n = 9). Hence, intracellular blockade of K+ (and Na+) channels presumably obviated any progressively increasing shunting of recorded signals during trains in addition to improving the signal/noise ratio (24–26).
The experiments were performed in neurons voltage clamped at −80 mV to minimize postsynaptic contributions of voltage-dependent Ca2+ conductance (27).
Drug application
The slices were perfused on a nylon mesh with oxygenated ACSF and drugs. The drugs were prepared in distilled water, firstly as stock solutions at ∼1000 times the required concentration and then frozen. Just before the experiment, the stock solutions were thawed and diluted in ACSF for application. D-2-amino-5-phosphono-valerate (APV, 50 μM (Sigma)) was used to block receptors for N-methyl D-aspartate. Receptors for γ-amino butyrate of type A (GABAA) were blocked by picrotoxin (50 μM). The drugs were diluted in ACSF and the pH adjusted to 7.3–7.4. Extracellular solutions were delivered in two ways: 1), bath applications performed using a roller-type pump at a rate of 2 mL/min through a submersion-type chamber with a volume of ∼0.3 mL, and 2), local application by a glass pipette (∼100- to 200-μm tip diameter) connected by polyethylene tubes to various reservoirs. The local application approach allowed for a rapid switch (within <5 s) between the various drugs (28).
Corticothalamic EPSCs
EPSCs were evoked by stimulating corticothalamic projections to ventrobasal neurons (held at −80 mV), using a bipolar tungsten electrode positioned over the internal capsule at a 0.2- to 0.3-mm distance from the recording electrode. For identification of corticothalamic pathways, the internal capsule was first stimulated with a strong (100 V) stimulus pulse (100–200 μs). As the electrode was moved progressively closer to the slice surface, the stimulus amplitude was reduced to the minimum value (range 5–20 V) that evoked responses to every stimulus. Once the electrode was just above, but not touching, the surface of the internal capsule, the stimulus amplitude was again adjusted to twice the minimum value. This procedure produced a stable stimulation of a small number of afferent axons, evident from a steady average and <∼10% variation in the trial-to-trial fluctuation of the first EPSC amplitude (12), and a lack of drift in time of equilibrium EPSC size as trains were iterated. Subsequent examination of data showed no need for rejection because of possible intermittent failure of axon stimulation, or branch failure, which would be evident in sudden increases in the variance/mean ratios after the first few EPSCs (see Theory).
Stimulation trains
After preliminary experiments, it was decided to use trains of length 20 pulses delivered at 2.5, 5, 10, and 20 Hz with a 20-s intertrain interval, chosen as sufficient to allow complete poststimulation recovery. The trains were applied in a sequence that included all possible combinations of frequencies, avoiding a bias in results resulting from possible “memory” of the previous train (10, 10, 20, 20, 5, 5, 2.5, 2.5, 10, 2.5, 20, 10, 5, 20, 2.5, 5). In each train, the 11th stimulus was omitted (see Theory).
Deconvolution of signals
In principle, any time series, y(t), can be expressed as the convolution of a “forcing function” and a prescribed function. For simple prescribed exponential functions with time constant τ, the forcing function is expressed as y(t) + τdy(t)/dt, also known as the “augmented derivative”. In practice, with an array of point values y[k] with τ > ∼10 sample times, this is approximated as (y(k) − a∗y(k − 1))/(1 − a) with a = exp(−1/τ), or (y[k]-a∗y[k-2])/(1a) with a = exp(−2/τ), the latter being equivalent to the former with two-point running average smoothing, and therefore less noisy. Deconvolution with an exponential function is the exact converse of integrative “smoothing” sm[k] = (1 − a)∗y[k] + a∗sm[k − 1], which was used twice, with a = exp(−1/2), for the deconvoluted records shown in the Results section.
Measurement of signals
Three different measures were made of EPSCs: 1), average of values around the peak minus baseline (average of points for a period of 10 ms before the stimulus extrapolated with τ to the time of measurement, for all stimuli except the first); 2), average of five values at the time of the peak of averages of signals for the particular stimulus number minus baseline; 3), area of deconvoluted signals as the sum of values in a broad window (determined from averages) minus an interpolated baseline at each point from linear regression with time of values before the stimulus and after the window period. The method for determining baseline was selected as the one, of several that were tried, that most successfully minimized correlation of baseline with amplitude of antecedent EPSCs. Otherwise, measure 1 was prone to find a signal where there was none (because a maximum within a window is likely to be at a point where there is a spontaneous event), an error not found with measure 2. All subsequent calculations were done with all three measures, and gave essentially the same results regarding evolution of means, variances, and covariances (and sampling errors), and derived values.
For brevity, the data presented in Results are those using measure 2, with the exception of EPSCs recorded in the presence of cyclothiazide and kynurenate, where measure 3 was used. In these, the overlap of successive EPSCs was considerable, and the chosen measure was that which, in theory, most avoided any artifactual covariances. EPSC amplitudes have been designated S1, S2, S3, etc.
Estimates of p, α, equilibrium variance/mean, and N
As explained in the theoretical section, these parameters are accessible only with the unrealistic assumption that p, α, and quantal amplitude are constant in the train. Then, at stimulus 1 the fraction of filled sites f1 is 1 and at every subsequent stimulus fj+1 = α + fj(1 − α)(1 − p). Equilibrium (final) ff is the same as equilibrium S (Sf) divided by 〈S1〉 and is α/(α + p − αp). Thus, for any given p, α = pff/(1 − ff + pff). For each set of average values of S in a train, Sf was determined as the average of S values for stimuli 5–10 and 15–20. A subroutine then went through all possible values of p, from 0.15 to 0.95, to obtain the least-squares best fit of predicted values of Sj/S1 to data, for j = 2–6. Then, assuming constancy of p, one has QA = vmf/(1 − pff) and, since 〈S1〉 = pQN, NA = 〈S1〉/p/QA ((〈S1〉/p − Sf)/vmf), where vmf is the equilibrium variance/mean. vmf was determined as the average of var(Sj)/〈Sj〉 for j = 5–10 and 15–20, variance being the mean-square of deviations from the mean of values at the same stimulus number, j, in the iterated trains. Calculation of variances (and covariances) using adjacent trains (11,12) made no appreciable difference to the values obtained.
Quantal size: “corrected” variance/mean
“Corrected” variance/mean was determined in three ways. Using “C” language terminology for clarity and designating vm[j] ≡ var(Sj)/〈Sj〉:
-
1.
, with NA as determined using best-fitting p and α;
-
2.
, with ;
-
3.
.for j = 9 or 19). (This is the method used by Scheuss and Neher (11).)
In addition, a theoretically partially corrected variance/mean was determined using variance within trains, for near equilibrium S, j = 5–9, 15–19:
-
4.
.
In the Results section, equilibrium cvm (“eq_cv” or “cvmf”) is identical to the Q found with p, α, and N, and eq_Qc is the average of Qc[j], for j = 5–10 and 15–20; Qt is the average of all Qt[j], all nominally equilibrium values.
Results
Database
EPSCs evoked by trains of stimuli at 2.5, 5, 10, and 20 Hz, with 20 iterations at each frequency, in a “balanced” sequence (see Methods) were successfully recorded from six neurons.
Later examination showed that for neuron 1, the 20-Hz data showed major differences from the other neurons, and from the same neuron at 2.5, 5, and 10 Hz, in that there was marked nonstationarity, manifested as a sudden increase of average late EPSC amplitude around the middle of the sequence. Also, the Qt within trains was ∼20% of the equilibrium vm (variance/mean ratios, with variance calculated between trains). The data from this neuron was therefore excluded from this analysis, but the original numbering of neurons has been retained as a reminder that behavior of EPSCs was not always the same.
Unless otherwise noted, the data presented below are from neurons 2–6 of this series. In each of another six neurons, six trains of EPSCs at 10 Hz were obtained in control bathing medium and in the presence of both cyclothiazide and kynurenate to block receptor desensitization and saturation (12), and these results are also presented here.
Rundown of EPSCs in trains
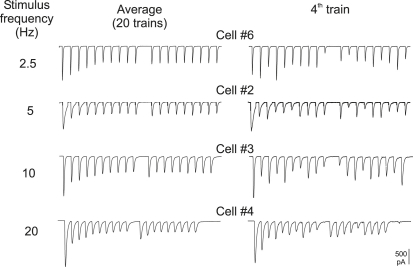
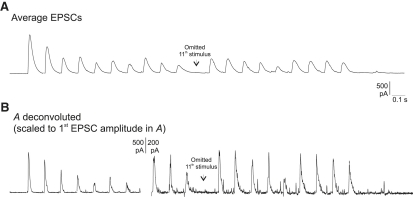
Repetitive stimulation produced a rundown of EPSC amplitude early in the train, with a “jump” in EPSC amplitude after the omitted stimulus. This short-term depression was frequency-dependent. Fig. 1 shows, at left, averages of records at each stimulation frequency, a different cell having been arbitrarily chosen for each, and at right, arbitrarily, the fourth train alone for each of these, illustrating the fluctuation of signals within any individual train. For 20-Hz trains, the records are continuous. In the other trains, some dead time between responses has been omitted. The impression of a constant time course of the EPSCs is reinforced in Fig. 2 A, where the same record as the last train of Fig. 1 is shown inverted, and on a faster time base. However, in Fig. 2 B, the augmented derivative of this record (i.e., the deconvoluted record) using the apparent time constant (τ) of late decline of signal averages (10.85 ms), shows that individual signals have time courses that are sometimes fragmented, as might be expected if each EPSC is composed of varying units that also appear as little bumps scattered between stimuli (23,29). The deconvolution producing the record in Fig. 2 B may be regarded as a convenient method of either bringing out detail or actually showing the timing of channel opening implied by the original record, assuming that τ is the time constant of monoexponential channel closing. This particular example (cell 4) was chosen for low noise and relative clarity of spontaneous or asynchronous activity, which was a little more prominent than in the other cells. It may be noted that in some records, particularly from cells where the effect of cyclothiazide/kynurenate was tested, the deconvolution of signals showed complexity in time course—“tails” that progressively diminished after stimulus1—that might indicate subpopulations of release sites with delayed release and more-than-average rundown.
Figure 1.
Examples of average corticothalamic EPSCs in trains (left) and a single train (right) at each stimulation frequency. Except at 20 Hz, some dead time between stimuli has been eliminated. Note jumps in EPSC amplitude visible in the averages, after the omitted 11th stimulus.
Figure 2.
A single EPSC train at 20 Hz, inverted, and the same train after “deconvolution” to bring out the variability of time course of signals and visualization of “asynchronous” events.
Correlations between EPSCs
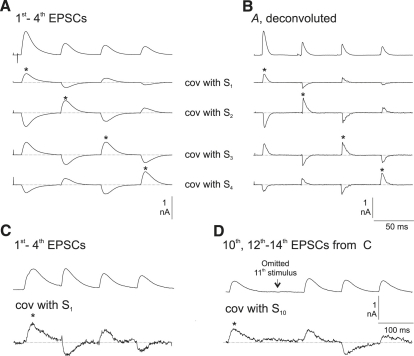
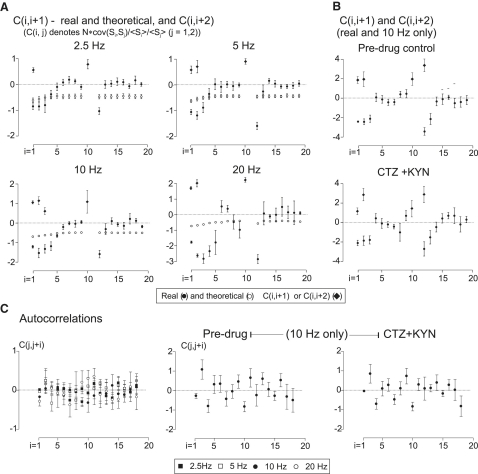
Mutual correlation of signals, illustrated in Fig. 3, showed results both consistent with the depletion model—negative covariances with adjacent signals—and contrary to this model—positive correlation of the first and third signals, and, to a lesser extent, of the second and fourth signals. In Fig. 3 A, under the (inverted) average of the records for the same period, are shown the correlations of all the points in the time period, including the first four signals with heights of, respectively, the first, second, third, and fourth signals in each train (i.e., average y[iter][j] ∗ (S[iter][k] − 〈S[k]〉), where y[iter][j] is the jth point in train number iter, and S[iter][k] is the height of the kth signal in train number iter). The above data are for cell 6 at 20 Hz. However, a virtually identical picture was obtained for the other neurons, and at all stimulation frequencies. The correspondence in time course of average signals and “self-covariance” (the part of the record where points have been correlated with the height of the corresponding signal, i.e., time-partitioned variance) is very obvious. The actual scaling of the covariances here was such as to make the maximum of the average self-covariance of equilibrium signals the same as the maximum of their average. The relatively low self-covariance of the first signal reflects a variance/mean less than that of equilibrium signals.
Figure 3.
(A) Covariance of continuous records with height of S1, S2,S3, and S4, respectively, under the average inverted original. Each signal-signal covariance is present at all relevant points. (B) Same records as in A, but deconvoluted. Note the relative brevity of signals. (C) Procedure similar to that in A, but only for covariances with height of S1. Data are from a neuron in cyclothiazide/kynurenate, which broadens EPSCs. (D) The same train set as in C, showing positive correlation across the omitted stimulus. Note the appearance of covariances despite there being only six trains.
Fig. 3 B shows the same data as in Fig. 3 A, but with deconvoluted records (τ = 9.1 ms), and covariances with areas instead of signal heights. Using original heights gave traces indistinguishable from those shown here, indicating that they were adequate surrogates for area. In theory, all bumps (inverted or not) should have the same time course as the corresponding averages if the measured signal heights are good surrogates for area of signals (see Theory). Also, the peak heights of the nondeconvoluted records (Fig. 3 A) are at a time where the deconvoluted records show the bulk of release included. It is also notable that for the third signal the self-covariance shows tiny irregularities that are duplicated in the covariances with the other signals but not apparent in the average. Similar deviations from theoretical expectation were seen with other neurons and at all stimulation frequencies, and will be considered elsewhere. The EPSCs recorded in the presence of cyclothiazide plus kynurenate (“ctz_ky”) were considerably more prolonged than controls, resulting in an inherent difficulty in defining “height”, except for the first in the 10-Hz train. Correlation of all points in the record with height of the first (illustrated in Fig. 3 C for one of these neurons) showed the same general picture as in Fig. 3 B, but with bumps—negative and positive correlations—superimposed on a “tail” reflecting late self-covariance of the first EPSCs. Fig. 3 D shows correlation of the time period corresponding to the 10th–14th stimuli with the height of signal 10 (which may have included some of signal 9). The positive correlation with signal 12 (i.e., the EPSC after the omitted stimulus at 11) occurred in all six sets of ctz_ky data, and in their controls, and in all the main series at all Hz, but varied considerably in magnitude. The subsequent bumps corresponding to correlations of signals 13–15 with signal 10 were very variable between data sets and, overall, not statistically significant.
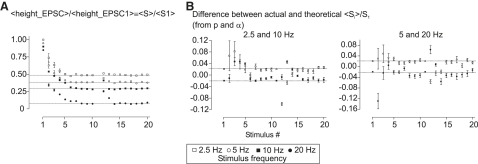
The scattergraphs in Fig. 4 make clear the existence and magnitude of the correlations between amplitudes of successive EPSCs. Fig. 4 A shows a plot of the data from neuron 2: the height of the second EPSC versus the height of the first (S2 versus S1) for the 20 iterated trains. The negative correlations are very obvious for data at each stimulation frequency. For the depletion model, the slope of correlation, b, should be −p in the absence of refill and otherwise less negative. In other words, the observed slopes, especially at 20 Hz, indicate rather high p. Using normalized values—S1/〈S1〉, S2/〈S2〉 etc.—allows points for trains from different cells to be put on the same graphs (Fig. 4 B). Now, the depletion model with no refill predicts b equal to −p/(1 − p) for S2/〈S2〉 versus S1/〈S1〉. For S3/〈S3〉 versus S1/〈S1〉, the observed positive slopes are quite different from the predicted slope, which is negative. The slopes of S3/〈S3〉 versus S2/〈S2〉 accord with theory in that they are negative, but turn out (see below) to be too negative.
Figure 4.
(A) Scatterplots of S2 versus S1 for one neuron only at 2.5, 5, 10, and 20 Hz. The 30 pairings available in each are sufficient to see the negative correlations. (B) Using data from all five neurons, by normalizing each set of Ss by dividing by the means. The slope of the correlation between S2/〈S2〉 versus S1/〈S1〉 is −p/(1 − p), in the absence of refill, or less negative if refill is appreciable. The positive correlation of S3/〈S3〉 versus S1/〈S1〉 is contrary to theoretical expectation.
Derived measures and parameters
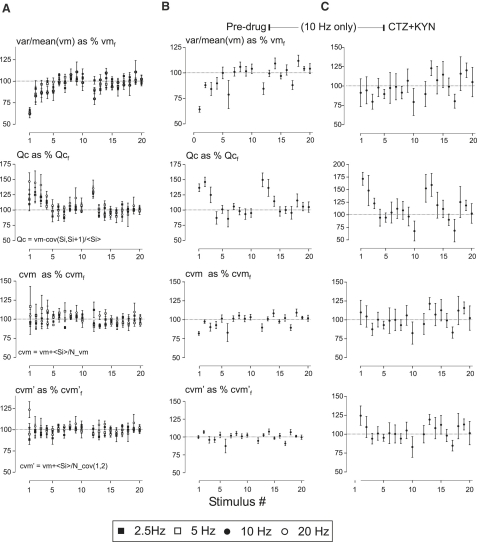
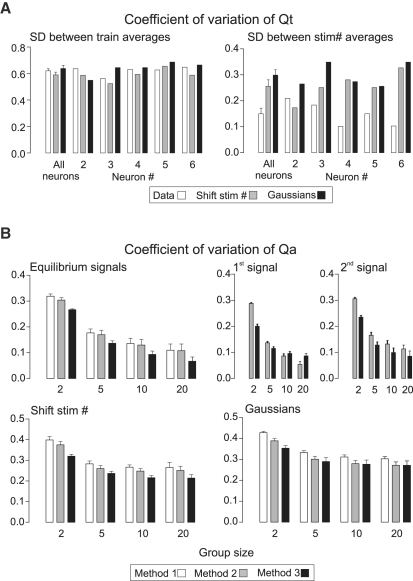
The bar graphs in Fig. 5 summarize some results from the five neurons where data was obtained at 2.5, 5, 10, and 20 Hz. Values of 〈S1〉 varied between cells, but equilibrium values (averages for stimuli 5–10 and 15–20, equilibrium S = Sf) were in proportion. That is, at each Hz, the fall of signal amplitude was virtually identical in all five neurons. Equilibrium values of variance/mean (“vmf”) were only slightly different between cells, with no consistent variation with stimulation frequency. Qt was on average very close to vmf, as were also equilibrium Qc. In other words, “correction” of variance/mean ratios to obtain true quantal size (cf. (11) re Qc) produced values almost identical to vmf. Very notably, the sampling errors of vmf, Qt, and Qcf (and also QA, not illustrated) were consistently less than expected—variance has an expected SE ±10% of mean for 200 samples, and each of the above values was obtained for 10 EPSCs with 20 iterations. This phenomenon is considered in more detail below.
Figure 5.
Various measured and derived release parameters. (A and C) Measured S1, S1/Sf, and derived parameters (vmf, Qt, Qc, and ratios) are given for each neuron. (B) Between-neuron variations for Qt/vmf and Qc/vmf ratios and SE/mean values.
The simplifying assumption of constant Q, p, and α for each train gave nominal values for both these parameters, and for N and Q (see Theory and Methods sections), as pA, αA, QA, and NA. These showed no consistent trend with stimulus frequency, except for αA which, as expected, declined with less time for “refill” between stimuli. Since nominal p was always ∼0.4, QA (vmf/(1 − pASf/〈S1〉) were between 10 and 20% more than vmf, with no significant variation with stimulus frequency and little difference between neurons. Sampling errors were 10–20% less than for vmf.
The NA for each of the neurons showed unexpectedly high variation with different stimulation frequencies. Further examination showed that this arose primarily from variation in estimates of pA rather than QA. Using the data for all stimulation frequencies in the algorithm for computing a common least-squares-fitting pA, pA varied among neurons between 0.44 and 0.38, with an average of 0.42; variation of NA between stimulation frequencies virtually disappeared, and values for each neuron were close to the average of the values illustrated.
The last panel shows values of NA multiplied by -cov(S1,S2)/〈S1〉/〈S2〉, the latter being 1/Ncov (see Theory). For these, unless “refill”, α, is appreciable, values of ∼1 are to be expected, otherwise, <1. Values of NA/Nx, Nx being the N calculated by correlating vmj with 〈Sj〉, had high SEs, as expected (see Theory), but average values close to 1 in every neuron. The alternative methods of finding N (also see Theory) using “finite summations” gave values (not shown) that differed from NA much more than in simulations and in most cases in the opposite direction to that expected with desensitization. In other words, the time course of rundown differed from that expected with constant p and α (also see below).
Tests of nonstationarity and nonlinearity/desensitization
In view of the above results, and those in the next section, these were partly redundant, since nonstationarity would introduce a positive component to every cov, denied in the data shown in Fig. 4. Using the method for finding δ2 described in the Theory section, in all but one of the 20 data sets (five neurons at four stimulation frequencies) this value was negative, with an average of −0.0011 ± 0.0003 and no significant difference with stimulation frequency. Theoretical values were all close to −0.0029, for the depletion model. Thus, either there was a tiny nonstationarity or overall covariances were less than expected for the depletion model.
With nonlinear summation, the apparent quantal size should be smaller for large, early signals than at equilibrium, and with desens the opposite should be true. The data gave estimates of Qa1/QA equal to 0.96 ± 0.08, and weighted averages of Qa for the first four stimuli, divided by QA, of 0.975 ± 0.070. Weighted averages of cvm/QA for the first four stimuli gave 1.01 ± 0.026. Based on simulation results (see Theory), these measures are incompatible either with desensitization or nonlinear summation, with c (in apparent S = trueS/(1 + trueS/c) < ∼20 × 〈S1〉.
With desens one would expect quantal amplitude at equilibrium, QA, to be more reduced the higher the stimulation frequency and rundown of signals, but the numbers, given as a percentage of the average for the four stimulation frequencies, were 102 ± 5 at 2.5 Hz, 102 ± 3 at 5 Hz, 98 ± 3 at 10 Hz, and 99 ± 5 at 20 Hz. That is, there was no significant trend in the direction expected if rundown had a postsynaptic component.
Evolution of estimated values of quantal amplitude
In Fig. 6, the evolution in trains of variance/mean ratios and derived values for quantal amplitude are shown for the five neurons at 2.5–20 Hz (Fig. 6 A), and for the six neurons in which results were obtained in control medium and in the presence of cyclothiazide and kynurenate (Fig. 6, B and C). Although the latter two data sets were from only six iterations, they show the same features that appear for the main data set in Fig. 6 A. The variance/mean ratio for S1 was consistently less than the equilibrium average, as expected. In partial agreement with Scheuss et al. (12), Qc was consistently high for the first few stimuli; here, cyclothiazide/kynurenate made no difference. However, corrected vm using NA showed no significant trend, and the same was true for Qa (not illustrated). This was also true of cvm′ j, vmj corrected using at each j the same constant apparent Ncov given by cov(S1,S2)/〈S1〉/〈S2〉. Since the formula Qcj = vmj − cov(Sj,Sj+1)/〈Sj+1〉 is equivalent to Qcj = vmj + 〈S/〉N, with N at each stimulus given by cov(Sj,Sj+1)/〈Sj+1〉/〈Sj〉, it can be concluded that the apparent early decline of Qc appears not to represent any true change in quantal amplitude but instead to reflect a failure of cov(Sj,Sj+1) late in trains to properly reflect N.
Figure 6.
(A) Evolution in trains of variance/mean ratios (vm). (Upper) Qc, cvm, and cvm′. Note that only Qc declines in the train. Data in A, main set: five neurons at four stimulus frequencies. (B and C) Averages from six neurons before treatment and with cyclothiazide/kynurenate at 10 Hz only, and with only six trains in each. The latter signals were measured as areas in deconvoluted records.
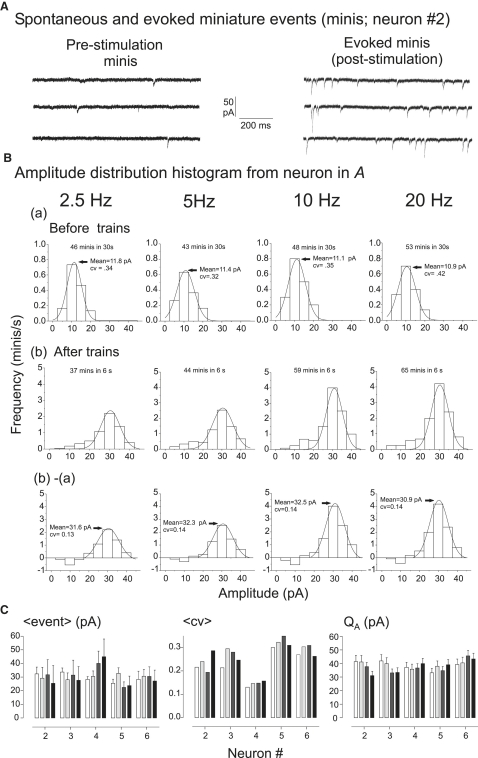
Relation between calculated quantal size and amplitude of spike-trigged miniature events
The logic employed for estimating the average size of spike-triggered miniature events is illustrated in Fig. 7. Invariably, events that could be “miniatures” (i.e., responses to individual quanta) occurred more often immediately after trains than before them. These were measured manually, and the amplitude was expressed as events/s so that the corresponding histogram for pretrain spontaneous events (expected to make the same contribution at all times) could be subtracted. The net results are summarized in Fig. 7 C. The coefficients of variation of spike-triggered event size were low enough that if the same applies to the quantal units of the signals, the terms in the equations for variance and covariance (see Theory) amount to no more than ∼1.1. Calculated quantal sizes (QA) were fairly consistently somewhat larger than mean event size (multiplied by 1 + cv2), but not by a large factor. It should be noted that, according to the depletion model, the release sites contributing to “asynchronous” release should mainly be those that did not release quanta in response to prior stimulation. That is, if release sites vary in p and α (“compound binomial”), the spike-triggered “miniatures” may come from release sites with relatively low p and/or high α; these would have relatively low 〈Q〉 if the sites are relatively distant from the soma and the miniatures are made small by filtering.
Figure 7.
Analysis of amplitude of evoked and spontaneous “miniature” events. (A) Evoked (spike-triggered) asynchronous miniature events were sampled immediately after stimulus trains (poststimulation), whereas “spontaneous” miniature events were sampled before stimulus trains (prestimulation). (B) Histograms expressed as events/s before and after trains give histograms for events evoked by the trains of stimuli. (C) Bar graphs show means at the different frequencies for the five neurons, the coefficients of variation, to be compared with the QAs for the antecedent trains.
Anomalies in EPSC rundown and covariances
The data consistently showed covariances that were different from those predicted by the depletion model. To be able to average results from the five neurons, with differing N, and therefore predicted values of covariances, a single value of N was calculated for each cell (from the common pA using data from all stimulation frequencies, and average QA), giving N = 〈〈S1〉〉/QA/pA). Each cov was then expressed as C(i,j) = N cov(Si,Sj)/〈Si〉/〈Sj〉. This procedure also allowed comparison of each covariance with the (always negative) theoretical value for the depletion model. For example, in theory, cov(S1,S2) = −〈S1〉〈S2〉(1 − α1/f2)/N and therefore, C(1,2) = −(1 − α1/f2), which can never be <–1 (Vere-Jones (9), and see Theory), unless N has been overestimated.
Some particularly notable values of C(i,j) are listed in Table 1 as averages ± SE (between cells). Even if one supposes that refill probability α is close to 0 at the start at 20 Hz, most of the listed values are significantly different from expected values. They are either too negative—e.g., C(1,2) at all but 2.5 Hz; α1/f2 should be appreciable at all but 20 Hz; C(2,3) is theoretically always less negative than C(1,2)—or they are positive: note, in particular, C(10,12), from the covariance of signals before and after the omitted stimulus, at all Hz. In all neurons, this follows a series of C(j,j + 2) with values near zero.
Table 1.
Selected values of C(i,j)
| Stimulus frequency (Hz) | C(1,2) | C(2,3) | C(1,3) | C(2,4) | C(10,12) |
|---|---|---|---|---|---|
| 2.5 | −0.85 ± 0.13 | −0.85 ± 0.14 | 0.53 ± 0.09 | −0.28 ± 0.39 | 0.76 ± 0.18 |
| 5 | −1.05 ± 0.10 | −1.18 ± 0.15 | 0.45 ± 0.19 | 0.62 ± 0.32 | 1.08 ± 0.14 |
| 10 | −1.21 ± 0.07 | −1.53 ± 0.25 | 0.99 ± 0.06 | 1.05 ± 0.15 | 1.16 ± 0.44 |
| 20 | −1.76 ± 0.07 | −2.62 ± 0.11 | 1.59 ± 0.11 | 1.95 ± 0.28 | 2.22 ± 0.18 |
C(i,j) ≡ N⋅cov(Si,Sj)/〈Si〉/〈Sj〉 ± SE between cells.
The evolution of covariances (Fig. 8) shows another anomaly, namely that from stimulus 4 or so, covariances of one signal with the next were essentially zero, as was already implicit in the correspondence of equilibrium Qc and Qt with equilibrium vm (Fig. 5), whereas theory predicts negative values. Note also the reappearance of (excessive) negative values for C(12,13)—after the omitted stimulus. Values for C(i,i + 3) were generally close to 0, except for small, usually significant, negative values for C(1,4). Note that similar patterns for C(i,i + 1) and C(i,i + 2) occurred in the data for the six neurons tested for an effect of cyclothiazide plus kynurenate (only six trains each at 10 Hz) both before and with ctz_ky (Fig. 8 B).
Figure 8.
(A) Evolution of covariances in trains expressed as C(i,j) to permit averaging for the five neurons, with theoretical values for C(i,i + 1). For C(i,i + 2), all theoretical values are about half of those for C(i,i + 1), i.e., always negative, and only significant values are shown. (B) Same as in A, for the six neurons before and with cyclothiazide\kynurenate.
All these features of the covariances were unaltered by elimination of covariances due to mutual correlation with antecedent signals (see Theory); the actual values were virtually unchanged.
In Fig. 8 C are shown autocorrelation functions for the data. Here, pairings giving obvious large covariances, C(1,i < 4), C(2,i < 4), C(12,13), have been omitted. These show an absence of net covariance, particularly for equilibrium signals, at all separations, for the main set of data at all stimulation frequencies. On the other hand, there is a hint of periodicity for the neurons studied before and with cyclothiazide and kynurenate, in which, remarkably, the same highs and lows occur at the same separations (iΔt) between stimuli (all at 10 Hz, Δt = 100 ms). However, this cycling, if any, has a period of ∼3Δt—somewhat higher than the 2Δt period necessary for any intrinsic cycling of p to account for the positive and excessively negative covariances early in the train.
Differences in rundown of EPSCs from predicted rundown
The depletion model with constant p and α (and fixed 〈Q〉) implies predicted values for EPSC average heights with 〈Sj〉/〈S1〉 independent of N (varying between neurons). Averages of these values for the five neurons are shown in Fig. 9 A. These are also graphs of quantal content relative to the first in the train. Deviations from predicted values (Fig. 9 B) occur early in the trains: S2 is notably low at 20 Hz, whereas S3–S5 are high at 10 Hz. The largest deviations from prediction are for stimuli after the omitted stimulus at position 11: at 2.5 Hz and 5 Hz, values are less than predicted, whereas at 10 Hz and 20 Hz, values are higher. In other words, the “jumps” in EPSC heights after the omitted stimulus were inconsistent with the postulate of constant p and α, with the jump being much less than predicted for 2.5 Hz and 5 Hz, and much more than predicted at 20 Hz. This is consistent with α at 2.5 and 5 Hz being much less in the extra gap than between stimuli, and p at 20-Hz equilibrium having risen from its initial value.
Figure 9.
(A) Evolution of mean EPSC height in trains. Since values are expressed as a fraction of 〈S1〉 and quantal heights did not change in trains, these are also plots of quantal content as a fraction of that of the first signal. To avoid overlapping points, the values for successive stimulation frequencies are displaced downward. (B) Deviations from theoretical expectation for a constant p and α model.
For the other six neurons, before and with cyclothiazide/kynurenate, with data (not shown) for 10 Hz only, rundown showed no significant differences from values predicted by the depletion model.
Pool-refill rate (rα) as a function of stimulus frequency
As explained in Theory, α is implicitly a function of the time interval between stimuli (Δt), but this should not be true of pool-refill rate (rα), calculated as rα = ln(1α)/Δt, provided refill at any moment is on average proportional to the extent to which sites have been “emptied” by release. In Table 2 are listed averages of these values for the five neurons (each of which gave nearly identical values), for each stimulation frequency. These data show that rα is not independent of Δt, but is rather a rising, but saturating, function of stimulation frequency.
Table 2.
Saturating rise of pool-refill rate and output/site/s with stimulus frequency
| Stimulus frequency (Hz) | True rα |
rα with fit |
||
|---|---|---|---|---|
| Fit(i) | Fit(ii) | Fit(iii) | ||
| 2.5 | 0.84 ± 0.01 | 0.90 | 0.86 | 0.84 |
| 5 | 1.39 ± 0.02 | 1.48 | 1.44 | 1.51 |
| 10 | 2.53 ± 0.02 | 2.11 | 2.31 | 2.26 |
| 20 | 2.69 ± 0.07 | 2.72 | 2.73 | 2.81 |
rα = equilibrium pool-refill rate/s = −ln(1 − α)⋅Hz. See text for a description of fits. All SEs are among values from the five neurons.
This result could arise, for example, if every stimulus injected something (say A) that accumulated with a time constant that was of the order of 100 ms, with rα proportional to the amount of AX,A combined with a receptor (X). At equilibrium, one has rα = k[AX]/[Xt] = k[A]/([A] + KA), where k and KA are constants to be fitted to the data. This model turns out to be indistinguishable from rα = kHz/(Hz + KHz) and the resulting least-squares best fit to the four points available (fit(i)) shows an rα at 10 Hz ∼15% lower than observed.
Differences between real and fitted values are less if one postulates that the amount of A injected by each stimulus is proportional to the output, Sj, i.e., that there is feedback, with refill stimulated by the transmitter itself, or something released as a consequence of transmitter action (fit(ii)). The “model” inherent in fit(ii) has a large element of tautology, and Monte Carlo simulation shows that one must have a component of injected A independent of outputs to avoid outputs eventually going to 0 or rising to be equal to S1. However, such a model generates positive covariances—it can account for positive C(10,12)—but C(10,12) in the simulation is never more than C(7,9), contrary to reality, and C(1,3) can scarcely be raised to an appreciable positive value. The third fitting function in Table 2 simply puts rα proportional to Hz × (1 − exp(−Δt/K)), an arbitrary saturating function with no theoretical basis—the resulting χ2 was about half that for fit(i) and double that for fit(ii).
Evolution of p and α in trains
As explained in Theory, the depletion model implies two equations that are independent of the mechanism of quantal transmitter release or action, namely, for each stimulus, 1), 〈Sj〉 = pjfj〈Qj〉N, and 2), fj+1 = αj + fj(1 − pj)(1 − αj), where fj is the fraction of sites with an available, releasable quantum, presumed to be unity at the beginning of a train (f1 = 1). With unchanging Q (Fig. 6), the decline in EPSC heights in trains must reflect a fall in either f or p, (since N, the number of sites, is fixed, and if some fail to be stimulated this can be regarded as a fall in 〈p〉 for all the sites). With the Pdown model, α is always 1 and f is always 1, i.e., the fall in S becomes entirely attributed to a fall in p, but the equations remain valid.
It follows from the two equations that for any arbitrary set of pj, the observed set of Sj/S1 dictates a corresponding set of αj. Conversely, given αj, there is a set of pj values that exactly fit the Sj/S1. In both cases, the only constraint is that no p or α can be 〈0 or 〉1. The calculated results in Fig. 10 A (averaged for the five neurons) show the evolution of α (and corresponding pool-refill rates, rα) on the assumption of constant p—this had to be raised to 0.53 (from the average of 0.42 for the five neurons, with no significant difference between them)—to prevent any negative α, and were assumed to be the same for the five neurons.
Figure 10.
(A) Plots of calculated α on the left and corresponding pool-refill rate, rα, on the right, calculated for each neuron at each stimulus frequency and then averaged, on the assumption of constant p. Note high early values and subsequent fall to a plateau, as well as dependence of rα on stimulus frequency. (B) Calculated p on the assumption of two different scenarios as to how α may be generated. See text for an explanation.
With p set constant, there appeared, at all frequencies, after an initial low α1 (set at 0 for 20 Hz), a progressive fall of α from an early maximum to a plateau. Subsequently, at 2.5 and 5 Hz, there was a profound fall of α within the time gap corresponding to the omitted stimulus. Setting a lower value for constant p (i.e., allowing negative α1 values at 20 Hz) produced the same features. In other words, the data actually show that if p is constant, α is not. The rough parallel between α1 and Sj/S1 provides a rationale for the assumption that the probability for refilling sites was proportional to previous transmitter release (Table 2, Fit(ii)). In fact, at 20 Hz, there is an apparent rise in α at the time the stimulus was omitted, suggesting that whatever causes pool-refill rate to rise reflects some kind of integral of previous events.
The converse situation, pj with constant α, consistently gave implausible results (e.g., an abrupt fall at stimulus 2, a large rise then fall, a progressive rise after the omitted stimulus) even with α for the time of the omitted stimulus set low. The results shown in Fig. 10 for model I are for pool-refill rates, rα, proportional to [AX] (see above), with constant injection of hypothetical A at each stimulus, falling and accumulating with a time constant of 100 ms—changing this parameter made little difference. Here, initial p1 was set at 0.42—any higher p1 gave a higher maximum p at 20 Hz. For model II, the preset α series was made by supposing hypothetical A injected at each stimulus in proportion to Sj/S1; p1 = 0.48 (cf. 0.53 above for constant p) was the highest that produced no p >1. In both cases, the large SEs for 20 Hz reflect solely the divergence of cell 2 from the others, which dominate the mean values. Also, in both cases, choosing an initial low p1 produced pj that initially fell, then rose, and then fell again from stimulus 2 to stimulus 10. The near correspondence of final (equilibrium) pj to p1 is artificial; it comes from adjusting, for each Hz in each cell, the proportionality factor for converting [AX] to pool-refill rate to make equilibrium α the same as the observed value. As pointed out above, model II, which corresponds to fit(ii) in Table 2, is not a true model, since rα. proportional to outputs that are themselves proportional to rα gives excessive positive or negative feedback. However, something between models I and II might be considered, a real model—partial dependence of pool-refill rate on antecedent outputs could partially explain the nonconstant α and positive covariances.
The result of both these exercises is the same. The rundown of signals is consistently different from the predictions of the simple depletion model, with either α falling from early high values (except for α for refill between the first and second stimulus at 20 Hz) or p rising and then falling, or both. In any case, pA values, and consequently αA and NA values, will be incorrect. What validity, if any, then attaches to these values, and to QA? The answer is that QA is nearly independent of moderate error in pA, which might underestimate p by no more than 25% or so. Correspondingly, α at equilibrium might be different from αA by as much as 25%. True N might be as much as 30% lower than NA. This would do little to bring the anomalous covariances into agreement with the theoretical.
Sampling error of vm and related measures
It was pointed out above, with regard to consideration of the derived values in Fig. 5, that between-stimulus-number SEs of vmf, Qcf, and Qt were all substantially less than those predicted from theory. The same was true of QA, and it soon became clear that it was estimates of variance that had SEs lower than expected. To check whether there was some computing error, simulations were done several hundred times for each model (see Theory), with varying parameters, and invariably using the same subroutine as for the actual data, SEs conformed to theory, with particular exceptions that will be described below.
Invariably, in deriving vm, etc., the averages and variance were determined between trains, i.e., independently at each stimulus number, there being no alternative when 〈S〉 runs down (Fig. 11 A). However, equilibrium values did give an alternative. For stimulus numbers 6–10 and 16–20, Qt was calculated for each trio of signals. Averaging the values within each train, and then taking SD(Qt)/〈Qt〉 vis-à-vis these averages gave the same values for SD(Qt)/〈Qt〉 as with two controls (Fig. 11 A, left). These controls were 1), altering in each train the sequence of S, e.g., S[9] to S[6], S[10] to S[7]…S[20] to S[17], S[6] to S[18], S[7] to S[19], S[8] to S[20] (Fig. 11 B, Shift stim no.), the starting number being determined by random numbers (30); and 2), replacing each S by a Gaussian variable (30) scaled to have variance/mean similar to that of real data. In contrast, making an average Qt at each stimulus number, across trains, and then getting an SD(Qt)/〈Qt〉 vis-à-vis these averages gave SD(Qt)/〈Qt〉 substantially less than in the controls. Here, the values plotted and SE bars are for averages over different Hz of stimulation (Fig. 11 A, right). It should be emphasized that 〈Qt〉 was just the same whichever procedure was used, and just the same for control A. Total shuffling of the positions of each signal within each train gave the second, between-signal SD(Qt)/〈Qt〉, the same as with Gaussians.
Figure 11.
Sampling errors expressed as a coefficient of variation of Qt (A) and Qa (B), depending on how variances are measured (see text). There are two sets of controls, one generated by shifting the position of S in each train (shift stim no.) and the other by replacement of real data with Gaussian variates (normally distributed). The latter conform to theoretical expectation, whereas the real data does not.
For Fig. 11 B, the data was treated in a slightly different way, to determine whether the same phenomenon was to be found assessing variance in other ways. Here, Qa was used, as essentially invariant with stimulus number. In method 1, Qa was found at each stimulus number (across trains), and the mean and variance were determined across all stimulus numbers. In method 2, the variance and means, and hence cv_Qa = SD(Qa)/〈Qa〉, of the same Qa as in method 1, were assessed across the values from the four different stimulation frequencies. In method 3, cv_Qa was estimated using adjacent pairs of Qa values. Qa across trains was done in four different ways: 1), using variance and mean across all 20 trains; 2), dividing the 20 Ss at each stimulus number into two groups of 10, and averaging the two pairs of values; 3), using four groups of 5; and 4), using 10 groups of 2. For all but the first case, a total of 1000 permutations of train location were used (and the final results averaged) to avoid the possibility that train groupings might make a difference. Theoretically, and in practice, Gaussians substituted for the data showed SD/mean of variance/mean diminishing from groups of 2 to groups of 20, with some difference between the methods. However, the real equilibrium signals showed a large decline with group size of cv_Qa, whereas control A (shift stim no.) gave an intermediate result, closer to the Gaussians than the unaltered data. Again, it should be emphasized that 〈Qa〉 was the same regardless of the method used to assess variance. Moreover, the equilibrium signals were the same for all stimulus numbers in terms of means, variances, and third and fourth moments. There were also (on average) no covariances between adjacent Ss for adjacent stimulus numbers.
Methods 2 and 3 could also be applied to the first and second signals, (sets of S1 and S2). The results (Fig. 11 B, 1st signal and 2nd signal) indicate that whatever causes the failure of variances to vary is operative from the start of the trains, rather than developing within it.
The exception to the rule that all simulations yielded values the same as theoretical came with models in which there was imposed a substantial extra between-train variance that was essentially the same for all stimulus numbers. This could be accomplished by making p vary at random (e.g., modulated by a gasdev() or vis-à-vis the sum of noncoherent oscillations) at all release sites together at each stimulus number, so that quanta always tend to be released in tandem, to make cv_Qa less than half its theoretical value. Such a scenario is so implausible as to be hardly worth mentioning, and it is contrary to the data in that it gives vm, etc., proportional to N. Moreover, if indeed the low sampling error of variances (and derived values) arises from a large extra variance at all stimulus numbers in the train, we must suppose that the extra variance parallels the variance produced by the binomial nature of outputs, to account for the low vm values associated with the largest signals (Fig. 6). Nevertheless, the implication of an SD/mean of variance that is one-quarter of the theoretical value, because of extra variance, is that the true quantal unit is of the order of one-quarter (!) that given by fluctuation analysis and by the stimulation-evoked “miniatures”.
Discussion
Perhaps the most striking outcome of this study is the abundance of information obtainable using repeated stimulus trains (11) at a conventional (corticothalamic) synapse; this experimental approach seems likely to be useful for the study of changes of synaptic function produced with longer-lasting forms of plasticity or with changed ambient conditions or drugs. Here, we have used several new methods for estimating quantal release based on an expanded theoretical framework. Briefly, the analysis starts with obtaining, as a first approximation, a description of tetanic rundown (“short-term depression”) in terms of the four constant-within-train parameters of a simple binomial-depletion model (9,10): number of release sites (N), quantal size (Q), output probability if a quantum is “available” (p), and probability of between-stimulus “refill” (α). Using several alternative estimates of N, corrected variance/mean ratios constitute estimates of quantal amplitude at each stimulus number. Monte Carlo simulation indicates that this procedure enables detection of any fall in Q if it occurs, which was not the case for the data presented here. Moreover, the data also showed Q to be independent of stimulation frequency. Thus, tetanic rundown at this conventional (nongiant) synapse is purely presynaptic, as at the (giant) neuromuscular junction (5).
Subsequent analysis showed deviations from the simple depletion model: “anomalous” covariances and EPSC rundowns per se not compatible with constant release probability (p) and refill (α). These deviations preclude an extrapolation to what would happen with irregular stimulus trains. Although covariances are indeed sometimes negative, this cannot be read as supporting the depletion scenario over others (Pdown, Ndown1, and Ndown2 in the Theory section). Thus, there are two important implications, namely, that release sites are not entirely independent of one another (see below) and that negative covariance does not arise only from depletion, if indeed depletion has anything to do with negative covariance.
Estimating quantal size during rundown
Whether quantal amplitudes change during repetitive stimulation (31–33) has been a long-standing question. Here, we have estimated quantal amplitudes (Q) as “corrected” variance/mean ratios (cvmj), with a rather wide latitude in the estimate of N in the equation, cvmj = vmj + 〈Sj〉/N. One guess at N comes from the equivalence, at equilibrium, of the latter equation with cvmf = vmj/(1 − pff) (with ff estimated as 〈Sf〉/〈S1〉, and p as the p governing rundown). These equations, used to estimate Q, are all model-independent (except for the implausible Ndown3 scenario in the Theory section). Using these approximations, we obtained, in each set of repeated trains, an array of cvmj values that should have revealed any systematic change in Q that may have occurred (Fig. 6). In general, whenever a synapse shows large rundown (〈Sj〉 much less than 〈S1〉), suggestive of high release probability (p), the uncorrected equilibrium variance/mean ratios (vmj) become nearly equal to cvmj and, therefore, represent legitimate (though biased) estimates of Q—unit quantal response. Another legitimate quantal size estimator is Qt, which needs no repetition of trains, but is available only for near-equilibrium signals. On the other hand, when synapses show no signal rundown, indicative of low p, both the variance/mean ratio and Qt represent valid quantal size estimates regardless of which model is used. Combining signal amplitudes and quantal size estimates, one can determine whether drug interventions or long-term plasticity are attributable to changes in quantal content (S/Q)—entirely presynaptic—or quantal amplitude—either pre- or postsynaptic.
Our conclusion that quantal size is invariant during tetanic rundown at corticothalamic synapses differs from that of Scheuss et al. (12) regarding the Calyx of Held. Nevertheless, we also find that Qc—quantal size by correcting variance/mean ratio using covariances of successive EPSCs (used by (12))—falls early in the stimulus train. In our data, this fall occurs for two reasons: early in the train cov(Sj,Sj+1) is excessively negative, and after the first few stimuli, cov(Sj,Sj+1) becomes near zero instead of approximating cov(Sj,Sj+1) = −〈Sj〉〈Sj+1〉/N. Corrected variance/mean ratios, using constant (and plausible) N, do not show a fall in putative quantal amplitude. However, there are two important differences between our results and those of Scheuss et al. (12). First, our data shows no change in this phenomenon during combined application of cyclothiazide and kynurenate (to block desensitization and saturation of receptors). Second, the N obtained by Scheuss et al. (12) from (simplified) cov(S1,S2) = −〈S1〉〈S2〉/N coincided with that obtained using the method of Elmqvist and Quastel (5), which is upwardly biased by any appreciable refill. In contrast, our Ns derived from cov(S1,S2) were always less than that obtained by a method that is less up-biased and depends on the same assumptions. The disparity between our results and those of Scheuss et al. (12) suggests that whatever (unknown) process produces overly negative cov(S1,S2) at corticothalamic synapses is less operative at the calyx of Held, and that whether postsynaptic factors play a role in rundown may vary between types of synapse.
Validity of the Q estimate
The classical test of the validity of quantal size estimates is that the values of Q should correspond to the amplitude (multiplied by 1 + cv2) of “miniatures” that represent responses to single quanta of transmitter (23). In the data presented here, Q was consistently a little (∼20%) higher than expected from the average amplitude, and variation of spike-triggered, asynchronous—long-latency—events presumably representing such miniatures. However, it may be argued (from the depletion model) that the latter largely represent responses to quanta from sites that did not produce “synchronous” release; there is no way of knowing if these belong to the same population. Nevertheless, it is possible that the discrepancy is real. In theory, this could arise from nonindependence of release sites (see below) causing a tendency of quanta to be released in tandem. The small-average events appearing between stimulus trains presumably represent spontaneous miniatures or EPSCs originating at synapses distinct from and more distant from the soma than those generating the EPSCs.
Complexity of refill rate
An unexpected finding was that the between-stimulus pool-refill rate, a parameter that limits the drop in quantal outputs within trains, was not only frequency-dependent (neuromuscular junction (5) or central synapses using visual probes (34–38)), but also declined within trains (Fig. 10) in parallel with outputs (except for the first few signals). It is conceivable that whatever makes outputs fall also makes pool-refill rate fall. For example, as pure speculation, the parallel fall of outputs and pool-refill rate might both reflect a rundown in Na+ (or Mg2+ or Ca2+) entry per stimulus. An alternative explanation is that a local feedback mechanism makes refill a function of previous outputs. Such a hypothesis would explain, at least in part, the appearance of positive or null covariances where negative ones were expected (see below).
Problem(s) posed by positive and overly negative covariances
A negative correlation between amplitudes of first and second EPSCs in trains (cov(S1,S2)) appeared prominently in all the data presented here (all cells, all stimulation frequencies, with modification by “refill” during interstimulus time much as expected), as at neuromuscular junctions (5), hair cell afferents (8), and calyx of Held (11,12), and with EPSPs from cerebral cortex (F. Tennigkeit, Max Planck Institute for Brain Research, Frankfurt, Germany, personal communication, 2004). However, there are indisputable counterexamples (14,15), indicating either that presynaptic physiology might differ fundamentally between types of synapses or that negative covariance may arise from mechanism(s) other than depletion.
The depletion model predicts that covariances between signal heights should always be negative and never more negative than to give Ncov(Sj,Sj+1) = −1. In contrast, our data show excessively negative covariance between the first and second, and particularly between the second and third, EPSCs. Although our estimates of N are intrinsically subject to error, they would have to be around three times too high for the observed values (especially cov(S2,S3)) not to exceed this limit (Table 1). In addition, there was always positive correlation between the first and third EPSCs (cov(S1,S3)) and between the 10th and 12th EPSCs (cov(S10,S12)), across an omitted stimulus. It is equally anomalous that equilibrium covariances (cov(Sj,Sj+1)) were near zero (also indicated by equilibrium quantal size estimators Qc and Qt indistinguishable from “final” variance/mean ratios (vmf)). In brief, the negative covariances must arise largely from mechanisms other than depletion.
In searching for possible mechanisms of the anomalous covariances, we must first emphasize that there can be no model with independent release sites by which the release of a quantum at one stimulus is succeeded by less than zero release at the next stimulus (implicit in Ncov(Sj,Sj+1) < −1). Therefore, the only explanation for the overly negative covariances is that release at a site is profoundly affected by antecedent release at other sites, presumably in the vicinity. The positive covariances should also be viewed in light of an expected negative covariance, either from continued depletion or persistence of whatever causes the excessively negative covariance. An obvious explanation for the anomalous covariances is feedback, namely, the released transmitter acts presynaptically either directly or through something released locally by the postsynaptic cell or glia. There are numerous possibilities for inhibitory and facilitatory feedback at corticothalamic (39,40) and other synapses (41–46), including (glial regulated) raised extracellular K+ implicated in short-term potentiation (47). It should be noted that neighboring axon terminals are electrotonically coupled (48,49) and that, in our experiments, the postsynaptic neurons were voltage-clamped and produced no action potentials. Given that transmitter release at a site is influenced by activity at neighboring sites supplied by the same axon(s), it is not unreasonable to infer the existence of heterosynaptic inhibition and facilitation subserving a mechanism for associative forms of synaptic plasticity (e.g., Hebbian learning).
The problem in finding a mathematical model to account for the anomalous covariances lies in their timing. Whatever the mediators, any postulated negative and positive feedback must have a time course, with decay faster for inhibition than for facilitation, but any set of parameters that might fit for one stimulus frequency cannot fit at the other frequencies. For example, the covariance across the omitted stimulus is positive at 10 Hz. That is, at a separation of 200 ms, with no intervening stimulus, an above-average EPSC10 is associated with above-average EPSC12. In other words, the above-average EPSC10 has produced net facilitatory feedback. In contrast, at equilibrium in 5 Hz trains, covariances between adjacent signals (with 200 ms separation and no intervening stimulus) are zero. Similarly, the early covariances appear to be related to stimulus number rather than to time between signals. A possible explanation is that presynaptic action potentials modulate the decay (and accumulation) of presynaptic inhibition and facilitation. But what combination of time and stimulus-number dependence allows the system to “know” that a stimulus has been omitted? So far, our Monte Carlo simulations have failed to match the timing of anomalous covariances.
Transmitter release revisited: stochastic or deterministic?
Our most perplexing observation is that the between-stimulus-number sampling errors of between-train variance (and, hence, estimated Q) were consistently and significantly less than expected for a binomial (or Poisson or Gaussian) distribution of quantal outputs. For equilibrium signals, with indistinguishable averages, this low sampling error disappeared with any shuffling of signal values, as though the system “knew” the stimulus number in each train and what the variance should be. An explanation for this behavior completely eludes us. The only models we have found that produce a low variation of variance do so by introducing a common “extra” variance at each stimulus in the train. If such extra variance exists, then true Q is less than estimated Q by a factor of ∼3. Why, then, the correspondence of estimated Q from between-train variances with Qt (from within-train variances) and with the size of spike-triggered asynchronous miniatures? Moreover, if our Q values are too high, our N values are correspondingly lower than true values, resulting in even more overly negative covariances. In this regard, our neuron 1 (omitted from our main data set) sometimes showed a within-train variance/mean ratio (Qt at 20 Hz) much lower than other Q. This unusual behavior is consistent with a shift to a subquantal release mode (cf. (50,51)). It is conceivable that the low sampling errors could reflect some kind of deterministic/chaotic process underlying quantal formation, as well as pseudostochastic release (19,52–55). However, our data is insufficient to permit the use of the relatively sophisticated analysis that has led to the identification of deterministic chaos associated with recurrent feedback networks (56). In retrospect, our experimental paradigm would have been much improved by including a few very long trains.
To conclude, the behavior of pool-refill rate, anomalous covariances, and sampling errors in our results, which imply unexpected complexity in presynaptic physiology, were readily detectable and measurable. Therefore, the mechanisms that give rise to these phenomena should be amenable to investigation using agents with known effects on receptors and metabolic systems. For example, pharmacological blockade of inhibitory (39,40) or facilitatory (41,43) presynaptic receptors might well lead to identification of specific components of feedback and how these may vary between synapses, alter with long-term plasticity, and contribute to optimization of transfer of information across the synapse.
Acknowledgments
The authors acknowledge excellent technical assistance from Viktoriya Dobrovinska and Christian Caritey. In addition, we thank Frank Tennigkeit for providing us with records of cortical EPSPs. This work was supported by the Canadian Institutes for Health Research (E.P. and D.M.), the Jean Templeton Hugill Foundation (E.P. and I.R.), Mathematics in Information Technology and Complex Systems (I.R.), and the Muscular Dystrophy Association of Canada (D.Q.).
Footnotes
Israeli Ran's present address is Département de Physiologie, 2960, Chemin de la Tour, Université de Montréal, Montréal, Quebec, Canada H3C 3J7.
Appendix: Monte Carlo modeling
The following subroutines in C make, for any of five scenarios, NT sets of S[train#][stim#] for NS stimuli with quanta of initial size Q0, with N sites, with an omission of the stimulus at stimulus number 10. The numbering of stimuli starts at 0.
modparam(f,al,p,pfail,tr) float ∗f,∗al,∗p,∗pfail,∗tr;
{ int i,j; float a,b,c,d,x,y,z;
/∗alp0 and p0 are globals∗/
for (j=0;j<NS;j++) { al[j]=alp0; p[j]=p0;pfail[j]=0;}
p[10]=0;/∗omission at #10∗/
f[0]=1;
if(Pdown||Ndown)
for(j=0;j<NS-1;j++) f[j+1]=al[j]+f[j]∗(1-al[j])∗(1-p[j]);
if(Pdown) for(j=0;j<NS;j++) p[j]=f[j]∗p0;/∗mimicking depletion∗/
if(Ndown==2) /∗stochastic irreversible ‘disabling’complete by tenth stim∗/ for(j=1;j<10;j++) pfail[j-1]=1-f[j]/f[j-1];if(trend>1)/∗ here trend is up..makes no difference∗/ { /∗want (1+x)/(1-x)=t=trend; 1+x= t-t∗x; t∗x+x=t-1; x=(t-1)/(t+1);∗/
x=trend-1;x/=trend+1; tr[0]=y=1-x; z=1+x; a=(z-y)/(NT-1);
/∗ also get square of cv produced by trend ∗/
c=tr[0];d=tr[0]∗tr[0];
for(i=1;i<NT;i++) {c+=tr[i]=tr[i-1]+a;d+=tr[i]∗tr[i];}
d -= c∗c/NT;d/=NT-1; c/=NT; trend2=d/c/c; } }
makesig() {
int i,j,k,n,t,site;
float c,Q,f[NS];
static int count=0,ok[N][NS];
static float al[NS],p[NS],pfail[NS],tr[NT],cnonlin;
if (count==0) {
modparam(f,al,p,pfail,tr);
for(site=0;site<N;site++) for(i=0;i<NS;i++) ok[site][i]=1; if(Ndown==3) /∗always same series of disabled sites∗/
for(j=1;j<NS;j++) {k=(1-f[j])∗N+0.5; for(site=0;site<k;site++) ok[site][j]=0; }
if(abs(nonlin)>1) cnonlin=nonlin∗p0∗N∗Q0;
count++; }
for (t=0;t<NT;t++) /∗t is train#∗/
{ for (j=0;j<NS;j++) S[t][j]= 0.001;/∗avoid 0's∗/ for(site=0;site<N;site++) { n=1; Q=Q0; for(j=0;j<NS;j++) {
if(ok[site][i]&&n>0)
if (frand<p[j]) {/∗release∗/
S[t][j]+=Q;
qs[0][j]+=Q;qs[1][j]+=Q∗Q;qs[2][j]++;/∗track Q∗/
if(depl) n=0;
if(desens) Q=0;/∗complete desens∗/ }
if(Ndown==1) if(frand<p[j]) n=0;
if(Ndown==2) if(frand<pfail[j]) break;
/∗ site disabled irreversibly ∗/
if (n<1) {if (frand<al[j]) n=1;} /∗refill∗/
if (desens) Q+=aH∗(Q0-Q);/∗non-stoch recovery from desens∗/
}/∗end doing for NS stimuli w/ omission at #10∗/
} /∗ end doing for N0 sites∗/
}/∗end NT trains∗/
if(trend>1) for(t=0;t<NT;t++) for(j=0;j<NS;j++) S[t][j] ∗= tr[t];if (abs(nonlin)>1) { if(trend>1) c=cnonlin∗tr[NT-1];else c=cnonlin;
for(t=0;t<NT;t++) for(j=0;j<NS;j++) S[t][j] /= 1+S[t][j]/c; }}
Any desired modification of the evolution of p and α may be specified in modparam(). If Q is to vary between sites, “S[t][j]+=Q;” becomes “S[t][j]+=Q∗q[site];” For within-site variation of Q, “S[t][j]+=Q∗q[site];” becomes “S[t][j]+=Q∗q[site]∗randlist[frand∗10000];”, where randlist[] is a preset list of 10000 log-normally distributed numbers (to avoid negative values) with an average of 1. For a “compound binomial”, one has different p[j] and/or alpha[j] at each site—i.e., the relevant lines have p[site][j] and al[site][j]. Of course, all these arrays must be specified before makesig(). If one wants entire pseudosignals, then whenever there is release, a position for the start of the quantum must be specified: “pos = latency-log(frand)∗tau1-log(frand)∗tau2; x= frand; ar[pos]+=x∗Q; ar[pos+1]+=(1-x)∗Q;” will produce a dispersion of release fitting an “α function” with these τ values. Integrating the array, twice, with the two τ values for a quantum fitting, an α function gives the same record as adding a whole quantum to the array whenever one is released.
For full flexibility in modeling, one can save at each j the output and state (n = 1 or 0 (full or empty, respectively)) of all N sites, and make al[j] and/or p[j + 1] for each site any arbitrary function of the output history of any group of sites, and then go on to the next stimulus.
References
- 1.Hirst G.D., McLachlan E.M. Post-natal development of ganglia in the lower lumbar sympathetic chain of the rat. J. Physiol. 1984;349:119–134. doi: 10.1113/jphysiol.1984.sp015147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Abbott L.F., Varela J.A., Sen K., Nelson S.B. Synaptic depression and cortical gain control. Science. 1997;275:220–224. doi: 10.1126/science.275.5297.221. [DOI] [PubMed] [Google Scholar]
- 3.Chen C., Blitz D.M., Regehr W.G. Contributions of receptor desensitization and saturation to plasticity at the retinogeniculate synapse. Neuron. 2002;33:779–788. doi: 10.1016/s0896-6273(02)00611-6. [DOI] [PubMed] [Google Scholar]
- 4.Liley A.W., North K.A. An electrical investigation of effects of repetitive stimulation on mammalian neuromuscular junction. J. Neurophysiol. 1953;16:509–527. doi: 10.1152/jn.1953.16.5.509. [DOI] [PubMed] [Google Scholar]
- 5.Elmqvist D., Quastel D.M. A quantitative study of end-plate potentials in isolated human muscle. J. Physiol. 1965;178:505–529. doi: 10.1113/jphysiol.1965.sp007639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Thies R.E. Neuromuscular depression and the apparent depletion of transmitter in mammalian muscle. J. Neurophysiol. 1965;28:428–442. doi: 10.1152/jn.1965.28.3.427. [DOI] [PubMed] [Google Scholar]
- 7.Walmsley B., Edwards F.R., Tracey D.J. Nonuniform release probabilities underlie quantal synaptic transmission at a mammalian excitatory central synapse. J. Neurophysiol. 1988;60:889–908. doi: 10.1152/jn.1988.60.3.889. [DOI] [PubMed] [Google Scholar]
- 8.Furukawa T., Hayashida Y., Matsuura S. Quantal analysis of the size of excitatory post-synaptic potentials at synapses between hair cells and afferent nerve fibres in goldfish. J. Physiol. 1978;276:211–226. doi: 10.1113/jphysiol.1978.sp012229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vere-Jones D. Simple stochastic models for the release of quanta of transmitter from a nerve terminal. Aust. J. Stat. 1966;8:53–63. [Google Scholar]
- 10.Quastel D.M. The binomial model in fluctuation analysis of quantal neurotransmitter release. Biophys. J. 1997;72:728–753. doi: 10.1016/s0006-3495(97)78709-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Scheuss V., Neher E. Estimating synaptic parameters from mean, variance, and covariance in trains of synaptic responses. Biophys. J. 2001;81:1970–1989. doi: 10.1016/S0006-3495(01)75848-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Scheuss V., Schneggenburger R., Neher E. Separation of presynaptic and postsynaptic contributions to depression by covariance analysis of successive EPSCs at the calyx of Held synapse. J. Neurosci. 2002;22:728–739. doi: 10.1523/JNEUROSCI.22-03-00728.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Taschenberger H., Scheuss V., Neher E. Release kinetics, quantal parameters and their modulation during short-term depression at a developing synapse in the rat CNS. J. Physiol. 2005;568:513–537. doi: 10.1113/jphysiol.2005.093468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin J.W., Faber D.S. Synaptic transmission mediated by single club endings on the goldfish Mauthner cell. II. Plasticity of excitatory postsynaptic potentials. J. Neurosci. 1988;8:1313–1325. doi: 10.1523/JNEUROSCI.08-04-01313.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Waldeck R.F., Pereda A., Faber D.S. Properties and plasticity of paired-pulse depression at a central synapse. J. Neurosci. 2000;20:5312–5320. doi: 10.1523/JNEUROSCI.20-14-05312.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li J., Bickford M.E., Guido W. Distinct firing properties of higher order thalamic relay neurons. J. Neurophysiol. 2003;90:291–299. doi: 10.1152/jn.01163.2002. [DOI] [PubMed] [Google Scholar]
- 17.Li J., Guido W., Bickford M.E. Two distinct types of corticothalamic EPSPs and their contribution to short-term synaptic plasticity. J. Neurophysiol. 2003;90:3429–3440. doi: 10.1152/jn.00456.2003. [DOI] [PubMed] [Google Scholar]
- 18.Reichova I., Sherman S.M. Somatosensory corticothalamic projections: distinguishing drivers from modulators. J. Neurophysiol. 2004;92:2185–2197. doi: 10.1152/jn.00322.2004. [DOI] [PubMed] [Google Scholar]
- 19.Del Castillo J., Katz B. Biophysical aspects of neuro-muscular transmission. Prog. Biophys. Biophys. Chem. 1956;6:121–170. [PubMed] [Google Scholar]
- 20.Boyd I.A., Martin A.R. The quantal composition of the mammalian end-plate potential. J. Physiol. 1955;129 14–15P. [PubMed] [Google Scholar]
- 21.Martin A.R. A further study of the statistical composition of the end-plate potential. J. Physiol. 1955;130:114–122. doi: 10.1113/jphysiol.1955.sp005397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hubbard J.I., Llinás R., Quastel D.M.J. Arnold; London: 1969. Electrophysiological analysis of synaptic transmission. [Google Scholar]
- 23.Del Castillo J., Katz B. Quantal components of the end-plate potential. J. Physiol. 1954;124:560–573. doi: 10.1113/jphysiol.1954.sp005129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Budde T., White J.A., Kay A.R. Hyperpolarization-activated Na+-K+ current (Ih) in neocortical neurons is blocked by external proteolysis and internal TEA. J. Neurophysiol. 1994;72:2737–2742. doi: 10.1152/jn.1994.72.6.2737. [DOI] [PubMed] [Google Scholar]
- 25.Cahalan M.D., Almers W. Interactions between quaternary lidocaine, the sodium channel gates, and tetrodotoxin. Biophys. J. 1979;27:39–55. doi: 10.1016/S0006-3495(79)85201-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Konishi T. Voltage-gated potassium currents in myelinating Schwann cells in the mouse. J. Physiol. 1990;431:123–139. doi: 10.1113/jphysiol.1990.sp018323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hernandez-Cruz A., Pape H.C. Identification of two calcium currents in acutely dissociated neurons from the rat lateral geniculate nucleus. J. Neurophysiol. 1989;61:1270–1283. doi: 10.1152/jn.1989.61.6.1270. [DOI] [PubMed] [Google Scholar]
- 28.Quastel D.M., Hackett J.T., Cooke J.D. Calcium: is it required for transmitter secretion? Science. 1971;172:1034–1036. doi: 10.1126/science.172.3987.1034. [DOI] [PubMed] [Google Scholar]
- 29.Scheuss V., Taschenberger H., Neher E. Kinetics of both synchronous and asynchronous quantal release during trains of action potential-evoked EPSCs at the rat calyx of Held. J. Physiol. 2007;585:361–381. doi: 10.1113/jphysiol.2007.140988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Press W.H., Flannery B.P., Teukolsky S.A., Vetterling W.T. Cambridge University Press; Cambridge, United Kingdom: 1992. Numerical Recipes in C: The Art of Scientific Computing. [Google Scholar]
- 31.Biro A.A., Holderith N.B., Nusser Z. Quantal size is independent of the release probability at hippocampal excitatory synapses. J. Neurosci. 2005;25:223–232. doi: 10.1523/JNEUROSCI.3688-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Highstein S.M., Bennett M.V. Fatigue and recovery of transmission at the Mauthner fiber-giant fiber synapse of the hatchetfish. Brain Res. 1975;98:229–242. doi: 10.1016/0006-8993(75)90003-7. [DOI] [PubMed] [Google Scholar]
- 33.Morishita W., Alger B.E. Sr2+ supports depolarization-induced suppression of inhibition and provides new evidence for a presynaptic expression mechanism in rat hippocampal slices. J. Physiol. 1997;505:307–317. doi: 10.1111/j.1469-7793.1997.307bb.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Crowley J.J., Carter A.G., Regehr W.G. Fast vesicle replenishment and rapid recovery from desensitization at a single synaptic release site. J. Neurosci. 2007;27:5448–5460. doi: 10.1523/JNEUROSCI.1186-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lee J.S., Kim M.H., Ho W.K., Lee S.H. Presynaptic release probability and readily releasable pool size are regulated by two independent mechanisms during posttetanic potentiation at the calyx of Held synapse. J. Neurosci. 2008;28:7945–7953. doi: 10.1523/JNEUROSCI.2165-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Richards D.A., Bai J., Chapman E.R. Two modes of exocytosis at hippocampal synapses revealed by rate of FM1–43 efflux from individual vesicles. J. Cell Biol. 2005;168:929–939. doi: 10.1083/jcb.200407148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sara Y., Mozhayeva M.G., Liu X., Kavalali E.T. Fast vesicle recycling supports neurotransmission during sustained stimulation at hippocampal synapses. J. Neurosci. 2002;22:1608–1617. doi: 10.1523/JNEUROSCI.22-05-01608.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Vanden Berghe P., Klingauf J. Synaptic vesicles in rat hippocampal boutons recycle to different pools in a use-dependent fashion. J. Physiol. 2006;572:707–720. doi: 10.1113/jphysiol.2005.100842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Alexander G.M., Godwin D.W. Presynaptic inhibition of corticothalamic feedback by metabotropic glutamate receptors. J. Neurophysiol. 2005;94:163–175. doi: 10.1152/jn.01198.2004. [DOI] [PubMed] [Google Scholar]
- 40.Garduno-Torres B., Trevino M., Gutierrez R., Arias-Montano J.A. Pre-synaptic histamine H3 receptors regulate glutamate, but not GABA release in rat thalamus. Neuropharmacology. 2007;52:527–535. doi: 10.1016/j.neuropharm.2006.08.001. [DOI] [PubMed] [Google Scholar]
- 41.Guo J.Z., Tredway T.L., Chiappinelli V.A. Glutamate and GABA release are enhanced by different subtypes of presynaptic nicotinic receptors in the lateral geniculate nucleus. J. Neurosci. 1998;18:1963–1969. doi: 10.1523/JNEUROSCI.18-06-01963.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Khanin R., Parnas I., Parnas H. On the feedback between theory and experiment in elucidating the molecular mechanisms underlying neurotransmitter release. Bull. Math. Biol. 2006;68:997–1009. doi: 10.1007/s11538-006-9099-3. [DOI] [PubMed] [Google Scholar]
- 43.McGehee D.S., Heath M.J., Gelber S., Devay P., Role L.W. Nicotine enhancement of fast excitatory synaptic transmission in CNS by presynaptic receptors. Science. 1995;269:1692–1696. doi: 10.1126/science.7569895. [DOI] [PubMed] [Google Scholar]
- 44.Morishige K., Inanobe A., Yoshimoto Y., Kurachi H., Murata Y. Secretagogue-induced exocytosis recruits G protein-gated K+ channels to plasma membrane in endocrine cells. J. Biol. Chem. 1999;274:7969–7974. doi: 10.1074/jbc.274.12.7969. [DOI] [PubMed] [Google Scholar]
- 45.Murase S., Schuman E.M. The role of cell adhesion molecules in synaptic plasticity and memory. Curr. Opin. Cell Biol. 1999;11:549–553. doi: 10.1016/s0955-0674(99)00019-8. [DOI] [PubMed] [Google Scholar]
- 46.O'Dell T.J., Hawkins R.D., Kandel E.R., Arancio O. Tests of the roles of two diffusible substances in long-term potentiation: evidence for nitric oxide as a possible early retrograde messenger. Proc. Natl. Acad. Sci. USA. 1991;88:11285–11289. doi: 10.1073/pnas.88.24.11285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Djukic B., Casper K.B., Philpot B.D., Chin L.S., McCarthy K.D. Conditional knock-out of Kir4.1 leads to glial membrane depolarization, inhibition of potassium and glutamate uptake, and enhanced short-term synaptic potentiation. J. Neurosci. 2007;27:11354–11365. doi: 10.1523/JNEUROSCI.0723-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Dityatev A.E., Clamann H.P. Reliability of spike propagation in arborizations of dorsal root fibers studied by analysis of postsynaptic potentials mediated by electrotonic coupling in the frog spinal cord. J. Neurophysiol. 1996;76:3451–3459. doi: 10.1152/jn.1996.76.5.3451. [DOI] [PubMed] [Google Scholar]
- 49.Pereda A.E., Bell T.D., Faber D.S. Retrograde synaptic communication via gap junctions coupling auditory afferents to the Mauthner cell. J. Neurosci. 1995;15:5943–5955. doi: 10.1523/JNEUROSCI.15-09-05943.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Vautrin J., Kriebel M.E., Holsapple J. Further evidence for the dynamic formation of transmitter quanta at the neuromuscular junction. J. Neurosci. Res. 1992;32:245–254. doi: 10.1002/jnr.490320214. [DOI] [PubMed] [Google Scholar]
- 51.Vautrin J., Schaffner A.E., Barker J.L. Quantal and subquantal GABAergic transmissions in cultured rat hippocampal neurons. Hippocampus. 1993;3:93–101. doi: 10.1002/hipo.450030110. [DOI] [PubMed] [Google Scholar]
- 52.Bennett M.R., Farnell L., Gibson W.G. Quantal transmitter release at somatic motor-nerve terminals: stochastic analysis of the subunit hypothesis. Biophys. J. 1996;70:654–668. doi: 10.1016/S0006-3495(96)79606-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fatt P., Katz B. Spontaneous subthreshold activity at motor nerve endings. J. Physiol. 1952;117:109–128. [PMC free article] [PubMed] [Google Scholar]
- 54.Katz B. Prologue. In: Cottrell G.A., Usherwood D.N.R., editors. Synapses. Academic Press; London: 1977. pp. 1–5. [Google Scholar]
- 55.Kriebel M.E., Vautrin J., Holsapple J. Transmitter release: prepackaging and random mechanism or dynamic and deterministic process. Brain Res. Brain Res. Rev. 1990;15:167–178. doi: 10.1016/0165-0173(90)90017-i. [DOI] [PubMed] [Google Scholar]
- 56.Faure P., Korn H. A nonrandom dynamic component in the synaptic noise of a central neuron. Proc. Natl. Acad. Sci. USA. 1997;94:6506–6511. doi: 10.1073/pnas.94.12.6506. [DOI] [PMC free article] [PubMed] [Google Scholar]