A biomechanical rationale for C1-ring osteosynthesis as treatment for displaced Jefferson burst fractures with incompetency of the transverse atlantal ligament

Abstract

Nonsurgical treatment of Jefferson burst fractures (JBF) confers increased rates of C1–2 malunion with potential for cranial settling and neurologic sequels. Hence, fusion C1–2 was recognized as the superior treatment for displaced JBF, but sacrifies C1–2 motion. Ruf et al. introduced the C1-ring osteosynthesis (C1–RO). First results were favorable, but C1–RO was not without criticism due to the lack of clinical and biomechanical data serving evidence that C1–RO is safe in displaced JBF with proven rupture of the transverse atlantal ligament (TAL). Therefore, our objectives were to perform a biomechanical analysis of C1–RO for the treatment of displaced Jefferson burst fractures (JBF) with incompetency of the TAL. Five specimens C0–2 were subjected to loading with posteroanterior force transmission in an electromechanical testing machine (ETM). With the TAL left intact, loads were applied posteriorly via the C1–RO ramping from 10 to 100 N. Atlantoaxial subluxation was measured radiographically in terms of the anterior antlantodental interval (AADI) with an image intensifier placed surrounding the ETM. Load–displacement data were also recorded by the ETM. After testing the TAL-intact state, the atlas was osteotomized yielding for a JBF, the TAL and left lateral joint capsule were cut and the C1–RO was accomplished. The C1–RO was subjected to cyclic loading, ramping from 20 to 100 N to simulate post-surgery in vivo loading. Afterwards incremental loading (10–100 N) was repeated with subsequent increase in loads until failure occurred. Small differences (1–1.5 mm) existed between the radiographic AADI under incremental loading (10–100 N) with the TAL-intact as compared to the TAL-disrupted state. Significant differences existed for the beginning of loading (10 N, P = 0.02). Under physiological loads, the increase in the AADI within the incremental steps (10–100 N) was not significantly different between TAL-disrupted and TAL-intact state. Analysis of failure load (FL) testing showed no significant differences among the radiologically assessed displacement data (AADI) and that of the ETM (P = 0.5). FL was Ø297.5 ± 108.5 N (range 158.8–449.0 N). The related displacement assessed by the ETM was Ø5.8 ± 2.8 mm (range 2.3–7.9). All specimens succeeded a FL >150 N, four of them >250 N and three of them >300 N. In the TAL-disrupted state loads up to 100 N were transferred to C1, but the radiographic AADI did not exceed 5 mm in any specimen. In conclusion, reconstruction after displaced JBF with TAL and one capsule disrupted using a C1–RO involves imparting an axial tensile force to lift C0 into proper alignment to the C1–2 complex. Simultaneous compressive forces on the C1-lateral masses and occipital condyles allow for the recreation of the functional C0–2 ligamentous tension band and height. We demonstrated that under physiological loads, the C1–RO restores sufficient stability at C1–2 preventing significant translation. C1–RO might be a valid alternative for the treatment of displaced JBF in comparison to fusion of C1–2.

Electronic supplementary material

The online version of this article (doi:10.1007/s00586-010-1380-3) contains supplementary material, which is available to authorized users.

Introduction

Modern instrumentation techniques are causing new interest in the treatment and outcome of upper cervical spine injuries. Jefferson burst fractures (JBF) of C1 resemble one of these injuries, where consensus lacks concerning its ideal classification and treatment. Currently, the definition of JBF comprises the net effect of a continuum of axial forces traversing through the atlas ring [61] causing varying fractures where they exit, with different number, spread and comminution of fragments. Concerning stability assessment in JBF, literature reflects consensus with most surgeons determining instability when the transverse atlantal ligament (TAL) is disrupted or avulsed at its osseus insertion [13, 15, 27, 37, 39, 56] causing spread of the C1-lateral masses. Accordingly, most surgeons rely on radiographic criteria of instability including a C1-lateral mass displacement exaggerating a net sum of 6.9 mm [57], or an anterior atlantodental interval (AADI) greater than 3 mm [21], suggesting failure of the TAL [9, 17, 21, 27, 37, 39, 56].

Dvorak [20] showed that clinical outcome in terms of validated measures was poor using non-surgical treatment for displaced JBF, frequently resulting in malunion of C1–2. Very early, the Halo, being a theoretically motion sparing technique, was shown inadequate to maintain reduction in displaced JBF and sufficiently immobilize the C1–2 junction [30, 40]. Hence, current strategies encompass non-surgical treatment for the non-displaced JBF, but fusion of C1–2 for the displaced JBF with incompetency of the TAL and fusion of C0–2 for JBF with a comminuted lateral mass of C1 [20, 56]. Ruf [55] presented a motion sparing technique of C1-ring osteosynthesis (C1–RO) using an anterior C1-lateral mass screw-plate construct. Clinical results were good with 39° axial rotation of C1–2 in dynamic MRI. The technique was not without criticism [15] because CT and MRI data on the integrity of the TAL were not reported in detail. Dickman [15] hypothesized that, when the TAL is torn, permanent anterior instability of C1–2 exists. In reverse, TAL integrity was suggested to have been maintained in most of Ruf’s cases. Dickman stressed that if there was an MRI-proven TAL disruption in a C1 fracture, C1–2 fusion is required because neither an external brace nor C1–RO will correct the incompetency of the TAL. Notably, in addition to Ruf, Anderson [2] and Boehm [7] did not report on late instability at C1–2 in a total of nine cases treated with C1–RO for displaced JBF. Clinical data indicate that C1–RO might be a valuable adjunct to the surgeon’s armamentarium because it reconstructs C1–2 congruency preventing late sequels from C1–2 malunion [11, 20, 36, 56] in the displaced JBF and preserves important C1–2 motion [36]. However, whether an MRI-proven incompetency of the TAL is a contraindication for C1–RO indicating fusion of C1–2 to prevent late translational instability was not sufficiently investigated [2, 7, 55].

Therefore, our objectives were to investigate the effect of C1–RO on the reconstruction of translational stability C0–2 in an unstable, displaced JBF model with incompetency of the TAL.

Materials and methods

Five fresh-frozen cervical spines C0–T2 were harvested from 1 female and 4 male cadavers (mean age at death 65 years, range 58–69 years). Biplanar radiographs were taken to exclude abnormalities of the bony structures. Medical histories and radiographs showed no evidence of pathological conditions or remote trauma to the occipitocervical junction (OCJ). Afterwards, cadavers were stored frozen at −20° in triple sealed bags until preparation. After thawing specimens were prosecured at C2–3 and the skull was osteotomized at the level of the occipital bone. Soft tissue was removed while the integrity of ligaments and osseous structures at C0–2 was maintained. During preparation, specimens were kept moist with the saline solution.

Two polyaxial 3.5-mm diameter polyaxial screws, ≥40 mm in length (Axon, Synthes, Switzerland) were inserted bicortically into the lateral masses of C1 according to Goel-Harms [23, 25] enabling linkage of screws by a transverse rod. Care was given that the screws were placed far cranial at the posterior C1-lateral mass surface and that the screw-heads and -shafts did not contact the Isthmus of C2. After screw insertion and each biomechanical testing, specimens were wrapped in saline-soaked gauze to prevent dehydration [64].

The C2 vertebra was potted in an aluminum loading fixture and embedded in polymethylmethacrylate (PMMA, Technovit 3040, Heraeus Kulzer GmbH, Wehrheim/Germany). Care was taken that only the inferior third of C2 was embedded and that the bottom line of C2 was horizontal and parallel to the PMMA pot. The potted specimens were fixed in the center of a cross table of an electromechanical testing machine (ETM; Z010, Zwick, Ulm/Germany). The pot was placed perpendicular to the floor with C1 facing downward (Fig. 1; Electronic suppl material Fig. 1). The C0–1 joint was left unconstrained.

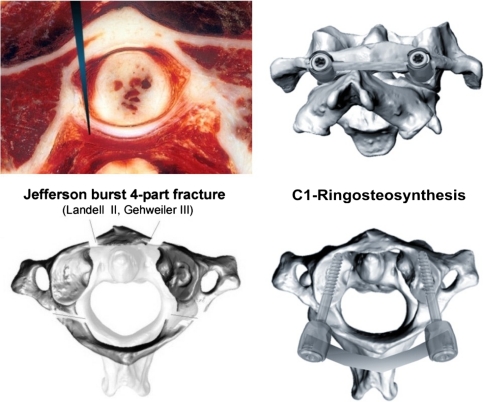
Fig. 1.

Top image on the left cryosection at C1 revealing the atlantodental joint and transverse atlantal ligament (TAL). The long arrow head denotes the level of osteotomy performed in our specimens to transect the TAL before the cyclic loading started. The bottom image on the left illustrates the recreation of the Jefferson burst fracture (JBF) model with the fracture traces being characteristic for JBF. In the current study, a classic four-part JBF was created classified as type II according to Landell [38] and type III according to Gehweiler [22]. The images on the right reveal the C1-ring osteosynthesis with 3.5-mm shaft-screws placed into the C1-lateral mass and linked with a 3.5-mm rod

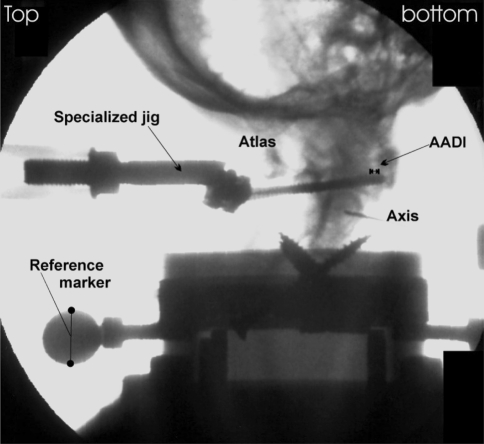
An image intensifier (Siremobil Compact L, Siemens, Erlangen/Germany) was placed surrounding the ETM to assess sagittal displacement of C1 and C2 radiographically. Images were performed at each increment of loading except for the cyclic loading part. In addition, displacement (mm) was recorded by the ETM. Radiographs for each incremental step of loading were processed digitally and analyzed using a customized software programm (Escape Medical Viewer V3, Escape, Greece). The degree of anterior translation of C1 on C2 was determined by monitoring the radiographic AADI. It was measured on all radiographs (mm) according to recommendations of the Spine Trauma Study Group [8] by one of the authors (HK). Inter- and intraobserver reliability of AADI measurements have been shown to be good [8, 16, 54]. To exclude measurement errors related to trigonometric projection, each radiograph was pre-calibrated referencing the radiologic size of a metal ball-type marker fixed to the specimen’s pott to its real size (17.5 mm, Fig. 2). The radiographic AADI resembled the true anterior translation of C1 on C2, the displacement at distinct loads, while the ETM collected load displacement data in posteroanterior direction including bending properties of the screw-bone osteosynthetic construct and tilting of C1. Differences between the radiographic measurement technique and recorded displacement data of the ETM were analyzed for each test separately. We also calculated the differences concerning any change in the AADI at each incremental loading. The difference was expressed as Δload–displacement (in mm, see Fig. 3).

Fig. 2.

Radiograph illustrating the testing set-up and radiographic assessment of AADI. Loads were applied in posteroanterior direction with the specimens placed perpendicular to the ground

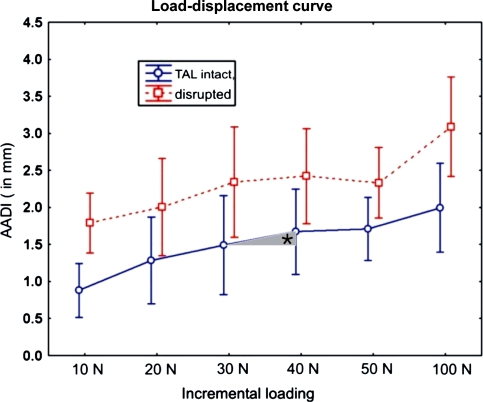
Fig. 3.

The displacement of C1 on C2 in terms of the radiographically assessed AADI in the TAL-intact state (solid line) and TAL-disrupted state (dotted line). Differences just yielded significance for the initialization of forces at 10 N (P = 0.02) and at 100 N loading (P = 0.049). The asterisk marks the increase or decrease of the AADI at each incremental loading expressed as Δload–displacement (mm)

All specimens were subjected to a protocol that included three steps as follows:

1. Physiological incremental loading of C1 on C2 at TAL-intact state with C1–RO from 10 to 100 N.

2. Cyclic loading (1,000 cycles) of C1 on C2 in posteroanterior direction with the TAL disrupted using physiologic loads (20–100 N).

3. Physiologic incremental loading of C1 on C2 at TAL-disrupted state and with the C1–RO accomplished from 10 to 100 N. Application of further loads >100 N to determine failure loads.

In detail, with the first step the specimen’s C1-lateral mass screws were linked posteriorly with a 3.5-mm rod (Axon, Synthes, Switzerland). A customized jig (see Electronic supplement material) was mounted onto the ETM transmitting the anteriorly directed loads to C1. The jig had a fish-mouth shaped opening that enabled perpendicular mid-sagittal contact to the posterior rod at the level of the posterior C1 arch. Next, the specimens were subjected to non-destructive sagitally oriented posteroanterior loading. We controlled for appropriate position of the specimen and that the posteroanterior force was applied inline with the neutral position of C1 on C2. With the TAL left intact, loads were applied in increments of 10 N ramping from 0 to 50 N and then with 50 N increments from 50 to 100 N. A 10 N preload was utilized for all tests to absorb any slack in the system. Speed was 0.1 mm/s breaks between incremental increases were 10 s. At each load increment, radiographs were taken and load–displacement data of the ETM stored digitally.

For the second step, the TAL was sectioned: after training on formalin-fixed specimens, we placed a left anterolateral vertically oriented osteotomy centered at the anterior arch of C1 using a small chisel. Then, osteotomy was opened with a small arthrodesis spreader. Using a scalpel, a longitudinal cut was made to a depth of 15 mm directly beneath the odontoid tip going downward in craniocephalad direction until the scalpel abutted the C2-vertebral body (Fig. 1). The transsection of the TAL was felt as a sudden break. Sectioning of the TAL was confirmed by dissection of C1–2 after biomechanical testing. To complete the JBF model, a contralateral osteotomy at the anterior C1 arch and two bilateral osteotomies at the lateral aspects of the posterior C1 arch close to the vertebral artery groove were placed. In addition to the transsection of the TAL, the capsule of the left C1–2 lateral joint was sectioned resulting in a floating’ left C1-lateral mass. After surgery, instability was assessed by the removal of the posterior rod-linkage and all specimens revealed unstable JBF equivalents in the coronal and sagittal plane and against rotation, with the lateral masses being easily displaced off the C1–2 joint boundaries. Next, the C1–RO was accomplished by reduction of the fragments, compressing the lateral masses of C1 against the condyles of C0 and linkage of the C1-lateral mass screws with the 3.5-mm rod. With the C1–RO, a tight, pre-tensioned OCJ could be reconstructed. Afterwards, the specimens were exposed to cyclic loading (triangulated force curve). Each specimen was loaded cyclically for a total of 1,000 cycles, ramping from 20 N to a maximum of 100 N and then back to 20 N in posteroanterior direction. Speed was 2.5 mm/s. This amount of fatigue was intended to simulate at least a week of post-surgery in vivo loads and normal stress on the osteosynthesis. Loads were applied as pure weights at the posterior rod ensuring that the secondary ligamentous restraints of C1–2 that take in place for the TAL after its sectioning, took over the direct loads. The maximum displacement of C1 on C2 at 100 N loading was recorded by the ETM.

Finally, with the third step, the specimens at TAL-disrupted state were subjected to incremental loadings with physiologic loads ramping from 10 to 100 N (same setting as in the first test), subsequently further loads with 10 N increments were applied to obtain failure load (FL) data with a maximum set at 500 N. Load and related displacement data derived by the ETM were taken continuously as well as radiographic images performed at each increase of load until the C1–2 complex failed. The displacement at each load was recorded using a computerized data collection system (TestXpert V11.02, Zwick Roell, Germany). Failure load was defined according to the study of Fielding [21]: after TAL rupture, at the instant of partial functional failure of some of the secondary restraints, the forces reach a peak and decline momentarily, then rise again as the forward shift of C1 continues and the remaining functionally active parts of the auxiliary ligament system come under load. Therefore, load and displacement data at the first instant of partial failure of secondary restraints were documented as failure loads in the current study. In addition, a descriptive assessment of failure was documented for each specimen.

Statistical analysis included computation of descriptive statistics, such as means and standard deviations. A repeated measure ANOVA with Fisher’s LSD test for post hoc comparisons was used to compare different groups (AADI, Δ-AADI, load–displacement and Δload–displacement). Whisker plots with 95% confidence intervals were used to illustrate results (Fig. 3). A P < 5% considered statistically significant. All analyses were done using Statistica 6.1 (StatSoft, Tulsa, USA).

Results

The means, standard deviation and ranges of radiographic assessment of AADI at the TAL-intact state derived from the first test using physiological loads are summarized in Table 1.

Table 1.

Radiographic measurements of AADI (mm) under physiological loading conditions (10–100 N), TAL intact

Loading	10 N	20 N	30 N	40 N	50 N	100 N
Mean	0.88	1.28	1.49	1.67	1.71	1.99
SD	0.35	0.34	0.31	0.34	0.21	0.24
Range	0.45–1.22	0.94–1.81	1.14–1.96	1.10–1.98	1.41–1.98	1.60–2.21

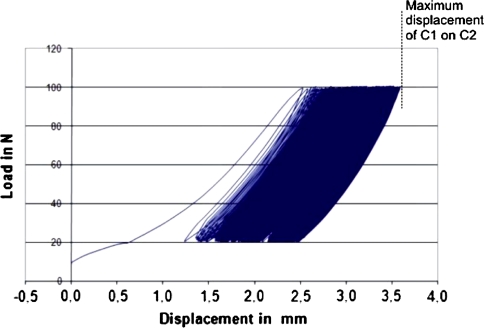
After transsection of the TAL, all specimens succeeded the cyclic loading without implant loosening or gross failure. The maximum displacement of C1 on C2 during the cyclic loading recorded by the ETM was 3.6 ± 1.19 mm (range 2.01–5.33 mm) on average. Figure 4 illustrates a load–displacement curve of one specimen at the TAL-disrupted state during the cyclic loading.

Fig. 4.

Load–displacement curve of one specimen during cyclic loading. After testing on the TAL-intact state, all specimens were subjected to cyclic loading with the TAL transsected. Maximum displacement under physiologic loading, ramping from 20 to 100 N, was 3.6 ± 1.19 mm (range 2.01–5.33 mm) on average

We observed that after creation of the JBF model the C1–RO reconstructed a tight ligamentous coupling at C0–2 in all specimens. Figure 5 illustrates the effect of the C1–RO on the JBF and the ligamentous complex at C0–2. All specimens did undergo the third tests, including the incremental loading from 10 to 100 N, as tested in the TAL-intact state and further incremental increase of loads until failure.

Fig. 5.

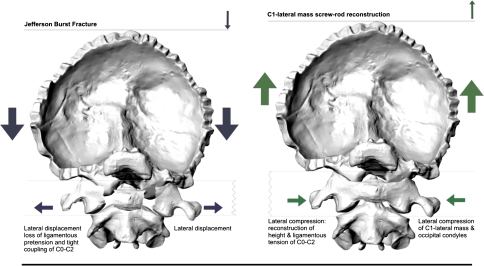
Biomechanical effect of C1-ring osteosynthesis on C0–2 alignment. Left schematic illustration of forces involved in the creation of a Jefferson burst fracture (JBF). Axial compressive forces (large dark arrows) on C0 result in a failure of the C0–C1–C2 ligamentous tension band through loss of height and fracture of the bony C1 ring, causing a lateral displacement (small dark arrows) of the C1-lateral masses from the anterior and posterior ring arches. Right reconstruction after a JBF involves imparting an axial tensile force (large gray arrows) to lift C0 into proper alignment to the C1–2 complex. Simultaneous compressive forces (small gray arrows) on the C1-lateral masses and occipital condyles allow for the recreation of the functional C0–C1–C2 ligamentous tension band and C0–C height

Radiographic assessment, TAL-disrupted state

Analysis of differences between the radiographically assessed AADI at each incremental loading revealed a statistically significant increase only at the beginning of the load transfer (10–20 N, P = 0.02) and it yielded significance at 100–150 N (Table 2). There were no significant differences for the Δload–displacement in terms of the AADI during the incremental loadings as assessed on the radiographs.

Table 2.

Radiographic measurements of AADI (in mm) under incremental failure-load testing (10 N to failure), TAL disrupted

Loading	10 N	20 N	30 N	40 N	50 N	100 N	150 N	200 Na	250 Na	300 Nb
Mean	1.97	2.44	2.71	2.78	2.71	3.38	3.73	4.25	4.50	5.66
SD	0.49	1.16	1.13	1.02	0.97	0.97	1.21	1.12	0.80	0.69
Range	1.41–2.68	1.11–4.16	1.43–4.19	1.68–4.20	1.73–4.20	2.25–4.56	2.36–5.36	3.25–5.55	3.70–5.41	5.17–6.14

^aData of four specimens succeeding loading condition

^bData of two specimens succeeding loading condition

Assessment with the ETM

Our analysis of differences between the load–displacement data at each incremental loading when using the ETM revealed a significant increase at incremental loading from 100 to 150 N (P = 0.03, Table 3). Figure 6 illustrates the load–displacement curve of one specimen from physiologic loading to failure. When concerning the Δload–displacement data, the statistical analysis showed no significant difference up to incremental loading of 90 N, whereas a significantly increased Δload–displacement existed between loading from 90 to 100 N (P < 0.001). Further loading by 50 N increments did not cause a significantly increased displacement between each loading increment, but it remained significant when compared with the initial loadings at 10–90 N (P < 0.001).

Table 3.

Assessment of atlantoaxial load–displacement (mm) under incremental failure-load testing (10 N to failure) with electromechanic testing machine, TAL disrupted

Loading	10 N	20 N	30 N	40 N	50 N	100 N	150 N	200 Na	250 Na	300 Nb
Mean	0.01	0.37	0.67	0.90	1.10	1.92	2.79	3.52	4.63	5.97
SD	0.01	0.25	0.33	0.42	0.48	0.70	0.95	1.38	1.94	1.33
Range	0.01–0.02	0.01–0.72	0.17–1.10	0.27–1.41	0.34–1.60	0.73–2.40	1.12–3.44	1.54–4.61	2.05–6.39	5.03–6.91

^aData of four specimens succeeding loading condition

^bData of two specimens succeeding loading condition

Fig. 6.

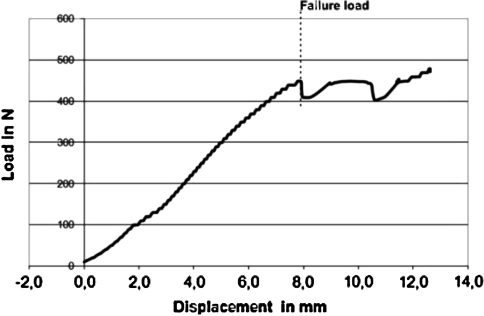
Failure-load curve of one tested C1-ring osteosynthesis with TAL disrupted. The load–displacement tracing illustrates a continuous load–displacement curve increasing until the system fails (here under loads >400 N at a displacement of about 8 mm). At the instant of partial functional failure of some of the secondary restraints, the forces reach a peak and decline momentarily, then rise again as the forward shift of C1 continues and the remaining functionally active parts of the auxiliary ligament system come under load

Differences between assessment of displacement on radiographs and using the ETM

Slight differences concerning the means existed between the radiographic assessment of the AADI and the assessment by the ETM. With the latter, increased displacement data at higher loads were explained by tilting of C1 on C2 with slight flexion or extension as well as construct bending. However, the statistical analysis revealed no significant differences among the radiologically assessed displacement in terms of the AADI and ∆load–displacement data derived by the ETM (P = 0.5).

Comparison of load–displacement data at the TAL-intact and the TAL-disrupted state

Although differences existed concerning means between the measurements of the radiographic AADI under physiological loading conditions (10–100 N) with the TAL-intact compared with the TAL-disrupted state (Tables 1 and 2; Fig. 3), these differences were small, on average ranging between 1 and 1.5 mm, yielding significance only for the beginning of loading (at 10 N, P = 0.02) and when reaching the upper limits of physiological loads (at 100 N, P = 0.049).

In the TAL-disrupted state, there was a larger AADI at the beginning of the incremental loading revealing an initial slack in the system. The analysis of further incremental loads showed that the increase in the AADI (ΔAADI) between the incremental steps (10–100 N) was not significantly different from the TAL-intact stage under physiological loading conditions (Fig. 3). With subsequent loading beyond the physiologic condition (10–100 N), the load–displacement characteristics remained similar between the TAL-disrupted and the TAL-intact state.

Characteristics of load to failure testing

After transsection of the TAL, the mean FL of the system (C1–RO with TAL and one-sided capsule incompetency with secondary ligamentous restraints intact) was 297.5 ± 108.5 N (range 158.8–449.0 N). The related load–displacement data assessed by the ETM was 5.8 ± 2.8 mm (range 2.3–7.9 mm) on an average. All five specimens succeeded a FL greater than 150 N, four of five greater than 250 N and three of five greater than 300 N. It is of note that failure, identified as a peak with sudden decline in the load–displacement curve, did not occur as gross construct failure in any specimen, but rather as shearing of the screws through the C1-lateral masses, tilting of C1 on C2, bending of the screw-rod construct, stretching of the secondary ligaments or at worst rupture of the C1–2 right lateral joint capsule or C1–2 anterior and posterior membranes (including combinations of failure characteristics). Figure 6 illustrates a typical FL curve of one specimen. With the TAL disrupted, this load–displacement tracing illustrates a rather continuous increase until the system fails the first time, e.g., with partial disruption, stretch or loss of one of the secondary ligamentous restraints. At this moment of functional failure, the applied forces peak sharply, decline momentarily and then rise again as the forward shift of C1 continues and remaining functionally active parts of auxiliary ligaments step in.

Discussion

The TAL is a strong ligament about 3-mm thick and 8-mm wide (Fig. 1) [42, 46, 67], the primary stabilizing component against translational forces at C1–2 [21]. The main auxiliary restraints include the tectorial membrane, the crucial ligament, the alar ligaments and the capsular ligaments as well as the apical odontoid ligament, and the atlantoaxial anterior and posterior membranes with descending order of importance [21, 32, 34, 46, 47, 65, 67]. Based on the previous biomechanical studies that were performed to identify the failure loads of the TAL and displacement at failure [19, 21, 28, 49, 57, 63], most physicians assumed that traumatic disruption of the TAL causes translational instability of C1–2 that places the spinal cord at risk [13, 15, 27, 37, 39, 56]. However, the current study showed that with C1–RO in an unstable JBF model with disrupted TAL and unilateral capsule, there was no gross translational instability or spinal canal compromise under physiologic loads and even beyond.

We defined a translational load of 100 N as the upper limit of physiological loading and we selected pure weight loading directly onto the screw-bone C1 construct, because flexion moments acting on C0 were difficult to control in their ability to perform translational posteroanterior stress at C1 provoking atlantoaxial subluxation. Actually, this is the first study on translational stability assessment of a C1–RO and there are no published tolerance values. Hence, our applied loads and related displacement data have to be placed into perspective of TAL failure loads reported in the literature ranging from a mean of 354–824 N [44, 52, 57, 61]. In several studies, a full physiologic flexion–extension range of C0–2 could be reproduced under bending moments of 1.5 Nm applied through C0 [44, 49, 51, 52]. Applying the 1.5 Nm bending loads to C0, Puttlitz [51] characterized the load transfer through the TAL during physiologic range of motion. In their finite element rheumatic generation model, the authors analyzed the ligament involvement during the development and advancement of atlantoaxial subluxation by calculating the AADI after reduction in transverse, alar and capsular ligament stiffness. The force resulting by contact of the TAL to the posterior odontoid surface at the odontoid process-TAL junction was 25.2 N. The axial contact forces of the lateral C1–2 joints were reported to be 35.2 N (right) and 44.3 N (left) for the TAL-intact state. The model predicted a normal AADI of 2.9 mm under physiologic loading. Consequently with our model, 100 N posteroanterior loads transferred through the C1–RO and the secondary ligamentous stabilizers were defined as physiologic upper limits to be sure simulating a clinical worse case scenario.

In our study, creating a JBF model with TAL rupture caused height loss at C0–2 with lateral displacement of the C1-lateral masses. In reverse, pretension of the coupled ligamentous C0–2 system was achieved when the C1–RO was accomplished, and thus was the ability of the secondary ligamentous restraints to resist translation loads (Fig. 3). Our observations echoed a previous biomechanical study [46] demonstrating that the moments applied to the head and C1, whether they are produced by posteroanterior or tensile forces, must be resisted by a force couple at C0–2. During flexion, the couple is primarily generated by tensions in the C0–2 ligamentous complex. Taking the AADI as a surrogate for C1–2 translational instability, our analysis showed that with the TAL disrupted, loads up to 150 N were transferred to C1, but the radiographically measured AADI did not exceed a mean of 3.7 mm, with displacement of C1 on C2 according to the ETM data of only 2.8 mm on average (see Tables 1 and 2). These displacement data at the limits of physiological loading have to be interpreted in perspective of physiologic data for the AADI: Rojas [54] studied the AADI in 200 adults on CT scans. In a supine position, the AADI was 1.3 ± 0.4 mm (range 0.5–2.4 mm). Other authors suggest a normal radiographic AADI to be 3 mm [9, 17, 21, 27, 37, 39, 56]. Hence, our results showed that after C1–RO anterior displacement of C1 on C2 under physiologic loading conditions (100 N) and even under higher loads was not much different from the intact state. The posterior atlantodental interval (PADI) that is complimentary to the AADI delineates the space for the spinal cord between the odontoid and the anterior surface of the posterior C1 arch. In an analysis of 100 sets of biplanar radiographs of healthy adults [33], the PADI was a mean of 24.1 ± 2.7 mm (range 19–33.1 mm). Although we did not measure the PADI during loading, our assessed load–displacement data at the limits of physiological loading delineate that, calculated from the results of the AADI, the PADI was reduced by 2.8 mm on average at loading of 150 N (illustrated in Table 3) and such a displacement would resemble a PADI of still >20 mm that does not endanger the spinal cord [17, 50].

This is the first biomechanical study of C1–RO, therefore comparisons to prior studies are not available and comparison to fusion C1–2 is not appropriate. However, the results of our load–displacement data can be further delineated in view of Puttlitz’ results [51]: In a fully intact TAL, the C1–2 capsular ligaments demonstrated tensions of 0.8 N anteriorly and 33.9 N posteriorly under posteroanterior loading. Complete TAL disruption resulted in a C1–2 load transfer increase of about 50% through the posterior capsules that acted as secondary stabilizers. During loading of the intact TAL, the AADI increased by 2.92 mm. Substantial increase and displacement >1.5 mm (AADI > 4.5 mm) was not obtained until the TAL stiffness was reduced by 75%. With simulated TAL disruption (100% TAL stiffness reduction) and 50% reduction in capsular ligament reduction, resembling the model replicated in our study, the finite element model [51] predicted an increase of 2.9 mm with an AADI of 5.8 mm, albeit resembling the displacement we documented in one of our specimens (specimen #2, AADI: 5.33 mm) during the cyclic testing. Puttlitz confirmed that the TAL is a main stabilizer of posteroanterior translation stability at C1–2, but emphasized that the alar and capsular ligaments function as secondary stabilizers to sagittal plane translation. The influence of the tectorial membrane was not analyzed [51], but was included in the current study that might explain our smaller mean displacement under physiologic loading (Table 1). In Puttlitz’s study [51] atlantoaxial subluxation did not exceed pronounced levels (defined as AADI >6 mm) until the alar and/or capsular ligament stiffness were reduced by 75% in addition to the TAL rupture. Findings agree with the cadaver investigation of Fielding [21], in which the TAL and alar ligaments were implicated as the main resistors to translation, comparing well to our findings. In light of Puttlitz’ findings, our study stressed that with the axial loading injury of the C1 ring and the C1–2 joints, the alar ligaments, portions of the facet capsules, and other secondary restraints to flexion remain intact, while the TAL can be ruptured. With the TAL rupture, some instability in flexion may be present, but it is limited by the remaining intact structures when the force couple at C0–2 is reconstructed using the C1–RO (Fig. 3). After C1–RO, the stability provided by the secondary ligaments seems sufficient to maintain C1–2 stability and translation of C1 on C2 within limits that do not endanger the spinal cord during physiological loading and even at the limits thereof. The AADI was within a limit of 5 mm (2.3–4.6 mm) in all cases at loading up to 100 N after the C1–RO. In contrast, in the intact state, the AADI was 1.99 mm on average at 100 N loading, with a maximum of 2.2 mm in one specimen. The results go in concert with data of normals by Rojas [54] where the AADI was <2 mm in 97.5% of individuals in supine CT-scan position.

In previous biomechanical studies [19, 21, 28, 49, 57, 63] clinical inferences about the integrity of the TAL were based on the threshold of the TAL rupture (3–5 mm). We scrutinized whether rigid radiographic criteria are appropriate to infer traumatic rupture of the TAL and ligamentous instability of C1–2 in a clinical scenario. We observed that with the TAL and one C1–2 joint capsule disrupted, the smallest AADI under the smallest loading condition (10 N) was 1.41 mm with a mean of 1.97 (Table 1), remaining within normal limits for two specimens up to 30 N and for one up to 50 N loading. Our study stressed that the secondary stabilizers can mask a TAL injury with the AADI being within normal limits confirming findings of Dickman [14, 15] that the AADI can be normal radiographically due to the resistance of secondary stabilizers.

The current study has limitations. The limited number of specimens is similar to other biomechanical studies on the OCJ and refers to the difficulties and costs acquiring fresh-frozen specimens [12, 19, 29, 41, 66]. But, as our testing echoed results derived in a validated finite element model [51], changes in main findings were not expected with increased sample size. Healed ligamentous properties and the support by the cervical neck muscles were not assessed in the current model. The paraspinal muscles have vital importance as contributors to OCJ stability because C1 is largely stabilized by ligaments and muscles interposed between C0 and C2 [4]. The effect of muscle forces would most likely have increased spinal stability at C0–2. Hence, we assume in vivo stability of C0–2 being not less than revealed in our biomechanical model after C1–RO. We did not assess the impact of TAL disruption on rotational stability. As the TAL was found to be the main stabilizer resisting translational forces in sagittal plane and the alar ligaments to be the main stabilizers against rotation at C0–2 [19, 21, 28, 49, 57, 63], we do not expect our main conclusions to be changed significantly. Previous studies demonstrated that strengths of the ligaments at the C0–2 complex vary in individuals [19, 21, 28, 67]. Hence, the results derived from the current study do not preclude individual assessment of the strength of the secondary stabilizers in unstable JBF with TAL disruption; neither vertical stability when conservative treatment nor a C1–RO is considered.

Clinical inferences

In a multicenter study, Dvorak et al. [20] reported the outcome of 34 patients treated conservatively for JBF demonstrating that displaced JBF can show significant long-term sequels due to C1–2 malunion. Patients in whom JBF were displaced ≥7 mm had significantly worse outcomes. Inferior clinical outcomes with non-surgical treatment of displaced JBF were also reported by others [2, 11, 18, 24, 27, 38–40] bearing the risk of late C1–2 deformity that can cause cranialization of the odontoid, C0–2 joint deformity and arthritis requiring C0–2 fusion [56]. As a consequence of the prevailing reports of inferior outcomes following conservative treatment, open reduction and instrumented fusion of C1–2 for displaced JBF are increasingly recognized as the preferred treatment with favorable outcomes, using posterior transarticular screw fixation of C1–2 with fusion [24, 27, 43, 56, 58], anterior transarticular screw fixation of C1–2 [3, 24, 35] or C1-lateral mass/C2 pedicle screw fixation [1, 25, 26, 60, 62]. C0–2 fusion is retained for the non-reductable JBF, those with a comminuted lateral mass or chronically and rigid displaced JBF with fixed cranial settling [11, 56, 58]. Concerning motion sparing techniques, some authors reported implant removal after C1–2 osteosynthesis for JBF to gain some rotation of C1–2, but results differed [5, 25, 59]. Subsequently, Ruf [55], Böhm [7] and Anderson [2] reported on C1–RO for JBF. Böhm [7] used a posteroanterior instrumented approach and reported favorable results in eight JBF. All cases had suspected TAL injury. At follow-up CT-based fusion was documented in all patients, which were reported to have ‘no’ restriction of rotation. Ruf [55] reported on six JBF treated with anterior transoral screw-rod fixation. In five cases, dynamic MRI revealed a mean C1–2 rotation to the right of 20.6° and 18.6° to the left. The outcome was good to excellent except in one patient who had C1–2 incongruency and poor outcome referred to a distorted C1–2 articular configuration. Even in seriously displaced JBF treated with C1–RO, these authors did not report on late sagittal or rotational instability, neither did Anderson who reported on a successful outcome following a posterior screw-rod based C1–RO for a displaced JBF [2]. In the context of sagittal instability concerns, the literature on the natural course of conservatively treated displaced JBF with TAL incompetency, including also individuals with severely displaced JBF, lacks reports concerning late sagittal instability of C1–2 [37, 39, 40]. In contrast, vertical settling C0–2 with basilar invagination [56] as well as painful C1–2 incongruency and painful loss of rotation due to C1–2 malunion is rather a problem in conservative treatment [11, 36, 40, 56]. It is important to recognize that only a few C1 injuries do show acute translational instability, but these patients frequently show vertical instability as part of a major ligamentous trauma to the OCJ (Electronic supplement material) [10, 31, 40, 53].

In degenerative cases, the AADI and PADI were used to delineate the space available for the cord at C1 and to predict the risk for increasing stenosis, myelopathy and death [6, 17, 33, 48, 50, 54]. Several authors suggested an AADI of 8 mm to be a sound threshold opting for fusion of C1–2. Although none of our specimens exceeded a displacement greater than 5.33 mm during the cyclic loadings and during the incremental loading from 10 to 100 N with the TAL disrupted, a distinct morphometric threshold cannot be given concerning when sagittal displacement of C1–2 confers ‘instability’ causing pain and, thus, indicating fusion C1–2 [28]. But, the current study was performed to gain first baseline data on the biomechanical characteristics of a C1–RO in a TAL-deficient JBF model that serve for better understanding of the clinical success reported with C1–RO in such injuries [2, 7, 55]. Reconstruction after a JBF using a C1-ring construct involves imparting an axial tensile force to lift C0 into proper alignment to the C1–2 complex. Simultaneous compressive forces on the C1-lateral masses and occipital condyles allow for the recreation of the functional C0–2 ligamentous tension band and C0–2 height (Fig. 3).

The C1–RO was shown to be a biomechanically sound treatment for JBF and a potential alternative to fusion. Displaced JBF carry a high risk of C1–2 incongruency, symptomatic malunion and late risk of arthrosis C1–2 [11, 36, 40]. In worst case, basilar invagination from cranial settling C0–2 occurs conferring neurological risks. C1–RO reconstructs atlantoaxial alignment, while it has the potential to restore atlantoaxial motion. Nevertheless, further clinical and biomechanical studies are indicated to elucidate the characteristics and limits of C1–RO. The limits of C1–RO arise in JBF where damage to the articular facets of C1–2 causes multiple fragments, imparts incongruency at C1–2 and precludes screw placement in the C1-lateral mass. The literature serves evidence that fractures including a comminuted articulating surface of C1 are difficult to reduce and fix by either a transarticular screw or a C1-lateral mass screw, so these fractures are still better managed with C0–2 fusion while non-displaced JBF with maintained C1–2 congruency can be successfully treated in a rigid collar [11, 27, 45, 56, 58].