Abstract
In quantitative perfusion imaging using arterial spin labeling (ASL), variable blood transit times and post-labeling delays are two confounding factors that may compromise the accuracy of perfusion quantifications. In the present study, theoretical analyses and experimental data at 9.4 T demonstrate that increasing labeling duration not only enhances the contrast of the ASL signal, it could also minimize the effect of variable post-labeling delays in multi-slice ASL acquisitions. With a labeling duration of 6.4 s, ASL signal acquired in multi-slice mode (11 slices) is very similar to that acquired in single slice mode. Previous studies have shown that inserting a delay between the spin labeling pulse and the image acquisition pulse could reduce confounds resulting from variable blood transit times at the expense of ASL sensitivity. Our simulations suggest that enhancing the contrast of ASL signal offers the opportunity for extending the post-labeling delay to a longer duration, minimizing systematic errors associated with a wide range of blood transit times, which could have significant implications for applying ASL techniques to perfusion imaging of pathological conditions in animal models.
Keywords: perfusion, blood transit time, brain, cerebral blood flow
INTRODUCTION
Cerebral blood flow (CBF) is an important physiological parameter that reflects brain tissue viability, metabolism and function (1). Arterial spin labeling (ASL) techniques (2–7) allow non-invasive assessment of CBF by observing the inflow of the labeled arterial blood into an imaging slice. ASL techniques have been implemented in both continuous (2–3) and pulsed versions (4–7), and are based on the detection of magnetization difference caused by the mixing of labeled/unlabeled arterial water with tissue water. As the ASL occurs outside the region of interest, one has to wait for the labeled water to transit from the labeling region to the region of interest and to mix with the local tissue. During this transit time, the labeled spins are decaying due to longitudinal relaxation, introducing a dependence of the ASL signal on the T1 of arterial water, which is itself dependent on the strength of the magnetic field, B0.
Perfusion imaging at high fields offers several advantages. First, the T1 value of arterial water increases with B0. At 1.5 T, T1 of arterial water is ~1.2 s (8), while at 9.4 T it is ~2.3 s (9). A longer T1 value allows for labeled spins to decay at a slower rate during the transit time from the labeling plane to the imaging plane, thus improving the sensitivity of the ASL signal (10). Second, the signal-to-noise ratio (SNR) is enhanced at high fields, allowing tissues with low perfusion levels to be imaged with improved accuracy. However, a potential concern in performing ASL experiments at high fields relates to the assumption of “steady-state” condition that has been widely applied in perfusion quantifications (except in cases where it is not required, such as the kinetic model (11)). When T1 values are markedly increased at high fields, such as 9.4 T, the steady-state condition may not be satisfied if the labeling duration is not sufficiently long, potentially underestimating cerebral perfusion. To the best of our knowledge, this issue has not been fully addressed in the literature.
In quantitative ASL, the transit time from the labeling plane to the imaging plane is a confounding factor, which is of particular importance for multi-slice ASL, since the transit times are known to be variable across slices and even within different structures in the same slice depending upon vasculature geometry (12,13). Furthermore, each slice has a distinct post-labeling delay. For example, assuming a data acquisition time of 35 ms per slice using echo planar imaging (EPI), perfusion imaging of eleven slices would result in a post-labeling delay difference of 350 ms between the first and the last slices, causing variable decays of the labeled spins across slices. In general, variable blood transit times and post-labeling delays remain intrinsic limitations in quantitative ASL of multiple slices, particularly in pathological conditions.
Several methods have been proposed to address the above-mentioned issues. Alsop and Detre (14) proposed to apply a delay following the labeling pulse. A pulsed version of this technique was introduced by Wong et al. (7) and was further elaborated in a later study (15). These approaches elegantly minimize systematic errors resulting from variable blood transit times, but they also reduce the sensitivity of the ASL signal by a factor exponentially dependent upon the duration of the post-labeling delays. Velocity-selective labeling (16,17) and territory labeling techniques (17) are also under development to mitigate these problems.
In the present continuous ASL (CASL) study, we propose to apply a labeling pulse of long-duration. Theoretical analyses and experimental data at 9.4 T demonstrate that long labeling duration enhances the contrast of the ASL signal and ensures the assumption of “steady-state condition” to be satisfied at high B0; more importantly, it could minimize systematic errors associated with variable post-labeling delays inherent in multi-slice ASL. It is further shown that enhancing the contrast of the ASL signal offers the opportunity for extending the duration of the post-labeling delay, thus minimizing systematic errors associated with a wide range of blood transit times. Together, these benefits not only permit quantitative perfusion imaging of the entire rat brain, they also provide the possibility for extending ASL techniques to perfusion imaging of pathological conditions.
THEORY
Assuming negligible magnetization transfer (MT) effects and fast water exchange between blood and tissue, time-dependent tissue water magnetization with blood perfusion can be derived from the Bloch equation, given by (4,18):
| [1] |
Here, f is the tissue perfusion rate defined as the volume of blood deliverd to capillary bed per unit volume of brain tissue per unit time; λ is the brain:blood partition coefficent (19); T1app = 1/(1/T1+f/λ) and α is the arterial blood labeling efficiency defined as with being the longitudinal magnetization per unit volume of arterial blood. The superscript “0” indicates longitudinal magnetization under fully relaxed conditions. Equation [1] suggests that the ASL signal is a function of perfusion rate and T1 value of brain tissue. When the labeling duration is sufficiently long, 1 − exp(−t/T1app) ≈1, and equation [1] reduces to the steady-state solution (18).
Equation [1] does not take blood transit time into account. In practice, variations in blood transit times are a major concern in quantitative ASL of multiple slices. The perfusion signal in the imaging plane has intraluminal and tissue compartments. Labeled water spins experience signal decay during the transit time (δ) defined as the interval between the time of spin labeling and time of water exchange in capillaries. When intraluminal signal is crushed by diffusion gradient (20), equation [1] can be modified to include the effect of blood transit time as follows:
| [2] |
Here T1a is the T1 value of arterial blood and δ is the blood transit time. It is shown that the effect of δ on the ASL signal can be reduced to some degree when a long labeling pulse is applied (see Results). When a delay (w) following the labeling pulse is introduced (14) to reduce the effect of variable transit times, the resulting ASL signal would be (10):
| [3a] |
| [3b] |
Here τ is the labeling duration, and min (δ − w, 0) is a fuction to find the smaller between δ − w and 0. It can be shown that when w>δ, equation [3a] becomes:
| [4a] |
In essence, this approach takes advantage of the fact that the T1 values of arterial blood and gray matter are similar. As a result, the effect of δ on ASL signal is minimal (since exp[−δ (1/T 1a −1/T 1app)]≈1). But the sensitivity of the ASL signal is reduced by a factor of exp(−w/T1app). For example, for human brain perfusion imaging at 1.5 T with a w of 1.5 s, the ASL signal reduces to 0.5% (14). In our experience, this is the practical low end of sensitivity necessary for an in-vivo MRI experiment to be peformed within a reasonable period of time, considering the fact that non-Gaussian noises resulting from cardiac pulsation, respiratory motion and slow spontaneous physiological fluntutations are unavoidable (21).
In multi-slice CASL using EPI, in addition to the transit time (δ) as discussed above, there is a cumulative increase in time delays as the slice acquisition progresses since it takes certain amount of time (η) to acquire a slice. As a result, there are incremental post-labeling delays across imaging slices, and the effective post-labeling delay for the nth slice is (w = w1 + (n − 1) · η), here w1 is the post-labeling delay for the first slice. Anatomically, the labeled blood is distributed to the anterior, middle and posterior cerebral arteries via the Circle of Willis, as shown in Fig. 1. During the time the first slice is being acquired, the labeled blood is also circulating through the rest of the slices, leading to different effective labeling duration across imaging slices. Such effect occurs when w < δ and τ + w > δ, and the ASL signal can be expressed as:
| [4b] |
Figure 1.

A schematic drawing illustrating the dynamics of the labeled blood in the vascular system of the rat brain (ventral view). Horizontal open bars with dashed thin border lines represent imaging slices. Bold dark lines indicate incoming labeled arterial blood from the internal carotid arteries (ICA), which is distributed to the anterior, middle and posterior cerebral arteries (ACA, MCA and PCA) via the Circle of Willis. Note that the imaging plane is approximately perpendicular to the three major arteries. (a) when τ + w < δ, labeled spins would remain in large arteries, and the effective labeling duration τeff = 0. (b) when w < δ and τ +w > δ, during the time the first slice is being acquired, labeled arterial blood that still remains in large arteries is also perfusing the rest of the imaging slices, leading to longer effective labeling durations.
As shown in Eqs. [4a] and [4b], when w1 + (n − 1) · η > δ, there are incremental post-labeling delays in multi-slice ASL; when w1 + (n − 1) · η < δ and τ + w1 + (n − 1) · η > δ, there are variable effective labeling durations across imaging slices (τ + w1 + (n − 1) · η − δ). The latter effect could be significant when δ is substantially increased under certain pathological conditions, such as stroke. Increasing τ could not only enhance the contrast of ASL signal, but also minimize this effect. Equation [4b] assumes inflowing labeled spins are simultaneously perfusing all imaging slices. This is the case in rat brain imaging since rat data are typically acquired in the coronal orientation to minimize susceptibility effects, and the imaging slices are approximately perpendicular to the three major feeding cerebral arteries. It should be noted that slice excitation/refocusing pulses could disturb the dynamics of labeled blood flow. In the current study, we acquired data in an interleaved order instead of a sequential order as typically applied in human ASL. The purpose of such a slice acquisition order is to minimize the interference caused by imperfect slice profile in neighboring slices while minimally interfering with the flow of tagged blood.
MATERIALS AND METHODS
Numerical Simulations
The effect of labeling duration, T1 value and perfusion rate on the ASL signal is quantitatively expressed in Eq. [1]. We simulated this effect with T1 = 1.9 s (22), T1a = 2.3 s (9), T1a = 2.3 s (19), and α = 0.76. Here α is the measured labeling efficiency. In our hardware and software environment, the inversion of arterial spins reaches a maximum when the labeling power is 0.14 Watt and plateaus at greater labeling power; α is found to be 76.2 ± 3% (n = 6, mean ±SD).
Blood transit time is known to be region-specific. Previous studies reported blood transit times in normal rat brain ranging from 0.3 to 0.5 s, which could change under different physiological and pathophysiological conditions (9,23,24). The ASL signal as a function of blood transit time and labeling duration is given in Eq. [2]. We define ASL signal perturbation caused by variable blood transit time (δ) as follows:
| [5] |
We simulate the effect of blood transit time on ASL signal under the following three conditions: i) normal conditions where δ is within a narrow range (0.3–0.5 s, Refs. (9,24), and ii) conditions where δ is in a slightly wider range to account for transit time changes caused by physiological challenges (0.1–0.7 s, Refs. (23). The simulations are performed without applying a post-labeling delay (w1 = 0), as described in Eq. [2]. We also simulate the scenario when blood transit times vary dramatically to account for certain pathological conditions. In this case, δ ranges from 0 to 8 s, and w is 0, 0.6, 1, 2, 3, 4, or 5 s. The simulations are based upon Eq. [3].
In multi-slice ASL, each slice has a distinct effective post-labeling delay. We simulated the effect of variable post-labeling delays on the resulting ASL signal. The number of slices n was either 11 or 1. With a slice thickness of 1.5 mm, eleven slices would effectively cover the entire rat brain. We define the ASL signal perturbation caused by variable post-labeling delays as follows:
| [6] |
Here S(ms,τ) and S(ss,τ) are ASL signals acquired with multi-slice (MS) and single slice (SS) EPI, respectively. The multi-slice ASL data are acquired with 11 slices. S(ms,τ) is the data from the last of the 11 slices, and S(ss,τ) is the single slice data acquired at the same location (see Data Acquisition). η = 35.7 ms, δ = 0.35 s. All simulations are performed using MATLAB in Linux (The MathWorks, Inc. Natick, MA, USA).
Animal Preparation
Fourteen male Sprague-Dawley rats weighing 250–350 g were used in this study. Animal preparation procedures were generally similar to a previous report (25), and was approved by the Animal Care and Use Committee at NIDA, NIH. Briefly, animals were initially anesthetized with isoflurane (5% induction followed by 2% maintenance) in oxygen-enriched air for surgical preparation. A double-lumen catheter was inserted into a femoral vein for drug delivery, and a femoral artery was catheterized for blood pressure monitoring and blood gas sampling. Rats were intubated for artificial ventilation (SAR-830 ventilator; CWE, Ardmore, PA) and received a neuromuscular blocking agent (Pancuronium Bromide, Sicor Pharmaceuticals, Inc., Irvine, CA) with a loading dose of 2.0 mg/kg followed by a constant infusion of 2.0 mg/kg/hr (Harvard Apparatus, Holliston, MA). Animals were secured via a customized head holder with bite bar and ear bars and positioned at the center of the magnet. End-tidal CO2 and O2 were continuously monitored (GEMINI Respiratory Gas Analyzer, CWE, Ardmore, PA) and core body temperature was maintained at 37.0 ± 0.3°C with a water-circulating bed. Anesthesia was maintained with 1.5% isoflurane during the scan sessions. Blood gases were sampled and maintained within normal range (PH = 7.39 ± 0.04, PaCO2 = 41.8 ± 3.7 mmHg, PaO2 = 146.6 ± 26.8 mmHg). As a control procedure to examine potential MT effect on ASL signal, two rats were euthanized with an overdose of pentobarbital sodium (100 mg/kg, I.V.) while maintained at the same location inside the magnet.
Data Acquisition
MRI experiments were performed on a Bruker Biospin 9.4 T scanner (Bruker, Karlsruhe, Germany). A three-coil continuous ASL technique (26,27) was implemented. A single-turn labeling coil was designed to have a curvature that minimizes the distance between the coil surface and the common carotid artery, and was driven by a separate RF amplifier (Communication Power Corporation, Hauppauge, New York). A volume coil was used for RF excitation and a surface coil was used for MR signal reception (both from InsightMRI, Worcester, MA). These three coils were actively decoupled using a decoupling box (InsightMRI). The labeling efficiency was measured using a method previously described (28).
For slice localization and image registration, high-resolution T2-weighted anatomical images were acquired using a rapid acquisition with relaxation enhancement (RARE) sequence: repetition time (TR) = 2650 ms, effective echo time (TE) = 50 ms, RARE factor = 8. The total number of slices was 23 with the slice thickness of 1 mm. The anterior commissure was used as a reference point for image acquisition, which approximately corresponds to −0.36 mm from rat bregma (29). ASL data were acquired using single-shot EPI sequences with the control and the labeling scans alternated. To examine the effect of labeling duration on ASL signal, we used gradient-echo EPI. Scan parameters were: FOV = 3.2 × 3.2 cm2, matrix size = 64×64, TE = 12 ms, slice thickness = 1.5 mm, bandwidth = 250 KHz, TR = 9.6 s. Here TR is defined as “labeling time (τ) + post-labeling delay (w1) + image acquisition time (η × number of slices) + recovery time”. A total of 7 slices were acquired in an interleaved fashion. The labeling pulse was a continuous square wave. The pulse duration alternated between 1.2, 3.2, 4.8, 6.4 and 9.6 s, in a pseudo-random order; each repeated 2–3 times. Forty labeling-control pairs were acquired when the labeling duration was 3.2 s and beyond, while sixty labeling-control pairs were acquired when labeling duration was 1.2 s to enhance the SNR. The location of the labeling plane was determined for each animal by taking flow-weighted anatomical images with the labeling coil operating in transmission/reception mode, and was typically 2.1 cm away from the isocenter of the magnet. During both the labeling and the control periods, a Z gradient of 1 Gauss/cm was applied. The central frequencies of the labeling and control pulses were adjusted symmetrical to that of the central slice to control for potential MT effects. No post-labeling delay between the labeling pulse and the slice excitation pulse was employed (w=0). Instead, bipolar diffusion weighting gradients were simultaneously applied along X, Y and Z (b = 149 s/mm2) to minimize ASL signal originating from relatively large arteries. The above experiments were performed on 7 animals.
To investigate whether long labeling duration could reduce confounds resulting from variable post-labeling delays intrinsic in multi-slice ASL, we also acquired ASL data using spin-echo EPI. Given the fact that the time for acquiring a single slice is longer in spin-echo EPI than in gradient echo-EPI, the effect of variable post-labeling delays is expected to be more pronounced. Furthermore, spin-echo EPI is less sensitive to signal drop out in areas with inadequate shimming, allowing for whole rat brain coverage. Scan parameters were the same as described above except that TR = 6810 ms, TE = 25 ms, the total number of slices was 11; labeling duration was either 2 s or 6.4 s. Forty labeling-control pairs were acquired. The time for acquiring a single slice was 35.7 ms. The tenth slice was acquired last, and its total post-labeling delay was 357 ms longer than that of the first slice. We also acquired single-slice (the 10th slice only) ASL data to compare the ASL signals acquired under multi- and single-slice conditions. The scan parameters were the same as in multi-slice ASL except that the number of slice was set to 1. The above experiments were performed on 5 animals, each repeated 3 times.
Geometric distortions in EPI images were corrected using the PLACE scheme proposed by Xiang and Ye (30). This was done by acquiring an additional set of EPI data with the phase-encoding blip offset by −1 and 0. This dataset was used to derive pixel-wise displacement maps, which were subsequently applied to correct for images acquired with the same EPI parameters.
Data Analysis
Fractional ASL signal is calculated as ΔS/S0. Here, ΔS is the signal difference between the control and labeled images calculated by pair-wise subtractions of neighboring control-labeling pairs, which are then averaged across multiple repetitions. S0 is the averaged signal intensity during the control period. To quantify the relationship between the labeling duration and the resulting ASL signal, we chose the caudate putamen (CPu) and the primary somatosensory in the forelimb region (S1FL) as two representative regions of interest (ROIs), and identified these areas based on a digital rat brain atlas. The method for co-registering the EPI images with the digital atlas has been described elsewhere (31). Briefly, a high-resolution coronal digital rat brain atlas (29) with similar coordinates relative to bregma as the MRI coronal slices was processed in MATLAB so that the matrix size and the format of those digital images were consistent with the MRI images. The dimensions of the digital atlas were also linearly scaled in the X and Y directions so that the outer contour of individual digital images matched that of anatomical images acquired with RARE sequence. A dataset from an animal with the best positioning inside the magnet was identified as the master dataset. Datasets from other animals were manually registered to the master dataset with a least-squares algorithm built in AFNI (32). The transformation matrix was subsequently applied to the EPI time series.
To quantify the effects of variable post-labeling delays in multi-slice ASL, we compared the ASL signals acquired in MS mode (11 slices) and SS mode. Only the slice acquired at the same location in both modes is compared. Since this slice is quite far from bregma (5.64 mm), the number of voxels inside the brain is limited and thus we included all voxels inside the brain for the calculation. Two-tailed paired t-tests were applied to compare the ASL signals acquired with different labeling durations as well as ASL signals acquired at MS vs. SS mode. p < 0.05 was considered significant.
RESULTS
Long labeling duration enhances the contrast of ASL signal
The effect of labeling duration on the resulting ASL signal was simulated with a range of perfusion rates. Results are shown in Fig. 2. In the case of low perfusion rate, a relatively short labeling duration is sufficient in order for the ASL signal to reach a plateau. For example, when f = 50 ml/100g/min, the ASL signal plateaus with a labeling duration of ~5 s, and the maximum ASL signal is 2.6%. However, when the perfusion rate is relatively high, for example, 200 ml/100g/min, labeling duration has to be increased to 6 s in order for the ASL signal to reach a plateau, yielding a maximum ASL signal of 9.8%. This is analogous to the classical resistor-capacitor electrical circuit while a capacitor is being charged; the time for the charges across a capacitor to reach a plateau is determined by the voltage source. The higher a voltage, the longer it takes to reach a plateau.
Figure 2.

Simulated ASL signal as a function of labeling duration and perfusion rate. Note that in the case of high perfusion rate, long labeling duration is required for the ASL signal to reach a plateau.
Experimental results are consistent with the above analysis. Figure 3a shows ASL signal measured in S1FL and CPu (n = 7). The boxes in Fig. 3b indicate regions of interest overlaid on raw percent ASL signal maps. In S1FL, the ASL signal is 3.5 ± 0.4% at a labeling duration of 1.2 s; it increases to 7.9 ± 0.9% at a labeling duration of 9.6 s. With a labeling duration of 3.2 s, the ASL signal is about 30% smaller than that at 9.6 s (p < 0.01, two-tailed paired t-test). There are no significant differences in ASL signals at labeling durations of 6.4 s and 9.6 s (p > 0.05, two-tailed paired t-test). Similar patterns are seen in the CPu.
Figure 3.
Measured ASL signal as a function of labeling duration. (a) ASL signal in S1FL and CPu is enhanced with increased labeling duration. Boxes in (b) indicate regions of interest on fractional ASL maps. (c) Normalized labeling-control signal time courses from one voxel with labeling durations of 3.2 s (red) and 9.6 s (blue). To examine potential magnetization transfer effects on the ASL signal, the animal was euthanized while maintained at the same location, and was scanned using the same sequence to serve as a control. Note that there is no systematic signal modulation between the labeling and control conditions when the animal was euthanized (black), indicating minimal magnetization transfer effects. Abbreviations: S1FL, primary somatosensory cortex of the forelimb region; CPu, caudate putamen.
Long labeling durations are known to induce significant MT effects in single-coil ASL that need to be controlled (18,20). Given the fact that the ASL signal was enhanced at longer labeling duration, a concern was whether this was caused by potential MT effects, even though a separate small coil was used for labeling. As a control procedure, two rats were euthanized while maintaining the same location inside the magnet. The same ASL experiment was repeated. As seen in Fig. 3c (black curve), there is no systematic modulation of the signal between the labeling and control pairs. For comparison, time courses before sacrifice are also shown. These data demonstrate that the enhanced ASL signal at longer labeling durations was not due to potential MT effects.
Long labeling duration reduces the effects of variable post-labeling delays inherent in multi-slice ASL
In multi-slice ASL, each slice has a different effective post-labeling delay. We simulated the effect of variable post-labeling delays on the resulting ASL signal (δ = 0.35 s, η = 35.7 ms). The number of slices n was either 11 or 1. Results are shown in Fig. 4a. When the labeling duration is longer than 3 s, the ASL signal difference acquired with multi-slice and single slice EPI is about 5%, and is negligible when the labeling duration is longer than 6 s. However, the difference is greater than 10% when the labeling duration is shorter than 2 s.
Figure 4.
The effects of variable post-labeling delays in multi-slice (MS) ASL. Eleven slices were acquired in MS ASL; only one slice was acquired in single slice (SS) ASL (the last slice with the longest post-labeling delay). (a) Simulated effects of variable post-labeling delays in MS ASL as a function of labeling duration. Percent ASL signal perturbation is defined as: (S(ms,τ) − S(ss,τ))/S(ss,τ). (b) Measured ASL signal in MS vs. SS mode with a labeling duration of 2 s and 6.4 s, respectively. Note significant difference in MS vs. SS ASL when labeling duration was 2 s (p < 0.01, two-tailed paired t-test); there was no difference with a labeling duration of 6.4 s.
Figure 4b shows experimental data acquired in SS and MS mode respectively (n = 5). Fractional ASL signal maps (ΔS/S0) acquired in the MS mode (11 slices) from a representative animal are shown in Fig. 5. Images were acquired in an interleaved fashion. The tenth slice was acquired last; its slice location (+5.64 mm from bregma) was the same as the slice acquired in SS mode and thus was used for comparison. As shown in Fig. 4b, with a labeling duration of 2 s, the ASL signal in the SS mode was 4.1 ± 0.9%, which was 19% smaller than that acquired in the MS mode (p < 0.01, two-tailed paired t-test). However, with a labeling duration of 6.4 s, the difference between SS and MS ASL was virtually identical (5.6 ± 1.1% vs 5.5 ± 0.7%).
Figure 5.

Fractional ASL signal (ΔS/S0) maps of the rat brain acquired using single-shot spin-echo EPI. Numbers below images are coordinates relative to bregma.
Long labeling duration reduces the effect of variable blood transit times
The effect of variable blood transit times on the ASL signal is expressed in Eq. [3]. As shown in Fig. 6a, under normal physiological conditions when δ is within a relatively narrow range (δ1 = 0.3 s and δ2 = 0.5 s), ASL signal perturbation caused by variable transit times decreases when the labeling duration is relatively long. It is 25% when τ = 1.5 s and reduces to 9% when τ = 10 s. Under certain physiological conditions when blood transit times are more inhomogeneous, e.g. from 0.1 to 0.7 s, the resulting ASL signal is perturbed more profoundly, particularly when the labeling duration is relatively short. It is 99% when τ = 1.5 s and reduces to 30% when τ = 10 s.
Figure 6.
Simulated ASL signal as a function of blood transit time and labeling duration. Percent ASL signal perturbation is defined as: (S(δ1, τ) − S(δ2, τ))/S(δ1, τ). (a) ASL signal perturbations caused by blood transit times are reduced, but are still significant even when long labeling duration is applied. This is more prominent when blood transit times are in a slightly wider range (solid curve, δ1 = 0.1 s, δ2 = 0.7 s). The effects of blood transit times are further reduced when a delay is applied following continuous labeling of the arterial spins, but at the penalty of reduced sensitivity. (b) ASL signal as a function of blood transit times and post-labeling delays when a 10 s labeling pulse is applied (f = 100 ml/100g/min, see text for details on other parameters).
The above simulations suggest that although increasing labeling duration could reduce the effect of variable blood transit times, it is still a confounding factor when δ is in a wider range. This effect can be further reduced by introducing a post-labeling delay (14). Figure 6b illustrates simulated results with a flow rate of 100 ml/100g/min, τ = 10 s. When w = 0 or w < δ, ASL signal decays with blood transit time by a factor of exp(−δ/T1a). When w = 1 s, the ASL signal is 3.4–3.6% with δ ranging from 0 to 1 s; when w = 5 s, the ASL signal is 0.5–0.6% with δ ranging from 0 to 5 s.
DISCUSSION
Summary of findings
In quantitative perfusion imaging using ASL, variable blood transit times and post-labeling delays are two confounding factors (7,13,14). In the present study, we demonstrate that, by increasing the labeling duration from 1.2 s to 6.4 s (≥3×T1), the ASL signal enhanced 84–109% as measured in S1FL and CPu (Fig. 3). It is further shown that the confounds resulting from variable post-labeling delays are essentially eliminated, and the ASL signal acquired in multi-slice ASL is virtually the same as that acquired in single slice ASL (Fig. 4). Enhancing the contrast of the ASL signal offers the opportunity for extending the post-labeling delay to a longer duration, minimizing systematic errors associated with a wide range of blood transit times (Fig. 6b), and thus permitting quantitative perfusion imaging of the entire rat brain. There are four reasons for such improvement: first, the T1 values of both blood and tissue at high field strengths increase substantially compared with that at low field, leading to slower T1 decays after labeling and thus improving effective labeling efficiency. Second, a labeling pulse with long duration enhances the contrast of ASL signal (Figs. 2 and 3). Third, a separate small labeling coil minimizes the MT effects (18), and the labeling RF power is only 0.14 Watt, allowing a long labeling pulse to be applied. Finally, since the ASL signal is approximately proportional to CBF (see Eq. [1]), the high perfusion rate in small animals enhances ASL signal sensitivity, providing the opportunity for such improvement.
It is noted that, with a labeling duration of 2 s, ASL signal in multi-slice acquisition (11 slices) is greater than that acquired with a single slice (see Fig. 4b). This appears counterintuitive since there are intrinsic post-labeling delays in multi-slice ASL, which should presumbly reduce ASL signal. There are several reasons for such counterintuitive findings. In rat brain imaging, data are typically acquired in the coronal plane to minimize the susceptibility effect as opposed to the axial plane that has been typically applied in human brain imaging. Anatomically, after the carotid arterial blood has been labeled, it is distributed to the anterior, middle and posterior cerebral arteries via the Circle of Willis, perfusing all slices simultaneously (Fig. 1). Under normal physiological conditions, each slice has distinct blood transit times but within a narrow range. During the time the first slice is being acquired, the labeled blood is also perfusing the rest of the slices. The effective labeling duration for the second slice would be η ms longer than the first slice. Thus, the last slice has the longest effective labeling duration as shown in Eqs. [4a] and [4-b]. At 9.4 T, the effect of labeling duration on the ASL signal is particularly prominent when the labeling duration is shorter than 4.8 s (Fig. 3a). But ASL signal perturbation caused by variable labeling duration tapers off when the labeling duration is sufficiently long (Figs. 2 and 3). It should be noticed that Eq. [4b] is valid only when (δ − (n− 1)·η ≥ 0) or (n ≤ δ/η+1), which implies that the additional post-labeling delays in multi-slice ASL must be shorter than blood transit time, and the maximum number of slices (nmax) is limited to (δ/η+1). For example, assuming δ = 400 ms in rat brain and η = 36 ms for spin-echo EPI acquisition, nmax is 12.
The above analyses are based on Eq. [2] where a post-labeling delay is not applied between the labeling pulse and the slice excitation pulse (w = 0). When a post-labeling delay (w) is applied, and w > δ, it can be shown from Eq. [4a] that the ASL signal perturbation caused by intrinsic variable post-labeling delays in multi-slice ASL is:
| [7] |
The resulting ASL signal is modulated by n and η, and is independent of the labeling duration. For example, assuming n = 12, η = 36 ms, f = 100 ml/100g/min, the ASL signal perturbation caused by intrinsic variable post-labeling delays is up to 17%. However, such perturbation can be readily corrected based on Eq. [7].
SNR considerations
From a SNR perspective, although increasing the labeling duration enhances the contrast in CASL, the temporal resolution of this method is limited by the duration of the labeling pulse. In pulsed ASL, improved SNR could also be achieved by data averaging where a shorter repetition time is typically applied (33,34). A previous study by Wong et al. (35) has shown that both the pulsed and continuous ASL techniques achieve similar SNR per unit time. However, under pathophysiological conditions, such as stroke, the blood transit times are heterogeneous and are substantially increased (36). Furthermore, perfusion is reduced in infarct areas, leading to a small ASL signal. These factors impose special challenges for perfusion imaging using ASL. It is likely that CASL would be advantageous in such circumstances. In order to minimize transit time effects, it may be necessary to apply a post-labeling delay (w) of long duration; however, this approach further sacrifices sensitivity. High field strength offers new opportunities to deal with this dilemma given its enhanced sensitivity. This could have implications for applying ASL techniques to preclinical perfusion studies under pathological conditions. The current study was performed with normal rat brain and there was not an easy approach to increase the blood transit times. It would be of significance to test the capability of the proposed method in an acute stroke model and to compare the results against a classical method, such as tracer autoradiography.
The effect of the recirculation of labeled blood on ASL signal
Physiologically, after the blood is labeled in the common carotid artery, it circulates through the brain and returns to the heart, where it mixes with the venous blood returning from the rest of the body, and subsequently enters the pulmonary circulation. About 4% of the resulting oxygenated blood perfuses the rat brain, although the human brain receives about 13% of the cardiac output (37,38). Given the long blood T1 values at high field strength and high cardiac rate in small animals (~350 beats/min in rats), a potential consequence of long labeling duration is the recirculation of labeled spins into the labeling plane before complete relaxation. This would decrease the apparent labeling efficiency in subsequent spin inversions. A similar issue was discussed in the context of pulsed ASL using the FAIR technique with short repetition times (34). We approach this problem by solving the Bloch equation with several assumptions detailed below.
1) Slow water exchange regime
In the case of slow exchange between labeled blood water and cerebral tissue water, we assume that the labeled spins experience spin-lattice relaxation with arterial blood T1 value (see Appendix for physiological justifications). In general, immediately following the ith inversion, the longitudinal magnetization becomes (see Appendix):
| [8] |
Here is the fully relaxed blood longitudinal magnetization. Tc is the time interval between two consecutive circulations. A is the mixture fraction of the labeled blood re-circulating back to the brain; (1-A) is the mixture fraction of the blood from the rest of the body that is to circuit the brain. for i = 1; for i = 2.
At the extreme case when all the labeled blood circulates back to the brain and does not mix with the blood from the rest of the body, i.e. A = 1, the magnetization after the ith inversion (i ≥ 3) becomes (see Appendix):
| [9] |
for i = 1; for i = 2.
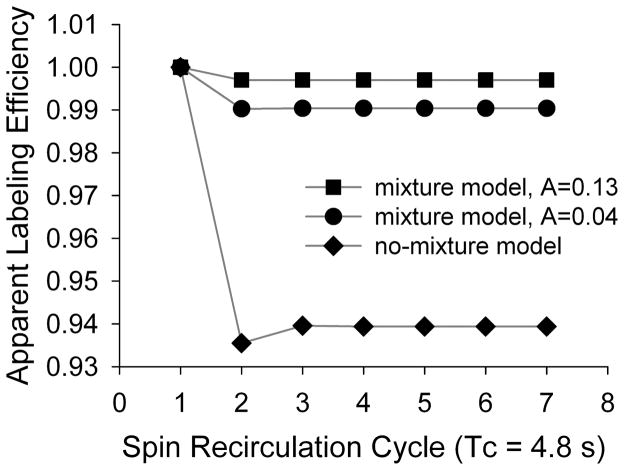
We calculate the longitudinal magnetization using Eqs. [7–8] with up to 7 labeling pulses. Immediately following the ith inversion, the magnetization is represented as: . Here αi is the apparent labeling efficiency during the ith inversion, which is normalized to α1 by: αi/α1. Tc is estimated to be 4.8 s based upon perfusion imaging of the rat brain using first-pass susceptibility contrast agent (39). A is set to 1 in the no-mixture model, and it is set to 0.04 and 0.13 to simulate two different conditions in the full-mixture model. Figure 7 shows the results calculated based on the assumption of slow exchange, a scenario where the recirculation of the labeled spin is expected to have the greatest effect. In the no-mixture model, the effect is the greatest during the second spin recirculation cycle, with the apparent labeling efficiency drops to 93.5%. But the effect plateaus at 93.9% after the third inversion. In the full-mixture model, when A = 0.13, the apparent labeling efficiency drops to 99% in the second inversion and beyond; when A = 0.04, it changes to 99.7% in the second inversion and beyond.
Figure 7.
The recirculation of labeled blood into the labeling plane leads to a reduction in apparent labeling efficiency in the no-mixture model. But this effect is much smaller in the mixture model (see text for details about the two models).
2. Fast water exchange regime
In the fast water exchange regime, the labeled water fully exchanges with tissue spins before entering venous vessels. Since cerebral blood volume is only about 5% of the total brain volume, the spins leaving capillaries (where the exchange takes place) could be assumed to have the same longitudinal magnetization as brain tissue, which is approximately fully relaxed with a long TR (≥ 3 T1), thus the effect of the recirculation of the labeled blood on ASL signal would be small. In addition, the blood circulating the brain is expected to mix with that circulating the rest of the body, further reducing this effect.
In a realistic experiment, the no-mixture model in the slow water exchange regime predicts the maximum possible effect that the recirculation of labeled blood could have on the ASL signal (Fig. 7); the full-mixture model in the fast water exchange regime predicts the minimum possible effect. Based upon above analysis, it appears unlikely that such effect would be significant.
In summary, given increased T1 values and enhanced SNR at high field strength, we propose to mitigate confounds resulting from variable blood transit times and post-labeling delays by applying a labeling pulse of long duration in combination with a post-labeling delay. This approach is straightforward, robust and can have implications for extending ASL techniques to perfusion imaging of such pathological conditions as stroke. However, the proposed method requires an additional RF amplifier, a separate labeling coil and associated coil-decoupling hardware as well as the imaging sequence, which are not currently available in commercial MRI scanners.
Acknowledgments
This work was supported by the Intramural Research Programs of the National Institute on Drug Abuse and the National Institute of Neurological Disorders and Stroke, National Institutes of Health.
Appendix
1. The no-mixture model
In the no-mixture model, we assume the labeled blood circulates back to the brain and does not mix with the blood from the rest of the body. This represents an extreme scenario where the recirculation of the labeled blood would have the maximum effect. Blood water magnetization immediately before and after individual spin inversion can be derived from the Bloch equation, and is detailed below:
Immediately following the first inversion, blood water magnetization is:
| [A1.1] |
Here is the fully relaxed blood longitudinal magnetization. Given the fact that it takes 100–300 ms for the red blood cells to pass the capillary network (40), which is much shorter than the labeling duration, the effect of the slice excitation pulse on the labeled spins could be ignored since a majority of the recirculating spins would not experience the slice excitation pulse. Therefore, by the end of the first circulation (right before the second inversion), blood water magnetization is:
| [A1.2] |
Here Tc is the time interval between two consecutive circulations. Immediately following the second inversion, blood water magnetization is:
| [A2.1] |
By the end of the second circulation (right before the third inversion), blood water magnetization is:
| [A2.2] |
In general, the magnetization right before the ith inversion (i ≥ 3) can be expressed as follows:
| [A3] |
2. The full-mixture model
In a more realistic scenario, the labeled blood circulating back to the brain mixes with that from the rest of the body before entering the pulmonary circulation. The time for blood to circulate the rest of the body is variable and is much longer than that of the brain. For example, it takes about 60 s for the bolus of contrast to pass the rat kidney (Fig. 3 in Ref. (41)). Therefore, we assume the blood magnetization has fully relaxed before circulating back to the heart.
Immediately following the first inversion, blood water magnetization is:
| [A4] |
Immediately following the second inversion, blood water magnetization is:
| [5] |
Here A is the mixture fraction of the labeled blood re-circulating back to the brain; (1−A) is the mixture fraction of the blood from the rest of the body that is circuiting to the brain.
In general, immediately following the ith inversion (i ≥ 3), the longitudinal magnetization can be expressed as the following:
| [A6] |
References
- 1.Iadecola C, Nedergaard M. Glial regulation of the cerebral microvasculature. Nat Neurosci. 2007;10:1369–1376. doi: 10.1038/nn2003. [DOI] [PubMed] [Google Scholar]
- 2.Kim S. Quantification of relative cerebral blood flow change by flow-sensitive alternating inversion recovery (FAIR) technique: application to functional mapping. Magn Reson Med. 1995;34:293–301. doi: 10.1002/mrm.1910340303. [DOI] [PubMed] [Google Scholar]
- 3.Kwong K, Belliveau J, Chesler D, Goldberg I, Weisskoff R, Poncelet B, Kennedy D, Hoppel B, Cohen M, Turner R. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci U S A. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Williams D, Detre J, Leigh J, Koretsky A. Magnetic resonance imaging of perfusion using spin inversion of arterial water. Proc Natl Acad Sci U S A. 1992;89:212–216. doi: 10.1073/pnas.89.1.212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Detre J, Leigh J, Williams D, Koretsky A. Perfusion imaging. Magn Reson Med. 1992;23:37–45. doi: 10.1002/mrm.1910230106. [DOI] [PubMed] [Google Scholar]
- 6.Edelman R, Siewert B, Darby D, Thangaraj V, Nobre A, Mesulam M, Warach S. Qualitative mapping of cerebral blood flow and functional localization with echo-planar MR imaging and signal targeting with alternating radio frequency. Radiology. 1994;192:513–520. doi: 10.1148/radiology.192.2.8029425. [DOI] [PubMed] [Google Scholar]
- 7.Wong E, Buxton R, Frank L. Quantitative imaging of perfusion using a single subtraction (QUIPSS and QUIPSS II) Magn Reson Med. 1998;39:702–708. doi: 10.1002/mrm.1910390506. [DOI] [PubMed] [Google Scholar]
- 8.Haacke EM, Brown RW, Thompson MR, Venkatesan R. Magnetic resonance imaging: physical principles and sequence design. John Wiley & Sons, Inc; 1999. [Google Scholar]
- 9.Kim T, Kim S. Quantification of cerebral arterial blood volume and cerebral blood flow using MRI with modulation of tissue and vessel (MOTIVE) signals. Magn Reson Med. 2005;54:333–342. doi: 10.1002/mrm.20550. [DOI] [PubMed] [Google Scholar]
- 10.Wang J, Alsop D, Li L, Listerud J, Gonzalez-At J, Schnall M, Detre J. Comparison of quantitative perfusion imaging using arterial spin labeling at 1.5 and 4.0 Tesla. Magn Reson Med. 2002;48:242–254. doi: 10.1002/mrm.10211. [DOI] [PubMed] [Google Scholar]
- 11.Buxton R, Frank L, Wong E, Siewert B, Warach S, Edelman R. A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magn Reson Med. 1998;40:383–396. doi: 10.1002/mrm.1910400308. [DOI] [PubMed] [Google Scholar]
- 12.Yang Y, Engelien W, Xu S, Gu H, Silbersweig D, Stern E. Transit time, trailing time, and cerebral blood flow during brain activation: measurement using multislice, pulsed spin-labeling perfusion imaging. Magn Reson Med. 2000;44:680–685. doi: 10.1002/1522-2594(200011)44:5<680::aid-mrm4>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- 13.Buxton R. Quantifying CBF with arterial spin labeling. J Magn Reson Imaging. 2005;22:723–726. doi: 10.1002/jmri.20462. [DOI] [PubMed] [Google Scholar]
- 14.Alsop D, Detre J. Reduced transit-time sensitivity in noninvasive magnetic resonance imaging of human cerebral blood flow. J Cereb Blood Flow Metab. 1996;16:1236–1249. doi: 10.1097/00004647-199611000-00019. [DOI] [PubMed] [Google Scholar]
- 15.Luh W, Wong E, Bandettini P, Hyde J. QUIPSS II with thin-slice TI1 periodic saturation: a method for improving accuracy of quantitative perfusion imaging using pulsed arterial spin labeling. Magn Reson Med. 1999;41:1246–1254. doi: 10.1002/(sici)1522-2594(199906)41:6<1246::aid-mrm22>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 16.Wong E, Cronin M, Wu W, Inglis B, Frank L, Liu T. Velocity-selective arterial spin labeling. Magn Reson Med. 2006;55:1334–1341. doi: 10.1002/mrm.20906. [DOI] [PubMed] [Google Scholar]
- 17.Paiva F, Tannus A, Silva A. Measurement of cerebral perfusion territories using arterial spin labelling. NMR Biomed. 2007;20:633–642. doi: 10.1002/nbm.1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang W, Silva A, Williams D, Koretsky A. NMR measurement of perfusion using arterial spin labeling without saturation of macromolecular spins. Magn Reson Med. 1995;33:370–376. doi: 10.1002/mrm.1910330310. [DOI] [PubMed] [Google Scholar]
- 19.Herscovitch P, Raichle M. What is the correct value for the brain--blood partition coefficient for water? J Cereb Blood Flow Metab. 1985;5:65–69. doi: 10.1038/jcbfm.1985.9. [DOI] [PubMed] [Google Scholar]
- 20.Ye F, Mattay V, Jezzard P, Frank J, Weinberger D, McLaughlin A. Correction for vascular artifacts in cerebral blood flow values measured by using arterial spin tagging techniques. Magn Reson Med. 1997;37:226–235. doi: 10.1002/mrm.1910370215. [DOI] [PubMed] [Google Scholar]
- 21.Hyde JS, Biswal BB. Physiological noise in fMRI. In: Moonen C, Bandettini PA, editors. Functional MRI. Springer-Verlag; 1999. [Google Scholar]
- 22.Tsekos N, Zhang F, Merkle H, Nagayama M, Iadecola C, Kim S. Quantitative measurements of cerebral blood flow in rats using the FAIR technique: correlation with previous iodoantipyrine autoradiographic studies. Magn Reson Med. 1998;39:564–573. doi: 10.1002/mrm.1910390409. [DOI] [PubMed] [Google Scholar]
- 23.Zhang W, Williams D, Detre J, Koretsky A. Measurement of brain perfusion by volume-localized NMR spectroscopy using inversion of arterial water spins: accounting for transit time and cross-relaxation. Magn Reson Med. 1992;25:362–371. doi: 10.1002/mrm.1910250216. [DOI] [PubMed] [Google Scholar]
- 24.Thomas D, Lythgoe M, van der Weerd L, Ordidge R, Gadian D. Regional variation of cerebral blood flow and arterial transit time in the normal and hypoperfused rat brain measured using continuous arterial spin labeling MRI. J Cereb Blood Flow Metab. 2006;26:274–282. doi: 10.1038/sj.jcbfm.9600185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lu H, Patel S, Luo F, Li S, Hillard C, Ward B, Hyde J. Spatial correlations of laminar BOLD and CBV responses to rat whisker stimulation with neuronal activity localized by Fos expression. Magn Reson Med. 2004;52:1060–1068. doi: 10.1002/mrm.20265. [DOI] [PubMed] [Google Scholar]
- 26.Silva A, Zhang W, Williams D, Koretsky A. Multi-slice MRI of rat brain perfusion during amphetamine stimulation using arterial spin labeling. Magn Reson Med. 1995;33:209–214. doi: 10.1002/mrm.1910330210. [DOI] [PubMed] [Google Scholar]
- 27.Zhang X, Nagaoka T, Auerbach E, Champion R, Zhou L, Hu X, Duong T. Quantitative basal CBF and CBF fMRI of rhesus monkeys using three-coil continuous arterial spin labeling. Neuroimage. 2007;34:1074–1083. doi: 10.1016/j.neuroimage.2006.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhang W, Williams D, Koretsky A. Measurement of rat brain perfusion by NMR using spin labeling of arterial water: in vivo determination of the degree of spin labeling. Magn Reson Med. 1993;29:416–421. doi: 10.1002/mrm.1910290323. [DOI] [PubMed] [Google Scholar]
- 29.Paxinos G, Watson C. The rat brain in stereotaxic coordinates. Elsevier Inc; 2007. [DOI] [PubMed] [Google Scholar]
- 30.Xiang Q, Ye F. Correction for geometric distortion and N/2 ghosting in EPI by phase labeling for additional coordinate encoding (PLACE) Magn Reson Med. 2007;57:731–741. doi: 10.1002/mrm.21187. [DOI] [PubMed] [Google Scholar]
- 31.Lu H, Scholl C, Zuo Y, Demny S, Rea W, Stein E, Yang Y. Registering and analyzing rat fMRI data in the stereotaxic framework by exploiting intrinsic anatomical features. Magn Reson Imaging. 2010;28:146–152. doi: 10.1016/j.mri.2009.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cox R. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- 33.Duhamel G, Callot V, Cozzone P, Kober F. Spinal cord blood flow measurement by arterial spin labeling. Magn Reson Med. 2008;59:846–854. doi: 10.1002/mrm.21567. [DOI] [PubMed] [Google Scholar]
- 34.Pell G, Thomas D, Lythgoe M, Calamante F, Howseman A, Gadian D, Ordidge R. Implementation of quantitative FAIR perfusion imaging with a short repetition time in time-course studies. Magn Reson Med. 1999;41:829–840. doi: 10.1002/(sici)1522-2594(199904)41:4<829::aid-mrm24>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 35.Wong E, Buxton R, Frank L. A theoretical and experimental comparison of continuous and pulsed arterial spin labeling techniques for quantitative perfusion imaging. Magn Reson Med. 1998;40:348–355. doi: 10.1002/mrm.1910400303. [DOI] [PubMed] [Google Scholar]
- 36.Wang J, Alsop D, Song H, Maldjian J, Tang K, Salvucci A, Detre J. Arterial transit time imaging with flow encoding arterial spin tagging (FEAST) Magn Reson Med. 2003;50:599–607. doi: 10.1002/mrm.10559. [DOI] [PubMed] [Google Scholar]
- 37.Sasaki Y, Wagner HJ. Measurement of the distribution of cardiac output in unanesthetized rats. J Appl Physiol. 1971;30:879–884. doi: 10.1152/jappl.1971.30.6.879. [DOI] [PubMed] [Google Scholar]
- 38.Stott W, Dryzga M, Ramsey J. Blood-flow distribution in the mouse. J Appl Toxicol. 1983;3:310–312. doi: 10.1002/jat.2550030607. [DOI] [PubMed] [Google Scholar]
- 39.Liu H-S, Yang Y, Guillem K, Rea W, Vaupel DB, Chefer S, Stein EA, Peoples LL, Lu H. Decreased regional cerebral blood volume during abstinence as studied by dynamic MR imaging in rats with long-access regimen of cocaine self-administration. Society for neuroscience poster, 1587/O35; 2009. [Google Scholar]
- 40.Hudetz A. Blood flow in the cerebral capillary network: a review emphasizing observations with intravital microscopy. Microcirculation. 1997;4:233–252. doi: 10.3109/10739689709146787. [DOI] [PubMed] [Google Scholar]
- 41.Baumann D, Rudin M. Quantitative assessment of rat kidney function by measuring the clearance of the contrast agent Gd(DOTA) using dynamic MRI. Magn Reson Imaging. 2000;18:587–595. doi: 10.1016/s0730-725x(00)00134-x. [DOI] [PubMed] [Google Scholar]