Spatio-Temporal Point-Spread Function of Functional MRI Signal in Human Gray Matter

Abstract

This study investigated the spatio-temporal properties of blood-oxygenation level-dependent (BOLD) functional MRI (fMRI) signals in gray matter (GM), excluding the confounding, inaccurate contributions of large blood vessels. Specifically, we quantified the spatial specificity of the BOLD response, and we investigated whether this specificity varies as a function of time from stimulus onset.

fMRI was performed at 7 Tesla, where mapping signals of parenchymal origin are easily detected. Two abutting visual stimuli were adjusted to elicit responses centered on a flat GM region in V1. fMRI signals were sampled in high-resolution orthogonal to the retinotopic boundary between the representations of the stimuli. Signals from macro-vessels were masked out.

Principal component analysis revealed that the first component in space accounted for 96.2±1.6% of the variance over time. The spatial profile of this time-invariant response was fitted with a model consisting of the convolution of a step function and a Gaussian point-spread-function. The mean full-width at half-maximal-height of the fitted point-spread-function was 2.34±0.20 mm. Based on simulations of confounding effects, we estimate that BOLD point-spread-function in human GM is smaller than 2 mm. A detailed time-point to time-point analysis revealed that the estimated point-spread-function obtained during the 3rd (1.52 mm) and 4th (1.99 mm) seconds of stimulation were narrower than the mean estimated point-spread-function obtained from the 5th second on (2.42±0.15 mm, mean ± SD). The position of the edge of the responding region was offset (1.72±0.07 mm) from the boundary of the stimulated region, indicating a spatial non-linearity.

In conclusion, the point-spread-function of the hyper-oxygenated BOLD response in human GM is narrower than that reported at 1.5 Tesla, where macro-vessels dominate the mapping signals. The initial phase of this response is more spatially specific than later phases. Data acquisition methods that suppress macro-vascular signals should increase the spatial specificity of BOLD fMRI. The choice of optimal stimulus duration represents a trade-off between the spatial specificity and the overhead associated with short stimulus duration.

Introduction

The majority of functional brain imaging studies in humans rely on fMRI (Bandettini et al., 1992; Kwong et al., 1992; Ogawa et al., 1992). fMRI utilizes task-invoked metabolic and hemodynamic responses to infer the underlying local changes in neuronal activity. Thus, the fMRI signal is an indirect measure of changes in neuronal activity. Its ultimate specificity in space and changes of this specificity as a function of time are subject to limitations introduced by intermediary non-neuronal events. The present study investigates and quantifies these limitations in the form of a spatio-temporal point-spread function (PSF) in human gray matter (GM).

The most commonly used fMRI approach is based on gradient echo (GE) BOLD contrast (Ogawa et al., 1990). The BOLD signal is inversely proportional to the local content of deoxy-hemoglobin (deoxyHb) (Ogawa et al., 1990). Following increases in neuronal activity, local arterial cerebral blood flow (CBF) increases are larger than the increases in oxygen consumption (Fox and Raichle, 1986; Hoge et al., 1999), resulting in lower deoxyHb content in the capillaries. This change in deoxyHb content propagates from the capillaries at the sites of increased neuronal activity downstream to the draining veins. Therefore, large veins distant to sites of increased neuronal activity become a source of functional mapping signals (Ugurbil et al., 2003), impairing the spatial specificity of fMRI and augmenting any intrinsic imprecision that may exist in the coupling between CBF and neuronal activity.

The first study (Engel et al., 1997) that quantified the spatial specificity of the GE BOLD response used an elegant paradigm to show that at 1.5 Tesla (T) the full width at half maximal height (FWHM) of the PSF of the BOLD response is 3.5 mm (Engel et al., 1997). Similar values (3.9 mm for GE BOLD and 3.4 mm for Spin Echo [SE] BOLD) have been reported at 3 T (Parkes et al., 2005) using a paradigm similar to that used by Engel et al. (1997). These measures are comparable to the estimated extent of changes in oxygenation of venous blood which extend without dilution along veins (4.2 mm; Turner, 2002). The BOLD response from microvasculature (i.e. capillaries and small post-capillary venules) is virtually undetectable at 1.5 T (Frahm et al., 1994; Hoogenraad et al., 1999; Kim et al., 1994; Lai et al., 1993; Menon et al., 1993; Ugurbil et al., 2003). Even at 3 T and irrespective of whether GE or SE acquisition is used, BOLD fMRI signals are dominated by contributions from blood, and hence large veins (Jochimsen et al., 2004). Consequently, inaccuracies introduced through this mechanism are likely to dominate the PSFs measured at these fields (Parkes et al., 2005) and lead to degradations in the spatial correlation with the actual locus of neuronal activity (Disbrow et al., 2000).

Recent studies implemented fMRI in humans at ultrahigh magnetic fields (e.g. 7 T) (Yacoub et al., 2001a). Although the contribution of signals from blood to GE fMRI is smaller at this magnetic field, large vessel contribution still persists (Yacoub et al., 2001a). However, unlike lower magnetic fields (Haacke et al., 1994; Lai et al., 1993; Song et al., 1996), at 7 T or higher magnetic fields functional signals of microvascular origin confined to GM become robustly detectable (Duong et al., 2003; Haacke et al., 1994; Lee et al., 1999; Silva and Koretsky, 2002; Song et al., 1996; Yacoub et al., 2001a; Yacoub et al., 2003). Furthermore, an increased signal-to-noise ratio (SNR) at ultrahigh fields permits high resolution imaging, and the consequent decrease in partial volume effects minimizes obfuscation of microvascular signals from GM by large pial vessel contributions. As a result, at such ultrahigh fields it is possible to measure specifically the PSF of GE BOLD fMRI in GM by restricting the analysis to the GM. In addition, given the dynamic nature of deoxyHB alterations in the vascular tree, the PSF of fMRI signals may evolve over time as deoxyHb changes propagate from capillaries to small and large veins (Goodyear and Menon, 2001; Lee et al., 1995). The high SNR at high magnetic fields provides an opportunity to examine this possibility at high temporal and spatial resolution for signals restricted to GM.

Overall, the specificity of the fMRI signals in the GM and its dependence on time remain uncertain. This study is aimed at characterizing the spatio-temporal PSF of the BOLD response in human GM. To this end, we imaged the fMRI response at high-resolution in space and time at high magnetic-field (7 T). The BOLD response was sampled orthogonal to and across a retinotopic boundary in area V1. We found that the PSF of the BOLD response in GM is narrower than the PSF reported previously under conditions where macro-vessel contributions dominate. The initial phase of this response is more spatially specific than later phases. Therefore, fMRI methods for acquiring signals restricted to the GM are expected to increase the spatial specificity of fMRI. The choice of optimal stimulus duration represents a trade-off between the spatial specificity and the overhead associated with short stimulus duration.

Materials and Methods

Subjects

Four healthy subjects (two female, two male, aged 20–35 years) participated in this study. All subjects gave their informed consent to the experimental protocol, which was approved by the institutional review board at the University of Minnesota.

Visual stimulation

Visual stimuli were presented via a fiber-optics system (Silent Vision, Avotec, Stuart, FL). After the position and focus were adjusted by the subjects, the goggles were mechanically fixed to the RF coil holder. To encourage fixation, the subjects were instructed to detect and report luminance changes in the fixation point timed randomly. The relative fixation point/background contrast switched between the values of 0.37 and 0.60.

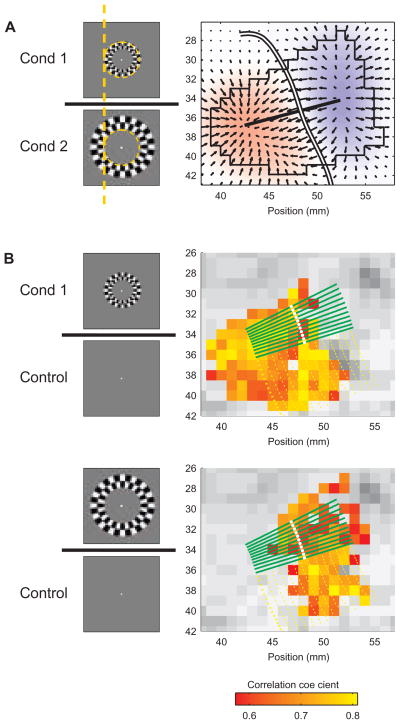
Each of the two stimuli consisted of a 3° wide iso-eccentricty (around ≈6° and ≈9°) ring of high-contrast checkers, flickering at 8 Hz (Fig. 1; each pixel changed its luminance 8 times per second). The exact eccentricities of the stimuli were adjusted so that their combined response was centered on the imaged flat GM region (see below). Outside the checkers, the image was a uniform gray field of luminance equal to the mean luminance of the checkers. The same luminance was used in the blank gray image presented to the subjects during the control periods (Fig. 1). Each scan consisted of a control period (40 s) followed by eight epochs of 16 s stimulus-on and 20 s stimulus-off. Each of the two stimuli was presented in alternating stimulus-on epochs.

Figure 1.

Delineation of the border between the representations of the stimuli, and sampling of the BOLD response. Two visual stimuli of iso-eccentricity rings composed of flickering checkers were used. The inner edge of condition 2 abutted (eccentricity-wise) the outer edge of condition 1, as demonstrated by the dashed orange circle and line (shown for presentation purposes here only). A blank gray image was presented during control periods.

A Delineation of the border between the retinotopic representations of the two stimuli. XCorr analysis was used for each of the two conditions. The map of correlation of the more peripheral stimulus (condition 2) was subtracted from the map of the more central stimulus (condition 1). The smoothed resulting map is presented in the background. Superimposed in black are arrows representing the gradient field of the differential response, the outline of the ROI, and the straight line that connects the points of maximal and minimal differences. The white curve depicts the border, computed by starting at the anchor point on the straight line with difference closest to zero and following the direction orthogonal to the local gradient. Subject, S2.

B Sampling of the BOLD response orthogonal to the border. Colored voxels in the background responded significantly to condition 1 (top) or condition 2 (bottom). The BOLD response was sampled along the green lines. The white dots on the green lines mark the position of the border. The yellow dotted lines represent potential sampling lines which were excluded (see methods). For clarity of presentation, only every seventh line (either green or yellow) is shown. Note that the threshold was applied to the functional maps for presentation purposes only. The actual sampled data were in units of change relative to baseline with no thresholding.

Hardware for BOLD imaging

MR imaging was performed on a 7 Tesla human magnet (Magnex Scientific, Abingdon, UK), controlled by an INOVA console (Varian Inc., Palo Alto, CA). An actively switched combination Radio-Frequency coil was used (Pfeuffer et al., 2002a), with a large transmit quadrature coil pair (18 × 12 cm²) and a small receive quadrature coil pair (6 cm average diameter). To minimize head motion, a bite bar was molded for each volunteer and rigidly attached to the coil holder.

Data Acquisition

Inversion recovery images were initially obtained to localize one oblique slice around the midline, parallel to- and centered on either the upper or lower bank of the calcarine sulcus. The position of the slice along the Z axis and the angle of the imaged plane relative to the XY plane were determined based on sagittal T₁-weighted scout images acquired before fMRI. The position and angle of the slice were optimized to maximize the overlap with the largest area of flat GM within the upper or lower bank of the calcarine sulcus in one hemisphere (Supplementary Fig. [SupFig] 1). In order to monitor any possible movement of the subject orthogonal to the slice plane, T₁-weighted sagittal images were taken from the midline towards the imaged hemisphere before the first - and after each - fMRI scan. In the event of subject motion relative to the initial position, the slice was repositioned to match the original slice position.

T2*-weighted functional images were acquired using a GE echo planar imaging (EPI) sequence with a field of view of 12.8×12.8 cm, an in-plane resolution of 1.0×1.0 mm and a 3-mm slice thickness. Images were acquired in four segments, with a total readout time of 30 ms per segment, TR of 250 ms, and an acquisition time of 1000 ms per acquired volume. A TE of 20 ms (T2* of GM = 25 ms, (Yacoub et al., 2001a)) and a flip angle of 30° were used.

The spatial resolution along the phase-encoding direction is expected to be blurred because of the T₂* filter effect during the EPI readout. In our case, the effective spatial resolution in the tissue, determined by the full width at half maximum of the point spread function of the T₂* filter effect, was only slightly (4%) larger than the nominal spatial resolution. This was because the readout time for one segment was approximately equal to the T₂* of the tissue (Haacke et al., 1999; Jesmanowicz et al., 1998).

Data Preprocessing

The measured k space data were preprocessed using DORK to remove respiration-induced fluctuations in resonance frequency (Pfeuffer et al., 2002b). Subsequently, a fast Fourier transformation was applied to transform the data to the image space. The reconstructed image series were preprocessed and analyzed using routines in MATLAB (The MATHWORKS Inc., Natick, MA). The first ten volumes of each scan were discarded to account for non-steady state effects. Motion correction within scans and registration between scans of each session were applied, using MCFLIRT (Jenkinson et al., 2002). Subsequently, voxel-wise linear trend removal and temporal high-pass filtering were applied. Frequencies with a cycle longer than the duration of 3 trials, i.e. longer than 108 s, were filtered out.

Analysis of the BOLD Response: Functional Maps

For each voxel in each scan a baseline value was computed by averaging over all the volumes before the first stimulation and the four volumes before each successive stimulation. We used only the four volumes before each stimulation rather than using all volumes in the non-stimulated state in order to minimize residual post-stimulus undershoot effects¹. For each voxel in each scan the signal change relative to the scan- and voxel-specific baseline was computed. The signal change image series were averaged across multiple scans from the same session. The averaged image time series were processed by voxel-wise cross-correlation (XCorr) analysis (Bandettini et al., 1993), using templates of the stimulation paradigm convolved with a model of the hemodynamic response (Boynton et al., 1996; Glover et al., 1999). For presentation purposes only (Fig. 1B), a threshold was applied to the XCorr maps, followed by the application of a minimal spatial cluster operator of at least four significantly responding voxels. The eight immediate neighbors of a pixel were defined as contiguous.

Mask Calculation and ROI

An ROI was defined, delineating a connected region within a flat part of GM in the calcarine sulcus in one hemisphere. The ROI was approximately centered on the border between the regions that responded to the two stimuli, and included all voxels that responded to at least one of the two stimuli.

A mask was computed in order to exclude voxels including significant signals from blood vessels from further analysis. First, the GE EPI signal intensity for each voxel was normalized to compensate for the decreasing signal intensity with increasing distance from the surface coil (SupFig 2 A–D). An exponential function was fitted to the mean anterior-posterior intensity profile, averaged along the medial-lateral axis. Each voxel was divided by the corresponding value of the fitted exponential function.

The mask was then computed based on two criteria (SupFig 2 E–F). Large veins appear as dark lines and spots in the T2* images, as demonstrated by Ogawa and Lee (1990), Menon et al. (1993), Reichenbach and Haacke (2001) and others. These veins show large response amplitude, as demonstrated by Menon et al. (1993), Kim et al. (1994), Cheng et al. (2001), Yacoub et al (2001, 2005), and others. Voxels were masked out if their signal intensity was below a threshold adjusted for each data set based on visual inspection, or if they demonstrated 10% or larger signal change (Cheng et al., 2001; Kim et al., 1994; Fig. 4 in Yacoub et al., 2005) in response to at least one of the two conditions relative to baseline.

Determination of the border between the cortical representations of the stimuli

The two stimuli shared a common iso-eccentricity edge. Iso-eccentricity rings in the visual space map to V1 as smooth, almost linear 2D curves (Tootell et al., 1988).

The map of correlation of the more peripheral stimulus (condition 2) was subtracted from the map of the more central stimulus (condition 1) (Fig. 1A). The map of differential correlation was resampled at higher resolution (100 μm × 100 μm) for further sub-voxel processing. The re-sampled map was spatially smoothed (only for the purpose of determining the border; the smoothed data were not used for estimating the PSF) by convolution with a 2D Gaussian (sigma = 1.5 mm).

The positions of maximal and minimal smoothed re-sampled differential map were determined, and a line was computed between them (Fig. 1A). The position on this line with differential response closest to 0 served as the anchor point for the computation of the border between the two responding regions. Next, the gradient vector field of the differential response was computed. Lastly, a continuous curve was computed, starting at the anchor point, and running along the two directions orthogonal to the local gradient. The differential response along this curve remained equal to that in the anchor point, i.e. approximating zero, because:

For any 2D continuous function f (x, y), the value of f (x, y) along the entire length of curves that are locally orthogonal to the gradient vector field of f (x, y) is constant, as shown below.

Let v(x,y) be the vector orthogonal to the gradient vector field ∇f (x,y). This is equivalent to:

$$\nabla f(x,y)·\mathit{v}(x,y)=0$$ (I)

Assuming that f (x, y) is continuous, equation (I) can be rewritten as:

$$\frac{\partial f(x,y)}{\partial x}{v}_x(x,y)+\frac{\partial f(x,y)}{\partial y}{v}_y(x,y)=\frac{\partial f(x,y)}{\partial \mathit{v}(x,y)}=0$$ (II)

i.e. the derivative of f (x, y) along the vector v(x,y) is 0, and thus f (x, y) stays constant in that direction.

Sampling of the Spatio-Temporal BOLD response

Lines were drawn across the border curve and orthogonal to it at the point at which the border was crossed (Fig. 1B). The lines were drawn at intervals of 0.05 mm along the border, and extended 5 mm on each side of it. For estimating the response from GM, lines extending beyond the limits of the ROI or going through voxels that were masked out by the blood vessel mask were excluded from further processing. The spatio-temporal BOLD response relative to the baseline (i.e., from single-condition response, Fig. 1B; not from the differential response) was sampled at intervals of 0.1 mm from the underlying original voxels representing the non-smoothed map along the remaining lines, separately for each condition. All spatio-temporal samples corresponding to one condition were averaged. The SD and SEM were updated during the averaging process.

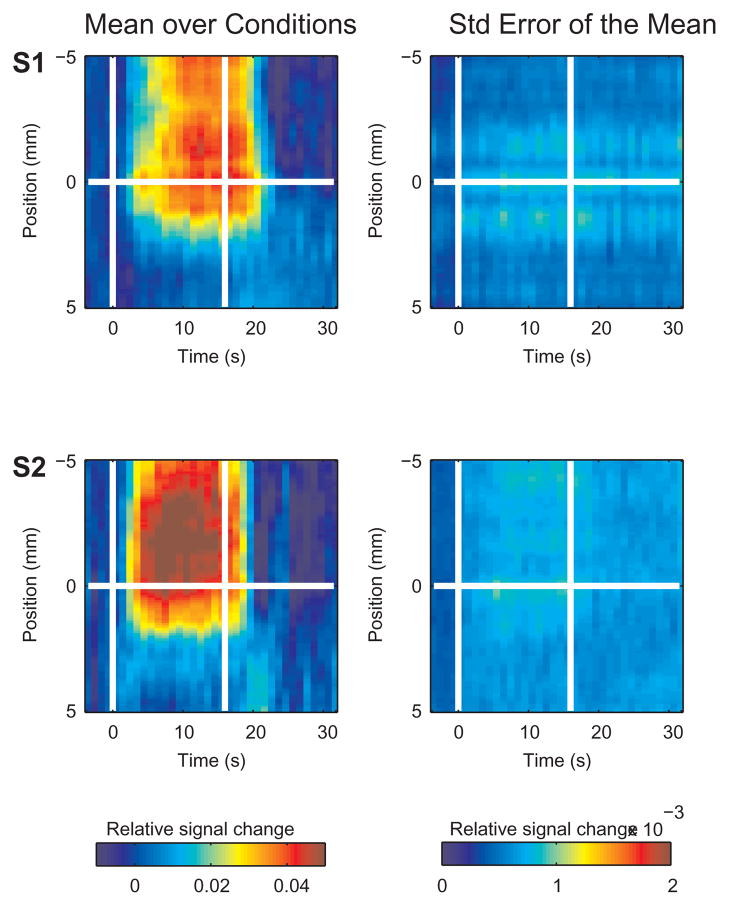
Given the continuity of V1, the neuronal and BOLD response to the two stimuli should be approximately symmetrical across the border between them. The mean spatio-temporal BOLD response to condition 2 was spatially mirrored across the position of the border, so that it spatially matched the response to condition 1. Subsequently, the mean response over the two conditions was computed (Fig. 2).

Figure 2.

Spatio-temporal BOLD response across the edge of the stimulated region. The mean relative signal change averaged over conditions and lines is presented as a function of time and position within the left column. To the right is the standard error of the mean. The horizontal white line at position 0 in each plot represents the position of the retinotopic boundary between the two conditions. The two vertical lines mark the onset and cessation of the stimulus. Subjects: S1 and S2. The mean SEM averaged over the stimulated region and time from peak response to stimulus offset (S1, 5.87E-04; S2, 6.50E-04; S3, 9.11E-04; S4, 8.33E-04; mean, 7.45E-04) was much smaller than the mean response (factor of 0.015 ± 0.005, averaged over subjects).

Principal Component Analysis

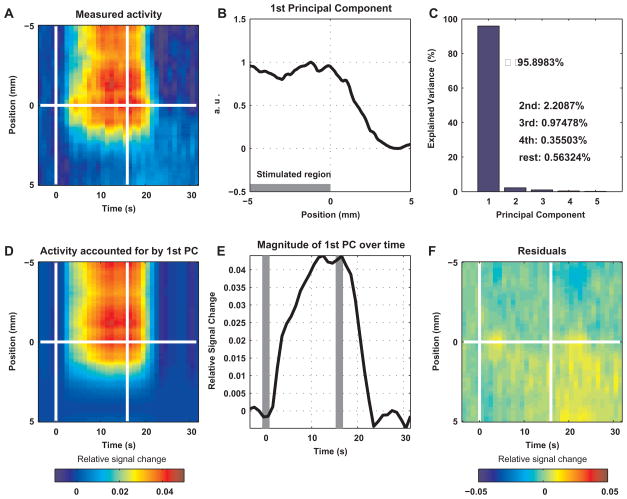
To compute the PSF of the BOLD response, we first obtained the spatial profile of the time-invariant part of this response. For each time point, the BOLD signal in space was considered as a vector. Principal component (PC) analysis was applied to these vectors over the time domain. The first PC, representing the spatial vector that accounted for the largest amount of variance among all components, was normalized so that its maximum was equal to one. The time-dependent magnitude of the first PC was computed by projecting the time-series of the fMRI spatial response vectors onto the subspace spanned by the normalized first PC (Fig. 3).

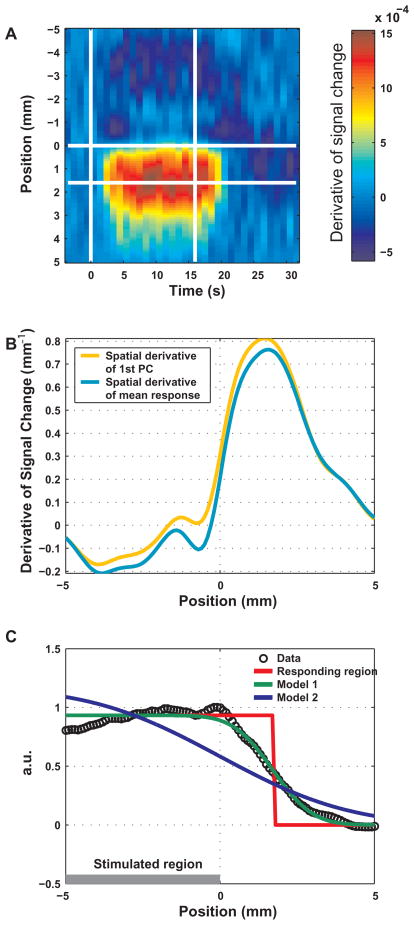
Figure 3.

Principal component analysis of the BOLD response across the edge of the stimulated region, presented for subject S1. A The measured spatio-temporal BOLD response. The mean relative signal change averaged over conditions and lines is presented as a function of time and position. The horizontal white line at position 0 represents the position of the retinotopic boundary between the two conditions. The two vertical lines mark the onset and cessation of the stimulus. B BOLD response as a function of position relative to the edge of the stimulated region: the normalized first PC. Principal component analysis over time was applied to the spatio-temporal response in A. C The variance accounted for by the PCs. The first PC accounted for 95.9% of the variance. D The part of the spatio-temporal BOLD response accounted for by the first PC. For each time point, the presented response as a function of space is the result of projecting the corresponding measured response onto the first PC. E Magnitude of the first PC over time. For each time point, the magnitude of the projection described in D is shown. The vertical gray bars indicate the onset and cessation of the stimulus. F The part of the BOLD signal that could not be accounted for by the first PC. The differences between the measured signal and the activity accounted for by the first PC are shown.

Spatial Derivative of the BOLD Response

Two derivatives were computed: 1) the spatial derivative of the first PC, and 2) the mean over time of the derivatives with respect to space of the BOLD response spatial vectors. To compute the latter, we first computed the derivative of the spatio-temporal response with respect to space:

Let r: R × R → R be the spatio-temporal response. We calculated the spatial derivative as a function of time d_r: R × R → R as:

$$d_r(x,t):=\frac{\partial r(x,t)}{\partial x}.$$

We then computed the mean over time of this derivative from 3 s after stimulus onset until 3 s after cessation of the stimulus.

Both derivatives were smoothed by convolving them with a Gaussian (sigma = 0.5 mm).

Computation of the Point-Spread Function by Fitting of a Kernel Model

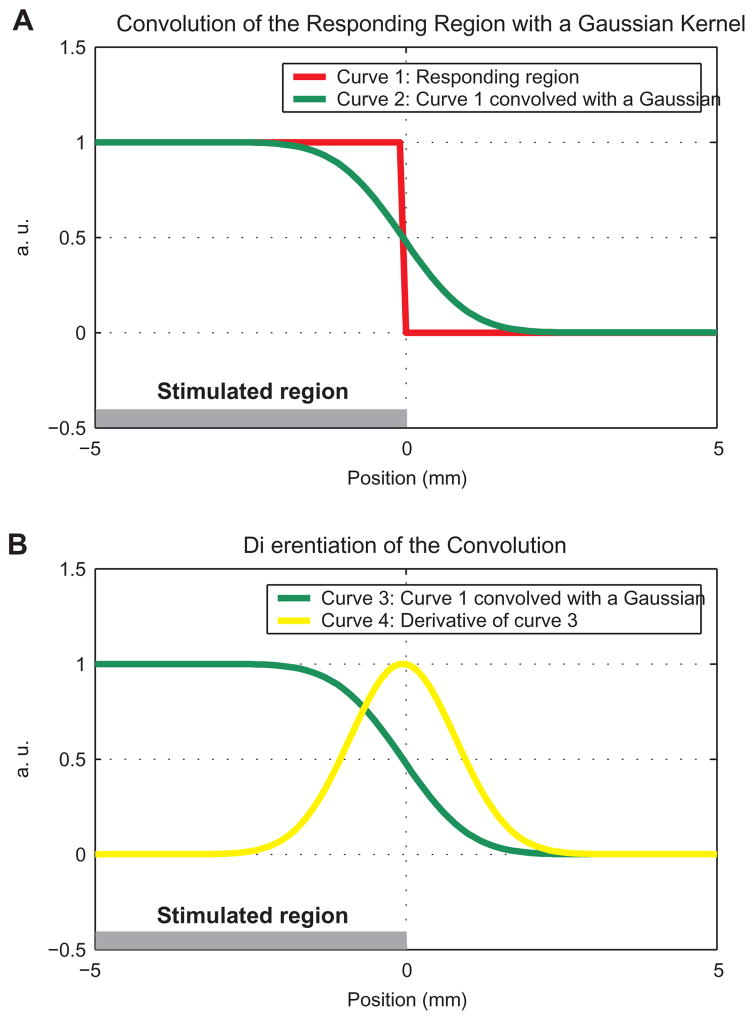
A model was fitted to the measured BOLD response in space. The model consisted of a convolution of the responding region (modeled as a step function) with a Gaussian PSF. Three free parameters of the model were determined by the fitting process: 1) the position of the edge of the step-like responding region, assuming that it does not necessarily fall exactly on the edge of the stimulated region (see Fig. 4), 2) the width of the Gaussian PSF, and 3) a multiplicative constant. For comparison, we also fitted a model with only two free parameters, with the position of the edge of the responding region set to the border between the regions responding to the two stimuli. The fitting with two free parameters assumed that the edge of the responding region coincides with the edge of the stimulated region.

Figure 4.

A model for signal spread of the BOLD response in one dimension. A The horizontal gray bar shows the retinotopic representation in V1 of a stimulus in the visual space. The stimulus subtends part of the visual field, with the edge of the retinotopically-stimulated region at position 0. The red curve shows the responding region in V1. The green curve represents the convolution of the responding region with a PSF (Gaussian, 2 mm FWHM). B Convolution of a step function with a kernel is equivalent to integration of the kernel over space. Therefore, differentiation of the convolution should result in the original kernel positioned at the original step. The green curve represents the convolution, identical to the one shown in A. The yellow curve represents the original Gaussian kernel computed by differentiation of the convolution with respect to space. In the scheme presented here, the edge of the stimulated region (horizontal gray bar) and the edge of the responding region (step in the red curve and peak of the derivative in yellow) are identical.

Estimation of the Point-Spread Function as a function of time

To investigate possible changes in the spatial specificity of the BOLD response as a function of time, we fitted the kernel model to the spatial pattern of the response time-point by time-point. The changes in PSF as a function of time were fitted with an exponential function (with 3 free parameters: a·exp(−b·x) + c) and a linear function (with 2 free parameters: a·x + b).

Estimation of errors caused by finite voxel-size and inaccurate localization of border

The response was modeled in space as a convolution of a step function and a Gaussian function. In stage 1, the effect of the voxel size (1 mm) was simulated by randomly aligning the modeled response to an array of voxels. The resulting value of each voxel was calculated as the mean underlying response averaged over the voxel. In stage 2, the effect of uncertainty in localizing the border was simulated. The vectors of simulated response based on the calculated voxel values from stage 1 were averaged relative to a border position that jittered randomly relative to the true border position. The shifts in border position were drawn from a Gaussian distribution. A spatial model was then fitted to the mean simulated sampled data and the edge position and FWHM of the PSF was estimated.

Results

This section describes the stimulus and sampling of the fMRI response (Figures 1 and 2), computes the time-invariant part of the spatial profile of the response (Fig. 3), estimates the parameters in space of this profile (Figures 4 and 5), presents changes in the specificity of the BOLD response as a function of time (Fig. 6), and analyzes the sensitivity of the estimation to confounding effects (Figures 7 and 8).

Figure 5.

Spatial differentiation of - and fitting a model to - the BOLD response in space. A The spatial derivative of the fractional signal change as a function of time and position. The horizontal white line at position 0 mm marks the edge of the stimulated region. The other horizontal line shows the position of the maximum of the mean (over time) spatial derivative. The two vertical lines mark the onset and cessation of the stimulus. B The spatial derivative of the first PC is shown in orange. The mean spatial derivative of the response, obtained by averaging the spatial derivative over the stimulation period, is shown in cyan. Position 0 marks the edge of the stimulated region. C Fitting a model to the BOLD response in space. The curve in black circles is the first PC. A model was fitted consisting of the convolution of a step function with a Gaussian kernel. Model 1 (in green) had 3 free parameters: the position of the edge of the responding region, the width of the kernel and a multiplicative constant. Model 2 (in blue) had 2 free parameters: the position of the edge of the responding region was set to the edge of the stimulated region.

Figure 6.

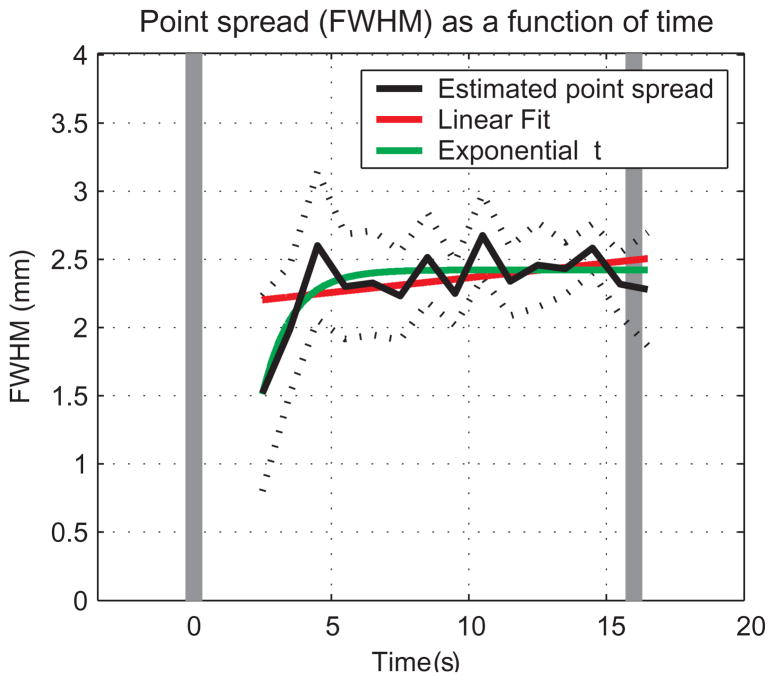
Point-spread function of the BOLD response from GM as a function of time from stimulus onset. For each time point, a model (with 3 free parameters) was fitted to the spatial pattern of the response averaged over lines, conditions and subjects. In dark, estimated PSF as a function of time. The dashed curves show the 95% confidence intervals around the estimated PSFs. The red and green curves represent linear and exponential functions, respectively, fitted to the PSF estimated between 2 and 16 s after stimulus onset. The confidence intervals obtained for the fitting of data from 0 to 2 seconds after stimulation onset were too wide and therefore uninformative. The vertical gray bars indicate the onset and cessation of the stimulus.

Figure 7.

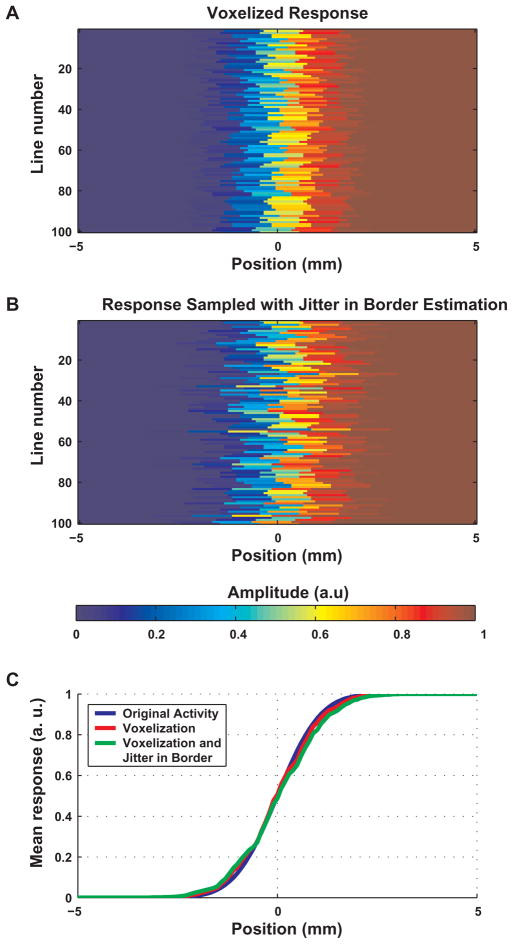
Estimation of errors caused by finite voxel-size and inaccurate localization of border: simulation of the sampling process in 1D. A The effect of voxel size (1 mm) on the measured pattern of activity across the edge of the responding region. The BOLD response across the edge of the responding region was modeled as a convolution of a step function (with the step at position 0) and a Gaussian with FWHM = 2 mm. It was then aligned randomly to a vector of voxels; each voxel was 1 mm long. The value shown for a voxel is the mean underlying BOLD signal. Each row shows the values in one alignment. B The effect of uncertainty in the position of the edge of the stimulated region (= the boundary between the two responses). This uncertainty is reflected by a random shift of the zero position for each line from A. The shifts were drawn from a Gaussian distribution with FWHM = 1 mm. C The BOLD response as a function of space. The original modeled convolution is shown in blue. The red curve represents the effect of voxel size (this is the mean averaged over all 100 vectors in A). The green curve shows the accumulated effects of voxel size and uncertainty in the estimation of the border (this is the mean averaged over all 100 vectors in B).

Figure 8.

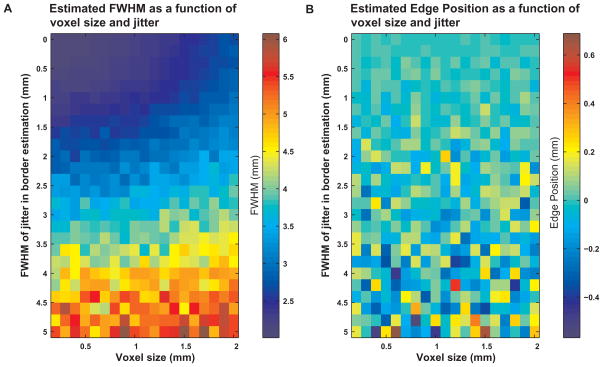
Dependence of the estimation of parameters on voxel size and on the uncertainty in estimation of the border. A The estimated FWHM of simulated data (with true FWHM = 2 mm) is shown as a function of voxel size and FWHM of the Gaussian used to simulate the uncertainty in localization of the border. B Sensitivity of the estimated edge of the responding region to voxel size and noise in localizing the boundary. The estimated position of the edge of the responding region (with true edge position 0 mm) is presented as a function of voxel size and FWHM of the Gaussian used to simulate the uncertainty in localization of the border. No systematic bias toward underestimation or overestimation could be seen. The variability, however, increased with increasing noise in localizing the boundary. For a voxel size of 1 mm and an error in boundary localization modeled using a Gaussian with FWHM 1 mm, the variability was in the relatively low range of −0.1 – 0.1 mm, while the mean position (−0.007 ± 0.044, mean ± SD) was close to the ‘true’ position (0 mm).

To study the spatio-temporal characteristics of the BOLD response in the GM, we used fMRI in a region of V1 that was approximately flat (SupFig 1). Subjects fixated on a spot at the center of the image during the entire scan. Two stimuli of iso-eccentricity rings composed of flickering checkers were used. The eccentricity of the outer edge of condition 1 (the condition which was more central in the visual field) was identical to the eccentricity of the inner edge of condition 2 (Fig. 1). The eccentricities of both stimuli were adjusted so that they activated parts of the imaged flat cortex in V1, with the shared edge of the two stimuli falling approximately in the center of that flat region.

As expected, condition 1 and 2 activated the more posterior and anterior parts of the calcarine sulcus, representing the more central and peripheral portion of the visual field, respectively (Fig. 1B). Differential analysis of the responses to the two stimuli revealed the retinotopic boundary between their representations (Fig. 1A). Multiple lines were drawn locally orthogonal to this boundary (Fig. 1B), and the single-condition responses relative to baseline along these lines were re-sampled at high resolution (0.1 mm). Data from blood vessels were excluded by masking out voxels with low-intensity T2* signals or with a high-amplitude (> 10%) response to at least one condition (SupFig 2; Fig. 1B). Data from the multiple lines were co-registered according to the location of the boundary within each line, with the stimulated region on the same side of the boundary. The registered data from multiple lines were averaged, resulting in the spatio-temporal response (Fig. 2).

To estimate the PSF of the BOLD response, we first obtained the time-invariant part of the spatial profile of that response. To this end, we applied principal component analysis over time to the spatial response (Fig. 3 A-C). Fig. 3A depicts the mean spatio-temporal BOLD responses averaged over the two conditions and all lines in a single subject. The white horizontal line within each image (coordinate 0 mm) represents the boundary of the retinotopic representation of the stimulus. The stimulated region extended from this line up. Fig. 3B shows the first spatial principal component (PC), with the stimulated region to the left of position 0 mm. Fig. 3C depicts the variance of the response accounted for by each of the 36 PCs present in this PC analysis. The first PC accounted for 96.18% ± 1.64% (mean ± SD averaged over subjects) of the variance over time of the response in space. In other words, the spatio-temporal response was well approximated by the spatial profile represented by the first PC, with changes as a function of time only in a scalar representing its magnitude. To verify this conclusion, we projected the vectors of the response in space as a function of time onto the normalized first PC. Fig. 3E presents the resulting series of magnitude values, with a time course reminiscent of the BOLD response. We then multiplied the first PC with this series of magnitude values to obtain the part of the response accounted for by the first PC (Fig. 3D). This part (Fig. 3D) approximated the measured response (Fig. 3A) with good fidelity. Lastly, Fig. 3F shows the residuals obtained by subtracting the approximated response (Fig. 3D) from the measured response (Fig. 3A). Overall, the spa-tio-temporal BOLD response could be closely approximated by a series of vectors that were scaled versions of the first PC. We concluded that the spatial pattern of fMRI BOLD response in GM was approximately time invariant.

To estimate the PSF of the BOLD response and to test the spatial linearity of that response across the edge of the stimulated region, we approximated the time-invariant spatial profile of the response using a model consisting of the convolution of a step function with a Gaussian (Fig. 4A, green curve). The step function and the Gaussian represented the stimulated region and the assumed PSF, respectively. The free parameters were the location of the step and the width and maximal height of the Gaussian. Assuming a spatially linear process of BOLD response convolved with neuronal response convolved with the stimulated retinotopic region, the spatial derivative of the response is expected to show its maximum on the edge of the stimulated region (Fig. 4B, yellow curve).

Fig. 5A depicts the mean derivative of the spatio-temporal response with respect to space (data pooled from all subjects). Fig. 5B shows the profile of this derivative (in cyan), and the derivative with respect to space of the first PC (in orange). Consistent across subjects, the maximal derivative was offset from the edge of the stimulated region, indicating spatial non-linearity of the BOLD response across the edge of the stimulated region. Similarly, the fitted location of the step (edge of the responding region) was 1.72 ± 0.07 mm away from the border (Fig. 5C, in red; Table I). The green-colored curve in Fig. 5C depicts the model with 3 free parameters (the width and maximal height of the Gaussian, and the position of the edge of the responding region) fitted to the response as a function of space. The blue colored curve depicts a model fitted with only two parameters (the width and maximal height of the Gaussian), while setting the edge of the responding region to coincide with the edge of the stimulated region (position 0 mm). This model clearly did not fit as well as the model that allowed the position of the responding region to be determined according to the data (Table I). The FWHM of the fitted Gaussian PSF was 2.34 ± 0.20 mm (obtained from data pooled from all subjects using the model with the 3 free parameters).

Table 1.

Estimated parameters in space, and goodness of fit

Subject	% of total variance explained by 1st PC	Point Spread Function FWHM (mm)	Position of edge of responding region (mm)	Fitting model (3 PRMS) in space: adjusted Rsquare	Fitting model (2 PRMS) in space: adjusted Rsquare
s1	95.9	2.13±0.18	1.87±0.06	0.990	0.814
s2	97.3	2.50±0.19	1.49±0.06	0.988	0.791
S3	94.0	2.57±0.60	1.71±0.18	0.890	0.733
S4	97.6	2.28±0.58	1.68±0.18	0.888	0.580
mean±SD	96.2±1.6	2.37±0.20	1.69±0.15	0.939±0.058	0.730±0.105
pooled data	97.9	2.34±0.20	1.72±0.07	0.988	0.786

The intervals attached to the PSF and to the position of the edge of the responding region are 95% confidence intervals. PRMS = parameters. Adjusted Rsquare = the fraction of variance explained by fitting the specific model using parameter-adjusted Rsquare statistics.

This PSF with FWHM of 2.34 mm was obtained from lines that were within the ROI encompassing GM regions, and that did not overlap any of the voxels that belonged to the blood-vessel mask. To evaluate how signal from vessels modify the PSF, we repeated the analysis without imposing the ROI or the blood-vessel mask. The FWHM of the fitted Gaussian PSF from GM and vessel regions was 3.15 ± 0.13 mm, wider than that of the PSF restricted to GM regions.

Although the spatial pattern of the fMRI BOLD response in GM was found to be approximately time invariant (Fig. 3), this does not necessarily mean that the spatial specificity of the response does not change as a function of time. Specifically, even if the PSF would change continuously, the evolving spatial patterns would still be correlated, and the spatiotemporal response would be expected to be well approximated by one spatial PC. Therefore, the PSF estimated in Fig. 5 is an estimate of the overall specificity of the BOLD response, while changes in this specificity as a function of time are possible. To investigate possible changes in the spatial specificity of the BOLD response as a function of time, we fitted the model to the spatial pattern of the response time-point by time-point. Fig. 6 shows that whereas the PSF remains stable from ~4 s from stimulation onset, it is smaller before that time point. The 95% confidence interval around the PSF obtained during the 3^rd second of stimulation did not overlap with those obtained during the 11^th and 15^th seconds. Therefore, the PSF obtained during the 3^rd second was narrower than the latter PSFs (p < 0.05; note that the confidence intervals obtained for the fitting of data from the 1^st and 2^ed seconds after stimulation onset were too wide and therefore uninformative). The estimated PSF obtained during the 3^rd (1.52 mm) and 4^th (1.99 mm) seconds of stimulation were smaller than the mean estimated PSF obtained during the 5^th to 16^th seconds (2.42 ± 0.15 mm, mean ± SD; p < 0.0001 and p < 0.02 respectively, two-tailed t-test). The changes in PSF as a function of time were approximated better by an exponential function (−8.148×exp(−0.8776×t) + 2.43, t = 2.5 s from stimulus duration and on, in green, adjusted R2 = 0.31) rather than a linear function (in red, adjusted R² = 0.17; note that R² values are relatively low because in part they reflect the fluctuations of the PSF after it reaches the steady state), indicating that the increase in PSF saturates rather than increases continuously. Overall, the initial phase of the positive hyper-oxygenated BOLD response from GM was more spatially specific than later phases.

Our estimates of PSF and position of the edge of the responding region assume infinitely high resolution of sampling and precise localization of the boundary between the two stimulated regions (the process described in Fig. 1A). Figures 7 and 8 demonstrate the sensitivity of the parameters estimated in space to voxel size and to uncertainty in localization of the retinotopic border. Figure 7 simulates the sampling process by finite voxels (1 mm long) and noise (drawn from a Gaussian distribution with FWHM of 1 mm) in the positioning of the boundary. It shows that neither voxel size nor noise in the positioning of the boundary cause a systematic bias in the localization of the edge of the responding region. However, each of the simulated effects does cause smearing of the response compared to the real response around the boundary.

Figure 8A depicts the FWHM of the estimated PSF as a function of simulated voxel size and uncertainty in localizing the boundary. The FWHM of the assumed ‘real’ PSF used for simulation was 2 mm. The FWHM of the estimated PSF increased with increasing voxel size and/or uncertainty in localizing the boundary. For a voxel size of 1 mm and an error in boundary localization modeled using a Gaussian with FWHM 1 mm, the FWHM of the detected PSF was 2.43 ± 0.04 mm (mean ± SD), ~20% wider than the FWHM of the ‘real’ PSF. Figure 8B demonstrates the influence of voxel size and uncertainty in localizing the boundary on the estimated position of the edge of the responding region. No systematic bias in estimating the position of the edge of the responding region can be seen with changes in these parameters. The variability in this estimation does increase, however, with increasing noise in the boundary estimation.

Discussion

BOLD point spread function in gray matter

The PSF that we measured (2.34±0.20 mm FWHM) is an upper bound of BOLD PSF in GM in response to a point-like increase in neuronal activity. It is in fact a convolution of PSFs due to eye movements, neuronal response, the BOLD response in GM and the PSF of the data acquisition process, including contributions to the signals from inflow effects² that admix the BOLD and flow contrast. Based on our simulations (Figures 7 and 8) we expect the combined neuronal and BOLD response PSF in V1 GM to be less than 2 mm.

Stimulus-evoked CBF changes must occur in all vessels that feed or drain the region where neuronal activity is increased. CBF control does exist in the sub-millimeter scale of columns (Duong et al., 2001; Zhao et al., 2004; Zhao et al., 2006). The specificity of arteries and veins with respect to territory of altered neuronal activity is expected to be lower because of the relatively large regions that they feed and drain, respectively. The contribution of the arteries to the BOLD signal is small, because deoxyHb content in the arteries is minimal. The relative contribution from large veins to the overall functional mapping signals is reduced at 7 T for two reasons. First, the micro-vascular signals are substantially enhanced: they increase approximately quadratically with field magnitude. Second, intravascular BOLD signals, the main mechanism responsible for the large vessel effects in fMRI, are substantially reduced at this high magnetic field strength (Yacoub et al., 2001a). However, GE fMRI at 7 T still includes contributions from veins of all sizes due to the extra-vascular BOLD effect. These remaining confounding signals of extra-vascular BOLD from large draining veins were reduced here by selecting the imaged slice within the GM and thus largely excluding blood vessels within the pia matter, and by masking out large vessels (Cheng et al., 2001).

Therefore, except for the spatially specific signals from capillaries, we are left with intracortical venules and veins. These are largely perpendicular to the cortex. They are classified in 5 classes (Duvernoy et al., 1981) with diameters from 20 μ (group 1) to 120 μ (group 5). They drain capillaries from regions with radii of 200 μ (group 1) to 500–2000 (group 5) μ (Duvernoy et al., 1981). These small intracortical venules and veins are expected to have a significant extra-vascular effect. They are large enough to be outside the dynamic averaging regime³ (Ogawa et al., 1993) at 7 T which diminishes the magnitude of the BOLD effect. Therefore, in the present study, these in-tra-cortical veins are expected to dominate the PSF of the GE fMRI signal. This is consistent with our estimation that after taking into account confounding effects, the combined neuronal and GE BOLD PSF should be below 2 mm. Therefore, intra-cortical veins and venules appear to be the limiting factor for high-resolution GE fMRI.

The FWHM of the PSF that we report in GM (2.34±0.20 mm FWHM) is narrower than those reported previously (3.5 mm at 1.5 T (Engel et al., 1997), and 3.9 mm at 3 T (Parkes et al., 2005)). We attribute this difference to magnetic field effects on the functional mapping signals and to our experimental procedure aimed at restricting the analyzed data to GM. First, while the large vessel contributions to GE BOLD persist at high magnetic fields such as 7 T, their relative contribution to fMRI signals is diminished: the BOLD effect at 7 T is biased towards signals from GM (Yacoub et al., 2001a). The mechanisms underlying this effect include larger functional signals from capillaries and smaller contribution of intravascular BOLD signals compared to lower magnetic fields (Ugurbil et al., 2003; Yacoub et al., 2001a; Yacoub et al., 2003). The reduction in intravascular BOLD signals is due to the rapidly decreasing venous blood T₂ with increasing magnetic field (Duong et al., 2003). In contrast, the BOLD response at 1.5 T is dominated by signals from large draining veins, with micro vascular contributions essentially undetectable at this field strength. Similarly, we attribute the relatively wide (3.4 mm) PSF of SE signals at 3 T (Parkes et al., 2005) to the presence of large vessel contamination to SE BOLD fMRI at 3 T due to intravascular, blood-related BOLD effects (Duong et al., 2003; Lee et al., 1999). Stimulus evoked signals from blood can originate from all blood vessels in the venous system, and, at 3 T, ~50% of the SE fMRI signals were shown to originate from blood alone (Jochimsen et al., 2004). The contribution from blood becomes negligible only at fields of ~7 T or above (Duong et al., 2003). Second, selecting flat GM regions and masking out blood vessels in the present study made it possible to reduce contributions from draining veins, in addition to the magnetic field effect described above. Supporting this interpretation, avoiding the post-processing procedures that masked out blood vessels yielded a PSF with FWHM 3.15 ± 0.13 mm, wider than that obtained from GM regions and more similar to the PSF reported at 1.5T (Engel et al., 1997). Third, the higher resolution that we could apply because of the increased SNR at high field made it possible to reduce partial volume effects with vessels, cerebro-spinal-fluid and white matter. Our work (JC Park and K Ugurbil, unpublished results) in the anesthetized cat visual cortex shows that the PSF of GE BOLD at 9.4 T is ~1.7 mm, consistent with the smaller PSF in humans at high- compared to low magnetic field, and in agreement with our estimate of PSF of less than 2 mm in human GM.

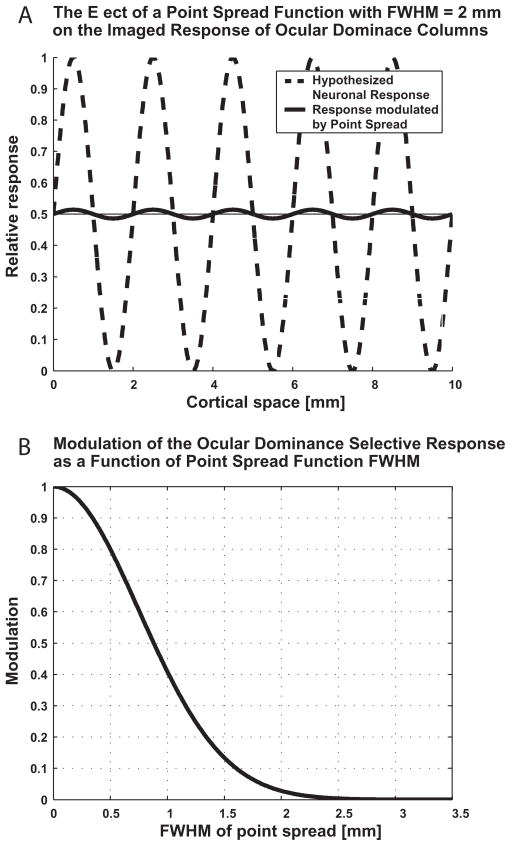
The PSF that we have measured reflects the resolution of fMRI for single-condition mapping rather than its resolving power in differential mapping. Single-condition mapping refers to the subtraction of the imaging signals obtained under baseline conditions without stimulation from the response to a stimulus (Grinvald et al., 2000; Ugurbil et al., 2003). The parameters that ultimately determine whether two functional domains can be resolved by single-condition imaging are the distance between the domains, the responses they elicit, the variability in the measured signals, and the point spread function of the imaging signal. The FWHM of PSF presented here is wider than the peak to peak distance between neighboring human ocular dominance columns (~0.8–1.2 mm (Horton et al., 1990)), and is comparable to the cycle of the organization of these columns (~2 mm). Fig. 9 shows the consequence of detecting the selective response of ocular dominance columns using an imaging method with a PSF whose FWHM is equal to the cycle of the organization. The effective contrast (i.e. the signal intensity difference between the active and non-active columns) is approximately 25-fold reduced. We therefore expect that GE BOLD does not have the power of resolving human ocular dominance columns by means of single-condition imaging. In conclusion, we anticipate that it will not be possible to resolve a columnar organization by means of an imaging signal with PSF comparable to the cycle of the organization (Fig. 9).

Figure 9.

Decreased selective response of ocular dominance columns caused by spatial convolution with a Gaussian point spread function.

A The dashed curve represents in 1D the functional cortical preference of ocular dominance columns. The selective response (either single condition or differential) is approximated here by a sinusoidal profile in space, along a direction orthogonal to the ocular dominance slabs. The continuous curve depicts the reduced selective response of ocular dominance columns following the convolution with a Gaussian point spread with FWHM of 2 mm. B Fraction of the full selective response of ocular dominance columns as a function of the FWHM of the point spread function used for convolution. Amplitude 1 represents the full selective response with no convolution at all (or with convolution with a point spread function with FWHM = 0).

The PSF of an imaging signal does not necessarily reflect its resolving power in differential imaging. Differential mapping relies on the subtraction of the response to one stimulus from that to a second one. If the two stimuli are known a priori to have both spatially overlapping and orthogonal components in their cortical representation, their subtraction removes the overlapping component from the maps, enhances the orthogonal component and reduces common non-specific responses from draining veins (Grinvald et al., 2000; Ugurbil et al., 2003). Specifically for ocular dominance columns, we expect that GE BOLD obtained at high signal to noise ratio, restricted to the GM and in regions that are not adjacent to vessels, should be able to differentially resolve these columns (Cheng et al., 2001; Menon et al., 1997), because of reduction in common non-specific responses from cortical veins of group 5 and in extra-vascular BOLD originating in veins within the pia. The contrast between active and inactive columns, however, will still be small unless the differential analysis reduces the effective PSF to well below the dimensions of the columns. The expected small contrast should make the resolving power of differential GE imaging susceptible to signals from large blood vessels that might not be completely subtracted out due to their large and variable response.

Spatial non-linearity near the edge of the retinotopically stimulated region

The edge of the responding region was offset (1.72 ± 0.07 mm; Fig. 5; Table I) from the boundary of the stimulated region, indicating a spatial non-linearity.

The offset in the edge of the responding region compared to the stimulated region cannot be attributed to our analysis method. If the BOLD response triggered by the neuronal response evoked by the retinotopic stimulus represents a spatially linear process, the spatial derivative of the BOLD response would be expected to have its maximum on the edge of the stimulated region (Fig. 4B). The maximum in spatial derivative, however, was offset relative to this location (Fig. 5), inconsistent with a purely linear process. Given these results, we fitted the data with both a model that included the offset as a parameter and a model that did not. The analysis that we applied took into account the number of fitted parameters, and resulted in improved goodness of fit across all subjects using the model that included the offset as a parameter (Table I).

This offset cannot be attributed to subject head movement or non-perfect fixation. Our motion detection and correction routines detected fluctuations on the order of 0.1 mm, an order of magnitude smaller than the detected offset. In addition, head movements and eye movements are expected to cause fluctuations in the position of the edge of the retinotopically responding region, rather than an extended plateau of activated region. Overall, head movements and eye movements would be expected to smear the edge of the responding region, rather than cause an offset in its position.

The spatial non-linearity that we demonstrate is not at odds with the spatial linearity of large-scale responses measured at relatively low resolution from V1 regions (Hansen et al., 2004), because we report a fine-scale non-linearity near the edge of the retinotopically stimulated region. We conclude that the BOLD response to a stimulus in V1 extends beyond what would be expected from a linear retinotopic representation of the stimulus.

We hypothesize that this offset reflects mostly neuronal activity rather than vascular effects. The underlying neuronal mechanisms are likely to involve the two representations of the visual field by the interleaved left and right ocular dominance columns. These two representations imply that neuronal retinotopic borders cannot be defined at a resolution higher than the dimension of ocular dominance columns along the line of the measurement. In support of this hypothesis, the neuronal cortical magnification factor of visual field representation in monkey V1 is 1.8 times larger along the axis orthogonal compared to parallel to the ocular dominance slabs (Grinvald et al., 1994). Additional neuronal contributions could be due to the saturation type non-linear contrast response function across the edge of the stimulated region (Heeger, 1992), in combination with receptive-field scatter (Hubel and Wiesel, 1962). The saturation of the neuronal response in V1 is expected to take place within the stimulated regions, in which all receptive-fields fully ‘see’ a stimulus with 100% contrast. As one approaches the retinotopic boundary and moves beyond it, the proportion of receptive-fields that are fully stimulated with this contrast decreases. The spatial mapping of the saturation effect is expected to cause a spatial non-linearity of the neuronal response across the edge of the stimulated region.

Changes in the specificity of BOLD response as a function of time

Whereas the PSF remains stable from ~4 s from stimulation onset, it is smaller before that time point. The PSF estimated based on data from the 3^rd and 4^th seconds after stimulation onset was smaller than that estimated from data obtained later. Overall, the initial phase of the positive hyper-oxygenated BOLD response from GM was more spatially specific than later phases.

It has been demonstrated (Malonek and Grinvald, 1996) and confirmed (Devor et al., 2005; Hu et al., 1997; Menon et al., 1995; Thompson et al., 2003; Yacoub et al., 2001b) that the spatio-temporal oxygenation response is biphasic, with an early, spatially-specific negative response (‘initial dip’) and a second, less accurate positive response. Our current study was not optimized to detect the initial dip, which is transient and has low amplitude to noise ratio. Our findings show that also the initial phase of the positive hyper-oxygenated BOLD response from GM was more spatially specific than later phases.

The changes we detected in the spatial specificity of the BOLD response from the GM as a function of time are not at odds with the finding on the approximate time-invariance of the spatial profile of this response. Simulations that we carried out show that even if the PSF would change continuously, the evolving spatial patterns would still be highly correlated, and the spatiotemporal response would be well approximated by the first spatial PC. Therefore, the PSF estimated in Fig. 5 is an estimate of the overall specificity of the BOLD response averaged over time, while changes in this specificity as a function of time are possible. Specifically, whereas the width of the PSF increases with time before 4 s from stimulation onset, it stays approximately constant after that time point, contributing to the overall approximate time invariance of the spatial response.

A previous high-resolution optical imaging study in rats (Devor et al., 2005) reported separability in space and time for the total hemoglobin and oxyhemoglobin (oxyHb) responses to short stimulus duration, but only to a lesser extent for the deoxyHb response (mean percent variance explained by first PC, 49.4%). Interestingly, the time over which Devor et al. (2005) applied their principal component analysis is identical to the time for which we found changes in the PSF of the BOLD response from GM. Taking into account that BOLD reflects deoxyHb content, our findings of changes in the specificity of the BOLD response during its initial positive response are in agreement with those by Devor et al. (2005). The quantitative differences between their results and ours concerning the extent to which the pattern changes can be accounted for by the ‘initial dip’ detected by their optical imaging method but not in our study.

A time dependence of the BOLD response at low (Lee et al., 1995) and high (Goodyear and Menon, 2001) resolution was demonstrated by studies carried out at 1.5 and 4 Tesla, respectively. We expect that the relatively late changes observed by Lee et al. (1995) but not in our study are of large vessel origin, which our overall approach minimized. Our findings of increased specificity of BOLD during the initial phase of the hyper-oxygenated response are in agreement with those presented by Goodyear and Menon (2001). Even using differential imaging preserved this higher specificity at the initial phase, estimated as 6 s by Goodyear and Menon (2001). The selective signal obtained from 4 s stimulus duration was higher than that obtained from 6 s duration, in which the selective signal seemed to saturate. The time measures we report are in close agreement with those reported by Goodyear and Menon (2001).

Implications for high-resolution functional MRI

The PSF from GM presented here is narrower than that based on signals that arise mainly from large draining veins (Engel et al., 1997). Extrapolating this approach to methods that can further suppress signals from intracortical veins should further increase the spatial specificity. SE and CBF fMRI are both capable of such suppression (Ugurbil et al., 2003). We therefore anticipate that the PSFs of these imaging methods should be even narrower than the one presented here. Because both methods use long acquisition time per volume, they require long stimulation duration. However, the PSF achievable by HSE BOLD and CBF imaging, presumably narrower than the steady state PSF we report here, should allow them to achieve the resolution of cortical columns even when using long stimulation duration. Therefore SE- and CBF-based fMRI are expected to further enhance the spatial specificity of fMRI, provided that the lower contrast-to-noise ratios of these methods can be overcome.

For GE imaging, the choice of optimal stimulus duration represents a trade-off between the spatial specificity and the overhead associated with short stimulus duration. Long stimulation reduces the overhead time spent on the onset and offset of the response, and makes it possible to achieve higher fractional amplitudes, thus increasing the contrast-to-noise ratio. If an intermediate level of spatial resolution is required (i.e. not as high as that needed for mapping cortical columns) the relatively narrow steady-state PSF is an argument in favor of long stimulation paradigms, provided that signals from large vessels are efficiently suppressed.