Sodium Inversion Recovery MRI of the Knee Joint In Vivo at 7T

Abstract

The loss of proteoglycans in the articular cartilage is an early signature of osteoarthritis. The ensuing changes in the fixed charge density in the cartilage can be directly linked to sodium concentration via charge balance. Sodium ions in the knee joint appear in two pools: in the synovial fluids or joint effusion where the ions are in free motion and bound within the cartilage tissue where the Na⁺ ions have a restricted motion. The ions in these two compartments have therefore different T₁ and T₂ relaxation times. The purpose of this study is to demonstrate the feasibility of a fluid-suppressed 3D ultrashort TE radial sodium sequence by implementing an inversion recovery (IR) preparation of the magnetization at 7T. This method could allow a more accurate and more sensitive quantification of loss of PG in patients with OA. It is shown that adiabatic pulses offer significantly improved performance in terms of robustness to B₁ and B₀ inhomogeneities when compared to the hard pulse sequence. Power deposition considerations further pose a limit to the RF inversion power, and we demonstrate in simulations and experiments how a practical compromise can be struck between clean suppression of fluid signals and power deposition levels. Two IR sequences with different types of inversion pulses (a rectangular pulse and an adiabatic pulse) were tested on a liquid phantom, ex vivo on a human knee cadaver and then in vivo on 5 healthy volunteers, with a (Nyquist) resolution of ~3.6 mm and a signal-to-noise ratio of ~30 in cartilage without IR and ~20 with IR. Due to specific absorption rate limitations, the total acquisition time was ~17 min for the 3D radial sequence without inversion or with the rectangular IR, and 24:30 min for the adiabatic IR sequence. It is shown that the adiabatic IR sequence generates a more uniform fluid suppression over the whole sample than the rectangular IR sequence.

1. Introduction

Osteoarthritis (OA) is a degenerative cartilage disease and is a leading cause of chronic disability. It is clinically characterized by joint pain, tenderness, limitation of movement, crepitus, occasional effusion and variable degrees of local inflammation. The World Health Organization (WHO) estimates that worldwide ~ 10% of men and ~ 18% of women over 60 years of age have symptomatic OA [1] and that 80% of those with OA will have limitations in movement and 25% cannot perform their major daily activities of life.

Articular cartilage is a dense connective tissue that consists mainly of an extracellular matrix (ECM) composed of collagen (15–20%), proteoglycan (PG, 3–10%) and water (65–80%). Biochemically, OA is associated with reduction of PG content, increase of water content and change in the arrangement of collagen molecules. There is currently no cure for OA, but some therapeutic modalities exist that are generally more useful in the early stages of the disease. An early detection of OA and an accurate method for quantifying the effects of treatments under investigation are therefore of fundamental importance. Although plain radiography is the most common technique for the diagnosis of OA in the knee, magnetic resonance imaging (MRI) is the most promising technique because it offers better soft tissue contrast and allows a non-invasive evaluation of cartilage morphology and function. Also, quantitative MRI methods such as T_1ρ relaxometry [2], T₂ relaxometry [3], Gd contrast enhanced T₁ relaxometry [4], gagCEST [5] and sodium MRI [6] are capable of characterizing the changes in the molecular composition in the ECM of cartilage and can help in the diagnosis of early OA prior to the appearance of irreversible morphological changes [7].

It has been shown that the loss of PG is a signature of early OA and that sodium concentration correlates linearly with PG concentration in cartilage [8, 9, 10, 11]. PG is a complex molecule composed of sulfate and carboxylate groups whose negative charges endow the cartilage with a fixed charge density (FCD). This FCD attracts free floating positive sodium ions Na⁺ in the ECM and these ions in turn attract the water molecules through osmotic pressure. The quantitation of FCD through sodium concentration is straightforward using an ideal Donnan equilibrium [12].

The goal of this preliminary work is to test the feasibility of a magnetization prepared 3D ultrashort TE (UTE) radial sodium MRI sequence which suppresses the free sodium signal from synovial fluids outside the cartilage or joint effusion in the knee joint at 7T. The objective is to allow a more accurate quantitation of the bound sodium concentrations in the ECM of the cartilage and increase the sensitivity of sodium MRI to the loss of PG for patients with OA. Note that sodium concentration in healthy cartilage is in the range of 240–300 mM [11] while it is in the range of 140–150 mM for synovial fluid or saline solution. For this purpose, an inversion recovery (IR) preparation was implemented in a 3D UTE sequence [13, 14]. Two kinds of inversion pulses were compared: rectangular and adiabatic. Sodium quantitation was performed by using Agar gel calibration phantoms with known sodium concentrations placed on top of the samples. The IR sequence was first applied to a fluid phantom, a human knee cadaver for optimization of its parameters (pulse length, pulse power, inversion times) and then applied in vivo on 5 healthy volunteers with a 3D Nyquist resolution of ~3.6 mm, giving a signal-to-noise ratio (SNR) of ~20 in cartilage. SNR was ~30 in cartilage with the 3D UTE sequence without IR.

The adiabatic pulses are particularly useful for allowing the sequence to become robust towards B₁ and B₀ inhomogeneities, which are commonplace in vivo. Also, in our particular implementation, no shimming was done prior to the image acquisition, since a singly-tuned sodium coil was used. On the other hand, the swept pulses require long irradiation if the sequence is to satisfy the specific absorption rate (SAR) requirements in vivo. We show below in both simulations and experiments how a balance can be struck between a long inversion pulse and efficacy of suppression of fluids and quantitativity in vivo at 7T.

2. Materials and Methods

MRI acquisition

The sodium images were acquired on a 7T whole-body Siemens scanner (Siemens Medical Solution, Erlangen, Germany) using a single tuned quadrature birdcage RF coil (Rapid MR International, Columbus, OH, USA) of length 27 cm and inner diameter 21 cm, tuned to 78.6 MHz. The data was acquired with a 3D ultrashort TE (UTE) radial sequence [15] written with SequenceTree 4.2.2 [16] and compiled with the Siemens pulse development environment IDEA VB15A. For the inversion recovery preparation, two types of non-selective inversion pulses were added in the sequence and tested: a rectangular pulse of 1 ms duration and an adiabatic WURST (Wide-band Uniform Rate and Smooth Truncation) pulse [17] of duration 8 to 10 ms (depending on the experiments). The linear frequency sweep of the WURST pulse was optimized using simulations and experiments on phantoms. The sweep range covered 2 kHz for the in vivo experiments. The WURST pulse was chosen here for its large effective bandwidth and lower peak radiofrequency level than an equivalent adiabatic hyperbolic secant pulse. Three different images were acquired during each session: 3D radial, 3D radial with the rectangular inversion pulse (subsequently referred to the “IR RECT” experiment), 3D radial with the adiabatic WURST inversion pulse (“IR WURST” experiment).

The acquisition parameters were: number of projections N_proj = 10000, flip angle FA = 90° with a pulse duration of 0.5 ms, TE = 0.4 ms, TR = 100 ms, 128 points of acquisition for each radial projection, dwell time = 80 μs, field of view FOV = 200×200×200 mm³. Prior to data acquisition, 100 projections were acquired with FA = 0° for noise measurements, followed by 30 projections for reaching the steady state. The total acquisition time was 16:50 min. Note that the TE was calculated from the center of the 90° pulse to the beginning of the data acquisition, leaving a delay of 150 ρs between the end of the transmit pulse and the start of the signal reception, in order to protect the preamplifier in the coil.

Image reconstruction

Images were reconstructed offline using a combination of MATLAB (Mathworks, Natick, MA, USA) and FORTRAN code. The image (ρ(x)) was estimated by solving the linear system arising from the discretized imaging equation:

$$s({\mathbf{k}}_i)=\sum _p\rho ({\mathbf{x}}_p)e^{i{\mathbf{k}}_i\sigma {\mathbf{x}}_p},$$ (1)

where s(k) is the signal in k-space expressed as the Fourier transform of the image. Briefly, optimal density compensation weights were calculated according to the following formula [18]:

$$w_i=\frac{1}{{\sum }_j{\text{sinc}}^2({\mathbf{k}}_i-{\mathbf{k}}_j)},$$ (2)

and used as a diagonal pre-conditioner in an iterative least-squares algorithm similar to [19]. The Fast Sinc Squared Transform [20] and the Non-Uniform Fast Fourier Transform (NUFFT) [21, 22] algorithms were used to accelerate the computations.

The image ρ(x) can only be estimated up to a resolution determined by the Nyquist criterion [15]:

$$k_{\mathit{max}}=\sqrt{\frac{N_{\mathit{proj}}}{4\pi }}.$$ (3)

For 10,000 projections, k_max = 28, therefore, for a field of view of 200 mm, images can be reconstructed at ~ 3.6 mm isotropic Nyquist resolution. We chose to interpolate by a factor of 2 in each direction and output images of size (112 × 112 × 112) and nominal resolution ~ 1.8 mm.

Inversion pulse simulations

Magnetization inversion using the rectangular and adiabatic WURST pulses was simulated for sodium in the fluid state for different frequency offsets, using the relaxation times T₁ ~ 43 ms and $T_2^{\ast }\sim 20\text{ms}$ (values from measurements on Phosphate Buffer Solution or PBS). For fluid sodium, Bloch equations adequately represent the magnetization dynamics, since only rank one tensors are created during evolution. For cartilage sodium, the simulations were run as a first approximation with the Bloch equations with T₁ ~ 26 ms and the short component $T_{2s}^{\ast }\sim 5\text{ms}$ (or sodium with restricted motion) to study the effect of the pulse on the sodium short $T_2^{\ast }$ components. These T₁ and $T_{2s}^{\ast }$ values come from the measurements on human cartilage ex vivo. The relaxation times of different tissues are given in Table 1. All simulations were done using the Bloch equations in Matlab and using Brian Hargreaves’ Bloch Equation Simulator (Stanford University, Radiology Department, Stanford, CA, USA) [23].

Table 1.

Sodium relaxation times at 7T and parts of signal coming from the short and long ${\text{T}}_2^{\ast }$ components ( $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$) of sodium in gels and cartilage. The relaxation times were measured on a human knee cadaver, 1 PBS tube and 5 Agar gel tubes. The signal was taken in 4 ROIs over 4 slices and then averaged before fitting. The uncertainties are the average standard deviations obtained from the fitting algorithm.

	T1 (ms)	$T_{2s}^{\ast }(\text{ms})$	% of signal	$T_{2l}^{\ast }(\text{ms})$	% of signal
Gels Agar 4% (100 to 300 mM)	26.4 ± 3.3	2.9 ± 0.7	67 ± 10 %	13.1 ± 7.6	33 ± 10 %
PBS	43 ± 4	-	-	18.9 ± 6	100 %
Human cartilage (ex vivo)	26 ± 6	4.8 ± 0.2	45 ± 11 %	12 ± 2	55 ± 11%

The WURST pulse is characterized by a a linear frequency sweep ( $\frac{d\phi }{dt}=\lambda t$), and the phase changes accordingly as

$$\phi (t)=\frac{1}{2}\lambda t^2,$$ (4)

with the frequency sweep slope $\lambda =\frac{2\pi \mathrm{\Delta }f}{T_p}$, where T_p is the duration of the pulse and Δf is the frequency sweep (here Δf = 2 kHz), and the time 0 ≤ t ≤ T_p. The amplitude of the pulse is given by

$${\omega }_1(t)=2\pi {\nu }_1(1-{\mid sin(\beta )\mid }^n),$$ (5)

where $\beta =\frac{\pi }{2}\frac{2t-T_p}{T_p}$ so that $-\frac{\pi }{2}\le \beta \le \frac{\pi }{2}$, and v₁ is the amplitude of the pulse in Hz. In our experiments and simulations, the factor n was fixed and chosen to be 20 [17], which provides a smooth rise and fall of the pulse shape at the beginning and the end.

Phantom experiments

The effect of the inversion pulses was first tested on a liquid filled phantom (0.45% by weight aqueous NaCl). One tube filled with PBS (154 mM of NaCl) and 5 tubes filled with 4% Agar and NaCl concentrations of 100, 150, 200, 250 and 300 mM were placed within the FOV. These were later used in vivo as calibration phantoms for the sodium concentration map calculations. The inner diameter of the tubes was 20 mm for the PBS and 10 mm for the gels. The length of all the tubes was 70 mm.

Ex vivo experiments

In order to optimize the parameters of the pulses (duration, pulse power and frequency sweep for the adiabatic pulse) for best inversion while minimizing the SAR of the sequence calculated by the scanner, the IR RECT and IR WURST sequences were tested on a a human knee cadaver (female 63 years old, from Science Care, Phoenix, AZ, USA). The sodium T₁ and $T_2^{\ast }$ relaxation times of the calibration tubes and of cartilage were measured in order to take into account the relaxation in the sodium quantitation. All images were acquired with the PBS and calibration gels phantoms placed on top of the sample.

Relaxation time measurements

The sodium T₁ relaxation time was measured with a saturation recovery method with the 3D radial sequence for different TR: 30, 50, 70, 90, 110, 150 ms. The $T_2^{\ast }$ relaxation time was measured with the 3D radial sequence for different TE: 0.4, 0.8, 1.2, 1.6, 2, 3, 5, 8, 12, 18, 24, 30 ms. The average signal of the calibration tubes and of the cartilage was measured over 4 consecutive slices in regions of interest (ROI) selected at different locations in the image and the data was then fitted with a mono-exponential function for T₁ and bi-exponential function for $T_2^{\ast }$, giving a short component $T_{2s}^{\ast }$ and a long component $T_{2l}^{\ast }$. The results are summarized in Table 1.

In vivo experiments

Five healthy volunteers (1 female, 4 males) were scanned, with an average age of 26 ± 2.7 years. The study was approved by the institutional review board (IRB) and all the patients signed an informed consent form prior to the experiments.

Sodium maps

All images were acquired with the same calibration tube phantoms as for the ex vivo experiments that were placed on the kneecap and included in the FOV. Sodium quantitation was then calculated using linear regression in Matlab as follows: ROIs were drawn in 4 calibrations phantoms (150, 200, 250 and 300 mM NaCl) over 4 consecutive slices and their average signal intensities $I_{\mathit{measured}}^{\mathit{gels}}$ were corrected for T₁, $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$ of the gels according to the following equations:

For the sequence without IR,

$$I_{\mathit{corrected}}^{\mathit{gels}}=\frac{I_{\mathit{measured}}^{\mathit{gels}}}{\left(1-e^{-\frac{\text{TR}}{T_1}}\right)\pm \left(0.67\pm e^{-\frac{\text{TE}}{T_{2s}^{\ast }}}+0.33\pm e^{-\frac{\text{TE}}{T_{2l}^{\ast }}}\right)}\mathrm{..}$$ (6)

For the sequence with IR,

$$I_{\mathit{corrected}}^{\mathit{gels}}=\frac{I_{\mathit{measured}}^{\mathit{gels}}}{\left(1-{\alpha }_s{e}^{-\frac{\text{TI}}{T_1}}+e^{-\frac{\text{TR}}{T_1}}\right)\pm 0.67\pm e^{-\frac{\text{TE}}{T_{2s}^{\ast }}}+\left(1-{\alpha }_l{e}^{-\frac{\text{TI}}{T_1}}+e^{-\frac{\text{TR}}{T_1}}\right)\pm 0.33\pm e^{-\frac{\text{TE}}{T_{2l}^{\ast }}}},.$$ (7)

with α_s and α_l the inversion parameters, related respectively to $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$, that depend on the effect of the tissue relaxation times T₁ and $T_2^{\ast }$ during the inversion pulses. These α parameters were evaluated from the Bloch equation simulations of the inversion pulses by measuring the longitudinal magnetization M_z just after the inversion pulse (M_z = 1 before the pulse) with no frequency offset (ideal case of no static field inhomogeneities). For the Agar gels, we used α_s = 1.82 and α_l = 1.94 for IR RECT, α_s = 1.20 and α_l = 1.43 for IR WURST. For complete inversion, we should have α = α_s = α_l = 2 (M_z = −1 after inversion). The weighting factors (0.67 and 0.33) before the $T_2^{\ast }$ exponentials are given in Table 1 and calculated from the $T_2^{\ast }$ bi-exponential fittings. A linear regression curve of these corrected intensities $I_{\mathit{corrected}}^{\mathit{gels}}$ versus sodium concentrations was then calculated and used to extrapolate the sodium 3D maps of the whole sample.

For a better estimation of the sodium concentration in cartilage in vivo, after the regression curve calculation from the gel signals but before extrapolation of the images to sodium maps, the images were corrected for the T₁, $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$ of cartilage measured on the human knee cadaver, using the same equations as for the gels but with the α parameters for cartilage and weighting factors given in Table 1 (0.45 and 0.55 instead of 0.67 and 0.33, respectively). For the cartilage, we used α_s = 1.88 and α_l = 1.94 for IR RECT, α_s = 1.30 and α_l = 1.42 for IR WURST. Note that in the resulting maps the sodium concentrations in the calibration phantoms were therefore incorrect but the cartilage ones were more correctly assigned. As 75% of the volume in cartilage is extracellular and composed of water, and sodium ions are mainly present in this space, the sodium maps were divided by 0.75 in order to get the real sodium concentration [24, 25]. Less than 5% of the cartilage volume is composed of cells [26] and the intracellular sodium concentration, estimated around 5–10 mM, is considered negligible in the present study.

Fixed Charge Density (FCD)

Considering ideal Donnan equilibrium, the FCD can be calculated from sodium concentrations using the equation [12]:

$$\mathit{FCD}=\frac{{[{Na}^{+}]}_{\mathit{bath}}^2}{{[{Na}^{+}]}_{\mathit{tissue}}}-{[{Na}^{+}]}_{\mathit{tissue}},$$ (8)

where ${[{Na}^{+}]}_{\mathit{bath}}^2\sim 150\text{mM}$ is the sodium concentration in the bath (typically synovial fluid) and [Na⁺]_tissue is the sodium concentration in the tissue of interest. All processing was done in Matlab.

3. Results and discussion

Biexponential $T_2^{\ast }$ analysis

For the gels, the proportions for $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$ are 67% and 33% with a standard deviation of 10%, which is relatively close to the usual 60/40% proportions for biexponential T₂ relaxation. This 60/40% ratio corresponds to the T₂ relaxation in homogeneous samples with a dominant quadrupolar relaxation in the slow motion approximation. For cartilage, we measured the proportions to be 45% for $T_{2s}^{\ast }$ and 55% for $T_{2l}^{\ast }$, with a standard deviation of 11%. These values were measured on human cartilage ex vivo on a cadaver from a 63 year-old female. The cartilage is likely relatively degraded which can lead to some inaccuracies in the results. We also wish to point out that the appearance of residual quadrupolar couplings will further skew the ratio. This is at present an unsolved problem, which is the subject of further exploration.

Inversion pulse simulations

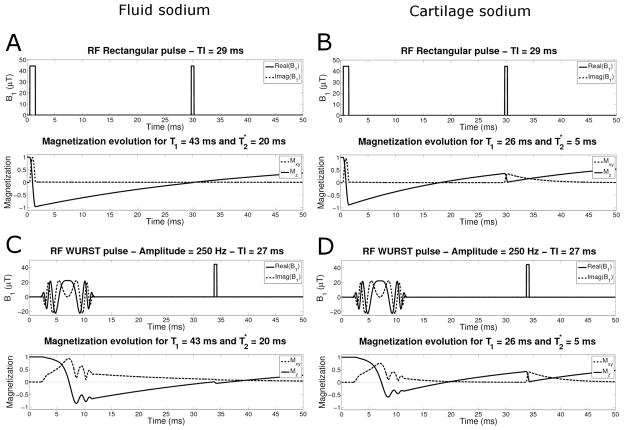
Figure 1A and 1C shows the simulation of the evolution of the longitudinal M_z and transverse M_xy magnetizations during the IR RECT and IR WURST pulse sequences for sodium ions in a fluid environment. The inversion time TI was optimized to 29 ms for IR RECT and 27 ms for IR WURST, and was chosen such as to minimize the M_xy just after the 90° pulse. Figures 1B and 1D show the simulation of the evolution of the longitudinal M_z and transverse M_xy magnetizations during the IR RECT and IR WURST pulse sequences for sodium ions with restricted motion (such as sodium in cartilage). The inversion times were kept the same as for the fluid suppression in Figure 1A and 1C. These simulations were used to estimate the signal suppression in an ideal uniform magnetic field B₀ by taking the difference between the transverse magnetization M_xy = 1 without IR and M_xy with IR (IR RECT and IR WURST), see Table 2. The WURST pulse had an amplitude of 250 Hz and a duration of 10 ms in all simulations. A fluid signal suppression of 99% is expected in the images acquired with the IR RECT sequence pulse and 92% with the IR WURST sequence. For the agar gels and cartilage, the suppressions are expected to be 65% with IR RECT, and 60% with IR WURST. The cartilage suppression is slightly stronger with IR RECT because of the short length of the pulse (1 ms) and short $T_2^{\ast }$ effects prevent the inversion of the bound sodium magnetization during the long WURST of 10 ms, which is better for our purpose as we only want to suppress the fluids.

Fig. 1.

RF pulse sequence and sodium magnetization evolution during the IR sequence. A and C: Fluid sodium (T₁ = 43 ms and ${\text{T}}_2^{\ast }=20\text{ms}$) with the rectangular pulse (with TI = 29 ms) and WURST pulse (with TI = 27) respectively. B and D: Cartilage sodium short component (T₁ = 26 ms and ${\text{T}}_2^{\ast }=5\text{ms}$) with the rectangular pulse and WURST pulse respectively, and the same TI as for fluid sodium.

Table 2.

Image signal loss when IR is applied with a rectangular and an adiabatic WURST pulse (in % of the signal of the image without IR). The inversion time TI was optimized to 29 ms for IR RECT and 27 ms for IR WURST for the simulations, and TI = 28 ms for IR RECT and 24 ms for IR WURST for the experiments (optimized on the fluid phantom).

Signal loss (%)	Simulation		Measured on liquid phantom		Measured ex vivo1		Measured in vivo2
Inversion pulse	Rect.	WURST	Rect.	WURST	Rect.	WURST	Rect.	WURST
PBS	99	92	78	88	73 ± 5	96 ± 2	76 ± 6	79 ± 9
Fluid (phantom)	99	92	87 ± 0.2	94 ± 0.7	-	-	-	-
Blood	-	-	-	-	-	-	73 ± 11	65 ± 11
Gels 4% Agar	65	60	39 ± 4	60 ± 15	53 ± 8	52 ± 10	62 ± 5	54 ± 6
Cartilage	65	60	-	-	23 ± 2	23 ± 2	43 ± 6	40 ± 10

¹Average of the values measured on hum an knee phantom. WURST pulse: 250 Hz, 10 ms.

²Average of the values measured on 5 volunteers. WURST pulse: 220 Hz, 8 ms.

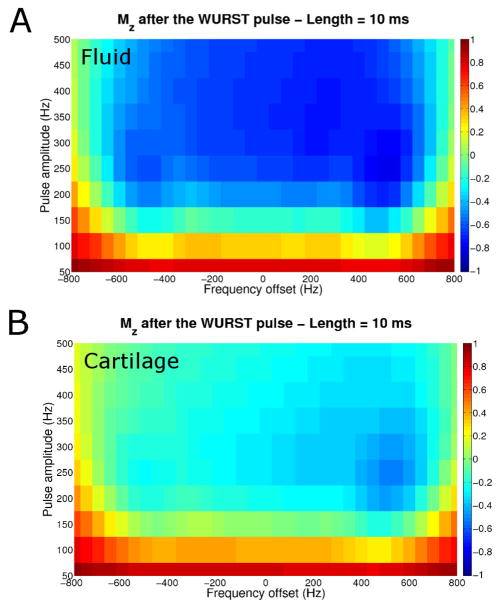
Figure 2 shows the effect of the WURST pulse on the longitudinal magnetization M_z of fluid sodium and cartilage sodium for different frequency offsets and different pulse amplitudes. It can be seen that for a good inversion of the fluid M_z over a frequency offset range of around 1.2 kHz, a WURST pulse of amplitude > 250 Hz and length 10 ms would be ideal, while the cartilage M_z is not completely inverted, leading to a more complete recovery before application of the 90° readout pulse.

Fig. 2.

M_z just after the 10 ms WURST pulse for different amplitudes and different frequency off sets. A: Fluid sodium (T₁ = 43 ms and ${\text{T}}_2^{\ast }=20\text{ms}$). B: Cartilage sodium short component (T₁ = 26 ms and ${\text{T}}_2^{\ast }=5\text{ms}$).

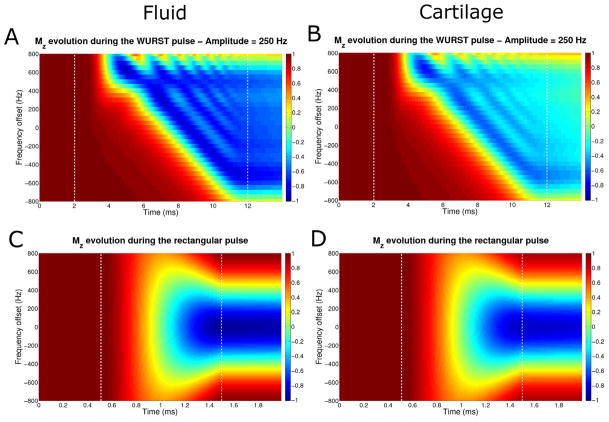
Figures 3A and 3B show the evolution of M_z (starting with M_z = 1) during an inversion WURST pulse with a fixed amplitude of 250 Hz and 10 ms duration for fluid sodium (T₁ = 43 ms and $T_2^{\ast }=20\text{ms}$) and for the short $T_2^{\ast }$ component of the cartilage sodium (T₁ = 26 ms and $T_2^{\ast }=5\text{ms}$) respectively, for different frequency offsets. The inversion is relatively uniform over a frequency offset of the sodium nuclei of approximately 1.2 kHz, but is incomplete for the cartilage.

Fig. 3.

Evolution of the longitudinal magnetization M_z during the WURST pulse of amplitude 250 Hz and length 10 ms (top row) and during the rectangular pulse of 1 ms length (bottom row) for different frequency offsets. A and C: Fluid sodium (T₁ = 43 ms and ${\text{T}}_2^{\ast }=20\text{ms}$). B and D: Cartilage sodium short component (T₁ = 26 ms and ${\text{T}}_2^{\ast }=5\text{ms}$). The pulse is applied between the white dash vertical lines.

Figures 3C and 3D show the evolution of M_z during a rectangular inversion pulse of 1 ms duration for fluid sodium and of the $T_{2s}^{\ast }$ component of cartilage respectively. The inversion is uniform over a smaller frequency offset range (approximately 400 Hz) than with the adiabatic pulse.

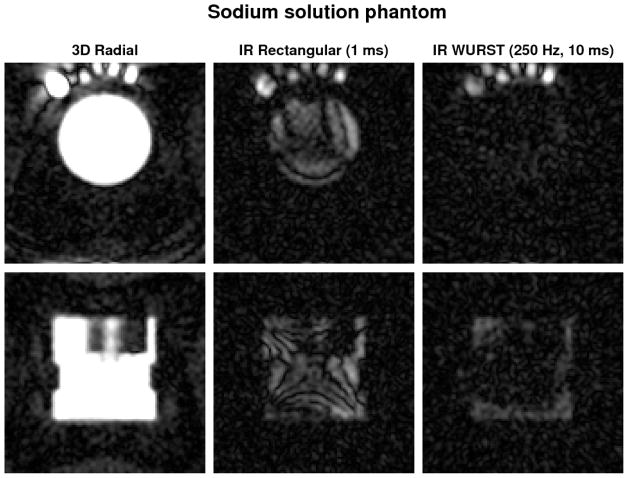
Phantom experiments

The inversion times were first optimized experimentally: TI = 28 ms for IR RECT and 24 ms for IR WURST, which are very close to the simulated ones (29 and 27 ms respectively). From Figure 4 we can see that fluid suppression from IR RECT is very non-uniform in the PBS sample in the left outer part of the FOV (top row images) and even in the uniform liquid sample in the middle of the FOV. IR with the WURST pulse (250 Hz, 10 ms) shows a more spatially uniform and more effective liquid suppression in the liquid-filled phantom and in the PBS sample. The numerical results can be seen in Table 2. The IR WURST gives very similar results as the simulation but the IR RECT exhibits a much less efficient suppression than expected, likely as a result of inhomogeneities.

Fig. 4.

Two different slices (first row: transverse, second row: coronal) of the images obtained without and with IR on a calibration phantom filled with a sodium solution. In the top images, the PBS tube is on the top left of the calibration phantom, and 5 gels tubes (100, 150, 200, 250, 300 mM of NaCl) are respectively placed on its right. The images are averaged over 2 slices for better visualization. The same range scaling is applied to all the images. The images on the first column (no IR) look therefore saturated in order to allow a better visualization of the low signal in the other images (with IR). Note the more uniform fluid suppression with the WURST inversion pulse than with the rectangular pulse in both the phantom solution (complete suppression) and the PBS (incomplete suppression).

Ex vivo experiments

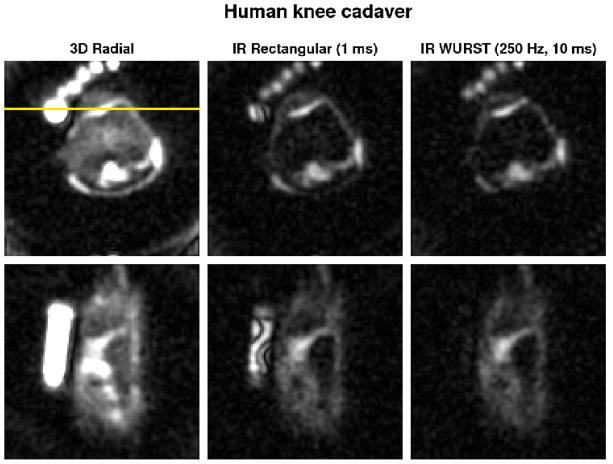
Figure 5 shows transverse and coronal sodium images obtained on the human knee cadaver. PBS suppression is not complete and not uniform with the IR RECT sequence as expected from the simulations. PBS suppression with IR WURST (250 Hz, 10 ms) is much more efficient and very uniform. Note the very non-uniform inversion of signal in the PBS tube on the left hand side of the coronal images (bottom row) for IR RECT compared to IR WURST. Numerical results are also shown in Table 2. In that case, IR WURST and IR RECT present similar results compared to the phantom experiments for PBS and gels, but both of them exhibit a very different signal suppression for the cartilage (only 23%). No satisfactory explanation has been found for the moment for this low signal suppression in cartilage ex vivo. We would expect that the cadaver tissue probably has very little fluid so almost all the sodium signal comes from cartilage in that case, and its magnetization is not inverted due to its short $T_2^{\ast }$, but from relaxation measurements we can see that 55% of the signal comes from the long $T_2^{\ast }$ component, which seems to contradict the previous statement. We can also note that the T₁ of the cadaver cartilage is very close to the Agar gel T₁ ~ 26 ms, which could confirm the fact that the cadaver tissue has little fluid (as fluid T₁ ~ 40 ms). This problem has no consequences for the conclusions of this present study, and in vivo measurements of the relaxation times are now under investigation so that we do not need to use the human knee cadaver data for future studies.

Fig. 5.

Transverse (top row) and coronal (bottom row) sodium MRI of the human knee ex vivo without and with IR (rectangular and WURST pulses). The images are averaged over 2 slices for better visualization. The same range scaling is applied to all the images. Human knee images were acquired with 10000 projections. The coronal slice was chosen to pass through the PBS tube in order to show the strong suppression inhomogeneities of the rectangular inversion pulse (horizontal yellow line). Note the uniform and complete fluid suppression with the WURST inversion pulse in the PBS tube and the very non-uniform fluid attenuation obtained with the rectangular pulse.

In vivo experiments

Due to SAR limitations during the in vivo experiments, it was impossible to apply a WURST pulse of 250 Hz and 10 ms while keeping the same total time of acquisition for all the experiments (16:50 min), therefore a WURST pulse of 220 Hz and 8 ms was applied, leading to a scanner-reported SAR in the range 90–99% depending on the volunteers. SAR is reduced by ~ 60% when going from a 250Hz/10 ms to a 220Hz/8 ms WURST pulse. For the IR RECT sequence with a 1 ms inversion pulse, SAR was also in the range 90–99%. Without IR, SAR was in the range of 35–40%. When asked after the experiments, none of the volunteers felt any RF heating in the knee area during the sequences applications.

From the in vivo experiments, as shown in Table 2, the suppression of the fluid sodium signal is smaller (76% and 79%, respectively for IR RECT and IR WURST) than expected from simulation. The signal loss in the cartilage was also smaller (43% for IR RECT and 40% for IR WURST) compared to simulations. This finding can be explained by the fact that tissues in vivo probably have different relaxation times from the ones used for the simulation (relaxation times measured on a knee cadaver). Furthermore, B₁ inhomogeneities for the rectangular pulse and the lower efficiency of the adiabatic pulse with lower power are additional causes of nonidealities.

Figure 6 shows a comparison of some transverse, coronal and sagittal images obtained on one volunteer where the IR WURST sequence was applied with a TR of 145 ms instead of 100 ms, thus allowing to use a WURST pulse of 240 Hz and 10 ms, with a SAR of 99%, but with a total acquisition time of 24:30 min. As expected, the PBS signal (transverse and sagittal images, top and bottom rows) and the artery signal (coronal images, middle row) are almost completely uniformly suppressed.

Fig. 6.

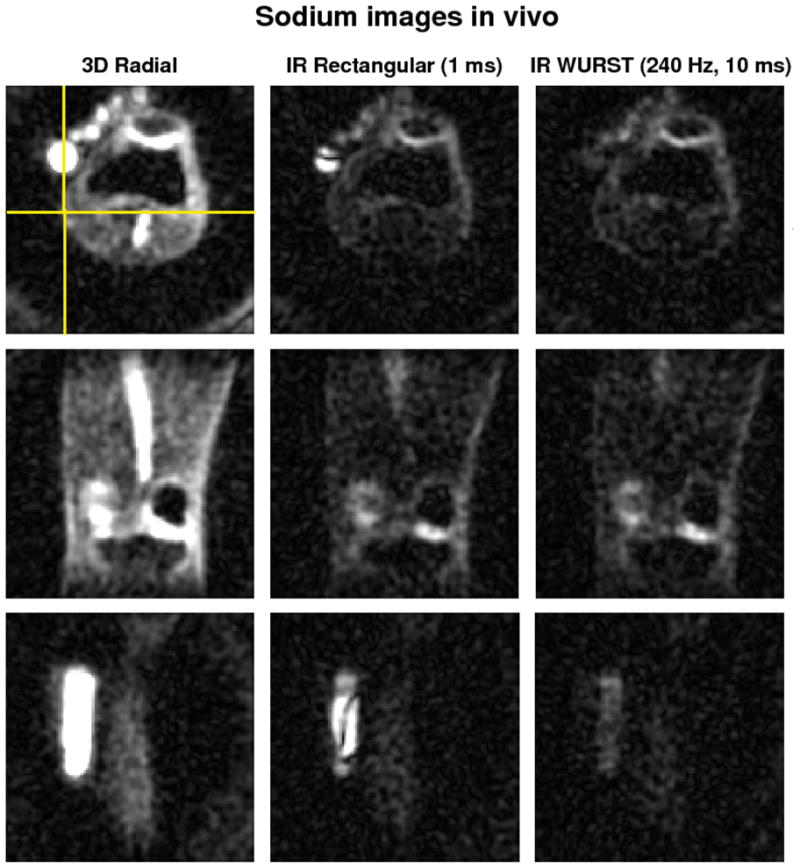
Transverse (top row), coronal (middle row) and sagittal (bottom row) sodium images of the knee joint of a volunteer at 7T. The total acquisition time of the 3D radial sequence without inversion and IR with rectangular pulse was 16:50 min. The WURST inversion pulse had an amplitude of 240 Hz and duration 10 ms, but due to SAR limitations, the TR was extended to 145 ms, leading to a total time of acquisition of the adiabatic IR sequence of 24:30 min. The images are averaged over 2 slices for better visualization. The same range scaling is applied to all the images. The coronal slice is represented by the horizontal yellow line drawn on the transverse image. The sagittal slice was chosen to pass through the PBS tube in order to show the strong suppression inhomogeneities of the rectangular inversion pulse (vertical yellow line). Note the uniform and complete fluid suppression with the WURST inversion pulse in the PBS tube and the very non-uniform fluid attenuation obtained with the rectangular pulse.

The IR RECT method could theoretically be improved by using a shorter rectangular pulse, increasing its power and bandwidth, but due to SAR limitations in vivo, the length of the pulse was limited to a minimum of 1 ms.

Sodium maps and FCD

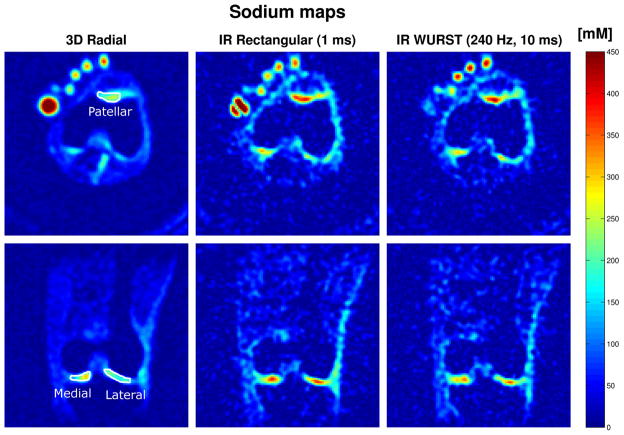
Figure 7 shows the sodium map calculated using the outlined procedures on transverse and coronal images without inversion, with IR RECT, and with IR WURST (240 Hz, 10 ms) corresponding to the data shown on Figure 6 (different slices). For sodium concentration measurements, ROIs were drawn over 4 consecutive slices for each volunteer in the regions indicated on the patella on the transverse images and in the femoro-tibial (FT) medial and lateral joint on the coronal images.

Fig. 7.

Transverse (top row) and coronal (bottom row) sodium maps of the knee joint of a volunteer at 7T. The sodium concentrations on all the volunteers were measured in ROIs as indicated on the images of the first row (patellar, FT medial and FT lateral cartilage). Sodium concentrations are given in mM (color bar). Data from the same volunteer as on Fig. 6. Note the uniform and almost complete fluid suppression with the WURST inversion pulse in the PBS tube and the very non-uniform fluid attenuation obtained with the rectangular pulse.

The results of average sodium concentrations of 5 patients and average FCD are shown in Table 3 for the 3 sequences (3D radial, IR RECT and IR WURST). For people in the range 30–40 years old, FCD is usually in the range (−150) – (−250) mM, and for people of age 60–70 years, the FCD ~ (−80) – (−200) mM, depending on the location [27, 10]. Sodium concentrations in healthy human cartilage are usually in the range of 240–300 mM [11, 8]. We can see that in all experiments, the mean patellar [Na⁺] is higher than the one in the FT medial region which is also higher than in the FT lateral region. For the 3D radial sequence without IR, the sodium concentrations and FCD calculated here seem in the lower range of typical values.

Table 3.

Average sodium concentrations and fixed charge densities (FCD) measured on 5 volunteers on the patellar, FT medial and FT lateral cartilage (FT stands for femoro-tibial, each measurement was averaged over 2 slices/volunteer). Results are given as average ± standard deviation.

Concentration (mM)	Patellar		FT Medial		FT Lateral
	[Na+]	FCD	[Na+]	FCD	[Na+]	FCD
3D Radial	254 ± 48	−165 ± 31	223 ± 36	−122 ± 19	196 ± 26	−81 ± 10
IR Rectangular pulse	383 ± 37	−324 ± 31	363 ± 52	−301 ± 43	355 ± 69	−291 ± 56
IR WURST pulse	351 ± 50	−286 ± 41	315 ± 22	−243 ± 17	296 ± 32	−220 ± 24

For IR RECT, [Na⁺] is always greater than 350 mM, giving high absolute values of the FCD which seem larger than typical values found in the literature. This result is likely due to the RF inhomogeneities of the rectangular inversion pulse leading to a non-uniform fluid suppression over the sample and the calibration phantoms, therefore the sodium quantification is biased. Note also the higher standard deviations of the results for IR RECT compared to IR WURST and 3D radial for FT medial and lateral cartilage.

For IR WURST, the [Na⁺] and absolute FCD are in the upper part of the range of “normal” values for FT cartilage and particularly high for patellar cartilage (but with a big variability in this latter case). This effect can also be due to residual RF inhomogeneities in the outer part of the FOV where the calibration tubes are located. Another possible reason may be an inaccuracy in the α inversion parameters in Eq. (7). These coefficients were initially estimated from the simulations based on the T₁ and $T_2^{\ast }$ values measured ex vivo on a human knee cadaver (of a 63 year-old female), where the cartilage was probably very degraded. These relaxation times are not very accurate for quantitation of sodium in vivo on healthy young volunteers of an average age of 26 years. The reliable measurement and study of ²³Na T₁ and $T_2^{\ast }$ parameters in vivo will lead to a great improvement for quantitation, but was not yet undertaken due to imaging time constraints.

Moreover, another limitation to this method is that the relaxation times in OA patients may be significantly different from the relaxation times in healthy volunteers, therefore the correction factors obtained from healthy volunteers may not be applicable for OA patients. From the Bloch simulations and the values given in Table 1, uncertainties of the correction factors used in equations (6) and (7) can be calculated using the standard error propagation method. The uncertainties in T₁, $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$ induce errors in α_s and α_l of approximately 5%, which in return generate uncertainties in the correction factors (and sodium quantification) of a maximum of 3%. The variations of the fractions of signal with $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$ are both approximately 10% and induce an error of the correction factor of the same order (10%). The $T_{2s}^{\ast }$ and $T_{2l}^{\ast }$ standard deviations cause an uncertainty of a maximum of 3% in the correction factors, for both gels and cartilage. The more sensitive parameter seems to be the T₁: the given variations in T₁, however, induce a variation of only 2% in the correction factor without IR, but provoke uncertainties for IR WURST of the order of 10% (gels) and 20% (cartilage), and even larger ones for IR RECT which are approximately 20% (gels) and 40% (cartilage). IR WURST hence is also the more robust sequence with respect to quantification based on independently-determined T₁ and $T_2^{\ast }$ values.

In vivo sodium relaxation times with and without IR at 7T are now under investigation in healthy and OA volunteers in order to quantify their variations with cartilage degradation.

4. Conclusion

This study demonstrates the feasibility of sodium MRI with uniform fluid suppression in articular cartilage in vivo at 7T within a reasonable image acquisition time (~24:30 min) for a 3D Nyquist resolution ~3.6 mm. It was shown that the fluid signal is uniformly suppressed by a simple inversion recovery sequence using an adiabatic wide-band WURST pulse. Although the application of adiabatic pulses may be limited by SAR considerations, we show here that suboptimal WURST pulses can still be be used for very efficient fluid suppression, while keeping the total acquisition time practical. The results with the adiabatic pulse were more reliable than the ones of the rectangular pulse IR sequence because of the robustness against B₀ and B₁ inhomogeneities. Due to the relatively poor resolution of ²³Na MRI, the use of fluid suppression is an important aspect of quantitative sodium MRI.

Optimization of the adiabatic IR sequence is now under investigation in order to decrease the RF power dissipation in the subject due to the inversion pulse by testing different other kinds of adiabatic pulses (hsec, chirp, BIR…) [28] or designing special pulses for fluid suppression with optimal control theory [29, 30]. The fluid suppressed sodium concentrations and FCD calculated from IR WURST are expected to be more sensitive to PG changes in patients with OA. The next step of this study is therefore a comparison of IR sodium MRI in controls and OA patients.