Why Copy Others? Insights from the Social Learning Strategies Tournament

Abstract

Social learning (learning through observation or interaction with other individuals) is widespread in nature and is central to the remarkable success of humanity, yet it remains unclear why it pays to copy, and how best to do so. To address these questions we organised a computer tournament in which entrants submitted strategies specifying how to use social learning and its asocial alternative (e.g. trial-and-error) to acquire adaptive behavior in a complex environment. Most current theory predicts the emergence of mixed strategies that rely on some combination of the two types of learning. In the tournament, however, strategies that relied heavily on social learning were found to be remarkably successful, even when asocial information was no more costly than social information. Social learning proved advantageous because individuals frequently demonstrated the highest-payoff behavior in their repertoire, inadvertently filtering information for copiers. The winning strategy (discountmachine) relied exclusively on social learning, and weighted information according to the time since acquisition.

Human culture is widely thought to underlie the extraordinary demographic success of our species, manifest in virtually every terrestrial habitat (1–2). Cultural processes facilitate the spread of adaptive knowledge, accumulated over generations, allowing individuals to acquire vital life skills. One of the foundations of culture is social learning – learning influenced by observation or interaction with other individuals (3) – which occurs widely, in various forms, across the animal kingdom (4). Yet it remains something of a mystery why it pays individuals to copy others, and how best to do this.

At first sight, social learning appears advantageous because it allows individuals to avoid the costs, in terms of effort and risk, of trial-and-error learning. However, social learning can also cost time and effort, and theoretical work reveals that it can be error prone, leading individuals to acquire inappropriate or outdated information in nonuniform and changing environments (5–11). Current theory suggests that to avoid these errors individuals should be selective in when and how they use social learning, so as to balance its advantages against the risks inherent in its indiscriminate use (9). Accordingly, natural selection is expected to have favoured social learning strategies, psychological mechanisms that specify when individuals copy, and from whom they learn (12–13).

These issues lie at the interface of multiple academic fields, spanning the sciences, social sciences and humanities, from artificial intelligence to zoology (5, 14–18). Formal theoretical analyses (e.g. 2, 5–9, 11–13, 19) and experimental studies (20–21) have explored a small number of plausible learning strategies. While insightful, this work has focussed on simple rules that can be studied with analytical methods, and can only explore a tiny subset of strategies. For a more authoritative understanding of when to acquire information from others, and how best to do so, the relative merits of a large number of alternative social learning strategies must be assessed. To address this, we organised a computer tournament in which strategies competed in a complex and changing simulation environment. €10,000 was offered as first prize. The organisation of similar tournaments by Robert Axelrod in the 1980s proved an extremely effective means for investigating the evolution of cooperation, and is widely credited with invigorating that field (22).

The tournament

The simulated environment for our tournament was a ‘multi-armed bandit’ (18), analogous to the ‘one-armed bandit’ slot machine but with multiple ‘arms’. In the tournament, the bandit had 100 arms, each representing a different behavior, and each with a distinct payoff drawn independently from an exponential distribution. Furthermore, we posited a temporally varying environment, realised by changing the payoffs with a probability, p_c, per behavior per simulation round, with new payoffs drawn from the same distribution. The possibility of acquiring outdated information is seen as a crucial weakness of social learning (e.g. 6).

Entered strategies had to specify how individual agents, in a finite population, choose between three possible moves in each round, namely INNOVATE, OBSERVE and EXPLOIT. INNOVATE represented asocial learning, that is individual learning stemming solely through direct interaction with the environment, for example, through trial-and-error. An INNOVATE move always returned accurate information about the payoff of a randomly selected behavior previously unknown to the agent. OBSERVE represented any form of social learning or copying through which an agent could acquire a behavior performed by another individual, whether by observation of or interaction with that individual (3). An OBSERVE move returned noisy information about the behavior and payoff currently being demonstrated in the population by one or more other agents playing EXPLOIT. Playing OBSERVE could return no behaviour if none were demonstrated, or if a behaviour that was already in the agent’s repertoire is observed, and always occurred with error, such that the wrong behaviour or wrong payoff could be acquired. The probabilities of these errors occurring, and the number of agents observed, were parameters we varied. Finally, EXPLOIT represented the performance of a behavior from the agent’s repertoire, equivalent to pulling one of the multi-armed bandit’s levers. Agents could only obtain a payoff by playing EXPLOIT.

Evolutionary dynamics were realised by a death-birth process (23). Agents died with a constant probability of 1/50 per round, and were replaced by the offspring of another agent. The probability that an agent was chosen to reproduce was proportional to its mean lifetime payoff, calculated as its summed payoff from playing EXPLOIT divided by the number of simulation rounds it had been alive. The obtained payoffs thus directly affected an agent’s fitness. Offspring inherited their parent’s strategy unless mutation occurred, in which case the offspring was given a strategy randomly chosen from the others playing in that simulation. We recorded the average frequency of each strategy in the population over the last 2,500 rounds of each 10,000 round simulation, and gave each strategy a ‘score’ that was the mean of these values over the simulations in which it participated.

Axelrod’s cooperation tournaments were based on a widely-accepted theoretical framework for the study of cooperation – the Prisoner’s Dilemma. While there is no such currently established framework for social learning research, multi-armed bandits have been widely deployed to study learning across biology, economics, artificial intelligence research and computer science (e.g. 18, 24, 25–28) because they mimic a common problem faced by individuals that must make decisions about how to allocate their time in order to maximize their payoffs. Multi-armed bandits capture the essence of many difficult problems in the real world, for instance, where there are many possible actions, only a few of which yield a high payoff, where it is possible to learn asocially or through observation of others, where copying error occurs and where the environment changes. When the payoffs of a multi-armed bandit change over time, as in our tournament, the bandit is termed ‘restless’, and the framework has the advantage of proving extremely difficult, perhaps impossible, to optimize analytically (e.g. 29). Thus we could be confident that our tournament would be a genuine challenge for all entrants.

In all other respects we attempted to keep the model structure as simple as possible to maintain breadth of applicability and ease of understanding, and attract the maximum number of participants. We balanced this simplicity with the inclusion of three features we considered critical, namely, individual memories (to facilitate learning), a degree of error associated with social learning (the existence of which nearly all the current literature agrees on), and replicator dynamics with mutation, to allow an evolutionary process. We used a common currency for costs – time – and made each possible move cost the same, to minimise structural assumptions about learning costs. The agents in our simulations could not identify or communicate directly with each other, an assumption that precluded the deployment of some model-based strategies present in the cultural evolution literature (e.g. prestige bias 30). Nonetheless, we reasoned that the simplicity, accessibility and generality of the proposed tournament structure outweighed the benefits of further complexity.

Results

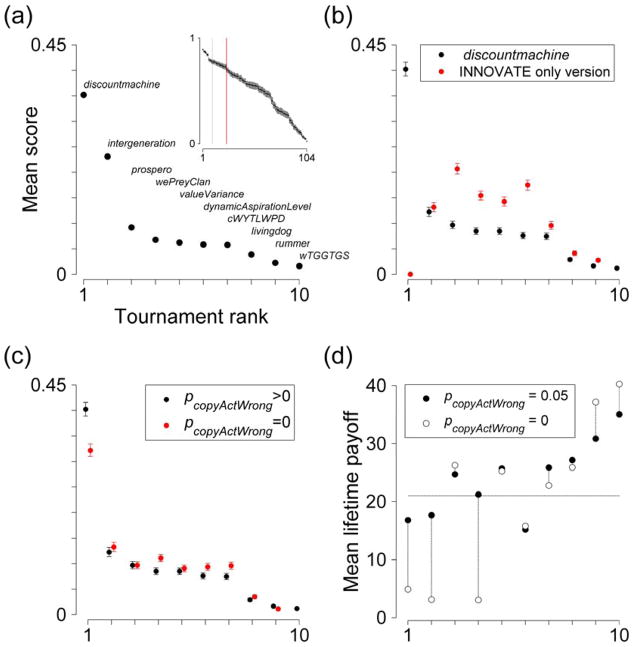
We received 104 entries, most, though not all (31), from academics across a wide range of disciplines, and from all over the world. The tournament was run in two stages. Strategies first competed in pairwise round-robin contests, taking turns to invade, or to resist invasion by, another strategy under a single set of conditions (32). The ten best performers progressed to a second stage, where all ten strategies competed simultaneously in melee contests over a range of simulation conditions (33). Scores in the first stage ranged from 0.02 to 0.89 (with a theoretical maximum of 1), indicating considerable variation in strategy effectiveness (Figure 1a).

Figure 1.

Performance of entered strategies. (a) Ranked overall strategy scores in the final stage of the tournament (cWYTLWPD = copyWhenYoungThenLearnWhen-PayoffsDrop and wTGGTGS = whenTheGoingGetsToughGetScrounging). Scores are averaged over all final stage simulations. Inset shows scores for all 104 entered strategies. Dotted black line indicates the ten highest scoring strategies; solid red line indicates the 24 strategies entered into further pair-wise conditions. (b) Ranked scores from those final stage simulations in which conditions were chosen at random (33), and under the same conditions but with the tournament winner, discountmachine, re-coded to learn only with INNOVATE and never OBSERVE (red). (c) As (b) but comparing original results with p_copyActWrong fixed at 0 (red). (d) Average individual fitness, measured as mean lifetime payoff, in populations containing only single strategies for each of the final stage contestants, ranked by tournament placing. Data are average values from the last quarter of single simulations, run under the same conditions as the first stage of the tournament, and also under the same conditions except with p_copyActWrong = 0. The horizontal dashed line represents the mean lifetime payoff of individuals when all strategies are played together under the same conditions. Strategies relying exclusively on social learning are those ranked 1, 2 and 4. Error bars are ± SEM, but mostly not visible as all SEMs<0.004.

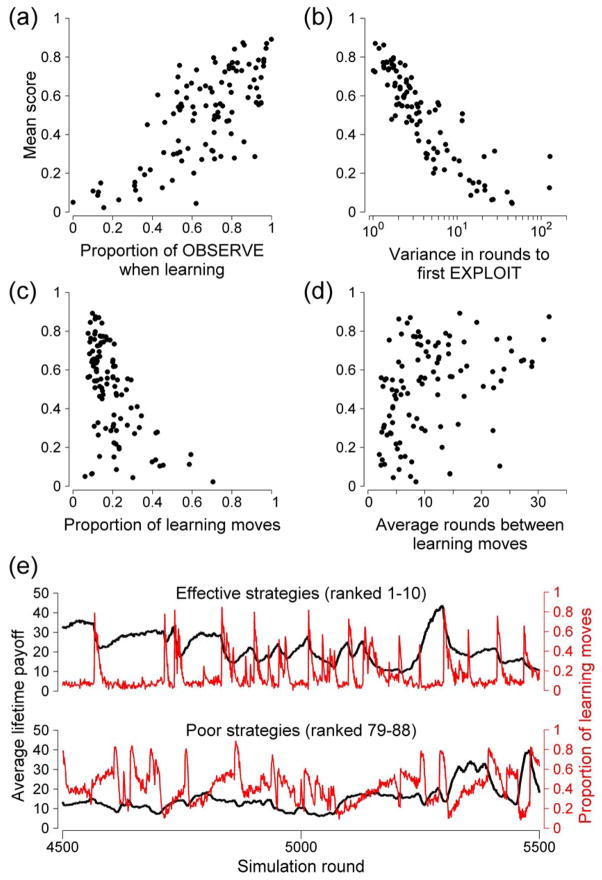
Statistical analysis indicates that much of this variation is explained by the extent to which strategies utilized social learning – more social learning being associated with higher payoffs. We examined the factors that made strategies successful using linear multiple regression and model selection using Akaike’s Information Criterion (AIC) (33). The best-fit model contained 5 predictors (Table 1). Two predictors had effect sizes more than twice the magnitude of the others – the proportion of those learning moves that were OBSERVE and the variance in the number of rounds before a strategy first played EXPLOIT. The proportion of learning moves dedicated to OBSERVE had a strong positive effect on a strategy’s score (Figure 2a). Even though INNOVATE cost no more than OBSERVE, the best strategies relied almost entirely on social learning, that is, when learning they almost exclusively chose OBSERVE rather than INNOVATE. The proportion of moves that involved learning of any kind had a negative effect, indicating that it was detrimental to invest too much time in learning, since payoffs came only through EXPLOIT. The data reveal a surprisingly low optimum proportion of time spent learning (Figure 2c).

Table 1.

Parameters of the AIC best-fit model predicting strategy scores in the first, pairwise, tournament stage. Adjusted R²=0.76.

Predictor	Effect size (β weight)	β	S.E.	t	p(>|t|)
(Intercept)	-	0.32	0.06	5.43	<0.0001
Proportion of learning that is OBSERVE	0.42	0.43	0.06	7.15	<0.0001
Variance in rounds to first EXPLOIT*	−0.42	−0.06	0.01	−6.62	<0.0001
Proportion of learning moves	−0.17	−0.34	0.12	−2.79	0.0063
Average rounds between learning moves	0.16	0.01	<0.01	3.09	0.0026
Estimate pc? (Y=1, N=0)	−0.07	−0.04	0.03	−1.47	0.1452

^*We used the natural log of this predictor to give a better linear relationship

Figure 2.

Key variables affecting strategy performance. (a) Final score plotted against the proportion of learning (i.e. INNOVATE or OBSERVE) moves that were OBSERVE in the first tournament stage. (b) Final score against the variance in the number of rounds before the first EXPLOIT. (c) Final score against the proportion of rounds spent learning in the first tournament stage. In both, each point represents the average value for one strategy. (d) Final score against the mean number of rounds between learning moves. (e) Time series plots of the per-round average individual mean lifetime payoff in the population and proportion of learning moves, from 1000 simulation rounds run under identical conditions with the final stage contestants (top panel) and the strategies ranked 79–88 in the first tournament stage (lower panel).

The timing of (either form of) learning also emerged as a crucial factor. Strategies with a high variance in the number of rounds spent learning before the agent first played EXPLOIT, caused by occasionally waiting too long before beginning to exploit, tended to do poorly (Figure 2b). Conversely, strategies that engaged in longer bouts of exploiting between learning moves tended to do significantly better (Figure 2d). Successful strategies were able to target their learning to coincide with periods when average population payoffs dropped, indicating a change in the environment that had rendered a behavior less profitable (Figure 2e). This pattern was observable statistically as the lagged correlation between the time series of average payoff and the proportion of learning moves in the population. We calculated Pearson correlation coefficients between the average payoff at simulation round t and the proportion of learning moves at round t + Δ, with 0 < Δ < 10,000. Accurate targeting of learning to periods where payoffs are dropping produces large negative correlation coefficients for small Δ. We compared the correlations for populations containing the ten strategies that progressed to the final stage with the correlations from simulations run with strategies ranked 78–88 in the first stage of the tournament (i.e. markedly less successful strategies). For the final stage strategies, the strongest negative correlations were always found with lags of less than 3 (Δ<3), and were significantly stronger than the strongest correlations found for the less successful strategies (2-sample t-test, p<0.0001; Figure S9). Successful strategies targeted learning to periods when it was likely to be most valuable (i.e. when the environment changed) but otherwise minimised learning, allowing them both to improve their payoffs through learning, and to maintain high rates of exploiting (Table 1). The issue of when to break off exploiting current knowledge in order to invest in further knowledge gain – the exploitation/exploration trade-off – had not been incorporated into previous theory in this field, and our tournament introduces this new dimension into the domain of understanding social learning.

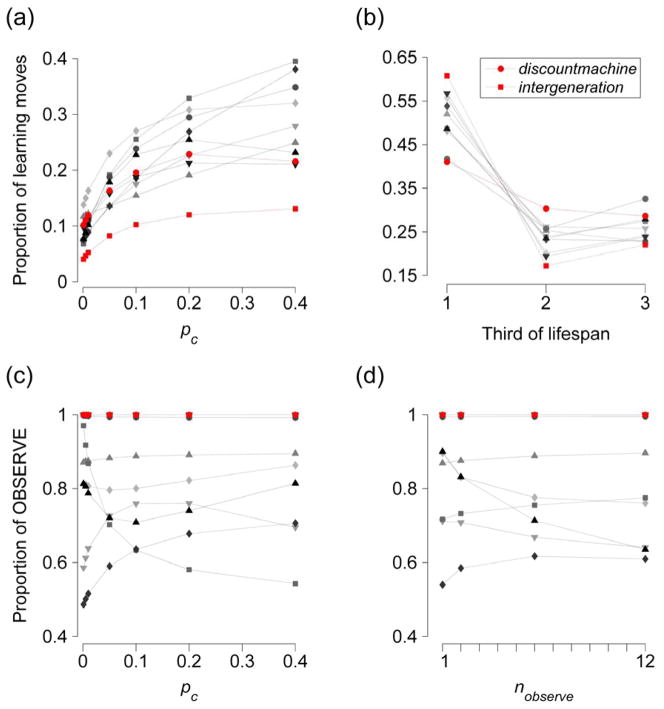
The strategy discountmachine (34) emerged as a convincing winner (Figure 1a) in the second stage of the tournament, which pitted the ten best performers in the first stage against each other in simultaneous competition under a range of conditions (it was also the winner of the pairwise phase). Strikingly, both discountmachine and the runner-up, intergeneration, relied virtually exclusively on OBSERVE as their means to learn (Figure 3c–d), and at least 50% of the learning of all of the second stage strategies was OBSERVE. Although all second stage strategies increased their amount of learning as the rate of environmental change increased, the best performers capped the level of learning to a maximum to maintain payoffs (Figure 3a). The winning strategy stood out by spreading learning more evenly across agent lifespans than any other second stage strategy (Figure 3b). It did this by, uniquely among the finalists, using a proxy of geometric discounting to estimate expected future payoffs from either learning or playing EXPLOIT.

Figure 3.

Why the winner won. (a) Proportion and (b) timing of learning moves in the final tournament stage. First and second place strategies are highlighted; the rank of the other strategies is indicated by shading, with darker shading indicating higher rank. (c–d) Variation in the proportion of learning moves that were OBSERVE with (c) variation in the rate of environmental change (p_c) and (d) the number of agents sampled when playing OBSERVE (n_observe), in the final tournament stage. Error bars are ± SEM, but mostly not visible as all SEMs<0.003.

Winning strategies also relied more heavily on recently acquired than older information. The top two strategies shared the following expression for estimating the expected payoff (w_expected) of a known behavior:

$$w_{\mathit{exp}}=w{(1-p_{\mathit{est}})}^i+{\overline{w}}_{\mathit{est}}(1-{(1-p_{\mathit{est}})}^i),$$ (1)

where w is the current payoff held in the agent’s memory and acquired i rounds ago, w̄ _est is the estimated mean payoff for all behavior, and p_est is an estimate of p_c, the probability of payoff change. This expression weights expected payoffs increasingly towards an estimated mean as the time since information was last obtained increases. Given the uncertain and potentially conflicting nature of information obtained through social learning, the winning strategy used a further weighting based on its estimate of p_c, discounting older social information more severely in more variable environments than in relatively constant ones. No other strategies in the melee round evaluated payoffs in this way.

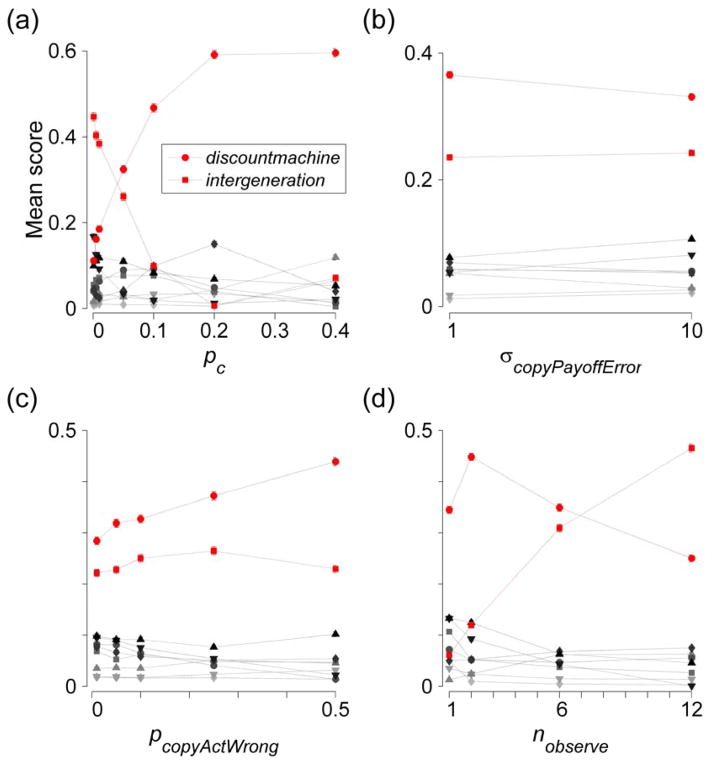
In the melee round, simulations were run to explore the effects of varying the rate of environmental change (p_c), the probability and scale of errors associated with social learning, and the relative costs of the two forms of learning, the last achieved by increasing the number of other agents sampled when playing OBSERVE (social learning being cheap when multiple individuals are observed). We found the tournament results to be unexpectedly robust to variation in these factors (Figure 4). The first and second place strategies switched rank in some conditions, namely when the environment was more stable (Figure 4a) and when social learning was cheap relative to asocial learning (i.e. the number of agents sampled by OBSERVE was high; Figure 4d). Increasing the probability and magnitude of the errors associated with social learning made virtually no difference to the strategy rankings (Figure 4b–c); even at extreme values, strategies heavily reliant on social learning thrived (Figure S11). This implies that social learning is of widespread utility even when it provides no information about payoffs. Nor does this utility rest on our assumption that copying errors can introduce new behaviors (Figure S13). These are surprising results, given that the error-prone nature of social learning is widely thought to be a weakness of this form of learning, whilst the ability to copy multiple models rapidly or preferentially copy high-payoff behavior are regarded as strengths (1). Strategies relying heavily on social learning did best irrespective of the number of individuals sampled by OBSERVE (Figure 4d). These findings are particularly striking in the light of previous theoretical analyses (5–8, 10–11, 13), virtually all of which have posited some structural cost to asocial learning and errors in social learning.

Figure 4.

Social learning dominates irrespective of cost across a broad range of conditions. Plots show mean strategy scores (± variance) across systematic melee conditions with respect to (a) variation in the rate of environmental change (p_c), (b) σ_{copyPayoffError}, the standard deviation of a normally distributed error applied to payoffs returned by OBSERVE, (c) p_copyActWrong, the probability that OBSERVE returned a behaviour selected, at random from those not actually observed, and (d) the number of other agents sampled when playing OBSERVE (n_observe). First and second place strategies are highlighted; the rank of the other strategies is indicated by shading with darker shading indicating higher rank. Error bars are ± SEM, but mostly not visible as all SEMs<0.01.

Previous theory also suggests that reliance on social learning should not necessarily raise the average fitness of individuals in a population (6–7, 10), and may even depress it (35). However, this was not the case for the strategies successful enough to make the second stage; in this second round average individual fitness in mixed-strategy populations was positively correlated with the proportion of learning in the population that was social (r = 0.16, p = 0.02; Figure S9). In contrast, for poorly performing strategies the relationship between average individual fitness and the rate of social learning was strongly negative (r = −0.71, p < 0.001; Figure S9). This highlights the importance of the strategic use of social learning in raising the average fitness in a population (5, 12, 19).

Strategies that did well were not, however, those that maximized average individual fitness when fixed in a population. Instead, we found a strong inverse relationship between the mean fitness of individuals in populations containing only one strategy and that strategy’s performance in the tournament (Figure 1d). Furthermore, the mean lifetime payoff in the population when all strategies competed together under the same conditions was lower than the levels achieved by lower ranking strategies when playing alone. This illustrates the parasitic effect of strategies that rely heavily on OBSERVE (e.g. discountmachine, intergeneration, wePreyClan and dynamicAspirationLevel, ranked 1, 2, 4 and 6, all played OBSERVE on at least 95% of learning moves). From this we can conclude that strategies using a mixture of social and asocial learning are vulnerable to invasion by those using social learning alone, which may result in a population with lower mean fitness. An established rule in ecology specifies that, among competitors for a resource, the dominant competitor will be the species that can persist at the lowest resource level (36). Recent theory suggests an equivalent rule may apply when alternative social learning strategies compete in a population: the strategy that eventually dominates will be the one that can persist with the lowest frequency of asocial learning (13). Our findings are consistent with this hypothesis.

Discussion

The most significant outcome of the tournament is the remarkable success of strategies that rely heavily on copying when learning, in spite of the absence of a structural cost to asocial learning, an observation evocative of human culture. This outcome was not anticipated by the tournament organisers, nor by the committee of experts established to oversee the tournament, nor, judging by the high variance in reliance on social learning (Figure 2a), by most of the tournament entrants. While the outcome is in some respects consistent with models that used simpler environmental conditions and in which individual learning is inherently costly relative to social learning (5), in our tournament the environment was complex and there was no inherent fitness cost to asocial learning. Indeed, there turned out to be a considerable cost to social learning, as it failed to introduce new behaviour into an agent’s repertoire in 53% of all the OBSERVE moves in the first tournament phase, overwhelmingly because agents observed behaviors they already knew. Nonetheless, social learning proved advantageous because other agents were rational in demonstrating the behavior in their repertoire with the highest payoff, thereby making adaptive information available for others to copy. This is confirmed by modified simulations wherein social learners could not benefit from this filtering process, in which social learning performed poorly (Figure S12). Under any random payoff distribution, if one observes an agent using the best of several behaviors that it knows about, then the expected payoff of this behavior is much higher than the average payoff of all behaviors, which is the expected return for innovating. Previous theory has proposed that individuals should critically evaluate which form of learning to adopt in order to ensure that social learning is only used adaptively (11), but a conclusion from our tournament is that this may not be necessary. Provided the copied individuals themselves have selected the best behavior to perform from at least two possible options, social learning will be adaptive. We suspect that this is the reason why copying is widespread in the animal kingdom.

That social learning was critical to the success of the winning strategy is shown by the results of running the random conditions portion of the second tournament stage with a version of discountmachine recoded to learn only by INNOVATE – it came last (Figure 1b). We also found that discountmachine dominated its recoded cousin across a large portion of the plausible parameters space with respect to environmental change (Figure 5), with payoffs needing to change with 50% probability per round before the INNOVATE-only version could gain a foothold. This is another way that our tournament challenges existing theory, which predicts that evolution will inevitably lead to a stable equilibrium where both social and asocial learning persist in a population (e.g. 6).

Figure 5.

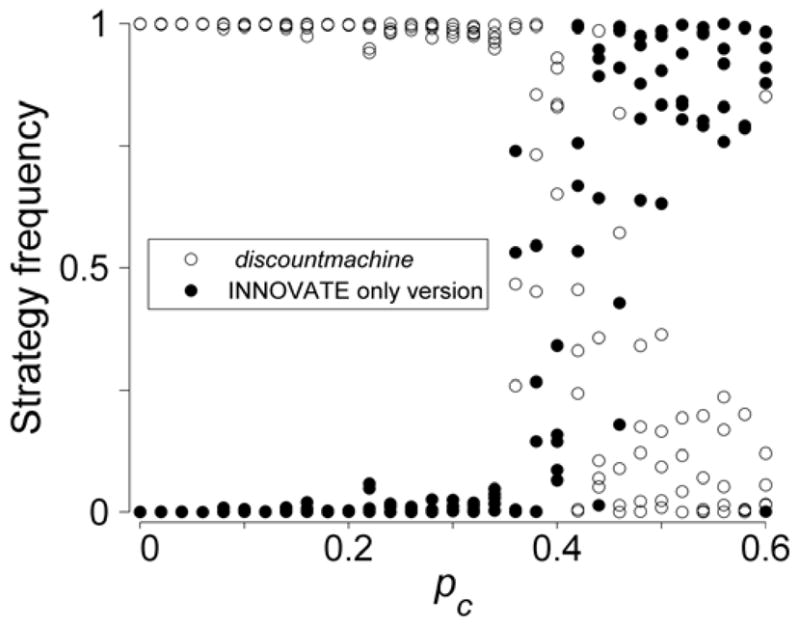
Results of a series of simulations in which the tournament winner played against a version of itself altered to learn only by INNOVATE. The rate of environmental change (p_c) was systematically varied. Five simulations were run at each level of p_c. Other parameters were fixed at n_observe=1, p_copyActWrong=0.05, and σ_payoffError=1.

It is important to note that, while our tournament may offer greater realism than past analytical theory, the simulation framework remains a simplification of the real world where, for instance, model-based biases and direct interactions between individuals (15) operate. It remains to be established to what extent our results will hold if these are introduced in future tournaments, where the specific strategies that prospered here may not do so well. Nonetheless, the basic generality of the multi-armed bandit problem we posed lends confidence that the insights derived from the tournament may be quite general.

The tournament also draws attention to the significance of social learning errors as a source of adaptive behavioral diversity. In our tournament, there was a probability, p_copyActWrong, that a social learner acquired a randomly selected behavior rather than the observed behavior. Modelling social learning errors in this way means new behavior can enter the population without explicit innovation. The importance of these errors is illustrated by the fact that strategies relying exclusively on social learning were unable to maintain high individual fitness when p_copyActWrong = 0 (Figure 1d). This does not mean that the success of the winning strategy depended on the condition p_copyActWrong > 0 – in the presence of other strategies providing the necessary innovations, discountmachine and intergeneration maintain their respective first and second places when p_copyActWrong = 0 (Figure 1c). Other models have highlighted copying errors as potentially important in human cultural evolution (37), but the extent to which adaptive innovations actually come about through such errors is an important empirical question ripe for investigation.

The ability to evaluate current information based on its age, and to judge how valuable that information might be in the future, given knowledge of rates of environmental change, is also highlighted by the tournament. There is limited empirical evidence that animals are able to discount information based on the time since it was acquired (38), but little doubt that humans are capable of such computation. Our tournament suggests that the adaptive use of social learning could be critically linked to such cognitive abilities. There are obvious parallels with the largely open question of mental time-travel, the ability to project current conditions into the future, in non-humans (39), raising the hypothesis that this cognitive ability could be one factor behind the gulf between human culture and any non-human counterpart. A critical next step will be to evaluate experimentally to what extent human behaviour mirrors that of the tournament strategies (e.g. 40). By drawing attention to the importance of adaptive filtering by the copied individual and temporal discounting by the copier, the tournament helps to explain both why social learning is common in nature and why human beings happen to be so good at it.