Determination of Cross Sections by Overtone Mobility Spectrometry: Evidence for Loss of Unstable Structures at Higher Overtones

Abstract

Overtone mobility spectrometry (OMS) is examined as a means of determining the collision cross sections for multiply-charged ubiquitin and substance P ions, as well as for singly-charged rafinose and melezitose ions. Overall, values of collision cross section measured by OMS for stable ion conformations are found to be in agreement with values determined by conventional ion mobility spectrometry (IMS) measurements to within ~1%, relative uncertainty. The OMS spectra for ubiquitin ions appear to favor different conformations at higher overtones. We propose that the changes in the distributions as a function of the overtone region in which they are measured arise from the elimination of ions that undergo structural transitions in the drift regions. Kinetics simulations suggest that structural transitions occurring on the order of a few ms and resulting in a ~4% change in ion collision cross sections are detected by OMS measurements. The unique method of distinguishing ion mobilities with OMS reveals these structural transitions which are not readily apparent from traditional IMS measurements.

Introduction

Overtone mobility spectrometry (OMS)^1,2 is a gas-phase separation method that filters ions according to differences in mobilities through an inert buffer gas. Selection is achieved by applying time-dependent fields to drift tube segments creating periodic ion elimination regions. Ions with mobilities that are resonant with the field application frequency pass through these regions and are transmitted to the detector. Measurement of ion intensity as field application frequency is scanned generates the OMS spectrum. While the method is very similar to IMS, there are some interesting differences. First, because transmission is based on the drift field application frequency, no initial pulse is required to initiate experiments. Instead the beam emerges as pulses of ions that remained stable throughout the drift region. Additionally, because the approach is based on the elimination of ions, the OMS resolving power (R_OMS) scales with the number of drift regions. Thus, whereas the resolving power for IMS (R_IMS) is proportional to the square root of the drift tube length, theory and experiments show that OMS resolving power scales in a roughly linear fashion with length.^1,2

Because OMS measurements are carried out using weak, uniform fields and the basis of ion selection is mobility matching with the field application frequency, ions of specific cross sections can be transmitted by fixing the frequency of the applied drift field. The relationship of the ion cross section to the drift field frequency is given by²

$$\mathrm{\Omega }=\frac{{(18\pi )}^{1/2}}{16}\frac{ze}{{(k_{b}T)}^{1/2}}{\left[\frac{1}{m_I}+\frac{1}{m_B}\right]}^{1/2}\frac{E[\phi (h-1)+1]}{f(l_t+l_e)}\frac{760}{P}\frac{T}{273.2}\frac{1}{N}.$$ (1)

In Equation 1, k_b, z, e, N, T, and P correspond to Boltzmann’s constant, the ion’s charge, the charge of an electron, the neutral number density, and the temperature and pressure of the buffer gas, respectively. The parameters E, m_I, and m_B represent the electric field and the masses of the ion and buffer gas, respectively. Other variables include the OMS parameters field application frequency (f), operational phase (φ), harmonic index (h), and ion transmission (l_t) and elemination (l_e) region lengths. For comparisons of features in OMS (and IMS) datasets (especially when values of z, and m are not known), it is useful to report reduced mobilities (K₀) using the relationship shown in Equation 2.

$$K_0=\frac{f(l_t+l_e)}{E[\phi (h-1)+1]}\frac{P}{760}\frac{273.2}{T}$$ (2)

From an understanding of how OMS and IMS measurements are carried out, one predicts that the distributions that are measured may show different features. For example, if an ion undergoes structural transitions as it migrates through a drift tube, the IMS approach would record the average drift time associated with all structures that were sampled during the time in the drift tube. On the other hand, if ions change structure during an OMS experiment, the new structure may not be mobility matched with the field frequency. Thus we expect new structures, having non-resonant mobilities, to be eliminated. Here, we investigate the ability of OMS measurements to provide reliable structural information as ion collision cross sections. Overall good agreement between OMS and IMS measurements is observed. However, examination of OMS spectra reveals that some features in OMS distributions are not observed in higher frequency spectral regions. It appears that the loss of these ions arises because structural transitions lead to a mismatch in mobility and field application frequency. Simulations suggest that such structural transitions occur on the ms timescale supporting results obtained from earlier studies of protein ions.^3–5

Since the introduction of electrospray ionization (ESI)⁶, a number of experiments designed to study macromolecular ion structures have been presented.^7–28 There is substantial interest in understanding transitions between conformational states. The development of a technique that allows transmission of stable structures would be useful as a means of purifying ions prior to other spectroscopic studies. Other analytical techniques that provide a means of ion filtering based on their mobilities include field assymetric ion mobility spectrometry (FAIMS)^29–32 and differential mobility analysis^33–37. An advantage of the OMS approach is that accurate collision cross sections can be obtained directly from the measurement. Additionally, an understanding of transitions between states, and development of methods that allow unstable states to be eliminated will be valuable in the development of higher resolution mobility measurements.

Experimental Methods

Overview

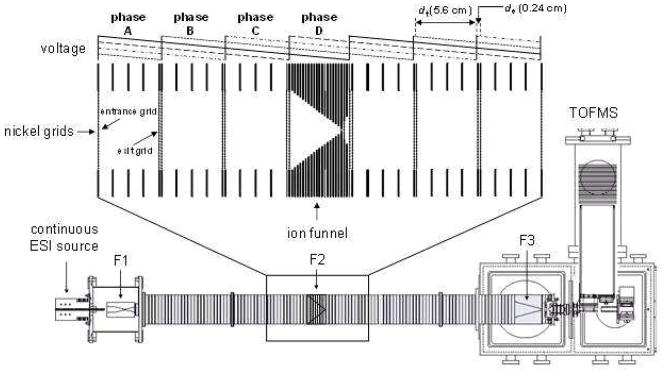
Detailed descriptions of IMS theory,^38–42 instrumentation,^43–48 and techniques^26,49–51 are described elsewhere. Additionally, details regarding the OMS method and instrument as well as the general theory behind OMS measurements have been reported.^1,2 Here only brief description of the OMS instrument and its operational mode used for these studies is given. Figure 1 shows a schematic diagram of the experimental apparatus. The OMS instrument includes an ESI source, a drift tube, ion focusing elements, and a time-of-flight (TOF) mass spectrometer. Direct infusion of the analyte solution through a pulled-tip capillary maintained at 2200 V relative to the ESI source entrance generates the protonated ions. Ions are focused into a drift tube through an ion funnel (F1) interface.^52,53 Ions are then transmitted through a portion of the drift tube under the influence of a uniform electric field (9 V·cm⁻¹) maintained at a pressure of ~2.95 Torr of 300 K He buffer gas. Ions exiting the OMS region drift through the rest of the drift tube and are extracted into the TOF instrument for mass analysis.

Figure 1.

Schematic diagram of the OMS-TOF instrument used to measure the collision cross section distributions. The drift tube assembly consists of three ion funnels (F1 to F3) and multiple segmented drift regions (22 sections). The segmented regions are divided by lenses containing nickel mesh grids. Each section is operated using an electric field of 9 V·cm⁻¹ (ion transmission region, 5.6 cm). Periodic repulsive fields of 963 V·cm⁻¹ are created between specific sets of grids (d_e regions, 0.24 cm). The four-phase system applied in these studies utilizes four distinct drift field settings (phases A, B, C, and D). These fields are modulated at different frequencies to allow the ions with appropriate mobilities to move through the drift tube.

OMS-MS instrumentation: general aspects of OMS

The OMS drift region is comprised of 22 segments (see insert in Figure 1) divided by nickel grids (90% transmittance, Buckbee-Mears, St. Paul, MN). Each segmented region contains both an ion transmission (d_t) and an ion elimination region (d_e). A sawtooth potential gradient is applied to multiple adjoining segmented regions and is modulated between a number of different settings. This generates a uniform DC field (9 V·cm⁻¹) across the coupled d_t (5.6-cm long) regions as well as a repulsive field (963 V·cm⁻¹) in multiple interfacing d_e (0.24 cm long) regions (see Figure 1). Field modulation causes the repulsive field to shift between alternate d_e regions. Ions with mobilities that do not match the field application frequency eventually locate in one of these d_e regions during transmission, and are neutralized on the wire mesh. Ions with mobilities that are in resonance with the field application frequency are transmitted through the drift tube. Scanning this field application frequency over a relevant range generates a complete OMS distribution.

OMS-MS instrumentation: drift fields setting in the segmented drift tube

The designated phase (φ, the number of distinct field settings) of the OMS instrument defines the mode of operation.^1,2 For these experiments, fields are created across four contiguous drift tube segments (Figure 1) and are modulated between four different field settings. This mode of operation is identified as a four-phase (φ = 4) system. The field application frequency coinciding with ions of resonant mobilities is termed their fundamental frequency (f_f).^1,2 The d region (d_t + d_e) residence times (and thus the mobilities) of the ions can be determined from OMS spectra. For example, a dataset feature with a f_f of 2000 Hz would require 500 μs to traverse a single d region. At this frequency, the phase A field (see Figure 1) is activated for a period of 500 μs; phase B, C, and D are turned off for the same time. After 500 μs, phase A is turned off and phase B is activated; phases C and D remain unchanged. The field setting shifts from one phase to another every 500 μs (e.g., A → B → C → D → A → …, see Figure 1).

A feature of the OMS system is the observation that transmission of ions is possible at overtone frequencies (f_m) that are exact multiples of the f_f (i.e., f_m = m · f_f, where m is the harmonic frequency number).^1,2 Values of m are defined as φ(h − 1) + 1, where h is a positive number termed the OMS harmonic index. For a four-phase system, OMS distribution peaks for a given ion conformation appear at 5·f_f, 9·f_f, 13·f_f, … frequencies.

OMS resolving power

The resolving power of OMS (R_OMS) is given by²

$$R_{\mathit{OMS}}=\frac{1}{1-\left[1-\frac{C_2}{R_{\mathit{IMS}}}\right]\left[\frac{mn-\left[\phi -1-\frac{l_e}{l_t+l_e}\right]}{mn}\right]},$$ (3)

where n and C₂ correspond with the number of segmented d regions and a correction factor allowing for the relating of R_OMS to the R_IMS, respectively.² While the equation is a little complicated, it does indicate the R_OMS scales in a nearly linear fashion with the number of drift segments as well as the overtone number.

Experimental collision cross sections

Cross sections from IMS measurements are obtained using³⁹

$$\mathrm{\Omega }=\frac{{(18\pi )}^{1/2}}{16}\frac{ze}{{(k_{b}T)}^{1/2}}{\left[\frac{1}{m_I}+\frac{1}{m_B}\right]}^{1/2}\frac{t_{D}E}{L}\frac{760}{P}\frac{T}{273.2}\frac{1}{N},$$ (4)

where t_D and L correspond to the ion’s drift time and the drift tube length, respectively. The ability to determine accurate collision cross sections is governed by how well each parameter is measured experimentally. Because experimental parameters such as buffer gas pressure and temperature and drift field can be precisely controlled, collision cross section measurements of well-characterized systems usually show agreement to within 2% relative uncertainty.⁵⁰ For OMS measurements, field application frequencies are highly tunable and thus comparable levels of precision are achieved.

Sample preparation

Bovine ubiquitin (90% purity, 76 amino acid residues, M_r = 8.6 kDa) was purchased from Sigma (St. Louis, MO) and used without further purification. Multiply charged ubiquitin ions were generated by electrospraying a 2.3 X 10⁻⁵ M protein solution dissolved in 49:49:2 (% vol) water: methanol: acetic acid. The sample solution was infused through a pulled capillary (75 μm i.d., 360 μm o.d.) tip at a flow rate of 0.3 μL·min⁻¹ using a syringe pump (KD Scientific, Holliston, MA). A peptide solution (49:49:2% vol., water: methanol: acetic acid) of 1.5 X 10⁻⁴ M substance P (98% purity, Sigma) was electrosprayed using identical conditions. Finally, melezitose (99% purity) and raffinose (98% purity) were purchased from Sigma (St. Louis, MO) and used without further purification. Oligosaccharide solutions (5.0 X 10⁻⁴ M in 50:50% vol., water: acetonitrile and 2 mM sodium chloride) were infused through the capillary tip using similar flow rates.

Results and Discussion

OMS distributions for ubiquitin

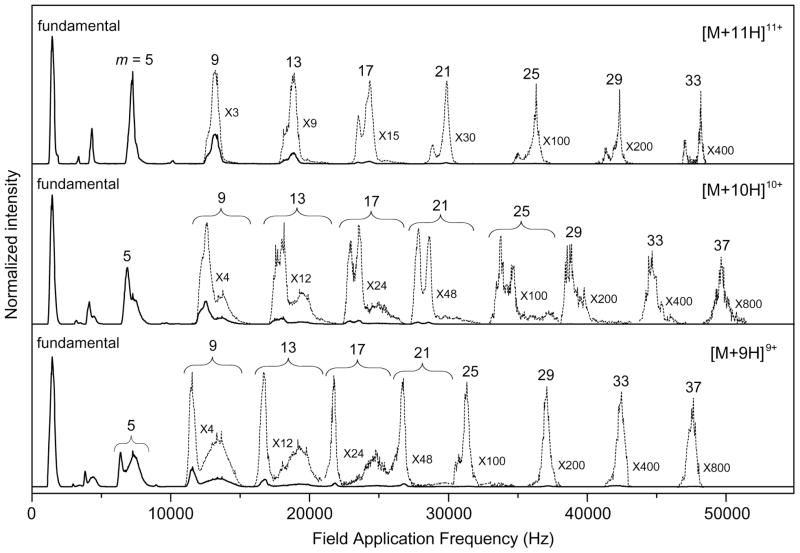
Figure 2 shows OMS distributions for the [M+9H]⁹⁺, [M+10H]¹⁰⁺, and [M+11H]¹¹⁺ charge states of electrosprayed ubiquitin ions that are obtained by scanning the drift field application frequency from 0 to 55,000 Hz. For individual charge states, the most intense peak is observed as the lowest frequency feature corresponding to ion transmission in the f_f range. The peaks in the fundamental region are centered at f_f = 1470, 1455, and 1470 Hz for the [M+9H]⁹⁺, [M+10H]¹⁰⁺, and [M+11H]¹¹⁺ charge states, respectively. Overtone frequency peaks are observed over a wide frequency range. The 37·f_f overtone peak is the highest frequency OMS distribution peak observed in the range studied here.

Figure 2.

Experimental OMS distributions for the [M+9H]⁹⁺ to [M+11H]¹¹⁺ charge states of electrosprayed ubiquitin ions. The data are plotted as a function of field application frequency over a range of 0 to 55,000 Hz. Low intensity features of each charge state are magnified (dashed lines). m indicates the harmonic frequency number permitting ion transmission (see text for details).

In general, as the frequency is increased, a more complicated pattern of overtone peaks of decreasing intensities is observed. For example, the [M+9H]⁹⁺ charge state shows only a single feature in the relatively narrow frequency range corresponding to the f_f. However, two features are observed in the 5·f_f region. We also observe that the intensities of higher-frequency peaks decrease. Additionally, the OMS resolving power ( $R_{\text{OMS}}=\frac{f}{\mathrm{\Delta }f}$) improves in higher overtone regions.^1,2 For example, a very high R_OMS value of 220 obtained at the 33·f_f overtone peak (47,820 Hz) for the [M+11H]¹¹⁺ charge state ions of ubiquitin. The origin of increasing R_OMS with increasing frequency is discussed elsewhere.² The loss in signal intensity at successive higher overtone frequency regions has been ascribed to ion diffusion, and depletion due to losses associated with operation at higher overtone numbers.² In OMS experiments these factors coupled with the use of wire mesh grids limit the overall ion signal. Of note is that the specification for 90% transmittance grids is an optical transmittance value and under the relatively high-pressure conditions of the drift tube greater ion loss may occur. That said, one advantage of the OMS method is that as opposed to IMS which utilizes discrete packets of ions, OMS imposes a mobility filter on ions originating from a continuous beam. The experiments performed here demonstrated sufficient ion signals to obtain OMS distributions up to the 37·f_f region. Current studies are focused on the use of a circular drift tube geometry^54,55 that can be used to perform OMS separations employing dynamic fields without requiring grids on drift tube lenses.

The OMS distributions gradually change in terms of the resolved species in the high frequency region. Consider the [M+11H]¹¹⁺ ions. By the 17·f_f region, two features are resolved at field application frequencies of 23,470 and 24,280 Hz. In the 21·f_f region, the intensity ratio of lower to higher frequency peaks decreases. This is slightly reversed from the 29·f_f to the 33·f_f regions. The [M+9H]⁹⁺ and the [M+10H]¹⁰⁺ ions show the resolution of multiple species upon reaching the 5·f_f region. These multiple features are preserved at higher overtone frequency regions (i.e., the 9·f_f to the 21·f_f and the 9·f_f to the 29·f_f regions for the [M+9H]⁹⁺ and the [M+10H]¹⁰⁺ ions, respectively). However, single features are observed for these ions at the highest OMS frequencies. Below we present a model that describes the origin of the observed OMS distribution changes.

OMS distributions for substance P, melezitose, and raffinose

Although we do not show the distribution, the OMS spectrum recorded over the f_f region for substance P ions shows two distinct features corresponding to the [M+3H]³⁺ and the [M+2H]²⁺ ions as confirmed by mass spectrometry analysis. Single features have been observed for the [M+H]⁺ ions of the oligosaccharides melezitose and rafinose. Here, we note that because datasets for these species were only recorded in the f_f region, relatively broad peaks have been obtained. Although peak centers have been used to obtain collision cross section measurements, it is not possible to draw conclusions about the numbers of stable conformations for these ions. The data are reported here to provide additional comparisons to IMS measurements.

Collision cross sections from OMS measurements

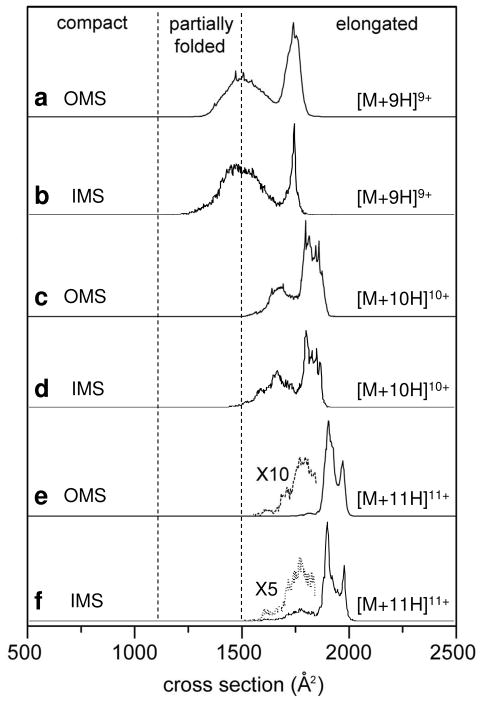
Table 1 lists the collision cross sections that have been obtained from OMS datasets of the protein ubiquitin, the peptide substance P and the oligosaccharides melezitose and raffinose. It is instructive to compare cross sections obtained from OMS measurements with those obtained from IMS experiments, which are also included in Table 1. For ubiquitin ions, the comparison is achieved by selecting overtone regions exhibiting collision cross section distributions that most closely resemble those obtained from IMS. Figure 3 shows a comparison of cross section distributions for the [M+9H]⁹⁺ to [M+11H]¹¹⁺ ions from OMS and IMS measurements. Consider the distribution of the 9·f_f overtone region for the [M+9H]⁹⁺ ubiquitin ions (Figure 3). The IMS distribution for this charge state shows a population of structures existing over a broad range in size (from ~1150 to ~ 1660 Ų). A sharp peak is also observed at Ω = 1733 Ų. Similarly, the 9·f_f overtone spectrum displays a broad distribution that includes a range of partially-folded conformations and a single narrow peak at Ω = 1741 Ų. The peak intensity ratios for the broad and narrow features are similar (~1:2) for the OMS and IMS distributions. OMS and IMS collision cross section distributions of the [M+10H]¹⁰⁺ and [M+11H]¹¹⁺ ubiquitin ions are also very similar (Figure 3). This similarity in collision cross section distribution exists over a limited field application frequency range; for this instrument, the OMS measurement at low field application frequencies (f_f and 5·f_f) does not have the required resolving power to distinguish peaks to the same degree the high-resolution IMS measurement does. At higher field application frequency settings, the OMS collision cross section distribution is once again dissimilar to the IMS distribution as ions undergoing structural changes are eliminated (see explanation below).

Table 1.

Comparison of OMS and IMS cross sections

Ions	OMS ccs (Å2)a										IMS ccs (Å2)
	mb = 1	m = 5	m = 9	m = 13	m = 17	m = 21	m = 25	m = 29	m = 33	m = 37
Ubiquitin [M+5H]5+	966.9	1019.6	1013.0								1045c
Ubiquitin [M+6H]6+	1092.3	1012.0	1015.9								1004c
		1058.8	1059.9								1050c
Ubiquitin [M+7H]7+	1109.0	1053.2	1056.4								1050c
		1099.1	1092.2								1113c
		1287.2	1328.2								1258c
		1541.9	1554.9
Ubiquitin [M+8H]8+	1371.6	1228.6	1384.2								1063c
		1374.1	1713.1								1217c
		1714.1									1367c
											1670c
											1695c
Ubiquitin [M+9H]9+	1531.8	1746.0	1471.3	1472.2	1531.8	1750.9	1748.5	1742.5	1744.1	1738.1	1500c
		1534.7	1508.8	1518.2	1742.4						1733c
			1741.2	1743.1
Ubiquitin [M+10H]10+	1787.9	1693.0	1682.6	1635.8	1804.2	1806.9	1808.1	1804.8	1854.5	1857.2	1590c
		1791.7	1792.8	1686.9	1854.7	1857.6	1854.7	1853.7			1660c
				1791.3							1790c
				1852.1							1850c
Ubiquitin [M+11H]11+	1885.9	1875.7	1880.2	1882.1	1787.1	1883.4	1879.4	1881.2	1883.61		1750c
				1963.2	1879.8	1950.0	1952.1	1953.7	953.5		1879c
					1944.7						1953c
Ubiquitin [M+12H]12+	2009.8	2003.0	2003.9	2001.5	2000.5	1999.3	2003.0	2002.3			1767c
											1845c
											1998c
											2072c
Ubiquitin [M+13H]13+	2120.7	2124.8	2123.8	2118.2	2102.0						2115c
Substance P [M+2H]2+	311.7										313.8d
											285e
											273f
Substance P [M+3H]3+	321.5										319.7d
Melezitose [M+H]+	129.8										131g
Raffinose [M+H]+	142.9										138g

^aCross sections correspond to peak maxima in the distributions.

^bValues of m depend on the magnitude of φ (see text for details).

^cFrom Reference ⁵⁹.

^dValues that have been calculated from data reported previously (reference ⁶²).

^eFrom Reference ⁶³.

^fFrom Reference ⁶⁰.

^gValues as measured on a prototype 3 m drift tube (not published).

Figure 3.

Cross section distributions for the [M+9H]⁹⁺ to [M+11H]¹¹⁺ charge states of ubiquitin ions obtained from OMS (a, c, and e) and IMS (b, d, and f) measurements. For OMS distributions, the 9·f_f, 13·f_f, and 17·f_f overtone spectra have been chosen for the [M+9H]⁹⁺, [M+10H]¹⁰⁺, and [M+11H]¹¹⁺ ions, respectively. Regions divided by dashed lines correspond to compact, partially-folded, and elongated conformations, as defined previously.⁵⁶ IMS distributions are obtained by taking slices from a two-dimensional t_D(m/z) dataset. The OMS distributions are plotted by determining the cross sections from overtone frequencies (Equation 1).

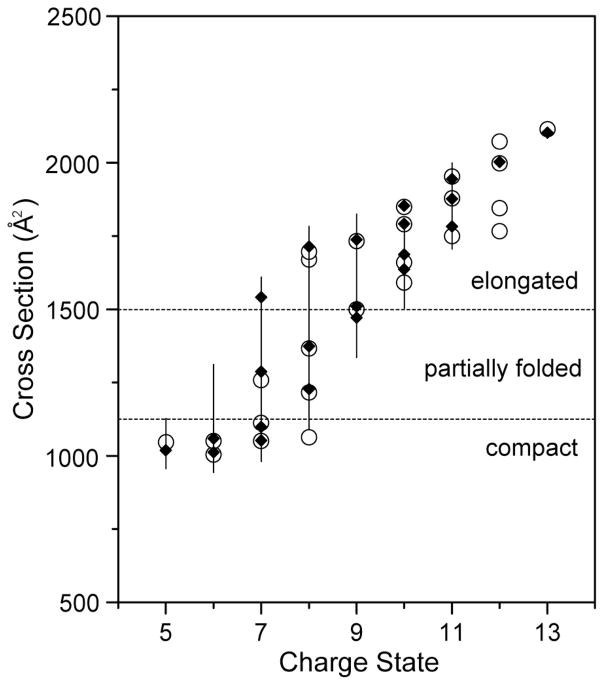
The general agreement in collision cross sections obtained from OMS and IMS⁵⁶ measurements for what appears to be similar conformations of ubiquitin ions observed in both datasets can be observed by examining Figure 4. For given charge states, corresponding structures observed with OMS have nearly identical collision cross section distributions as those observed in IMS distributions. There are instances where specific conformational types are observed for one technique but are not present in the other (see for example the [M+7H]⁷⁺, [M+8H]⁸⁺, and [M+12H]¹²⁺ ions in Figure 4). The origin of some differences in OMS distributions are discussed below. However, in general, the agreement between OMS and IMS collision cross sections for peaks that are observed in both techniques is good. In general, comparison of any OMS cross section with an IMS value for the same conformer shows agreement to within ±1% relative uncertainty. Thus, the OMS approach is a reliable means of obtaining cross sections. The good agreement in collision cross sections also suggests that the dynamic nature of OMS drift fields as well as the highly repulsive fields in the d_e regions do not significantly alter the mobilities of the ions.

Figure 4.

Cross sections for the [M+5H]⁵⁺ to [M+13H]¹³⁺ charge state ions of ubiquitin. The open circles correspond to data recorded using IMS.⁵⁹ The solid diamonds indicate data obtained by OMS. The vertical lines show a range of cross sections that are associated with unresolved conformations. Dashed lines indicate divisions for compact, partially folded, and elongated conformational states. Different overtone spectra for individual charge states have been analyzed to calculate the cross sections (the 5·f_f overtone spectra for the [M+5H]⁵⁺ to [M+8H]⁸⁺ ions, the 9·f_f overtone spectrum for the [M+9H]⁹⁺ ions, the 13·f_f overtone spectrum for the [M+10H]¹⁰⁺ ions, and the 17·f_f overtone spectra for the [M+11H]¹¹⁺ to [M+13H]¹³⁺ ions).

Evidence for structural changes

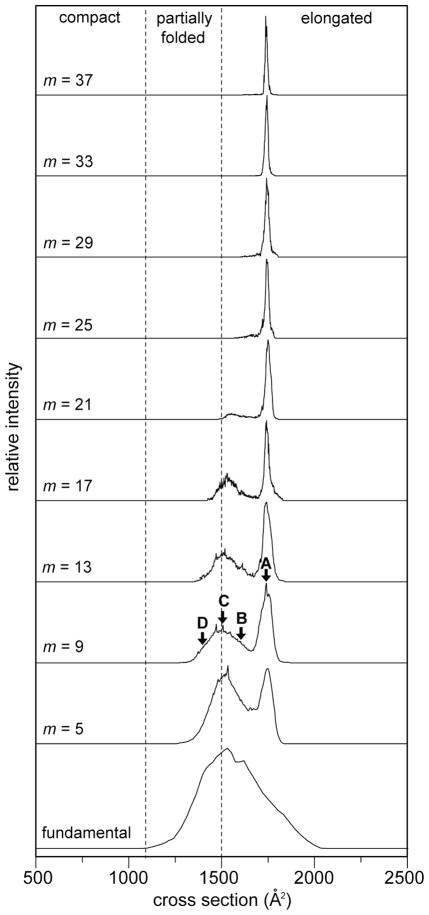
Figure 5 shows cross section distributions for the [M+9H]⁹⁺ charge state ions obtained at each of the frequency regions (f_f and m = 5 to 37) studied here. At the f_f setting, a broad, unresolved distribution of conformations is observed extending from Ω ≈ 1100 to 2000 Ų. When the field application frequency range is increased to the 5·f_f region, two features of equal intensity are present in the spectrum. A broad feature of unresolved, partially-folded structures is observed over the cross section range of Ω ≈ 1300 to 1660 Ų. The second, narrower feature corresponds with ions having a collision cross section of Ω = 1741 Ų. As the field application frequency range is increased to the 9·f_f region, the intensity level of the broad feature decreases relative to the more elongated conformation. In the 13·f_f and 17·f_f regions, a greater valley is observed between the two dataset features indicating a more rapid loss of ions with conformations of sizes intermediate to the partially-folded and elongated conformations. Additionally, ions with the smallest conformations are also lost. The feature representing the elongated conformation also becomes narrower. As the field application frequency is increased to the 21·f_f region, a large decrease in the proportion of the partially-folded states is observed. In the 25·f_f and 29·f_f regions, only the largest partially-folded states remain. Upon reaching the 33·f_f regions, only the most elongated conformation persists. The dataset feature corresponding to this conformation continues to narrow from the 25·f_f region to the 37·f_f regions.

Figure 5.

Cross section distributions for the [M + 9H]⁹⁺ charge state of electrosprayed ubiquitin ions obtained from OMS measurements. The OMS spectrum has been recorded from the f_f to the 37·f_f overtone. m indicates the harmonic frequency number allowing the ion transmission. Dashed lines indicate divisions for compact, partially folded, and elongated conformational states. Four conformations (labeled A, B, C and D, Ω= 1417, 1508, 1612, and 1741 Ų, respectively) have been chosen to simulate structural transitions (see Figure 6 and the text for details).

In addition to the distributions described in each of the overtone frequency regions described above, additional dataset features are observed between the f_f and the 5·f_f frequency regions. These distributions are similar to those observed in the 5·f_f regions for all three charge states. These features have been observed previously in OMS measurements and are more prevalent in operational modes employing larger values of φ.² In general such peaks are more highly resolved and appear to belong to a separate overtone series. Because the origin of these peaks is currently under investigation, they will not be discussed further here.

Ion trajectory simulations

In order to understand the evolution of the OMS distributions with increasing overtone frequency, it is useful to consider that the physical size of the transmissible portion of the ion beam decreases with increasing frequency.² Species that undergo structural transitions may be eliminated at some overtones, but not others. That is, the stable region of the ion beam is a factor of 37 times shorter for the 37·f_f overtone peak than for the f_f. Because of this, the rates that structures change will influence the spectrum differently for different overtone regions. These changes in OMS distributions in different frequency regions can be modeled theoretically to bracket the kinetics associated with these changes. Here, we present three models describing possible structural transitions for ubiquitin.

In this analysis, the simulation monitors the time-dependent displacement of individual ions. The total displacement per time step is calculated by summing the contributions from the electric field as well as random variations associated with diffusion. The electric field at each ion location point is obtained from field array files similar to that produced by Simion.⁵⁷ Because experiments have been carried out using a four phase (φ = 4) system, four separate field array files are used. Each contains repulsive fields in a unique set of d_e regions signaling ion neutralization. The accumulated drift time and user-defined field application frequency dictates which field array file is used for each time step displacement calculation.

Initially the algorithm selects one field array file and reads in the four array points immediately surrounding the two-dimensional position of the ion. Using the distance of the ion to each point, a weighted-average field is then calculated for both the x- and y-dimensions representing the field at the ion location. The drift velocity of the ion (v = KE) as well as the defined time step (typically ≤ 2μs) is then used to calculate the displacement of the ion resulting from its mobility.

Displacement of ions due to diffusion is simulated by considering the root mean-square displacement of the ion as given by³⁸

$$\sqrt{\overline{r^2}}={(4D\mathrm{\Delta }t)}^{1/2}.$$ (5)

Δt represents the user-defined time increment. Ion diffusion coefficients can be obtained using the mobilities of the ions ( $D=\frac{k_{b}TK}{e}$). For these studies, K is obtained from the experimentally determined values in the OMS instrument for the [M+9H]⁹⁺ ubiquitin ions. To randomize the contribution to ion displacement in two dimensions due to diffusion, $\sqrt{\overline{r^2}}$ is converted into a polar coordinate vector by randomizing a single angle (Θ). It is straightforward to use $\sqrt{\overline{r^2}}·\mathit{sin}\mathrm{\Theta }$ and $\sqrt{\overline{r^2}}·\mathit{cos}\mathrm{\Theta }$ to represent the y- and x-axis vector components, respectively. Thus ion diffusion can range from $-\sqrt{\overline{r^2}}$ to $+\sqrt{\overline{r^2}}$ in each dimension for each timestep. This displacement due to diffusion is then added to that from the mobility calculation to produce a net ion displacement for each time increment. Ion trajectory simulations using this treatment for diffusion show that with the use of a sufficient number of separate calculations (separate ions) Gaussian shaped peaks of the appropriate width are produced for model ion packets. Additionally, the modeling of diffusion in this manner leads to the accurate representation of the dependence of ion intensity on field application frequency for OMS experiments.²

For the calculations, ions originate in positions are referenced with respect to the d_t(1) region immediately preceding the first ion elimination region [d_e(1)]. These regions are equal in size to all other d_t and d_e regions. The same total number of d regions (22) is used for the simulation and the experiment. The d_t(1) region is 354 grid units long and the trajectories for 10 ions beginning at each grid unit are determined resulting in a total of 3540 separate calculations.

Kinetics models

The simplest model simulated for structural transitions is that a conformer C changes into a conformer C′, where C′ has an off-resonant mobility with respect to the field application frequency. Structural transformations are considered to occur as a first order reaction where the residual starting conformation is determined according to⁵⁸

$$I=I_0{e}^{-kt}.$$ (6)

Here I and I₀ represent the intensity of C for given experiments and the initial intensity of C, respectively. These values are obtained from peak heights in the experimental datasets (see Figure 5) and from the numbers of transmitted ions of a population for respective frequency settings in the simulations. Here we note that a more accurate treatment of the data would be to utilize peak areas. However, because individual conformations are not resolved in the partially-folded region of the OMS distribution (Figure 5), this is currently not possible for this system. The first-order rate constant, k, corresponds to conversion of C into conformer C′. The second model takes into account structural transformations approaching equilibrium where C changes into C′ which can subsequently change back into conformer C. Here, the amount of the initial conformation is determined according to⁵⁸

$$I=\frac{k_2+k_1{e}^{-(k_2+k_1)t}}{k_2+k_1}{I}_0$$ (7)

where k₁ and k₂ represent the rate constants for the forward and reverse reactions respectively (see below for more details). For all simulations reported here, ion mobilities have been varied by ±4%. That is, the ratio of size of C to C′ is 1.04. We note that smaller and larger variations were tested and did not fit the experimental data as well.

Simulation results

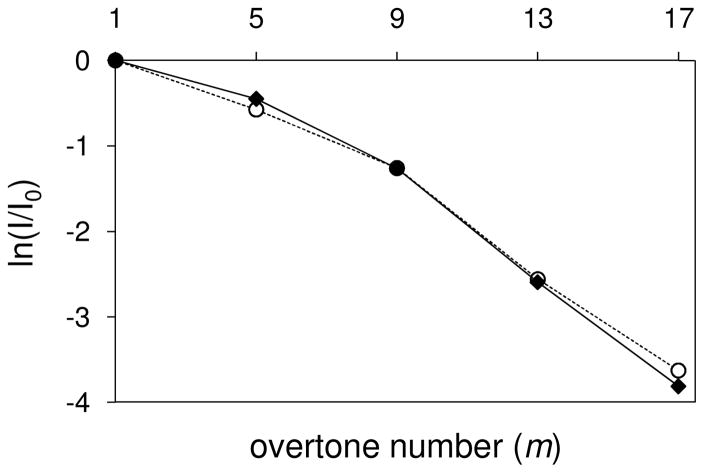
For this analysis, it is important to begin by understanding the ion losses that are due to diffusion alone for a stable state that undergoes no structural changes during the measurement. The elongated conformer (labeled A in Figure 5, K = 0.0795 m²·V⁻¹·sec⁻¹) persists to the highest frequency regions for the [M+9H]⁹⁺ ubiquitin ions, albeit at reduced intensity levels. Ion trajectory simulations for loss of the elongated form of conformer A include losses from ion diffusion (see above) but exclude structural transitions (mobility variation). Figure 6 shows that the decrease in the calculated intensity with increasing frequency is nearly identical to the decrease observed experimentally. This is consistent with a peak centered at 1741 Ų that corresponds to a relatively stable elongated conformer (or set of similar stable conformers). All of the ion losses with increasing overtone number can be ascribed to losses expected from diffusion alone.

Figure 6.

Plot of calculated (◆) and experimental (○) relative intensity ratios as a function of m for the elongated conformation (labeled A in Figure 5) of the [M+9H]⁹⁺ charge state of ubiquitin ions. Relative intensities obtained from ion trajectory simulations were calculated accounting for a contribution from ion diffusion but excluding structural transitions.

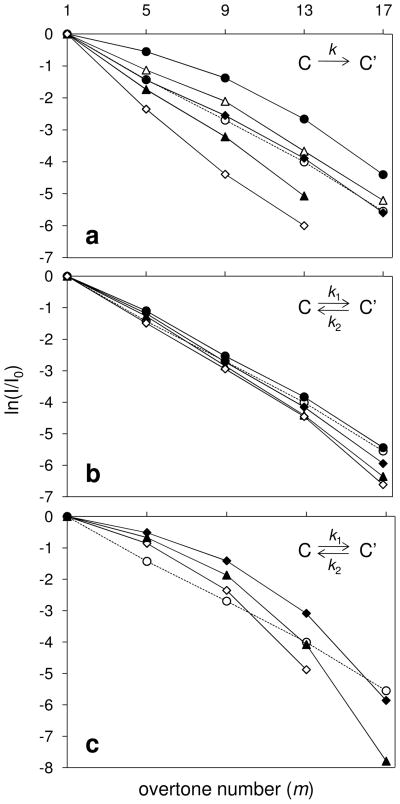
As shown in Figure 5, the broad feature corresponding to ions with more compact conformations is lost more rapidly with increasing overtone number than the elongated ions. Ion trajectory simulations for select, partially-folded states (labeled C in Figure 5, K = 0.0920 m²·V⁻¹·sec⁻¹) for the [M+9H]⁹⁺ charge state of ubiquitin ions have been performed. Figure 7 shows a comparison of the calculated and experimental intensity ratios ( $\frac{I}{I_0}$) for conformer C as a function of the harmonic number using the two different kinetics models.

Figure 7.

Plot of calculated and experimental relative intensity ratios as a function of m for the partially folded conformation (labeled C in Figure 5) of the [M+9H]⁹⁺ charge state of ubiquitin ions. The dashed trace represents relative intensities obtained from the experimental results. Relative intensities obtained from ion trajectory simulations were calculated utilizing ±4% variation in mobility (see text for details). The three kinetics models used to simulate the intensities of conformer C during ion transmission are: (a) an irreversible reaction (●k = 10; △k = 100; ◆k = 150; ○exp.; ▲k = 200; ◇k = 300); (b) a reversible reaction at relatively low rates (k₁ = 200 for all; ●k₂ = 200; ○ exp.; ◆k₂ = 150; ▲k₂ = 100; ◇k₂ = 50); (c) a reversible reaction at relatively high rate constant (k₁ = k₂; ◆k = 6932; ○ exp.; ▲k = 2310; ◇k = 1155).

For the irreversible kinetics model (Figure 7a), the rate constants tested extend over a 30 fold range. At higher rate constants, a greater number of ions exhibiting conformer C convert to conformer C′ during the simulated drift time. Overall more ions–compared with the experimental results– are neutralized in the d_e regions due to the greater time with an altered mobility. Thus, we conclude we need to tune either the rates, or structures, or both. Simulations using very small rate constants show that an insufficient number of ions is eliminated. For this model, the simulation with a rate constant of 150 s⁻¹ provides the best fit to the experimental data.

A reversible conformational transition has also been modeled utilizing different rate constants. Figure 7b shows the ion trajectory modeling results for the reversible system in which the conversion of conformer C′ to C is equal to or slower than the process of converting from C to C′. For this analysis k₁ was maintained at 200 s⁻¹ while k₂ was varied from 50 to 200 s⁻¹ (increments of 50). The modeling data utilizing k₁ = 200 s⁻¹ and k₂ = 150 s⁻¹ is the most similar to the experimental intensity trace. It is noteworthy that an increase of 33% in the forward reaction rate (to a value of 200 s⁻¹) requires a sizeable reverse reaction rate (almost equal at 150 s⁻¹).

Another possible structural variation is that ions rapidly interconvert between two conformations. In this model, the average mobility associated with the conformational changes is set to the resonant mobility. For example, conformers C and C′ are assigned mobilities that are 2% higher and lower, respectively, than the resonant mobility. If values of k₁ and k₂ are large (>10³), multiple structural transformations occur for each field application setting. This ensures that the average mobility is sufficiently sampled such that most of the ions can make it through the instrument at lower and intermediate overtone frequencies. However, at higher overtone frequencies, the transmissible portion of the ion beam decreases (according to a factor of 1/m) to a size where ions having off-resonant mobilities even for a short period of time are eliminated. Figure 7c shows that for all values of k₁ and k₂ tested, such a fast reversible model underestimates and overestimates ion loss at low and high frequencies, respectively.

Both the irreversible and the reversible models provide reasonable fits to the experimental data. These best fits require similar rate constants (e.g., k = 150 and k₁ = 200 s⁻¹ for the respective models). The half lives (τ, where $\frac{I}{I_0}=0.5$) obtained from the best fits are τ ≈4.62 and 5.94 ms for the irreversible and reversible models, respectively. This result suggests that these ions change structures on a few millisecond timescale. This is consistent with our previous data showing structural transitions of ubiquitin ions with no activation (i.e., conformational changes were observed when a relatively unstable ion was selected).⁵⁹ Because partially-folded conformations are those that undergo structural transformations, it is possible that Coulomb repulsion causes these species to gradually elongate over this time period. Previous studies have monitored the elongation of proteins ions over tens of ms.^3–5 This would also explain the relative stability of the elongated conformation as the balance between Coulomb repulsion and attractive intramolecular interactions results in a more stable structure. Finally, this argument may somewhat favor the irreversible process as such species may initially elongate minimally to relieve strong Coulomb repulsion prior to the more extensive elongation observed previously.^3–5 That said, the data are insufficient to rule out either process.

As a final note, the OMS distributions for the [M+9H]⁹⁺ ubiquitin ions (Figure 5) demonstrate that structural transformations of specific partially-folded conformations occur over varying timescales. It is worthwhile to consider the rates of change for other species. Simulations for Conformers B and D (labeled in Figure 5, K = 0.0883 and 0.0998 m²·V⁻¹·sec⁻¹, respectively) have been performed using the irreversible model system. Based on the modeling results, conformers B and D undergo structural transitions at a higher rate than conformer C with rate constants of 190 and 280 s⁻¹, respectively.

Conclusions

OMS measurements have been performed for a number of gas-phase ions produced by direct electrospray of ubiquitin, substance P, rafinose, and melezitose solutions. Overall, collision cross sections obtained from OMS measurements are in good agreement with those obtained by IMS. Additionally, the production of similar collision cross section distributions at specific overtone frequency regions indicates the robust nature of the OMS technique for determining ion mobilities. Modeling structural transitions by fitting experimental peak intensity ratio data obtained from OMS distributions for [M+9H]⁹⁺ ubiquitin ions indicates that a portion of the ion population undergoes a structural transition on a few ms timescale. Because IMS measurements occur on this timescale, they do not expose these structural transitions as drift time distributions provide the average mobilities for these ions. Such determinations are also problematic for multidimensional IMS techniques as multiple mobility selections using variable time delays would require a substantial amount of time to monitor a single dataset feature. By allowing the tuning of the transmissible portion of the ion beam to very short lengths, OMS offers the unique advantage of elucidating such conformational changes for multiple gas-phase ions over a relatively short time period.