Genetic Introgression and the Survival of Florida Panther Kittens

Abstract

Estimates of survival for the young of a species are critical for population models. These models can often be improved by determining the effects of management actions and population abundance on this demographic parameter. We used multiple sources of data collected during 1982-2008 and a live recapture-dead recovery modeling framework to estimate and model survival of Florida panther (Puma concolor coryi) kittens (age 0 – 1 year). Overall, annual survival of Florida panther kittens was 0.323 ± 0.071 (SE), which was lower than estimates used in previous population models. In 1995, female pumas from Texas (P. c. stanleyana) were released into occupied panther range as part of an intentional introgression program to restore genetic variability. We found that kitten survival generally increased with degree of admixture: F₁ admixed and backcrossed to Texas kittens survived better than canonical Florida panther and backcrossed to canonical kittens. Average heterozygosity positively influenced kitten and older panther survival, whereas index of panther abundance negatively influenced kitten survival. Our results provide strong evidence for the positive population-level impact of genetic introgression on Florida panthers. Our approach to integrate data from multiple sources was effective at improving robustness as well as precision of estimates of Florida panther kitten survival, and can be useful in estimating vital rates for other elusive species with sparse data.

1. Introduction

Rigorous estimates of survival rates and understanding factors influencing those rates are critical for discerning proximate and ultimate causes of dynamics, regulation, and persistence of populations (Newton 2004; Ozgul et al. 2006) and for devising and implementing management interventions for species conservation (Davis et al. 2007). Population dynamics of many vertebrate species are strongly influenced by changes in survival rates (Heppell et al. 2000; Oli and Dobson 2003; Stahl and Oli 2006). Estimates of survival also are necessary for the parameterization of population models, which are essential tools in conservation biology for evaluating population performance, diagnosing the causes of low numbers or population declines, developing solutions to those problems, and determining research priorities (Caswell 2001; Caughley and Gunn 1996; Fujiwara and Caswell 2001). These population models can often be improved by including the estimated effects of factors such as population density or genetic diversity on survival.

The Florida panther (Puma concolor coryi) is a subspecies of puma that once ranged throughout the southeast United States. Florida panthers give birth to 1-4 kittens, which remain in the den for approximately 7-8 weeks (Maehr et al. 1990). Average age of independence is just over 1 year (mean = 397 days, SD = 75 days, n = 35; FWC & NPS, unpublished data). The Florida panther is now restricted to <5% of its historic range in south Florida (Maehr et al. 2002), where it occurs in a single population with ca. 100 sub-adults and adults (McBride et al. 2008). It has been federally listed as endangered since 1967. Small population size, isolation, loss and fragmentation of habitat, road-related mortalities, and other anthropogenic influences continue to threaten the long-term persistence of Florida panthers (Kautz et al. 2006).

Small populations are expected to suffer from inbreeding depression (Frankham et al. 2002); earlier studies of Florida panthers found evidence of inbreeding and recommended genetic introgression via the introduction of a subspecies of puma whose range historically abutted with the range of the Florida panther (Barone et al. 1994; Roelke et al. 1993). Based on this recommendation, 8 female Texas pumas (P. c. stanleyana) were released into the Florida panther population in 1995. Although the panther population has experienced an almost fourfold increase since 1995 (McBride et al. 2008), the success of the introgression continues to be a topic of debate (Maehr et al. 2006; Onorato et al. 2010; Pimm et al. 2006). There have also been non-management releases of captive pumas into south Florida; some of these (between 1957 and 1967) resulted in a genetic population with partial Central American ancestry in the Everglades (O’Brien et al. 1990).

In 2003, the U.S. Fish and Wildlife Service (USFWS) and the Florida Fish and Wildlife Conservation Commission (FWC) convened the Scientific Review Team (SRT) to review the status of Florida panther science, and to make research and management recommendations. The SRT thoroughly reviewed existing literature on demography and population ecology of the panther, and found that rigorous estimates of age- or stage-specific survival rates and cause-specific mortality rates were not available. Furthermore, SRT found that previously reported estimates of the survival rate of Florida panther kittens (Maehr and Caddick 1995) and those used in population viability analyses (Maehr et al. 2002) were not based on reliable inference methods and raised doubt on predictions regarding the persistence of the panther population (Beier et al. 2003; Beier et al. 2006; Gross 2005). The SRT recommended reanalysis of existing data to rigorously estimate age-specific survival rates and test hypotheses regarding factors influencing survival rates (Beier et al. 2003).

In accordance with SRT recommendations (Beier et al. 2003), our goals were to provide rigorous estimates of survival of Florida panther kittens (defined here as age 0 – 1 year), and to evaluate factors influencing kitten survival. We analyzed long-term radio-telemetry (1982-2008) and Passive Integrated Transponder (PIT)-tagging (1995-2008) data within a live-recapture, dead recovery modeling framework (Burnham 1993; Williams et al. 2002). We tested the hypotheses that kitten survival: (1) would not differ between sexes, due to little or no sexual dimorphism during this stage of life; (2) would decrease with increasing litter size due to large litters potentially being more energetically demanding to dams and more difficult to protect from predators; (3) would be higher during the wet season (June – November) than during the dry season (December – May), due to potential higher prey availability during the wet season; and (4) would be negatively influenced by population abundance due to density-dependent effects. In many species of carnivores, survival of neonates is generally lower compared to older juveniles (Garrison et al. 2007; Logan and Sweanor 2001). Thus, we also hypothesized that kitten survival (5) would increase with age during their first year.

Results of rigorous analyses evaluating the effects of genetic introgression on kitten survival could assist in setting future management and research priorities. Thus, we tested these additional hypotheses: (6) kitten survival probability would increase with average heterozygosity, because loss of genetic variation (especially due to inbreeding) has been shown to negatively influence fitness and its components (Crnokrak and Roff 1999; Ralls and Ballou 1983); and (7) survival probability would be higher for admixed kittens than for canonical (i.e., pure Florida panther) kittens as outcrossing has been shown to increase various measures of fitness for small, inbred populations (Heschel and Paige 1995; Madsen et al. 1999; Vrijenhoek 1994).

2. Materials and methods

2.1 Field methods

Florida panthers and Texas pumas were captured and monitored by radio-telemetry from 1982-2008 across the range of the subspecies in south Florida, USA (Kautz et al. 2006) by biologists from the FWC and National Park Service (NPS) using methods described by Belden et al. (1988) and Land et al. (2008). Age of captured panthers (if unknown) was estimated using a combination of toothwear, pelage characteristics, size, and developmental stage of teats and reproductive organs. Blood and tissue samples were collected for health assessment and genetic analysis. Radio collars were affixed on captured adults, sub-adults, and older kittens (occasionally as young as 5 months old; age and size qualifications for collaring varied over time).

Successive locations of females were continually assessed to determine the commencement of denning behavior; lack of movement between 3-4 fixes was taken as evidence of possible denning (Land et al. 1998). We visited dens 4-35 days post-partum (approximate median = 14 days). Kittens in dens were counted, sexed, sampled for genetic material, and implanted with passive integrated transponder (PIT) tags. Occasionally, dens were checked after dams vacated the area for evidence of dead kittens.

Females that denned ≤ 12 months after giving birth to a previous litter were classified as having lost that previous litter because 1) females are unlikely to copulate while they have dependent kittens, 2) the gestation period is about 3 months (Maehr 1992), and 3) the minimum age of independence recorded is 9 months (D. Onorato, unpubl. data). Similarly, litters whose dams died ≤ 9 months after denning were classified as having failed. These two types of litter failure data generally do not provide an estimated death date for individual kittens, only an upper limit on the date when litters could have failed.

2.2 Heterozygosity and genetic ancestry

We extracted total genomic DNA from blood and tissue samples obtained from wild-caught panthers and captive pumas from south Florida and west Texas during 1982-2007. We amplified and scored 23 microsatellite loci following previously described PCR amplification conditions (Menotti-Raymond et al. 1999; Menotti-Raymond et al. 1997). Derived genotypes were used to calculate average individual heterozygosity using the program MICROSAT (Minch et al. 1995).

A Bayesian procedure, implemented in the program STRUCTURE (Pritchard et al. 2000) was used to identify populations or genetic clusters (run without preset groups/training individuals) and to estimate the genetic origin of individuals. The STRUCTURE approach assumes departures from both Hardy-Weinberg and complete linkage equilibriums to be indications of population substructure (Pritchard et al. 2000).

We used results from the STRUCTURE analysis along with pedigree information and field evidence to assign panthers to groups that reflect the genetic makeup of the southern Florida population: canonical panthers (92 total panthers; 50 kittens), backcrossed to canonical admixed panthers (92 total panthers; 80 kittens), backcrossed to Everglades admixed panthers (19 total panthers; 18 kittens), backcrossed to Texas admixed panthers (42 total panthers; 38 kittens), and F₁ admixed panthers (15 total panthers; 13 kittens). Canonical Florida panthers showed no evidence of non-Florida genetic admixture (no direct non-Florida relatives or < 10% non-Florida genetic contribution based on STRUCTURE analyses). Admixed panthers were mostly the descendents of the introduced female Texas pumas released in 1995, except for 6 radio-collared individuals (0 kittens) that were genotypically similar to pumas maintained in a large enclosure on the Seminole Indian Reservation (SIR) adjacent to Big Cypress National Preserve. These SIR panthers, panthers of unknown ancestry (4 kittens), and admixed panthers whose ancestry could not be accurately determined (total = 54, of which 43 were kittens) were excluded from the survival analysis that incorporated ancestry.

Backcrossed to canonical panthers were admixed panthers with predominantly (>50%) canonical heritage resulting from admixed panthers breeding with canonical panthers. Backcrossed to Everglades were admixed panthers with predominantly (>50%) Everglades heritage resulting from breeding events between admixed and Everglades panthers. Backcrossed to Texas admixed panthers were admixed panthers of predominantly (>50%) Texas heritage resulting from admixed panthers breeding with introduced Texas pumas. We defined F₁ admixed panthers as any offspring produced by matings between a Texas female and a pre-introgression type male (either canonical Florida panther or Everglades panther). In theory, Everglades panthers (with documented genetic links to Central American pumas) represent a sixth genetic population; however, there were no recorded kittens of this group during the post-introgression study period (June 1995 – May 2008).

We also repeated our analyses based on a simpler ancestry classification (canonical, F₁ admixed, and other admixed) that allowed the inclusion of admixed panthers with unknown ancestry; results of these analyses are presented in Appendix A.

2.3 Index of abundance

To examine the potential effects of panther density on kitten survival, we used minimum population counts as an index of abundance (McBride et al. 2008). These minimum counts were based on radio-tracking and field evidence of sub-adult and adult panthers (tracks, scat, kills, and scrapes) and collected for calendar years (e.g., total number of sub-adult and adult panthers known to have been alive in the wild over the period January 2005 – December 2005). In contrast, we analyzed annual kitten survival for periods extending from June – May. We applied the sub-adult/adult calendar year count for year x to the kitten June x – May x + 1 year, because puma kitten mortality is generally highest in the first three months of life (see Results), so adult abundance during that period seemed most likely to affect survival. In 2004, the panther survey was incomplete, so the minimum count is unknown. We followed McBride et al. (2008) and extrapolated it halfway between the 2003 and 2005 counts.

2.4 Data preparation and analysis

We used two datasets for the analysis of kitten survival. The first contained the capture (of live panthers) and recovery (of dead panthers) histories, observations of litter-failures (i.e., loss of entire litters), and radio-tracking data for panthers that were initially PIT-tagged in the den between June 1995 and May 2008 (13 years). The second contained the capture, recovery, and radio-tracking histories of all other panthers between n June 1982 and May 2008 (26 years). Details of data preparation can be found in Appendix B.

We analyzed data using the R (R Development Core Team 2010) package RMark (Laake and Rexstad 2010) as an interface for program MARK (White and Burnham 1999) and Burnham’s live-recapture dead-recovery modeling framework (Burnham 1993; Williams et al. 2002). The Burnham model has four parameters: survival probability (S), recapture probability (p), recovery probability (r), and fidelity (F). For all models, we fixed F=1 for all panthers, as the recapture and recovery areas are the same and encompass the entire range of the Florida panther. We set p and r for radio-collared animals to 1, because we could count on knowing their status each year.

Although the focus of our study was kitten survival, we also used data from sub-adult and adult panthers to efficiently parameterize the likelihood functions. For example, the likelihood of a kitten being PIT-tagged in the den and then recaptured as a 2-year old panther depends on the probability of it surviving as a kitten, the probability of it surviving the first year of being a sub-adult, and the probability of recapture as a sub-adult. Thus, to estimate the kitten survival probability from data such as these, we also need to estimate the other aforementioned probabilities. We used a model with an interaction of sex and age class (sub-adult or adult), a reasonably well supported model (Benson et al. 2009) that could be applied to all individuals, to estimate the survival of sub-adults and adults. The boundary between sub-adult and adult panthers was originally defined at age 2.5 for females and age 3.5 for males (Benson et al. 2009). Transitions at these ages were impossible with a one-year time step; therefore, we fitted survival models with those ages rounded up and down to the nearest integer (to 2 and 3 for females and 3 and 4 for males). We used an information-theoretic approach (Akaike’s Information Criterion adjusted for overdispersion and small sample size; QAIC_c) for model selection and statistical inference (Burnham and Anderson 2002). We calculated QAIC_c values, Akaike differences (ΔQAIC_ci, difference between QAIC_c value of the ith model and the top-ranked model) and Akaike weights (the weight of evidence that a model is the best model of the models being considered given the data) as in Burnham and Anderson (2002). We calculated model-averaged estimates of annual survival and unconditional variance for each level of categorical variables and across continuous covariates (Burnham and Anderson 2002; Tinker et al. 2006). To generate these model-averaged estimates of survival we used all models included in the model selection process for a given analysis, with model-specific estimates weighted by their Akaike weights. Models with no effects of the covariates being presented were included in the averages.

We commenced by testing all a priori models for recapture and recovery combined with a priori models for survival of kittens, sub-adults, and adults with various divisions of age classes. Because kittens could only be recaptured as sub-adults the following year, there was no capture probability parameter for kittens (e.g., Pollock 1981); for sub-adult and adult panthers we estimated a single capture probability. We used models that estimated separate recovery rate for kittens and older panthers as well as those that estimated a single recovery rate for all panthers.

We used a model that allowed kitten survival to vary between sexes and recapture probability to be different for kittens (the most parameterized model that applies to the full dataset) to test for overdispersion of the data due to lack of independence within litters ( ĉ ) using the data bootstrap approach developed by Bishop et al. (2008); a ĉ > 1 indicates overdispersion. We estimated ĉ as the ratio of the replication-based estimate of the variance of bootstrapped survival estimates (this variance incorporates overdispersion associated with lack of independence) to the model-based estimate of variance of survival (estimated from the original dataset). For the bootstrap approach, we sampled litters from the dataset with replacement. Panthers first captured as sub-adults or adults were treated as litters of size 1 for the bootstrapping. If the model failed to estimate kitten survival parameters, the iteration was discarded. We repeated the resampling and estimation until we had 1,000 estimates of female and male kitten survival and estimated the mean ĉ as in Bishop et al. (2008). The estimate of overdispersion was 1.37 for females and 1.60 for males, with a mean ĉ of 1.48, indicating slight overdispersion of data. We used this value as a variance inflation factor and to calculate QAIC_c.

We selected the model with the lowest QAIC_c from preceding analyses as the base model to test hypotheses regarding factors affecting kitten survival (Table 1). The models for ancestry (Table 1A, models 3-6, Table 1B) and heterozygosity (Table 1A, models 7-10) were run on data collected between 1995 and 2008 only due to the absence of admixed panthers in Florida before 1995. We tested for the effect of ancestry and heterozygosity on survival of (1) kittens only; (2) sub-adult and adult panthers only; (3) kittens and older panthers considered separately; and (4) panthers of all ages. Based on previous results (Benson et al. 2009), however, we only considered 2 ancestry categories for sub-adult and adult panthers (F1Adv; Table 1B).

Table 1.

A) All a priori models that were used to test hypotheses regarding the effect of covariates on kitten survival probability (S) and B) definitions of ancestry models. All models are based on the additive effects of covariates on survival of kittens (unless otherwise noted) from the base model(s) (base; see Table 2). s&a indicates an effect on sub-adult and adult survival and k indicates an effect on kitten survival.

A. All Models
Model	Description
1. S(base + k:sex)	Additive sex effect
2. S(base + k:LS)	Additive linear litter size effect
3. S(base + k:Ancestry)*	Additive ancestry effect (see below) on kitten survival
4. S(base + Ancestry)*	Additive ancestry effect (see below) on survival of panthers of all ages
5. S(base + s&a:F1Adv)*	Additive F1 ancestry effect (see below) on survival of sub-adult and adult panthers only
6. S(base + k:Ancestry + s&a:F1Adv)*	Separate additive ancestry effects (see below) on kitten survival and sub-adult and adult survival (F1 only)
7. S(base + k:Het)	Additive linear heterozygosity effect on kitten survival
8. S(base + Het)	Additive linear heterozygosity effect on survival of panthers of all ages
9. S(base + s&a:Het)	Additive linear heterozygosity effect on survival of sub-adults and adults only
10. S(base + k:Het + s&a:Het)	Separate additive linear heterozygosity effects on survival of kittens and survival of sub-adults and adults
11. S(base + k:Abundance)	Additive linear effect of abundance index
B. Ancestry Models
Term	Definition	Hypothesis
IntAdv	2 ancestry categories: 1) Canonical; 2) Backcrossed to Canonical, Backcrossed to Everglades, Backcrossed to Texas, and F1.	General introgression advantage (or disadvantage).
AdmAdv	2 ancestry categories: 1) Canonical and Backcrossed to Canonical; 2) Backcrossed to Everglades, Backcrossed to Texas, and F1.	General admixture advantage (or disadvantage), but with Backcrossed to Canonical reverting to Canonical.
50TexAdv	2 ancestry categories: 1) Canonical, Backcrossed to Canonical, and Backcrossed to Everglades; 2) Backcrossed to Texas, and F1.	Survival advantage (or disadvantage) for those ≥50% Texas.
CanDisF1Adv	3 ancestry categories: 1) Canonical; 2) Backcrossed to Canonical, Backcrossed to Everglades, and Backcrossed to Texas; and 3) F1.	Differences in survival between pre-introgression types, backcrosses, and F1’s.
CanDis50TexAdv	3 ancestry categories: 1) Canonical; 2) Backcrossed to Canonical and Backcrossed to Everglades; 3) Backcrossed to Texas and F1.	Differences in survival between pre-introgression types, ≥50% Texas, and intermediate types.
F1Adv	2 ancestry categories: 1) Canonical, Backcrossed to Canonical, Backcrossed to Everglades, and Backcrossed to Texas; and 2) F1.	Survival advantage (or disadvantage) for F1’s.

^*Ancestry stands for 6 different hypothesis driven models of the effect of ancestry on survival; specifically, F1Adv divides F₁ admixed from other panthers. See part B of this table for descriptions of ancestry models.

We tested for the effect of abundance on kitten survival (Table 1A, model 11) using data collected between 1995 and 2008. Data on kittens collected prior to 1995 were insufficient to test for the effect of abundance on kitten survival.

Finally, we estimated process variance (random effect of year; a critical parameter for stochastic population models) in kitten survival using the Markov Chain Monte Carlo (MCMC) option in MARK (Lukacs et al. 2009; White et al. 2009). We used the Bayesian MCMC approach instead of a method of moments approach because some missing kitten survival estimates for specific years (fixed effects categorical model used as an input for method of moments) made the method of moments approach unreliable (G. White pers. comm.). We estimated process standard deviation in logit survival from the mean and 95% credible interval of the posterior distribution. To estimate the temporal variation beyond that explained by abundance, we also estimated the temporal standard deviation associated with year in the model that included abundance index as a covariate. Temporal standard deviations were converted from the logit scale using the mean kitten survival (to σ̂; without abundance index model) and the kitten survival computed for the mean abundance (to σ_res; abundance index model). We estimated percentage of the temporal variance explained by abundance as $({\widehat{\sigma }}^2-{\sigma }_{\mathit{res}}^2)/{\widehat{\sigma }}^2$ (Loison et al. 2002).

We used the same non-informative priors as White et al. (2009); estimates from the fixed effects models were used as starting values where appropriate. We tested for lack of convergence using 10 Markov chains for each model (Gelman 1996) and found no evidence of lack of convergence. For each chain we sampled the MCMC for 50,000 iterations, after 4,000 tuning samples and 1,000 burn-in samples.

2.5 Three-month time step data preparation and analysis

Using the data organized on an annual time scale, it was not possible to test for seasonal variation in kitten survival and age-specific variation in survival within the first year of life. Therefore, we recoded data into 3-month time intervals. This necessitated leaving out litter failure data, because information about the 3-month interval in which actual kitten deaths occurred was generally not available from these data. We also did not include the recapture/recovery histories of panthers not PIT tagged in the den (without working radio-collars), for computation efficiency (Appendix C).

Analysis of the data with a 3-month time step was similar to the annual time step analysis, except that there was now a possibility of recapture as a kitten. We commenced by testing all a priori models for recapture and recovery combined with a priori models for survival of kittens based on age (Appendix C). We report model-specific and model-averaged estimates of annual kitten survival probability and model-averaged estimates of 3-month kitten and annual sub-adult and adult survival probabilities (Burnham and Anderson 2002).

3. Results

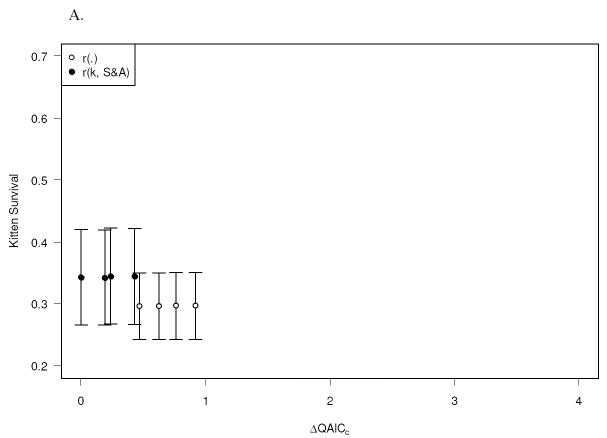
The most parsimonious model (model 1, Table 2) indicated that survival (S) and recapture (r) probabilities differed between kittens and older panthers, and that S differed between sex and age classes among older panthers, with the sub-adult to adult transition at the upper age limit for both sexes. The four models with lowest QAIC_c provided similar estimate of kitten survival (Table 2); the model-averaged estimate of annual kitten survival was 0.323 ± 0.071 (± 1 SE).

Table 2.

Model comparison table to estimate annual kitten survival and select t base model. For each model, we present the number of parameters (K), the difference from the top model in Akaike’s Information Criterion adjusted for overdispersion and small sample size (ΔQAIC_c), the model QAIC_c weight, and the estimate of annual kitten survival with standard error. The base model selected is in bold (representing survival differing between kittens, females age 1 and 2, females 3 and older, males age 1-3, and males 4 and older; recapture the same for all uncollared panthers; and recovery differing between uncollared kittens and uncollared older panthers).

Model	K	ΔQAICc	Weight	Annual Kitten Survival Estimate (SE)
1. S(k, 1≤f<3, f≥3, 1≤m<4, m≥4)p(.)r(k, s&a)	8	0.00	0.155	0.343 (0.077)
2. S(k, 1≤f<3, f≥3, 1≤m<3, m≥3)p(.)r(k, s&a)	8	0.19	0.141	0.342 (0.077)
3. S(k, 1≤f<2, f≥2, 1≤m<4, m≥4)p(.)r(k, s&a)	8	0.24	0.138	0.345 (0.078)
4. S(k, 1≤f<2, f≥2, 1≤m<3, m≥3)p(.)r(k, s&a)	8	0.43	0.125	0.344 (0.077)
5. S(k, 1≤f<3, f≥3, 1≤m<4, m≥4)p(.)r(.)	7	0.47	0.123	0.296 (0.054)
6. S(k, 1≤f<3, f≥3, 1≤m<3, m≥3)p(.)r(.)	7	0.62	0.114	0.296 (0.054)
7. S(k, 1≤f<2, f≥2, 1≤m<4, m≥4)p(.)r(.)	7	0.76	0.106	0.297 (0.054)
8. S(k, 1≤f<2, f≥2, 1≤m<3, m≥3)p(.)r(.)	7	0.92	0.098	0.297 (0.054)
9. S(k + sex, 1≤f<3, f≥3, 1≤m<4, m≥4)p(.)r(k, s&a)	9	2.02	0.267	0.349 (0.084)a 0.335 (0.089)b

^aFemale kitten survival.

^bMale kitten ten survival.

We selected the most parsimonious model from the initial model set (model 1, Table 2) as a base model for testing the effects of covariates on kitten survival. There was no evidence of an effect of sex (Table 2) or litter size (ΔQAIC_c of litter size model = 2.04) on kitten survival.

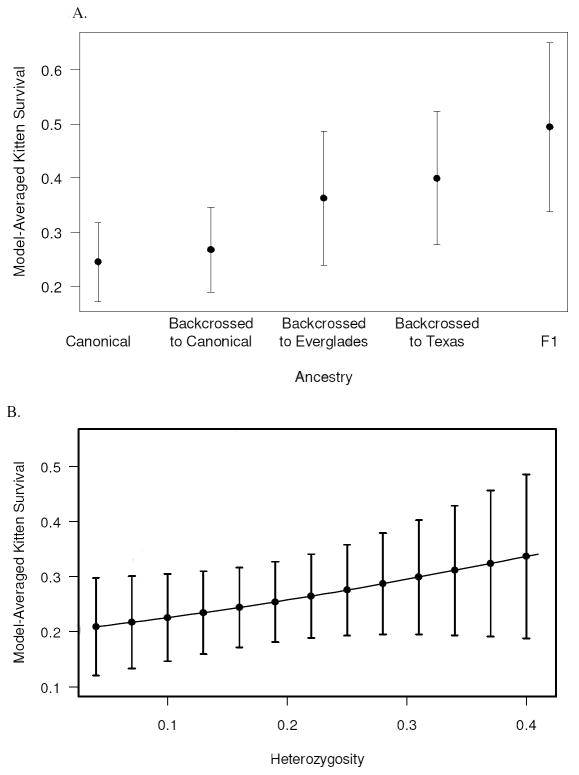
Two of the ancestry models (base + k:CanDisF1Adv and base + k:F1Adv) failed to estimate a kitten survival parameter and were discarded. There was considerable evidence that ancestry influenced kitten survival; the 6 most parsimonious models all included ancestry effects on kitten survival (models 1-6, Table 3A). The top 2 models indicated that survival of kittens differed substantially between two ancestry categories: 1) canonical and backcrossed to canonical kittens and 2) F₁, backcrossed to Texas, and backcrossed to Everglades kittens (Table 3A). Model-averaged kitten survival was lowest for canonical kittens and highest for F₁ kittens (Figure 1A).

Table 3.

Model selection table for A) ancestry effects on kitten and older survival, B) heterozygosity effects on kitten and older survival, and C) abundance index effects on kitten survival. These analyses were performed on subsets of the data (excluding panthers before 1995 for all analyses and panthers of unknown ancestry for A, and panthers before their heterozygosity was successfully sampled for B). For each model, we present the number of parameters (K), the difference from the top model in Akaike’s Information Criterion adjusted for overdispersion and small sample size (ΔQAIC_c), and the model QAIC_c weight. See Table 1 for descriptions of the covariate models and Table 2 for the base model. All models estimate constant recapture rates and recovery rates that differ between kittens and older panthers (p(.)r(k, s&a)).

A. Ancestry models
Survival Model	K	ΔQAICc	Weight
1. base + k:AdmAdv + s&a:F1Adv	10	0.00	0.242
2. base + AdmAdv	9	1.34	0.124
3. base + F1Adv	9	1.44	0.118
4. base + CanDisF1Adv	10	1.99	0.090
5. base + k:50TexAdv + s&a:F1Adv	10	2.38	0.074
6. base + k:AdmAdv	9	3.27	0.047
7. base + s&a:F1Adv	9	3.35	0.045
8. base + 50TexAdv	9	3.43	0.044
9. base + k:F1Adv + s&a:F1Adv	10	3.46	0.043
10. base + k:IntAdv + s&a:F1Adv	10	3.49	0.042
11. base + k:CanDis50TexAdv + s&a:F1Adv	11	3.98	0.033
12. base + k:CanDisF1Adv + s&a:F1Adv	11	4.22	0.029
13. base + CanDis50TexAdv	10	4.92	0.021
14. base + IntAdv	9	5.56	0.015
15. base + k:50TexAdv	9	5.80	0.013
16. base + k:IntAdv	9	7.34	0.006
17. base + k:CanDis50TexAdv	10	7.36	0.006
18. base	8	7.43	0.006
B. Heterozygosity models
Survival Model	K	ΔQAICc	Weight
1. base + Het	9	0.00	0.325
2. base + s&a:Het	9	0.75	0.223
3. base	8	0.91	0.206
4. base + k:Het	9	1.88	0.127
5. base + k:Het + s&a:Het	10	2.00	0.119
C. Abundance index models
Survival Model	K	ΔQAICc	Weight
1. base + k:Abundance	9	0.00	0.988
2. base	8	8.79	0.012

Figure 1.

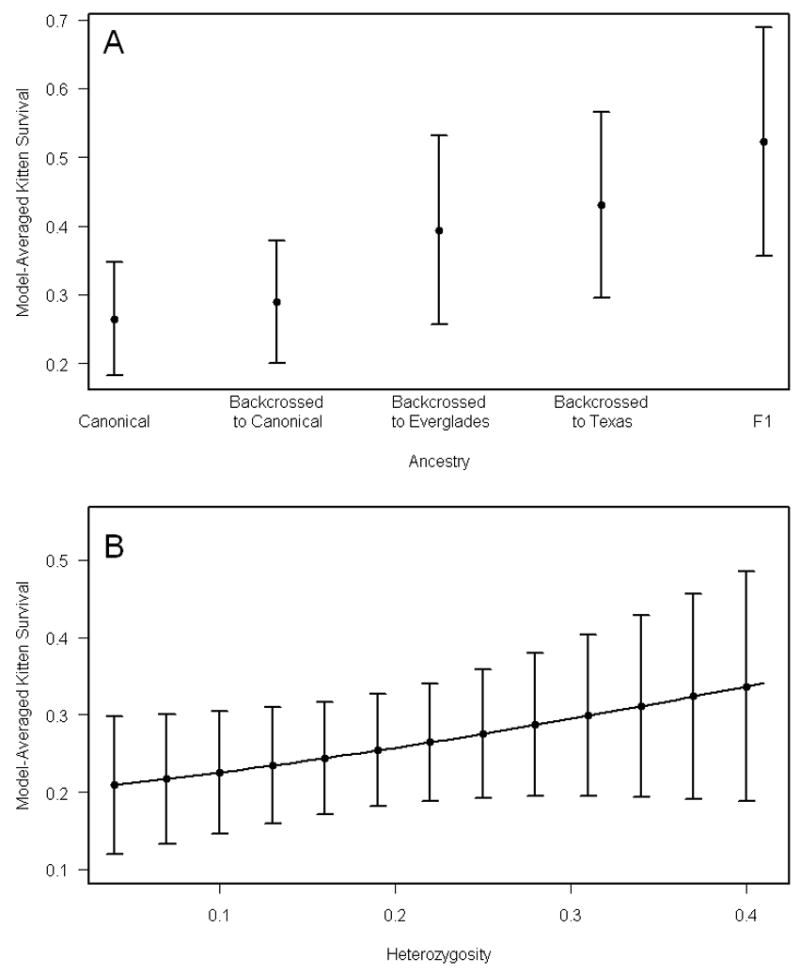
The effect of genetic variables on model-averaged kitten survival estimates. A) Annual survival plotted against ancestry category. B) Annual survival plotted against heterozygosity. Error bars represent unconditional standard errors.

The most parsimonious model including the effects of heterozygosity on survival indicated that survival of panthers of all ages (including survival of kittens) was positively affected by average heterozygosity (Table 3B, model 1). Although this model differed from the base model by ΔQAIC_c <2, the 95% confidence interval for the slope parameter did not include zero (β = 2.89; 95% CI: 0.16 – 5.63) suggesting a positive effect of average heterozygosity on panther survival. Model-averaged kitten survival increased with heterozygosity (Figure 1B).

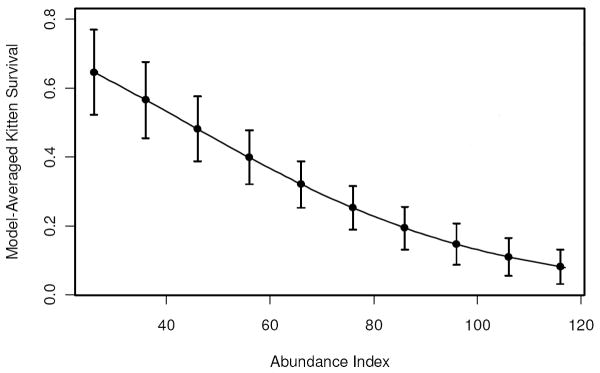
There was considerable evidence that abundance negatively influenced kitten survival, with the model with no such effect having a ΔQAIC_c of 8.79 (Table 3C). Kitten survival declined with increasing population size (Figure 2; β = -0.034, 95% CI = -0.053 – -0.016).

Figure 2.

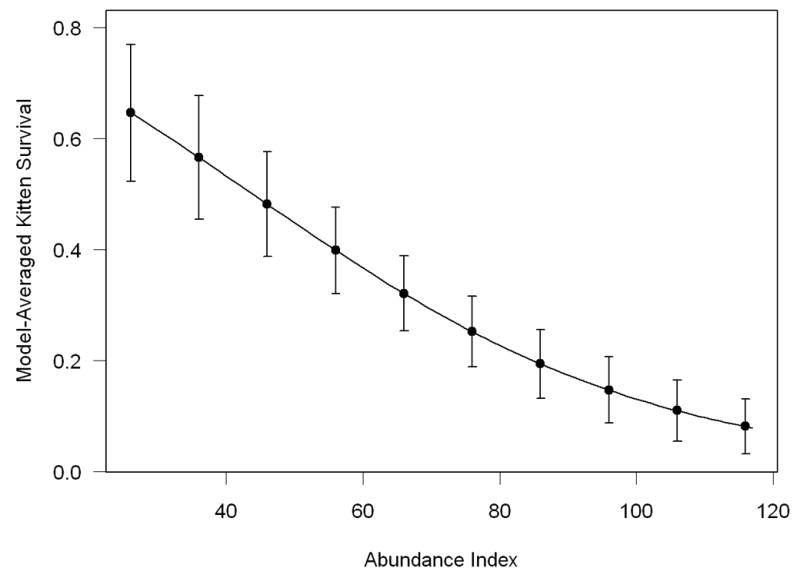
The effect of a panther abundance index on model-averaged kitten survival estimates. Error bars represent unconditional standard errors.

We estimated temporal standard deviation of kitten survival (σ) at 0.228 (95% credible interval = 0.019 – 0.431) and 0.098 (95% credible interval = 0.004 – 0.286) using models without and with the abundance index, respectively. Abundance index explained 81.5% of the temporal variation in kitten survival.

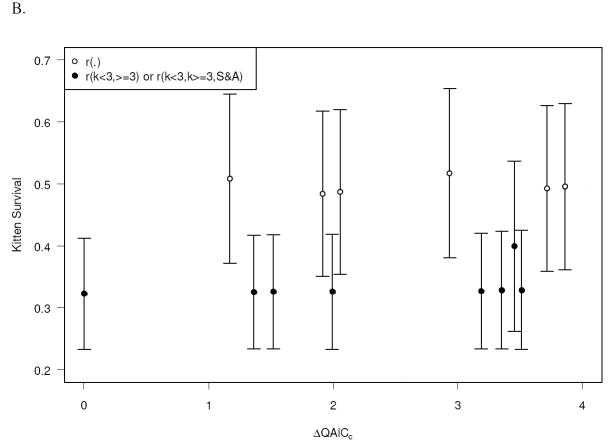
There was considerable uncertainty in the base model selection, with 8 models in Table 2 having ΔQAIC_c < 1. We reran all covariate tests using model 5 from Table 2 as a base model (model 5 was the highest ranked model with a different estimate of kitten survival than model 1). Model selection and statistical inference were barely affected by the switch of base models, and model averaged estimates that included both sets of models were somewhat lower, but generally had similar precision (Appendix D).

There was strong evidence that kitten survival was lowest in the first 3 months of life (Figure 3). There was no evidence for seasonal variation in kitten survival (Appendix C). Details of results based on the analysis of data organized using 3-month time steps are presented in Appendix C.

Figure 3.

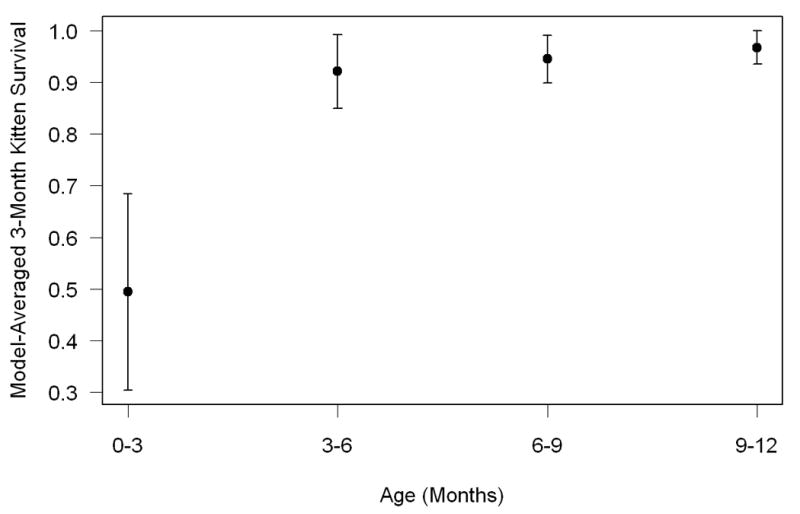
Model-averaged kitten survival by 3-month age interval within the first year. Error bars represent unconditional standard errors.

4. Discussion

Models developed for population conservation and management have historically focused on either population dynamics (Morris and Doak 2002) or threshold numbers required to avoid genetic problems (Franklin 1980). The population ecology and population genetics of a species are frequently not integrated in these models. When they are, the demographic effects of inbreeding are often based on data from captive animals and/or program defaults (e.g., Brito 2009; Maehr et al. 2002; Nilsson 2004). An important first step towards developing integrated models is determining the functional relationship between measures of inbreeding and juvenile survival in the wild, especially for managed populations.

Overall, the model-averaged estimate of annual survival probability of Florida panther kittens was 0.323 ± 0.071; this estimate is lower than those reported for western North American populations of pumas (range: 0.44 to 0.72; Lambert et al. 2006; Laundré et al. 2007; Logan and Sweanor 2001; Robinson et al. 2008). Our estimate of kitten survival also is substantially lower than those used in earlier demographic analyses of the Florida panther (Maehr and Caddick 1995: 0.84 - 0.87; Maehr et al. 2002: 0.735 - 1.0; Root 2004: 0.62). Although our estimates of kitten survival varied slightly depending on the model (0.30 to 0.34; Table 2), they were consistently lower than those used in previous analyses. Furthermore, kittens were not tagged immediately after birth, and we could have missed kittens that had died before they were PIT-tagged at the den site; thus, true survival may be slightly lower. However, since most of our data on kitten survival came from a period of population growth (McBride et al. 2008), we have no reason to believe that the kitten survival rate for this population is unsustainable. Ongoing work developing updated population models for Florida panthers may shed additional light on the role of kitten survival in determining population dynamics.

Survival rates did not differ between male and female kittens. This result was as expected due to the lack of sexual dimorphism among kittens, although some authors have suggested sex-specific differences in survival of puma kittens (Logan and Sweanor 2001). There was no evidence that litter size influenced survival of kittens. This may reflect the possibility that females most able to successfully raise large litters are those most likely to produce them.

Perhaps the most dramatic panther conservation measure undertaken to date is the release of 8 female Texas pumas into the Florida panther population in 1995 (Seal 1994). Genetic introgression has been highly controversial (e.g., Maehr and Caddick 1995; Maehr et al. 2006; Pimm et al. 2006). Pimm et al. (2006) reviewed the arguments for and against genetic introgression in general, and in the Florida panther population in particular. They reported that admixed kittens are more than three times as likely to survive as purebred Florida panthers. Pimm et al’s (2006) conclusions were based solely on the proportion of kittens PIT-tagged in the den that were subsequently captured and (generally) radio-collared. These kittens were recaptured at ages ranging from 6.5 months to 3.5 years and detection probability was not taken into account, so it is unclear how well these ratios represent differences in kitten survival.

In the present study, we used multiple sources of field data, a thorough determination of ancestry of nearly all kittens captured since genetic introgression occurred in 1995, and a statistically rigorous live-recapture dead-recovery modeling approach that takes detection probabilities into account to test for the effect of genetic introgression on the survival of Florida panther kittens. As recommended by Creel (2006), we limited this portion of the analysis to a period when both canonical and admixed kittens were on the landscape. We also were able to examine the effects of heterozygosity, which differed dramatically between canonical Florida panthers (0.161) and Texas pumas (0.318; Driscoll et al. 2002; W. Johnson, unpubl. data). Furthermore, we were able to determine ancestry of panther kittens at a much finer scale than Pimm et al. (2006). We found that admixed kittens generally survived better than kittens born to canonical Florida panthers. Furthermore, F₁ admixed kittens had the highest survival, followed by backcrossed to Texas kittens (Fig. 1A). Finally, we found that average heterozygosity positively influenced survival of Florida panther kittens (Fig. 1B). These results provide unambiguous evidence for the positive, population-level impact of genetic introgression.

Index of panther abundance negatively influenced kitten survival, which is suggestive of a density dependent effect. This could result from infanticide by sub-adult and adult males during territorial disputes or for mating opportunities (Garrison et al. 2007; Logan and Sweanor 2001; Packer et al. 2009), from deaths of the dependent kittens’ dams due to intraspecific aggression, or from competition for food or other resources. We note, however, that our results are based on an index of abundance, and thus may not be sufficient to conclusively demonstrate density-dependent influence on kitten survival. Interestingly, a substantial proportion of temporal variation in kitten survival was explained by temporal variance in index of abundance.

Analysis of data organized with 3-month time intervals revealed no evidence for seasonal (i.e., wet vs. dry) variation in survival of kittens. However, we found that survival was lowest during the first 3 months of life, which is consistent with other large carnivore populations (Garrison et al. 2007; Logan and Sweanor 2001). These results point to the fact that young kittens are particularly vulnerable to various mortality factors.

Estimating survival of young can be challenging in elusive carnivores because they are rarely observed. Additionally, in the case of panthers, kittens are typically too small to be fitted with radio-transmitters when sampled at the den site – a method that would be effective for monitoring their fate during the first year of life. Furthermore, the small population size of endangered species and invariably small sample sizes may not be adequate for rigorous estimates of survival of the young. For example, estimates of kitten survival that did not include litter failure data lacked robustness as well as precision; models that were similarly ranked based on QAIC_c provided very different estimates of kitten survival (Appendix C). We addressed this challenge by using a modeling framework that can utilize multiple data sources. Resulting estimates of kitten survival were more robust and precise, and also allowed us to test various hypotheses regarding factors influencing survival of Florida panther kittens. Similar approaches can be used to estimate survival of young in other elusive species that occur in low numbers.

Our study is the first to provide rigorous estimates of survival of Florida panther kittens. We found that kitten survival in our study population was lower than reported for western cougars, and substantially lower than values used in previous demographic analyses of Florida panthers. These results are consistent with an earlier suggestion that results of a previous PVA (Maehr et al. 2002) that assumed kitten survival of up to 87% may be unreliable (Beier et al. 2003). Finally, we found strong evidence that survival of admixed (particularly, F₁) kittens was substantially higher than that of purebred kittens, and that heterozygosity positively influenced survival of Florida panther kittens. These results are consistent with hybrid vigor theory (Crow 1948; Frankham et al. 2002), and suggest that genetic introgression had positive population-level effects in our study population. Although there are concerns that genetic introgression can have undesirable or even negative impacts on populations (Edmands 2007; Maehr and Caddick 1995; Shields 1993), our analyses revealed beneficial results of deliberate introgression for this population. A combination of these results with other recently published or on-going assessments of demography pre- and post-introgression should assist in directing management and research priorities that will ensure the continued persistence the critically endangered Florida panther.

Appendix A

Analysis of Florida Panther Kitten Survival Based on 3 Ancestry Categories

Methods

We used results from the STRUCTURE analysis along with pedigree results and field evidence to assign panthers to 3 groups that reflect the genetic makeup of the southern Florida population (canonical panthers, F₁ admixed panthers, and other admixed panthers). Canonical and F₁ admixed ancestry categories are defined in the main text. The other admixed category includes: backcrossed to canonical (admixed panthers with predominantly (>50%) canonical heritage); backcrossed to Everglades (admixed panthers with predominantly (>50%) Everglades heritage resulting from breeding events between Texas admixed and Everglades panthers); backcrossed to Texas (admixed panthers of predominantly (>50%) Texas heritage resulting from admixed panthers breeding with introduced Texas cougars); unknown admixed; and Seminole admixed panthers (these last two categories were not included in the analyses presented in the text). Based on these 3 ancestry categories, we formulated alternative hypotheses regarding the effect of ancestry on kitten survival (Table A1).

We selected model 1 in Table 4 as the base model because this model had the lowest QAIC_c among candidate models (Table 4), and used model selection to draw inferences for hypotheses about the effects of ancestry on kitten survival (Table A1). For these analyses, we used a subset of data collected between 1995 and 2008, due to the absence of admixed panthers in Florida before 1995. We tested for the effect of ancestry on survival of (1) kittens only; (2) sub-adult and adult panthers only; (3) kittens and older panthers considered separately; and (4) panthers of all ages. Based on previous results (Benson et al. 2009), however, we only considered 2 ancestry categories for sub-adult and adult panthers (Ancest2; Table A1). We report model-averaged annual estimates of kitten survival probability (Burnham and Anderson 2002).

Results and Discussion

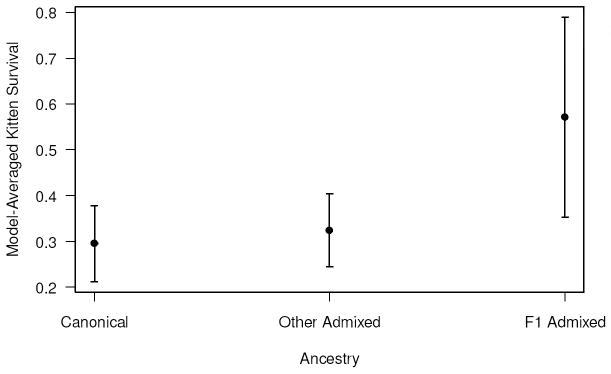
Three models (base + k:Ancest1, base + k:Ancest1 + s&a:Ancest2, and base + k:Ancest2) failed to estimate a kitten survival parameter and were discarded. The most parsimonious model testing for the effect of simple ancestry on survival indicated that survival of panthers of all ages (including survival of kittens) was higher for F₁ admixed (Table A2, model 1). Although this model differed from the model where ancestry only affects the survival of sub-adults and adults (model 3) by ΔQAIC_c <2, the 95% confidence interval for the slope parameter did not include zero (β = 1.55; 95% CI: 0.46 – 2.65) providing strong evidence of a difference between the survival of F₁ admixed and other panthers. Model-averaged estimated kitten survival increased from canonical to other admixed to F₁ admixed panthers (Figure A1).

These results suggest that although there are subtle differences in survival of kittens with various genetic ancestries, the main difference is that between F1 admixed kittens and those of all other ancestry categories. F1 admixed kittens survived substantially better than kittens with other ancestry categories. This F1 admixed kitten survival advantage was also found in the ancestry analysis presented in the text. One difference in that analysis is that we found that some of the other admixed categories (specifically backcrossed to Texas and possibly backcrossed to Everglades) also had higher survivals than the canonical kittens. We believe that those results represent real differences within the other admixed category, and are not an artifact of the exclusions required for that analysis.

Table A1.

Definitions of simple ancestry models, and the hypotheses they represent.

Term	Definition	Hypothesis
Ancest1	3 ancestry categories: 1) Canonical; 2) Other Admixed; and 3) F1 Admixed.	Different survival probability for each ancestry group.
Ancest2	2 ancestry categories: 1) Canonical and Other Admixed; and 2) F1 Admixed.	First generation survival advantage (or disadvantage).
Ancest3	2 ancestry categories: 1) Canonical; and 2) Other Admixed and F1 Admixed.	General admixed survival advantage (or disadvantage).

Table A2.

Model selection table for testing hypotheses regarding the effect of genetic ancestry on survival of kittens and older panthers based on 3 ancestry categories. These analyses were performed on a subset of the data (excluding panthers before 1995 and panthers of unknown ancestry). For each model, we present the number of parameters (K), the difference from the top model in Akaike’s Information Criterion adjusted for small sample size and overdispersion (ΔQAIC_c), and the model QAIC_c weight. See Table A1 for descriptions of the covariate models and Table 4 for the base model. All models estimate constant recapture rates and recovery rates that differ between kittens and older panthers (p(.)r(k, s&a)). Model 1 in Table 2 was used as the base model for these analyses. Ancestry categories are defined in Table A1.

Survival Model	K	ΔQAICc	Weight
1. base + Ancest2	9	0.00	0.367
2. base + Ancest1	10	1.15	0.207
3. base + s&a:Ancest2	9	1.86	0.145
4. base + k:Ancest2 + s&a:Ancest2	10	2.04	0.132
5. base + k:Ancest3 + s&a:Ancest2	10	2.52	0.104
6. base + Ancest3	9	5.81	0.020
7. base	8	6.46	0.015
8. base + k:Ancest3	9	6.91	0.012

Figure A1.

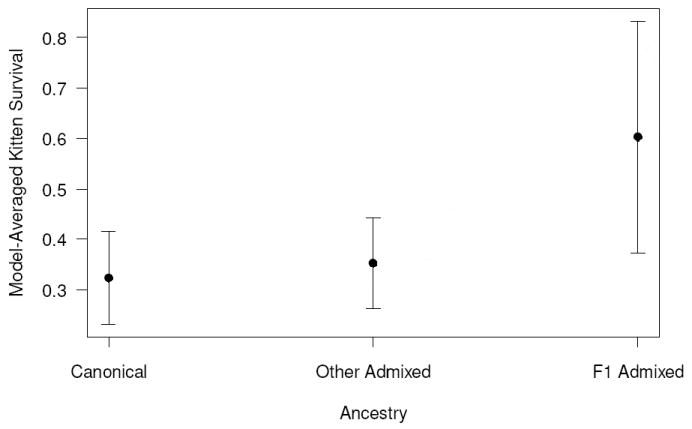
Model-averaged estimates of annual survival of Florida panther kittens based on 3 ancestry categories (Table A1). Error bars represent unconditional estimated standard errors.

Appendix B

Data Preparation

We used two datasets for the analysis of kitten survival. The first contained the capture (of live panthers) and recovery (of dead panthers) histories, observations of litter-failures (i.e., loss of entire litters), and radio-tracking data for panthers that were initially PIT-tagged in the den between June 1995 and May 2008 (13 years). The second contained the capture, recovery, and radio-tracking histories of all other panthers between June 1982 and May 2008 (26 years). We used a live-dead data input format (Cooch and White 2008).

We coded the data with a 1-year time step. All litter failures were treated as recoveries within the first year, because all known litter failures occurred within the first year of kittens’ lives (after which the kittens’ fates were considered to be independent of their dams’). For panthers that were not PIT-tagged in the den, captures and radio-failures were coded as occurring on the closest June 1, and known deaths were coded as occurring in the June-May interval in which they occurred. PIT-tagging events of kittens in the den were also coded as occurring on the closest June 1. Subsequent captures, radio-failures, and known deaths of that group were coded to happen at the correct age, rather than the correct year, on the occasions when those were in conflict.

Panthers that would have died if we had not removed them to captivity were treated as having died on the date of removal. One exception was a panther whose injuries were apparently capture related; it was right-censored on the capture date and added again to the analysis on the date it was returned to the wild. Kittens that were found dead during the initial den visit (n=7) were not included in the survival analysis, but were included in the litter size counts of PIT-tagged kittens in their litters.

The ages of 91 radio-collared panthers not handled as kittens in the den were estimated as previously described; 11 were estimated to be < 1 year of age. When ages were estimated as a range in the field (e.g., 5-6 years old), we used the average of the range for assigning age class transitions. The influence of estimated age on the estimates of survival of adult panthers was insubstantial (Benson et al. 2009: Appendix A); this effect is likely even smaller for survival of kittens.

The sex of two kittens from a single litter was not recorded in the field; since their fates were the same and the overall numbers of kittens PIT-tagged for each sex were similar (119 females and 131 males), we randomly assigned one as a female and the other male. We did not have covariate data for all panthers included in the analyses. Thus, we tested for the effect of litter size and ancestry on survival separately after excluding kittens or all panthers, respectively, with missing values. For average heterozygosity, we ran a separate analysis excluding panthers that had not been genotyped, as well as captures of panthers that occurred before they were successfully genotyped. This approach removed the potential bias in survival estimates by heterozygosity that would be caused by only excluding those that were never genotyped (Nichols et al. 2004).

Appendix C

Analysis of Survival of Florida Panther Kittens Using Data Organized in 3-month Time Steps

Methods

Using the data organized on an annual time scale, it was not possible to test for seasonal variation in kitten survival and changes in survival within the first year of life. Therefore, we recoded the data with 3-month time steps. This necessitated leaving out litter failure data, because the 3-month interval in which actual kitten deaths occurred was generally not available from these data. The large number of capture occasions (26*4 = 104) made it computationally necessary to divide the sampling period in half. All data from panthers PIT tagged in the den were in the second half and could be handled normally, but all other panthers were only followed while radio-collared to accommodate the half transition. The analyses of data organized in 3-month time step also allowed us to compare sub-adult and adult survival with the results of Benson et al. (2009), because we were now able to put the transition from sub-adult to adult at the same age as in their analyses (2.5 years old for females and 3.5 years old for males).

Analysis of the data with a 3-month time step was similar to the annual time step analysis, except that there was now a possibility of recapture as a kitten. We set recapture probability (p) and recovery probability (r) for radio-collared animals to 1, and p for 3-month old panthers to 0, because none of the few panthers captured and radio-collared at <6 months of age were PIT-tagged first. The FWC and National Park Service (NPS) instituted a policy in November 2001 restricting the capturing and radio-collaring of kittens < 12 months in age. Therefore we fixed p at 0 for 6-month old kittens starting at that date.

Data analysis proceeded as described in the text. We commenced by testing all a priori models for recapture and recovery combined with a priori models for survival of kittens based on age (Table C1). The kittens of Texas cougars may have been more likely to be captured than other kittens, due to greater efforts expended to capture those kittens (model 1, Table C1A). The justification for the separate recovery rate for kittens ≤3 months of age (models 4 and 5, Table C1B) is that a different series of events leads to recovery of kittens in the den (approximately the first 7-8 weeks, Maehr et al. 1990) compared to older panthers. For a kitten in the den to be recovered, it has to be PIT-tagged, die, and then be found in a subsequent visit to the den. For an older (non-radio-collared) panther that was handled and marked with a PIT tag as a kitten to be recovered, it has to die (most likely due to a vehicle collision), and subsequently be reported to panther researchers. A cause-specific mortality analysis of radio-collared sub-adult and adult panthers suggests that the probability of a panther’s death being due to vehicular collision is independent of sex or age class (Benson et al. 2009).

We tested all combinations of survival, recapture, and recovery models from Table C1 and selected the most general model that converged successfully (if there was a tie, we selected the model with the lowest AIC_c). We used that model to test for overdispersion of the data due to lack of independence within litters using a data bootstrap (Bishop et al. 2008). We sampled litters from the dataset with replacement. Panthers first captured as sub-adults or adults were treated as litters of size 1 for the bootstrapping. We estimated annual survival of kittens as a derived parameter of the model. If the model failed to estimate any parameters, the iteration was discarded. We repeated the resampling and estimation until we had 1,000 estimates of kitten survival. We calculated the mean and standard deviation of the estimates, and estimated the overdispersion parameter (ĉ) as [(bootstrap standard deviation of estimates of kitten survival) / (standard error of kitten survival obtained from the original model run)]². An estimated ĉ > 1 indicates overdispersion. We used the estimated ĉ to calculate the QAICc for each model and as a variance inflation factor.

We selected the model or set of models with the lowest QAIC_c as the base model(s) to test our hypothesis that kitten survival varies seasonally. We report model-specific and model-averaged 3-month and annual estimates of kitten survival probability and model-averaged estimates of recapture, recovery, and sub-adult and adult survival probabilities (Burnham and Anderson 2002).

Results and Discussion

Of the 72 models run (all permutations from Table C1), 14 failed to estimate all parameters and were discarded, including all models using survival model 7 (Table C1C). From the most general models remaining (with 13 parameters), the model S(k<3, 3≤k<9, k≥9) p(k:DO, s&a) r(k<3, k≥3, s&a) had the lowest AIC_c and was used in the litter bootstrap to estimate ĉ. We estimated ĉ at 2.20, which is only slightly less than the average litter size of PIT tagged kittens used in the analysis (mean litter size = 2.47).

There was strong support for kitten survival being lowest in the first 3 months of life (Table C2; main text Figure 1). Several closely ranked models yielded very different estimates of annual kitten survival, and variances of most estimates were substantial (Table C2, Fig. C1). These results suggest that estimates of kitten survival obtained from data organized in 3 month-time steps lacked precision and robustness, most likely due to sample size limitations. Among the top models, the main factor that affected estimated kitten survival was whether recovery of dead panthers differed between kittens in the first 3 months of life and other panthers (low estimates of survival, about 0.33) or not (high estimates of survival, about 0.50). The model-averaged estimate of annual kitten survival from the 3-month analysis was 0.404 (95% CI: 0.169 – 0.693). The uncertainty of this estimate was high due to 1) small sample sizes and uncertainty about the fates of individual kittens leading to large standard errors for estimates from individual models; 2) further increase of these standard errors by the variance inflation factor, to account for overdispersion; and 3) different models often producing very different estimates of kitten survival, and the unconditional confidence interval presented here incorporates that uncertainty.

Estimated annual survival rates of sub-adults and adults were fairly consistent among models and the model-averaged estimates were similar to those from the corresponding model in Benson et al. (2009; Table C3). The slightly lower estimate of sub-adult female survival may be in part due to a death of a female panther near her estimated 1^st birthday that was categorized as a sub-adult in the kitten analysis and as a kitten in the adult analysis.

We selected two highly ranked models with differing estimates of kitten survival (models 1 & 2, Table C2) as base models for testing the effects of season on kitten survival. There was no evidence of an effect of season on kitten survival (Table C4).

Table C1.

A priori models used for the analysis of A) recapture probability (p), B) recovery probability (r), and C) survival probability (age models only; S), using a 3-month time step. All combinations of p, r, and S models in this table were run. We also tested for the effect of season (wet vs. dry) on S, using the top model(s) from this analysis. For all models, p and r were fixed at 1 for radio-collared panthers. We fixed p at 0 for kittens younger than 6 months old and for kittens younger than 9 months old after November 2001 for all models. All models estimated non-kitten survival as the interaction of sex and age-class (sub-adult or adult); therefore, we only describe how kitten survival was modeled.

A) Model for p	Description
1. p(k:DO, s&a)	Recapture probability differs between kittens and older panthers, and between kittens with dam origin of Florida and Texas.
2. p(k, s&a)	Recapture probability differs between kittens and older panthers.
3. p(.)	Recapture probability is the same for all panthers.
B) Model for r	Description
4. r(k<3, k≥3, s&a)	Recovery probability differs between kittens in their first three months, older kittens, and non-kittens.
5. r(k<3, ≥3)	Recovery probability differs between kittens in their first three months and older panthers.
6. r(.)	Recovery probability the same for all panthers.
C) Model for S	Description
7. S(k<3, 3≤k<6, 6≤k<9, k≥9)	Age effect (survival differs between each of 4 3-month age intervals)
8. S(k<6, 6≤k<9, k≥9)	Age effect (survival same for first two age intervals)
9. S(k<3, 3≤k<9, k≥9)	Age effect (survival same for second two age intervals)
10. S(k<6, k≥6)	Age effect (survival same for first two age intervals, same for second two age intervals)
11. S(k<3, k≥3)	Age effect (survival same for last three age intervals)
12. S(AT)	Age trend (survival over the first 4 3-month intervals as a linear trend)
13. S(.)	Survival same for all kittens

Table C2.

Kitten survival models to examine the effects of age (3-month time step). For each model, we present the number of parameters (K), the difference from the top model in second-order Quasi-Akaike’s Information Criterion (ΔQAIC_c), the model QAIC_c weight, and the estimate of annual kitten survival with standard error. See Table C1 for descriptions of models. The base models selected are in bold.

Model	K	ΔQAICc	Weight	Annual Kitten Survival Estimate (SE)
1. S(k<3, k≥3)p(k, s&a)r(k<3, ≥33)	10	0	0.170	0.323 (0.090)
2. S(k<3, k≥3)p(k, s&a)r(.)	9	1.170	0.095	0.508 (0.136)
3. S(k<3, 3≤k<9, k≥9)p(k, s&a)r(k<3, ≥3)	11	1.361	0.086	0.326 (0.091)
4. S(k<3, k≥3)p(k, s&a)r(k<3, k≥3, s&a)	11	1.518	0.079	0.326 (0.092)
5. S(AT)p(k, s&a)r(.)	9	1.914	0.065	0.484 (0.133)
6. S(k<3, k≥3)p(k:DO, s&a)r(k<3, ≥3)	11	1.991	0.063	0.326 (0.093)
7. S(k<3, 3≤k<9, k≥9)p(k, s&a)r(.)	10	2.057	0.061	0.487 (0.133)
8. S(k<3, k≥3)p(k:DO, s&a)r(.)	10	2.935	0.039	0.517 (0.136)
9. S(k<3, 3≤k<9, k≥9)p(k, s&a)r(k<3, k≥3, s&a)	12	3.188	0.034	0.327 (0.093)
10. S(k<3, 3≤k<9, k≥9)p(k:DO, s&a)r(k<3, ≥3)	12	3.354	0.032	0.329 (0.095)
11. S(AT)p(k, s&a)r(k<3, ≥3)	10	3.454	0.030	0.399 (0.137)
12. S(k<3, k≥3)p(k:DO, s&a)r(k<3, k≥3, s&a)	12	3.512	0.029	0.329 (0.096)
13. S(AT)p(k:DO, s&a)r(.)	10	3.717	0.026	0.493 (0.134)
14. S(k<3,3≤k<9, k≥9)p(k:DO, s&a)r(.)	11	3.863	0.025	0.496 (0.134)
15. S(.)p(k, s&a)r(k<3, ≥3)	9	4.42	0.019	0.770 (0.137)
16. S(AT)p(k, s&a)r(k<3, k≥3, s&a)	11	4.58	0.018	0.355 (0.111)
17. S(k<3, 3≤k<9, k≥9)p(k:DO, s&a)r(k<3, k≥3, s&a)	13	5.18	0.013	0.330 (0.097)
18. S(AT)p(k:DO, s&a)r(k<3, ≥3)	11	5.36	0.012	0.411 (0.1 48)
19. S(k<6, k≥6)p(k, s&a)r(.)	9	5.63	0.010	0.498 (0.138)
20. S(k<6, 6≤k<9, k≥9)p(k, s&a)r(.)	10	5.67	0.010	0.481 (0.133)
21. S(.)p(k:DO, s&a)r(k<3, ≥3)	10	5.98	0.009	0.775 (0.135)
22. S(.)p(k, s&a)r(k<3, k≥3, s&a)	10	6.43	0.007	0.781 (0.267)
23. S(AT)p(k:DO, s&a)r(k<3, k≥3, s&a)	12	6.54	0.007	0.361 (0.118)
24. S(.)p(k, s&a)r(.)	8	7.12	0.005	0.590 (0.129)
25. S(k<6, 6≤k<9, k≥9)p(k, s&a)r(k<3, k≥3, s&a)	12	7.22	0.005	0.400 (0.154)
26. S(k<6, k≥6)p(k:DO, s&a)r(.)	10	7.40	0.004	0.507 (0.139)
27. S(k<6, 6≤k<9, k≥9)p(k:DO, s&a)r(.)	11	7.49	0.004	0.490 (0.135)
28. S(k<6, k≥6)p(k, s&a)r(k<3, k≥3, s&a)	11	7.74	0.004	0.404 (0.163)
29. S(k<3, k≥3)p(.)r(k<3, ≥3)	9	8.13	0.003	0.307 (0.076)
30. S(.)p(k:DO, s&a)r(.)	9	8.79	0.002	0.595 (0.128)
31. S(k<6, 6≤k<9, k≥9)p(k:DO, s&a)r(k<3, k≥3, s&a)	13	9.13	0.002	0.414 (0.172)
32. S(k<3, 3≤k<9, k≥9)p(.)r(k<3, ≥3)	10	9.62	0.001	0.308 (0.077)
33. S(k<6, k≥6)p(k:DO, s&a)r(k<3, k≥3, s&a)	12	9.62	0.001	0.422 (0.189)
34. S(k<3, k≥3)p(.)r(.)	8	9.91	0.001	0.437 (0.118)
35. S(k<3, k≥3)p(.)r(k<3, k≥3, s&a)	10	9.95	0.001	0.308 (0.077)
36. S(AT)p(.)r(.)	8	10.77	0.001	0.420 (0.113)
37. S(k<3, 3≤k<9, k≥9)p(.)r(.)	9	10.98	0.001	0.423 (0.113)
38. S(k<3, 3≤k<9, k≥9)p(.)r(k<3, k≥3, s&a)	11	11.57	0.001	0.308 (0.0 77)
39. S(AT)p(.)r(k<3, ≥3)	9	11.97	0.000	0.355 (0.101)
40. S(AT)p(.)r(k<3, k≥3, s&a)	10	12.59	0.000	0.326 (0.086)
41. S(k<6, k≥6)p(.)r(.)	8	14.13	0.000	0.428 (0.117)
42. S(.)p(.)r(k<3, ≥3)	8	14.18	0.000	0.640 (0.184)
43. S(k<6, 6≤k<9, k≥9)p(.)r(.)	9	14.39	0.000	0.417 (0.112)
44. S(.)p(.)r(k<3, k≥3, s&a)	9	14.57	0.000	0.426 (0.144)
45. S(k<6, 6≤k<9, k≥9)p(.)r(k<3, k≥3, s&a)	11	14.99	0.000	0.350 (0.099)
46. S(.)p(.)r(.)	7	15.09	0.000	0.487 (0.125)
47. S(k<6, k≥6)p(.)r(k<3, k≥3, s&a)	10	15.21	0.000	0.350 (0.101)
48. S(k<6, k≥6)p(.)r(k<3, ≥3)	9	15.87	0.000	0.491 (0.218)
49. S(k<6, 6≤k<9, k≥9)p(.)r(k<3, ≥3)	10	16.01	0.000	0.488 (0.211)

Table C3.

Estimates of annual sub-adult and adult survival from the 3-month kitten survival analysis and the adult analysis of Benson et al. (2009). Sub-adult is defined as ages 1-2.5 for females and 1-3.5 for males; adult is defined as ages 2.5 and up for females and 3.5 and up for males. The results from the kitten analysis are the model-averaged survivals from all models in the 3-month analysis; the results from the adult analysis are from the Sex * Age1 model (Benson et al. 2009).

		Annual Survival Estimates (SE)
Sex	Age Class	Kitten Analysis	Adult Analysis
Female	Sub-Adult	0.929 (0.051)	0.954 (0.032)
Female	Adult	0.858 (0.03)	0.852 (0.023)
Male	Sub-Adult	0.723 (0.066)	0.712 (0.05)
Male	Adult	0.774 (0.049)	0.782 (0.035)

Table C4.

Model comparison table for examining the effects of season on kitten survival. For each model, we present the number of parameters (K), the difference from the top model in second-order Quasi-Akaike’s Information Criterion (ΔQAIC_c), the model QAIC_c weight, and the estimate of seasonal kitten survival with standard error. The same recapture model (p(k, s&a)) was used in all models. See Table C1 for descriptions of models.

				6-Month Kitten Survival
Model	K	ΔQAICc	Weight	Wet Season	Dry Season
1. S(k<3, k≥3)r(k<3, ≥3)	10	0.00	0.469	0.568 (0.079)
2. S(k<3, k≥3)r(.)	9	1.17	0.261	0.713 (0.096)
15. S(k<3, k≥3 + season)r(k<3, ≥3)	11	2.01	0.172	0.564 (0.102)	0.572 (0.093)
16. S(k<3, k≥3 + season)r(.)	10	3.14	0.098	0.736 (0.144)	0.703 (0.107)

Figure C1.

Individual model estimates of annual kitten survival A) from the 1-year time step analysis and B) from the 3-month time step analysis. All models are shown in A, whereas only top models (the difference from the top model in second-order Quasi-Akaike’s Information Criterion or ΔQAIC_c < 4) are plotted in B. Models are aligned by their ΔQAIC_c value on the x-axis. Error bars represent standard errors (adjusted by the variance inflation factor).

Appendix D

Including another Base Model

Methods

To examine the effects of base model uncertainty on covariate testing, we ran all covariates with the highest ranked model from Table 2 that had a different estimate of kitten survival than the base model (this was model 5). This model (hereafter called base2) modeled survival identically to the base model but estimated one recovery rate for all panthers instead of dividing it between kittens and older panthers. All covariate analyses were performed the same way as in the main text. We report full model average estimates based on all models run with both base models.

Results

All covariate models using base2 could estimate all parameters. There was still no evidence that sex or litter size affected kitten survival (Table D1). There was still considerable evidence that ancestry influenced kitten survival; the 7 most parsimonious models all included ancestry effects on kitten survival (models 1-7, Table D2A). The top 2 models indicated that survival of kittens differed substantially between two ancestry categories: 1) canonical and backcrossed to canonical kittens and 2) F₁, backcrossed to Texas, and backcrossed to Everglades kittens (Table D2A). Full model-averaged kitten survival was lowest for canonical kittens and highest for F₁ kittens (Figure D1A), and were slightly lower for all ancestry classes than model averages from the base model alone (Figure 1A).

The most parsimonious model testing for the effect of heterozygosity on survival indicated that survival of panthers of all ages (including survival of kittens) was positively affected by average heterozygosity (Table D2B, model 1). Full model-averaged estimated kitten survival increased with heterozygosity (Figure D1B).

The evidence for the effect of abundance index on kitten survival was even stronger using base2 (Table D2C). Full model-averaged estimated kitten survival declined with abundance index (Figure D2). We estimated temporal standard deviation of kitten survival (σ) at 0.199 (95% credible interval = 0.011 – 0.380) and 0.077 (95% credible interval = 0.003 – 0.234) using models without and with abundance index, respectively.

The most parsimonious model testing for the effect of simple ancestry on survival indicated that survival of panthers of all ages (including survival of kittens) was higher for F₁ admixed (Table D3, model 1). Full model-averaged estimated kitten survivals increased from canonical to other admixed to F₁ admixed (Figure D3), and were slightly lower for all ancestry classes than model averages from the base model alone (Figure A1).

Interestingly, unconditional standard errors estimated for the full model set tended to be lower than those estimated for the base model set alone, even when the full model-averaged estimate was closer to 0.5.

Table D1.

Model selection table for A) sex effect on kitten survival and B) litter size effect on kitten survival. For each model, we present the number of parameters (K), the difference from the top model in Akaike’s Information Criterion adjusted for overdispersion and small sample size (ΔQAIC_c), the model QAIC_c weight, and the estimates of annual kitten survival with standard error (for both sexes and the highest and lowest litter sizes). The QAIC_c values of the top models are 857.23 and 845.66, respectively (compare to QAIC_c values for the base models run with the same datasets of 856.76 and 845.64, respectively). See Table 1 for descriptions of the covariate models and Table 2 (model 5) for the base2 model. The litter size analysis was performed on a subset of the data (excluding kittens from litters of unknown size). All models estimate constant recapture and recovery rates (p(.)r(.)).

A. Sex models				Annual Kitten Survival Estimate (SE)
Survival Model	K	ΔQAICc	Weight	Female	Male
1. base2	7	0.00	0.725	0.296 (0.054)
2. base2 + k:sex	8	1.94	0.275	0.311 (0.068)	0.282 (0.065)
B. Litter size models				Annual Kitten Survival Estimate (SE)
Survival Model	K	ΔQAICc	Weight	1 kitten	4 kittens
1. base2	7	0.00	0.735	0.280 (0.050)
2. base2 + k:LS	8	2.04	0.265	0.279 (0.109)	0.280 (0.081)

Table D2.

Model selection table for A) ancestry effects on kitten and older survival, B) heterozygosity effects on kitten and older survival, and C) abundance index effects on kitten survival. These analyses were performed on subsets of the data (excluding panthers before 1995 for all analyses and panthers of unknown ancestry for A, and panthers before their heterozygosity was successfully sampled for B). For each model, we present the number of parameters (K), the difference from the top model in Akaike’s Information Criterion adjusted for overdispersion and small sample size (ΔQAIC_c), and the model QAIC_c weight. The QAIC_c values of the top models are 623.98, 577.80, and 716.22, respectively (compare to QAIC_c values for the top models of Table 3 of 624.41, 577.37, and 716.46, respectively). See Table 1 for descriptions of the covariate models and Table 2 (model 5) for the base2 model. All models estimate constant recapture and recovery rates (p(.)r(.)).

A. Ancestry models
Survival Model	K	ΔQAICc	Weight
1. base2 + k:GenAnc2 + s&a:GenAnc6	9	0.00	0.232
2. base2 + GenAnc2	8	1.18	0.128
3. base2 + GenAnc6	8	1.35	0.118
4. base2 + GenAnc4	9	1.83	0.093
5. base2 + k:GenAnc3 + s&a:GenAnc6	9	2.07	0.082
6. base2 + k:GenAnc6 + s&a:GenAnc6	9	3.20	0.047
7. base2 + GenAnc3	8	3.21	0.047
8. base2 + s&a:GenAnc6	8	3.23	0.046
9. base2 + k:GenAnc1 + s&a:GenAnc6	9	3.71	0.036
10. base2 + k:GenAnc5 + s&a:GenAnc6	10	3.84	0.034
11. base2 + k:GenAnc2	8	3.85	0.034
12. base2 + k:GenAnc4 + s&a:GenAnc6	10	4.29	0.027
13. base2 + GenAnc5	9	4.69	0.022
14. base2 + GenAnc1	8	5.55	0.014
15. base2 + k:GenAnc3	8	5.94	0.012
16. base2 + k:GenAnc6	8	6.44	0.009
17. base2 + k:GenAnc4	9	7.53	0.005
18. base2	7	7.54	0.005
19. base2 + k:GenAnc5	9	7.72	0.005
20. base2 + k:GenAnc1	8	7.93	0.004
B. Heterozygosity models
Survival Model	K	ΔQAICc	Weight
1. base2 + Het	8	0.00	0.320
2. base2 + s&a:Het	8	0.53	0.245
3. base2	7	0.78	0.216
4. base2 + k:Het + s&a:Het	9	2.07	0.114
5. base2 + k:Het	8	2.22	0.105
C. Abundance index models
Survival Model	K	ΔQAICc	Weight
1. base2 + k:Abundance	8	0.00	0.992
2. base2	7	9.65	0.008

Table D3.

Model selection table for three category ancestry effects on kitten and older survival. These analyses were performed on subsets of the data (excluding panthers before 1995 and panthers of unknown ancestry). For each model, we present the number of parameters (K), the difference from the top model in Akaike’s Information Criterion adjusted for overdispersion and small sample size (ΔQAIC_c), and the model QAIC_c weight. The QAIC_c value of the top model is 716.21 (compare to QAIC_c value for the top model of Table A2 of 715.74). See Table A1 for descriptions of the covariate models and Table 2 (model 5) for the base2 model. All models estimate constant recapture and recovery rates (p(.)r(.)).

Survival Model	K	ΔQAICc	Weight
1. base2 + Ancest2	8	0.00	0.321
2. base2 + Ancest1	9	1.04	0.191
3. base2 + s&a:Ancest2	8	1.68	0.138
4. base2 + k:Ancest2 + s&a:Ancest2	9	1.77	0.133
5. base2 + k:Ancest3 + s&a:Ancest2	9	2.68	0.084
6. base2 + k:Ancest1 + s&a:Ancest2	10	3.19	0.065
7. base2 + k:Ancest2	8	5.50	0.020
8. base2 + Ancest3	8	5.74	0.018
9. base2	7	6.58	0.012
10. base2 + k:Ancest1	9	6.92	0.010
11. base2 + k:Ancest3	8	7.50	0.008

Figure D1.

The effect of genetic variables on model-averaged kitten survival estimates, including two different base models (base and base2). A) Annual survival plotted against ancestry category. B) Annual survival plotted against heterozygosity. Error bars represent unconditional estimated standard errors.

Figure D2.

The effect of a panther abundance index on model-averaged kitten survival estimates, including two different base models (base and base2). Error bars represent unconditional estimated standard errors.

Figure D3.

Model-averaged estimates of annual survival of Florida panther kittens based on 3 ancestry categories, including two different base models. Error bars represent unconditional estimated standard errors.