Abstract
How phenomena like helping, dispersal, or the sex ratio evolve depends critically on demographic and life-history factors. One phenotype that is of particular interest to biologists is genomic imprinting, which results in parent-of-origin specific gene expression and thus deviates from the predictions of Mendel’s rules. The most prominent explanation for the evolution of genomic imprinting, the kinship theory, originally specifies that multiple paternity can cause the evolution of imprinting when offspring affect maternal resource provisioning. Most models of the kinship theory do not detail how population subdivision, demography, and life-history affect the evolution of imprinting. In this work, we embed the classic kinship theory within an island model of population structure and allow for diverse demographic and life-history features to affect the direction of selection on imprinting. We find that population structure does not change how multiple paternity affects the evolution of imprinting under the classic kinship theory. However, if the degree of multiple paternity is not too large, we find that sex-specific migration and survival, and generation overlap, are the primary factors determining which allele is silenced. This indicates that imprinting can evolve purely due to sex-related asymmetries in the demographic structure or life-history of a species.
Subject headings: kinship theory, overlapping generations, sex-biased dispersal, dominance, sex-specific selection
1. Introduction
Although Mendel’s rules provide the conceptual bedrock for most population genetic and evolutionary theory, deviations from these rules are eagerly studied as they often involve unusual phenotypes and pose novel evolutionary questions. One such deviation, genomic imprinting, has received a great deal of interest from both empirical and theoretical biologists (Bartolomei and Tilghman 1997; Wilkins and Haig 2003). In genomic imprinting, the expression level of a given allele is conditional on the parent-of-origin of that allele, and typically involves the silencing of either the maternally or the paternally-derived allele.
A number of theories have been developed to explain the evolution of genomic imprinting. One recent hypothesis suggests that imprinting can evolve in response to sex-specific selection or so-called sexual conflict (Day and Bonduriansky 2004; Van Cleve and Feldman 2007). In this scenario, alleles donated by the sex-experiencing stronger selection against deleterious alleles are predicted to be expressed, while alleles donated by the other sex are silenced. Another recent theory suggests that expression of maternally-derived alleles and silencing of paternally-derived alleles evolved due to selection for coadaptation between maternal and offspring phenotypes (Wolf and Hager 2006).
The most prominent explanation for the evolution of genomic imprinting, however, is the kinship hypothesis (Haig 1992). This explanation is predicated on the assumption that offspring can influence the allocation of maternal resources post-fertilization, which is the case for placental mammals and marsupials. The kinship hypothesis predicts that maternally-derived copies of genes that increase the uptake of maternal resources will be silenced and paternally-derived copies of the same gene will be expressed when relatedness between maternal gene lineages within offspring competing for maternal resources is higher than relatedness between paternal gene lineages. Such a relatedness asymmetry may be created when the offspring of a given female have multiple fathers. The pattern would then be expected to be reversed for genes that decrease maternal resource uptake.
Previous analyses of the kinship hypothesis have assumed additive genetic effects and a family structured population in which interactions among kin only take place between offspring of the same brood in an otherwise panmictic population (Greenwood-Lee et al. 2002; Haig 1992; Haig and Wilkins 2000; Mills and Moore 2004; Mochizuki et al. 1996; Spencer et al. 1998, 2004; Úbeda 2008). But many natural populations consist of local demes that are connected by dispersal (Lawson Handley and Perrin 2007). This spatial structure can have strong consequences for the evolution of populations (Wright 1931). In particular, gene frequency fluctuations induced by finite population size and limited migration (e.g. genetic drift) lead to the build up of relatedness among neighbors, where asymmetries in genetical ties can be shaped by various life-history factors (e.g. Charnov 1982; Frank 1998; Hamilton 1967). These factors suggest that population structure (Haig 1997, 2000a; Spencer and Clark 2006) and life-history factors could have an important role in the evolution of genomic imprinting, either for the direction of imprinting or the level of imprinted gene expression.
Here, we address these issues and embed the key life-history and mating system assumptions of the kinship hypothesis into a metapopulation system with an island model of population structure. In order to investigate the impact of demography on the evolution of imprinting under the kinship hypothesis, we construct a mathematical model based on a weak selection approximation for the change in the frequency of a focal allele that causes a specified phenotypic effect (Rousset 2004; Rousset and Billiard 2000). This model allows us to study the effect of finite population size, limited migration, biased sex ratios, the effect of sex-specific values of viability selection and migration, the effect of generation overlap, and the effect of allelic dominance on the predictions of the classical result from the kinship hypothesis (Haig 1992); namely, that under multiple paternity, alleles that increase resource uptake should be expressed when paternally-derived and silenced when maternally-derived.
2. Model framework
2.1. Life cycle
We consider an island model of population structure (Wright 1931); there are D demes (or patches) each equally connected to one another through migration. Although we formulate the model generically for a finite number of demes, we will analyze the model in the limit as the number of demes becomes very large (D → ∞). Each deme is assumed to contain N diploid individuals, Nf = (1 − r)N females and Nm = rN males, where r is the fraction of males.
The life cycle of the individuals begins with random mating among adult males and females. A very large number of juvenile males and females are produced and suffer density-independent mortality during their development into adults; we assume that this mortality depends on the phenotypes of individuals and their sex. Juveniles who survive then migrate independently of each other to a different deme with probability mf for females and mm for males. During each iteration of the life cycle, adults who currently reside in the deme suffer mortality based on their phenotype and sex. Finally, as juveniles mature into adults, they compete for the open patches vacated by dying adults. Density-dependent effects at this stage maintain the male and female adult population sizes at constant sizes Nf and Nm, respectively.
The classic kinship hypothesis (Haig 1992, 1997) assumes that females have an opportunity to mate with more than one male. Here, we use the simplest such mating scheme and assume that each female randomly chooses τ males with replacement from the Nm males in her deme; this mating system can be classi3ed as a type of polygynandry. Thus, τ can be thought of as a measure of how many males sire offspring in a brood, or as the degree of multiple paternity.
Following classical analyses of the kinship hypothesis (Haig 1992, 1997; Mochizuki et al. 1996), the phenotype we focus on is the level of expression of a resource enhancer (Úbeda 2008) gene that increases the rate of uptake of maternal resources by offspring during development. In order to track the evolutionary dynamics of this phenotype, we develop a population genetic model using the weak selection approach developed by Rousset and colleagues (e.g., Rousset 2004; Rousset and Billiard 2000; Roze and Rousset 2004, 2008) for the study of evolution in subdivided populations.
2.2. Genotypes and phenotypes
We assume that a mutant allele, denoted A, and a wild-type allele, denoted a, segregate at the locus controlling the level of gene expression. Since we are interested in exploring the possibility that expression levels may differ based on the sex of the parent who donated the allele, we write the phenotype of an individual homozygous for the resident allele as zaa = xa + ya, where xa is the gene expression level of a when maternally derived and ya when paternally derived (both xa and ya take only positive values). The phenotype of an individual homozygous for the mutant allele is assumed to be given by zAA = xa +ya +δx +δy, where the parameters δx and δy measure how much the maternally derived and paternally derived expression levels of A deviate from those of a and can take both positive or negative values so long as the resulting expression levels of A are non-negative. Finally, we allow dominance interactions between the level of paternal and maternal gene expression so that the phenotype of heterozygote individuals having received A (or a) maternally is assumed be to be given by zAa = xa + ya + 2(1 − h)δx (or zaA = xa + ya + 2(1 − h)δy), where h may be thought of as measuring the level of penetrance of the expression level induced by the a allele. When h = 1, the mutant allele has no effect on expression level, and the expression levels from both maternally- and paternally-derived copies are fully affected when h = 0.
It will be convenient for our analysis to introduce the allele frequency variable pufij (pumij) that is equal to 1 when the maternally (paternally)-derived allele in focal individual j of sex u (u = m or f) in deme i is A and 0 otherwise. With this, we can write the phenotype of individual j of sex u in deme i as
| (1) |
The crucial life-history assumption in the kinship hypothesis is that the phenotype z of an offspring affects both the survival of the offspring itself and the total maternal fertility due to differential consumption of maternal resources during development (Haig 1992). Since females have a finite amount of resources to devote to offspring development, a high rate of consumption of maternal resources by each each offspring during development results in a smaller brood size; that is, there is a trade-off between offspring survival and maternal fertility. In order to formalize this trade-off, we let the probability sf(z) (or sm(z)) that a given juvenile female (or male) survives density-independent selection be an increasing function of its phenotype z, where the shape of the function expresses diminishing return. In an extension of the kinship hypothesis, we assume that adult phenotype also affects survival to the next generation; for simplicity, an adult female (or male) survives with the same probability as a juvenile, sf(z) (or sm(z)). In the second part of the trade-off, we suppose that the fertility b (z̄) of a focal adult female is a decreasing function of the average gene expression level z̄ among her offspring. During mating, females mate with τ males with replacement as described above and produce a single brood from the stored sperm of those matings. A large number of zygotes are produced from those sperm and grow to the juvenile stage.
2.3. Change of allele frequency
The fitness of a focal adult individual is defined as the expected number of offspring that survive to adulthood. Since we allow for sex-specific survival and a flexible sex-ratio, we must account for fitness is a sex-specific way. Let Wuvij be the expected number of adult offspring of sex v produced by adult j of sex u in deme i. Then, there are four fitness functions, Wffij, Wfmij, Wmfij, and Wmmij. Using these fitness functions, we can write the expected change in the frequency of allele A over a single generation, Δp, as
| (2) |
where p = αfpf + αmpm is the reproductive value weighted average of the frequency of A in all females in all demes, pf, and all males in all demes, pm, with αf and αm being the reproductive values of males and females, respectively (Taylor 1990); pfij is the realized frequency of A in female j in deme i in the current generation and can take the values 0, 1/2, or 1; pmij is defined similarly for male j. The fitness functions depend on full genotype frequencies, but these can be expressed as functions of the frequency variables pfij and pmij, which will be illustrated below. The factor of 1/2 in equation (2) accounts for the frequency of transmission of genes from parent to offspring due to meiosis.
3. Analysis
3.1. Weak selection approximation
3.1.1. Fitness function
In order to evaluate a weak selection approximation to Δp, we build a first-order Taylor expansion of Δp about δx = 0 and δy = 0. Since fitness is a function of phenotype, assuming that δx and δy are small entails that selection is weak (Wild and Traulsen 2007). In order to calculate the weak selection approximation to Δp, we need first-order approximations of the four fitness functions. As is commonly found in island models (e.g.,(Lehmann et al. 2007; Rousset and Roze 2007; Roze and Rousset 2004)), we can approximate the expected number of adult offspring of sex v left by individual j of sex u in deme i when the number of demes grows large as (see Appendix A.1)
| (3) |
where εuv is equal to 1 when parent and offspring are of the same sex (i.e., v = u) and to 0 when they are of opposite sexes (i.e., v ≠ u). The probability that adult j of sex u living in deme i survives is given by Suij = su(zuij), where the phenotype zuij is a function of the mutant allele frequency (0, 1/2, or 1) in individual j. The average of Suij over all individuals of sex u in deme i is given by Sui, and the average over all demes is given by Su. Juvij is the expected number juveniles of sex v produced by individual j of sex u in deme i that survive to the migration stage. Averaging over all individuals of sex u in the deme yields Juvi and over all demes yields Juv. The factor of 2 for the survival probability of the focal adult in equation (3), Suij, accounts for the fact that an adult that survives to the next generation “inherits” both of its alleles in the next generation whereas its offspring only inherit one due to meiosis.
3.1.2. Fertility
In simple cases where mating is random and the phenotype under consideration has an effect only on survival or fertility, the expected number of juveniles produced by each sex that survive to the migration stage becomes a simple function of the phenotype of a focal individual and the average phenotype in a focal deme (Rousset 2004). However, our model assumes that there is a trade-off between female fertility and offspring survival so that evaluating these expectations requires a careful accounting of how the mating system operates and how offspring survival and female fertility interact due to their shared genetic basis. In Appendix A.2, we show that, despite this complexity, a first-order expression for the expected number of juveniles is still a function of the phenotype of the focal individual and the focal deme. For example, the expected number of juveniles of sex v produced by female j in deme i can be expressed as
| (4) |
which is simply the product of female fertility and offspring survival where z(pfij, pmi) is the average gene expression in offspring of a focal female and δ is the largest of the two phenotypic deviations δx and δy. Since we assume that females choose males randomly with respect to their genotype, the average gene expression in the focal female’s offspring is a function of her allele frequency, pfij, and the average allele frequency in males in the focal deme i, pmi.
The expected number of juveniles of sex v produced by a focal male is more complex due to female control of reproduction and because females mate τ times:
| (5) |
Here, the fertility of a focal male is determined by the average gene expression in all offspring of all females with which the male mates. This expression level, given by the argument to the fertility function b in equation (5), is the sum of the average gene expression in offspring of the focal male, z(pfi, pmij), weighted by the average fraction of paternity the focal male has in each clutch of offspring, 1/τ, and the average expression level in all offspring of all males (and females) in the deme, z(pfi, pmi), weighted by the remaining paternity, 1 − 1/τ, where pfi is the average allele frequency in females in the focal deme i. The fraction Nf/Nm in equation (5) reflects the effect of the sex ratio on absolute male fertility.
3.1.3. Selection gradient
Using the definition of gene expression level z in equation (1) and the number of juveniles produced by females and males in (4) and (5), respectively, we can calculate first-order expressions for the fitness function given by equation (3), as is usually carried out with the direct fitness method (Rousset 2004; Taylor and Frank 1996). Inserting these functions into the equation for Δp given in (2), we arrive at (see Appendix A.6)
| (6) |
where p(1 − p) is the variance in gene frequency in an individual, Sy is the selection gradient on the mutant allele resulting from its expression when paternally inherited, and Sx is the selection gradient on the mutant allele when maternally inherited. These two selection gradients are given by
| (7) |
and
| (8) |
where su is the probability that an adult of sex u with the resident phenotype survives to the next generation, and are the female and male reproductive values, and β = αf(1 − sf) = αm(1 − sm). The functions in the selection gradients (a prime denotes a derivative) can be interpreted as the direct survival benefits to focal offspring of sex u stemming from increase in its gene expression level and C = −b′/b is the associated indirect fertility cost to a parent stemming from the focal offspring raising gene expression level.
The coefficients Ras,uv, Rjs,uv, and Rb,uv can be interpreted as imprinted measures of relatedness between different classes of individuals based on the effect of the mutant allele on adult survival (Ras,uv), juvenile survival (Rjs,uv), and fertility (Rb,uv), where the subscripts u and v specify the class of the actor. Recipients of fitness effects are adults since we measure fitness at the adult stage. For example, Rjs,mf can be interpreted as the relatedness value between a maternally-derived allele (f) in a male (m) focal juvenile, the actor, and an allele in one of its own parents, where male and female parents are sampled with equal probability due to fair meiosis. Since the fertility of a female depends on the genotype of all offspring in her clutch, Rb,ff can be interpreted as the relatedness between a maternally-derived allele (f) in a focal female (f) juvenile and a random allele in one of the parents of the clutch. Interpretations for the other relatedness coefficients are analogous.
3.1.4. Scaled relatedness
Importantly, the coefficients Ras,uv, Rjs,uv, and Rb,uv are scaled measures of relatedness where the effect of local competition (sometimes referred to as kin competition) on the the selection gradient is taken into account (Queller 1994). Hence, Ras,uv, Rjs,uv, and Rb,uv depend, as in previous models for subdivided populations (e.g. Lehmann et al. 2007; Rousset and Roze 2007; Roze and Rousset 2004; Taylor 1992), on various coefficients of probabilities of identity by descent (IBD) between sets of genes, and on the parameters of the model (see equations (12), (14), (19), and (22)). The evaluation of these probabilities of identity is carried out in Appendix A.4. However, without fully evaluating Ras,uv, Rjs,uv, and Rb,uv, we can infer from equation (6) and (A.21)–(A.23) how female fertility, offspring survival, and allelic dominance will affect the change in mutant frequency.
3.1.5. Dominance
The degree of dominance or penetrance of the allele a, namely the coefficient h, affects Δp by adding genetic identity terms in the Rjs,uv and Rb,uv coefficients in equations (A.21)–(A.23) that contain products of three allele frequencies. These terms are scaled by 1 −2(1−h) so that the dominance terms augment Δp when h < 1/2, and decrease Δp when h > 1/2. The dominance terms do not depend on whether the focal allele is maternally or paternally-derived, which means that the dominance terms affect both gene expression level deviations, δx and δy, identically. In contrast, the “additive” terms that do not disappear when h = 1/2 scale δx and δy independently. In order for selection to increase the degree of imprinting through an increase in the frequency of the allele A, the expression level deviations δx and δy must have independent effects on Δp. Thus, dominance cannot by itself select for imprinting; rather, dominance can exert selection on the total expression level of both maternally and paternally-derived alleles and in doing so may affect the strength of selection for imprinting. We examine this effect of dominance explicitly in Appendix A.7. In the rest of the paper, we assume that h = 1/2.
3.1.6. Direction of selection on imprinting and evolutionary stability
Under additive gene action and using our weak selection approximation, the selection gradients, Sx and Sy are frequency independent. This lack of frequency dependence allows us to derive candidate evolutionarily stable (ES) values of xa and ya since a newly arisen mutant A will either invade and increase in frequency to fixation or will go extinct. We denote the candidate ES values of xa and ya by and , respectively. In order to find and , we define and to be nonzero solutions of
| (9) |
and
| (10) |
respectively. If a maternally inherited allele completely determine the total expression level, then can be seen as a candidate ES level of expression from the perspective of maternally-derived expression; can be seen as the analogous quantity from the perspective of paternally-derived expression.
In order for a phenotype to evolve to a candidate ES value, mutant alleles may invade the population and reach fixation only when they bring the phenotype in the population closer to the ES value. This property, convergence stability, can be expressed mathematically as and for the candidate ES values and , respectively, and is a necessary condition for long-term evolutionary stability (Eshel 1983). In general, we will assume that all candidate ES phenotypes are also convergence stable.
When the selection gradients are equal, Sx = Sy, and the candidate ES gene expression levels are the same for maternally and paternally-derived alleles. In this case, any and that sum to are ES. This means that selection is indifferent to whether the total amount of expression is generated by Mendelian ( ) or imprinted ( ) gene expression.
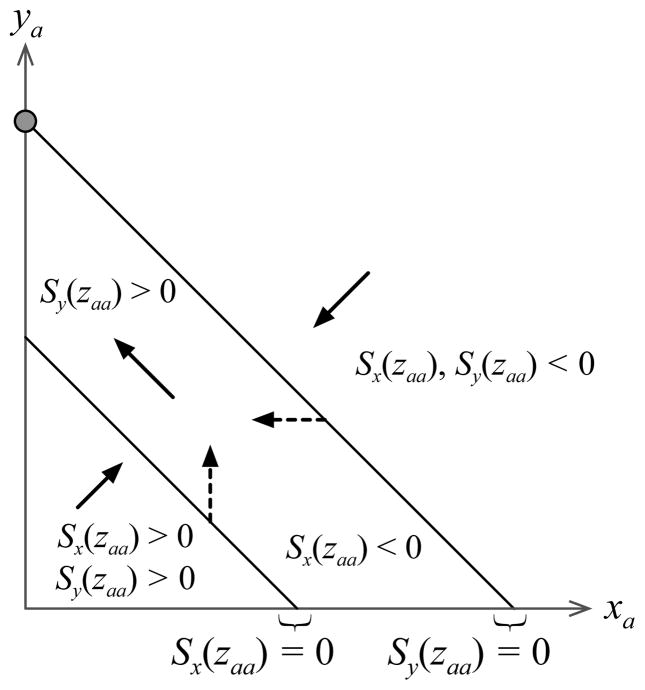
When the selection gradients Sy and Sx are not equal and the maternally and paternally-derived gene expression levels have different candidate ES values, no values of and can simultaneously sum to both and . As Figure 1 shows, this results in silencing of one of the alleles and expression from the other allele at its maximal possible value, either for or for (Greenwood-Lee et al. 2002 provide an alternative dynamical explanation of this process). Which allele is silenced is determined by whether is greater or less than . In other words, which allele is imprinted depends on whether Sy is greater or less than Sx (at the point where the first of the two selection gradients vanishes).
Fig. 1.
Convergence stability of and xa = 0, denoted by the grey circle, when h = 1/2 and τ > 1. The lower black diagonal line indicates all xa and ya that solve Sy(zaa) = 0 and the upper black diagonal line is defined similarly for Sx(zaa) = 0. The arrows indicate the general direction that a vector of δx and δy must have so that Δp > 0. Given and , this leads to the ES values and xa = 0.
In order to understand this result, suppose that Sy > Sx and note that when xa and ya entail a gene expression level that is less than , Sx (zaa) and Sy (zaa) are positive and equation (6) shows that A increases in frequency when it increases both maternally and paternally-derived expression levels. A series of mutant allele invasions and fixations lead xa and ya to approach . When , allele A increases in frequency if it increases expression from the paternal allele, δy > 0. Once the maternally and paternally-derived expression levels evolve so that they are both less than and greater than , then allele A invades the population when it induces decreased expression from the maternally-derived allele and increased expression from the paternally-derived allele. This leads to silencing of the maternally-derived allele, , and (see Figure 1). Similar reasoning shows that the ES expression levels and are approached when Sx > Sy.
In the next sections, we will show how various combinations of life-history factors can lead the selection gradients Sy and Sx to differ and thus lead to the evolution of genomic imprinting.
4. Results
4.1. Multiple paternity
4.1.1. Direction of imprinting
We begin by analyzing the case with equal migration rates in the sexes (mf = mm = m) and no generation overlap (sf = sm = 0 for adults). In this case, the selection gradients in (7) and (8) simplify so that Rjs,fu = Rjs,mu = Rjs,u, Rb,fu = Rb,mu = Rb,u, and terms with Ras,uv disappear, which gives the selection gradients on the mutant allele as
| (11) |
Substituting the probabilities of genetic identity from Appendix A.4 into the scaled relatedness coefficients weighting the benefits in equation (11) yields
| (12) |
where Quv denotes the probability that two alleles in different adults, one sampled from sex u and one from sex v, are identical by descent.
Equation (12) accounts for two different types of inclusive fitness effects accruing to the mutant gene lineage from increasing the gene expression of an allele donated by a parent of sex u in a focal juvenile (the actor). The first fitness effect is a benefit to the parents of the focal juvenile (recipients) that stems from the juvenile having a higher survival probability. This is accounted for by the first term in equation (12), (1 + Qfm)/4 + Qfm/2, namely the probability of identity between a focal allele sampled in the focal juvenile, which is derived from a parent of sex u, and an allele randomly sampled from a parent of the focal juvenile. The parent that has contributed the focal allele to the juvenile is sampled with probability 1/2 (meiosis is fair), and the probability of identity between the two alleles is then (1 + Qfm)/2, where Qfm has to be understood in this equation as the inbreeding coefficient (at equilibrium, the inbreeding coefficient is equivalent to the probability of identity between two alleles, one randomly sampled in an adult male and the other in a female (Gandon and Michalakis 1999)). With probability 1/2 the other parent is sampled and the probability of identity between the two alleles is Qfm.
The second term in equation (12) accounts for the increase in local competition experienced by relatives of the focal juvenile and stems from it having a higher survival rate so that it is more likely to compete with other juveniles from its deme for open breeding spots. With probability (1 − m)2 the focal juvenile competes with another juvenile produced in the focal deme and with probability 1/Nu the competitor and the focal juvenile share the same parent of sex u. By having a higher survival probability and remaining philopatric, the focal juvenile may thus displace a fraction (1 − m)/Nu of juveniles produced on the focal patch that are related to it by (1 + Qfm)/4 + Qfm/2 and it will displace a fraction (1 − m)(1 − 1/Nu) of juveniles that descend from a different parent of sex u that are related to it by (Quu + Qfm)/2. The second term in equation (12) is thus the increase in kin competition due to increasing the gene expression of the allele donated by a parent of sex u in a focal juvenile.
Substituting the probabilities of genetic identity from Appendix A.4 into the scaled relatedness coefficients weighting the costs in equation (11) gives
| (13) |
and
| (14) |
where the only difference from equation (12) is that the inclusive fitness effects are functions of the probability of identity between a gene sampled in the focal juvenile derived from a male parent and a gene sampled randomly from a parent of the clutch of the juvenile (first line in equation (14)), which is a decreasing function of the number of matings. Hence, Rb,m < Rb,f for τ > 1. Finally, we mention that Quv simplifies so that
| (15) |
Because multiple paternity affects only the identity between a paternally-derived allele in the focal offspring and an allele sampled randomly from one of the parents of its clutch, relatedness factors out of Sx and implies that Sx = 0 is equivalent to
| (16) |
Since the ES level of maternally-derived gene expression solves (16), is independent of the demographic structure of the population and depends only on the balance of the costs and benefits of gene expression.
Setting and using equation (8), we can show that must satisfy
| (17) |
where the ratio Rb,m/Rjs,m varies between zero (no indirect fertility cost to paternally-derived gene expression) and one. When τ = 1 and there is no multiple paternity, paternally-derived relatedness values for fertility and survival effects are also the same and Rjs,m = Rb,m. Thus, Sy = Sx, which implies that and that selection is indifferent to Mendelian or imprinted gene expression.
When there is multiple paternity and τ > 1, the ratio Rb,m/Rjs,m decreases. Equation (17) shows that a smaller value of Rb,m relative to Rjs,m implies a reduction in the indirect fertility cost associated with paternally-derived resource-enhancing gene expression, δy, relative to the direct survival benefit. Though the strength of the reduction is a function of the demographic parameters of the model such as the sex ratio, migration rate, and population size, a reduction of Rb,m/Rb,f always occurs so long as τ > 1. This results in due to the stronger selection pressure on paternally-derived gene expression (Sy) than on maternally-derived gene expression (Sx) and in silencing of the maternally-derived allele.
4.2. Sex-specific migration
The results of section 4.1 show that demographic parameters including local deme size, migration rate, and sex ratio have no effect on selection for imprinting of a resource-enhancing allele; multiple paternity is sufficient for exclusive expression by the paternally-derived allele. The reason for this is that multiple paternity creates asymmetry between the relatedness among maternally and paternally-derived alleles in the offspring of a given female. On average, maternally-derived alleles are then more likely to be identical by descent within a clutch than paternally-derived ones (Haig 1992). Sex-specific dispersal may also generate asymmetry in relatedness and has been hypothesized to generate selection for imprinting (Haig 2000a). We will study this proposition next.
In order to isolate the effect of sex-specific dispersal on relatedness from other factors, we assume that there is no multiple paternity (τ = 1), and that there are an equal number of males and females within each deme (r = 1/2 and Nf = Nm = N). The IBD probabilities Qff, Qfm, and Qmm now take different values since juveniles of different sexes migrate at different rates (see Appendix A.4). Under these conditions, the selection gradients on the mutant allele resulting from its expression when paternally and maternally inherited are given, respectively, by
| (18) |
where
| (19) |
is a scaled imprinted measure of relatedness that depends on sex-specific migration probabilities.
The interpretation of this relatedness coefficient is similar to that of equation (12): the first term in square brackets is the probability of identity between an allele sampled in a focal offspring of sex u, which was inherited from a parent of sex v, and an allele sampled in a random parent of that offspring. The second term in square brackets in equation (19) is the probability of identity between an allele sampled in the focal offspring and an allele sampled from a random parent that has produced an offspring entering in competition with the focal offspring, which occurs with probability (1 − mu)2. The second term in (19) thus reflects the loss in inclusive fitness by an individual carrying the mutant allele stemming from how the mutant increases the intensity of local competition.
The first thing to note about equation (18) is that sex-specific selection, Bf ≠ Bm, and migration, mf ≠ mm, are necessary for there to be selection for imprinting. If there is no sex-specific selection, Bf = Bm = B, then Sx and Sy are both proportional to B − C and . Although sex-specific migration may generate asymmetry in relatedness between maternally and paternally-derived alleles, these differences do not affect the trade-off between the fertility costs and survival benefits when survival is independent of sex. When migration is independent of sex, mf = mm = m, relatedness among surviving adults is independent of sex, Rjs,ff = Rjs,mf = Rjs,fm = Rjs,mm, and the benefits and costs of gene expression to survival and fertility are the same for both maternally- and paternally-derived alleles. This means that Sx = Sy and again . In order to generate selection for imprinting, sex-specific viability and migration must co-occur so that the trade-off between the benefits and costs of gene expression is different between maternally- and paternally-derived alleles.
Recall that the maternally-derived allele is silenced when and the paternally-derived allele is silenced when (see section 3.1.6). The effect of sex-specific migration on the direction on imprinting can be discerned by determining which of the selection gradients, Sx (zaa) or Sy (zaa), vanishes first as the level of gene expression zaa increases. We perform this analysis in Appendix A.5 and show that the strength of sex-specific selection, independent of which sex migrates more often, determines which of or is larger. That is, the maternally-derived allele is silenced if
| (20) |
and if the reverse inequality holds, the paternally-derived allele is silenced.
That the sex bias in viability selection, and not migration, determines which allele is silenced is due to the symmetric effects of migration on the local competition components of the Rjs,uv coefficients defined in equation (19). If one sex migrates less frequently than the opposite sex (i.e. the first sex is philopatric), this increases the chance that both juveniles and adults of the philopatric sex will compete with relatives locally, which decreases relatedness coefficients that measure identity between alleles of the philopatric sex. Since we assume an even sex ratio, the magnitude of this increase in local competition is the same for females when migration has a female bias of a certain amount as it is for males when migration has a male bias of the same amount. This means that sex biases in migration affect the selection gradients in (18) symmetrically leaving the sex-bias in viability selection to determine which allele is silenced and which is expressed.
More generally for τ ≥ 1 and any sex ratio, which allele is silenced by a particular sex-bias in viability selection is determined by whether the effect of local competition on relatedness is stronger when philopatric alleles are found in both parent and offspring or are found apart. If the increase in local competition for alleles donated by parents of the philopatric sex to offspring of that sex, which can be measured by the geometric mean , is weaker than that for alleles where only one of the donating parent or the offspring is of the philopatric sex, measured by , then Rjs,ff Rjs,mm > Rjs,mf Rjs,fm. In this case, stronger viability selection on males, Bm > Bf, leads to expression of paternally-derived alleles and silencing of maternally-derived alleles, and the opposite expression pattern is expected for stronger viability selection on females, Bf > Bm. The effect of sex-specific viability is reversed when the increase in local competition is weaker for alleles for which only one of the donating parent or the offspring is of the philopatric sex; i.e. Rjs,ff Rjs,mm < Rjs,mf Rjs,fm means that Bm > Bf implies silencing of paternally-derived alleles and Bf > Bm means silencing of maternally-derived alleles. This latter case leads to inequality (20) when τ = 1 and r = 1/2.
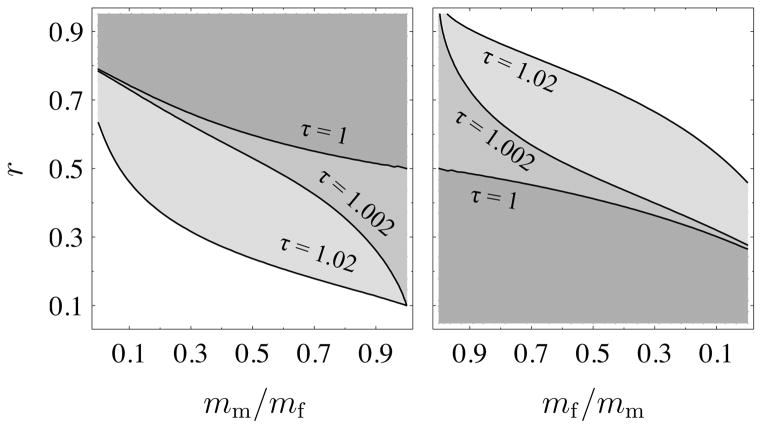
By itself, an uneven sex ratio strongly affects the degree of population structure (this can be seen in Figure A.1 in the Appendix); for this case, r ≠ 1/2, sex-specific migration does play a role in determining which allele is imprinted. Since the expression for Δp is sufficiently complex in this case, we present numerical results in Figure 2 that show which gene expression level, or , is greater under a range of sex ratios and sex-biased migration rates. We assume that N = 10, m = 0.01 for the non-philopatric sex, and that viability selection affects males more strongly than females, Bm > Bf. Focusing on the τ = 1 line, we can see that as expected for all migration rates when r = 1/2. If the sex ratio is female-biased (r < 1/2), then for all levels of female-biased migration, which we see in the lefthand plot. If migration is male-biased, when this bias is weak and when this bias is strong. The level of male bias in migration required for to become greater than increases as the sex ratio become more female-biased to the point where for any level of male-biased migration. For male-biased sex ratios, the pattern is reversed; any male-biased migration yields , and female-biased migration yields only when the migration bias is sufficiently strong. Figure 3 in the Appendix shows that this qualitative pattern holds across a range of populations sizes and migration rates. An analogous pattern also results when viability selection affects females more strongly and is predicted at an even sex ratio. Thus, condition (20) holds when the sex ratio and migration rates are biased towards the same sex or when migration is strongly biased and the sex ratio is close to even.
Fig. 2.
Plot of the sign of for h = 1/2 and N = 10 as a function of sex-specific migration and the sex ratio when there is no generation overlap. In the left graph, mf = 0.01, and in the right graph, mm = 0.01. We assume that Bm > Bf. In the left panel, the region above a given τ contour line indicates , and the region below the contour line indicates . The pattern is reversed in the right panel where the region below a given τ contour line indicates and the region above the contour line indicates .
Figure 2 also shows what happens when as τ increases beyond one and females mate multiply. When migration is either weakly male- or female-biased, multiple paternity immediately results in the classical result of silencing of the maternally-derived allele for almost all values of r. As the sex ratio and migration rates become increasingly biased towards the same sex, and the paternally-derived allele is silenced. As the degree of multiply paternity increases, the threshold levels of bias in the sex ratio and migration rates required for this shift rapidly increase; long before τ = 2, no amount of bias in the sex ratio and migration rates can generate silencing of the paternally-derived allele. In addition, Figure 3 in the Appendix shows that increasing the population size makes it much more difficult to reverse the classical result and generate lower ES gene expression from the paternally-derived allele. Taken together, these results reveal that sex-biased migration rates and sex ratios can counterbalance the effect of a small degree of multiple paternity on patrilineal relatedness when viability selection is stronger on males and the population size is small.
4.3. Overlapping generations
Asymmetry in relatedness between males and females can be produced by differential adult survival when generations are overlapping. If adult individuals of one sex have a lower mortality than adults of the other sex, then alleles drawn from individuals of the first sex are more likely to be identical by descent than alleles drawn from the other sex. If this effect on relatedness is strong enough, it may generate selection for imprinted gene expression and possibly result in silencing of the paternally-derived allele even when there is multiple paternity.
Assuming that males and females disperse at equal rates and that there is no multiple paternity (τ = 1), the relatedness coefficients in the selection gradients in equations (7) and (8) simplify so that Rjs,fu = Rjs,mu = Rjs,u, Rb,fu = Rb,mu = Rb,u, and Rb,u = Rjs,u, which is given by (12). Therefore,
| (21) |
We show in Appendices A.3 and A.4 that the remaining coefficient in these selection gradients, Ras,uv, which is due to the survival of adults from one generation to the next, is given by
| (22) |
where Qu[ũ]v[ṽ] are imprinted IBD coefficients that measure the probability that an allele in an adult of sex u that came from a parent of sex ũ is identical to an allele from another adult of sex v that came from a parent of sex ṽ. Methods for calculating such imprinted IBD coefficients are given in Appendix A.4.
As was the case above, the scaled relatedness given by equation (22) accounts for two different types of inclusive fitness effects accruing to an individual carrying the mutant allele. The first term, (1 + Qfm)/2, is the probability of identity between an allele sampled in an adult of sex u (the actor), which was inherited from a parent of sex v, and the adult itself (the adult is here also the recipient of the act). The second term in equation (22) accounts for the increase in local competition affecting the relatives of the actor when it has a higher adult survival probability through an increase in gene expression level. Then, all offspring produced in the focal patch that remain philopatric (a fraction 1 − m of the productivity of the focal patch, which includes the offspring of the focal actor) are less likely to find an open breeding space. The increase in survival of the focal adult then displaces offspring, which are related to it by the relatedness term given in square braces in equation (22) divided by 1/2.
Given the selection gradients in equation (21), we show in Appendix A.6 that the maternally-derived allele is silenced if
| (23) |
and if the reverse inequality holds, the paternally-derived allele is silenced. The numerator of the first term in inequality (23) measures the relatedness between a paternally-derived allele in a random surviving adult and a random allele in that adult where surviving males and females are sampled according to their reproductive-value-weighted survival probabilities. The numerator of the second term is interpreted analogously for maternally-derived alleles. As in section 3.1, the denominators are the relatedness values between paternally and maternally-derived alleles in offspring and random parents. Thus, inequality (23) says that evolutionarily stable gene expression of the paternally-derived allele will be larger than expression of the maternally-derived allele when paternally-derived alleles have a higher relatedness in surviving adults relative to random adults than do maternally-derived alleles. In effect, higher patrilineal relatedness among surviving adults selects for higher expression of the paternally-derived allele, since survival rates increase with gene expression levels.
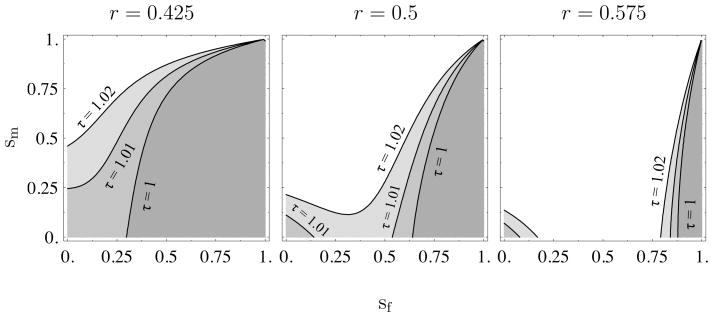
To evaluate the effect of the demographic parameters on the relatedness values in (23), we resort to numerical analysis since the IBD equations are quite complicated. For a range of female and male survival probabilities, Figure 4 shows which of or is greater for N = 10 and m = 0.01. The sex ratio is female-biased in the left plot, male-biased in the right plot, and even in the middle plot. Above a given τ contour line, , and below the contour line. Focusing on the even sex-ratio case in the middle plot and the τ = 1 (no multiple paternity) line, we can see that for weak generation overlap (small sf and sm) with any sex bias, , which results in silencing of the paternally-derived allele. This effect is likely due to the fact that when females mate only once, the probability that two random offspring share a mother, 1/Nf, is lower than the probability of sharing a father, 1/Nf + 1/Nm(1 − 1/Nf), which increases kin competition among patrilineal lines. This increase in kin competition decreases Ras,fm and Ras,mm relative to Ras,ff and Ras,mf for small amounts of generation overlap. High survival rates in females and low rates in males can counterbalance this effect by strengthening kin competition among matrilineal lines enough to yield .
Fig. 4.
Plot of the sign of for h = 1/2, N = 10, and mf = mm = 0.01 as a function of female and male adult survival rates, sf and sm. The value of the sex ratio is listed at the top of each plot. The region below a given τ contour line indicates , and the region above the contour line indicates .
For both female and male-biased sex ratios, high female and low male survival yield and maternal silencing. Even so, the direction of sex-ratio bias changes the degree of bias in survival rates needed for . A female-biased sex ratio requires a smaller female bias in survival rates in order for than a male-biased sex ratio. At first, this seems surprising since a female-biased sex ratio should increase the effect of kin competition among patrilineal lines, which would further decrease Ras,fm and Ras,mm relative to Ras,ff and Ras,mf. However, the effect of the sex ratio on kin competition is stronger on the within-generation relatedness values Rjs,m and Rjs,f where Rjs,m decreases relative Rjs,f for female-biased sex ratios. Thus, a female-biased sex ratio increases patrilineal relatedness among surviving adults relative to random adults, which increases the scope for silencing of the maternal allele. For analogous reasons, a male-biased sex ratio makes it easier to silence the paternal allele.
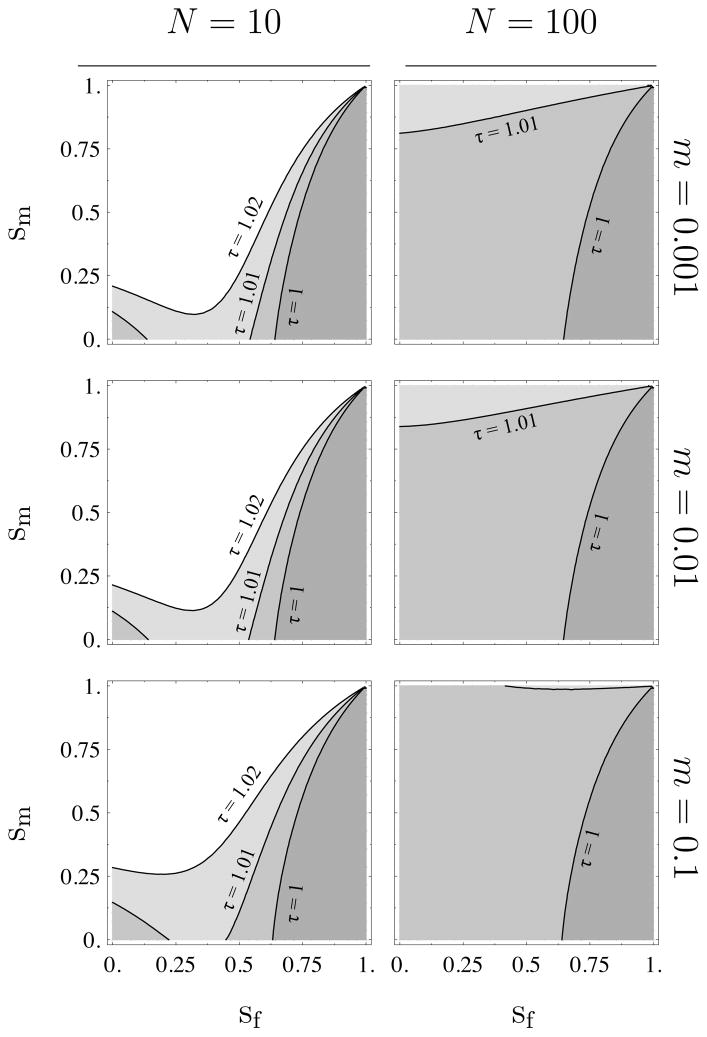
Figure 4 also shows what happens to the ES expression levels when multiple paternity is rare. Regardless of the sex-ratio bias, multiple paternity reduces the bias in survival rates needed for maternal silencing. Figure 5 in the Appendix suggests that, as was the case for sex-specific migration, the strength of the effect of multiple paternity is roughly independent of the migration rate but increases with increasing population size. Increasing τ to 2 (not shown) under the sex ratios used in Figure 4 erases any opportunity for even for N = 10. Taken together, these results suggest that for mating systems that are close to monogamous, the reverse pattern of the classical result, paternal silencing of a resource-enhancing gene, should hold in small or moderate sized populations so long as the survival rates and the sex ratio are not too female biased. When there is a significant degree of multiple paternity, we predict maternal silencing independent of the other demographic parameters.
5. Discussion
The original formulation of the kinship hypothesis for the evolution of genomic imprinting used inclusive fitness theory to show that the asymmetry in relatedness between maternally and paternally-derived alleles generated by multiple paternity can lead to silencing of genes that enhance offspring growth if this growth benefits offspring individually, but comes at the cost of future female fertility (Haig 1992, 1997). Later models showed that the same result holds when offspring growth decreases current female fertility due to scramble competition (Greenwood-Lee et al. 2002; Haig and Wilkins 2000; Kondoh and Higashi 2000; Mochizuki et al. 1996). All of these previous models, however, assumed a family-structured population and additive interactions between alleles. They did not address how genomic imprinting might evolve due to relatedness asymmetries induced by local genetic drift due to finite population size and migration, by dominance, by sex-specific effects on migration and selection, and by generation overlap. The model presented in this paper addresses these issues by embedding the basic life-history assumption of the kinship hypothesis within an island model of population structure.
5.1. Multiple paternity
If there is no generation overlap and migration is independent of sex, our model reproduces the predictions of the classic kinship hypothesis; multiple paternity results in silencing of the maternally-derived copy of the resource-enhancing gene and full expression of the paternally-derived copy. This analysis easily extends to resource-inhibiting genes and predicts that such loci will be expressed by the maternally-derived copy if they have opposite effects on survival and fertility to resource-enhancing genes. These results are independent of the demographic parameters of the model including local deme size, migration rate, and sex ratio; since these parameters determine the degree of population structure due to local drift, we can conclude that local drift within a deme does not affect long-term predictions of which allele will be silenced. The reason that the degree of multiple paternity has such a strong effect even in small local populations is that any amount of asymmetry between the matrilineal and patrilineal relatedness of developing offspring of a given female will result in asymmetric fertility costs of gene expression from maternally- and paternally-derived alleles; such costs result in different “optimal” levels of expression from maternally and paternally-derived alleles and in a convergence-stable level of gene expression at which one allele is silenced (see Figure 1).
It is important to note, however, that local drift and population structure will have an effect on the strength of selection for silencing of maternally-derived alleles. For a given level of multiple paternity, the effect of multiple paternity decreases rapidly with small deme size, a female-biased sex ratio, and weak migration, all of which increase local drift and decrease the efficacy of selection. Selection can also be weak when the fertility costs and survival benefits of gene expression are weak. If selection is weak, it may take a long time for imprinted gene expression to evolve since advantageous mutants will reach fixation at a rate only slightly higher than neutral mutants. This could allow for transient heterogeneity in imprinting status within a population as has been observed in some genes (Ogawa et al. 1993). It is possible that such heterogeneity could also be due to selection for a polymorphism, though we have not explored the possibility of such polymorphisms in our model due to over-dominance in gene expression.
5.2. Sex-specific migration
As with multiple paternity, sex-specific migration can generate relatedness asymmetries among alleles sampled from different sexes. Haig (2000a) suggested that sex-specific migration can generate selection for imprinting due to such asymmetries. After including sex-specific migration in our model, when females are monogamous and alleles interact additively, we find that sex-specific migration is not sufficient to generate selection for imprinting. Once migration occurs at different rates in the sexes, sex-specific selection is required to generate selection for imprinting, and the direction of sex-specific selection, not migration, is a better predictor of which allele is silenced. Specifically, when there is an even sex ratio, the sex experiencing stronger viability selection silences the resource-enhancing allele that it donates to offspring.
Sex-specific selection drives selection for imprinted gene expression because of the effect of sex-specific migration on competition within the sexes for resources or breeding sites during the density-dependent regulation phase of the life cycle. All else being equal, sex biases in migration affect the strength of local competition on each sex symmetrically in the sense that a given level of philopatry in males increases local competition among alleles in males as much as the same level of philopatry in females increase local competition among alleles in females. Since the selection gradients on maternally- and paternally-derived alleles both depend on relatedness between alleles in males and females, the sex bias in selection determines which allele is silenced. When selection is stronger on one sex, this results in an increased benefit to gene expression of an allele donated by a parent of the second sex and silencing of expression of the allele donated by a parent of the first sex, regardless of which sex is philopatric.
5.3. Sex-specific selection
Even in panmictic populations, sex-specific selection can generate selection for imprinting. In a two-locus population genetic model, Day and Bonduriansky (2004) found that a modifier allele that causes silencing of maternally-derived alleles increases in frequency when selection is stronger on males. Van Cleve and Feldman (2007) confirmed this result as a special case when there is no dominance at the locus under selection. In these models, imprinting can be seen as a way for phenotypes to more closely track selective pressures; the sex experiencing stronger selection will pass on a higher frequency to its offspring of the allele better adapted in that sex. In a quantitative genetic model of the evolution of X-linked genomic imprinting, Iwasa and Pomiankowski (2001) found a so-called “reversed” pattern in which stronger selection on one sex resulted in silencing of the alleles that sex donated to offspring. Their model contained the same life-history trade-off between female fertility and offspring survival due to increased offspring gene expression found in the classic kinship hypothesis and our model. The reversed pattern in X-linked imprinting was due to the fact that males obtain their only X-chromosome from their mothers. If viability selection is stronger on males than on females, then expression of maternally-derived alleles will be higher than expression from paternally-derived ones (and vice-versa). Our model contains the same reversed pattern, except that it derives from the effects of kin competition and sex-specific migration. In principle, it is possible to reconcile these two patterns by including in our model a modifier locus that controls the imprinting status of a major locus whose expression level has different effects on survival and fertility. It is likely that in this case recombination between the modifier and major loci will be crucial in determining whether the normal or reversed pattern of imprinting evolves.
5.4. Generation overlap
Our model shows how generation overlap affects patrilineal and matrilineal relatedness and how asymmetries in these relatedness values can drive silencing of either the paternally or maternally-derived resource-enhancing allele. Specifically, we show how a monogamous mating system can increase local competition among patrilines, which yields silencing of the paternally-derived allele for small degrees of generation overlap. This is in contrast to the classical result, which predicts that any pattern of gene expression, e.g. silencing of either allele or equal expression from both, is ES under monogamy (Haig and Wilkins 2000). The amount of generation overlap due to sex specific survival of adults also affects local competition in demes. Male-bias in adult survival rates generates more local competition among patrilines and results in silencing of the paternally-derived allele. Likewise, female-bias in adult survival rates can increase local competition among matrilines enough to counter the effect of monogamy on patrilines and result in maternal silencing. Female-biased sex ratios should yield more intense local competition among patrilines, but surprisingly, female-biased sex ratios make paternal silencing harder. This is due to the fact that sex-ratio bias has a stronger local competitive effect on fertility than adult survival. Our results suggest that when multiple paternity is infrequent, paternal silencing of a resource-enhancing gene can result as long as the sex ratio and adult survival rates are not too female biased.
5.5. Conclusions
In studying the kinship hypothesis in a subdivided population, we find that the trade-off between female fertility and offspring survival alongside significant levels of multiple paternity are sufficient to generate selection for imprinting. This occurs despite the effects that other demographic variables, including local deme size, migration, and sex ratio, have on population structure. When multiple paternity is infrequent, we find that the demographic variables become crucial in determining which allele will be expressed and which silent in the evolutionary long-term. In fact, the sex ratio, sex-specific selection, migration, and adult survival can all affect which allele is imprinted. Moreover, our results suggest that many perturbations in the sex symmetry of demographic variables will lead to genomic imprinting. Support for this idea comes from recent work by Úbeda and Gardner (in press) that predicts that genes for helping behaviors will be imprinted in a manner dependent on sex biases in migration or other demographic factors. If sex biases in demography can often generate selection for imprinting, then a reasonable next step in evaluating genomic imprinting in an evolutionary context is to determine why so few genes are imprinted (Franklin et al. 1996; Spencer 2000). It is possible that the recessivity of most deleterious mutations could partly explain this (Haig 2000b; Van Cleve and Feldman 2007), but more genomic work is needed to confirm this conjecture.
Some of the strongest empirical support for the kinship hypothesis comes from the fact that, among vertebrates, only eutherians (placental mammals) and marsupials but not monotremes (platypus and echidna) are known to harbor imprinted genes (Ferguson-Smith and Surani 2001). Among the known mammalian imprinted genes, many have effects related to growth or morphogenesis (Morison et al. 2005) and are active in placental tissue (Coan et al. 2005). However, a systematic test of the kinship hypothesis will require genome-wide data on gene function and imprinting status across a range of mammalian species with diverse mating systems and life histories. Genome-wide data on imprinting status using high-throughput sequencing technologies have been collected for mice (Wang et al. 2008) but remain to be collected for non-model mammal species. Once such data are available, demographically explicit models like the one we present here will become essential for testing quantitative predictions about patterns in imprinting status across the mammalian phylogeny.
Such demographically explicit models will allow us to use fixation probabilities and data on generation times to estimate how a variety of demographic and life-history variables affect the time scales required for the evolution of imprinting. In addition, we will be able to quantitatively assess the relative importance of different demographic factors in driving the evolution of imprinting in different species. For example, our model suggests that when multiple paternity is uncommon, we should be able to predict imprinting status based on other demographic variables. Though the degree of multiple paternity required for these variables to be important in our model is small, this is due to our assumption that competition for maternal resources is strong; in the likely case that competition for maternal resources is weaker (and better modeled by contest competition instead of scramble competition: see Haig and Wilkins 2000), demographic variables will be more important in predicting imprinting status. If genome-wide searches for imprinted genes find them in non-mammalian species such as birds, demographic factors will likely become an important component of explaining imprinting in these species since conflict over maternal resources is weaker.
Generally, basic demography and life history features, such as generation overlap and sex-bias in dispersal, are crucial to a more detailed and broader view of the phenotype of interest. Our model demonstrates this to be the case for genomic imprinting and suggests that such a detailed approach will be fruitful in the study of related problems including parent-offspring conflict and parental care.
Supplementary Material
Fig. 3.
Same plot as Figure 2, except that we vary the magnitude of the migration rate and the population size. In first and third columns, mf = m, where m is given on the right hand side of the plots, and in second and fourth columns, mm = m. In the first and third columns, the region above a given τ contour line indicates and the region below the contour line indicates . The pattern is reversed in the second and fourth columns where the region below a given τ contour line indicates and the region above the contour line indicates . The population size for the first two columns is N = 10 and N = 100 for the last two columns.
Fig. 5.
Same plot as Figure 4, except that we vary the magnitude of the migration rate and the population size and that the sex ratio is r = 0.5. The population sizes are listed in the first row and the migration rates along the last column where mf = mm = m. The region below a given τ contour line indicates and the region above the contour line indicates .
Table 1.
Variables and parameters in the model
| Symbol | Definition | |
|---|---|---|
| Nf [Nm] | Number of adult females [males] in each deme | |
| N | Total population size in each deme: Nf + Nm | |
| D | Number of demes | |
| τ | Number of males with which a female mates, with replacement | |
| r | Sex ratio = Nm/N | |
| m [mf, mm] | Migration rate [for females and males] | |
| h | Dominance coefficient of the resident allele a | |
| z | Level of expression from a resource enhancer gene in a focal individual | |
| zaa | Level of gene expression in an aa homozygote | |
| xa, ya | Gene expression level from maternally and paternally-derived a alleles | |
| δx [δy] | Deviations in gene expression level between alleles A and a for maternally-derived [paternally-derived] copies | |
| b(z) | Female fertility as a function of average offspring gene expression level z | |
| sf(z) [sm(z)] | Female [male] survival probabilities as a function of individual gene expression | |
| pfij, pf i, pf | Realized frequency of A in female j of deme i, average frequency of A in females in deme i, and average frequency of A in females across all demes; frequencies in males are defined similarly. | |
| αf [αm] | Class reproductive value of females [males] | |
| Quv | Probability that two alleles from different individuals of sex u and v sampled within a deme are identical by descent | |
| Sx(zaa) [Sy(zaa)] | Derivative of Δp with respect to δx [δy] (selection gradient of δx [δy]) | |
|
|
Maternally-derived [paternally-derived] expression levels that guarantee Sx(zaa) = 0 [Sy(zaa) = 0]. Expression levels are assumed to be convergence stable. |
Acknowledgments
J.V. was supported by a National Library of Medicine Training grant LM-07033. This research was supported in part by National Institutes of Health grant GM-28016 to M.W.F.
References
- Bartolomei MS, Tilghman SM. Genomic imprinting in mammals. Annual Review of Genetics. 1997;31:493–525. doi: 10.1146/annurev.genet.31.1.493. [DOI] [PubMed] [Google Scholar]
- Charnov EL. The theory of sex allocation. Vol. 18. Princeton University Press; Princeton, N.J: 1982. [PubMed] [Google Scholar]
- Coan PM, Burton GJ, Ferguson-Smith AC. Imprinted genes in the placenta–a review. Placenta. 2005;26(Supplement A):S10–20. doi: 10.1016/j.placenta.2004.12.009. [DOI] [PubMed] [Google Scholar]
- Day T, Bonduriansky R. Intralocus sexual conflict can drive the evolution of genomic imprinting. Genetics. 2004;167:1537–1546. doi: 10.1534/genetics.103.026211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eshel I. Evolutionary and continuous stability. Journal of Theoretical Biology. 1983;103:99–112. doi: 10.1006/jtbi.1996.0312. [DOI] [PubMed] [Google Scholar]
- Ferguson-Smith AC, Surani MA. Imprinting and the epigenetic asymmetry between parental genomes. Science. 2001;293:1086–1089. doi: 10.1126/science.1064020. [DOI] [PubMed] [Google Scholar]
- Frank SA. Foundations of Social Evolution. Princeton University Press; Princeton, NJ: 1998. [Google Scholar]
- Franklin GC, Adam GI, Ohlsson R. Genomic imprinting and mammalian development. Placenta. 1996;17:3–14. doi: 10.1016/s0143-4004(05)80638-1. [DOI] [PubMed] [Google Scholar]
- Gandon S, Michalakis Y. Evolutionarily stable dispersal rate in a metapopulation with extinctions and kin competition. Journal of Theoretical Biology. 1999;199:275–290. doi: 10.1006/jtbi.1999.0960. [DOI] [PubMed] [Google Scholar]
- Greenwood-Lee J, Taylor P, Haig D. The inclusive fitness dynamics of genomic imprinting. Selection. 2002;2:103–118. [Google Scholar]
- Haig D. Genomic imprinting and the theory of parent-offspring conflict. Seminars in Developmental Biology. 1992;3:153–160. [Google Scholar]
- Haig D. Parental antagonism, relatedness asymmetries, and genomic imprinting. Proceedings of the Royal Society B: Biological Sciences. 1997;264:1657–1662. doi: 10.1098/rspb.1997.0230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haig D. Genomic imprinting, sex-biased dispersal, and social behavior. Annals of the New York Academy of Sciences. 2000a;907:149–163. doi: 10.1111/j.1749-6632.2000.tb06621.x. [DOI] [PubMed] [Google Scholar]
- Haig D. The kinship theory of genomic imprinting. Annual Review of Ecology and Systematics. 2000b;31:9–32. [Google Scholar]
- Haig D, Wilkins JF. Genomic imprinting, sibling solidairity and the logic of collective action. Philosophical Transactions of the Royal Society B: Biological Sciences. 2000;355:1593–1597. doi: 10.1098/rstb.2000.0720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton WD. Extraordinary sex ratios. a sex-ratio theory for sex linkage and inbreeding has new implications in cytogenetics and entomology. Science. 1967;156:477–488. doi: 10.1126/science.156.3774.477. [DOI] [PubMed] [Google Scholar]
- Iwasa Y, Pomiankowski A. The evolution of X-linked genomic imprinting. Genetics. 2001;158:1801–1809. doi: 10.1093/genetics/158.4.1801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondoh M, Higashi M. Reproductive isolation mechanism resulting from resolution of intragenomic conflict. American Naturalist. 2000;156:511–518. doi: 10.1086/303409. [DOI] [PubMed] [Google Scholar]
- Lawson Handley LJ, Perrin N. Advances in our understanding of mammalian sex-biased dispersal. Molecular Ecology. 2007;16:1559–78. doi: 10.1111/j.1365-294X.2006.03152.x. [DOI] [PubMed] [Google Scholar]
- Lehmann L, Rousset F, Roze D, Keller L. Strong reciprocity or strong ferocity? A population genetic view of the evolution of altruistic punishment. American Naturalist. 2007;170:21–36. doi: 10.1086/518568. [DOI] [PubMed] [Google Scholar]
- Mills W, Moore T. Polyandry, life-history trade-offs and the evolution of imprinting at Mendelian loci. Genetics. 2004;168:2317–2327. doi: 10.1534/genetics.104.030098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mochizuki A, Takeda Y, Iwasa Y. The evolution of genomic imprinting. Genetics. 1996;144:1283–1295. doi: 10.1093/genetics/144.3.1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morison IM, Ramsay JP, Spencer HG. A census of mammalian imprinting. Trends in Genetics. 2005;21:457–465. doi: 10.1016/j.tig.2005.06.008. [DOI] [PubMed] [Google Scholar]
- Ogawa O, McNoe LA, Eccles MR, Morison IM, Reeve AE. Human insulin-like growth factor type i and type ii receptors are not imprinted. Human Molecular Genetics. 1993;2:2163–5. doi: 10.1093/hmg/2.12.2163. [DOI] [PubMed] [Google Scholar]
- Queller DC. Genetic relatedness in viscous populations. Evolutionary Ecology. 1994;8:70–73. [Google Scholar]
- Rousset F. Genetic Structure and Selection in Subdivided Populations. Princeton University Press; Princeton, NJ: 2004. [Google Scholar]
- Rousset F, Billiard S. A theoretical basis for measures of kin selection in subdivided populations: Finite populations and localized dispersal. Journal of Evolutionary Biology. 2000;13:814–825. [Google Scholar]
- Rousset F, Roze D. Constraints on the origin and maintenance of genetic kin recognition. Evolution. 2007;61:2320–2330. doi: 10.1111/j.1558-5646.2007.00191.x. [DOI] [PubMed] [Google Scholar]
- Roze D, Rousset F. The robustness of hamilton’s rule with inbreeding and dominance: kin selection and fixation probabilities under partial sib mating. American Naturalist. 2004;164:214–231. doi: 10.1086/422202. [DOI] [PubMed] [Google Scholar]
- Roze D, Rousset F. Multilocus models in the infinite island model of population structure. Theoretical Population Biology. 2008;73:529–542. doi: 10.1016/j.tpb.2008.03.002. [DOI] [PubMed] [Google Scholar]
- Spencer HG. Population genetics and evolution of genomic imprinting. Annual Review of Genetics. 2000;34:457–477. doi: 10.1146/annurev.genet.34.1.457. [DOI] [PubMed] [Google Scholar]
- Spencer HG, Clark AG. A chip off the old block: a model for the evolution of genomic imprinting via selection for parental similarity. Genetics. 2006;174:931–935. doi: 10.1534/genetics.106.060475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer HG, Feldman MW, Clark AG. Genetic conflicts, multiple paternity and the evolution of genomic imprinting. Genetics. 1998;148:893–904. doi: 10.1093/genetics/148.2.893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer HG, Feldman MW, Clark AG, Weisstein AE. The effect of genetic conflict on genomic imprinting and modification of expression at a sex-linked locus. Genetics. 2004;166:565–579. doi: 10.1534/genetics.166.1.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor PD. Allele-frequency change in a class-structured population. American Naturalist. 1990;135:95–106. [Google Scholar]
- Taylor PD. Altruism in viscous populations an inclusive fitness model. Evolutionary Ecology. 1992;6:352–356. [Google Scholar]
- Taylor PD, Frank SA. How to make a kin selection model. Journal of Theoretical Biology. 1996;180:27–37. doi: 10.1006/jtbi.1996.0075. [DOI] [PubMed] [Google Scholar]
- Úbeda F. Evolution of genomic imprinting with biparental care: implications for Prader-Willi and Angelman syndromes. PLoS Biology. 2008;6:e208. doi: 10.1371/journal.pbio.0060208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Úbeda F, Gardner A. A model for genomic imprinting in the social brain: Juveniles. Evolution. doi: 10.1111/j.1558-5646.2010.01015.x. in press. [DOI] [PubMed] [Google Scholar]
- Van Cleve J, Feldman MW. Sex-specific viability, sex linkage and dominance in genomic imprinting. Genetics. 2007;176:1101–1118. doi: 10.1534/genetics.107.071555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Sun Q, McGrath SD, Mardis ER, Soloway PD, Clark AG. Transcriptome-wide identification of novel imprinted genes in neonatal mouse brain. PLoS ONE. 2008;3:e3839. doi: 10.1371/journal.pone.0003839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wild G, Traulsen A. The different limits of weak selection and the evolutionary dynamics of finite populations. Journal of Theoretical Biology. 2007;247:382–390. doi: 10.1016/j.jtbi.2007.03.015. [DOI] [PubMed] [Google Scholar]
- Wilkins JF, Haig D. What good is genomic imprinting: the function of parent-specific gene expression. Nature Reviews Genetics. 2003;4:359–368. doi: 10.1038/nrg1062. [DOI] [PubMed] [Google Scholar]
- Wolf JB, Hager R. A maternal-offspring coadaptation theory for the evolution of genomic imprinting. PLoS Biology. 2006;4:e380. doi: 10.1371/journal.pbio.0040380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Evolution in mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.