Estimation of Future Glucose Concentrations with Subject-Specific Recursive Linear Models

Abstract

Background

Estimation of future glucose concentrations is a crucial task for diabetes management. Predicted glucose values can be used for early hypoglycemic/hyperglycemic alarms or for adjustment of insulin injections or insulin infusion rates of manual or automated pumps. Continuous glucose monitoring (CGM) technologies provide glucose readings at a high frequency and consequently detailed insight into the subject's glucose variations. The objective of this research is to develop reliable subject-specific glucose prediction models using CGM data.

Methods

Two separate patient databases collected under hospitalized (disturbance-free) and normal daily life conditions are used for validation of the proposed glucose prediction algorithm. Both databases consist of glucose concentration data collected at 5-min intervals using a CGM device. Using time-series analysis, low-order linear models are developed from patients' own CGM data. The time-series models are integrated with recursive identification and change detection methods, which enables dynamic adaptation of the model to inter-/intra-subject variability and glycemic disturbances. Prediction performance is evaluated in terms of glucose prediction error and Clarke Error Grid analysis (CG-EGA).

Results

Prediction errors are significantly reduced with recursive identification of the models, and predictions are further improved with inclusion of a parameter change detection method. CG-EGA analysis results in accurate readings of 90% or more.

Conclusions

Subject-specific glucose prediction strategy has been developed. Including a change detection method to the recursive algorithm improves the prediction accuracy. The proposed modeling algorithm with small number of parameters is a good candidate for installation in portable devices for early hypoglycemic/hyperglycemic alarms and for closing the glucose regulation loop with an insulin pump.

Introduction

With the current therapy for insulin-dependent patients, it is generally difficult to estimate future glucose levels and therefore to determine the required insulin amount/rate. Reliable glucose prediction models will simplify diabetes management. By predicting future glucose concentrations, the appropriate insulin amount for keeping normoglycemia can be calculated, hypoglycemic/hyperglycemic episodes can be prevented before they occur, and the amplitudes of glucose level variation can be reduced. The fully automated artificial pancreas with closed-loop administration of insulin will also require a model predicting future glucose concentrations.^1–3

Modeling glucose–insulin interactions has been an active research area.^4–8 Most of the proposed physiological models are nonlinear and are difficult to tune for individual patients. More precise glucose predictions require taking into account the intra-/inter-subject variability. Several techniques for glucose estimation from self-monitored glucose data have also been proposed.^9–13 Recent continuous glucose monitoring (CGM) technologies provide detailed insight into glucose variation,^14–16 and new methods have been emerging for analyzing a patient's own CGM data.^3,17–23 Finan et al.²² and Sparacino et al.²³ used the time-series identification methods. Similarly, we make use of time-series analysis for the development of subject-specific glucose prediction models from CGM data.

Time-series models are recursively identified at each sampling step and are integrated with a change detection method that enables dynamic adaptation of the model to inter-/intra-subject variability and glycemic disturbances. Prediction accuracy is evaluated in terms of error in glucose predictions and Clarke Error Grid analysis (CG-EGA).

Materials and Methods

Subject data

Two separate patient databases collected under (1) disturbance-free (hospitalized) and (2) normal daily life conditions are used. Both databases consist of glucose concentration data collected using a CGM device. The two study procedures were reviewed and approved by the University of Illinois at Chicago Institutional Review Board. Prior to participating in the study, all subjects completed consent and HIPPA documents. Data collection took place at the University's general clinical research center.

Study Group A

This study population consisted of healthy individuals (sample size n = 22, 43.50 ± 10.4 years old, body mass index [BMI] = 35.02 ± 3.4 kg/m²), glucose-intolerant subjects (n = 7, 45.00 ± 7.0 years old, BMI =34.88 ± 4.1 kg/m²), and subjects with type 2 diabetes (n = 11, 47.18 ± 5.1 years old, BMI = 36.80 ± 4.1 kg/m²). Data were originally collected to investigate the effect of moderate exercise (30-min walk on a treadmill performed before breakfast at an intensity of 65% maximal oxygen consumption (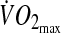) measured with indirect spirometry) on postprandial glucose during two separate randomized protocols (exercise and nonexercise).²⁴ Subjects were hospitalized for 48 h and were prescribed three standard meals for each day. A subject's glucose concentration was monitored with a CGM system (CGMS System Gold™, Medtronic MiniMed, Northridge, CA) for 48 h. In this paper, we used the CGMS data collected during the nonexercise protocol only.

Study Group B

This study population consisted of subjects with type 2 diabetes (n = 14, 47.93 ± 6.1 years old, BMI = 36.94 ± 4.9 kg/m²) and healthy subjects (n = 8, 42.75 ± 12.7 years old, BMI = 34.66 ± 5.8 kg/m²). The database consisted of glucose concentration data collected at 5-min intervals using the CGMS System Gold monitoring device. The subjects wore the CGMS at home for 48 h, with no additional instructions other than how to operate the monitor and calibration techniques of the device.

Low-order linear time-series models

With the intensive insulin therapy, patients with diabetes are constrained to check their blood glucose concentrations frequently, to closely follow their eating and exercise plan, and to avoid unexpected stress conditions. Physiological models that describe glucose–insulin dynamics under such disturbance-free conditions have been reported in the literature.^4–8 However, these nonlinear models have a large number of parameters to be identified, which makes it difficult to tune the model for individual patients. To overcome this limitation, we develop recursive linear models using the patient's own CGM data. Low-order linear models would be less accurate than nonlinear models for describing variations of a nonlinear system in a wide range of conditions. However, it will be shown that recursive identification of the model will compensate for its simplicity and improve its accuracy.

Current or future glucose concentrations can be expressed as a function of previous glucose measurements with autoregressive (AR) or autoregressive moving average (ARMA) models:

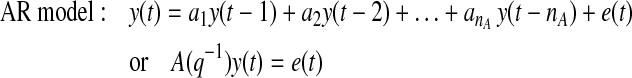(1)

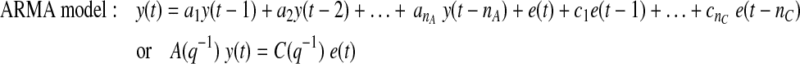(2)

where y(t) denotes the glucose measurement at current time instant t and y(t − k) is the glucose measurement k time-units before the current time t. e(t) = y(t) − ŷ(t) represents the residual terms caused by the difference between the patient's behavior and its model, where ŷ(t) is the predicted value of y(t). Parameters a_i and c_i are unknown and are identified by using the patient's GCM data. q⁻¹ is the back shift operator that transforms a current observation to a previous one [q^−ky(t) = y(t − k)]. Polynomials A(q⁻¹) and C(q⁻¹) in Eqs. 1 and 2 are:

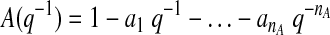(3)

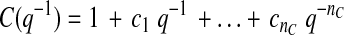(4)

Future glucose concentrations are estimated from recent glucose data, and models do not require any prior information about glycemic disturbances such as meal consumption or insulin administration.

Recursive identification of model parameters

Glucose–insulin dynamics show inter-subject variability. Metabolic changes caused by stress or changes in insulin sensitivity might also lead to variation in glucose–insulin dynamics of the same subject over time. Furthermore, subjects are exposed to glycemic disturbances such as meal consumption or physical activity on a daily basis. A reliable model for predicting glucose levels should address such variabilities and should be able to adapt to unexpected fluctuations in the system dynamics. Therefore, recursive identification of the glucose prediction models (Eqs. 1 and 2) is proposed. As a new glucose measurement becomes available at each sampling instant, model parameters are updated in order to include information about the most recent glucose concentration dynamics. The preferred recursive identification strategy is the weighted recursive least square (RLS) method with a forgetting factor, λ:

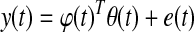(5)

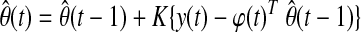(6)

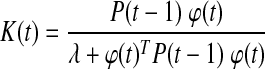(7)

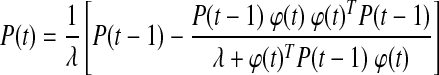(8)

where y(t) is the current glucose measurement, φ(t) represents the vector of past glucose observations, and θ(t) denotes the vector of model parameters, while 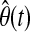is its estimate. For instance, for the ARMA model described by Eq. 2,

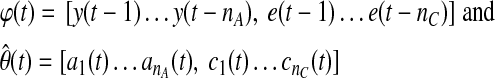K(t) and P(t) are the smoothing parameter and estimate of error variance, respectively. The forgetting factor (0 < λ ≤ 1) assigns relative weights on past data sequence. When λ = 1, all observations are equally weighted (infinite memory) in the identification. Small values of λ make the more recent data dominant for estimation of model parameters by assigning larger weights on recent observations and smaller weights on older ones (short memory).

Change detection method

In order to capture unpredicted glycemic disturbances rapidly and to provide quick response to such conditions, the RLS algorithm is integrated with a change detection method. When a persistent change in model parameters is detected, λ is decreased to a smaller value. This way, past observations (data before the change detection) are rapidly excluded, and faster convergence to new model parameters is ensured. However, to avoid parameter changes due to nonpersistent abnormalities in data such as sensor noise, λ is not reduced at the first instant of change detection. Instead, consistency of the change for several time steps (window size, T_W) is assured first. The proposed change detection method can be described by null and alternative hypotheses as:

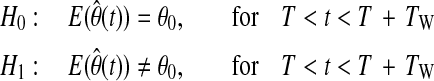(9)

where 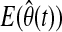represents the expected value of parameter estimates at current time t and θ₀ is the vector of unbiased parameter estimates computed by the RLS algorithm using data until time instant T. When a persistent change with the duration of the window size is detected, λ is reduced to a smaller value, and θ₀ is replaced with its new estimate.

k-steps-ahead glucose prediction

The k-steps-ahead glucose prediction, ŷ(t + k|t; θ) is a function of current and past glucose observations.²⁵ For the ARMA model (Eq. 2):

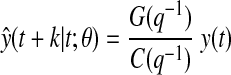(10)

The polynomial G(q⁻¹) (of order n − 1, n = max (n_A, n_C − k + 1,1)) is uniquely defined by:

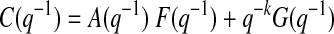(11)

where F(q⁻¹) has order of k − 1. Rearrangement of Eqs. 10 and 11 for AR models (Eq. 1) is straightforward.

Prediction performance analyses

Error in glucose predictions

Prediction accuracy, the deviation of predicted glucose values from the patient's GCM device data, can be expressed as the sum of squares of the glucose prediction error (SSGPE):

(12)

and relative absolute deviation (RAD):

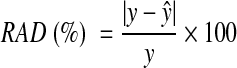(13)

In Eqs. 12 and 13, y denotes the actual glucose measurement (CGM data), and ŷ is the predicted glucose concentration. SSGPE and RAD do not depend on data magnitude, since they are normalized by actual glucose measurements. The CGM device is assumed to provide accurate (reference) glucose readings.

CG-EGA

Prediction performance is also evaluated using CG-EGA.^26,27 CG-EGA creates three error grid zones (clinically accurate, benign errors, and erroneous readings) for analyzing the prediction accuracy and provides separate analysis during hypoglycemia (blood glucose ≤ 70 mg/dL), normoglycemia (70 < blood glucose ≤ 180 mg/dL), and hyperglycemia (blood glucose > 180 mg/dL). We use the CGM data as reference and analyze how accurate are the predicted glucose values in terms of CG-EGA.

Results

Time-invariant models for disturbance-free case

Glucose prediction with time-invariant models is first demonstrated on the database of study Group A. In order to remove any noise in the sensor data, CGM data are smoothed using a low-pass filter (filter characteristics are defined later in the text). The first half of the smoothed CGM data is used for the development and identification of the linear models with constant parameters (Eqs. 1 and 2). Then, prediction performances of the models developed are validated on the patient's raw second-day data (second half). Models of various orders (n_A,n_C) are developed using the MATLAB (Natick, MA) System Identification Toolbox.²⁸ The best model order is determined based on a statistical model fit measure, Akaike's Information Criterion. Results show an AR model of order 3 (n_A = 3) and ARMA model of order (3,1) (n_A = 3, n_C = 1) to be satisfactory. Figure 1 demonstrates the predicted glucose values by these models for the representative subjects, with model parameters and prediction error terms provided in Table 1.

FIG. 1.

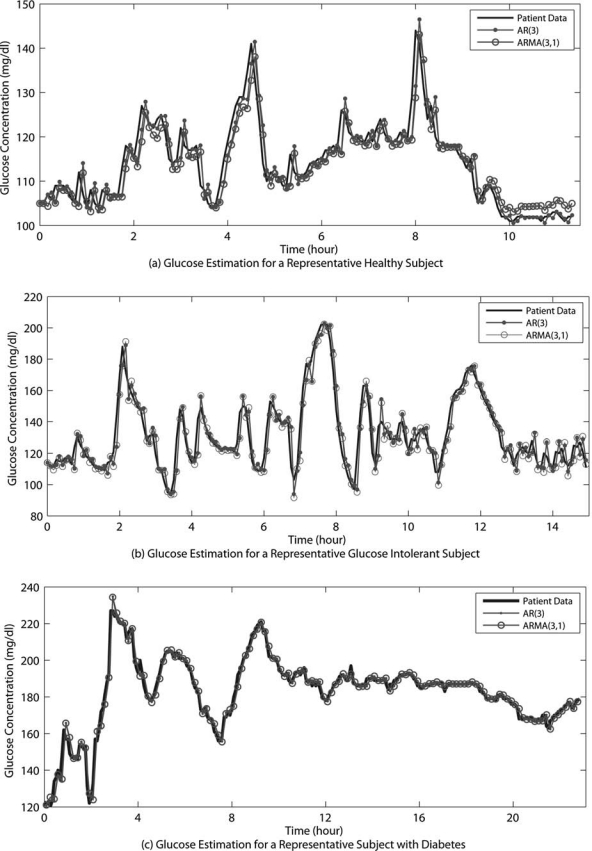
Prediction of blood glucose with time-invariant models for a representative (a) healthy subject, (b) glucose-intolerant subject, and (c) subject with type 2 diabetes for Group A with a PH of two time steps.

Table 1.

Model Parameters and Glucose Prediction Errors of Group A Presented in Figure 1

	Model Parameter
Patient group, model	a1	a2	a3	c1	SSGPE (%)	Mean RAD (%)
Healthy
AR(3)	1.294	−0.480	0.185	—	4.27	1.26 (0.27)
ARMA(3,1)	2.065	−1.237	0.172	−1.01	4.21	1.21 (0.28)
Glucose-intolerant
AR(3)	1.625	−1.019	0.392	—	4.81	1.43 (0.35)
ARMA(3,1)	1.241	−0.437	0.184	0.463	4.72	1.40 (0.32)
Diabetes
AR(3)	1.215	−0.154	−0.061	—	4.20	1.11 (0.24)
ARMA(3,1)	1.844	−0.886	0.042	−0.669	4.11	1.09 (0.24)

Results are for time-invariant models. SSPGE and RAD values are for a PH of two time steps (one step = 5 min). Mean RAD values are reported with standard deviations given in parentheses.

Effect of prediction horizon (PH)

Prediction accuracy defined as SSGPE or RAD (Eqs. 12 and 13) is highly affected by the PH, how far into the future one is trying to predict. Table 2 presents mean SSGPE and RAD values for several PH values for populations of both study groups. PH = 3 denotes that glucose value 3-steps-ahead (15 min) from the current time is predicted using the available history of glucose measurements. For 10-min-ahead prediction, results show around 4–5% SSGPE and 1–2% RAD. Prediction errors increase to around 11–12% SSPGE and 5–7% RAD for PH = 6. Even though prediction models are developed using filtered glucose data, SSGPE and RAD are computed as deviation of predicted glucose values from patient's raw GCM device data.

Table 2.

Prediction Performances for Several PH Values Using Time-Invariant Models: (A) SSGPE Values and (B) RAD Values

	Group A						Group B
	Healthy		Glucose-intolerant		Diabetes		Healthy		Diabetes
PH (step)	AR(3)	ARMA(3,1)	AR(3)	ARMA(3,1)	AR(3)	ARMA(3,1)	AR(3)	ARMA(3,1)	AR(3)	ARMA(3,1)
(A) SSGPE (%)
1	0.32 (0.12)	0.24 (0.09)	0.43 (0.16)	0.31 (0.11)	0.33 (0.15)	0.25 (0.10)	0.30 (0.08)	0.21 (0.06)	0.36 (0.16)	0.27 (0.12)
2	4.43 (0.72)	4.40 (0.72)	4.13 (1.06)	4.07 (1.05)	4.63 (1.24)	4.59 (1.26)	4.88 (1.69)	4.83 (1.75)	3.80 (2.05)	3.73 (2.10)
3	6.48 (1.02)	6.45 (1.02)	6.16 (1.47)	6.06 (1.47)	6.79 (1.73)	6.73 (1.74)	7.13 (2.11)	7.03 (2.18)	5.69 (2.59)	5.58 (2.65)
4	8.21 (1.24)	8.17 (1.25)	7.98 (1.76)	7.84 (1.76)	8.64 (2.10)	8.57 (2.10)	9.05 (2.29)	8.84 (2.39)	7.40 (2.82)	7.21 (2.90)
5	9.78 (1.41)	9.73 (1.42)	9.67 (1.98)	9.51 (1.97)	10.35 (2.45)	10.26 (2.44)	10.82 (2.38)	10.46 (2.49)	9.04 (2.92)	8.78 (3.01)
6	11.24 (1.55)	11.19 (1.56)	11.25 (2.15)	11.08 (2.14)	11.95 (2.80)	11.90 (2.79)	12.55 (2.43)	11.97 (2.53)	10.66 (2.95)	10.32 (3.04)
(B) RAD (%)
1	0.20 (0.08)	0.15 (0.06)	0.31 (0.13)	0.23 (0.10)	0.21 (0.11)	0.16 (0.07)	0.19 (0.07)	0.15 (0.06)	0.22 (0.10)	0.17 (0.08)
2	1.14 (0.22)	1.08 (0.19)	1.08 (0.40)	0.97 (0.43)	1.15 (0.52)	1.07 (0.47)	1.75 (0.46)	1.75 (0.49)	1.01 (0.33)	0.95 (0.32)
3	2.19 (0.39)	2.11 (0.35)	2.12 (0.68)	2.07 (0.65)	2.25 (1.05)	2.15 (0.98)	3.31 (0.71)	3.30 (0.77)	1.94 (0.60)	1.85 (0.61)
4	3.29 (0.56)	3.21 (0.50)	3.23 (0.97)	3.15 (0.95)	3.45 (1.62)	3.35 (1.56)	4.59 (0.83)	4.55 (0.89)	2.95 (0.90)	2.83 (0.92)
5	4.38 (0.71)	4.31 (0.65)	4.28 (1.32)	4.20 (1.28)	4.68 (2.20)	4.62 (2.19)	5.67 (0.97)	5.64 (1.04)	4.00 (1.22)	3.87 (1.25)
6	5.44 (0.83)	5.40 (0.79)	5.42 (1.68)	5.29 (1.67)	5.92 (2.78)	5.90 (2.80)	6.64 (1.06)	6.58 (1.10)	5.07 (1.56)	4.93 (1.60)

Data are population mean SSGPE and RAD values with standard deviations given in parentheses. Results are for time-invariant models. One step = 5 min.

For constant parameter models, prediction error is also affected by the likeness between data used for model development and data used for validation. Reducing the interval of data used in model development from 24 h to 12 h (from one-half to one-fourth) does not significantly alter the SSGPE and RAD values: e.g., for PH = 2 and ARMA(3,1), SSGPE is 5.10 ± 0.97%, 4.25 ± 0.93%, and 5.20 ± 1.06%, and RAD is 1.42 ± 0.15%, 1.21 ± 0.38%, and 1.47 ± 0.37% for the healthy, glucose-intolerant, and type 2 diabetes populations of Group A, respectively. Since glucose concentrations are relatively constant at night and most of the glucose variation occurs during daytime, the model from the first 12-h data is able to capture the dynamics of the remaining data. However, using the first 6-h data for model development significantly increases the error terms for PH = 2 and ARMA(3,1) to 8.37 ± 0.96%, 7.28 ± 1.26%, and 8.05 ± 2.21% SSGPE and 3.38 ± 0.37%, 3.31 ± 0.70%, and 3.54 ± 0.72% RAD for healthy, glucose-intolerant, and type 2 diabetes populations, respectively.

Recursive models

For the recursive modeling, we selected the ARMA model type over AR since the model error information is leveraged by the ARMA model structure [C(q⁻¹) term in Eq. 2]. During recursive identification, simultaneously an online filter is utilized to remove the sensor noise and consequently enhance the prediction accuracy. Figure 2 illustrates 5-min- (PH = 1) and 30-min-ahead (PH = 6) glucose predictions for representative subjects of Group B. Results are for ARMA(2,1) with T_W = 5 (25 min) and λ = 0.5. The forgetting factor λ is reduced to 0.005 in case of change detection. The model is able to track and predict 30-min-ahead glucose concentrations accurately with 3.03% and 6.14% SSGPE and 2.62 ± 0.83% and 3.78 ± 1.12% RAD for the representative healthy and type 2 diabetes subjects, respectively.

FIG. 2.

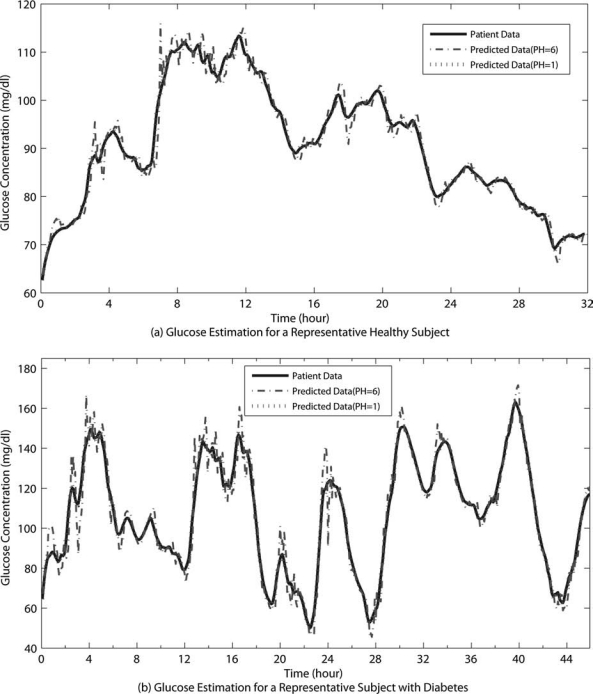
Glucose prediction results with the recursive algorithm for a representative (a) healthy subject and (b) subject with type 2 diabetes for Group B.

Increasing the autoregressive term of ARMA(p,q), p, results in more oscillatory predictions with larger overshoots that cause increase in prediction errors. For instance, the error terms increase to 3.84% and 7.40% SSGPE and 2.85 ± 0.78% and 4.02 ± 1.00% RAD for the representative healthy subject and patient with diabetes in Figure 2, for ARMA(3,1) with PH = 6. On the other hand, as the model order is reduced to ARMA(1,1), prediction profiles become much smoother; however, they result in larger delays in predictions. Reducing the moving average part (q), ARMA(2,0) or AR(2), leads to consistent overshoot and higher SSGPE and RAD values (3.81% and 6.76% SSGPE and 2.80 ± 0.81% and 3.87 ± 1.09% RAD for representative healthy and type 2 diabetes subjects, respectively, in Fig. 2 with PH = 6), whereas ARMA(2,2) does not significantly improve the prediction performance.

Prediction capability of the recursive algorithm for model ARMA(2,1) with T_W = 5 (25 min) and λ = 0.5 is evaluated in terms of SSGPE and RAD in Table 3. Means and standard deviations of the error terms, up to six time steps of PH are provided for both subject groups. Comparing results of Table 2 with Table 3, for PH = 1, the SSGPE and RAD values are slightly lower for time-invariant models because the transition period (start with an untuned model) in the recursive strategy may lead to large error terms at the beginning and constant-parameter models may yield smaller error terms for small PH values. As PH increases, the superior predictive capability of the recursive identification is shown by significantly smaller SSGPE and RAD values compared to time-invariant models. Comparison of the results between the study groups in Tables 2 and 3 reveals lower prediction errors for the hospitalized group because glucose variation will be reduced under controlled conditions.

Table 3.

Prediction Performances Using the Recursive Algorithm With and Without the Change Detection Strategy: (A) SSGPE Values and (B) RAD Values

	Group A						Group B
	Healthy		Glucose-intolerant		Diabetes		Healthy		Diabetes
	Change detection		Change detection		Change detection		Change detection		Change detection
PH (step)	With	Without	With	Without	With	Without	With	Without	With	Without
(A) SSGPE (%)
1	0.32 (0.06)	0.48 (0.15)	0.50 (0.16)	0.65 (0.18)	0.42 (0.21)	0.70 (0.24)	0.35 (0.12)	0.74 (0.38)	0.45 (0.17)	1.06 (0.45)
2	0.91 (0.18)	1.32 (0.40)	1.50 (0.54)	1.93 (0.54)	1.22 (0.63)	1.99 (0.65)	1.02 (0.33)	1.74 (1.03)	1.32 (0.51)	2.39 (0.86)
3	1.80 (0.38)	2.45 (0.75)	3.00 (1.13)	3.76 (1.51)	2.44 (1.28)	3.02 (1.08)	1.95 (0.66)	2.78 (1.72)	2.57 (1.00)	3.84 (1.42)
4	2.57 (0.76)	3.94 (1.25)	4.12 (1.46)	5.35 (1.76)	4.16 (1.71)	5.20 (1.94)	2.95 (1.00)	3.84 (1.44)	4.28 (1.73)	5.36 (2.04)
5	2.84 (0.80)	4.28 (1.42)	4.75 (1.66)	7.31 (1.97)	4.35 (2.22)	6.45 (2.74)	3.16 (1.05)	4.92 (2.18)	4.90 (2.17)	6.98 (2.76)
6	3.02 (1.05)	5.80 (1.96)	5.42 (1.90)	8.91 (2.51)	5.30 (2.36)	9.09 (3.65)	3.60 (1.24)	5.99 (2.23)	5.56 (2.38)	8.65 (3.52)
(B) RAD (%)
1	0.25 (0.07)	0.31 (0.10)	0.39 (0.14)	0.46 (0.13)	0.29 (0.14)	0.33 (0.16)	0.25 (0.08)	0.53 (0.23)	0.32 (0.13)	0.78 (0.33)
2	0.69 (0.19)	0.89 (0.28)	1.15 (0.42)	1.38 (0.41)	0.85 (0.41)	0.97 (0.46)	0.73 (0.25)	1.23 (0.58)	0.94 (0.40)	1.77 (0.66)
3	1.32 (0.33)	1.66 (0.54)	2.24 (0.82)	2.65 (0.80)	1.69 (0.83)	1.88 (0.90)	1.39 (0.51)	1.97 (0.97)	1.81 (0.77)	2.84 (1.07)
4	2.11 (0.49)	2.59 (0.85)	3.04 (1.17)	3.27 (1.25)	2.64 (1.15)	3.17 (1.33)	2.22 (0.83)	3.58 (1.94)	2.90 (1.22)	3.94 (1.50)
5	2.17 (0.67)	2.98 (0.66)	3.21 (1.19)	4.19 (1.25)	2.94 (1.45)	4.27 (2.16)	2.39 (0.89)	4.10 (2.27)	3.57 (1.60)	5.09 (1.97)
6	2.55 (0.79)	3.92 (0.90)	3.67 (1.31)	5.96 (1.76)	3.53 (1.88)	5.77 (2.86)	2.70 (0.99)	4.67 (2.64)	3.83 (1.63)	6.26 (2.44)

Data are population mean SSGPE and RAD values with standard deviations given in parentheses. Results are for a forgetting factor λ of 0.5 and T_W = 5. One step = 5 min.

Accuracy of the predictions is also evaluated using CG-EGA. Table 4 demonstrates CG-EGA error matrix for 30-min-ahead glucose predictions using the recursive algorithm with change detection. There were no CGM data in the hyperglycemic range for the healthy population; therefore Table 4A does not include columns for hyperglycemia. In the hypoglycemic range, 92.31%, 7.69%, and 0% of the data result in accurate readings, benign errors, and erroneous readings for the healthy population and 92.94%, 5.29%, and 1.77% for the population with type 2 diabetes. These values are 91.50%, 7.87%, and 0.63% during normoglycemia and 89.79%, 8.70%, and 1.51% during hyperglycemia for the population with type 2 diabetes. In contrast, 95.47%, 4.53%, and 0% of the healthy group data are considered as accurate, benign errors, and erroneous readings during normoglycemia.

Table 4.

Error Matrix of CG-EGA for Predicted Glucose Values with PH = 6 of Group B: (A) Healthy Subgroup and (B) Type 2 Diabetes Subgroup

	Point error grid zones
	Hypoglycemia (BG ≤ 70 mg/dL)			Normoglycemia (70 < BG ≤ 180 mg/dL)			Hyperglycemia (BG > 180 mg/dL)
Rate error grid zone	A	D	E	A	B	C	A	B	C	D	E
(A) Healthy
A	92.31%	0%	0%	85.17%	0.46%	0%	—	—	—	—	—
B	0%	0%	0%	9.52%	0.32%	0%	—	—	—	—	—
uC	0%	0%	0%	1.74%	0.23%	0%	—	—	—	—	—
lC	7.69%	0%	0%	2.29%	0.27%	0%	—	—	—	—	—
uD	0%	0%	0%	0%	0%	0%	—	—	—	—	—
lD	0%	0%	0%	0%	0%	0%	—	—	—	—	—
uE	0%	0%	0%	0%	0%	0%	—	—	—	—	—
lE	0%	0%	0%	0%	0%	0%	—	—	—	—	—
(B) Diabetes
A	81.76%	1.18%	0%	72.43%	1.18%	0%	70.23%	1.00%	0%	0.08%	0%
B	11.18%	0.59%	0%	17.05%	0.84%	0.04%	18.23%	0.33%	0.17%	0%	0%
uC	2.35%	0%	0%	3.49%	0.30%	0%	4.10%	0.25%	0%	0%	0%
lC	2.94%	0%	0%	3.58%	0.25%	0%	4.01%	0.17%	0%	0%	0%
uD	0%	0%	0%	0.04%	0%	0%	0.17%	0%	0%	0%	0%
lD	0%	0%	0%	0.04%	0.17%	0%	0.08%	0%	0.17%	0%	0%
uE	0%	0%	0%	0.21%	0%	0%	0.42%	0%	0%	0%	0%
lE	0%	0%	0%	0.30%	0.08%	0%	0.59%	0%	0%	0%	0%

The healthy subgroup had no measurements in the hyperglycemic range. The normal type, italic type, and bold type represent accurate readings, benign errors, and erroneous readings, respectively. BG, blood glucose; l, lower; u, upper.

Variations in model parameters

To enhance change detection in model parameters, noisy data are smoothed with an online filter. A low-pass equirriple finite impulse response filter is used with normalized pass-band edge frequency of 0.42 and stop-band edge frequency of 0.5. Initial values for model parameters (θ(t = 0)) are 0; therefore, initialization does not require any prior glucose concentration data. Model parameters converge to good parameter values rapidly, and reliable glucose concentration predictions are made in less than 2 h after starting the recursive algorithm (Fig. 3). This period can be reduced further for a specific patient who uses this method routinely, by assuming as the initial value the parameter values from an earlier prediction series.

FIG. 3.

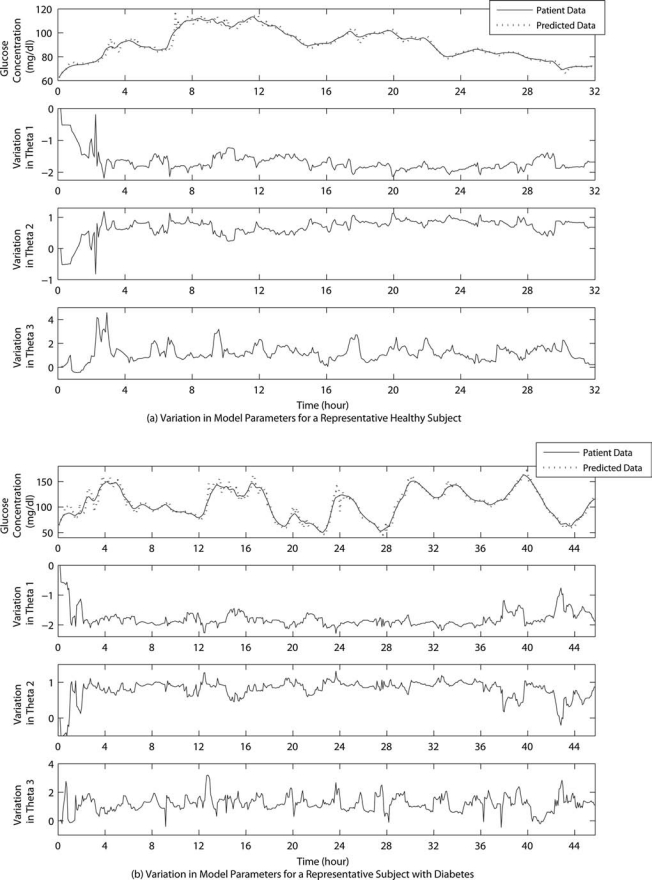
Variation in model parameters for a representative (a) healthy subject and (b) subject with type 2 diabetes for Group B. Predicted glucose concentrations are for a PH of six time steps. Representative subjects are the same as in Figure 2.

Discussion

A reliable subject-specific glucose prediction algorithm has been proposed. Results in Table 3 reveal that more accurate glucose predictions necessitate recursive identification of the model parameters.

Prediction accuracy is improved by continued adaptation of the model to a subject's glucose–insulin dynamics. Some previous studies have suggested adaptive strategies for glucose–insulin modeling.^2,29,30 The proposed recursive glucose prediction algorithm can dynamically adapt to inter-/intra-subject variability because models are derived from the patient's own CGM data and are recursively updated at each sampling step to include the most recent glucose dynamics. Integrating the recursive modeling strategy with a change detection method further facilitates the prediction performance, as the effects of glycemic disturbances are more rapidly captured and a faster model convergence is ensured.

To our knowledge, the work of Sparacino et al.²³ is the only previous study that specifically focused on recursive time-series model identification of a real patient's CGM data. They used a first-order polynomial and AR model. Criteria used in our algorithm are based on a different model type and order, and more optimized model identification and glucose predictions are achieved with integration of the change detection strategy to the recursive algorithm. We believe that simple linear time-series models provide satisfactory glucose predictions and therefore can replace detailed nonlinear physiological glucose–insulin models.

The computational simplicity of the proposed algorithm makes it a good candidate for early warning hypo-/hyperglycemic alarms or closing the glucose regulation loop with an automated pump. Depending on the purpose of glucose predictions, different PH values may play a significant role. For instance, in case of hypo-/hyperglycemia detection, higher PH values (e.g., 20–30-min-ahead) will be of greater importance. However, for closing the loop with model-based control strategies, even one-step-ahead prediction will play an important role in computations of the required insulin infusion rate.

Acknowledgments

This work was partially supported by grant RO1 NR07760-01 from the National Institutes of Health and by the General Clinical Research Center at the University of Illinois at Chicago, which is funded by grant M01-RR-13987 from the National Institutes of Health.

Author Disclosure Statement

No competing financial interests exist.