Abstract
Based on data from 760 centenarians and 1060 middle-age controls (all Han Chinese), this article contributes biodemographic insights and syntheses concerning the magnitude of effects of the FOXO genotypes on longevity. We also estimate independent and joint effects of the genotypes of FOXO1A and FOXO3A genes on long-term survival, considering carrying or not-carrying the minor allele of the single-nucleotide polymorphism of another relevant gene. We found substantial gender differences in the independent effects; positive effects of FOXO3A and negative effects of FOXO1A largely compensate each other if one carries both, although FOXO3A has a stronger impact. Ten-year follow-up cohort analysis shows that at very advanced ages 92–110, adjusted for various confounders, positive effects of FOXO3A on survival remain statistically significant, but no significant effects of FOXO1A alone; G × G interactions between FOXO1A-209 and FOXO3A-310 or FOXO3A-292 decrease survival likelihood by 32%–36% (p < .05); G × E interactions between FOXO1A-209 and regular exercise increase survival likelihood by 31%–32% (p < .05).
Keywords: Biodemographic analysis, FOXO genes, G × G and G × E interactions, Longevity, Mortality
FOXO1A and FOXO3A, also known as FKHR and FKHRL1, are two members of FOXO (Forkhead box, class O) subfamily of forkhead transcription factors and evolutionarily conserved across the species in their protein sequences (1). Recent studies have found that FOXO3A is associated with human longevity in Japanese-Americans from Hawaii (2), Italians (3), Ashkenazi Jews (4), Californians (4), New Englanders (4), Germans (5), and Han Chinese (6). The German study also showed that the FOXO3A variants were more frequent in centenarians than in 90-year-olds, indicating that these variants may extend life span even at very advanced ages. The genetic study by Li and colleagues (6) on which our current biodemographic analysis is based tested the genetic contribution of FOXO1A and FOXO3A genes to the longevity phenotype in the Han Chinese population. Six tagging single-nucleotide polymorphisms (SNPs) from FOXO1A and FOXO3A were selected and genotyped. All three SNPs of FOXO3A were positively associated with longevity in both genders (odds ratio [OR] = 1.61–1.73, p = .0002–0.005; dominant model). Two SNPs of FOXO1A (rs2755209 and rs2755213) were found to be negatively associated with longevity in women (OR = 0.70 and 0.71, p = .007 and .015; dominant model), whereas in the dominant model for men, FOXO1A-rs2755213 is marginally and negatively associated with longevity (OR = 0.65, p = .025) and the association of FOXO1A- rs2755209 is not significant (OR = 0.73, p = .093). One SNP (rs17630266) from FOXO1A was found not to be associated with longevity. The negative association of FOXO1A with female longevity was replicated in 350 centenarians and 350 younger individuals who were sampled in a geographically distinct region. FOXO1A and FOXO3A gene variants have also been linked to longevity in the Framingham cohort in the United States (7) and in the Leiden 85-plus study (8).
In her most recent Nature review article, Kenyon stated that the reason why FOXO variants are so consistently associated with longevity is perhaps because FOXO proteins act in many pathways to affect life span (9). In vivo, FOXO1A and FOXO3A regulate a group of gene’s expression, such as TRAIL, ApoC3, angiopoietin-2, ENOS, Agrp, pomc, FasL, and Bim. On the other hand, FOXO1A and FOXO3A, once phosphorylated by AKT, can bind to 14-3-3, leading to their functional inactivation by transferring from cell nucleus to cytoplasm (10,11). AKT1-FOXO–mediated signaling pathway is critical in regulation of cell cycle, apoptosis, stress resistance, and metabolism (12,13). Early studies have demonstrated that a genetic modification of DAF-16 or FOXO in Caenorhabditis elegans and Drosophila melanogaster significantly affects their maximum life span (14–16), indicating that FOXOs are involved in the aging process.
Previous case–control population association studies on genetic contributions to longevity (including those reviewed previously) estimate ORs that measure the differences in the frequencies of genetic variants between long-lived individuals and younger adults, usually following the conventional approach of logistic regression. If the ORs are significantly greater or less than 1, the conclusion can be drawn that the allele or genotype is positively or negatively associated with longevity. The ORs estimated in the conventional approach do not indicate, however, how much the probability of survival from younger ages to older ages would be increased or reduced due to genetic influences. In other words, they do not specify the magnitude of the genetic effects on the survival probability. Furthermore, previous studies (6,7) have shown that FOXO3A and FOXO1A influence longevity in opposite directions, but no investigation of their independent (ie, in the absence of the other), joint (presence of both), and interactive effects has been reported. Moreover, previous studies (2–7) did not investigate the impacts of various genotypes of FOXO1A and FOXO3A, interactions between these genotypes (G × G) and interactions between the genotypes and social-behavioral factors (G × E) on survival at advanced ages. Building upon previous relevant research (2–18), especially based on the genotypic data set produced in the study by Li and colleagues (6) on the association between FOXO genes and longevity in Han Chinese, we address the following previously unanswered questions, by a biodemographic analysis approach:
What are the magnitudes of the general effects of the genotypes of FOXO1A and FOXO3A on the probability of survival from middle age to ages 100+?
As compared with those who are neither a carrier of the genotype of FOXO1A nor a carrier of the genotype of FOXO3A, what are the differences in the probability of survival from middle age to age 100+ for those who are a carrier of a genotype of FOXO1A but not FOXO3A, a carrier of a genotype of FOXO3A but not FOXO1A, or a carrier of both? Are there any statistically significant effects of gene–gene interaction of FOXO1A and FOXO3A on survival from middle age to age 100+?
Does the carrying or not-carrying the genotypes of FOXO1A and FOXO3A, the G × G interactions among them, and their G × E interactions with social and behavioral factors significantly affect survival at very advanced ages? If yes, what are the direction and size of the effects?
MATERIALS AND METHODS
Data Sources
Our analyses are mainly based on DNA samples from 578 female centenarians and 182 male centenarians who survived to age 100+ when they participated in the interviews in baseline or the follow-up wave(s) of the Chinese Longitudinal Healthy Longevity Survey (CLHLS) study; all of them were at least 92 years old in 1998 baseline survey. The DNA samples of the middle-age controls (378 women and 682 men) were collected from the routine clinic health examinations involving ordinary people. These 760 centenarians and the 1060 middle-age controls were all from Southern China (China is traditionally and culturally considered to have Southern and Northern parts, although there is no legitimate or official administrative meaning to this division. The South and North are divided by the geographical line of the Qin Ling mountain and Huai River. The line crosses through four provinces of Shaanxi, Henan, Anhui and Jiansu. Among the 22 provinces where CLHLS was conducted, Liaoning, Jilin, Heilongjiang, Hebei, Beijing, Tianjing, Shanxi, and Shangdong belong to Northern China; Shanghai, Zhejiang, Fujian, Jiangxi, Hubei, Hunan, Guangdong, Guangxi, Sichuan, Chongqing belong to Southern China; and the northern and southern sides of the Qin Ling mountain—Huai River line in Shaanxi, Jiangsu, Anhui, Henan belong to Northern and Southern China, respectively), and their genotypic data used in this study were produced by and described in the genetic analysis by Li and colleagues (6). More specifically, we use the same genotypic data for the SNPs rs2755209 and rs2755213 of FOXO1A gene and the three SNPs rs2253310, rs2802292, rs4946936 of FOXO3A gene as that used in Li and colleagues (6). The internationally standardized technical procedures for producing the genotypic data were presented in Li and coworkers (6). The rs17630266 SNP of FOXO1A was found not to be associated with longevity and thus will not be used in our present more in-depth biodemographic analysis. The minor allele frequency (MAF) distributions of the SNPs, the single SNP association analysis, genotype association analysis with recessive and additive models, and the linkage disequilibrium and haplotype association analysis were presented in Li and colleagues (6), and thus there is no need to be repeated here. To ease the presentation, we abbreviate in this article the two SNPs rs2755209 and rs2755213 of FOXO1A gene as 1A-209 and 1A-213; we abbreviate the three SNPs rs2253310, rs2802292, rs4946936 of FOXO3A gene as 3A-310, 3A-292, and 3A-936, respectively.
To define the genotypes to be analyzed in this article, carrying or not-carrying the minor allele of one of the two SNPs of FOXO1A or of one of the three SNPs of FOXO3A is determined as “Yes (carrier)” or “No (noncarrier)” for each of the centenarians and controls, all based on the dominant model. In the dominant model, individuals who carry one or two copies of the minor allele are coded as Yes (carrier), and the individuals who do not carry the minor allele are coded as No (noncarrier) (ie, mm, Mm = 1, MM = 0; here, M: major allele, m: minor allele). Table 1 presents the frequency distribution of the genotypes defined by carrying the minor alleles of one of the two SNPs of FOXO1A or one of the three SNPS of FOXO3A based on the dominant model, for the male and female centenarians and middle-age controls. Tables 2 and 3 present the frequency distributions of the genotypes defined by combinations of whether carrying the minor allele of one of the three SNPs of FOXO3A and whether carrying the minor allele of 1A-209 (Table 2) or 1A-213 (Table 3), respectively, for the male and female centenarians and middle-age controls.
Table 1.
Frequency Distribution of the Genotypes Defined by Carrying the Minor Alleles of One of the Two SNPs of FOXO1A or One of the Three SNPS of FOXO3A Based on the Dominant Model, and the Estimates of the Odds Ratio of Survival Probability (RS) from Middle Age to Age 100+ Measuring the General Effects of the Genotypes
| Women |
Men |
|||||||
| Genotypes | Cent. %car. | Contr %car. | RS (95% CI) | p | Cent. %car. | Contr %car. | RS (95% CI) | p |
| Carrying minor allele of 1A-209 | 42.3 | 51.3 | 0.70 (0.53–0.91) | 0.0073 | 41.8 | 49.5 | 0.73 (0.51–1.05) | 0.093 |
| Carrying minor allele of 1A-213 | 57.8 | 65.8 | 0.71 (0.54–0.91) | 0.0152 | 58.8 | 68.6 | 0.65 (0.45–0.95) | 0.025 |
| Carrying minor allele of 3A-310 | 51.9 | 39.3 | 1.67 (1.27–2.18) | 0.0002 | 55.5 | 43.0 | 1.65 (1.19–2.30) | 0.003 |
| Carrying minor allele of 3A-292 | 51.7 | 39.8 | 1.62 (1.24–2.12) | 0.0004 | 56.3 | 42.7 | 1.73 (1.24–2.41) | 0.001 |
| Carrying minor allele of 3A-936 | 49.5 | 37.1 | 1.66 (1.26–2.18) | 0.0003 | 51.9 | 40.2 | 1.61 (1.16–2.24) | 0.005 |
Note: Sample size—centenarians: 578 women and 182 men; middle-age controls: 378 women and 682 men, all Han Chinese from Southern China. CI = confidence interval. Cent. %car. = Percentage of centenarians who carry the minor allele; Contr %car. = Percentage of middle-age controls who carry the minor allele; SNP = single-nucleotide polymorphisms.
Table 2.
Frequency Distribution of the Genotypes Defined by Combinations of Whether Carrying the Minor Allele of One of the Three SNPs of FOXO3A and Whether Carrying the Minor Allele of 1A-209, and the Estimates of the Odds Ratios of Survival Probability (RSij/00) from Middle Age to Ages 100+ Measuring the “Independent and Joint Effects” of the Genotypes
| Carrier or noncarrier of the minor allele of the SNPs of FOXO3A | Noncarrier of minor allele of 1A-209 (i = 0) | Carrier of minor allele of 1A-209 (i = 1) | ||||||
| Cent. % genotype | Contr % genotype | RSij/00 (95% CI) | p | Cent. % genotype | Contr % genotype | RSij/00 (95% CI) | p | |
| Women | ||||||||
| 3A-310, noncarrier (j = 0) | 27.8 | 26.6 | 1.00 | 20.2 | 34.0 | 0.57 (0.39–0.83) | 0.002 | |
| 3A-310, carrier (j = 1) | 29.9 | 21.7 | 1.32 (0.89–1.94) | 0.148 | 22.1 | 17.7 | 1.19(0.79–1.81) | 0.389 |
| 3A-292, noncarrier (j = 0) | 27.7 | 26.6 | 1.00 | 20.5 | 33.6 | 0.58 (0.40–0.85) | 0.004 | |
| 3A-292, carrier (j = 1) | 30.1 | 21.9 | 1.31 (0.89–1.93) | 0.148 | 21.7 | 17.9 | 1.16(0.76–1.76) | 0.462 |
| 3A-936, noncarrier (j = 0) | 28.8 | 28.2 | 1.00 | 21.6 | 34.6 | 0.61 (0.42–0.88) | 0.006 | |
| 3A-936, carrier (j = 1) | 28.9 | 19.9 | 1.41 (0.95–2.10) | 0.073 | 20.7 | 17.3 | 1.17(0.77–1.78) | 0.451 |
| Men | ||||||||
| 3A-310, noncarrier (j = 0) | 23.3 | 29.3 | 1.00 | 20.6 | 27.8 | 0.93 (0.55–1.55) | 0.755 | |
| 3A-310, carrier (j = 1) | 35.0 | 22.3 | 1.96 (1.23–3.15) | 0.003 | 21.1 | 20.6 | 1.28(0.76–2.16) | 0.322 |
| 3A-292, noncarrier (j = 0) | 23.8 | 29.6 | 1.00 | 19.9 | 27.8 | 0.89 (0.53–1.49) | 0.636 | |
| 3A-292, carrier (j = 1) | 34.8 | 22.0 | 1.96 (1.23–3.15) | 0.003 | 21.5 | 20.6 | 1.30(0.77–2.17) | 0.292 |
| 3A-936, noncarrier (j = 0) | 26.6 | 31.6 | 1.00 | 21.5 | 28.3 | 0.91 (0.55–1.49) | 0.686 | |
| 3A-936, carrier (j = 1) | 32.0 | 19.9 | 1.92 (1.20–3.06) | 0.004 | 19.9 | 20.2 | 1.17(0.70–1.96) | 0.522 |
Note: (1) The sample size is the same as that listed in Table 1. (2) The odds ratio 1.00 refers to the reference group with a genotype without carrying the minor allele of any of the two SNPs paired for the analysis; the values in italics in this table present the estimates of the “joint” effects of carrying the minor allele of SNP 1A-209 and carrying the minor allele of one of the three SNPs of FOXO3A; and the rest present the estimates of the “independent” effects of carrying the minor allele of one of the three SNPs of FOXO3A but not-carrying the minor allele of the SNP 1A-209, or carrying the minor allele of the SNP 1A-209 but not-carrying the minor allele of one of the three SNPs of FOXO3A. CI = confidence interval; SNP = single-nucleotide polymorphisms.
Table 3.
Frequency Distribution of the Genotypes Defined by Combinations of Whether Carrying the Minor Allele of One of the Three SNPs of FOXO3A and Whether Carrying the Minor Allele of 1A-213, and the Estimates of the Odds Ratios of Survival Probability (RSij/00) From Middle Age to Ages 100+ Measuring the “independent and joint effects” of the genotypes
| Carrier or noncarrier of the minor allele of the SNPs of FOXO3A | Noncarrier of minor allele of 1A-213 (i = 0) | Carrier of minor allele of 1A-213 (i = 1) | ||||||
| Cent. % genotype | Contr % genotype | RSij/00 (95% CI) | p | Cent. % genotype | Contr % genotype | RSij/00 (95% CI) | p | |
| Women | ||||||||
| 3A-310, noncarrier (j = 0) | 19.2 | 18.8 | 1.00 | 28.7 | 41.7 | 0.68 (0.45–1.00) | 0.043 | |
| 3A-310, carrier (j = 1) | 23.0 | 14.6 | 1.55 (0.97–2.48) | 0.052 | 29.1 | 24.9 | 1.15(0.76–1.75) | 0.489 |
| 3A-292, noncarrier (j = 0) | 19.0 | 18.8 | 1.00 | 29.1 | 41.3 | 0.70 (0.47–1.03) | 0.061 | |
| 3A-292, carrier (j = 1) | 23.2 | 14.8 | 1.55 (0.97–2.47) | 0.052 | 28.7 | 25.1 | 1.14(0.74–1.73) | 0.534 |
| 3A-936, noncarrier (j = 0) | 20.1 | 19 | 1.00 | 30.3 | 43.7 | 0.66 (0.45–0.97) | 0.029 | |
| 3A-936, carrier (j = 1) | 22.1 | 13.8 | 1.53 (0.95–2.47) | 0.066 | 27.5 | 23.5 | 1.12(0.73–1.71) | 0.595 |
| Men | ||||||||
| 3A-310, noncarrier (j = 0) | 13.9 | 17.5 | 1.00 | 30.0 | 39.5 | 0.96 (0.55–1.69) | 0.867 | |
| 3A-310, carrier (j = 1) | 27.2 | 14.7 | 2.34 (1.30–4.25) | 0.002 | 28.9 | 28.3 | 1.29(0.74–2.29) | 0.352 |
| 3A-292, noncarrier (j = 0) | 14.3 | 17.7 | 1.00 | 29.3 | 39.7 | 0.91 (0.53–1.59) | 0.712 | |
| 3A-292, carrier (j = 1) | 27.1 | 14.5 | 2.29 (1.28–4.14) | 0.003 | 29.3 | 28.1 | 1.28(0.74–2.26) | 0.357 |
| 3A-936, noncarrier (j = 0) | 17.2 | 19.3 | 1.00 | 30.9 | 40.6 | 0.86 (0.51–1.45) | 0.538 | |
| 3A-936, carrier (j = 1) | 24.3 | 12.8 | 2.14 (1.21–3.81) | 0.005 | 27.6 | 27.3 | 1.14(0.67–1.96) | 0.617 |
To conduct a novel biodemographic analysis, we also combine the genotypic data with the corresponding 10-year follow-up cohort phenotypic data from 760 individuals who were at least 92 years old in the CLHLS 1998 baseline survey, whereas 750 of them died after 1998 at ages 100+ and 10 still survived in the 2008 wave. The cohort follow-up data on survival and death, socioeconomics, lifestyle, psychological characteristics, and heath status, etc. of the participants used in the multivariate statistical survival analysis in this article are from the CLHLS conducted in 1998, 2000, 2002, 2005, and 2008 using questionnaires that followed the international standards adapted to the Chinese cultural context (19). The careful evaluations (such as reliability coefficients and factor analysis) have shown that the data quality of the CLHLS surveys was reasonably good (19). We use the centenarians’ age at death (or age in 2008 for the 10 centenarians who survived in the 2008 follow-up survey) in our case-control analysis. The mean age of the male and female centenarians samples were 101.9 and 103.2, respectively. The mean ages of the male and female controls were 46.0 and 45.4, respectively. Similar to the previously published studies on association between the FOXO genotypes and longevity (2–8), the centenarians and middle-age controls of this study are ethnically (all Han Chinese) and geographically (Southern China) compatible, and thus the population stratification problem is well under control.
The Extended Fixed Attribute Dynamics Method
The Fixed Attribute Dynamics (FAD) method belongs to the family of methods of case–control population association analysis, and it is designed to investigate the association of fixed attributes (including genotypes) on longevity. The initial use of the FAD method (known as the Survival Attribute Assay then) by Vaupel (20) and Yashin and colleagues (21) required knowledge of cohort age-specific mortality rates. The FAD method extended by Zeng and Vaupel (22) does not require these rates, which are not available in many practical applications.
The OR of survival from age x to x + n (RS) for those with the fixed attribute (eg, a genotype) to those without the attribute can be estimated as:
| (1) |
where p (x) is the proportion of individuals who are x years old and have the fixed attribute. Zeng and Vaupel (22) derived Formula (1) and empirically justified it.
Note that Formula (1) provides estimates of the general impacts of one genetic variant on survival from age x to x + n, regardless of carrying or not-carrying another relevant genetic variant. We extend the FAD method here to provide formulas to estimate the independent effect of a genetic variant in the absence of another relevant genetic variant, the joint effects when both are present and the effects of interactions between them.
Let i = 0, 1 represent not-carrying and carrying the genetic variant, abbreviated as “noncarrier” and “carrier” hereafter; and j = 0, 1 represent not having and having another fixed attribute (or genetic variant), abbreviated as “not-exposed” and “exposed” hereafter. Let p11(x) be the proportion of x-year-old individuals who are both carrier and exposed among all persons aged x. Similarly, define p10(x), p01(x), and p00(x) as the proportions who are a carrier and not-exposed, noncarrier and exposed, and neither carrier nor exposed. Note that the sum of p11(x), p10(x), p01(x) and p00(x) is equal to 1. The extended FAD method is expressed in the following formula; its mathematical and demographic derivation is presented in the Appendix 1:
| (2) |
If the OR of survival RSij/00 is significantly greater (or smaller) than 1.0, the i–j combination of the gene-fixed exposure is positively (or negatively) associated with longevity, and the difference between the OR of survival and 1.0 measures the magnitude of the genetic effects on longevity. Standard statistical significance tests including estimates of p values and 95% confidence intervals (CIs) (23) can be performed to assess whether the estimates of an OR of survival (RS in Formula (1) and RSij/00 in Formula (2)) is significantly different from 1.0, using a simple procedure in standard statistical software (eg, STATA, SAS or SPSS). Note that RS10/00 and RS01/00 represent the independent impact of the genetic variant (or another fixed exposure) on survival from age x to x + n, in the absence of another fixed exposure (including genetic variant) and that RS11/00 represents the joint impact of the genetic variant and the fixed exposure on survival from age x to x + n when both of them present.
In Formula (2), individuals are identified as “carriers” or “noncarriers,” and a carrier could have 1 or 2 copies of the minor allele of the SNPs in the application of our present study. Hence we are implicitly assuming that the minor allele is dominant rather than recessive or additive. A modified version of the FAD approach and application is required to analyze recessive or additive models.
Gene–environment interaction (G × E) is defined as “a different effect of an environmental exposure on disease and health risk in persons with different genotypes,” or, alternatively, “a different effect of a genotype on disease and health risk in persons with different environmental exposures” (24,25). Similarly, gene–gene interaction (G × G) is defined as “a different effect of a genotype on disease and health risk in persons with and without another genotype.” Applying the standard definition and method for estimating the G × E or G × G interactions (25), we present in Appendix 2 the procedures for estimating the effects of gene-fixed exposure interactions on survival from age x to x + n, using the ORs of survival (RSij/00, i = 0, 1; j = 0, 1) derived by Formula (2).
The basic and extended FAD methods expressed in Formulas (1) and (2) can be used to analyze cross-sectional data from different cohorts of long-lived cases and younger controls or follow-up data from the same cohort. In the case of analyzing the cross-sectional data, we actually connect the younger cohort and the long-lived cohort into what the demographic text books call “a hypothetical cohort,” and estimate the OR of survival based on proportions of the genetic variant and fixed exposure among the long-lived and younger cohorts (ie, at advanced and younger ages in the “hypothetical cohorts”).
It is important to note that, if one uses cross-sectional data, both the FAD method expressed in Formulas (1) and (2) and the conventional case–control statistical genetic approach assume that the initial distributions of the genetic variant, the fixed exposure and their combinations, and their association with longevity do not differ substantially between cohorts of long-lived individuals and younger controls, that is, there is no substantial problem of population stratification (see more detailed discussions in Appendix 1 on potential bias if this basic assumption is violated). If cohort follow-up data are used, one needs to assume that the loss to follow-up from age x to x + n is not correlated with respondents’ combination of the genetic variant and the fixed exposure under study. Serious attention must be paid to this issue in applying either the conventional statistical genetic approach or the FAD method for identifying genetic contributions to longevity. To control for population stratification in the FAD analysis in this article using the cross-sectional data of centenarians and middle-age controls, we have restricted our analysis to a single ethnic group (Han Chinese) residing in Southern China, and classified the samples by gender as well.
The basic and extended FAD methods are based on the fundamental demographic insight that the prevalence of a fixed attribute (eg, genetic variant, birth weight, childhood conditions, and serious disease(s) suffered earlier in life) and combinations of two fixed attributes in a population can change with age even though no individual can change his or her variant. Therefore, much can be learned about the impact of the fixed attribute (including genetic variant) and the combinations of the fixed attributes on survival.
Note that it is mathematically and numerically verified that, using the same genotypic data sets of the long-lived cases and younger controls, the estimates of the ORs of survival and their associated p values and 95% CI by our FAD method expressed in Formulas (1) and (2) are exactly the same as the corresponding numerical results produced by the logistic regression not adjusted for covariates, which is a conventional approach in genetic analysis on the association of a genetic variant with longevity (The mathematical proof and the empirical evidence, which verify that our FAD method and the conventional logistic regression without controlling for covariates produce exactly the same numerical results of ORs, p, and 95% CI are not presented here due to space limitation, but available upon request.). This fact verifies the statistical properties of our FAD method. More importantly, the ORs of survival based on the FAD method quantify the magnitude of the genetic effects on survival probability, namely how much the probability of survival from age x to x + n would be increased or reduced by carrying the genotype. In other words, the FAD method provides clearer demographic interpretations and presents meaningful demographic syntheses of the case–control genetic analysis on longevity. As the two approaches produce exactly the same numerical results, one may adopt the FAD’s demographic interpretation of the OR, namely the effects on survival probability from the average age of the younger controls to the average age of the long-lived cases, even if one still uses the conventional approach of logistic regression. From this point of view, we may consider that the FAD method contributes an additional new insight of demographic interpretation on the magnitude of the genetic effects on survival probability to the conventional approach of logistic regression in case–control genetic analysis on longevity.
The standard method of survival analysis using cohort follow-up data is limited because it requires prospective tracking of the mortality of study participants, with a follow-up period for estimating long-term survival probabilities that may be prohibitively expensive and time consuming (26). The FAD method circumvents this major limitation of standard survival analysis because it does not require expensive follow-up mortality data of study participants and it can be applied to both cohort and cross-sectional data sets if the basic assumption of no serious problems of population stratification is met. However, the FAD method has a major limitation: it permits an analysis to ascertain the “de facto” association of a fixed attribute (including genes) or the combination of gene-fixed exposure on longevity while usually controlling for age and sex. In theory, we can further control for other covariates by extending the FAD method through cross-tabulations of the study participants by confounding factors that are also fixed attributes and meet the assumption of no substantial problems of population stratification, but this may cause problems with small sample sizes of the subgroups. Thus, we applied both FAD methods and multivariate statistical modeling approaches whenever possible to complement each other and to maximize the utility of the available data sources.
Multivariate Hazards Model for Survival Analysis
The effects of the genotypes of the FOXO1A and FOXO3A, their G × G and G × E interactions on survival likelihood at very advanced ages 92–110 are examined based on Cox proportional hazard models using the available genotypic and longitudinal data from 727 interviewees (553 women and 174 men; the sample size used in our Cox proportional hazards model analysis is slightly smaller than that used in the FAD analysis because a very small number of cases who were interviewed and contributed DNA in 1998 were lost to follow-up and we had to drop them from the regression. Empirical testing has shown that dropping these few loss-to-follow-up cases does not affect the estimates) who were aged 92+ and contributed DNA in the CLHLS 1998 baseline survey and survived to age 100+ either in the baseline or in one of the subsequent follow-up surveys conducted in 2000, 2002, 2005, and 2008, but almost all of them died before 2008. The assumption of proportionality of the hazards was assessed and met the requirement for all of the models analyzed. Survival time is entered as days between the last interview date and date of death for those who died (or date at 2008 interview for the 10 individuals who still survived in 2008 follow-up survey), while using the exact age at last interview as a covariate (survival analysis in population aging studies usually does not use age at death or censoring as survival time because it could not easily identify the age effect on the mortality risk if the age is used as the survival time). Demographic characteristics (including exact age at 1998 baseline survey, gender and rural-urban residence, etc.), social connections, family support, health practices, the resilience score, and current health status (see Appendix 3) are included in the hazards models as covariates in a forward stepwise analysis. Results based on the sequential models are presented to show how the effects of genotypes on survival may be mediated by different confounders. We also tried to estimate the effects of all possible gene–environment interaction (G × E) and gene–gene interaction (G × G) terms in the Cox proportional hazards models.
Note that the statistically significant estimates of the interaction terms of G × E and G × G derived from the Cox proportional hazard models analysis represent the significant G × E and G × G synergistic effects, which may or may not exactly reflect the interaction effects of G × E and G × G, as the estimates may or may not be confounded by the gene–environment correlations (rGE) and gene–gene correlations (rGG). Thus, we need to do the following additional analysis to detect whether the rGE and rGG exist. For all significant gene–environment effects with a continuous environmental variable discovered in the Cox proportional hazards model analysis, we use the ANOVA model to test for differences in means of continuous environmental factors between the gene carriers and noncarriers. For all significant gene–environment synergistic effects with a discrete environmental variable and for all significant gene–gene synergistic effects discovered in the Cox proportional hazards models analysis, we use the chi-squared test to assess the genotype frequency difference across the environmental categories and across the genes. For all significant rGE and rGG detected by analysis of variance or chi-square test, we will need to conduct path analysis employing multivariate regression analysis or structural equation modeling, adjusted for various confounding factors, to further explore the interplay among genes, environment, and survival likelihood. Based on the path analysis, we may estimate the significant genotype effects that work through environmental exposure or another genotype, the direct genotype effect, and the significant gene–environment interaction or gene–gene interaction effects on survival likelihood.
RESULTS
General Effects of the Genotypes of FOXO1A and FOXO3A on Long-term Survival Probability From Middle Age to Age 100+
Table 1 presents estimates of the general effects of the genotypes of FOXO1A and FOXO3A on long-term survival probability from middle age to age 100+, regardless of carrying or not-carrying another relevant genotype, based on genotypic data from 760 centenarians and 1056 middle-age controls who reside in Southern China and the FAD method expressed in Formula (1) in The Extended Fixed Attribute Dynamics Method subsection. The genotypes presented in Table 1 are defined as carrying or not-carrying the minor allele of one of the two SNPs of FOXO1A or one of the three SNPs of FOXO3A regardless of whether carrying the minor allele of any other four SNPs of FOXO1A and FOXO3A. The results show that, as compared with noncarriers, the OR of survival from middle ages to age 100+ for women who are carriers of the minor alleles of 1A-209 and 1A-213 are 0.70 (p = .0073) and 0.71 (p = .0152), respectively; the corresponding OR estimates for men are 0.73 (p = .093) and 0.65 (p = .025). These estimates imply that the probability of survival from middle age to age 100+ for women who are a carrier of the minor alleles of the 1A-209 and 1A-213 are 30% and 29% lower than those who are noncarriers, and the estimates are statistically significant; those men who carry the minor alleles of 1A-209 and 1A-213 may have 27% and 35% lower probability of survival from middle age to age 100+, but the estimate for 1A-209 is not statistically significant and the estimate for 1A-213 is moderately significant (p = .025) (Table 1). As compared with noncarriers, the OR of survival for women and men who carry the minor alleles of 3A-310, 3A-292, and 3A-936 are 1.62–1.67 (p = .0002–.0004) and 1.61–1.73 (p = .001–.005), respectively. These estimates of the general effects imply that, on average, middle-age women and men who carry the minor allele of any one of the three SNPs of FOXO3A may have 62%–67% and 61%–73% higher probability of survival from middle age to age 100+, and all of the estimates are highly statistically significant.
The Independent and Joint Effects of the Genotypes of FOXO1A and FOXO3A on Long-term Survival From Middle Age to Age 100+
The analyses concerning FOXO1A presented in Table 1 of the present study employing Formula (1) of the FAD method and in previous relevant studies following the conventional genetic and statistical approach (6) are based on comparing the frequencies of carrying the minor allele of the SNPs of FOXO1A (regardless of whether carrying the minor allele of the SNPs of FOXO3A) between centenarians and younger controls. So are the analyses concerning FOXO3A presented in Table 1 and in the previous studies (2–7). Although they are useful in exploring the general impacts of one genotype on longevity regardless of carrying or not-carrying the other relevant genotype, these analyses cannot reveal the independent, joint, and interactive effects of the genotypes of FOXO3A and FOXO1A, which influence survival in opposite directions.
Applying our extended FAD method expressed in Formula (2), Tables 2 and 3 present the estimates of ORs of survival (RSij/00) from middle age to age 100+ reflecting the independent and joint effects of the genotypes of FOXO3A and FOXO1A. The genotypes presented in Tables 2 and 3 are defined by a combination of carrying or not-carrying minor alleles of one of the two SNPs of FOXO1A and minor alleles of one of the three SNPs of FOXO3A, with the reference group who carry neither the minor allele of the SNP of FOXO1A nor the minor allele of the SNP of FOXO3A. We choose these combinations because we aim to capture the independent effects (RS10/00 and RS01/00), joint effect (RS11/00) of the two genes of FOXO1A and FOXO3A that affect longevity in opposite directions, and the Gene × Gene interactions. We did not choose the combination of the pairs within the three SNPs of FOXO3A gene and the combinations of the pairs within the two SNPs of the FOXO1A gene, mainly because such haplotype-based analysis was already done in the previous publication (6).
The results show that, as compared with those who are noncarriers of the minor allele of one of the three SNPs of FOXO3A and noncarriers of the minor allele of 1A-209, the negative and independent effects of carrying the minor allele of 1A-209 on survival in women are all highly significant (p = .002–0.006) (Table 2), which is consistent with the general effects (regardless of carrying or not-carrying the minor allele of FOXO3A) presented in first row of the panel for women in Table 1. The corresponding negative and independent effects of 1A-213 in women are moderately (p = .029–.043) or marginally (p = .061) significant (Table 3), which are consistent in terms of impact direction and magnitude of the ORs but with lower level of significance as compared with the general effects (see second row of the panel for women in Table 1). As compared with those women who are noncarriers of the minor allele of 1A-209 and noncarriers of the minor allele of the corresponding SNP of FOXO3A, the independent effects of 3A-310 and 3A-292 are not significant, and the independent effect of 3A-936 is only marginally significant (p = .073) (Table 2). As compared with those women who are noncarriers of the minor allele of the 1A-213 and noncarriers of the minor allele of the corresponding SNP of FOXO3A, the independent effects of the three SNPs of FOXO3A are only marginally significant (p = .052–.066). These estimates of the independent effects of the three SNPs of FOXO3A in women are remarkably different from the general effects regardless of the carrying or not-carrying the minor allele of the two SNPs of FOXO1A estimated by the basic FAD analysis (Table 1) and the conventional genetic analysis (2–7).
In men, the patterns of the independent effects of FOXO1A and FOXO3A are substantially different from those of women. As compared with men who are noncarriers of the minor allele of one of the three SNPs of FOXO3A and oncarriers of the minor allele of the corresponding SNP of FOXO1A, the independent effects of the two SNPs of FOXO1A in men are all nonsignificant (see the panels for men in Tables 2 and 3). However, it is interesting to note that in men, as compared with those who are noncarriers of the minor allele of one of the two SNPs of FOXO1A and noncarriers of the minor allele of the corresponding SNP of FOXO3A, the independent effects of the three SNPs of FOXO3A are all highly significant (p = .002–.005; see panels for men in Tables 2 and 3), which are consistent with the general effects.
Dual presence of the minor allele of one of the three SNPs of FOXO3A and the minor allele of one of the two SNPs of FOXO1A may increase the chance of survival from middle age to age 100+ by 12%–19% in women and by 14%–30% in men, as compared with those who neither carry the minor allele of the corresponding SNP of FOXO3A nor carry the minor allele of the corresponding SNP of FOXO1A, but all of the estimates associated with the dual presence (ie, joint effects) of FOXO3A and FOXO1A are not statistically significant (see the italic and bold values in Tables 2 and 3). These results indicate that the positive effects of FOXO3A and the negative effects of FOXO1A substantially compensate each other, whereas the impacts of FOXO3A are somewhat stronger.
The Effects of Interaction Between FOXO1A and FOXO3A on Survival From Middle Age to Age 100+
The absolute values of the correlation coefficients between each of the two SNPs of the FOXO1A and each of the three SNPs of the FOXO3A are very small (about half <.01 and another half .01–.05). Moreover, FOXO1A and FOXO3A are located on different chromosomes (FOXO1A on chromosome 13, FOXO3A on chromosome 6), and they are physically independent in terms of linkage disequilibrium. Consequently, the assumption of independence between FOXO1A and FOXO3A is clearly met. We employed Formula (A6) of the FAD approach described in the Appendix 2, which is based on the multiplicative assumption to estimate the index of interactions between FOXO1A and FOXO3A on long-term survival; p and 95% CI are estimated by the bootstrap simulation method. The results show that all interactions between each of the two SNPs of the FOXO1A and each of the three SNPs of the FOXO3A are not statistically significant (data not shown).
The Effects of SNPs of FOXO1A and FOXO3A and Their G × G and G × E Interactions on Survival at Very Advanced Ages, Based on Longitudinal Cohort Data From the Long-Lived Cases
Note that the results presented in Tables 1, 2, and 3 and discussed in previous subsections are all based on cross-sectional data from long-lived cases and middle-aged controls and the FAD approach. In this subsection, we will present the multivariate survival analysis based on longitudinal cohort data from the long-lived cases only, given the fact that the follow-up data from the middle-age controls are not available. Tables 4 and 5 presents the estimates of the relative hazards for the genotypes, G × G (gene–gene) interactions, and the significant G × E (gene–environment) interactions on survival likelihood at very advanced ages 92–110, adjusted for 15 potentially confounding factors step by step, based on the cohort follow-up data from the Southern China Han samples. We present the definitions and how we estimated these 15 potentially confounding factors in Appendix 3. As discussed earlier, the FOXO1A and FOXO3A genes are not correlated with each other. However, among the Chinese male and female centenarians, the three SNPs within the FOXO3A are highly correlated with each other (with correlation coefficients ranging from 0.894 to 0.976), and the two SNPs within the FOXO1A are also highly correlated (with correlation coefficients ranging from .618 to .643). To avoid the problems of multicollinearity, we should not include more than one SNP of FOXO1A and more than one SNP of FOXO3A in each regression model. Instead, in Models I, II, III, and IV, which do not include any G × G and G × E interactions, we include one of the two SNPs of FOXO1A or one of the three SNPs of FOXO3A one by one. In other words, each of these four models has five submodels and each submodel includes one SNP only. Models I, II, III, and IV also sequentially introduce the potentially confounding variables step by step. Model I includes demographic and basic socioeconomic status: gender, single year of age, residence (urban vs rural), educational attainment and economic independence. Model II further includes family and social support variables (such as marital status, living arrangement, proximity to children, whether had family members as caregiver, and leisure activities score) and the resilience score. Model III adds health practice including regular exercise, smoking in recent 5 years, and heavy alcohol use. Model IV further includes the deficits index (DI), a summary indicator of cumulative deficits of different health dimensions of daily activities, physical performance, cognitive function, depressive symptoms, self-rated health, chronic disease, etc., at old ages (see Appendix 3). Models V, VI, and VII include the G × G interactions between 1A-209 and one of the three SNPs of FOXO3A, and Models VIII, IX, and X include the G × G interactions between 1A-213 and one of the three SNPs of FOXO3A. Models V, VI, VII, VIII, IX, and X also include all possible G × E interactions terms among the SNPs and the social and behavior confounders in the Cox hazards models; we only present the significant G × E estimates in Table 4.
Table 4.
Relative hazards of the genotypes, the G × G (gene–gene), and the significant G × E (gene–environment) interactions on survival likelihood at very advanced ages
| Excluding G × G and G × E |
Including G × G of 1A-209 and one of three SNPs of FOXO3A, and sign. G × E |
Including G × G of 1A-213 and one of three SNPs of FOXO3A, and sign. G × E |
||||||||
| Models | I | II | III | IV | V | VI | VII | VIII | IX | X |
| Demographic and basic SES | ||||||||||
| Male (female) | 1.15 | 1.21* | 1.21 | 1.34** | 1.33** | 1.33** | 1.33** | 1.34** | 1.34** | 1.33** |
| Age | 1.07*** | 1.06*** | 1.06*** | 1.06*** | 1.06*** | 1.06*** | 1.06*** | 1.06*** | 1.06*** | 1.06*** |
| Urban (rural) | 1.05 | 1.08 | 1.09 | 1.02 | 1.02 | 1.03 | 1.02 | 1.02 | 1.02 | 1.02 |
| 1+ year of schooling (0) | 0.97 | 1.05 | 1.05 | 1.05 | 1.06 | 1.06 | 1.07 | 1.05 | 1.05 | 1.06 |
| Economic independence (no) | 0.71 | 0.77 | 0.81 | 0.74 | 0.73 | 0.73 | 0.71 | 0.72 | 0.73 | 0.71 |
| Family and social support | ||||||||||
| Currently married (no) | 0.87 | 0.88 | 0.89 | 0.92 | 0.92 | 0.94 | 0.93 | 0.92 | 0.94 | |
| Living alone (no) | 0.99 | 1.02 | 1.01 | 1.03 | 1.03 | 1.03 | 1.03 | 1.02 | 1.02 | |
| Close proximity to child (no) | 0.95 | 0.94 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | |
| Family member as caregiver (no) | 0.97 | 0.96 | 1.04 | 1.00 | 1.01 | 0.99 | 1.02 | 1.02 | 1.00 | |
| Leisure activities score | 0.91** | 0.92** | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | |
| The resilience score | 0.93*** | 0.94*** | 0.99 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 0.99 | |
| Health practice | ||||||||||
| Regular exercise (no) | 0.82* | 0.92 | 1.11 | 1.11 | 1.10 | 0.93 | 0.93 | 0.93 | ||
| Smoking in recent 5 years (no) | 1.06 | 1.06 | 1.07 | 1.07 | 1.07 | 1.06 | 1.06 | 1.07 | ||
| Current heavy alcohol drinker (no) | 1.08 | 1.12 | 1.14 | 1.14 | 1.14 | 1.12 | 1.11 | 1.11 | ||
| DI | 19.47*** | 20.56*** | 20.71*** | 20.08*** | 18.75*** | 18.43*** | 18.26*** | |||
| Main effects of the SNPs | ||||||||||
| 3A-310 (noncarrier of the minor allele) | 0.84** | 0.84** | 0.85** | 0.86** | 0.76*** | 0.83 | ||||
| 3A-292 (noncarrier of the minor allele) | 0.76*** | 0.84 | ||||||||
| 3A-936 (noncarrier of the minor allele) | 0.77*** | 0.83 | ||||||||
| 1A-209 (noncarrier of the minor allele) | 0.86 | 0.85 | 0.91 | |||||||
| 1A-213 (noncarrier of the minor allele) | 0.95 | 0.94 | 0.99 | |||||||
| G × G interactions | ||||||||||
| (1A-209) × (3A-310) | 1.33* | |||||||||
| (1A-209) × (3A-292) | 1.36* | |||||||||
| (1A-209) × (3A-936) | 1.21 | |||||||||
| (1A-213) × (3A-310) | 1.05 | |||||||||
| (1A-213) × (3A-292) | 1.06 | |||||||||
| (1A-213) × (3A-936) | 0.98 | |||||||||
| Significant G×E interactions | ||||||||||
| (1A-209) × (regular exercise) | 0.68* | 0.68* | 0.69* | |||||||
| −2 Log likelihood | 7866 | 7838 | 7833 | 7762 | 7752 | 7752 | 7751 | 7759 | 7759 | 7756 |
| Number of observations | 727 | 727 | 727 | 727 | 727 | 727 | 727 | 727 | 727 | 727 |
Notes: Sample size: 553 women and 174 men, all were aged 92+ in 1998 CLHLS baseline survey and survived to age 100+ in 1998 or a follow-up wave of the CLHLS survey, all of them were Han Chinese from Southern China; the relative hazards (RH) = exp(B), where B is the coefficient of the categorical variable estimated in the Cox proportional hazard models. RH is the ratio of the hazard of death when the variable = 1 as compared to the reference group indicated in the parentheses. Each of the Models I, II, III, and IV has five submodels, and each submodel includes one of the five SNPs (ie, two SNPs of FOXO1A and three SNPs of FOXO3A). The estimates of the relative hazards of the potential confounders among the five submodels within each of the Models I, II, III, and IV are almost identical, with few minor differences up to the second decimal point. In other words, the estimates of the coefficients of the potential confounders in Models I, II, III, and IV were not affected by which SNP was included into the model. Thus, we present only one set of the estimates of the potential confounders in the Models I, II, III, and IV concerning the SNP 3A-310 in Table 4, and the estimates of the relative hazards of the main effects of the other four SNPs (1A-209, 1A-213, 3A-292, and 3A-936) are listed in Table 5. CLHLS = Chinese Longitudinal Healthy Longevity Survey; DI, deficits index; SES, socioeconomic status; SNP = single-nucleotide polymorphism.
*p < .10; **p < .05; ***p < .01.
Table 5.
Relative Hazards of the Main Effects of the SNPs 1A-209, 1A-213, 3A-292, and 3A-936 in the Models I, II, III, and IV excluding G × G and G × E Interactions
| Model | I | II | III | IV |
| Main effect of 1A-209 (noncarrier of the minor allele) | 1.00 | 1.01 | 1.02 | 0.94 |
| Main effect of 1A-213 (noncarrier of the minor allele) | 1.04 | 1.05 | 1.05 | 0.98 |
| Main effect of 3A-292 (noncarrier of the minor allele) | 0.83** | 0.83** | 0.84** | 0.86* |
| Main effect of 3A-936 (noncarrier of the minor allele) | 0.80*** | 0.80*** | 0.80*** | 0.82** |
SNP = single-nucleotide polymorphisms. *p < .10; **p < .05; ***p < .01.
Four interesting findings appeared from the estimates based on the follow-up cohort survival analysis presented in Tables 4 and 5. First, the positive effects of carrying the minor alleles of the three SNPs of FOXO3A on long-term survival from middle age to age 100+ discovered in our case–control analysis using the FAD method (Table 1) and in previous studies (2–7) remain statistically significant at very advanced ages 92–110. As shown by the estimates of Models I, II, and III, adding variables concerning family and social support and health practice into Models II and III only very slightly changed the estimates of previously included variables including five SNPs of the FOXO genes and the confounders. After the DI is added to Model IV, previously significant estimates of the leisure activities score, the resilience score, and regular exercise, which showed significantly positive impacts on increasing survival likelihood at very advanced ages, were no longer significant, indicating that their effects may be largely enforced through affecting health status. However, the positive effects of carrying the minor alleles of any one of the three SNPs of FOXO3A on enhancing survival slightly decreased from 15%–20% in Model III to 14%–18% but still remained significant after the DI is added in Model IV. After the G × G interaction terms between 1A-209 and the three SNPs of FOX3A are added into the model (Models V, VI, and VII), the positive effects of the three SNPs of FOXO3A even became stronger—increasing survival likelihood by 23%–24% (p < .01). These estimates confirm that FOXO3A has its own significant and positive impacts on survival at advanced ages independent of the effects of other potential social and behavioral mediators or confounders. This finding is in general consistent with the result of the German study (5) showing that the FOXO3A variants were more frequent in centenarians than in 90-year-olds based on cross-sectional comparison, but our result is derived from cohort follow-up data and adjusted for various confounders. Note that the main effects of the three SNPs of FOXO3A are no longer statistically significant in Models VIII, IX, and X when the interaction terms between 1A-213 and one of the three SNPs of FOXO3A are included.
Second, the negative effects of carrying the minor alleles of the SNPs 1A-209 and 1A-213 on long-term survival from middle age to age 100+ discovered by us employing the FAD approach in this article and by Li and colleagues (6) following the conventional genetic analysis are no longer statistically significant at very advanced ages, adjusted for the potentially confounding factors (see the estimates of 1A-209 and 1A-213 in Models I to X in Tables 4 and 5).
Third, the G × G interactions between 1A-209 and 3A-310 and between 1A-209 and 3A-292 significantly decrease the survival likelihood by 33%–36% (p < .05) at very advanced ages (see Models V and VI in Table 4), whereas we ruled out the possibility of their significant gene–gene correlation by the chi-square test (Table 6). The estimates of the relative hazards of the other G × G interaction terms between the SNPs of FOXO1A and the SNPs of FOXO3A on survival likelihood at very advanced ages are not statistically significant. Note that although the sample size of centenarians and younger controls in this study is larger than almost all previously published studies in the field, it may still not be large enough, especially for the estimates of the alleles with low frequency. Thus, in the case of chi-square tests presented in Table 6, the data do not support a correlation of rGG and rGE, but it does not prove there is no any correlation. It is possible that some of the nonsignificant p value in Table 6 and other tables may be because of the small sample size and low MAF. We need to keep this in mind and conduct the further investigations when the new data with larger sample size become available.
Table 6.
Chi-square tests to assess rGE and rGG for the significant G × E and G × G synergistic effects discovered by the Cox proportional hazards model analysis
| Significant Synergistic Effects | (1A-209) × (r.exercise) | (1A-209) × (3A-310) | (1A-209) × (3A-292) | (1A-209) × (3A-936) | ||||
| Regular exercise | 3A-310 | 3A-292 | 3A-936 | |||||
| Yes | No | Carrier | Noncarrier | Carrier | Noncarrier | Carrier | Noncarrier | |
| % carrying 1A-209 | 40.87 | 39.83 | 39.59 | 40.54 | 39.44 | 40.71 | 40.73 | 39.35 |
| P of chi-square test of rGE or rGG | .917 | .937 | .917 | .913 | ||||
| Conclusion | rGE does not exist | rGG does not exist | rGG does not exist | rGG does not exist | ||||
Note: rGE = gene–environment correlations; rGG = gene–gene correlations.
Fourth, after ruling out the possibility of the confounding effects of the rGE correlation of 1A-209 with regular exercise through the chi-square tests (Table 6), we conclude that the G × E interaction between 1A-209 and regular exercise significantly increase survival likelihood at very advanced ages by 31%–32% (p < .05) in the full Models V, VI, and VII that included all potentially confounding factors considered and the G × G interactions between 1A-209 and any of the three SNPs of FOXO3A.
DISCUSSION
As compared with previous genetic case–control studies on the effects of FOXO genes on longevity, the present study has made a few unique contributions. First, the extended FAD method derived and empirically applied in this article provides biodemographic syntheses and meaningful demographic interpretation to the conventional case–control ORs of genetic analysis on longevity. As discussed in The Extended Fixed Attribute Dynamics Method section, using the same data set, the FAD method produces exactly the same estimates of the ORs of survival and their associated p values and 95% CI as the corresponding estimates by the conventional case–control population association analysis on longevity using the logistic regression controlling for the same covariates as the FAD does. This fact verifies the statistical properties of our FAD method. More importantly, the results of the ORs of survival based on the FAD method quantify the magnitude of the genetic impacts on survival probability, namely, how much the probability of survival from age x to x + n would be increased or reduced by carrying the genetic variant. This is a significant addition to the conventional statistical genetic approach that presents ORs expressing the difference of frequencies of the genetic variant between long-lived individuals and younger controls without concrete demographic meaning about the magnitude of the genetic impacts on the probability of survival.
Second, we provided unique estimates of the independent, joint, and interactive effects of the genotypes of FOXO1A and FOXO3A on probabilities of survival from middle age to age 100+. In addition to the interesting findings of the independent effects of FOXO1A and FOXO3A, we discovered that the positive effects of FOXO3A and negative effects of FOXO1A substantially compensate each other if one carries both, although FOXO3A has a stronger impact. This is a significant step forward as compared with the conventional genetic analysis reported in previous publications on the association of FOXO3A or FOXO1A genes with longevity (2–7) that did not take into account the effects of whether carrying the minor allele of the SNP of another relevant gene (FOXO1A or FOXO3A) that affects longevity in opposite directions.
Third, we presented unique estimates of the genetic influence of FOXO1A and FOXO3A and their G × G interactions on survival at very advanced ages, adjusted for various potentially confounding factors, using prospective cohort data. We found that the positive effects of FOXO3A on survival from middle age to ages 100+ remain statistically significant at very advanced ages, but the corresponding negative effects of FOXO1A disappear. We also discovered that the interactions between 1A-209 and 3A-310 and between 1A-209 and 3A-292 significantly decrease the survival likelihood at very advanced ages by 33%–36%.
Fourth, this is the first study that investigates the impacts of G × E interactions between the FOXO genes and social-behavioral factors on survival at very advanced ages. Our new finding that G × E interaction between the SNP 1A-209 and regular exercise significantly increase the survival by 31%–32% (p < .05) at very advanced ages may have important policy and practical relevance.
We realize that there are several limitations in our present study and unanswered questions that need to be explored further. One limitation is that, as we stated in The Extended Fixed Attribute Dynamics Method section and expressed mathematically in Formulas A4 and A5 in the Appendix 1, both the FAD method employed in this article to produce the estimates of Tables 1–3 and the conventional case–control statistical genetic approach assume that (a) the initial distributions of the genetic variant and (b) their association with longevity do not differ substantially between cohorts of long-lived individuals and younger controls. However, although restricting our analysis to a single ethnic group (Han Chinese) residing in Southern China and classifying the samples by gender as well may reduce and hopefully minimize the bias, we are aware of that there may still be bias because of potential violation of the assumptions (a) and (b); and we do not know to what degree these assumptions may be violated in the real world. This implies that the results of the OR of survival probability from middle age to age 100+ measuring the general, independent, and joint effects of the FOXO genotypes based on data from the cases (centenarians) and controls (middle-age group), presented in Tables 1–3, may be subject to a bias of unknown magnitude because of confounding with birth cohorts of centenarians and middle-age individuals. Similar cautions were also raised in previous studies following the case–control approach (2–6), and the potential bias needs to be evaluated in the future when more sophisticated cohort follow-up data sources become available. Although Li and colleagues (6) have done the replication analysis on the general effects of FOXO1A on longevity using female samples from Southern and Northern China, we are not able to perform the replication for the independent, joint, and G × G interaction effects between FOXO1A and FOXO3A that are the themes of this study because the FOXO3A genotypic data from the Northern China samples are not available. We are so far not able to investigate the impacts of the G × G interactions between FOXO1A and FOXO3A as well as the G × E interaction on survival at ages younger than 92 years as the needed genotypic data matched with the follow-up survival-death observations for participants younger than age 92 are not available. We are also not able to interpret why the negative effects of FOXO1A on long-term survival from middle-age to age 100+ found in the cross-sectional case–control analysis diminished at very advanced ages 92–110 in the cohort survival analysis; it is not clear why there are substantial gender differences in the independent effects of the genotypes of FOXO1A and FOXO3A on probabilities of survival from middle age to ages 100+ discovered by us. The biological, epigenetic, and environmental mechanisms by which FOXO genes’ G × G combinations and interactions and G × E interactions may affect the human longevity at old ages are not investigated in our present biodemographic analysis but are warranted in the future interdisciplinary research (27–30). For example, a further study needs to investigate how G × E interaction between 1A-209 and regular exercise is translated into physiological effects on cellular responses that may significantly increase survival likelihood at advanced ages. More replication analyses and further biological functional study plus demographic–social research using genotypic and longitudinal phenotypic data may provide stronger scientific evidence and explanations for the findings presented in this article.
Finally, it is worth noting that, although the genetic effects of FOXO genes on longevity estimated in this article and the other studies (2–8) are fascinating, we are not able to estimate the proportion of variance in individuals’ probabilities of survival from middle age to age 100 explained by the FOXO genes. This is because the cohort data on outcome of that who (among the members of the middle-age control group) will survive to age 100 required for such variance analysis are not available. However, previous studies on elderly twins have shown that only one fourth of the differences in individual life span are determined by genetic inherence that involves multiple genes and the other three fourths are determined by social, behavioral, and environmental factors (31). Clearly, knowing which genotypes a person carries does not tell whether he or she may survive to age 100. The most important issue is to promote better social and environmental conditions and healthy behaviors that will affect health and longevity directly and indirectly through interactions with genetics. Our new finding that G × E interaction between the SNP 1A-209 and regular exercise significantly increase survival by 31%–32% at very advanced ages has provided a piece of strong empirical evidence to support this understanding.
FUNDING
This study is part of the project funded by National Institute on Aging/National Institutes of Health (NIH) (R01 AG023627 to Y.Z.), NIH Pepper Center Grant (P30AG028716 to E.R.H.), China Natural Science Foundation (70533010 to Y.Z.), and by National Basic Research Program of the Chinese Ministry of Science and Technology (973 grant 2007CB512100 to X.L.T.).
Acknowledgments
We thank Yang Li, Wen-Jing Wang, Chong Wu, Fang-Yuan Hu, Jian Guo, Ling Zhao, Fan Yang, Yi-Xin Zhang, Wei Li, and Gu-Yan Zheng for their efforts in the lab wok on DNA extractions and genotyping. We are grateful to Liqun Tao, Qin Xu, Ye Yuan, Jie Zhan, Jiehua Lu, Yun Zhou, and Jianxin Li for their contributions in the Chinese Longitudinal Healthy Longevity Survey and the DNA samples collection, and we thank all interviewees and their families for their voluntary participation in this study. We are very grateful for the thoughtful comments provided by Danyu Lin, Fengyu Zhang, Qiushi Feng and Jessica Sautter.
Competing Interests: The authors have declared that no competing interests exist.
Human Participation Protection: The Research Ethics Committees of Duke University and Peking University granted approval for the Protection of Human Subjects for each wave of the Chinese Longitudinal Healthy Longevity Survey, which is the data source of this study. The survey respondents gave informed consent before participating.
Author contributions: Y.Z. and X.L.T. designed the research; Y.Z. derived the extended FAD method, supervised data and DNA sample collection and data analysis, and wrote the paper; L.C. and H.C. analyzed data; X.L.T. and H.Q.C. led the laboratory work of DNA extraction and genotyping, Y.L. and Z.X. performed data and sample collection; E.R.H. and Q.T. analyzed data and suggested revisions of the article; J.W.V. devised the original FAD method, contributed to the data and DNA collection, and revised methodological portions of the article.
Appendix 1. Derivation of the Extended FAD Method for Estimating the Independent and Joint Effects of Genetic Variant and Fixed Exposure
The definition of pij(x) is given in the text of The Extended Fixed Attribute Dynamics Method section. Let s11(x), s10(x), s01(x), and s00(x) denote the conditional survival probability from age x to x + n for those who are both carrier and exposed, carrier and not-exposed, noncarrier and exposed, and neither carrier nor exposed, respectively (the terms “carrier, noncarrier, exposed and not-exposed” are defined in The Extended Fixed Attribute Dynamics Method section in the text); N(x), the total number of persons aged x; S(x), the overall average conditional survival probability from age x to x + n for all persons aged x.
Because N(x) pij(x) sij(x) = N(x) S(x) pij(x + n), it follows that
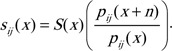 |
(A1) |
We choose the group of individuals who are neither a carrier nor exposed as a reference group, and it similarly follows that
| (A2) |
Dividing Formula (A1) by Formula (A2) gives the OR of survival from age x to age x + n of those with the i–j combination of the gene-fixed exposure to those who are neither a carrier nor exposed:
| (A3) |
Note that the above mathematical and demographic derivation is based on the framework of cohort survivorship. If the Formula (A3) is applied to follow-up data from the same cohort counted at different time points (ie, at ages x and x + n), one needs to assume that the loss-to-follow-up from age x to x + n is not correlated with respondents’ combination of the genetic variant and the fixed exposure under study. However, the cohort long-term follow-up data, such as the pij(x) at middle age and age 100+ from the same cohort, are usually not available. Consequently, one may use cross-sectional data from different cohorts of long-lived cases (e.g., centenarians) and younger controls (eg, middle-age group). In this case, we connect the younger cohort and the long-lived cohort into “a hypothetical cohort,” and we assume that the initial distributions of the combinations of the genetic variant and the fixed exposure at age x of the cohorts of long-lived individuals (denoted as pij1(x)) and younger controls (denoted as pij2(x)) do not differ substantially. We then compare the observed pij2(x + n) of the long-lived individuals (cases) and the observed pij2(x) of the middle-age controls, considering the cases and controls as members of a hypothetical cohort and derive the estimate of RSij/00. This basic assumption inherent in the FAD method is the same as the one adopted in the conventional case–control statistical genetic approach using cross-sectional data from long-lived individuals (as cases) and younger controls, namely assuming that there is no substantial problem of population stratification. We further explore in the following discussion the implications of this basic assumption adopted in both FAD and the conventional case–control statistical genetic approaches and its potential bias if the basic assumption is violated.
Let pij1(0) and pij2(0) denote the initial distribution of the combination of the genetic variant and the fixed exposure at birth among the individuals born x + n years ago and x years ago, respectively; Nij1(0) and Nij2(0), the initial size (number of births) of the cohorts of the individuals born x + n years ago and x years ago, respectively; S1 (0→x) and S2(0→x), the overall average probability of survival from age 0 to age x among all of the individuals born x + n years ago and x years ago, respectively; Cij1 and Cij2, the ratio of the probability of survival from age 0 to x among persons with the i – j combination of the genetic variant and the fixed exposure to the overall average probability of survival from age 0 to x for all of the cohort members born x + n years ago and x years ago, respectively; pij1(x) and pij2(0), the proportions of persons aged x with the combination of the genetic variant and the fixed exposure among all individuals aged x in the cohorts born x + n years ago and x years ago, respectively.
| (A4) |
Similarly,
| (A5) |
As discussed earlier, when the extended FAD method is applied to the cross-sectional data from the long-lived individuals aged x + n and the younger controls aged x, one in fact assumes that: pij1(x) = pij2(x) or pij1(0)Cij1 = pij2(0)Cij2, namely assuming (a) the initial distributions of the combinations of the genetic variant and the fixed exposure of the two cohorts born x + n years ago and x years ago are the same, that is, pij1(0) = pij2(0); (2) the associations between the genetic variant and longevity in the two cohorts are the same, Cij1 = Cij2. If these assumptions are met, the OR of survival RSij/00 produced by the Formula (A3) based on the cross-sectional data adequately provides the estimate of the effects of the i–j combination of the genetic variant and the fixed exposure on longevity. Based on equations (A-4) and (A-5), we observe that, theoretically speaking, the estimates of the OR of survival are not directly affected by the differences in the initial sizes (numbers of births) of the cohorts (ie, N1(0) and N2(0)) and the overall average probabilities of survival from birth to age x among all of the individuals born x + n years ago and x years ago (S1(0→x) and S2(0→x)), as they are canceled out during the process of derivation. However, there would be bias in the estimates of the OR if the basic assumptions (a) and (b) described previously are violated because of population stratification and/or the unknown interactions among the genetic variant, fixed exposure, the different socioeconomic environmental conditions, and mortality levels from birth to the middle age (ie, age x) (to our knowledge based on a careful literature search, there have been no previously published studies about the influences of FOXO genes on mortality from birth to middle age) in the different cohorts born x + n and x years ago. In this study, we control for population stratification in the FAD analysis using the cross-sectional data of centenarians and middle-age controls by restricting our analysis to a single ethnic group (Han Chinese) residing in Southern China and classifying the samples by gender as well. We believe that this may reduce and hopefully minimize the bias, but we are aware of that there may still be potential bias, which needs to be evaluated in the future when more sophisticated cohort data sources become available.
Appendix 2. Estimating the Effects of Interactions Between the Genetic Variant and the Fixed Exposure on Longevity Following the FAD Approach
We present the procedures for estimating the effects of gene-fixed exposure interactions on survival from age x to x + n, using the ORs of survival (RSij/00, i = 0,1; j = 0,1) derived by Formula (2).
On a multiplicative scale, the Interaction Index of Survival (ISm) is estimated as:
| (A6) |
On an additive scale, the Interaction Index of Survival (ISa) is estimated as:
| (A7) |
If ISm or ISa is significantly greater or less than 1, the interaction between the genetic variant and the fixed exposure positively or negatively affects survival from age x to x + n.
Note that assuming additive versus multiplicative interactions is not purely a statistical question but rather a one based on what we know about the social environment, behavior, and biology (25). In other words, it is content based, and we should determine whether we adopt an additive or multiplicative assumption case by case based on empirical data or through learning from literature.
Unlike the Formulas (1) and (2), we cannot simply use the standard statistical significance tests (23) to assess whether the interaction effects estimated by Formulas (A6) and (A7) are statistically significant because the functional distributions of Formulas (A6) and (A7) are unknown, at least to our knowledge. In theory, we may use multivariate Delta method to do the statistical significance tests. However, in this case the Delta method is not feasible because we have eight variables (ie, Pij(x) and Pij(x + n)); the sample size may usually not be large enough to estimate the 72 parameters (8 variances plus 64 (= 8 × 8) covariants) in most applications including ours. Based on a careful literature search, we believe that a bootstrap simulation approach is most appropriate for estimating the confidence intervals and P values of ISm and ISa (32,33).
Appendix 3. Potentially Confounding Factors Included in the Cox Hazards Regression Models
We choose the following variables as relevant covariates based on reviews of previous studies in this field and our understanding of the Chinese social context.
Demographic and socioeconomic variables.—
Demographic and socioeconomic variables include age, gender, residence (rural vs urban), education (no schooling vs ≥1 year of schooling; note that two thirds of the Chinese oldest old aged 80+ reported “no schooling”) and economic independence (having his or her own retirement wage and/or earnings vs no income).
Social and family support and connections.—
Marital status refers to currently married vs unmarried. Proximity to children was measured dichotomously (participants who lived with their children or had at least one child nearby, ie, in the same village or on the same street, vs those who had neither co-resident children nor children living nearby). We also examined whether the study participant lived alone. Instrumental social support was measured by a question that asked participants whether their spouse or other family members took care of them when they were sick. The Leisure Activities score is based on frequency of participation in seven activities: personal outdoor activities, gardening, raising domestic poultry and/or pets, playing cards or mah-jong, participating in organized social activities other than religion, reading newspapers and books, and watching TV and listening to the radio. Respondents who reported engaging in the activity once or more per week were coded 1, otherwise, 0. We then summed the seven scores; the resulting scale has a range from 0 to 7.
The resilience score.—
The resilience score was constructed based on the more straightforward and simplified definition of resilience specified in Lamond and colleagues (34), namely, resilience connotes the ability to adapt positively to adversity (i.e. ability of coping and adjustment). We selected seven available and relevant items in the demographic study CLHLS to construct the resilience score, which is actually a simplified version (focusing on coping and adjustment) of the resilience index used in the in-depth psychological study (35).
Health practices.—
Cigarette smoking was assessed by the following question: “Do you smoke regularly at the present time?” Response options were “no” (coded 0) and “yes” (coded 1). Based on relatively detailed information concerning the frequency, quantities and types of alcohol consumed, we coded participants as “heavy alcohol drinker” (defined as having at least 200 g of liquor or 400 g of beer per day) (code = 1) versus “not heavy alcohol drinker” (code = 0). Exercise was assessed by the following question: “Do you exercise regularly at the present time?” Response options were “yes” and “no,” coded 1 and 0, respectively.
Deficits index.—
We constructed an index of overall health status, known as the deficits index (DI) (also called frailty index), which has been validated and widely applied as a proxy for biological age; as a predictor of death, health change, and utilization of health services and has implications for public health monitoring and intervention (36). DI is defined as the proportion of observed deficits divided by the total number of possible deficits for a given individual and is posited to capture the cumulative deficits of the sampled persons. Following the general practice in constructing the DI, we estimated the DI for each oldest old interviewee based on 39 variables that include cognitive function, instrumental activities of daily living, activities of daily living, physical performance functional limitations, self-reported health, self-reported changes in health during the past year, interviewer-reported health, hearing loss and vision loss, heart rhythm, psychological distress, any serious illness in the past 2 years, and reports of specific chronic diseases. With an exception for the number of times of hospitalization in the past year for which a score of 2 was given if the number of times was greater than 2, each variable is coded 1 when the deficit is present, and 0 otherwise. We then summed up these 39 variables and divided by 40 to obtain the DI. The possible range of the DI is 0 to 1. A detailed list of variables used to construct the DI is available elsewhere (37).
The frequency distributions of the 15 covariates included in our Cox proportional hazards regression models are not presented in this article due to space limitation, and are available upon request.
References
- 1.Birkenkamp KU, Coffer PJ. FOXO transcription factors as regulators of immune homeostasis: molecules to die for? J Immunol. 2003;171:1623–1629. doi: 10.4049/jimmunol.171.4.1623. [DOI] [PubMed] [Google Scholar]
- 2.Willcox BJ, Donlon TA, He Q, et al. FOXO3A genotype is strongly associated with human longevity. Proc Natl Acad Sci U S A. 2008;105:13987–13992. doi: 10.1073/pnas.0801030105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Anselmi CV, Malovini A, Roncarati R, et al. Association of the FOXO3A locus with extreme longevity in a southern italian centenarian study. Rejuvenation Res. 2009;12:95–104. doi: 10.1089/rej.2008.0827. [DOI] [PubMed] [Google Scholar]
- 4.Pawlikowska L, Donglei H, Scott H, et al. Association of common genetic variation in the insulin/IGF1 signaling pathway with human longevity. Aging Cell. 2009;8:460–472. doi: 10.1111/j.1474-9726.2009.00493.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Flachsbart F, Caliebe A, Kleindorp R, et al. Association of FOXO3A variation with human longevity confirmed in German centenarians. Proc Natl Acad Sci U S A. 2009;106:2700–2705. doi: 10.1073/pnas.0809594106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li Y, Wang W, Cao H, et al. Genetic association of FOXO1A and FOXO3A with longevity trait in Han Chinese populations. Hum Mol Genet. 2009;18:4897–4904. doi: 10.1093/hmg/ddp459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lunetta KL, D’Agostino RB, Sr, Karasik D, et al. Genetic correlates of longevity and selected age-related phenotypes: a genome-wide association study in the Framingham Study. BMC Med Genet. 2007;8(suppl 1):S13. doi: 10.1186/1471-2350-8-S1-S13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kuningas M, Mägi R, Westendorp RGJ, et al. Haplotypes in the human Foxo1a and Foxo3a genes; impact on disease and mortality at old age. Eur J Hum Genet. 2007;15:294–301. doi: 10.1038/sj.ejhg.5201766. [DOI] [PubMed] [Google Scholar]
- 9.Kenyon CJ. The genetics of aging. Nature. 2010;464:504–512. doi: 10.1038/nature08980. [DOI] [PubMed] [Google Scholar]
- 10.Kim HK, Kim HY, Song I, et al. Down-regulation of a Forkhead Transcription Factor, FOXO3a, accelerates cellular senescence in human dermal fibroblasts. J Gerontol A Biol Sci Med Sci. 2005;60(1):4–9. doi: 10.1093/gerona/60.1.4. [DOI] [PubMed] [Google Scholar]
- 11.Dröge W. Oxidative aging and insulin receptor signaling. J Gerontol A Biol Sci Med Sci. 2005;60(11):1378–1385. doi: 10.1093/gerona/60.11.1378. [DOI] [PubMed] [Google Scholar]
- 12.Sundaresan NR, Gupta M, Kim G, et al. Sirt3 blocks the cardiac hypertrophic response by augmenting Foxo3a-dependent antioxidant defense mechanisms. in mice. J Clin Invest. 2009;119(9):2759. doi: 10.1172/JCI39162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Evans-Anderson HJ, Alfieri CM, Yutzey KE. Regulation of cardiomyocyte proliferation and myocardial growth during development by FOXO transcription factors. Circ Res. 2008;102(6):686–694. doi: 10.1161/CIRCRESAHA.107.163428. [DOI] [PubMed] [Google Scholar]
- 14.Lin K, Dorman JB, Rodan A, Kenyon C. daf-16: an HNF-3/forkhead family member that can function to double the life-span of Caenorhabditis elegans. Science. 1997;278:1319–1322. doi: 10.1126/science.278.5341.1319. [DOI] [PubMed] [Google Scholar]
- 15.Ogg S, Paradis S, Gottlieb S, et al. The Fork head transcription factor DAF-16 transduces insulin-like metabolic and longevity signals in C. elegans. Nature. 1997;389:994–999. doi: 10.1038/40194. [DOI] [PubMed] [Google Scholar]
- 16.Giannakou ME, Goss M, Junger MA, Hafen E, Leevers SJ, Partridge L. Long-lived Drosophila with overexpressed dFOXO in adult fat body. Science. 2004;305:361. doi: 10.1126/science.1098219. [DOI] [PubMed] [Google Scholar]
- 17.Kenneth WW, Finch C. Between Zeus and the Salmon: The Biodemography of Longevity. Washington, DC: National Research Council, National Academy Press; 1997. [PubMed] [Google Scholar]
- 18.Ewbank DC. Mortality differences by APOE genotype estimated from demographic synthesis. Genet Epidemiol. 2002;22:146–155. doi: 10.1002/gepi.0164. [DOI] [PubMed] [Google Scholar]
- 19.Zeng Y, Poston D, Vlosky DA, Gu D. Healthy Longevity in China: Demographic, Socioeconomic, and Psychological Dimensions. Dordrecht, the Netherlands: Springer Publisher; 2008. [Google Scholar]
- 20.Vaupel JW. Analysis of population changes and differences. Presented at: the Annual Meeting of the Population Association of America; April 1992, Denver, CO. [Google Scholar]
- 21.Yashin AI, Benedictis GD, Vaupel JW, et al. Gene, demography and life span: the contribution of demographic data in genetic studies of aging and longevity. Am J Hum Genet. 1999;65:1178–1193. doi: 10.1086/302572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zeng Y, Vaupel JW. Association of late childbearing with healthy longevity among the oldest-old in China. Popul Stud. 2004;58(1):37–53. doi: 10.1080/0032472032000175437. [DOI] [PubMed] [Google Scholar]
- 23.Newman SC. Biostatistical Methods in Epidemiology. Wiley series in probability and statistics. New York: John Wiley and Sons; 2001. [Google Scholar]
- 24.Ottman R. Gene-environment interaction: definition and study designs. Prev Med. 1996;25:764–770. doi: 10.1006/pmed.1996.0117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hernandez LM, Blazer DG, editors. IOM (Institute of Medicine, National Academy of Sciences) Committee. Genes, Behavior, and the Social Environment: Moving Beyond the Nature/Nurture Debate. Washington, DC: National Academia of Sciences; 2006. [PubMed] [Google Scholar]
- 26.Hill ME. Multivariate survivorship analysis using two cross-sectional samples. Demography. 1999;36:497–503. [PubMed] [Google Scholar]
- 27.Williamson DL, Raue U, Slivka DR, Trappe S. Resistance exercise, skeletal muscle FOXO3A, and 85-year-old women. J Gerontol A Biol Sci Med Sci. 2010;65(4):335–343. doi: 10.1093/gerona/glq005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kahn AJ. Epigenetic and Mitochondrial Mechanisms in Aging and Longevity: A Report of a Meeting of the Longevity Consortium, Napa, California, October 25–27, 2006. J Gerontol: Biol Sci. 2007;62A(6):577–582. doi: 10.1093/gerona/62.6.577. [DOI] [PubMed] [Google Scholar]
- 29.Bradshaw JM. Genetic Influences on Social Life: Evidence, Pathways, and Implications for Sociological Inquiry [PhD dissertation] Austin, TX: The University of Texas at Austin; 2008. Approved by the Dissertation Committee co-chaired by Christopher G. Ellison and Mark D. Hayward. [Google Scholar]
- 30.Weinstein M, Hermalin AI, Stoto MA. Population Health and Aging: Strengthening the Dialogue between Epidemiology and Demography. New York, NY: New York Academy of Sciences; 2001. [Google Scholar]
- 31.Herskind AM, McGue M, Holm NV, Sorensen TA, Harvald B, Vaupel JW. The heritability of human longevity, a population-based study of 2872 Danish twin pairs born 1870–1900. Hum Genet. 1996;97:319–323. doi: 10.1007/BF02185763. [DOI] [PubMed] [Google Scholar]
- 32.Andersson T, Alfredsson L, Källberg H. “Calculating Measures of Biological Interaction”. Eur J Epidemiol. 2005;20(7):575–579. doi: 10.1007/s10654-005-7835-x. [DOI] [PubMed] [Google Scholar]
- 33.Cameron AC, Trivedi PK. Microeconometrics: Methods and Applications. Cambridge: Cambridge University Press; 2005. [Google Scholar]
- 34.Lamond AJ, Depp CA, Allison M, et al. Measurement and predictors of resilience among community-dwelling older women. J Psychiatr Res. 2009;43:148–154. doi: 10.1016/j.jpsychires.2008.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zeng Y, She K. Curr Gerontol Geriatr Res. In Press. Resilience significantly contributes to exceptional longevity in China. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kulminski AM, Ukraintseva SV, Kulminskaya IV, Arbeev KG, Land KC, Yashin AY. Cumulative deficits better characterize susceptibility to death in the elderly than phenotypic frailty: Lessons from the Cardiovascular Health Study. J Am Geriatr Soc. 2008;56:898–903. doi: 10.1111/j.1532-5415.2008.01656.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gu D, Dupre ME, Sautter J, Zhu H, Liu Y, Zeng Y. Frailty and mortality among Chinese at advanced ages. J Gerontol Soc Sci. 2009;64B(2):279–289. doi: 10.1093/geronb/gbn009. [DOI] [PMC free article] [PubMed] [Google Scholar]


