A Mathematical Model for Understanding the Statistical effects of k-space (AMMUST-k) preprocessing on observed voxel measurements in fcMRI and fMRI

Abstract

Image processing is common in functional magnetic resonance imaging (fMRI) and functional connectivity magnetic resonance imaging (fcMRI). Such processing may have deleterious effects on statistical maps computed from the processed images. In this manuscript, we describe a mathematical framework to evaluate the effects of image processing on observed voxel means, covariances and correlations resulting from linear processes on k-space and image space data. We develop linear operators for common image processing operations, including: zero filling, apodization, smoothing and partial Fourier reconstruction; and unmodeled physical processes, including: Fourier encoding anomalies caused by eddy currents, intra-acquisition decay and magnetic field inhomogeneities. With such operators, we theoretically compute the exact image-space means, covariances and correlations which result from their common implementation and verify their behavior in experimental phantom data. Thus, a very powerful framework is described to consider the effects of image processing on observed voxel means, covariances and correlations. With this framework, researchers can theoretically consider observed voxel correlations while understanding the extent of artifactual correlations resulting from image processing. Furthermore, this framework may be utilized in the future to theoretically optimize image acquisition parameters, and examine the order of image processing steps.

1 Introduction

Magnetic field gradients can be used in magnetic resonance imaging to encode the measured signal as a linear transformation of the object being imaged. An inverse transform is then applied to the acquired signal to reconstruct an image of the object. As the encoding and reconstruction are linear transformations, they can be considered through the constructs of linear algebra as multiplications of matrices upon vectors representing either the physical object or the acquired signal. Rowe et al. (2007) have recently published a description of this mathematical formalism, using Fourier encoding and reconstruction as a specific example. In the case of Fourier encoding, the acquired data is in the spatial frequency space, k-space, and it is reconstructed through the inverse Fourier transform to image-space. In addition to describing the mathematical formalism of image reconstruction, the work also illustrated that, because of the linear properties of the reconstruction, correlated observations in k-space lead to correlated volume elements, or voxels, in the reconstructed image.

Correlated voxels, which necessarily arise from correlated k-space measurements, are the basis of functional connectivity studies (Biswal et al., 1995). These connectivity studies determine voxels to be connected if their time series exhibit high correlations. Common techniques, including cross correlation analysis, principle component analysis (PCA), and independent component analysis (ICA), have been used to determine regions with high correlations in their time series (Biswal et al., 1995; Friston et al., 1993; van de Ven et al., 2004). Regardless of the analysis method, voxel correlation, and thus k-space correlation, affect the measured voxel connectivity.

The low temporal frequency physiologic processes upon which functional connectivity studies rely are clearly not the only sources of voxel correlation. Global signal fluctuation may arise from physiologic processes (Glover et al., 2000; Pfeuffer et al., 2002; Birn et al., 2006; Shmueli et al., 2007). As described by Rowe et al. (2007), temporal autocorrelation in the acquired signal also may lead to image-space voxel correlation. Artifactual time series correlations have also been observed in inanimate phantom studies (Kriegeskorte et al., 2008). Additionally, as this manuscript describes, operations on k-space data before reconstruction and image space data after reconstruction can produce correlations in voxels. Sequences of spatially correlated images lead to temporally correlated time series. Clearly one must be mindful of the effects of such operations when drawing conclusions from functional connectivity (fcMRI) and functional (fMRI) data.

In this manuscript we consider several operations. These include: Fourier encoding anomalies, k-space observation censoring, k-space line shifting, symmetric k-space generation, and smoothing through k-space windowing, zero filling, and image-space convolution. We first develop linear operators for the mentioned operations and show toy examples of each using an 8 × 8 data set. We then utilize the operators to theoretically examine image-space correlations associated with the operators under more relevant parametrizations, including 96 × 96 data acquisition arrays. Finally we illustrate the results of the operations in acquired 96 × 96 phantom data.

2 Theory

2.1 Operator Development

In this section we extend the mathematical formalism of image reconstruction presented by Rowe et al. (2007) to a more general case. We describe Cartesian Fourier reconstruction for the sake of demonstration, although the mathematics hold true for any linear reconstruction operator. Other linear operators may include regridding operators for non-Cartesian k-space sampling methods. First we further extend the previously published statistical model to include the data as it is ideally collected. This includes modeling the points acquired during the phase encoding blips of echo planar imaging (EPI), and the reversal of lines acquired with negative frequency encoding gradients. We describe models of Fourier encoding anomalies, k-space line shifting, symmetric k-space generation, zero filling, and multiplication of the k-space observations with a windowing function in light of the extended statistical model.

Rowe et al. (2007) have described complex-valued Fourier reconstruction through a real-valued isomorphism such that a vector of the reconstructed image, y, is the product of a Fourier reconstruction operator, Ω, with a vector of the observed k-space observations, s:

$$y=\Omega s.$$ [1]

In the above equation, if the reconstructed image is m rows by n columns, y is a vector with mn real image values stacked above mn imaginary image values, Ω is a reconstruction operator array with dimensions of 2mn × 2mn, and s is a vector of mn appropriately ordered real Cartesian k-space observations stacked above mn imaginary Cartesian k-space observations. The Cartesian Fourier reconstruction operator may be written as

$$\Omega =\left(\begin{array}{cc}\hfill \Re \left({\Omega }_C\right)\hfill & \hfill -\Im \left({\Omega }_C\right)\hfill \\ \hfill \Im \left({\Omega }_C\right)\hfill & \hfill \Re \left({\Omega }_C\right)\hfill \end{array}\right),$$ [2]

where ℜ(·) and ℑ(·) take the real and imaginary parts of the arguments respectively, and Ω_C is the Kronecker product of two matrices, Ω_x and Ω_y, which Fourier transform the columns and rows of the acquired k-space, respectively,

$${\Omega }_C={\Omega }_x\otimes {\Omega }_y.$$

The Kronecker product, denoted by ⊗, multiplies each element of the first matrix by the entire second matrix. The jk^th element of Ω_x, where j and k are indices from 0 to n − 1, may be written as

$${\left({\Omega }_x\right)}_{\mathit{jk}}=w^{\left(-\frac{n}{2}+j\right)\left(-\frac{n}{2}+k\right)},$$

where $w=\frac{1}{n}{e}^{\frac{i2\pi }{n}}$ for the inverse Fourier transform and $w=e^{\frac{-i2\pi }{n}}$ for the forward Fourier transform. A similar matrix of dimension m exists for Ω_y.

Under the formalism of Equation 1, if the k-space observations have a covariance matrix of cov(s) = Γ₀, the resulting reconstructed image-space values have a covariance matrix of ΩΓ₀Ω^T, where T denotes transposition. Here we develop operators, O, such that the acquired signal, S, may be processed as desired and transformed to image-space. It is helpful to note that s represents the properly ordered k-space data while S represents the real/imaginary k-space observation pairs acquired along the k-space trajectory, including points acquired during echo planar imaging phase encoding blips. With such operators developed, the original reconstruction relationship shown in Equation 1 may be more appropriately modeled as

$$y=O𝘴,$$ [3]

with a covariance matrix resulting from the k-space covariance matrix, Γ, calculated as

$$\mathrm{cov}\left(y\right)=O\Gamma O^T.$$ [4]

In light of the new parameterization, if the originally collected k-space data, S, has mean of S₀, the final reconstructed complex-valued image, y, has a mean of OS₀ and a covariance matrix as shown above.

The covariance structure of the square of the magnitude data may be derived from this complex data covariance matrix. The covariance matrix for the square of the magnitude data is considered as an analytical solution exists in the described linear framework. The magnitude operation, being non-linear in nature, does not extend well to the described framework. Nevertheless, it can be shown that the magnitude squared covariance asymptotically approaches the magnitude covariance. It will be seen that the magnitude squared correlation structure, which is asymptotically equal to the magnitude data correlation structure, is generally found to exhibit similar properties to the real and imaginary correlation structures. A brief derivation of the magnitude squared covariance matrix is included in Appendix A.

In light of this framework, the effects of several processing techniques will be considered. The mean, covariance, and correlations will be computed for each operation on the complex and magnitude squared data. A brief description of each operator follows, with expanded descriptions of their compositions included in the appendices.

2.1.1 Anomalies in Fourier Encoding

The k-space observation process is often assumed to be instantaneous at the echo time, TE (Haacke et al., 1999). Under that assumption, and assuming an exponential intra-acquisiton decay map of $T_2^{\ast }(x,y)$ and magnetic field inhomogeneity map of ΔB(x, y), the acquired k-space signal is

$$s(k_x,k_y)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\rho (x,y)e^{-\mathit{TE}∕T_2^{\ast }(x,y)}{e}^{i\gamma \Delta B(x,y)\mathit{TE}}{e}^{-i2\pi (k_{x}x+k_{y}y)}\mathrm{d}x\mathrm{d}y,$$ [5]

where γ is the proton gyromagnetic ratio and ρ is the proton spin density. The k-space points are defined by the temporal integral of the applied magnetic field gradients applied along the appropriate directions:

$$k_x=\frac{\gamma }{2\pi }{\int }_0^t{G}_x\left(t^{\prime }\right)\mathrm{d}{t}^{\prime },k_y=\frac{\gamma }{2\pi }{\int }_0^t{G}_y\left(t^{\prime }\right)\mathrm{d}{t}^{\prime }.$$

Thus, the observed k-space data, encoded in time, is assumed to be the Fourier transform of the proton spin density weighted by the intra-acquisition decay and with a phase determined by the magnetic field inhomogeneity. The image-space representation may then be recovered with an inverse Fourier transform. An image of the ideal 128 × 128 Fourier, Ω, operator, described above and in Rowe et al. (2007), for an 8 × 8 image array toy example is shown in Figure 1(a). Each column of this operator corresponds to either the real or imaginary part of a voxel of the original 8 × 8 image array, and each row corresponds to either the real or imaginary part of a voxel of the processed image array. This operator is described as ideal as it does not account for $T_2^{\ast }$ or ΔB effects.

Figure 1.

Toy example operators.

However, as the definition of k-space locations suggests, the k-space observation process occurs over a finite duration of time, with each k-space measurement being sampled at a unique time point. Thus, the k-space signal equation may be more appropriately considered as

$$s(k_x,k_y\mid t)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\rho (x,y)e^{-t∕T_2^{\ast }(x,y)}{e}^{i\gamma \Delta B(x,y)t}{e}^{-i2\pi (k_{x}x+k_{y}y)}\mathrm{d}x\mathrm{d}y,$$ [6]

when the k-space point (k_x, k_y) is sampled at time t = t(k_x, k_y). With the t(k_x, k_y) variable changing for each k-space measurement, image blurring from intra-acquisiton decay and image warping from magnetic field inhomogeneities may occur (Jesmanowicz et al., 1998; Jezzard and Balaban, 1995). Thus, the Fourier transform operator developed by Rowe et al. (2007) may be modified to account for non-instantaneous k-space observation in a modified Fourier operator, Ω_a. Each row of the operator is modified with exponential terms for $T_2^{\ast }(x,y)$ and ΔB(x,y) as described in Appendix B.

The inclusions of these parameters finely alter the structure of Ω to arrive at Ω_a. Two examples of Ω_a are shown in Figures 1(b) and 1(c). Figure 1(b) illustrates a Fourier matrix that accounts for a spatially uniform $T_2^{\ast }$ decay. The element values tend toward zero in the later portion of Ω_a because of the exponential decay. Figure 1(c) illustrates a Fourier matrix that accounts for a magnetic field gradient in the frequency encoding direction. This array is clearly different from the ideal Fourier array in Figure 1(a) and the array including decay in Figure 1(b). This Fourier array is essentially a skewed version of the ideal array. In both the cases of intra-acquisition decay and magnetic field inhomogeneity, an external measure of the perturber must be utilized. A $T_2^{\ast }(x,y)$ map may be acquired through the consideration of the magnitude of separate scans with varying echo times, and the ΔB(x, y) map may be acquired through the consideration of the phase of separate scans with varying echo times.

2.1.2 Obtaining s from S

In Equation 1, s is assumed to include only the properly ordered k-space observations located on the Cartesian k-space grid. However, as the k-space data is acquired in echo planar imaging (EPI), this is not true of the collected signal. Rather, the collected k-space data, S, is observed as real-imaginary pairs throughout the k-space traversal defined by the pulse sequence. Thus, in addition to including point-wise real-imaginary pairs instead of a column of real observations above a column of imaginary observations, the acquired data includes e extra points acquired during the phase encoding blips and incorrectly ordered observations from the negative frequency encoding lines in echo planar imaging. If the acquired k-space point at row r and column c on the desired k-space grid is denoted as s_r,c,R/I, where the final R/I index indicates that the observation is real or imaginary, and the extra k-space points acquired during the phase encoding blips are denoted as E_r,ep,R/I, with ep indexing the extra point number, the actually acquired data is the long vector

$$𝘴={[s_{1,1,R},s_{1,1,I},\dots ,s_{1,n,I},E_{1,1,R},\dots ,E_{1,e,I},s_{2,n,R},s_{2,n,I},s_{2,n-1,R},\dots ,E_{m,e,I}]}^{\prime }.$$

However, the data required for the reconstruction in Equation 1 is

$$s={[s_{1,1,R},s_{1,2,R},\dots ,s_{m,n,R},s_{1,1,I},\dots ,s_{m,n,I}]}^{\prime }.$$

Therefore, points in S must be censored and its component lines reordered to produce the s required in Equation 1. This can be performed in the three steps of censoring extra points, reversing alternating lines, and segregating real and imaginary observations. Censoring may be performed with a censoring matrix, C, row reversal may be performed with a permutation matrix, R, and the separation of real and imaginary data may be performed with another permutation matrix, P_C. The construction of these operators is discussed in Appendix C, and the operators are shown in Figures 1(d), 1(e), and 1(f), respectively.

Thus, the process of converting the acquired data to the required data for Equation 1 may be considered as

$$s=P_C\mathit{RC}𝘴.$$ [7]

As the operators in Equation 7 are censoring and permutation matrices, considering their effects on uncorrelated k-space observations is trivial. In the case of uncorrelated k-space observations, Γ = I_m(n+e). The covariance between the processed k-space observations, Γ_PcRC, is

$$\begin{array}{cc}\hfill {\Gamma }_{P_C\mathit{RC}}& =P_C{\mathit{RCI}}_{m(n+e)}{C}^T{R}^T{P}_C^T\hfill \\ \hfill {\Gamma }_{P_C\mathit{RC}}& =I_{\mathit{mn}}.\hfill \end{array}$$

Thus, the processes of censoring, reversing, and permuting uncorrelated k-space observations does not yield correlated k-space values as it can be shown that CC^T = I, RR^T = I and $P_C{P}_C^T=I$. However, if identity k-space covariance matrix Γ is not assumed, these processes will alter the covariance.

2.1.3 Line Shifting

Unmodeled gradient timing errors and eddy current effects may cause alternating k-space lines to be shifted in EPI acquisitions (Haacke et al., 1999). This shifting results in the N/2 or Nyquist ghost artifact associated with EPI. An offset term is introduced in the signal equation,

$$s(k_x,k_y\mid t)=\int \int \rho (x,y)e^{-t∕T_2^{\ast }(x,y)-i\gamma \Delta B(x,y)t+i{(-1)}^{\ell }2\pi \Delta k_{x}x}{e}^{-i2\pi (k_{x}x+k_{y}y)}\mathrm{d}x\mathrm{d}y$$ [8]

where Δk_x is the effective eddy current k-space shift and l is the frequency encoding line number in Equation 8. These shifts can be estimated and corrected to reduce such artifacts in the reconstructed images. Such shifts are often determined through the use of navigator echoes (Jesmanowicz et al., 1993) or reference scans (Bernstein et al., 2004). Thus, opposite shifts are then applied to the acquired k-space lines to realign them. The application of these shifts involves the use of the Fourier shift theorem. Each line is Fourier transformed, multiplied by a complex-valued exponential, and then inverse Fourier transformed to the shifted state. Thus, the process of shifting the k-space lines can be considered in several steps: The vector s is re-ordered to group real and imaginary observations from each line together; The lines are Fourier transformed; The transformed lines are multiplied by a complex-valued exponential; The phase altered lines are inverse Fourier transformed into shifted lines; The shifted lines are re-ordered to the original ordering of s. Thus, three operators need to be constructed: a permutation operator, P_R, to convert from s with the reals for the image stacked above the imaginaries for the image to a vector of reals stacked above imaginaries for each row; a row Fourier transform operator, Ω_row, to transform each of the rows; and a phase shift operator, Φ, to alter the phase of the transformed rows. Additionally, inverses of the permutation operator, trivially $P_R^{-1}=P_R^T$, and Fourier transform operator, ${\Omega }_{\mathit{row}}^{-1}$, are needed. The details of these three operators are given in Appendix D, and image representations of them are shown in Figures 1(g), 1(h), and 1(i).

With the permutation, Fourier transform and phase shift operators defined, shifting the acquired k-space lines alternating directions to yield a corrected set of k-space observations simply involves linear algebra:

$$s_{\mathit{corrected}}=P_R^{-1}{\Omega }_{\mathit{row}}^{-1}\Phi {\Omega }_{\mathit{row}}{P}_{R}s.$$ [9]

Thus, when performed on a time series of images, the reconstructed mean and covariance are altered by the processes in Equation 9 to

$$\mathrm{E}\left(y\right)=\Omega P_R^{-1}{\Omega }_{\mathit{row}}^{-1}\Phi {\Omega }_{\mathit{row}}{P}_R{s}_0$$ [10]

and

$$\mathrm{cov}\left(y\right)=\left(\Omega P_R^{-1}{\Omega }_{\mathit{row}}^{-1}\Phi {\Omega }_{\mathit{row}}{P}_R\right)\Gamma \left(P_R^{-1}{\Omega }_{\mathit{row}}^T{\Phi }^T{\left({\Omega }_{\mathit{row}}^{-1}\right)}^T{P}_R{\Omega }^T\right),$$ [11]

where s₀ = E(s) in Equation 10 is the mean k-space observation vector and Γ₀ = cov(s) in Equation 11 is the mean k-space covariance matrix. It should be once again noted that if Γ = I, then

$$\left(\Omega P_R^{-1}{\Omega }_{\mathit{row}}^{-1}\Phi {\Omega }_{\mathit{row}}{P}_R\right)\left(P_R^T{\Omega }_{\mathit{row}}^T{\Phi }^T{\left({\Omega }_{\mathit{row}}^{-1}\right)}^T{\left(P_R^{-1}\right)}^T{\Omega }^t\right)=I$$ [12]

because it can be shown that each of the operators in Equation 12 multiplied by their transposes yield identity matrices. If Γ ≠ I, the mean, covariance, and correlation will be altered by the operations, leading to the correlation of a voxel with its ghost location.

2.1.4 Symmetric k-space Generation

Symmetric k-space generation relies upon the symmetry of k-space about the origin under complex conjugation when a real-valued object is imaged. This symmetric generation has been used in partial Fourier acquisitions (Jesmanowicz et al., 1998). In the simplest case the first m/2 + 1 lines of k-space are acquired and the final m/2 − 1 lines are generated through the symmetry relationship. The partial Fourier interpolation matrix, H, is described in Appendix E. A graphical representation of H is shown in Figure 1(j) for the case of an 8 × 8 symmetric k-space generation from a 5 × 8 k-space acquistion.

With this partial Fourier reconstruction matrix, the omitted data is generated using the k-space symmetry relationship with the matrix multiplication s_S = H s. In the event of a full k-space acquisition, no symmetric data need be generated and H = I. Effects of partial Fourier processing on a data set may be considered with the modified reconstructed mean and covariance being

$$\mathrm{E}\left(y\right)=\Omega H{s}_0$$

and

$$\mathrm{cov}\left(y\right)=\Omega H{\Gamma }_0{H}^T{\Omega }^T.$$ [13]

Note that HH^T ≠ I when a partial k-space acquisition is made. It is seen that partial k-space reconstruction necessarily requires k-space observations to be correlated. Therefore, as the process of reconstruction is linear, image-space observations must exhibit a correlation. Thus, the operator modifies the covariance and correlation. Of course, the reconstruction of an image with fewer points in partial Fourier reconstruction additionally yields increased variance.

2.1.5 Smoothing with k-space Windowing and Image-Space Convolution

Smoothing of the complex-valued data may be performed during apodization, zero-filling, or explicit image smoothing operations. The Fourier convolution theorem allows complex-valued image-space convolution to be considered with k-space windowing. Thus, zero-filling, k-space apodization, and image-space complex data smoothing may be considered with operators of the same form. Because of the image-space convolution associated with these processes, it is obvious that they have a non-negligible effect on image-space voxel correlations. In Appendix F, we describe a zero filling operator, F, and an apodization operator, A. The apodization operator may include any windowing function, including the usual Fermi, Tukey, Hanning or Gaussian apodization windows. In Appendix F, we also describe an operator, S_m, which may be implemented on magnitude or magnitude squared data to yield image-space smoothing. The zero-filling operator is shown in Figure 1(k), the apodization operator in Figure 1(l), and the image-space magnitude smoothing operator in 1(m).

As it is well known, convolution alters the image mean, covariance, and correlation. Thus, even if Γ = I, the application of these operators alters the data as it will be shown.

3 Operator Implementation

With the above linear operators defined, it is possible to mathematically determine the image-space correlations resulting from applying the operators to k-space data with a covariance matrix, cov(S) = Γ. The image space covariance, cov(y), after applying an operator, O, to k-space data with a covariance matrix of Γ is defined in Equation 4.

Without loss of generality, we describe here the case of applying the operators to uncorrelated k-space data. Thus, Γ is assumed to be the identity matrix. Therefore, Equation 4 simplifies to cov(y) = OO^t. It is clear from this that if OO^t = δ²I, where δ² = 1/(m²n²) is a scalar introduced by the inverse Fourier transform, then the resulting image-space observations have scaled identity covariance matrices. With the covariance matrix known, the correlation matrix may be exactly calculated as

$$\mathrm{cor}\left(y\right)=D^{-1∕2}\mathrm{cov}\left(y\right)D^{-1∕2},$$ [14]

where D = diag(cov(y)).

As it was mentioned in the description of the operators, the censoring of the k-space observations, row reversal, reordering, and line shifting operators yield no image-space correlations in uncorrelated k-space data as in each case the operator multiplied by its transpose results in an identity matrix. If the k-space covariance matrix is not the identity, the operators will modify the covariance and correlation. More interesting results follow from the application of the operators including anomalies in the Fourier encoding process, partial Fourier reconstruction and k-space windowing or image-space convolution. In the following sections we consider these operators individually and serially in the case of a 96 × 96 data acquisition.

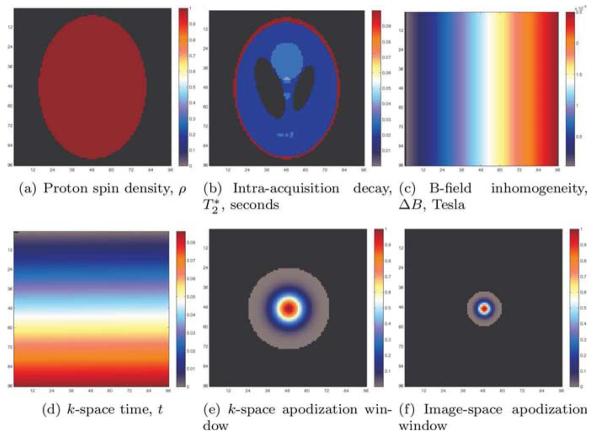
In the following calculations, physical parameters similar to those in typical fMRI studies were considered. The maps of the physical parameters and apodizers considered are shown in Figure 2. The proton spin density ρ shown in Figure 2(a), was assumed to be zero outside of the phantom, and unity within the phantom. The intra-acquisition decay, $T_2^{\ast }$ shown in Figure 2(b), was considered as a modified Shepp-Logan phantom which was scaled to physically relevant values from 10 to 100 ms. The B field inhomogeneity was considered as a horizontal gradient from 0 to 2.5 × 10⁻⁶ T, as shown in Figure 2(c). This B field inhomogeneity is significant, but on the order of the inhomogeneity observed in the inferior frontal lobe. The timing of the k-space observations is shown in Figure 2(d), and is representative of a standard EPI pulse sequence with an acquisition matrix of 96 × 96, bandwidth of 250 kHz, effective echo spacing of 0.96 ms, and echo time of 50 ms. The considered k-space apodization filter, shown in Figure 2(e), is a Gaussian window with an image-space representation shown in Figure 2(f). The image-space representation has a full width at half maximum of 3 pixels. Partial Fourier reconstruction was considered with 16 overscan lines. When the processes were not considered in the following calculations the parameters for the unconsidered processes are equivalent to: $T_2^{\ast }$ as a uniform, infinite map; ΔB as a map of zeroes; and the apodization window as a map of ones.

Figure 2.

Parameters considered in theoretical calculations.

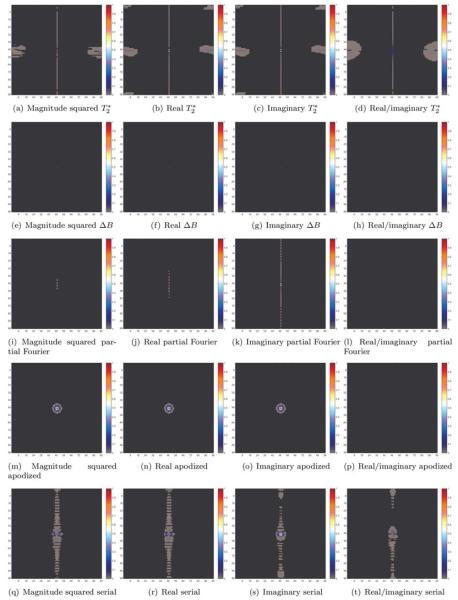
Calculations were made to examine the intra-acquisition decay, B field inhomogeneity, partial Fourier interpolation, and k-space apodization operators individually. Additionally, the combination of intra-acquisition decay, partial Fourier interpolation and k-space apodization performed serially was evaluated. Results illustrating the processed image means are shown in Figure 3, and the correlations for the center pixel in the processed images with all other pixels are shown in Figure 4. The first and second columns of Figure 3 illustrates the mean magnitude and phase images, while the third and fourth columns respectively illustrate the mean real and imaginary images. Each row of Figure 3 illustrates the results on the mean image in light of a different processing pipeline. Figure 4 illustrates the correlations for the center pixel for the same processing cases. Additionally, correlation coefficients for the four neighbors of the center pixel are shown in Table 1 for several processing pipelines.

Figure 3.

Reconstructed mean magnitude squared, phase, real and imaginary signal with various processes included. In each case, only the listed operator was included. In the serial case, $T_2^{\ast }$ decay, partial Fourier reconstruction, and k-space apodization were considered.

Figure 4.

Image-space correlations for the center pixel in magnitude squared, real, imaginary, and real/imaginary data with various processes included. In each case, only the listed operator was included. In the serial case, $T_2^{\ast }$ decay, partial Fourier reconstruction, and k-space apodization were considered.

Table 1.

Calculated correlation coefficients for the center voxel's nearest neighbors under several operations.

Operation	Left Neighbor Real	Left Neighbor Imaginary	Left Neighbor Real/Imaginary	Left Neighbor Magnitude2	Right Neighbor Real	Right Neighbor Imaginary	Right Neighbor Real/Imaginary	Right Neighbor Magnitude2
None	1.3e-16	1.3e-16	4.25e-17	3.3e-17	1.3e-16	1.3e-16	4.25e-17	3.3e-17
$\text{Uniform}{T}_2^{\ast }$	5.6e-8	5.6e-8	3.7e-5	1.2e-8	5.6e-8	5.6e-8	3.7e-5	1.2e-8
$\text{Varying}{T}_2^{\ast }$	4.9e-8	4.9e-8	3.4e-5	1.6e-8	4.9e-8	4.9e-8	3.4e-5	1.2e-8
B-Gradient	5.5e-7	5.5e-7	5.8e-10	7.5e-8	5.5e-7	5.5e-7	6.0e-10	7.7e-10
Partial Fourier	3.8e-5	8.9e-5	8.0e-17	7.0e-6	3.8e-5	8.9e-5	8.0e-17	7.0e-6
Partial Fourier and $\text{Uniform}{T}_2^{\ast }$	5.6e-5	4.0e-3	1.3e-6	1.3e-6	5.6e-5	4.0e-3	1.3e-6	1.3e-6
Partial Fourier and $\text{Varying}{T}_2^{\ast }$	7.7e-5	8.6e-4	9.3e-7	2.3e-6	7.7e-5	8.7e-4	1.3e-6	2.3e-6
Gaussian Smoothing	7.3e-1	7.3e-1	1.3e-16	7.3e-1	7.3e-1	7.3e-1	1.3e-16	7.3e-1
$\text{Varying}{T}_2^{\ast }$ Partial Fourier and Smoothing	7.5e-1	7.5e-1	2.2e-4	7.5e-1	7.4e-1	7.4e-1	1.0e-4	7.4e-1
$\text{Varying}{T}_2^{\ast }$ B-Gradient and Smoothing	8.2e-1	8.2e-1	2.9e-6	7.0e-1	7.5e-1	7.5e-1	2.7e-6	5.4e-1
Operation	Top Neighbor Real	Top Neighbor Imaginary	Top Neighbor Real/Imaginary	Top Neighbor Magnitude2	Bottom Neighbor Real	Bottom Neighbor Imaginary	Bottom Neighbor Real/Imaginary	Bottom Neighbor Magnitude2
None	5.4e-15	5.4e-15	9.2e-15	1.4e-15	5.4e-15	5.4e-15	9.2e-15	1.4e-15
$\text{Uniform}{T}_2^{\ast }$	4.9e-1	4.9e-1	2.0e-1	3.4e-3	4.9e-1	4.9e-1	2.0e-1	2.4e-3
$\text{Varying}{T}_2^{\ast }$	4.9e-1	4.9e-1	1.9e-1	5.2e-3	4.9e-1	4.9e-1	1.9e-1	3.6e-3
B-Gradient	2.7e-16	6.3e-17	8.1e-15	3.6e-17	1.5e-15	6.2e-20	1.1e-14	3.9e-16
Partial Fourier	2.6e-2	5.7e-1	1.0e-5	2.9e-3	2.6e-2	5.7e-1	1.0e-5	2.9e-3
Partial Fourier and $\text{Uniform}{T}_2^{\ast }$	5.3e-1	2.0e-1	1.1e-3	1.2e-1	5.3e-1	2.0e-1	1.1e-3	1.2e-1
Partial Fourier and $\text{Varying}{T}_2^{\ast }$	5.3e-1	1.1e-1	1.3e-3	1.0e-1	5.3e-1	1.1e-1	4.4e-4	1.2e-1
Gaussian Smoothing	7.3e-1	7.3e-1	2.8e-16	7.3e-1	7.3e-1	7.3e-1	2.8e-16	7.3e-1
$\text{Varying}{T}_2^{\ast }$ Partial Fourier and Smoothing	3.7e-1	6.1e-1	2.2e-2	3.7e-1	3.3e-1	6.1e-1	1.1e-2	3.3e-1
$\text{Varying}{T}_2^{\ast }$ B-Gradient and Smoothing	5.9e-1	5.9e-1	1.4e-1	5.8e-1	5.9e-1	5.9e-9	1.4e-1	5.9e-1

3.1 Fourier Anomalies

As it has previously been described, intra-acquisition decay yields an increase in the point spread function in the phase encoding direction (Jesmanowicz et al., 1998). The increase in the point spread function occurs preferentially in the phase encoding direction because of the decreased effective bandwidth in this direction in EPI. This can be seen through the apparent blurring of the edges of the phantom in the magnitude and real images in Figures 3(a) and 3(c). Nevertheless, slight correlation is noted between voxels in the frequency encoding direction as well in Table 1 due to the non-instantaneous acquisition of each k-space line. These correlations are dramatically less in the frequency encoding direction than in the phase encoding direction because of the remarkably higher bandwidth in the frequency encoding direction. Additionally, intra-acquisition decay leads to the appearance of edges in the mean phase and imaginary image in Figures 3(b) and 3(d). The increased point spread function in the phase encoding direction is clear in the correlation maps in Figures 4(a), 4(b), 4(c), and 4(d). The magnitude squared point spread function is less than the real and imaginary point spread functions. Moderate correlation between the real and imaginary data was observed along the phase encoding direction. The observation of the reduced magnitude squared point spread function holds true for each of the considered processing pipelines.

Also as previously described, static B field inhomogeneities lead to image warping and phase generation (Jezzard and Balaban, 1995). Thus, warping and a bulk shift in the phase encoding direction is apparent in the mean images that include B field inhomogeneities in the Fourier operators in Figures 3(e), 3(f), 3(g), and 3(h). More minor sub-voxel warping also occurs in the frequency encoding direction because of the higher sampling bandwidth in that direction. The phantom appears warped but uniform in Figure 3(e) as the magnitude data does not contain phase information, while the horizontally varying phase information is apparent in the phase, real and imaginary data in Figures 3(f), 3(g) and 3(h). Very small correlations are seen from the B field inhomogeneity in Figures 4(e), 4(f), 4(g), and 4(h). In fact, as seen in Table 1, higher correlation coefficients are observed in the frequency encoding direction than in the phase encoding direction. Such an observation may corroborate the observations of Kriegeskorte et al. (2008) where correlations in the frequency encoding direction appear to dominate. In this framework with uncorrelated data, B field inhomogeneities do not significantly alter observed variances.

3.2 Partial Fourier Reconstruction

In the ideal calculated case, partial Fourier reconstruction does not visually alter the mean reconstructed images in Figures 3(i), 3(j), 3(k), and 3(l). As expected with partial Fourier reconstruction, no obvious information is introduced into the phase or imaginary data. However, as described above, partial Fourier interpolation does slightly alter the mean image and correlation structure, even in this ideal case. Negligible correlation results between the real and imaginary data as seen in Figure 4(l). Figures 4(i), 4(j), and 4(k) illustrate slight correlations in the phase encode direction. Note that these correlations are less than those associated with intra-acquisition decay. In fact, as previously described by Jesmanowicz et al. (1998), when both partial Fourier reconstruction and intra-acquisition decay are considered, reduced correlation along the phase encoding direction is observed when compared to full Fourier reconstruction in the presence of intra-acquisition decay. Although Table 1 shows slight increases in correlation coefficients in neighboring voxels in the phase encoding direction with partial Fourier reconstruction, the effective point spread function in the phase encoding direction is reduced by partial Fourier reconstruction. It should be further noted that non-zero phase, caused by magnetic field inhomogeneities, exists in experimental data and leads to further alterations of the reconstructed mean images. Partial Fourier reconstruction was found to increase variance in the real and magnitude data while decreasing variance in the imaginary data, as expected.

3.3 k-space Windowing and Image-Space Convolution

Apodization with a Gaussian window clearly alters the reconstructed image means. The magnitude mean image in Figure 3(m) illustrates that the edge of the phantom is blurred and dilated as a result of convolution of the image-space apodization kernel. The real mean image shows the same result in Figure 3(o). As there is ideally no data in the imaginary data, apodization does not introduce significant information into the phase and imaginary mean images in Figures 3(n) and 3(p), although the noise appears to be smoothed. Correlations resulting from apodization, shown in Figures 4(m), 4(n), 4(o) , and 4(p), are as expected through the Fourier convolution theorem. Specifically, the image space-correlations resulting from k-space apodization are related to the image-space convolution with the Fourier transform of the k-space apodization window. As convolution with a real valued kernel does not induce correlations between the real and imaginary data, no correlations are seen in Figure 4(p). Apodization was found to decrease variance as expected with spatial smoothing.

3.4 Serial Processes

The results of serially considering intra-acquisition decay, partial Fourier reconstruction, and k-space apodization on the mean images are shown in Figures 3(q), 3(r), 3(s), and 3(t). The effects of intra-acquisition decay and apodization appear to dominate the reconstructed mean images. However, the computed image-space correlations, shown in Figures 4(q), 4(r), 4(s), and 4(t), are not simply the superposition of the correlations associated with each process. In this result, some of the utility of the theoretical framework is illustrated as the result of a series of complicated processing steps may be easily computed. The effects of smoothing from apodization were found to dominate the processed data variance as it was reduced to the level observed with apodization alone.

4 Experimental Illustration

To illustrate the performance of the operators, their application to phantom data was considered. Two experimental data sets were considered. The data sets were acquired on a 3.0 T General Electric Signa LX magnetic resonance imager, with a spherical doped agar phantom with $T_2^{\ast }=40.0$ ms as the subject. Each data set consisted of 1024 images of a single 2.5 mm thick, 24.0 cm field of view slice, with a 96 × 96 acquisition matrix, minimum full k-space echo time of 50.0 ms, effective echo spacing of 0.96 ms, 2000.0 ms repetition time, and 250 kHz acquisition bandwidth. The proton spins were excited with an 80 degree radio frequency pulse in one data set, and with a zero degree radio frequency pulse in the other data set. The data set with no excitation pulse was acquired to match the condition of pure noise considered in some of the above theoretical computations, while the data set with an excitation pulse more closely matches standard acquisitions.

Data were collected with a custom echo planar imaging pulse sequence, and reconstructed with locally developed software. With control of the entire acquisition and reconstruction pipeline, the confounds of unmodeled data processing are reduced. Nevertheless, some temporal filtering of the k-space acquisitions is performed to sub-sample the acquired 1 GHz samples to the collected 250 kHz samples. This processing may result in an autocorrelation of k-space observations, although such a correlation structure was not observed and is likely obscured by the noise in the experimental data.

Three navigator echoes of the center line of k-space were acquired to estimate error in the center frequency, and group delay offsets between odd and even k-space lines (Nencka et al., 2008). In the data acquired with an excitation pulse a group delay of 5.6 μs (1.4 k-space points) between odd and even lines was observed. Without correction of the group delay, severe Nyquist ghosting existed in the reconstructed data. This resulted in correlations between image voxels and ghost voxels. Correction of the group delay error greatly reduced the Nyquist ghost and resulting image-space correlations. The same group delay error was assumed on the data set acquired without an excitation pulse. No significant image-space correlations were apparent before or after application of the group delay error correction, in agreement with the theoretical result that the even and odd line shifts do not induce correlation in pure noise data. The data acquired with no radio frequency excitation was found to exhibit uncorrelated normally distributed noise in space and time with a mean of zero. Global, temporal phase structure was corrected in the data set acquired with radio frequency excitation to account for field shifts associated with gradient heating and radio frequency phase variation (Hahn et al., 2008). The data acquired with radio frequency excitation exhibited uncorrelated noise after phase correction. Thus, in both the no radio frequency excitation and the dynamic phase corrected data sets, there are no apparent structured correlations above the background correlations in the unprocessed data. Correlation coefficients in the experimental data for the four-neighbors of the center voxel under multiple processing conditions are shown in Table 2.

Table 2.

Correlation coefficients for the center voxel's nearest neighbors under several operations in experimental phantom data.

Operation	Left Neighbor Real	Left Neighbor Imaginary	Left Neighbor Real/Imaginary	Left Neighbor Magnitude2	Right Neighbor Real	Right Neighbor Imaginary	Right Neighbor Real/Imaginary	Right Neighbor Magnitude2
No RF, No Processing	1.6e-4	5.6e-4	1.4e-5	3.1e-4	1.8e-4	1.3e-4	8.0e-4	4.0e-4
Excitation	2.0e-5	1.2e-3	2.5e-3	2.9e-7	3.7e-4	1.6e-3	6.7e-10	8.3e-4
No RF, Partial Fourier	1.2e-3	2.2e-3	2.2e-3	2.8e-4	2.3e-4	5.0e-4	1.9e-4	1.3e-4
Excitation, Partial Fourier	2.5e-4	1.3e-4	4.4e-3	2.8e-4	1.1e-3	3.6e-4	8.0e-6	9.7e-4
No RF, Smoothing,	9.3e-1	9.3e-1	1.4e-5	8.7e-1	9.3e-1	9.4e-1	4.9e-4	8.7e-1
Excitation, Smoothing	9.8e-1	9.5e-1	1.2e-1	9.8e-1	9.8e-1	9.6e-1	2.3e-1	9.8e-1
Operation	Top Neighbor Real	Top Neighbor Imaginary	Top Neighbor Real/Imaginary	Top Neighbor Magnitude2	Bottom Neighbor Real	Bottom Neighbor Imaginary	Bottom Neighbor Real/Imaginary	Bottom Neighbor Magnitude2
No RF, No Processing	6.6e-3	2.1e-3	1.9e-5	1.8e-3	1.3e-4	1.1e-3	1.9e-3	1.1e-5
Excitation	1.4e-4	1.9e-5	3.2e-4	3.2e-4	1.9e-3	2.2e-3	4.1e-5	1.4e-3
No RF, Partial Fouier	1.2e-4	1.7e-3	6.3e-4	3.2e-3	1.0e-3	1.7e-3	5.1e-5	1.1e-7
Excitation, Partial Fourier	8.2e-4	7.4e-5	7.0e-4	7.7e-4	1.2e-3	8.7e-4	1.6e-4	1.3e-3
No RF, Smoothing	9.4e-1	9.3e-1	7.9e-4	8.8e-1	9.4e-1	9.4e-1	4.9e-6	8.8e-1
Excitation, Smoothing	9.7e-1	9.6e-1	1.6e-1	9.8e-1	9.7e-1	9.6e-1	1.6e-1	9.7e-1

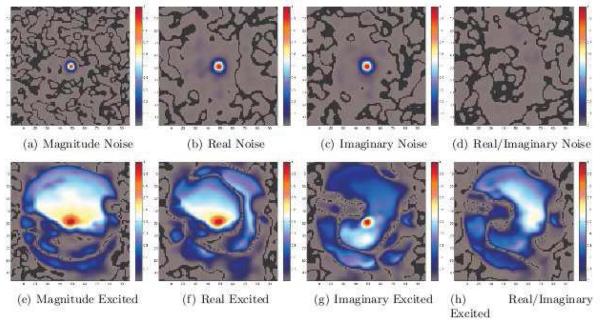
Smoothing of the noise data yields expected results, in agreement with those which are theoretically computed. The resulting images are shown in Figure 5. The similarity between the magnitude squared, real, imaginary, and real/imaginary correlations in the smoothed noise data in Figures 5(a), 5(b), 5(c), and 5(d) and the theoretical cases in Figures 4(m), 4(n), 4(o) , and 4(p) supports the validity of the theoretical method. Some residual phase correlation manifests itself in the correlation maps for the radio frequency excited data in Figures 5(e), 5(f), 5(g) and 5(h). Nevertheless, these results are similar to the theoretically expected case.

Figure 5.

Image space correlations for the center voxel in the acquired phantom data with no excitation pulse (noise) and with an excitation pulse (excited) in the magnitude squared, real, imaginary, and real/imaginary data after smoothing.

5 Discussion

This work extends a line of research which has been briefly mentioned in a paper (Rowe et al., 2007), and further developed in conference proceedings (Nencka and Rowe, 2007, 2008). In that work, the underlying theory for computing image-space correlations based upon k-space processes was developed. We have extended that work by developing multiple operators for common reconstruction processes which are defined in the first part of this manuscript. We have studied the results of those operators by theoretically computing image-space correlations associated with relevant implementations. We have examined the validity of the operators and the theoretical image-space correlations by verifying the results in acquired phantom data.

The results presented in this manuscript for individual operations may appear obvious, as relatively simple operations were considered. However, the utility of the method is demonstrated when multiple operations are considered at once. With this theoretical framework, the exact image-space point spread function may be computed following a string of processing operations on ideally uncorrelated data. This is useful as often a string of operations are performed on a data set. If all the common processes described here are implemented on a data set, the reconstructed image would be represented as

$$y=S_m{\Omega }_a{AFHP}_R^{-1}{\Omega }_{\mathit{row}}^{-1}\Phi {\Omega }_{\mathit{row}}{P}_R{P}_C\mathit{RC}𝘴.$$ [15]

The complicated process including all the described processing steps in Equation 15 lends itself well to this analytic mathematical model that is based upon simple linear algebra.

Furthermore, the alterations to an arbitrary covariance structure, Γ, may be examined. By computing the correlation structure following processing procedures on uncorrelated data, a reasonable null hypothesis threshold for experimental correlations may be considered. Thus, the theoretical method described in this manuscript and previous abstracts may be used to consider how much spatial processing is too much when considering functional connectivity or fMRI data.

This method may be further expanded with operators for additional processing operations. Operators for parallel acquisition image reconstruction, transmit/receive field inhomogeneities, non-cartesian gridding, masking, and image shifting could easily be developed for the described framework. Additionally, continuing work seeks to further extend this model to include more relevant temporal processing. A time series of images could be considered by stacking k-space observation vectors to create a time series observation vector, and performing Kronecker products between the operators and identity matrices with dimensions equal to the number of time series observations. Under such a parameterization, the effects of temporal processing may also be examined. Operators for dynamic magnetic field correction (Hahn et al., 2008, 2009), motion correction (Jenkinson et al., 2002), slice timing correction (Henson et al., 1999), temporal band-pass and notch filtering, and temporal smoothing (Gonzalez and Woods, 1992) may be developed by performing the Kronecker product with matrices other than identities. Thus, the full processing pipeline may be appropriately modeled with an extension to the described framework. In light of such a framework, statistical models may appropriately model the acquired data, rather than modeling data which has been preprocessed. Such models may allow scientists to statistically model the underlying physical changes associated with fcMRI and fMRI in more natural data (Rowe and Logan, 2004, 2005; Rowe, 2005), rather than modeling the observed indirect magnitude signal fluctuations.

Current computational limitations prevent the full implementation of such a statistical model. For a 96×96 k-space acquisition matrix, the described operators are 18432×18432. If all double precision elements are saved to an array, such an array requires over 2.5 gigabytes of memory. In many cases, sparse matrix representations may be considered, but in cases including the Fourier operator or a modified Fourier operator, each element must be computed. As the matrix multiplication required to compute the alteration of a covariance matrix based upon the operation, OΓO^T = Σ, requires three separate matrices in memory, O, Γ, and Σ, at least 7.5 gigabytes of memory must be addressed. Thus, 64-bit computing is essential. Further, hardware optimized matrix multiplication routines like the BLAS (Dongarra, 2002a,b) are essential for timely computations. If a time series of N images were to be considered, the memory requirements would grow by a factor of N² and the time for calculations would likewise grow. As the number of computing cores in personal computers continues to grow, and the availability of memory continues to increase, such calculations for reasonable time series will likely become possible in the relatively near future.

In spite of these technological issues, this manuscript presents an exact theoretical means of computing image-space correlations which arise from processing operations, describes the construction of several common operators, presents theoretical results for common image acquisition techniques, and verifies those theoretical results in acquired echo planar data. The results illustrate that processing operations and physical processes affect computed voxel correlations, especially in local neighborhoods of voxels. This has strong implications for methods which consider correlations between nearby voxels, as the choice of processing techniques and the physical properties of the imaging subject may substantially affect computed results.

Appendix

A Magnitude Squared Covariance

Consider two magnitude squared variables

$$\begin{array}{cc}\hfill y_1& =x_{1R}^2+x_{1I}^2,\hfill \\ \hfill y_2& =x_{2R}^2+x_{2I}^2,\hfill \end{array}$$ [A.1]

where x_1R and x_2R are the real components of the first and second observations while x_1I and x_2I are the imaginary components. For the sake of this derivation, let

$$\begin{array}{cc}\hfill \mathrm{E}\left(x_{1R}\right)={\rho }_1\cos {\theta }_1,\mathrm{var}\left(x_{1R}\right)={\sigma }_{1R}^2& \mathrm{cor}(x_{1R},x_{2I})={\Gamma }_{\mathit{RI}},\hfill \\ \hfill \mathrm{E}\left(x_{1I}\right)={\rho }_1\sin {\theta }_1,\mathrm{var}\left(x_{1I}\right)={\sigma }_{1I}^2& \mathrm{cor}(x_{1I},x_{2I})={\Gamma }_{\mathit{II}},\hfill \\ \hfill \mathrm{E}\left(x_{2R}\right)={\rho }_2\cos {\theta }_2,\mathrm{var}\left(x_{2R}\right)={\sigma }_{2R}^2& \mathrm{cor}(x_{1R},x_{2R})={\Gamma }_{\mathit{RR}},\hfill \\ \hfill \mathrm{E}\left(x_{2I}\right)={\rho }_2\sin {\theta }_2,\mathrm{var}\left(x_{2I}\right)={\sigma }_{2I}^2& \mathrm{cor}(x_{1I},x_{2R})={\Gamma }_{\mathit{IR}},\hfill \\ \hfill & \mathrm{cor}(x_{1R},x_{1I})={\Gamma }_1,\hfill \\ \hfill & \mathrm{cor}(x_{2R},x_{1I})={\Gamma }_2,\hfill \end{array}$$ [A.2]

where ρ represents an observation's magnitude and θ represents an observation's phase. The magnitude and phase may be obtained from the reconstructed image. Note that the Γ and variance values may be obtained from the complex correlation matrix.

The covariance between the magnitude squared variables assuming normally distributed noise is thus:

$$\begin{array}{cc}\hfill \mathrm{cov}(y_1,y_2)=& \mathrm{E}\left(y_1{y}_2\right)-\mathrm{E}\left(y_1\right)\mathrm{E}\left(y_2\right)\hfill \\ \hfill =& E\left(x_{1R}^2{x}_{2R}^2\right)+E\left(x_{1R}^2{x}_{2I}^2\right)+E\left(x_{1I}^2{x}_{2R}^2\right)+E\left(x_{1I}^2{x}_{2I}^2\right)-\hfill \\ \hfill & (E\left(x_{1R}^2\right)+E\left(x_{1I}^2\right))(E\left(x_{2R}^2\right)+E\left(x_{2I}^2\right))\hfill \\ \hfill =& 2({\Gamma }_{\mathit{RR}}^2{\sigma }_{1R}^2{\sigma }_{2R}^2+{\Gamma }_{\mathit{RI}}^2{\sigma }_{1R}^2{\sigma }_{2I}^2+{\Gamma }_{\mathit{IR}}^2{\sigma }_{1I}^2{\sigma }_{2R}^2+{\Gamma }_{\mathit{II}}^2{\sigma }_{1I}^2{\sigma }_{2I}^2)+\hfill \\ \hfill & 4({\Gamma }_{\mathit{RR}}{\sigma }_{1R}{\sigma }_{2R}{\rho }_1\cos \left({\theta }_1\right){\rho }_2\cos \left({\theta }_2\right)+\hfill \\ \hfill & {\Gamma }_{\mathit{RI}}{\sigma }_{1R}{\sigma }_{2I}{\rho }_1\cos \left({\theta }_1\right){\rho }_2\sin \left({\theta }_2\right)+\hfill \\ \hfill & {\Gamma }_{\mathit{IR}}{\sigma }_{1I}{\sigma }_{2R}{\rho }_1\sin \left({\theta }_1\right){\rho }_2\cos \left({\theta }_2\right)+\hfill \\ \hfill & {\Gamma }_{\mathit{II}}{\sigma }_{1I}{\sigma }_{2I}{\rho }_1\sin \left({\theta }_1\right){\rho }_2\sin \left({\theta }_2\right)).\hfill \end{array}$$ [A.3]

By letting x1 = (x1R,x_1I)′, x2 = (x_2R,x2I)′, E(x1) = μ1, E(x2) = μ₂, cov(x1) = Σ₁, cov(x₂) = Σ₂, and cov(x₁,x₂) = Σ₁₂, one can compactly write:

$$\begin{array}{cc}\hfill \mathrm{E}\left(y_j\right)=\mathrm{tr}\left({\Sigma }_j\right)+{\mu }_j^{\prime }{\mu }_j,\hfill & \hfill j=1,2,\hfill \\ \hfill \mathrm{var}\left(y_j\right)=2\mathrm{tr}\left({\Sigma }_j^{\prime }{\Sigma }_j\right)+4{\mu }_j^{\prime }{\Sigma }_j{\mu }_j,\hfill & \hfill j=1,2,\hfill \\ \hfill \mathrm{cov}(y_1,y_2)=2\mathrm{tr}\left({\Sigma }_{12}^{\prime }{\Sigma }_{12}\right)+4{\mu }_1^{\prime }{\Sigma }_{12}{\mu }_2,\hfill & \hfill \hfill \end{array}$$ [A.4]

where tr(·) denotes the trace operation.

B Fourier Anomalies

The standard Fourier operator, Ω, is described in Equation 2.1. This operator may be modified to include anomalies in the Fourier encoding procedure, produced by $T_2^{\ast }$ decay and B-field inhomogeneity. Each anomaly introduces time dependent exponential terms to the signal equation as shown in Equation 6. The exponential terms for $T_2^{\ast }$ and ΔB, denoted as ℰ(k_x,k_y,x,y), may be considered with their real and imaginary components through the Euler identity,

$$ℰ(k_x,k_y,x,y)=e^{-t(k_x,k_y)∕T_2^{\ast }(x,y)}{e}^{i\gamma \Delta B(x,y)t(k_x,k_y)}$$ [B.1]

$$\begin{array}{cc}\hfill =& e^{-t(k_x,k_y)∕T_2^{\ast }(x,y)}\cos \left(\gamma \Delta B(x,y)t(k_x,k_y)\right)\hfill \\ \hfill & +{\mathit{ie}}^{-t(k_x,k_y)∕T_2^{\ast }(x,y)}\sin \left(\gamma \Delta B(x,y)t(k_x,k_y)\right).\hfill \end{array}$$ [B.2]

These multiplicative terms may be included in the Fourier matrix with encoding anomalies as

$${\Omega }_a=\Omega .\ast \left(\begin{array}{cccccc}\hfill \Re \left(ℰ(1,1,1,1)\right)\hfill & \hfill \cdots \hfill & \hfill \Re \left(ℰ(m,n,1,1)\right)\hfill & \hfill -\Im \left(ℰ(1,1,1,1)\right)\hfill & \hfill \cdots \hfill & \hfill -\Im \left(ℰ(m,n,1,1)\right)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \Re \left(ℰ(1,1,m,1)\right)\hfill & \hfill \cdots \hfill & \hfill \Re \left(ℰ(m,n,m,1)\right)\hfill & \hfill -\Im \left(ℰ(1,1,m,1)\right)\hfill & \hfill \cdots \hfill & \hfill -\Im \left(ℰ(m,n,m,1)\right)\hfill \\ \hfill \Re \left(ℰ(1,1,1,2)\right)\hfill & \hfill \cdots \hfill & \hfill \Re \left(ℰ(m,n,1,2)\right)\hfill & \hfill -\Im \left(ℰ(1,1,1,2)\right)\hfill & \hfill \cdots \hfill & \hfill -\Im \left(ℰ(m,n,m,2)\right)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \Re \left(ℰ(1,1,m,n)\right)\hfill & \hfill \cdots \hfill & \hfill \Re \left(ℰ(m,n,m,n)\right)\hfill & \hfill -\Im \left(ℰ(1,1,m,m)\right)\hfill & \hfill \cdots \hfill & \hfill -\Im \left(ℰ(m,n,m,n)\right)\hfill \\ \hfill \Im \left(ℰ(1,1,1,1)\right)\hfill & \hfill \cdots \hfill & \hfill \Im \left(ℰ(m,n,1,1)\right)\hfill & \hfill \Re \left(ℰ(1,1,1,1)\right)\hfill & \hfill \cdots \hfill & \hfill \Re \left(ℰ(m,n,1,1)\right)\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \Im \left(ℰ(1,1,m,n)\right)\hfill & \hfill \cdots \hfill & \hfill \Im \left(ℰ(m,n,m,n)\right)\hfill & \hfill \Re \left(ℰ(1,1,m,n)\right)\hfill & \hfill \cdots \hfill & \hfill \Re \left(ℰ(m,n,m,n)\right)\hfill \end{array}\right),$$ [B.3]

where .* indicates point-wise multiplication of the matrices. Clearly the form of $T_2^{\ast }$ and ΔB are dependent upon the physical system being imaged.

C Censoring and Reordering Acquired Data

As acquired, the EPI k-space data is not in a format appropriate for the developed Fourier operators. Extra data must be censored, data acquired with negative frequency encoding gradients must be reversed, and the real data must be segregated from the imaginary data. First, the extra points acquired during the phase encoding blips must be censored. A binary censoring matrix of dimension 2mn × 2m(n + e) is used to multiply S. The censoring matrix is an identity matrix with the rows corresponding to the extra acquired points omitted. Mathematically, this can be described using the Kronecker product. Thus, the censoring matrix, C, is the Kronecker product of an identity matrix with a non-square matrix which includes an identity matrix and an 2n × 2e matrix of zeros denoted by Z(2n, 2e):

$$C=I_m\otimes [I_{2n},Z(2n,2e)].$$ [C.1]

Thus, the extraneous points acquired during the phase encoding blips are removed through the use of the censoring matrix, S_C = CS. A toy example of a censoring matrix for an 8×8 array of k-space measurements with 1 point acquired during the phase encoding blips is shown in Figure 1(d).

With the removal of the points acquired during the phase encoding blips, S_C contains only the k-space observations that are on the k-space grid. The second step is to reorder the alternating lines where the data is collected with negative frequency encoding gradients. This is slightly more complicated than simply reversing the data as it is still in real-imaginary pairs which would be swapped to imaginary-real pairs if only row reversal was performed. Again, a Kronecker product is used to construct the row reversal operator, R. To construct R, a Kronecker product between I, a “reverse identity” matrix, to reverse the row, and an identity matrix, to preserve the real-imaginary pairs, is used:

$$ℛ={ℐ}_n\otimes I_2.$$ [C.2]

To apply this row reversal to only even lines, an alternating row reversal matrix, R, must be constructed. This is the Kronecker product between an identity matrix and a block, B, which preserves one row and reverses one row. Thus, the block is defined to be

$$B=\left(\begin{array}{cc}\hfill I_{2n}\hfill & \hfill Z(2n,2n)\hfill \\ \hfill Z(2n,2n)\hfill & \hfill ℛ\hfill \end{array}\right),$$ [C.3]

and the alternating row reversal matrix is thusly

$$R=I_{m∕2}\otimes B.$$ [C.4]

Note that this assumes an acquisition with reversed even rows, although an acquisition with reversed odd rows would require the trivial change of switching the positions of I_2n and R in B. With the alternating row reversal matrix constructed, the alternating row reversal can be easily performed: S_RC = RS_C. A toy example of an alternating row reversal matrix for an 8 × 8 k-space data set is shown in Figure 1(e).

The final step of converting S to s involves reordering S_RC to include the real observations stacked above the imaginary observations. This operation is performed by a permutation matrix, P_C, which can be constructed by interleaving the columns of two non-square matrices. These matrices include P_C1 = [I_mn;Z(mn,mn)] and P_C2 = [Z(mn,mn);I_mn]. The columns of these matrices are interleaved to produce P_C by taking the first column of P_C1 followed by the first column of P_C2 and so on. This real-imaginary reordering can be performed through matrix multiplication to yield the data ordering required in Equation 1, s = P_CS_RC. An example assuming an 8 × 8 k-space acquisition is shown in Figure 1(f).

D Nyquist Ghost Correction

Even and odd lines may be shifted in opposite directions to correct for the Nyquist ghost introduced from eddy current effects in EPI. This may be performed through the use of the Fourier shift theorem. The three operators which are described in this section reorder the data into sets of real and imaginary data for each row, Fourier transform each row, and apply a phase shift to the Fourier transformed row.

The permutation matrix is a binary matrix which can be constructed by interleaving blocks of columns of two non-square matrices to create a square matrix. The two matrices to be interleaved are P_R1 = [I_mn, Z(mn,mn)] and P_R2 = [Z(mn,mn), I_mn]. The permutation matrix, P_R, results from taking the first n columns of P_R1 followed by the first n columns of P_R2, and so on. The signal is thus re-ordered to a column vector of the reals stacked above the imaginaries for each row through multiplication with P_R. As this is a permutation matrix, its inverse is simply its transpose. A graphical representation of P_R for an 8 × 8 k-space acquisition is shown in Figure 1(g).

The row Fourier transform matrix is the Kronecker product of an identity matrix with the Fourier transform matrix Ω_x, as defined earlier, Ω_row = I_m ⊗ Ω_x. A graphical representation of Ω_row for an 8 × 8 k-space acquisition is shown in Figure 1(h).

The phase shift operator is the final necessary operator for performing a line shift. This operator multiplies the complex-valued Fourier transform of the line by a complex-valued exponential to implement the Fourier shift theorem. For a shift of ϕ, the j^th element of the row must be multiplied by exp(−i2πϕj/n), or equivalently cos(2πϕj/n)−i sin(2πϕj/n). Thus, the real component of the phase shifted j^th element is ℜ(fj) cos(2πϕj/n)−ℑ(f_j) sin(2πϕj/n), where f_j is the j^th element of the Fourier transformed row. Similarly, the imaginary component of the phase shifted j^th element is ℜ(f_j) sin(2πϕj/n) + ℑ(f_j) cos(2πϕj/n). Thus, for a row, this phase shift matrix operator is

$$\zeta =\left(\begin{array}{cccccc}\hfill \cos (2\pi \varphi 1∕n)\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill -\sin (2\pi \varphi 1∕n)\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cos (2\pi \varphi n∕n)\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill -\sin (2\pi \varphi n∕n)\hfill \\ \hfill \sin (2\pi \varphi 1∕n)\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \cos (2\pi \varphi 1∕n)\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill \sin (2\pi \varphi n∕n)\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cos (2\pi \varphi n∕n)\hfill \end{array}\right).$$ [D.1]

Shifting a row to the right by ϕ pixels is denoted by ζ⁺ while shifting a row to the left by ϕ pixels is denoted by ζ⁻. With this representation, the phase shifting of lines in alternating directions is denoted by Φ = I_m/2⊗[ζ⁺, Z(2n, 2n);Z(2n, 2n), ζ⁻]. A graphical representation of Φ with ϕ = 0.5 and an 8 × 8 acquisition matrix is shown in Figure 1(i).

E Partial Fourier Interpolation

Conjugate symmetry ideally exists about the origin in k-space, as the reconstructed image is expected to be real-valued. This symmetry allows half of k-space to be generated without being acquired. Thus the acquired data array, s, only requires 2(m/2+1)n elements while the symmetrically generated data array s_S, is 2mn elements. For the sake of consistency in notation, we assume that the remaining 2(m/2−1)n elements in s are set to zero with the last (m/2−1)n real observations being zero and the last (m/2−1)n imaginary observations being zero. An equivalent symmetric k-space generation operator can be constructed which does not include these zero elements thereby reducing the operator size. However, in the considered case a square matrix, H, can be used for partial Fourier reconstruction. For the acquired real and imaginary points, the partial Fourier operator returns the observed values. For the generated point (k_x, k_y), the partial Fourier operator returns the complex conjugate of the observed point at (−k_x, −k_y). This partial Fourier operator multiplies the uncollected points by zero, so the values originally substituted into these points are irrelevant. The partial Fourier operator is thusly a 2mn×2mn matrix. This matrix which includes identity, I, “reverse identity,” I, and zero, Z, matrices is:

$$H=\left(\begin{array}{ccc}\hfill I_{(m∕2+1)n}\hfill & \hfill Z((m∕2+1)n,(m∕2-1)n)\hfill & \hfill Z((m∕2+1)n,\mathit{mn})\hfill \\ \hfill Z((m∕2-1)n,n)\hfill & \hfill {ℐ}_{(m∕2-1)n}\hfill & \hfill Z((m∕2-1)n,\frac{3}{2}\mathit{mn})\hfill \\ \hfill Z((m∕2-1)n,\mathit{mn})\hfill & \hfill I_{(m∕2+1)n}\hfill & \hfill Z((m∕2+1)n,(m∕2-1)n)\hfill \\ \hfill Z((m∕2-1)n,(m+1)n)\hfill & \hfill -{ℐ}_{(m∕2-1)n}\hfill & \hfill Z((m∕2-1)n,\frac{m}{2}n)\hfill \end{array}\right).$$ [E.1]

A graphical representation of H is shown in Figure 1(j) for the case of an 8×8 symmetric k-space.

F Convolution

We will first describe the zero filling operator, F, and then describe the apodization operator, A, which includes the typical Fermi apodization window and Gaussian smoothing window as specific cases. We will finally describe the image-space magnitude smoothing operator.

Zero-filling is often performed to yield an increase in apparent reconstructed resolution and to create an array which has dimensions of an integer power of two for fast Fourier transform routines (Gonzalez and Woods, 1992). In zero-filling, zeros are appended to the acquired k-space observations at higher spatial frequencies than are observed. It is well known that zero-filling is equivalent to image-space convolution with a sinc kernel. The zero-filling is done symmetrically to preserve the location of the k-space origin in the zero-filled array at (m/2+1, n/2+1). The zero filling matrix is a binary matrix containing blocks of zero and identity matrices. This parameterization of the zero-filling operator assumes that an even number of phase encode points, 𝒫, and an even number of frequency points, 𝓕, are to be added to the acquired data. The zero-filling operator is denoted as

$$F=I_2\otimes \left(\begin{array}{c}\hfill F_{𝒫}\hfill \\ \hfill I_m\otimes F_{ℱ}\hfill \\ \hfill F_{𝒫}\hfill \end{array}\right)$$ [F.1]

where

$$F_{𝒫}=Z(𝒫∕2,\mathit{mn})$$ [F.2]

and

$$F_{ℱ}=\left(\begin{array}{c}\hfill Z(ℱ∕2,n)\hfill \\ \hfill I_n\hfill \\ \hfill Z(ℱ∕2,n)\hfill \end{array}\right).$$ [F.3]

Thus, zeros are appended symmetrically around the acquired k-space matrix. It should be noted that this changes the dimensionality of s, and subsequent operators must be appropriately adjusted. An example of F is shown in Figure 1(k) for zero filling a 4 × 4 k-space data set to an 8 × 8 data set.

Apodization and filtering can be considered with the Fourier convolution theorem, where convolution with a kernel in image space is simply point-wise multiplication of the Fourier transform of the original kernel in k-space. Thus, any processing step which involves the point-wise multiplication of k-space observations with a kernel or the image-space convolution of the complex-valued image with a kernel can be considered with the apodization operator presented here. This apodization operator, A, is a diagonal matrix in which the non-zero elements correspond to the values of the k-space kernel for those points. If the values of the k-space kernel, K, are indexed across rows such that the first element of the first row is 1, the last element of the first row is n, the first element of the second row is n + 1, and so on, the elements of A are easily defined such that A_j,j = K(j). An example of A is shown in Figure 1(l) for the case of a simple 8 × 8 Hanning k-space window.

Explicit image smoothing is often performed on the reconstructed magnitude data. Such a process is different from smoothing the complex data (Lai et al., 1996) and is a non-linear process. However, with the magnitude squared covariance matrix known from the complex-valued covariance matrix, an operator, S_mm, may be developed to consider smoothing magnitude squared data. The first row of the operator consists of the kernel weights for each magnitude squared data point for the first smoothed magnitude squared data point. The second row includes the weights for the second point, and so on. An operator for smoothing an 8 × 8 data set with a Gaussian kernel with a 3 voxel FWHM is shown in Figure 1(m). If image-space smoothing of the complex-valued data were preferred over k-space apodization, a complex-data smoothing operator, S_m could be constructed as a block diagonal operator where the two diagonal blocks are filled with S_mm.