Probing Microsecond Time Scale Dynamics in Proteins by Methyl ¹H Carr−Purcell−Meiboom−Gill Relaxation Dispersion NMR Measurements. Application to Activation of the Signaling Protein NtrC^r

Abstract

To study microsecond processes by relaxation dispersion NMR spectroscopy, low power deposition and short pulses are crucial and encourage the development of experiments that employ ¹H Carr−Purcell−Meiboom−Gill (CPMG) pulse trains. Herein, a method is described for the comprehensive study of microsecond to millisecond time scale dynamics of methyl groups in proteins, exploiting their high abundance and favorable relaxation properties. In our approach, protein samples are produced using [¹H, ¹³C]-d-glucose in ∼100% D₂O, which yields CHD₂ methyl groups for alanine, valine, threonine, isoleucine, leucine, and methionine residues with high abundance, in an otherwise largely deuterated background. Methyl groups in such samples can be sequence-specifically assigned to near completion, using ¹³C TOCSY NMR spectroscopy, as was recently demonstrated (Otten, R.; et al. J. Am. Chem. Soc.2010, 132, 2952−2960). In this Article, NMR pulse schemes are presented to measure ¹H CPMG relaxation dispersion profiles for CHD₂ methyl groups, in a vein similar to that of backbone relaxation experiments. Because of the high deuteration level of methyl-bearing side chains, artifacts arising from proton scalar coupling during the CPMG pulse train are negligible, with the exception of Ile-δ1 and Thr-γ2 methyl groups, and a pulse scheme is described to remove the artifacts for those residues. Strong ¹³C scalar coupling effects, observed for several leucine residues, are removed by alternative biochemical and NMR approaches. The methodology is applied to the transcriptional activator NtrC^r, for which an inactive/active state transition was previously measured and the motions in the microsecond time range were estimated through a combination of backbone ¹⁵N CPMG dispersion NMR spectroscopy and a collection of experiments to determine the exchange-free component to the transverse relaxation rate. Exchange contributions to the ¹H line width were detected for 21 methyl groups, and these probes were found to collectively report on a local structural rearrangement around the phosphorylation site, with a rate constant of (15.5 ± 0.5) × 10³ per second (i.e., τ_ex = 64.7 ± 1.9 μs). The affected methyl groups indicate that, already before phosphorylation, a substantial, transient rearrangement takes place between helices 3 and 4 and strands 4 and 5. This conformational equilibrium allows the protein to gain access to the active, signaling state in the absence of covalent modification through a shift in a pre-existing dynamic equilibrium. Moreover, the conformational switching maps exactly to the regions that differ between the solution NMR structures of the fully inactive and active states. These results demonstrate that a cost-effective and quantitative study of protein methyl group dynamics by ¹H CPMG relaxation dispersion NMR spectroscopy is possible and can be applied to study functional motions on the microsecond time scale that cannot be accessed by backbone ¹⁵N relaxation dispersion NMR. The use of methyl groups as dynamics probes extends such applications also to larger proteins.

Introduction

To understand the function of a biological macromolecule, it is of critical importance to complement a high-resolution three-dimensional structure with a detailed insight in its molecular dynamics.^1,2 For a growing number of systems, it has been found that slow (microsecond to millisecond), collective motions can be rate limiting for biological function. Nuclear magnetic resonance (NMR) spectroscopy is an ideal technique for studying dynamical processes on this time scale, being capable of providing such information for many different nuclei with atomic resolution.³⁻⁵ Specifically, microsecond−millisecond dynamics can be studied through NMR relaxation dispersion experiments, and applications to protein folding,⁶⁻¹⁰ ligand binding,^10,11 enzyme catalysis,¹²⁻¹⁸ and allosteric regulation(19) have appeared.

Relaxation dispersion NMR spectroscopy investigates the influence of slow (μs−ms) stochastic processes on the nuclear spin relaxation. For a molecule undergoing a conformational exchange process described by

relaxation dispersion experiments yield information on (i) the exchange rate, k_ex = 1/τ_ex = k_AB + k_BA, (ii) the populations of the exchanging states, p_A and p_B, and (iii) the absolute difference between the chemical shifts of state A and B, |Δω|.^20,21

While the basic building block of these experiments, the spin−echo, dates back to the 1950s,(22) Carr−Purcell−Meiboom−Gill (CPMG)^23,24 relaxation dispersion spectroscopy has emerged over the past decades as a powerful tool to study motions on millisecond to second time scales in proteins, through combined advances in biochemical labeling techniques and NMR pulse scheme developments (see, for example, Lundström et al. and references therein(25)). In particular, for ¹³C CPMG experiments, it has been vital to prepare NMR samples with isolated ¹³C probes to remove artifacts in CPMG data sets due to the large one-bond and nonvanishing long-range homonuclear scalar coupling constants.²⁶⁻²⁸ As a result, a host of experiments are now available that exploit protein backbone nuclei (¹⁵N, ¹H^N, ¹H^α, ¹³C^α, and ¹³C)^6,7,29−39 as well as side chain nuclei (e.g., ¹³C^β, ¹⁵NH₂, ¹³C^methyl, and ¹H^methyl)^28,40−44 as reporters of the exchange process.

Most CPMG experiments to date aim at obtaining X-spin relaxation dispersion profiles for ¹H-X-spin systems in proteins, where X = ¹⁵N or ¹³C. These experiments have been employed to characterize exchange processes on the millisecond time scale, using maximum pulse repetition rates on the order of 1 kHz. This limitation is primarily a consequence of significant heating of the NMR sample at high duty cycles, as a result of dielectric losses, but hardware issues (e.g., power handling of the amplifiers and probehead and detuning of the RF circuit) also play a role.

The experimental constraints are less stringent if ¹H is used as nucleus to record the CPMG relaxation dispersion profiles, because sample heating at a certain duty cycle is much lower in that case.(45) The ability to use a wide range of effective CPMG field strengths makes it possible to accurately address faster processes (down to ∼10 μs) by sampling the spectral density curve over a wider range. It is also vital for the detection of multiple exchange processes occurring on different time scales. In addition, ¹H CPMG experiments have several other advantages. First, the 180° refocusing pulses in the ¹H CPMG element are significantly shorter than those used for ¹³C/¹⁵N, which reduces off-resonance effects(46) as well as artifacts arising due to evolution during 180° pulses.(47) Furthermore, the chemical shift perturbations measured by methyl ¹H CPMG relaxation dispersion experiments are complementary to those reported by backbone ¹³C and ¹⁵N measurements, because ¹H chemical shifts are extremely sensitive reporters of local tertiary, rather than secondary structure.(48)

Despite the above-mentioned advantages, the development of ¹H CPMG relaxation dispersion experiments has been comparatively limited, mainly due to difficulties in adequately suppressing homonuclear scalar couplings^26,34,49 and ¹H−¹H dipolar cross relaxation.^50,51 Meanwhile, some methods have emerged that use protons in the backbone as probes of protein dynamics. More specifically, ¹H CPMG relaxation dispersion experiments have been described for amide^30,31,34 and alpha^35,36 proton nuclei using (per-)deuterated NMR samples and an appropriate pulse scheme.

It would be of great interest to extend the ¹H CPMG relaxation dispersion methodology to side chain atoms, and methyl groups in particular. Not only are these moieties abundant in proteins, thereby supplying a lot of potential probes to measure dynamics, they are also often located at interesting positions (e.g., in the hydrophobic core and at the interface of complexes)(52) and possess favorable NMR properties. The rapid 3-fold jumps about the methyl symmetry axis scales the ¹³C relaxation rate(53) by 1/9, and the fact that the TROSY principle(54) can be employed⁵⁵⁻⁵⁷ assures that narrow NMR resonances are observed, even in the case of high molecular weight systems. In addition, high-quality data can be recorded over a large temperature interval, which is important for determining the thermodynamic parameters of the exchange process. Temperature-dependent studies using ¹H^N or ¹⁵N CPMG relaxation dispersion measurements are seriously hampered by spin decorrelation effects (e.g., exchange with the solvent), leading to loss of signal in ¹H−¹⁵N (TROSY-)HSQC experiments. Because methyl protons are nonlabile, they are not affected by this phenomenon, such that high-quality ¹H−¹³C correlation maps can also be recorded at elevated temperature and pH.

Here, we describe an approach to record ¹H CPMG relaxation dispersion data on methyl groups, selecting for the CHD₂ isotopomer. The production of protein samples by bacterial expression using U-[¹H, ¹³C]-d-glucose and ∼100% D₂O ensures the isotopic enrichment of all possible methyl groups together with high deuteration levels in the side chain.⁵⁸⁻⁶⁰ Because residual protonation at positions adjacent to the methyl group in the side chain will defeat our strategy, we first validated the proposed methodology on calbindin D_9k, which has been studied in great detail using NMR spectroscopy and where slow motions are absent.⁶¹⁻⁶⁴ We are able to demonstrate that ¹H CPMG relaxation dispersion profiles can be faithfully acquired using a standard CPMG pulse scheme for Ala, Val-γ1/γ2, Leu-δ1/δ2, Ile-γ2, and Met methyl groups, because of the high deuteration level (90−95%) in these amino acid side chains. Spurious dispersion profiles were observed in a few cases, and either resulted from significant protonation on neighboring carbon atoms (Ile-δ1 and Thr methyl groups) or strong ¹³C scalar coupling effects (Leu). A straightforward modification of the experiment is presented to remove artificial dispersion profiles originating from residual protonation, and solutions are described that resolve strong ¹³C scalar coupling artifacts, by using a biochemical or NMR approach.

The approach we have taken differs in an important way from alternative methods to measure slow (μs−ms) motions in proteins by ¹H relaxation dispersion NMR, as the previously described methods rely on the use of specifically methyl-protonated precursors on a fully deuterated background.^43,65 Although this is key for truly high (>100 kDa) molecular weight systems, specific labeling considerably limits the number of available probes. Depending on the type of precursor, samples labeled with I(δ1)LV,^66,67 Ala,^68,69 or Met(70) contain approximately 60%, 17%, or 3% of methyl groups in proteins, respectively.

The utility of our approach is illustrated with an application to the N-terminal receiver domain of the Nitrogen Regulatory Protein C (NtrC^r).⁷¹⁻⁷⁵ NtrC is a transcriptional activator, and the switch from an inactive to active conformation, triggered by phosphorylation of residue D54 in the N-terminal domain (NtrC^r), is accompanied by a considerable structural change. The proposed mechanism for the activation is a shift in the pre-existing equilibrium between inactive and active conformations. In a previous ¹⁵N relaxation dispersion study, the time scale for this process could only be approximated from the discrepancy of line broadening in the slow pulsing regime and the exchange-free line width obtained from separate experiments.(74) Application of ¹H CPMG relaxation dispersion NMR to CHD₂ methyl groups shows that 21 probes exhibit an exchange contribution. All relaxation data could be collectively fitted to a single, cooperative process (k_ex = 15 458 ± 452 s⁻¹). ¹H NMR extends the application of CPMG methodology to study microsecond time scale exchange processes, which is crucial to adequately map the chemical exchange spectral density function.

Materials and Methods

Sample Preparation

The heat- and IPTG-inducible pRCB1 expression vector, containing the P43G mutation, was used to obtain the coding sequence for calbindin D_9k by PCR using 5′-ggctcATGAAATCTCCGGAAGAACTG and 5′-cgctcatatggaTTTCTGGCAGGG (uppercase, annealing sequence; lowercase, primer overhang) as the forward and reverse primers, respectively. The PCR product was purified from agarose gel, cut with PagI/NdeI and ligated into the NcoI/NdeI digested pET-15b vector (Novagen). The resulting pET15b-calbindinP43G expression vector (IPTG-inducible, no His-tag) was sequenced (Service XS, Leiden, The Netherlands) and confirmed to be correct.

Escherichia coli BL21(DE3) was used to express recombinant calbindin D_9k. For the induction of protein synthesis, cells were grown at 37 °C in M9 minimal medium with 100 μg/mL ampicillin to an OD₆₀₀ ≈ 0.6 and incubated for 3 h at the same temperature in the presence of 1 mM isopropyl β-d-thiogalactoside (IPTG). To purify calbindin D_9k, cell pellets were resuspended in a buffer containing 20 mM Tris, pH 8.0 (buffer A) with 10 μg/mL DNase I and 0.5 mM phenylmethanesulfonyl fluoride (PMSF) added. After French press, the cell lysate was added to twice the volume of boiling buffer A, and under vigorous stirring it was heated until the temperature reached ∼95 °C. After quickly cooling the sample on ice−water slurry, the precipitated proteins and cell debris were removed by centrifugation. The supernatant was loaded onto a Q-Sepharose column (GE Healthcare) pre-equilibrated with buffer A. After extensive washing with buffer A, calbindin D_9k was eluted using a salt gradient of NaCl (0−200 mM). Fractions containing calbindin D_9k were pooled, dialyzed extensively against water, and the homogeneity was confirmed by 15% SDS-PAGE.

A U-[¹³C, ¹⁵N]-¹H/²H sample of calbindin D_9k was obtained using the general isotope labeling strategy outlined by Tugarinov et al.(76) Briefly, pET15b-calbindinP43G was transformed into E. coli BL21(DE3) and was grown in 200 mL of D₂O M9 medium containing 2 g/L U-[¹H, ¹³C]-d-glucose (Cambridge Isotope Laboratories) and 1 g/L ¹⁵NH₄Cl (Cambridge Isotope Laboratories) as the sole carbon and nitrogen sources, respectively. The calbindin D_9k (P43G) NMR sample contained ∼1 mM protein, pH 6.0 (93% H₂O and 7% D₂O) and was fully calcium-loaded.

NtrC^r was prepared and purified as described previously,(71) except that in this case [U-¹H,1-¹³C]-d-glucose was used as the sole carbon source and bacterial growth was performed in ∼100% D₂O. The NtrC^r NMR sample contained ∼0.75 mM protein and 50 mM sodium phosphate, 0.02% azide, pH 6.75 (90% H₂O and 10% D₂O).

NMR Spectroscopy

NMR experiments were performed on Varian Unity Inova spectrometers operating at 600 and 800 MHz, equipped with a triple-resonance room temperature (600 MHz) or a cryogenically cooled (800 MHz) probehead.

Relaxation dispersion experiments on calbindin D_9k were recorded at 28 °C on a 600 MHz spectrometer with the experimental schemes A and B (Figure 1) as a series of 25 2D data sets with T_CP set to 80 ms and the constant-time (CT) carbon evolution period equal to 28 ms. The CPMG field strengths, ν_CPMG (ν_CPMG = 1/(4τ_c), where 2τ_c is the interval between the 180° proton pulses during the CPMG element(40)), were equal to 25, 50, 75, 100, 200, 325, 400, 500, 600, 800, 1000, 1200, 1400, 1600, 1800, 2150, 2200, 2300, and 2500 Hz with duplicate experiments recorded at 100, 400, 800, and 1600 Hz. For the experiment performed using scheme C (Figure 1), a series of 23 2D data sets was recorded with CPMG field strengths, ν_CPMG, equal to 25, 50, 75, 100, 125, 150, 200, 250, 300, 400, 500, 600, 675, 750, 800, 900, 950, and 1000 Hz with duplicate experiments recorded at 100, 200, 400, 800, and 1000 Hz. The ¹³C CW decoupling field was centered at 25 ppm and had a field strength, ω₁/2π, varying between 1.2 and 2.1 kHz, following the procedure described by Vallurupalli et al.(77) The ¹³C B₁ field was calibrated using the method described by Mulder and Akke(63) from data recorded on the same protein sample. The reference experiment was performed by omitting the CPMG block in the pulse scheme and repeated two and four times for schemes A/B and C, respectively. The CHD₂-detected ¹H-CPMG experiments were acquired with 111 (¹³C) × 512 (¹H) complex points, with maximum evolution times equal to 27.75 (¹³C) × 64 (¹H) ms. An interscan delay of 1.5 s was used with four scans per transient, giving rise to a net acquisition time of ∼25 min per 2D spectrum.

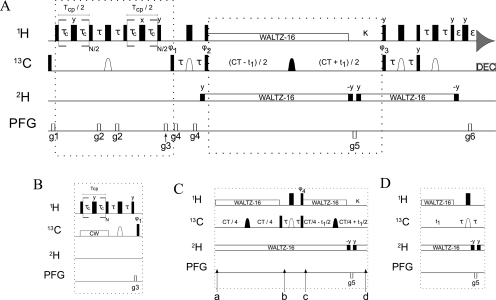
Figure 1.

Experimental schemes used to measure ¹H relaxation dispersion profiles of CHD₂ methyl groups.

Relaxation dispersion experiments on NtrC^r were recorded at 25 °C with the experimental scheme D (Figure 1) at two static magnetic fields, as a series of 55 (600 MHz) and 46 (800 MHz) 2D data sets, respectively, with T_CP set to 40 ms and the constant-time (CT) carbon evolution period equal to 28 ms. The CPMG field strengths, ν_CPMG, varied between 50 and 6000 Hz and included 18 (600 MHz) and 15 (800 MHz) duplicate points (see the Supporting Information for details, Table S1). The reference experiment was performed by omitting the CPMG block in the pulse scheme and was repeated four (600 MHz) or two (800 MHz) times. The CHD₂-detected ¹H-CPMG experiments were acquired with 111 (¹³C) × 512 (¹H) complex points and maximum evolution times equal to 27.75 (¹³C) × 64 (¹H) ms (600 MHz) or 140 (¹³C) × 640 (¹H) complex points and maximum evolution times equal to 28 (¹³C) × 64 (¹H) ms (800 MHz). An interscan delay of 1.5 s was used with 12 (600 MHz) or 4 (800 MHz) scans per transient, giving rise to a net acquisition time of 1.25 h (600 MHz) or 31.5 min (800 MHz) per 2D spectrum.

The heating of the protein sample due to the CPMG block in the pulse scheme was determined by comparison of the ¹H chemical shifts^78,79 between an experiment with and without the CPMG scheme and found to be 0.4 and 1.0 °C for calbindin D_9k and NtrC^r, respectively. The setting of the variable temperature (VT) unit was adjusted such that the “real” sample temperature was 28 °C for calbindin D_9k and 25 °C for NtrC^r. To ensure that the sample heating remains constant for each of the different experimental schemes and for different values of ν_CPMG, a period T_CP was added at the beginning of the interscan delay, d₁, such that the total number of 180° proton pulses was maintained.

Pulse Sequence

The experimental schemes for the sensitivity-enhanced ¹H-CPMG-CHD₂ experiment are shown in Figure 1. The core of the experiment is a CT-[¹H−¹³C]-HSQC pulse sequence to detect only the CHD₂ isotopomer as described earlier.(58) The CPMG part is implemented during the first INEPT period as a variable pulse spacing,^23,24 constant-time (CT) CPMG element,(40) either as relaxation-compensated variant(29) (rcCPMG; Figure 1, scheme A) or applied to the in-phase magnetization with ¹³C CW decoupling (cwCPMG; Figure 1, scheme B). Schemes C and D can be used to substitute for the conventional CT carbon evolution period. The individual schemes and their benefit for different experimental conditions and isotopically labeled protein samples are described in more detail in the Results and Discussion and in the Supporting Information.

Narrow (wide) filled bars indicate 90° (180°) RF pulses applied along the x-axis, unless otherwise indicated. The proton pulse train for heat-compensation at the beginning of the sequence (not shown in Figure 1) is performed 200 kHz off-resonance, and the ¹H carrier is moved to the water resonance (4.75 ppm) for weak (ω₁/2π = 30 Hz) continuous-wave (CW) irradiation to saturate the solvent water resonance for the remainder of the d₁ period. During the rest of the experiment, the ¹H carrier is centered in the middle of the methyl region (0.75 ppm), and proton pulses are applied with a field strength of ω₁/2π = 36.8 kHz. Rectangular ¹³C pulses are centered at 20 ppm and applied with ω₁/2π = 21.4 kHz. The shaped carbon pulses (open domes) have a REBURP profile(80) applied on resonance, with a peak RF field strength of ω₁/2π = 6.6 kHz and a pulse length of 1.0 ms (at 600 MHz), and thereby refocus only the methyl resonances (bandwidth ∼24 ppm). The other shaped carbon pulses (filled domes) have a REBURP profile (ω₁/2π = 19.0 kHz, 350 μs duration at 600 MHz) and are frequency shifted to 40 ppm, so as to cover all aliphatic carbon spins (bandwidth ∼67 ppm). The ¹³C CW field (scheme B) is centered at 25 ppm and applied with a varying strength, satisfying the relationship ν_CW = 2·k·ν_CPMG (where k is an integer number). Proton and deuterium decoupling are achieved by WALTZ-16,(81) using ω₁/2π = 7.0 and 0.7 kHz and the carrier positions at 0.75 and 4.75 ppm, respectively. Flanking 90° deuterium pulses are given at the same field strength and frequency. Values of the delays are τ = 1.98 ms, T_CP = constant-time CPMG relaxation period, τ_c = variable timing in the CPMG element, CT = 28.0 ms, ε = 0.4 ms, and d₁ = 1.5 s. The gradient strengths in G/cm (length in ms) are g₁ = 5.0 (0.5), g₂ = 3.0 (1.0), g₃ = 15.0 (1.0) and g₄ = 6.0 (0.3), g₅ = −27.15 (1.0), g₆ = 27.0 (0.25). All gradients are applied along the z-axis. The phase cycling is ϕ₁ = [x,−x], ϕ₂ = [x,x,−x,−x], ϕ₃ = [x], ϕ₄ = [y,−y], and ϕ_rec = [x,−x,x,−x].

Quadrature detection is obtained using the gradient sensitivity enhancement scheme:(82) the echo and antiecho signals are collected separately by inverting the sign of g₅ together with inversion of ϕ₃. The pulse sequences and parameter files can be obtained from the authors upon request.

Data Processing and Analysis

The data sets were processed with the NMRPipe/NMRDraw software package,(83) and peak intensities were extracted using the program Sparky.(84) The values of R_2, eff were calculated for each ν_CPMG value using the relationship:

where I(ν_CPMG) and I₀ are the intensities of the cross-peaks with and without the CPMG block, respectively, and T_CP is the constant-time CPMG relaxation period.

The data analysis and error estimation in the experimental data and fitted exchange parameters were performed as described earlier by Mulder et al.(28) Briefly, the uncertainty in the ratio of cross-peaks I(ν_CPMG)/I₀ was estimated from the rmsd in the intensities of the duplicate measurements according to the definition of pooled relative standard deviation, σ_r = (∑(ΔI/I_avg)²/2N)^1/2.^28,85

The exchange parameters can be obtained from fitting the relaxation dispersion profiles (R_2, eff as a function of ν_CPMG) to approximate analytical expressions for chemical exchange (see below) or by numerically solving the Bloch−McConnell equations.(86) The dispersion profiles for NtrC^r obtained at two B₀ fields were fitted together to three different models assuming (i) no exchange, (ii) a two-site fast-exchange process,(87) and (iii) a general two-site exchange process (described by Carver and Richardson and Jen, CRJ equation;^88,89 see eq 3 of Millet et al.(90)). In model 1, the experimental data points are fitted to flat lines with R_2, eff (ν_CPMG→∞) at each B₀ field as adjustable parameters. In the second model, there are two additional parameters, Φ_ex = p_Ap_Bδω² and τ_ex, included to describe the experimental data. In the case where the exchange is not fast (model 3, CRJ equation), it is often possible to separate the product Φ_ex into its components, and the five fitting parameters in this case are R_2, eff (ν_CPMG→∞) at the two B₀ fields, p_A, δω, and τ_ex. The increasing complexity of the functions will generally improve the fit, and, therefore, F-statistics were used to determine whether the description by a more complicated model was justified at the 99.9% confidence interval. The uncertainties in the fitting parameters were determined from the covariance matrix obtained by inverting the Hessian matrix.(91)

Results and Discussion

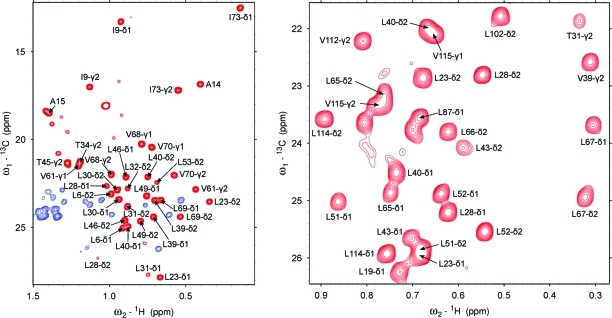
We have previously determined the isotopomer incorporation and residual protonation of methyl-containing amino acids for protein samples grown on U-[¹H, ¹³C]-d-glucose in ∼100% D₂O.(58) The desired CHD₂ isotopomer shows favorable incorporation levels with the lowest value around 30% for Met-ε and between 41% and 56% for all other methyl-containing amino acids. Because the incorporation of the CH₃ isotopomer is very low (<8%) for all amino acids, and signals from the CH₂D are easily suppressed in our experiment, it is possible to obtain a clean, high-resolution CHD₂ spectrum (see Figure 2).

Figure 2.

Two-dimensional ¹H−¹³C spectra recorded at 600 MHz using the ¹H-CPMG-CHD₂ experiment (scheme A, without the CPMG block). The complete methyl region of calbindin D_9k is shown in the left panel (blue signals have an opposite sign and originate from CHD methylene groups), while for NtrC^r an inset of the Leu region is shown (right panel).

Validation of the Methodology for a System That Does Not Display Microsecond−Millisecond Time Scale Dynamics

The underlying assumption in CPMG relaxation dispersion experiments is that, in the absence of exchange, the obtained dispersion profiles are flat (i.e., the signal intensity does not depend on the CPMG pulse repetition rate). In the case of calbindin D_9k, previous studies have shown that there is little or no chemical exchange present,⁶¹⁻⁶⁴ and, therefore, flat curves are expected for all residues.

In Figure 3, representative curves are shown for Ala, Ile-γ2, Met, and Val methyl groups (recorded with scheme A, Figure 1) for which we indeed observe flat “profiles”. Following Tugarinov et al.,(43) the pairwise root-mean-square deviation is used as a measure of how flat the curves are and is defined as

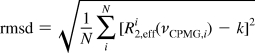where R_2, effⁱ(ν_CPMG, i) is the effective transverse relaxation rate, k is the best fit horizontal line to the experimental curve, and N is the number of experimental data points. For the above-mentioned residue types in calbindin D_9k, we obtain an average rmsd of 0.20 ± 0.04 s⁻¹, with a maximum of 0.27 s⁻¹.

Figure 3.

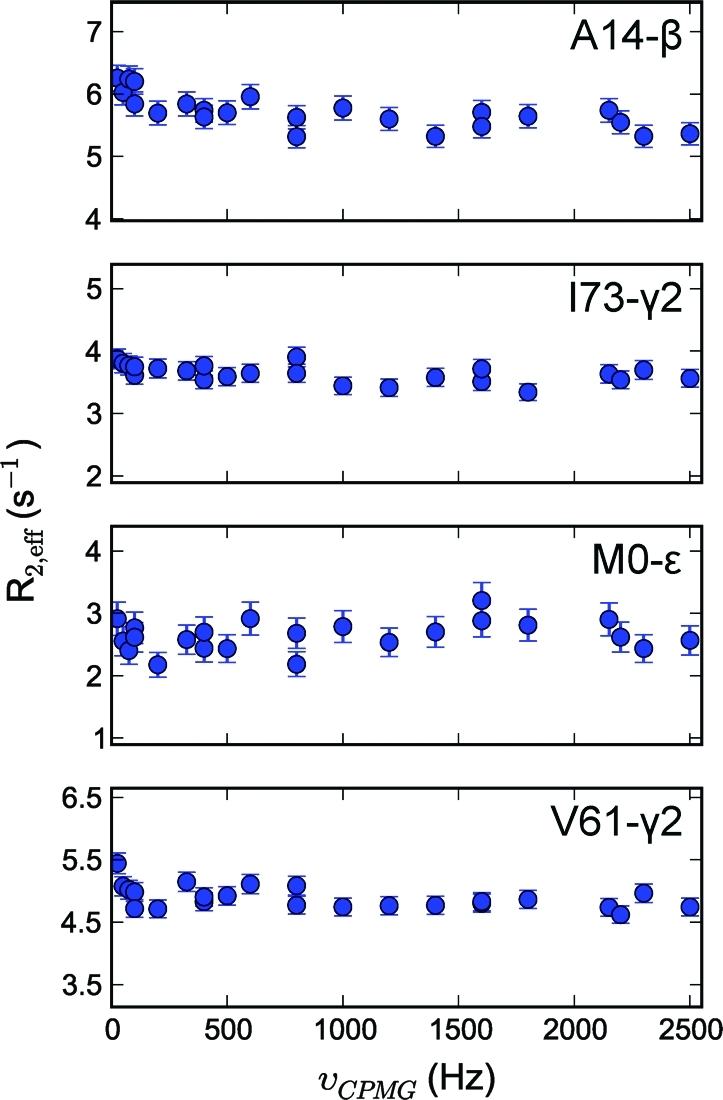
Representative methyl transverse ¹H relaxation dispersion profiles for Ala, Ile-γ2, Met, and Val methyl groups recorded at 600 MHz for calbindin D_9k.

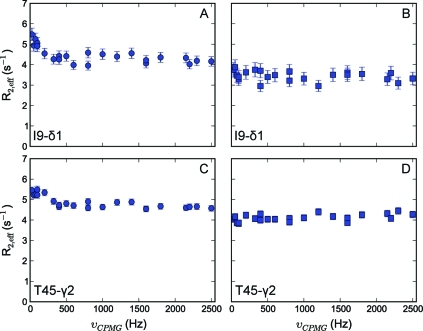
It is, however, anticipated that methyl groups will display artifacts depending on the protonation level of their neighboring carbon atom. We have shown earlier that the deuteration level of neighboring carbons in the side chains ranges between 90% and 95% for Ala-α, Leu-γ, Val-β, and Ile-β, but is significantly lower for Ile-γ1 and Thr-β positions (66% and 81%, respectively).(58) Of note, because of the high level of deuteration, the occurrence of a CH₂ methylene group is ≤5% and can, therefore, be neglected. Indeed, in the case of Ile-δ1 and Thr (Figure 4, panels A and C), spurious dispersion profiles are observed, because the positions adjacent to the methyl groups are protonated to a significant degree, and ¹H homonuclear scalar couplings affect the signal intensity due to Hartmann−Hahn mixing, to a degree that depends on the CPMG pulse repetition rate.(26) These artifacts can easily be suppressed, by selecting only the magnetization originating from methyl groups for which the neighboring carbon atom is fully deuterated (Figure 1, scheme C). This selection is achieved by dividing the CT period in two parts, separated by an INEPT period (see the Supporting Information for a detailed description).

Figure 4.

Representative methyl transverse ¹H relaxation dispersion profiles for Ile-δ1 and Thr methyl groups for calbindin D_9k recorded at 600 MHz. Panels A and C show spurious dispersion profiles originating from homonuclear scalar coupling; in panels B and D, the source of this artifact has been removed in the NMR experiment.

It is obvious from Figure 4 that significant artifacts arise from the protonation at the γ1-position of Ile and β-position of Thr residues, but also that these can be purged by choosing experimental scheme C (Figure 1). Using this pulse scheme, flat lines are obtained for Ile-δ1 and Thr methyl groups as well (Figure 4, panels B and D), with an average rmsd value of 0.22 ± 0.03 s⁻¹ for the two Ile-δ1 and one Thr of calbindin D_9k considered here. Of note, as expected, the background R_2, eff obtained using scheme C is also lower in this case because the ¹H−¹H dipolar interaction with the neighboring nuclei is removed.^33,34 Finally, it should be noted that in scheme C ∼14 ms is needed to evolve the J_CC coupling, which cannot be used at the same time for chemical shift encoding. Therefore, the resolution of the resulting 2D spectra is a factor of 2 lower than for scheme A. Although one could increase the period for chemical shift evolution from 1/(2J_CC) to 3/(2J_CC) to obtain a higher resolution, at the cost of signal intensity, scheme C is only advantageous for Ile-δ1 and Thr methyl groups, with the proposed labeling.

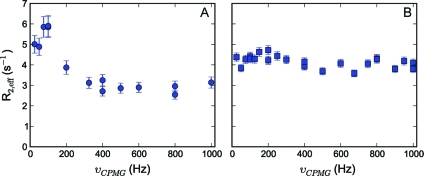
Another type of artifact was observed for several Leu methyl groups, where dispersion profiles showed enhanced R_2, eff values at low pulsing rates, as shown in Figure 5, panel A. Because the deuteration level of the Leu-γ position is ∼92%, it is unlikely that the spurious profiles originate from ¹H homonuclear scalar coupling. Furthermore, if ¹H−¹H coupling would be the source of the spurious profiles, then one would expect this to be similar for all Leu residues (and for both the δ1 and the δ2 methyl groups), which is not the case. Moreover, the profiles remain identical when scheme C is used to record the CPMG relaxation dispersion experiment (see the Supporting Information for all profiles, Figure S1). One potential source of deviation might be strong ¹³C scalar coupling. It is well-known that the difference between the downfield Leu-δ1/δ2 and the Leu-γ chemical shifts can be rather small (25.7 ± 1.2 versus 26.7 ± 1.3 ppm, respectively),(92) and there seems to be a (slight) correlation between this difference and how pronounced the artifacts are. Indeed, “strong coupling effects during X-pulse CPMG experiments on heteronuclear ABX spin systems” have been observed before in the case of ribose units of RNA.(77) Vallurupalli et al. showed that X-magnetization is lost during the CPMG element in the situation where spins A and B are strongly coupled (in our case: X = ¹H^M, A = Leu-C^δ1/C^δ2, and B = Leu-C^γ) and demonstrated that these artifacts can be removed by recording a CPMG relaxation experiment on in-phase proton magnetization, by applying a ¹³C continuous wave (CW) decoupling field during the CPMG element.(77)

Figure 5.

Methyl transverse ¹H relaxation dispersion profile, representative for many downfield resonating Leu-δ1/δ2 methyl groups in the case of strong ¹³C scalar coupling in the ABX spin system (see text). Panel A shows the spurious dispersion profile obtained for L40-δ1 of calbindin D_9k; in panel B, the source of this artifact has been removed in the NMR experiment.

We implemented this approach (Figure 1, scheme B), and in several cases the artifacts indeed disappeared and a flat line was obtained (Figure 5, panel B; rmsd = 0.28 s⁻¹). However, the minimal condition ν_CW = 2·k·ν_CPMG limits the maximum ν_CPMG values to ∼2.5 kHz because the maximum attainable ¹³C CW field strength for a period of 40−80 ms is around 5 kHz. In our case, the maximum value for ν_CPMG was equal to 1 kHz, and the ¹³C CW field strength determined according to the relationship above was between 1.2 and 2.1 kHz, and, therefore, complete decoupling will be achieved only for signals close to the carrier position. The offset between the ¹³C carrier position and L40-δ1 is small (∼0.8 ppm), and in such cases the strong ¹³C scalar coupling artifacts will be removed because even for the lowest ¹³C CW field the δ1-carbon is completely decoupled (Figure 5). We observe that especially at lower CPMG pulse rates and depending on the offset not all artifacts are removed and, in fact, sometimes even appear for residue types in situations for which none are present in the rcCPMG version (see the Supporting Information, Figure S1). Therefore, in protein applications the suppression of strong ¹³C scalar coupling artifacts using the above-mentioned pulse scheme, although possible, is rather inefficient. The use of [U-¹H,1-¹³C]-d-glucose as precursor provides an alternative, and fully effective, procedure for the elimination of strong ¹³C scalar coupling in Leu residues (see below).

The aim of this study was to use all available methyl-containing amino acids to record CPMG relaxation dispersion profiles, which requires uniform isotope labeling. Such labeling scheme potentially introduces artifacts, but we have demonstrated above that reliable profiles can be recorded for all methyl groups if an appropriate pulse scheme is employed. Alternatively, one could specifically introduce CHD₂ isotopomers in an otherwise deuterated background using specific precursors. Because of such a labeling scheme, CPMG relaxation dispersion profiles are guaranteed artifact free, but at the expense of a complete amino acid coverage. In a very recent NMR study of proteasome gating, Kay and co-workers have undertaken the latter approach and also considered the potential of CHD₂ methyl groups as probes of millisecond time scale dynamics.(65) In their study, CHD₂ probes were specifically introduced for methionine residues, which, due to their significant degree of fast (ps) side chain dynamics, can still give sensitive spectra, and for which the residue-specific assignment was obtained from a combination of NMR spectroscopy and mutagenesis.(93) Indeed, when dealing with very high molecular weight systems (the α7 subunit of the 20S core particle from T. acidiphilium weighs 180 kDa), it is necessary to introduce specific labels without isotope dilution into an otherwise strictly deuterated background. However, for many other smaller (<100 kDa) proteins or their assemblies, a near-complete assignment of methyl groups can be obtained cost-effectively using a partial deuteration scheme, as we have recently demonstrated.(58) Importantly, these samples, prepared using protonated glucose in D₂O, together with appropriate ¹H CPMG relaxation dispersion experiments, can be used to quantify microsecond−millisecond time scale motion for all methyl-containing amino acids. In addition, the same samples can also be used for a comprehensive analysis of fast (ps−ns) time scale dynamics.(58)

Application to Activation of the Signaling Protein NtrC^r

Given the fact that flat ¹H CPMG relaxation dispersion profiles can be obtained for all methyl groups in the absence of exchange, we now focus our attention on a system that displays functional dynamics on the microsecond time scale. The Nitrogen Regulatory Protein C (NtrC) is a bacterial enhancer-binding protein that activates transcription upon phosphorylation of residue D54 in its N-terminal, regulatory domain (NtrC^r). Kern and co-workers have demonstrated that the switch from an inactive to active species involves an extensive change in structure,(72) and that the mechanism of activation is best described by a population-shift model, where phosphorylation shifts the pre-existing equilibrium from inactive toward active conformations.(73) The exchange rate between these two conformations was determined on the basis of ¹⁵N CPMG data and the exchange-free transverse relaxation rates obtained from separate measurements and was shown to be 13580 ± 850 s⁻¹.^73,75 Moreover, the population of active NtrC^r was estimated to be 14 ± 2% in the unphosphorylated form of the protein, based on comparison of chemical shifts of the WT sample with respect to those of the fully active and inactive species.(75)

Relevant to the current study, NtrC^r contains 57 methyl-containing amino acids (15 Ala, 8 Ile, 14 Leu, 5 Met, 5 Thr, and 10 Val residues) supplying 89 potential probes for methyl relaxation dispersion spectroscopy. Initial investigations (data not shown) of methyl group dynamics using ¹³C T_1ρ measurements(92) have revealed that leucine residues, in particular, were subject to microsecond time scale dynamics. Ideally, one would like to obtain dispersion profiles for all different methyl-containing amino acids from a single experiment, but, as stated earlier, strong ¹³C scalar coupling in Leu residues remains problematic. As mentioned above, relaxation dispersion profiles for Leu methyl groups are of great interest in this system, and, therefore, it would be useful to remove the strong ¹³C scalar coupling phenomenon using a biochemical approach. As demonstrated earlier by Lundström et al.,(94)¹³C enrichment of the methyl groups, while the neighboring carbon atom is of the ¹²C variety, can be accomplished by the use of [U-¹H,1-¹³C]-d-glucose as sole carbon source. The ¹³C enrichment of the methyl groups using [U-¹H,1-¹³C]-d-glucose is a factor of 2 lower as compared to when U-[¹H, ¹³C]-d-glucose is used as precursor, but is still sufficiently high (between 35% for Met and 44% for Ala, Ile-γ2, Leu, and Val methyl groups, respectively).(94) For Ile-δ1 and Thr methyl groups, the ¹³C incorporation drops quite dramatically to ∼13%, and in only 25% of the cases are the Ile-δ1 and Thr methyl groups directly attached to a ¹³C spin(94) such that selection against protonation on the neighboring carbon could be performed. The resulting signal-to-noise ratio for these correlations is, therefore, too low, and these were not included in the analysis. It should be emphasized here that using [U-¹H,1-¹³C]-d-glucose we can reliably use 28 Leu methyl groups at the expense of 5 Thr and 8 Ile-δ1 probes. In addition, for Thr and Ile-δ1, one needs to resort to a less sensitive variant (scheme C, Figure 1) to obtain artifact free profiles, and this is simultaneously circumvented.

In the NtrC^r sample prepared using [U-¹H,1-¹³C]-d-glucose as precursor molecule, 76 methyl groups were labeled to a high extent, and 52 assigned and nonoverlapping cross-peaks were observed in the 2D ¹H−¹³C spectra and could be used in the analysis (Figure 2, right panel). Figure 6 shows representative relaxation dispersion profiles for some of the methyl groups in NtrC^r (see the Supporting Information for all profiles, Figure S2). Initially, the experimental data acquired at 600 and 800 MHz were fitted simultaneously on a per-residue basis to the appropriate model without restricting any of the fitting parameters (see the Supporting Information, Table S2). In total, for 31 residues, no significant exchange contribution to the methyl proton line width was observed (model 1), as indicated by the flat profiles. Furthermore, it was determined from F-statistic tests that 18 residues are best fitted using the fast-exchange equation (model 2), while the remaining three residues fall in the intermediate exchange regime and are, therefore, best fitted by the general two-site exchange (CRJ) equation (model 3).

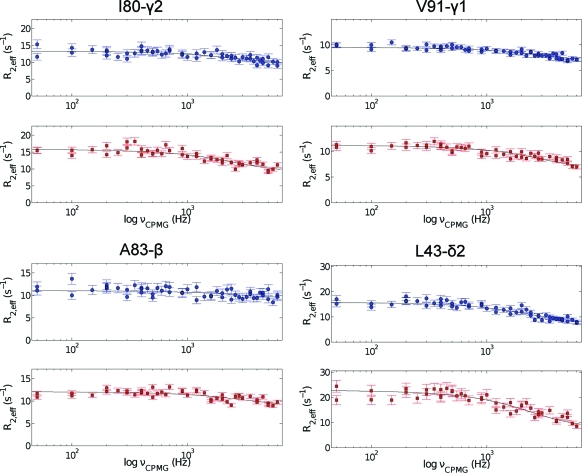
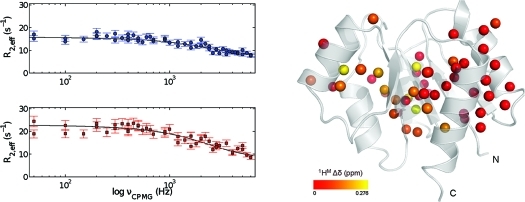
Figure 6.

Representative methyl transverse ¹H relaxation dispersion profiles for Ala, Val, Ile-γ2, and Leu methyl groups in NtrC^r recorded at 600 (upper panel) and 800 (lower panel) MHz. The solid lines correspond to the best curves, obtained from fitting the experimental data from both fields simultaneously to the appropriate two-site exchange equation.

In the case of model 2 (fast-exchange), only the product Φ_ex = p_Ap_Bδω² and τ_ex can be obtained from the analysis. In cases where the exchange is not fast (model 3), it is often possible to separate Φ_ex into its individual components (i.e., populations and chemical shift difference). In our case, however, the three residues that were best fitted to model 3 show very low values for the population of the minor state, p_B < 0.3%, and unrealistically large values for the chemical shift difference between the two states (|Δδ | between 1.8 and 3.2 ppm). Through independent experiments, Gardino et al.(75) reliably determined the population p_B to 14%, and we therefore used this value for the population of the minor state. By restricting the population to this value, the three residues initially following model 3 are now accurately described by the fast-exchange model. Of note, the fitting parameters of the 18 probes described by model 2 did not change by assuming a value for p_B, but the chemical shift difference between the two states can now be calculated according to

The dispersion profiles of all residues showing an exchange contribution are now accurately described by the fast-exchange model, as evidenced by the reduced χ², and the extracted exchange parameters are given in Table 1 (first row for every entry). Only for I55-γ2 the value for χ_red² increased significantly to 2.5 from an already rather high value of 1.6 in the free fitting procedure. The origin of the poor fit for this residue is not understood at this stage, and it is, therefore, excluded from further analysis.

Table 1. Relaxation Dispersion Parameters for Methyl Groups in NtrC^r at 25 °C^a,b.

methyl group	Δδc,d (ppm)	τex (μs)	R2,eff (νCPMG → ∞)d,e (s−1)		Rexd,e (s−1)		χred2d,f
V9-γ1	0.209 ± 0.010	76.3 ± 5.7	11.67 ± 0.22	11.44 ± 0.32	5.69	10.13	1.48
	0.231 ± 0.003	64.7 ± 1.9	11.31 ± 0.17	10.80 ± 0.18	5.92	10.53	1.51
V18-γ1	0.094 ± 0.057	47.7 ± 37.7	5.85 ± 0.35	5.24 ± 0.62	0.72	1.28	0.86
	0.076 ± 0.009	64.7 ± 1.9	5.95 ± 0.12	5.42 ± 0.18	0.63	1.12	0.85
L19-δ2	0.114 ± 0.033	62.3 ± 25.6	7.41 ± 0.29	7.01 ± 0.52	1.38	2.45	0.89
	0.111 ± 0.008	64.7 ± 1.9	7.44 ± 0.14	7.05 ± 0.24	1.36	2.42	0.88
L40-δ1	0.971 ± 47.384	4.0 ± 195.6	−0.02 ± 315.32	−6.00 ± 560.80	6.46	11.49	0.99
	0.071 ± 0.009	64.7 ± 1.9	5.90 ± 0.11	4.55 ± 0.18	0.55	0.99	1.02
L43-δ1	0.193 ± 0.016	70.8 ± 9.4	7.67 ± 0.26	7.01 ± 0.45	4.50	8.00	1.14
	0.204 ± 0.004	64.7 ± 1.9	7.51 ± 0.14	6.73 ± 0.23	4.60	8.18	1.14
L43-δ2	0.276 ± 0.019	65.0 ± 7.1	7.34 ± 0.41	7.83 ± 0.72	8.45	15.02	1.21
	0.277 ± 0.005	64.7 ± 1.9	7.33 ± 0.20	7.81 ± 0.35	8.46	15.04	1.20
V50-γ2	0.148 ± 0.021	68.3 ± 15.1	7.66 ± 0.25	5.95 ± 0.45	2.55	4.53	1.36
	0.153 ± 0.005	64.7 ± 1.9	7.60 ± 0.13	5.85 ± 0.20	2.59	4.61	1.34
I55-γ2	0.437 ± 0.062	36.1 ± 6.2	10.71 ± 1.42	8.36 ± 2.52	11.78	20.95	2.52
	0.285 ± 0.006	64.7 ± 1.9	13.97 ± 0.27	14.19 ± 0.41	8.95	15.92	2.68
L66-δ2g	0.150 ± 0.016	71.1 ± 12.1	7.07 ± 0.21	6.85 ± 0.36	2.72	4.84	0.96
	0.159 ± 0.004	64.7 ± 1.9	6.97 ± 0.12	6.67 ± 0.18	2.79	4.96	0.95
L76-δ1	0.083 ± 0.030	79.2 ± 43.4	5.87 ± 0.23	5.18 ± 0.43	0.93	1.65	0.88
	0.094 ± 0.010	64.7 ± 1.9	5.79 ± 0.15	5.04 ± 0.28	0.98	1.75	0.87
L76-δ2	0.064 ± 0.020	89.9 ± 42.8	6.67 ± 0.16	4.69 ± 0.24	0.62	1.11	0.86
	0.078 ± 0.009	64.7 ± 1.9	6.59 ± 0.14	4.54 ± 0.19	0.68	1.20	0.86
V78-γ1	0.092 ± 0.019	75.7 ± 23.9	8.03 ± 0.15	6.96 ± 0.28	1.08	1.93	1.07
	0.101 ± 0.005	64.7 ± 1.9	7.96 ± 0.08	6.83 ± 0.16	1.13	2.02	1.06
V78-γ2	0.108 ± 0.063	48.3 ± 37.0	8.68 ± 0.45	8.06 ± 0.79	0.96	1.70	0.93
	0.087 ± 0.009	64.7 ± 1.9	8.81 ± 0.14	8.30 ± 0.22	0.84	1.50	0.92
I79-γ2	0.116 ± 0.021	90.6 ± 26.8	9.36 ± 0.25	8.65 ± 0.44	2.08	3.70	0.75
	0.142 ± 0.008	64.7 ± 1.9	9.10 ± 0.19	8.18 ± 0.31	2.24	3.98	0.76
I80-γ2	0.190 ± 0.021	61.6 ± 10.1	9.55 ± 0.32	9.10 ± 0.54	3.78	6.73	1.23
	0.184 ± 0.005	64.7 ± 1.9	9.63 ± 0.17	9.25 ± 0.23	3.73	6.63	1.22
A83-β	0.139 ± 0.033	52.7 ± 17.2	9.32 ± 0.34	8.98 ± 0.56	1.74	3.09	1.38
	0.120 ± 0.005	64.7 ± 1.9	9.48 ± 0.15	9.28 ± 0.17	1.60	2.85	1.37
L87-δ1g	0.232 ± 0.138	27.1 ± 17.8	4.30 ± 1.36	3.07 ± 2.42	2.49	4.43	0.81
	0.117 ± 0.005	64.7 ± 1.9	5.37 ± 0.11	4.98 ± 0.17	1.51	2.68	0.85
A90-β	0.283 ± 0.041	49.4 ± 9.9	9.33 ± 0.75	15.33 ± 1.39	6.76	12.02	1.25
	0.235 ± 0.006	64.7 ± 1.9	10.15 ± 0.21	16.79 ± 0.50	6.11	10.87	1.26
V91-γ1	0.179 ± 0.028	49.7 ± 10.6	6.78 ± 0.32	6.35 ± 0.57	2.72	4.84	1.03
	0.149 ± 0.004	64.7 ± 1.9	7.11 ± 0.08	6.93 ± 0.15	2.46	4.38	1.04
A93-β	0.141 ± 0.100	34.5 ± 28.7	8.24 ± 0.73	7.93 ± 1.29	1.18	2.09	1.59
	0.087 ± 0.007	64.7 ± 1.9	8.62 ± 0.12	8.59 ± 0.17	0.84	1.49	1.58
L102-δ2	1.010 ± 72.520	3.9 ± 278.3	0.89 ± 485.4	−5.20 ± 863.3	6.76	12.03	0.94
	0.071 ± 0.008	64.7 ± 1.9	7.11 ± 0.10	5.86 ± 0.17	0.56	0.99	0.98
L114-δ1	0.202 ± 0.059	38.1 ± 14.0	4.14 ± 0.64	1.99 ± 1.14	2.65	4.72	1.20
	0.138 ± 0.005	64.7 ± 1.9	4.80 ± 0.10	3.16 ± 0.17	2.10	3.73	1.23

^aExchange parameters are obtained by fitting the dispersion profiles measured at 600 and 800 MHz simultaneously using p_B = 14%.

^bMethyl groups are stereospecifically assigned.

^cΔδ was calculated assuming the above-mentioned values for the populations. For other populations (p_C and p_D), the chemical shift difference can be calculated according to Δδ_CD = Δδ_AB((p_Ap_B)/(p_Cp_D))^1/2.

^dThe numbers in the second row indicate values obtained after fitting the profiles again, using k_ex = 15 458 s⁻¹ as determined from the global fit.

^eFirst column ω₀/2π = 600 MHz, and second column ω₀/2π = 800 MHz.

^fThe reduced χ² is calculated using χ_red² = χ²/(N − m), where N is the number of experimental data points and m is the number of fitting parameters.

^gResonances of δ1/δ2 methyl group overlap, assuming that only the listed probe exhibits an exchange contribution.

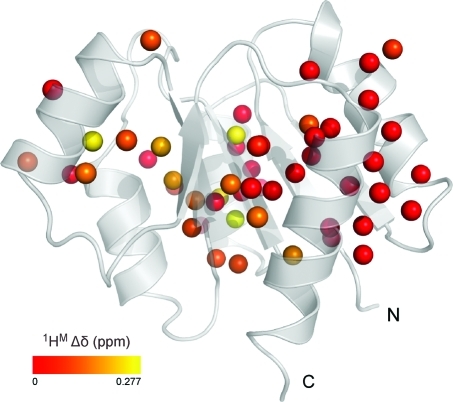
The values obtained for the exchange lifetime are rather similar (see Table 1, first row for each probe), suggesting an exchange process between two conformations via a single, cooperative process. A global analysis of the data for all methyl groups in Table 1 (except I55-γ2) was performed, and a value of 64.7 ± 1.9 μs was obtained for the exchange lifetime. The average χ_red² did not change when this global exchange lifetime was used to describe the dispersion profiles and thus supports the hypothesis of a single, cooperative exchange process. The results of the global analysis of all CPMG data, using p_B = 14% and τ_ex = 64.7 μs, are given in Table 1 (second row for every entry). The exchange rate obtained from the ¹H CPMG data, k_ex = 15 458 ± 452 s⁻¹, is in excellent agreement with the value of 13 580 ± 850 s⁻¹ obtained earlier from a suite of ¹⁵N relaxation data.(75) Notwithstanding the agreement between the exchange parameters obtained from the ¹⁵N and ¹H CPMG relaxation dispersion data, there is an obvious benefit of using the latter approach. In practice, due to the limited attainable ¹⁵N CPMG field strength, it is only possible to map about one-sixth of the chemical exchange spectral density function, when compared to ¹H CPMG relaxation dispersion NMR spectroscopy. Therefore, in previous studies,^74,75 it was necessary to extract the exchange parameters from fitting the initial part of the ¹⁵N CPMG dispersion profile, and the value of the exchange free component (i.e., R_2, 0), obtained from a separate experiment. On the contrary, complete microsecond time scale dynamics dispersion profiles are now obtained from a single experiment using the ¹H CPMG relaxation experiment (Figure 6). The chemical shift differences between the two exchanging states, determined from the group fit with p_B = 14%, are visualized on the three-dimensional structure of NtrC^r in Figure 7. Indeed, all methyl groups identified to experience a global dynamic process on a 15 000 per second time scale map to the interface between secondary structure elements that were previously identified to comprise the molecular switch.

Figure 7.

Cartoon representation of unphosphorylated, inactive state of NtrC^r. The spheres represent the carbon atoms of all available methyl group probes, and these are color-coded from red to yellow according to the value of Δδ. The structural representation was generated in PyMol.(95)

In conclusion, we have shown how reliable ¹H CPMG relaxation dispersion profiles up to 6 kHz field can be obtained for all methyl groups in protein samples grown on U-[¹H, ¹³C]-d-glucose in D₂O. A relaxation compensated ¹H CPMG experiment is presented for CHD₂ methyl groups and yields very good results for Ala, Ile-γ2, Met, and Val methyl groups. Residual protonation in the case of Ile-δ1 and Thr methyl groups leads to artifacts arising from ¹H homonuclear scalar coupling, but these effects can be easily eliminated. Leu residues for which the methyl carbon is strongly scalar coupled with the adjacent carbon spin remain problematic, and, even though the use of a special pulse scheme can avoid these artifacts, this only works over a limited bandwidth, making the approach nonoptimal for those methyl groups in proteins. To resolve this issue, we favor an approach where [U-¹H,1-¹³C]-d-glucose is used as carbon source, thereby eliminating strong ¹³C scalar couplings in Leu residues altogether.

The application to the N-terminal receiver domain of the Nitrogen Regulatory Protein C (NtrC^r) demonstrates that the experiment can be used to characterize exchange processes in the microsecond time scale, because high effective field strengths can be attained by using ¹H CPMG pulse trains. The fact that methyl groups, which exhibit narrow lines and high sensitivity, are used as probes to detect dynamics suggests a wide range of applications, including higher molecular weight systems, as well as temperature-dependent studies to characterize the thermodynamics of enzyme dynamics.

Supporting Information Available

A more detailed description of experimental scheme C, one figure showing all ¹H CPMG relaxation dispersion profiles of calbindin D_9k, one figure showing the ¹H CPMG relaxation dispersion profiles (at 600 and 800 MHz) for all methyl groups in NtrC^r showing exchange, one table with the effective field strengths used in the ¹H CPMG relaxation dispersion experiments on NtrC^r, and one table listing the exchange parameters obtained from fitting the NtrC^r data on both fields on a per-residue basis. This material is available free of charge via the Internet at http://pubs.acs.org.