Abstract
Currently, Granger-Geweke causality models have been widely applied to investigate the dynamic direction relationships among brain regions. In a previous study, we have found that the right hand finger-tapping task can produce relatively reliable brain response. As an extension of our previous study, we developed an algorithm based on the classical Granger-Geweke causality model to further investigate the effective connectivity of three brain regions (left primary motor cortex (M1), supplementary motor area (SMA) and right cerebellum) that showed the most robust brain activations. Our computational results not only confirm the strong linear feedback among SMA, M1 and right cerebellum, but also demonstrate that M1 is the hub of these three regions indicated by the anatomy research. Moreover, the model predicts the high intermediate node density existing in the area between SMA and M1, which will stimulate the imaging experimentalists to carry out new experiments to validate this postulation.
Keywords: Granger-Geweke causality model, time series, Computational Neuroscience, fMRI, finger-tapping, hand movement, Math modeling
Introduction
Recently, effective connectivity methods have been widely applied on the functional Magnetic Resonance Imaging (fMRI) data set to investigate the dynamic directional relationships among brain regions [1–5]. In particular, in generating the testable hypothesis regarding the function of human brain networks, directional information obtained from Granger-Geweke causality model [6–12] has played a pivotal role. The Granger-Geweke causality model[7, 13, 14], which is a well-developed statistical measure based on the concept of time series forecasting [5, 6, 11, 15–18], has been proposed for multivariate time series analysis to investigate the linear causal relationships among a set of univariate time series variables. For instance, Lin et al.[11] and Chen et al.[6] employed Granger–Geweke Causality model to investigate the interictal spike propagation and the effective connectivity of supplementary motor areas, respectively.
In a previous fMRI study, we [19] investigated the test-retest reliability of electroacupuncture stimulation, a mode of sensory stimulation and finger-tapping task. We found that compared with electroacupuncture stimulation, finger-tapping task can generate significant and reliable fMRI signal increases across different experimental sessions. Thus, in this study, we propose to reanalyze the finger-tapping data set (six subjects each repeated in 6 identical experimental sessions) using Granger-Geweke causality model to elucidate the effective connectivity among the key regions involved in the finger tapping. These three regions are left primary motor area (M1), medial supplementary motor area (SMA) and right cerebellum. Several reasons motivated selection of the data sets. First, right hand finger tapping task can produce robust and reliable fMRI signal increase; secondly, the brain regions involved in finger-tapping and their interaction are relatively clear.
The fMRI technology provides different types of time series for brain research, either stationary or non-stationary time series, but the classical Granger–Geweke Causality model can only process the stationary time series. For this reason, the aim of this research is developing a general algorithm developed from the Granger–Geweke Causality model to analyze the various types of fMRI time series us, such as our previous experimental data [19]. This algorithm is briefly described as follows. First, since fMRI will provide us a stationary or nonstationary time series, the augmented Dickey-Fuller (ADF) unit root test [20–22] will be implemented to test the stationarity of raw data. If the data are nonstationary, the plot of autocorrelation function will be applied to check the patterns and choose an appropriate smoothing technique to transform the raw data to stationary data. Next, the approximation to the critical values of Schwarz's Bayesian information criterion (SBIC) is computed by ARFIT algorithm [23] to determine the order of auto-regressive equation of the Granger–Geweke Causality model. Consequently, an time series autoregressive model with appropriate order will be developed to fit smoothed fMRI data. Lastly, the confidence intervals will be constructed for the measures of feedback. In the study, the results of the model not only agree with our previous experimental findings[19] that there are strong correlations among SMA, M1 and cerebellum, but also match the observations of the anatomy[24] that both SMA and cerebellum project to M1.
Materials and Methods
Experimental material and methods
In the present study, we reanalyzed the data from a previous study (experimental details described in the original paper). In summary, 6 healthy right handed subjects were included in this study. All experiments were conducted with the written consent of each subject and approved by the Massachusetts General Hospital’s Institutional Review Board
Experimental procedures
Each subject participated in 6 identical fMRI scanning sessions. Sessions 1 and 2 were separated by 20–30 minutes. Sessions 2 and 3 were separated by 3–6 days. After Session 3, the interval between subsequent sessions was 7–21 days. The block design was applied. The fMRI scan started with 30s baseline, four 30s blocks of stimulation (ON, right finger-tapping), were separated by four rest periods (OFF) of 30s, 60s, 30s and 30s respectively.
fMRI data acquisition and analysis
All brain imaging was performed with a 3-axis gradient head coil in a 3 Tesla Siemens MRI System (Erlagen, Germany) equipped for echo planar imaging. After automated scout and shimming procedures, functional MR images were acquired using gradient echo T2*-weighted sequence with TR 2000 ms, TE 40 msec and a flip angle of 90 degrees. Thirty slices (4 mm thick, 1 mm skip) oriented parallel to the AC-PC plane were collected to provide whole brain coverage. A high resolution 3D MPRAGE sequence was also collected. Pre-processing and statistical analysis were performed using SPM2 software (Wellcome Department of Cognitive Neurology). Pre-processing began with motion correction. All functional runs were realigned to the first volume acquired in the scan session. We set a movement threshold of 2mm within a scan to eliminate subjects with excessive head movement. However, none of the subjects had head movements that exceeded this threshold. Thus, all data were used for this analysis. All functional runs were normalized to MNI stereotactic space and spatially smoothed with an 8mm Gaussian kernel. A separate general linear model (GLM) for each session was specified across each subject with regressors for the difference from baseline for each of the four conditions. Global signal scaling was applied. Low-frequency noise was removed with a high-pass filter applied with default values to the fMRI time series at each voxel. For each individual session, a threshold of p<0.005 uncorrected with 10 contiguous voxels was used for finger-tapping; then for each predefined ROI, left M1, SMA and right cerebellum, the average time courses of 3mm sphere around the peak of the three regions were extracted for Granger causality analysis.
Mathematical model
Granger-Geweke Causality Model
In this study, the Granger–Geweke Causality model is employed as the major tool to analyze the fMRI imaging data and to reveal the relationships among those brain regions of interest. Consider two zero-mean vector time-series X and Y. The time-indexed observations are denoted as xt and yt, where t = 1,…,n is the time index. X, Y can be modeled as autoregressive (AR) processes of order p as
| (1) |
| (2) |
| (3) |
| (4) |
where a1i, b1i, a2i, b2i, c2i, d2i are coefficients of AR models, and u1t, v1t, u2t, v2t are the zero-mean residuals. Their variances Σ1, T1, Σ2, T2, respectively. Let U1n×k, V1n×l, U2n×k,V2n×lbe the respective residual matrix of equations 1 through 4, the variances can be estimated by ordinary least squares (OLS) method, such that . Then the measure of linear feedback is computed by equation 5 and 6.
| (5) |
| (6) |
where FY→X indicates the strength of time series Y Granger-causing X, and FX→Y indicates the strength of time series X Granger-causing Y. The measure of instantaneous linear feedback is computed by equation 7.
| (7) |
where Γ in equation 8 is the covariance matrix
| (8) |
and C denotes the covariance of u2t, v2t. The measure of linear dependence is the sum of the measures of the three types of linear feedback, which is referred as FX,Yin equation 9:
| (9) |
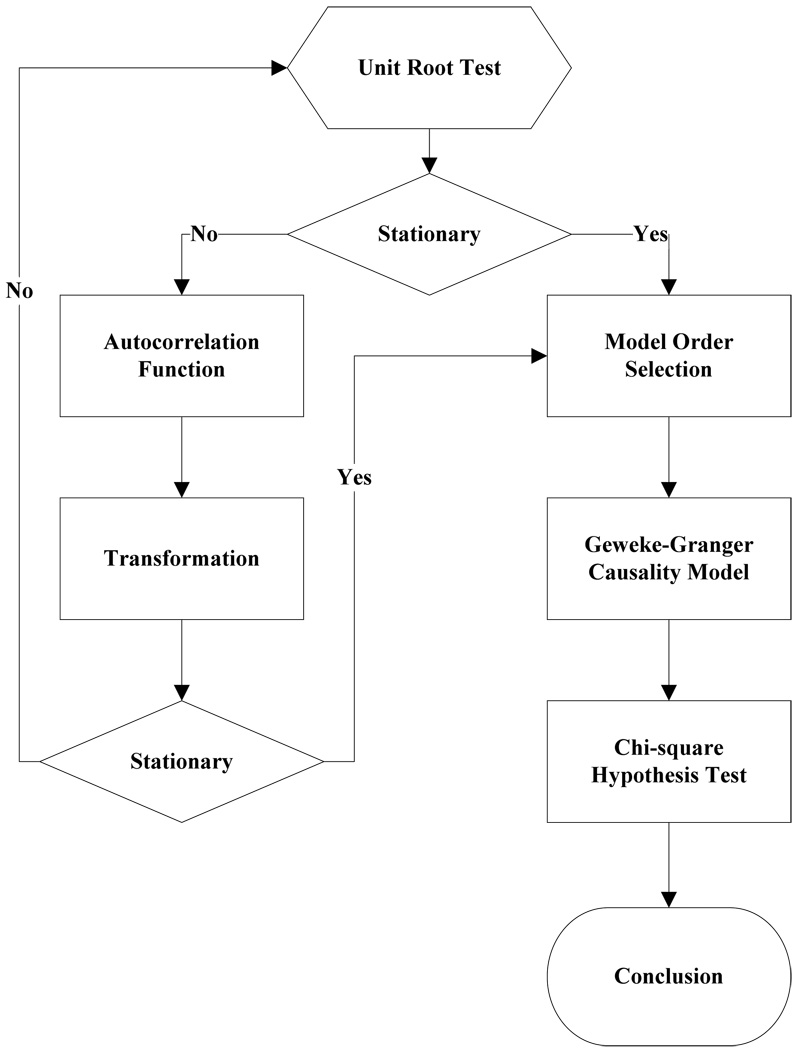
Typically, a time series can be described as either stationary or non-stationary, depending on the constancy of its statistical properties [25–27]. The stationary time series should have constant mean and variance over time as well as covariance which is a function of time difference only. The non-stationary time series may have either non-constant means, or non-constant variance or both, which results in spurious regression; [28, 29]. This poses a very serious problem for the estimation, and over-rejects hypothesis with T(true) or F(false) test statistics. Since Granger-Geweke Causality model focuses on the stationary purely nondeterministic multiple time series, the raw fMRI imaging data is confirmed to be stationary. If non-stationary, differencing method is employed to transform the non-stationary data to stationary data. For this reason, a general procedure to employ Granger-Geweke Causality model is presented and described by Figure 1. Next, we will illustrate each step in detail.
Figure 1.
A general procedure to employ Granger-Geweke Causality model to investigate the relations among the interesting regions of the brain.
Check if the dataset are stationary or non-stationary
The augmented Dickey-Fuller (ADF) unit root test [20, 21] and the plot of autocorrelation function (ACF) [27, 30] are most two common methods to test whether the dataset is stationary or non-stationary.
The ADF test statistics a numeric indicator such that the more negative it is, the stronger the rejection of the null hypothesis that there is a unit root (Data is not stationary) at some level of confidence. The ADF test model, referred as a random walk, is described by equation 10,
| (10) |
where k is the lag order, xt,xt−i xt−j are respective observations at time t, t−1, t−j, j = 2,…,k, in the time series X, η is the constant drift, λt is the time-trend term, γ, δ are coefficients, and εt is the noise with mean zero and constant variance. Since the well-developed auto regression (AR) models of Granger-Geweke causality model have neither time trend nor drift processes, the current ADF test model can be simplified as equation 11,
| (11) |
The number of lags is determined by the sampling frequency. If the sampling frequency is large, k should be small [31]. Because the time frequency of the fMRI experiments is 2 seconds long, we have to set k to 1, smallest lag number in this case. And then the unit root test is carried out under the null hypothesis γ = 1 against the alternative hypothesis of γ < 1. Once a value for the test statistic, equation 12 is computed, which can be compared to the relevant critical value derived in Monte Carlo study[22]
| (12) |
If the test statistic is smaller (this test is non symmetrical so we do not consider an absolute value) than the critical value at α significant level, then the null hypothesis of γ=1 is rejected and no unit root is present which means the data are stationary. Once the test results (Table 1) show that all fMRI time series are non-stationary, the next step is to choose the appropriate smoothing technique by ACF plot.
Table 1.
ADF test results for time series M1, SMA and cerebellum
| Subject | Session | M1 | SMA | cerebellum | Subject | Session | M1 | SMA | cerebellum |
|---|---|---|---|---|---|---|---|---|---|
| 1 | S1 | 0.6283 | 0.6988 | 0.7338 | 4 | S1 | 0.6256 | 0.8848 | 0.8332 |
| S2 | 0.8834 | 0.7967 | 0.8406 | S2 | 0.6981 | 0.7002 | 0.842 | ||
| S3 | 0.6915 | 0.7164 | 0.6593 | S3 | 0.7063 | 0.7429 | 0.9074 | ||
| S4 | 0.6321 | 0.524 | 0.6405 | S4 | −0.113 | −0.27 | −0.1072 | ||
| S5 | 0.5759 | 0.8567 | 0.8247 | S5 | 0.8579 | 0.7953 | 0.7811 | ||
| S6 | 0.7728 | 0.7533 | 0.9337 | S6 | 0.7594 | 0.9034 | 0.8619 | ||
| 2 | S1 | 0.7697 | 0.6838 | 0.7179 | 5 | S1 | 0.7073 | 0.7633 | 0.7659 |
| S2 | 0.5857 | 0.6571 | 0.6015 | S2 | 0.8368 | 0.8408 | 0.8512 | ||
| S3 | 0.7462 | 0.7352 | 0.7248 | S3 | 0.6926 | 0.8152 | 0.8125 | ||
| S4 | 0.6697 | 0.7857 | 0.7402 | S4 | 0.7143 | 0.7667 | 0.7999 | ||
| S5 | 0.6079 | 0.585 | 0.7134 | S5 | 0.6698 | 0.7242 | 0.6612 | ||
| S6 | 0.6473 | 0.6664 | 0.8495 | S6 | 0.8022 | 0.8728 | 0.8255 | ||
| 3 | S1 | 0.7059 | 0.8223 | 0.8381 | 6 | S1 | 0.5849 | 0.8409 | 0.6631 |
| S2 | 0.6882 | 0.7747 | 0.7634 | S2 | 0.807 | 0.7644 | 0.84 | ||
| S3 | 0.6972 | 0.8879 | 0.7782 | S3 | 0.6915 | 0.7164 | 0.6593 | ||
| S4 | 0.8751 | 0.782 | 0.6341 | S4 | 0.7688 | 0.5515 | 0.8083 | ||
| S5 | 0.6204 | 0.7089 | 0.6091 | S5 | 0.6908 | 0.6905 | 0.7162 | ||
| S6 | 0.7709 | 0.8331 | 0.8759 | S6 | 0.7811 | 0.8398 | 0.8479 |
The ACF plot is a powerful graphical tool to measure the correlation between observations at different distances apart, to check the randomness of data and to find repeating pattern in them. Given the time series X given in equation 1, the ACF between its observations xt and xt−i is defined as
| (13) |
where cov(xt−i,xt−i) is the covariance of xt and xt−i, and is the variance of the series [13, 21]. If the autocorrelation dies out quickly in the plot (with autocorrelations on the y axis and the different time lags on the x axis), the series should be considered as stationary [14, 32]; especially if the autocorrelations are close to zero, the data are considered as white noise. Otherwise, the data will be considered as non-stationary time series [33];.
Data preprocessing
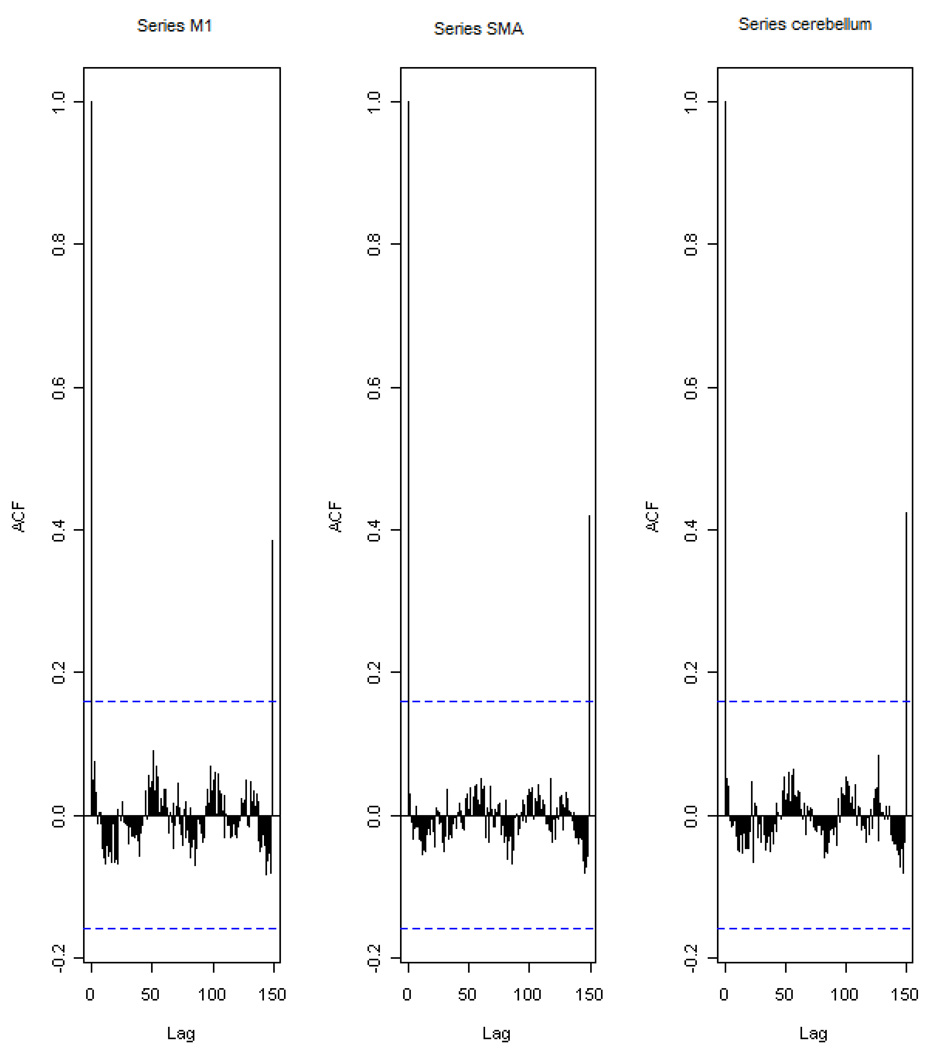
Differencing is a classical tool to transform the dataset from non-stationary to stationary. The first-order difference of a time series is the one that changes from one period to the next, that is, at time period t the first order difference of series X is xt − xt−1 denoted by Δxt. Here, we only list the ACF plots (Figure 2) for the subject 1 at section 1(see Table 1) restricted to the page limit. The rest of the ACF plots are very similar to Figure 2. Since Figure 2 shows seasonal trends for each time series, the differencing method is adopted to remove these trends from the time series.
Figure 2.
The ACF plot of observations within each brain area for the subject 1 in Session 1. The x axis represents the number of lag; the y axis represents the autocorrelation.
Therefore, the equation 1 through equation 4 can be rewritten as
| (14) |
| (15) |
| (16) |
| (17) |
After the first-order difference, ADF test is employed again of Δxt to evaluate whether the treated dataset is stationary or non-stationary. If it is still non-stationary, the second-order difference (Δ2xt = xt − 2xt−1 + xt−2) should be applied. However, if the series need differencing more than twice we should use other methods, such as log transformation. In the results section of the study, we are going to discuss the data preprocessing result in detail.
Model Selection
After the stationary data set is generated, the order of the equation 14 to 17 by computing the approximation to the criteria values of Schwarz's Bayesian information criterion (SBIC) is identified with ARFIT algorithm [23, 34]. SBIC is an information criterion used for goodness-of-fit model selection for fixed effects models with different number of parameters at some significance level, and the one with lower SBIC fits the data better. Given the time series X in equation 1, the corresponding SBIC can be calculated as
| (18) |
where n is the number of observations in X, p is the order of the AR model and U1 is the residual matrix of X. We choose the order of AR model, p, with smallest SBIC value.
Linear feedback calculation
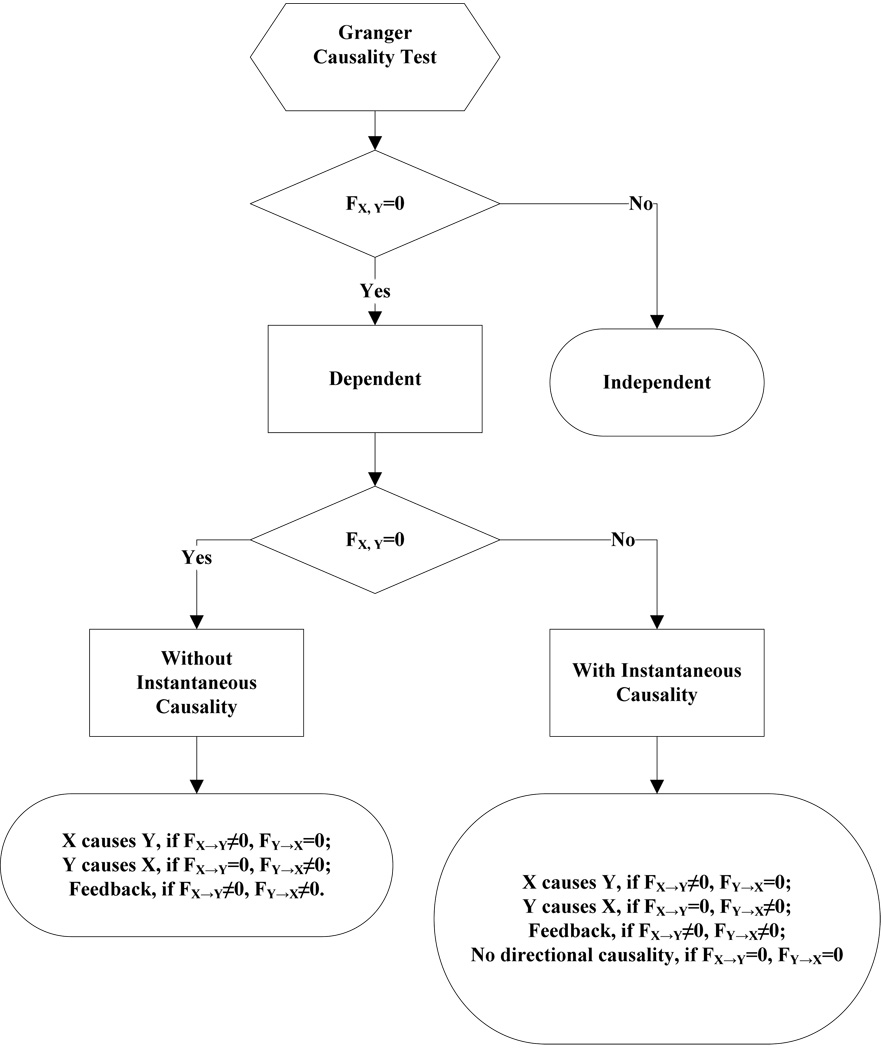
After the order of AR models is determined, the linear feedback for each pair of brain regions by equation 5 and 6 is computed. Then, the conventional large-sample distribution theory is used to test the null hypothesis that a given measure of feedback zero. As indicated by Geweke’s research[7] if FY→X = 0, then ; if FX→Y = 0, then ; if FX·Y = 0, then ; if FX,Y= 0, then . The k, l are the number of columns in the residual matrix U1n×k, V1n×l. And p is the lag of autoregressive models. With respect to this null hypothesis test, we can have the followed eight relations (equations 19.1–19.8) between two series X and Y [35] described by Figure 3.
| Relations | Sign | equation | |
|---|---|---|---|
|
X and Y are independent, if |
(x,y) | (equation 19.1) | |
| Instantaneous causality only without direction, if |
(x–y) | (equation 19.2) | |
|
X causes Y, with instantaneous causality, if |
(x→y) | (equation 19.3) | |
|
X causes Y, without instantaneous causality, if |
(x=>y) | (equation 19.4) | |
|
Y causes X, with instantaneous causality, if |
(x←y) | (equation 19.5) | |
|
Y causes X, without instantaneous causality, if |
(x<=y) | (equation 19.6) | |
| Feedback with instantaneous causality, if |
(x↔y) | (equation 19.7) | |
| Feedback without instantaneous causality |
(x⇔y) | (equation 19.8) |
Figure 3.
The relations between two time series
Results
Stationary check for the dataset
Table 1 shows the ADF test results for time series M1, SMA, and cerebellum. It indicates that each time series is non-stationary at 10% significant level. Restricting to page limit, Figure 2 shows the ACF plots of each time series for subject 1 at session 1. However, the ACF plots of the rest of persons are similar with Figure 2. For this reason, we should employ differencing method to transform the dataset from non-stationary to stationary time series.
Data transformation from non-stationary to stationary time series
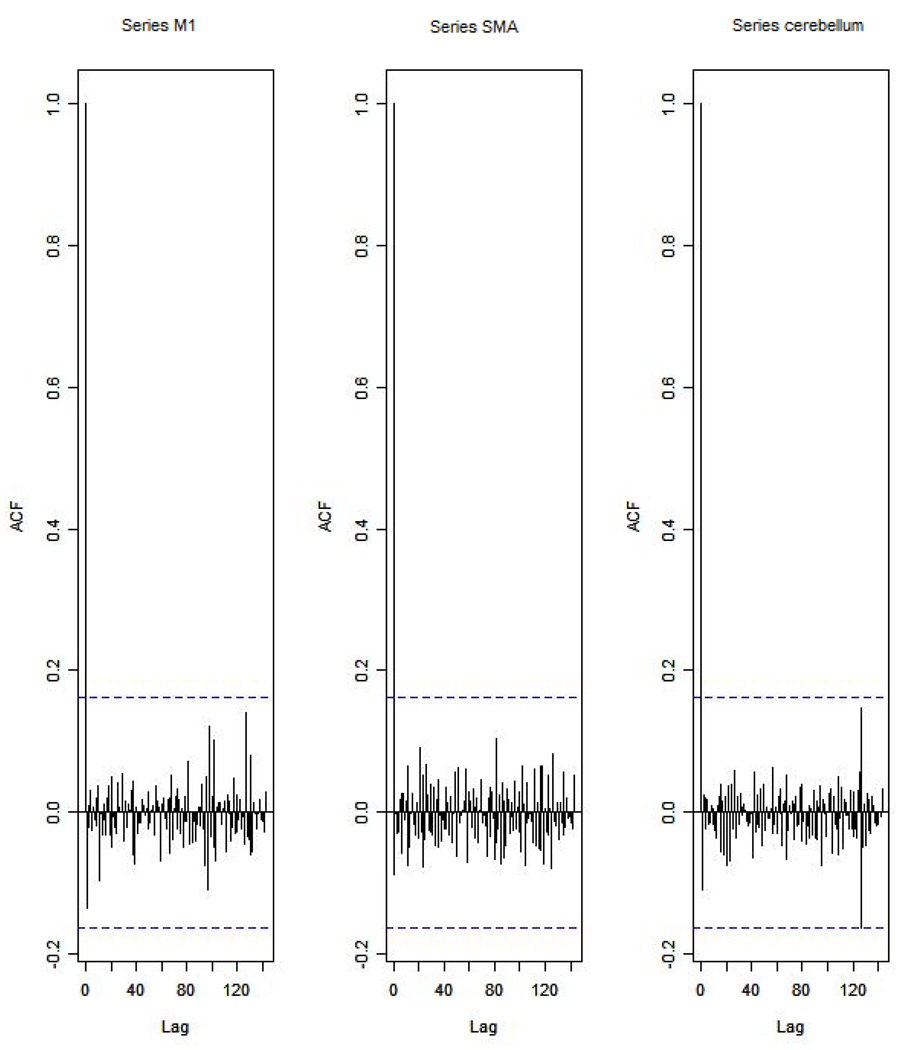
Table 2 shows ADF test results for time series M1, SMA, and cerebellum after the first-order differencing method is applied. Now each time series is stationary and the Hochberg’s[36] step-up multiple test procedure is implemented. This procedure is based on the individual P-value (Table 3) calculated by ADF test and concluded that the stationarity assumption has been satisfied. Figure 4 describes the ACF plot of these time series for subject 1 in session 1 restricting to the page limit. Figure 4 shows that seasonal trend has been removed from time series for subject 1 in session 1 after first-order differencing. Our results show that ACF plots for the remaining subjects are similar.
Table 2.
ADF test results for first-order differenced time series M1, SMA and cerebellum.
| Subject | Session | M1 | SMA | cerebellum | Subject | Session | M1 | SMA | cerebellum |
|---|---|---|---|---|---|---|---|---|---|
| Ay | S1 | −6.2401 | −5.1229 | −5.0559 | Mwe | S1 | −7.0335 | −5.207 | −3.9694 |
| S2 | −4.3975 | −4.481 | −4.7884 | S2 | −4.8556 | −7.1719 | −3.3872 | ||
| S3 | −5.1525 | −5.4316 | −4.5684 | S3 | −5.7965 | −5.4341 | −3.1331 | ||
| S4 | −7.2745 | −7.9421 | −6.2819 | S4 | −11.284 | −10.8797 | −12,0458 | ||
| S5 | −6.7513 | −3.1335 | −5.3833 | S5 | −5.1912 | −4.3987 | −4.286 | ||
| S6 | −4.4235 | −5.7843 | −3.0588 | S6 | −10.9812 | −8.8644 | −6.8167 | ||
| Mj | S1 | −4.613 | −7.0375 | −5.0471 | Wi | S1 | −4.8346 | −5.3248 | −4.772 |
| S2 | −6.8688 | −6.883 | −6.3738 | S2 | −2.8913 | −3.9684 | −2.2962 | ||
| S3 | −4.4981 | −4.0534 | −5.9015 | S3 | −4.6129 | −4.6122 | −3.9287 | ||
| S4 | −4.916 | −5.6706 | −4.2594 | S4 | −4.4593 | −4.5542 | −5.1556 | ||
| S5 | −7.5981 | −6.8371 | −6.4166 | S5 | −4.4734 | −6.0808 | −6.0491 | ||
| S6 | −7.4277 | −8.4613 | −3.4288 | S6 | −2.9585 | −2.5292 | −3.6465 | ||
| Mm | S1 | −4.2132 | −4.5137 | −2.3973 | Yt | S1 | −3.9059 | −5.5496 | −4.4626 |
| S2 | −3.0548 | −4.6281 | −4.3999 | S2 | −4.3165 | −5.5688 | −3.4785 | ||
| S3 | −4.066 | −3.7752 | −5.0195 | S3 | −5.1525 | −5.4316 | −4.5684 | ||
| S4 | −3.848 | −4.8816 | −6.1045 | S4 | −4.0086 | −5.6379 | −4.9253 | ||
| S5 | −5.6978 | −4.8186 | −5.2083 | S5 | −6.7513 | −3.1335 | −5.3833 | ||
| S6 | −2.8161 | −4.5713 | −2.4998 | S6 | −3.2064 | −3.5299 | −3.2231 |
Table 3.
The p-value of ADF test.
| Subject | Session | M1 | SMA | cerebellum | Subject | Session | M1 | SMA | cerebellum |
|---|---|---|---|---|---|---|---|---|---|
| 1 | S1 | 4.88·10−9 | 9.79·10−7 | 1.32·10−6 | 4 | S1 | 8.18·10−11 | 6.71·10−7 | 0.000115 |
| S2 | 2.15·10−5 | 1.53·10−5 | 4.23·10−6 | S2 | 3.17·10−6 | 3.92·10−11 | 0.000917 | ||
| S3 | 8.57·10−7 | 2.40·10−7 | 1.07·10−5 | S3 | 4.3·10−8 | 2.38·10−7 | 0.00211 | ||
| S4 | 2.26·10−11 | 5.86·10−13 | 3.96·10−9 | S4 | <2·10−16 | <2·10−16 | <2·10−16 | ||
| S5 | <2·10−16 | 2.07·10−9 | <2·10−16 | S5 | 7.2·10−7 | 2.14·10−5 | 3.37·10−5 | ||
| S6 | 1.94·10−5 | 4.45·10−8 | 0.00266 | S6 | <2·10−16 | 3.32·10−15 | 2.61·10−10 | ||
| 2 | S1 | 8.87·10−6 | 8·10−11 | 1.37·10−6 | 5 | S1 | <2·10−16 | 4.56·10−16 | <2·10−16 |
| S2 | <2·10−16 | <2·10−16 | <2·10−16 | S2 | 9.3·10−12 | 2.83·10−15 | 7.28·10−12 | ||
| S3 | 1.43·10−5 | 8.34·10−5 | 2.59·10−8 | S3 | 9.88·10−16 | 2.09·10−13 | 2.22·10−15 | ||
| S4 | 2.44·10−6 | 7.84·10−8 | 3.74·10−5 | S4 | <2·10−16 | 4.65·10−15 | <2·10−16 | ||
| S5 | 3.91·10−12 | 2.3·10−10 | 2.01·10−9 | S5 | 2.29·10−15 | <2·10−16 | <2·10−16 | ||
| S6 | 9.88·10−12 | 3.17·10−14 | 0.000797 | S6 | 1.4·10−10 | 2.89·10−10 | 3.97·10−13 | ||
| 3 | S1 | 4.49·10−5 | 1.34·10−5 | 0.0178 | 6 | S1 | 3.06·10−14 | <2·10−16 | 2.6· 10−16 |
| S2 | 0.0027 | 8.33·10−6 | 2.13·10−5 | S2 | 6.07·10−11 | <2·10−16 | 3.22·10−13 | ||
| S3 | 7.94·10−5 | 0.000235 | 1.55·10−6 | S3 | <2·10−16 | <2·10−16 | <2·10−16 | ||
| S4 | 0.00018 | 2.83·10−6 | 9.58·10−9 | S4 | 1.83·10−12 | <2·10−16 | 2.43·10−16 | ||
| S5 | 6.89·10−8 | 3.71·10−6 | 6.67·10−7 | S5 | 1.04·10−12 | 8.9·10−12 | 4.93·10−12 | ||
| S6 | 0.00556 | 1.06·10−5 | 0.0136 | S6 | 2.06·10−14 | 1.24·10−9 | <2·10−16 |
Figure 4.
The ACF plot of first-order differenced observations within each brain area for the subject 1 in session 1. The x axis represents the number of lag; the y axis represents the autocorrelation.
Order selection for the Geweke-Granger causality model
By equation 18, we evaluated the order p of the Geweke-Granger models with smallest SBIC values. With respect to the time interval of the previous fMRI experiments (2 seconds)[19], the candidates order p is limited from 1, 2 and 3. And the results in Table 4 show when p=1, for most of sessions, Geweke-Granger model will receive minimum SBIC value. Therefore, we choose p=1 as the order of the model.
Table 4.
The order of AR model for equation 14 to equation 17.
| Subject | Session | M1 | SMA | cerebellum | Subject | Session | M1 | SMA | cerebellum |
|---|---|---|---|---|---|---|---|---|---|
| 1 | S1 | 1 | 1 | 1 | 4 | S1 | 2 | 1 | 1 |
| S2 | 1 | 1 | 2 | S2 | 1 | 1 | 1 | ||
| S3 | 1 | 1 | 1 | S3 | 1 | 1 | 1 | ||
| S4 | 1 | 2 | 1 | S4 | 3 | 1 | 2 | ||
| S5 | 1 | 1 | 1 | S5 | 1 | 1 | 1 | ||
| S6 | 1 | 1 | 1 | S6 | 1 | 1 | 1 | ||
| 2 | S1 | 1 | 2 | 1 | 5 | S1 | 1 | 1 | 1 |
| S2 | 1 | 1 | 1 | S2 | 1 | 1 | 1 | ||
| S3 | 1 | 1 | 1 | S3 | 1 | 1 | 1 | ||
| S4 | 1 | 1 | 1 | S4 | 1 | 1 | 1 | ||
| S5 | 1 | 1 | 1 | S5 | 1 | 1 | 1 | ||
| S6 | 2 | 2 | 1 | S6 | 1 | 1 | 1 | ||
| 3 | S1 | 1 | 1 | 1 | 6 | S1 | 2 | 2 | 1 |
| S2 | 1 | 1 | 1 | S2 | 1 | 1 | 1 | ||
| S3 | 1 | 1 | 1 | S3 | 1 | 1 | 1 | ||
| S4 | 1 | 1 | 1 | S4 | 1 | 1 | 1 | ||
| S5 | 1 | 1 | 1 | S5 | 1 | 1 | 1 | ||
| S6 | 1 | 1 | 1 | S6 | 1 | 1 | 1 |
Causality among different brain regions
The Table 5 lists the directions among different brain regions by session. The sign is introduced by the equations 19.1–19.8. It reveals the following emergent phenomenon.
Most of the relations are instantaneous causality only without direction, X causes Y with instantaneous causality (X→Y) and Y causes X with instantaneous causality (Y→X). In the rest of the discussion, we denote the directed relation as X causes Y with instantaneous causality and Y causes X with instantaneous causality.
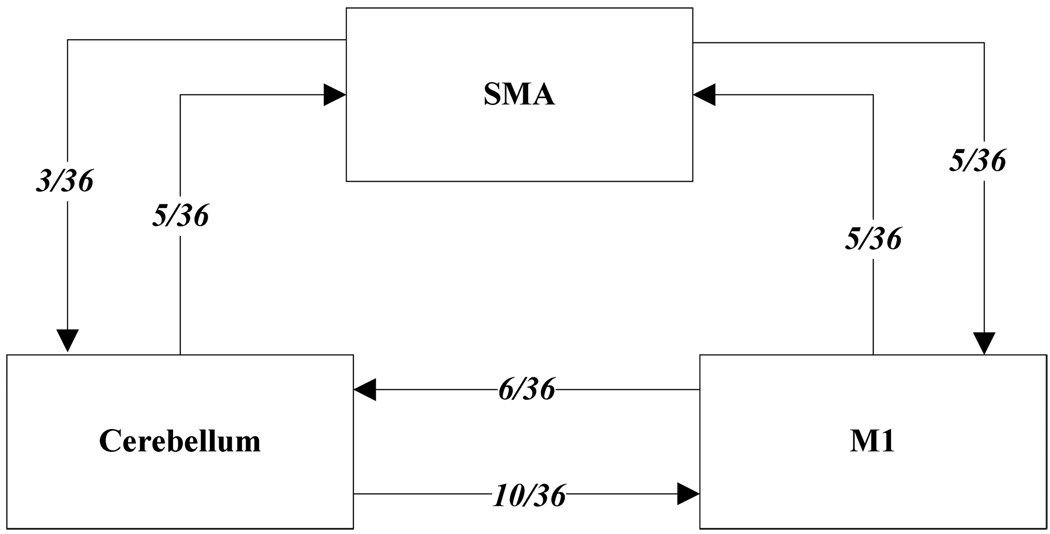
There should be strong directed relations between M1 and cerebellum, because we detect sixteen signals between these regions regarding to thirty six experiments as well as ten times the direction is from cerebellum to M1 and six times from M1 to cerebellum.
There should be strong directed relations between M1 and SMA because we detect ten signals between these regions regarding to thirty six experiments as well as five times the direction is from cerebellum to M1 and five times from M1 to cerebellum.
Table 5.
The relations between multivariate brain areas investigated by fMRI sort by sessions.
| subject | M1,SMA | M1, cerebellum | SMA, cerebellum | subject | M1,SMA | M1, cerebellum | SMA, cerebellum | ||
|---|---|---|---|---|---|---|---|---|---|
| S1 | 1 | – | → | – | S | 1 | – | – | – |
| 2 | – | – | – | 2 | – | – | – | ||
| 3 | – | ← | – | 3 | – | – | – | ||
| 4 | ⇔ | ← | → | 4 | ← | ← | – | ||
| 5 | ← | ← | – | 5 | – | ← | ← | ||
| 6 | – | – | – | 6 | ← | – | ← | ||
| S2 | 1 | → | → | – | S | 1 | – | – | – |
| 2 | – | – | – | 2 | – | – | – | ||
| 3 | – | ← | ← | 3 | – | – | – | ||
| 4 | – | – | – | 4 | → | ⇔ | – | ||
| 5 | – | ← | – | 5 | – | – | – | ||
| 6 | → | → | – | 6 | ← | → | → | ||
| S3 | 1 | – | – | – | S | 1 | – | ← | ← |
| 2 | – | – | – | 2 | – | – | – | ||
| 3 | ← | → | → | 3 | – | ← | – | ||
| 4 | – | ← | – | 4 | – | – | ← | ||
| 5 | – | – | – | 5 | → | – | – | ||
| 6 | – | → | – | 6 | → | – | – |
The Table 6 lists the directions among different brain regions by subject, which explores the following emergent phenomenon.
It shows that all the subjects response to the stimulation during right finger-tapping task.
Except one subject, the rest of the five subjects have the similar response pattern to the stimulation.
As we discussed in equation 9, the sum of the measure of linear dependence FX,Y is the linear combination of directed linear feedback FX→Y and FY→X as well as the instantaneous linear feedback (FX·Y). Here, the instantaneous linear feedback (FX·Y) takes very high percentage over the sum of the measure of linear dependence FX,Y, most of the percentage is more than 90%.
Table 6.
The relations between multivariate brain areas investigated by fMRI sort by subjects. The number in the paragraph shows the ratio of FX·Y / FX,Y.
| subject | M1,SMA | M1, cerebellum | SMA, cerebellum | subject | M1,SMA | M1, cerebellum | SMA, cerebellum | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | S1 | – | →(99.5%) | – | 4 | S1 | ⇔ | ←(95.4%) | →(95.4%) |
| S2 | →(96.1%) | →(92.4%) | – | S2 | – | – | – | ||
| S3 | – | – | – | S3 | – | ←(96.1%) | – | ||
| S4 | – | – | – | S4 | ←(67.9%) | ←(24.5%) | – | ||
| S5 | – | – | – | S5 | →(91.6%) | ⇔ | – | ||
| S6 | – | ←(96.7%) | ←(97.7%) | S6 | – | – | ←(93.3%) | ||
| 2 | S1 | – | – | – | 5 | S1 | ←(96.6%) | ←(99.7%) | – |
| S2 | – | – | – | S2 | – | ←(97.7%) | – | ||
| S3 | – | – | – | S3 | – | – | – | ||
| S4 | – | – | – | S4 | – | ←(96.3%) | ←(95.4%) | ||
| S5 | – | – | – | S5 | – | – | – | ||
| S6 | – | – | – | S6 | →(95.8%) | – | – | ||
| 3 | S1 | – | ←(96.9%) | – | 6 | S1 | – | – | – |
| S2 | – | ←(93.5%) | ←(94.6%) | S2 | →(96.9%) | →(97.5%) | – | ||
| S3 | ←(94.1%) | →(96.7%) | →(96.7%) | S3 | – | →(97.2%) | – | ||
| S4 | – | – | – | S4 | ←(99.2%) | – | ←(96.5%) | ||
| S5 | – | – | – | S5 | ←(92.3%) | →(92.9%) | →(92.2%) | ||
| S6 | – | ←(95.7%) | – | S6 | →(96.9%) | – | – |
Discussion and conclusion
This study applied Granger-Geweke Causality model to investigate the effective connectivity of M1, SMA and cerebellum during the finger-tapping task. Equation 9 shows that linear dependence FX,Y has three components, instantaneous linear feedback (FX·Y), directed linear feedback (FX→Y and FY→X). Especially, instantaneous linear feedback (FX·Y) describes the impact between time series X and Y at current time step. And directed linear feedback (FX→Y and FY→X) describes how the effect of time series X or Y in previous t−1 time steps affects time series Y or X at t time step. Actually, the relation between two time series could include more than one type of linear feedbacks simultaneously. Therefore, Kirchgässner and Wolters[35] classified these linear feedbacks to eight relations (equations 19.1–19.8), which are not independent each other.
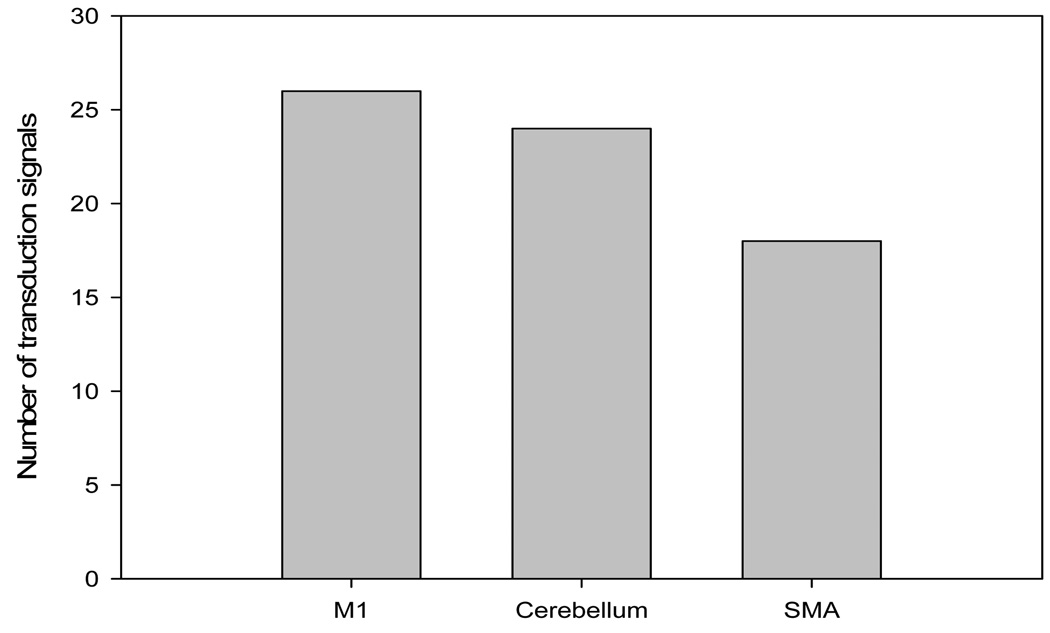
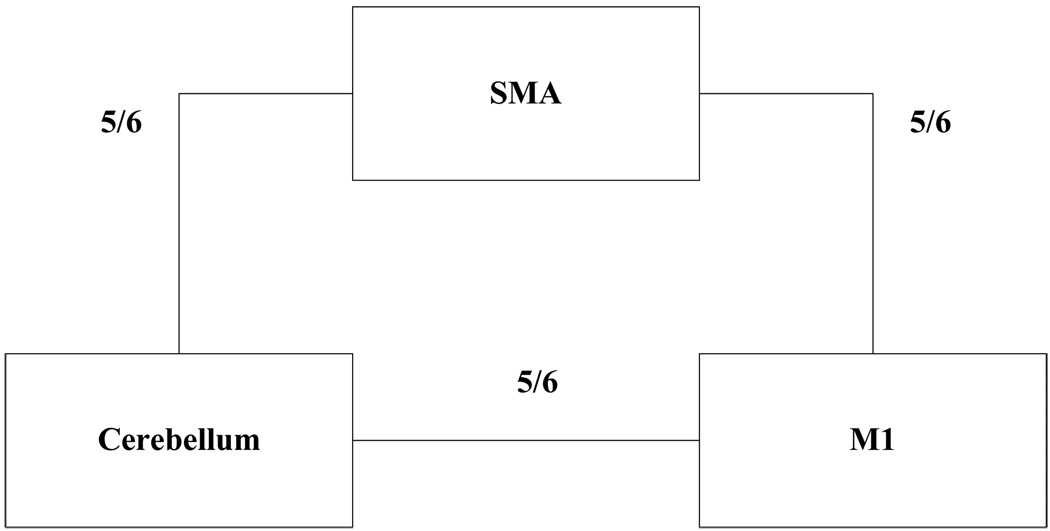
The current results show (Table 5) that most of the pair wise relations between the brain regions are instantaneous causality only without direction (equation 19.2), X causes Y with instantaneous causality (equation 19.3) and Y causes X with instantaneous causality (equation 19.5). The rest relation such as feedback without instantaneous causality (equation 19.8) only appears twice (Table 5). Here, we denote the relations like X causes Y with instantaneous causality (equation 19.3) and Y causes X with instantaneous causality (equation 19.5) as the directed relation in the rest of the discussion. Table 6 shows instantaneous causality only without direction (equation 19.2) is the most favorite relation in the results. More importantly, the most popular relation instantaneous linear feedback (FX·Y) component takes high percentage (mostly more than 90% (Table 6)) of the sum of the linear dependency (FX,Y). The phenomena imply that neurology response time period should be shorter than the fMRI time interval (2 seconds). Next, the directed relations among these brain regions were investigated. Figure 5 describes the directed relations between each pair of the brain regions. It shows strong directed relations between M1 and cerebellum, M1 and SMA, because there are sixteen and ten directed signals transductions occurred between the pair of these regions, respectively. Additionally, if we consider each region as a node of the brain network, Figure 6 demonstrates that M1 should be a busy node, since it is involved 26 directed signal transductions. Particularly, this finding matches the anatomical observations[24] that the both SMA and Cerebellum project to M1. Furthermore, Figure 5 shows that SMA and cerebellum are the regions which have less directed signal transductions. Due to that, we consider the number of intermediate nodes between SMA and cerebellum should be fewer than others which will not cause many latency of the signal transduction between these regions. Figure 7 shows the directed simulation response is stable and believable, since five out six subjects shows the directed relations.
Figure 5.
The directed relation between every two brain areas. The arrow indicates the direction of causality. The label of each link indicates the number of the directed signals.
Figure 6.
The number of directed signal transductions for each brain regions, M1, cerebellum and SMA.
Figure 7.
The directed relation between every two brain areas. The label of each link indicates the numbers of subject out of six have the relation between these two regions.
In summary, the results demonstrate strong linear feedback among SMA, M1 and cerebellum as our previous study. Especially, the instantaneous linear feedback plays the very important role. Also, strong directed relations were found between M1 and cerebellum, M1 and SMA. It derives that M1 should be the hub of these three regions and such findings agree with the observation of anatomy that both SMA and Cerebellum project to M1. Also, indicated by the anatomy field[24], the distance between SMA and M1 is the shortest, but a number of directed signals are detected (Figure 5), which implies a high intermediate node density existing in the area between these two regions. On the other hand, the distance between SMA and cerebellum is much longer than SMA and M1, but many directed relations between them cannot be obtained. We postulate that there are not many intermediate nodes in the area between SMA and cerebellum compared to the area between SMA and M1.
Acknowledgements
Funding and support for this study came from the startup funding of Michigan Tech University, NIH (NCCAM) K01 AT003883 and R21AT004497 to Jian Kong. M01-RR-01066 for Mallinckrodt General Clinical Research Center Biomedical Imaging Core, P41RR14075 for Center for Functional Neuroimaging Technologies from NCRR, and the MIND Institute.
References
- 1.Astolfi L, Cincotti F, Mattia D, Salinari S, Babiloni C, Basilisco A, Rossini PM, Ding L, Ni Y, He B, Marciani MG, Babiloni F. Estimation of the effective and functional human cortical connectivity with structural equation modeling and directed transfer function applied to high-resolution EEG. Magn Reson Imaging. 2004 Dec;vol. 22:1457–1470. doi: 10.1016/j.mri.2004.10.006. [DOI] [PubMed] [Google Scholar]
- 2.Brovelli A, Ding MZ, Ledberg A, Chen YH, Nakamura R, Bressler SL. Beta oscillations in a large-scale sensorimotor cortical network: Directional influences revealed by Granger causality. Proceedings of the National Academy of Sciences of the United States of America. 2004 Jun 29;vol. 101:9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Eichler M. A graphical approach for evaluating effective connectivity in neural systems. Philos Trans R Soc Lond B Biol Sci. 2005 May 29;vol. 360:953–967. doi: 10.1098/rstb.2005.1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sato JR, Amaro E, Takahashi DY, Felix MD, Brammer MJ, Morettin PA. A method to produce evolving functional connectivity maps during the course of an fMRI experiment using wavelet-based time-varying Granger causality. Neuroimage. 2006 May 15;vol. 31:187–196. doi: 10.1016/j.neuroimage.2005.11.039. [DOI] [PubMed] [Google Scholar]
- 5.Smith JF, Pillai A, Chen K, Horwitz B. Identification and validation of effective connectivity networks in functional magnetic resonance imaging using switching linear dynamic systems. Neuroimage. 2009 Dec 5; doi: 10.1016/j.neuroimage.2009.11.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen HF, Yang Q, Liao W, Gong QY, Shen S. Evaluation of the effective connectivity of supplementary motor areas during motor imagery using Granger causality mapping. Neuroimage. 2009 Dec; doi: 10.1016/j.neuroimage.2009.06.026. vol. doi:10.1016/j.neuroimage.2009.06.026. [DOI] [PubMed] [Google Scholar]
- 7.Geweke J. The Measurement of Linear-Dependence and Feedback between Multiple Time-Series - Rejoinder. Journal of the American Statistical Association. 1982;vol. 77:323–324. [Google Scholar]
- 8.Gow DW, Jr, Segawa JA, Ahlfors SP, Lin FH. Lexical influences on speech perception: a Granger causality analysis of MEG and EEG source estimates. Neuroimage. 2008 Nov 15;vol. 43:614–623. doi: 10.1016/j.neuroimage.2008.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liao W, Mantini D, Zhang Z, Pan Z, Ding J, Gong Q, Yang Y, Chen H. Evaluating the effective connectivity of resting state networks using conditional Granger causality. Biol Cybern. 2010 Jan;vol. 102:57–69. doi: 10.1007/s00422-009-0350-5. [DOI] [PubMed] [Google Scholar]
- 10.Liao W, Marinazzo D, Pan Z, Gong Q, Chen H. Kernel Granger causality mapping effective connectivity on FMRI data. IEEE Trans Med Imaging. 2009 Nov;vol. 28:1825–1835. doi: 10.1109/TMI.2009.2025126. [DOI] [PubMed] [Google Scholar]
- 11.Lin FH, Hara K, Solo V, Vangel M, Belliveau JW, Stufflebeam SM, Hamalainen MS. Dynamic Granger-Geweke Causality Modeling With Application to Interictal Spike Propagation. Human Brain Mapping. 2009 Jun;vol. 30:1877–1886. doi: 10.1002/hbm.20772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Marinazzo D, Liao W, Chen H, Stramaglia S. Nonlinear connectivity by Granger causality. Neuroimage. 2010 Feb 2; doi: 10.1016/j.neuroimage.2010.01.099. [DOI] [PubMed] [Google Scholar]
- 13.Box GEP, Jenkins GM, Reinsel GC. Time series analysis : forecasting and control. 3rd ed. Upper Saddle River, N.J: Prentice Hall; 1994. [Google Scholar]
- 14.Chatfield C. Time-series forecasting. Boca Raton: Chapman & Hall/CRC; 2001. [Google Scholar]
- 15.Londei A, D'Ausilio A, Basso D, Belardinelli MO. A new method for detecting causality in fMRI data of cognitive processing. Cogn Process. 2006 Mar;vol. 7:42–52. doi: 10.1007/s10339-005-0019-5. [DOI] [PubMed] [Google Scholar]
- 16.Nedungadi AG, Rangarajan G, Jain N, Ding MZ. Analyzing multiple spike trains with nonparametric granger causality. Journal of Computational Neuroscience. 2009 Aug;vol. 27:55–64. doi: 10.1007/s10827-008-0126-2. [DOI] [PubMed] [Google Scholar]
- 17.Roebroeck A, Formisano E, Goebel R. Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage. 2005 Mar;vol. 25:230–242. doi: 10.1016/j.neuroimage.2004.11.017. [DOI] [PubMed] [Google Scholar]
- 18.Zhang Y, Chen Y, Bressler SL, Ding M. Response preparation and inhibition: The role of the cortical sensorimotor beta rhythm. Neuroscience. 2008 Sep 22;vol. 156:238–246. doi: 10.1016/j.neuroscience.2008.06.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kong J, Gollub RL, Webb JM, Kong JT, Vangel MG, Kwong K. Test-retest study of fMRI signal change evoked by electroacupuncture stimulation. Neuroimage. 2007 Feb 1;vol. 34:1171–1181. doi: 10.1016/j.neuroimage.2006.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Greene WH. Econometric analysis. 5th ed. Upper Saddle River, N.J: Prentice Hall; 2003. [Google Scholar]
- 21.Yaffee RA, McGee M. Introduction to time series analysis and forecasting : with applications in SAS and SPSS. San Diego: Academic Press; 2000. [Google Scholar]
- 22.Dickey DA, Fuller WA. Distribution of the Estimators for Autoregressive Time-Series with a Unit Root. Journal of the American Statistical Association. 1979;vol. 74:427–431. [Google Scholar]
- 23.Neumaier A, Schneider T. Estimation of parameters and eigenmodes of multivariate autoregressive models. Acm Transactions on Mathematical Software. 2001 Mar;vol. 27:27–57. [Google Scholar]
- 24.Notle J. The Human Brain: An Introduction to Its Functional Anatomy. St. Louis, Missouri 63146: Mosby Inc; 1999. [Google Scholar]
- 25.Priestley MB. Spectral analysis and time series. London; New York: Academic Press; 1981. [Google Scholar]
- 26.Priestley MB. Non-linear and non-stationary time series analysis / M. B. Priestley. London; San Diego: Academic; 1988. [Google Scholar]
- 27.Wei W. Time Series Analysis. Boston, MA: Perrson Education, inc; 2006. [Google Scholar]
- 28.Pearl J. Causality : models, reasoning, and inference. Cambridge, U.K.; New York: Cambridge University Press; 2000. [Google Scholar]
- 29.Brooks C. Introductory econometrics for finance. 2nd ed. Cambridge [England]; New York: Cambridge University Press; 2008. [Google Scholar]
- 30.Baum CF. An introduction to modern econometrics using Stata. College Station, Tex: Stata Press; 2006. [Google Scholar]
- 31.Warner RM. Spectral analysis of time-series data. New York: Guilford Press; 1998. [Google Scholar]
- 32.Mills TC. Time series techniques for economists. Cambridge [England]; New York: Cambridge University Press; 1990. [Google Scholar]
- 33.Clements P, Hendry DF. Forecasting non-stationary economic time series. Cambridge, Mass: MIT Press; 1999. [Google Scholar]
- 34.Storch HV, Zwiers FW. Statistical analysis in climate research. Cambridge, U.K.; New York: Cambridge University Press; 1999. [Google Scholar]
- 35.Kirchgässner G, Wolters J. Introduction to modern time series analysis. Berlin; New York: Springer; 2007. [Google Scholar]
- 36.Hochberg Y. A Sharper Bonferroni Procedure for Multiple Tests of Significance. Biometrika. 1988 Dec;vol. 75:800–802. [Google Scholar]