Population clocks: motor timing with neural dynamics

Abstract

An understanding of sensory and motor processing will require elucidation of the mechanisms by which the brain tells time. Open questions relate to whether timing relies on dedicated or intrinsic mechanisms and whether distinct mechanisms underlie timing across scales and modalities. Although experimental and theoretical studies support the notion that neural circuits are intrinsically capable of sensory timing on short scales, few general models of motor timing have been proposed. For one class of models, population clocks, it is proposed that time is encoded in the time-varying patterns of activity of a population of neurons. We argue that population clocks emerge from the internal dynamics of recurrently connected networks, are biologically realistic and account for many aspects of motor timing.

The problem of time

The fact that people can communicate using a purely temporal code - as occurs when two individuals are receiving and sending messages in Morse code - is one of many pieces of evidence that the nervous system has evolved sophisticated mechanisms to tell time and process temporal information. Indeed, the sheer diversity of time scales and computational problems that rely on temporal processing suggests that multiple mechanisms are in place to tell time. The neural bases of timing have been the subject of a number of recent reviews [1–6] and one critical question addressed in these reviews is whether timing relies on dedicated (specialized) neural mechanisms or on an intrinsic and general ability of networks of neurons (Box 1). An equally important and related unanswered question is whether sensory and motor forms of timing share mechanisms and circuits. For example, does the discrimination of a 400- or 500-ms tone rely on the same neural circuitry as that required to generate a 400- or 500-ms depression of a piano key?

Box 1. Dedicated versus intrinsic neural mechanisms of timing.

Central to the issue of the neural basis of timing and temporal processing is the question of whether the brain uses dedicated or intrinsic neural mechanisms to tell time [3]. This distinction in many ways revolves around whether there are ‘clocks’ in the brain, that is, whether there are specialized systems that were ‘designed’ to tell time and are exclusively devoted to the problem of timing, or whether timing is a general and intrinsic ability of neurons and neural circuits. In this view the same circuits responsible for timing can process other aspects of sensory stimuli simultaneously in a multiplex fashion.

The classic internal clock model, composed of a pacemaker and accumulator, is an instantiation of a dedicated and centralized mechanism of timing [74,75]. By contrast, an example of an intrinsic model is a state-dependent network; in this class of models, sensory timing emerges from the interaction of the time-varying internal state of neural networks with incoming stimuli [13,14]. Although the notion that subsecond timing is performed locally has recently received experimental support [10–12,76], there is still little direct evidence of whether the brain relies on dedicated or intrinsic mechanisms.

Here we focus on the problem of motor timing and, although the issue of whether motor and sensory timing rely on the same circuitry remains open [7–12], we take the position that they generally rely on nonoverlapping networks. Specifically, we argue that motor timing relies on the internal dynamics that arise from the ability of recurrent neural networks to generate self-sustained, complex, time-varying patterns of neural activity, whereas, as previously proposed, sensory timing depends on the interaction between incoming stimuli and time-dependent changes in the internal state of recurrent networks [13,14]. A key distinction between models is the regime of recurrent networks. Motor timing would rely on regimes with strong internal connections capable of self-sustained activity, whereas sensory timing depends on with weak connections regimes, which do not support self-perpetuating dynamics. One consequence of these differences is that the circuits involved in motor timing can encompass longer time scales of many seconds.

Motor timing

Motor control, from catching a ball to playing the piano, requires the production of complex spatiotemporal patterns of muscle activity. The spatial dimension refers to which muscle groups are activated, and the temporal dimension to the timing of activity in relation to other muscle groups or to external sensory stimuli. Most motor tasks, including speech production and playing a musical instrument, require carefully orchestrated movements timed on the order of tens of milliseconds to a few seconds. In the following discussion we focus on motor problems that explicitly require timing, as opposed to the production of any sequence of movements, such as touching different points on a computer screen (which should not be taken to imply that we view the mechanisms as different).

Localization of motor timing

Many different neural structures are known to contribute to motor control. Most movements require a precise temporal structure, so it is not surprising that many of these areas have also been implicated in motor timing. One area known to be important for motor coordination, the cerebellum, was one of the first structures hypothesized to contribute to timing [15] and decades of research have provided compelling evidence that the cerebellum is critical to some forms of motor timing. For example, human studies have revealed that patients with cerebellar lesions exhibit a range of general motor coordination deficits [16,17]. In addition, this patient population has impairments in pure motor timing tasks, including the precision (standard deviation) of finger tapping ([18,19], but see [20]). More directly, animal studies have established that the appropriate timing of conditioned eyeblink responses, which are learned as a function of the conditioned stimulus–unconditioned stimulus interval, are abolished by localized cerebellar lesions [21,22].

Other areas also play an important role in timing, particularly in the timing of complex movements associated with recently learned motor tasks. Numerous studies indicate that the basal ganglia are involved in motor timing. Such a role has been inferred in part from pharmacological and Parkinson's disease studies that point to alteration in motor timing on a scale of seconds [23–25]. In addition, imaging studies have revealed changes in activity in the basal ganglia during motor production tasks [5,26–28].

Different neocortical areas have also been implicated in motor timing. Imaging studies have revealed a large, and as yet not agreed on, network of cortical areas that are activated during implicit and explicit timing tasks [5,26]. In addition, electrophysiological studies have revealed time-sensitive neuronal responses during motor timing tasks in many different cortical areas [29–32]. But converging evidence supports the role of pre- and supplementary motor areas [30,33], which are also known to contribute to sequence generation [34]. In subsequent sections, we argue that many aspects of motor timing can be addressed by models based on the internal dynamics of excitatory recurrent networks characteristic of neocortical circuits; for this reason, our discussion focuses primarily on timing in neocortical areas.

Models of timing

Timing has long been incorporated into abstract models of motor control [35]. However, relatively few biologically realistic neuron-based models of motor timing have been proposed. The internal clock model (Glossary), for instance, assumes the presence of a pacemaker and accumulator in the brain; however, evidence on the location of the pacemaker or nature of the accumulator has been elusive after several decades of research. Other models of motor control and sequence generation either have simply assumed that there is a population of neurons that fires selectively at different points in time, or have limited their focus to sequence generation [36–38].

Multiple oscillator models

Some models are based on the hypothesis that timing arises from a population of elements oscillating at different frequencies [39,40]. These multiple-oscillator models do not require integration or counting of pulses in any of the oscillators, but rely on detecting specific beats or synchronous patterns among the population of oscillators. This detection process can be performed by readout neurons that detect the coincident activity of a subset of oscillators corresponding to a specific point in time.

Labeled-line models

Other biologically inspired models have proposed that motor timing might rely on an array of neuronal elements that exhibit a spectrum of different time constants of some neuronal or synaptic property, implementing what is commonly referred to as a labeled line [37,41]. Biologically plausible implementations of such spectral, or delay line, models have been proposed, including the time constants of neurotransmitter receptors [42], the time constant of slow membrane conductances [43,44] and the decay time of inhibitory postsynaptic potentials [45,46]. In these models all elements share a common implementation, but at least one of the variables is set to a different value, which endows each unit with the ability to respond selectively to a different interval. In specialized domains, such as the auditory system of the bat, there is evidence that the duration of inhibitory postsynaptic potentials contributes to the detection of temporal windows of <50 ms. However, it seems unlikely that such mechanisms can be generalized to complex forms of temporal processing that require discrimination of the patterns generated by consecutive intervals and there is little evidence that they are involved in motor timing.

Population clock models

A distinct class of neural-based models proposes that time is both generated and represented in a population of essentially identical neurons [47]. Here timing emerges from the dynamics of the entire network and is encoded in the population vector of neurons that are active at any specific point in time (Box 2). Critical to the notion of a population clock is that the activity of neurons in the network is time-varying and that output units can be trained to recognize specific patterns of activity within the population clock network and thus serve as a readout of time. Note that as with multiple oscillator or labeled-line models, time can ultimately be read by a single output neuron; importantly, however, timing per se (the clock) is an emergent property of the network; in other words, it relies on the interaction between many units, and the time scale over which a network can time far exceeds the longest time constant of the individual elements.

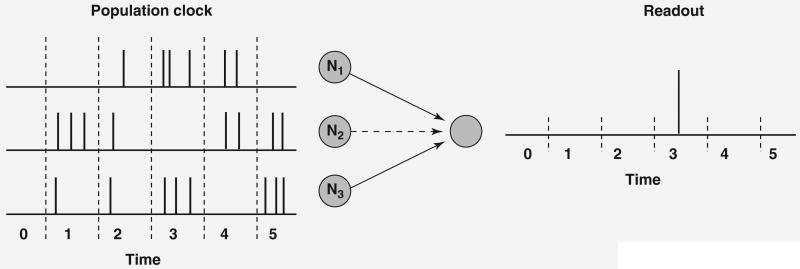
Box 2. Population clocks.

For a population clock it is assumed that a group of neurons exhibit time-varying activity and that each point in time is coded by a unique pattern of activity in the network [47–49]. Consider a group of three neurons (N₁–N₃) that in response to a start signal (t = 0) reliably produce a specific pattern of firing (represented as the number of spikes in a time bin, Figure I). In this example, each time step can be identified by a unique combination of the number of spikes in each cell: bin t₁ has the spike signature [0,3,1], whereas bin t₃ has the signature [3,0,3]. Time can be read by output units that receive synapses from all the neurons in the population clock network if the synaptic weights are adjusted appropriately. For example, to generate a motor response at time bin 3, the synapses onto the output neuron from N₁ and N₃ should be fairly strong, because both these neurons are strongly active at this time bin and not at the others (note that the synapses cannot be too strong because then the output would fire at other time points as well). In a network in which thousands of neurons fire in a time-varying manner, it is easy to establish a population code for time. A simple instantiation of a population clock consists of a chain of neural activity in a population of neurons. In this case, each point in time would be represented by the activity of a single or a small population of neurons [52,53,77,78]. This sparse code (which is essentially a labeled line) for time has been observed experimentally [79]

Figure I.

Reading a population clock.

The critical challenge to any population clock model is how a dynamic population of active neurons would be generated. In principle, any recurrent neural network (Glossary) can produce time-varying activity, which can be thought of as a neural trajectory (Box 3). Assuming that a network is in the appropriate regime, a given population of active neurons A could activate population B and so on, leading to the pattern A→B→C→…, in which each letter corresponds to a distinct but possibly overlapping population of neurons. The second challenge to population clock models is that the trajectory must be able to be elicited in a robust and reproducible manner. We address these two issues below and show that the dynamics of a recurrently connected neural network can subserve a population clock in neocortical circuits.

Box 3. Neural trajectory.

A complex and time-varying pattern of activity in a population of neurons can be thought of as a neural trajectory in neural space. In a network with three neurons, all possible patterns of activity can be represented in three-dimensional space, where each axis corresponds to the instantaneous firing rate of each neuron (or the presence or absence of a spike at each point in time). In a network composed of 1500 neurons, the trajectory takes place in a 1500-dimensional space that can nevertheless be visualized using dimension reduction methods. Figure I illustrates the simulated activity of 10 units from the network shown in Figure 1. In this simulation the activity of each unit is bounded between −1 and 1. The activity of the entire network can be visualized as a 3D neural trajectory by plotting the first three components of a principal component (PC) analysis on the activity of the entire network. Note that in the neural trajectory time is represented as a color gradient. Thus, the rate of color change provides information about the speed of the trajectory or the rate of change of the firing pattern. The same point in time could be represented by many nearby points in state space, and the output or downstream neurons that would fire with the network is somewhere within this cloud of points. The effect of both the input pulse and the output pulse (fed back) on the network activity is evident as large excursions in PC space.

Figure I.

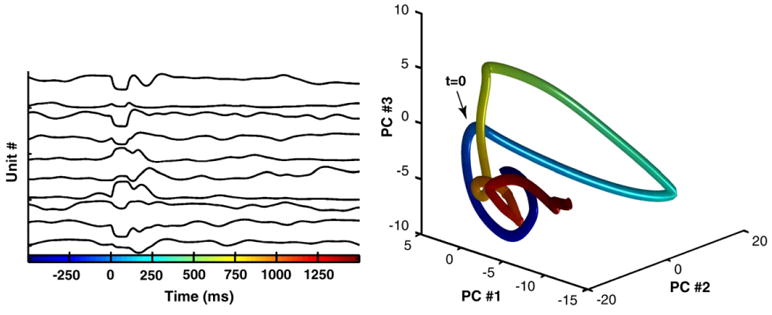
Low-dimensional representation of a high-dimensional neural trajectory. Left: activity of 10 sample units in a network of 1500 units. Right: Plot of the first three components of a Principal Component analysis on the activity of the whole network.

Dynamics in recurrent networks

The first population clock model was proposed by Michael Mauk in the context of the cerebellum [48–50]. In his model, a continuously changing population of granule cells encodes time, and specific time points are read by Purkinje cells that detect distinct patterns of granule cell activity. It is proposed that the evolving trajectory of granule cells arises from the interaction between a tonic input into the cerebellum and the internal state defined by the granule and Golgi cells. Granule cells excite, and are inhibited by, Golgi cells, thus creating a negative feedback loop that can result in a dynamic pattern of granule cell activity and implement a population clock. Realistic large-scale simulations based on spiking neurons have revealed that it accounts for many of the experimental observations on timing of eyeblink conditioning [50,51].

The cerebellar circuitry is unique for its absence of recurrent excitatory activity. Consequently, the cerebellum cannot sustain a self-maintaining and dynamic pattern of activity in the absence of an external input. By contrast, neocortical networks are characterized by robust excitatory connections capable of sustaining internal dynamics.

Critical to the dynamics of recurrent neural networks, and whether they support self-maintaining activity, is the average strength of the recurrent synaptic weights. It is evident that if the internal weights are on average very weak, there is little coupling between the units and in response to a brief input (or start signal) network activity will quickly fade away (this is generally the regime a state-dependent network model operates in for sensory timing). By contrast, if the recurrent weights are strong, it is easy to imagine that in response to a brief input the network could potentially enter a self-maintaining activity regime (which could be steady state, periodic or non-periodic in nature). Thus, the weights within the recurrent network are critical to the behavior of the circuits. Yet setting these weights in theoretical models has proven challenging because of the highly nonlinear nature of the internal dynamics. It has recently been shown that biologically plausible learning rules facilitate the development of spatiotemporal patterns that can be used for motor timing, although the patterns are simple and limited in time scale [52,53].

It seems likely that the brain harnesses the computational potential of recurrent networks by using the complex dynamic regimes that are ideally suited to generate population clocks. However, these regimes are precisely those that lead to chaotic dynamics [54]. In a system with chaotic activity, there is a critical dependence on the initial conditions and noise: tiny perturbations to the system will make the trajectory of a system diverge exponentially in time. It has been shown that feedback is a powerful tool for controlling the chaotic dynamics of nonlinear systems [55,56] and advances have provided insights into how recurrent networks can both generate complex patterns -that could be used for a population clock – and not be dominated by chaos. In the context of artificial networks, Jaeger and Haas [57] demonstrated that carefully controlled feedback can be used to generate complex yet reproducible patterns. Sussillo and Abbott [58] recently extended this approach and demonstrated how it can be used for networks that are spontaneously active (strong internal connections). The recurrent weights in these networks are set at random (with specific distributions), avoiding the need to carefully set them. Pivotal, however, are the weights of the recurrent network onto the output unit, because they define the output and feedback (if present). Different supervised learning rules have been used to effectively adjust these weights, and using both firing-rate and spiking models it has been shown that recurrent networks with feedback can generate time-varying outputs [57–60].

Recurrent networks with strong internal coupling, with or without feedback, are potentially well suited for timing tasks. Consider a psychophysical task that requires a subject to press a button 1 s after stimulus 1 and 2 s after stimulus 2. As shown in Figure 1, a recurrent network can be trained to solve this task; in response to a brief input representing stimulus 1, a well-timed response is generated with a delay of 1 s (the time constant of the elements in this circuit was 10 ms, which, along with the size of the network, determines the upper limit that can be timed [61]). Importantly, in response to a different input (stimulus 2) the same network can be trained to generate a response at 2 s. Specifically, different input patterns will set the network along different neural trajectories, and thus the same points in absolute time can be encoded in different network states, depending on the task. An inherent strength of this approach is that it provides a general and robust model of motor timing. As shown in Figure 2, it is easy to use the same network to generate temporal patterns (multiple time responses from the same output unit), each triggered by different inputs. Thus, the same network can be used to generate multiple distinct temporal or spatiotemporal output patterns [58].

Figure 1.

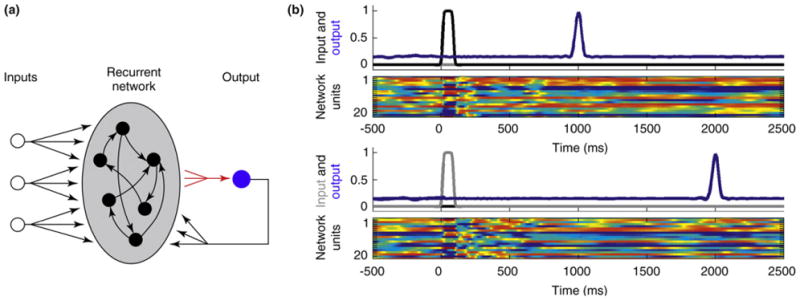
Simple interval timing with a population clock model. (a) The network architecture is composed of a population of 1500 firing-rate units (time constant 10 ms), all of which are connected to a single output unit that also provides feedback to the network. Each target output pattern (blue traces in panels b and c) is triggered by a combination of the three inputs to the network. Tonic input 3 sets the network to a ready state (not shown) and then pulses at inputs 1 or 2 are used to elicit either of two different trained output patterns. Training consists of adjusting the weights from the recurrent units onto the output unit (red arrows). Network architecture and the learning rule used to train the weights onto the output units were similar to those reported by Sussillo and Abbott [58]. The network connectivity matrix was sparse with probability of connection p = 0.1 and synaptic strength factor g of 1.35. A noise ‘current’ from a uniform distribution with a maximal amplitude of 0.001 was present in all the units. It should be stressed that although these simulations are biologically realistic in the sense that they rely on the interaction of neuron-like units, future work must use spiking units with realistic synaptic dynamics. In addition, the precise role of feedback when using nonperiodic targets must be examined; indeed, similar results can be obtained in the absence of feedback. (b) The upper panel shows the activity of the output unit trained to generate a delayed pulse-like response at 1 s to input 1 at time zero (traces from three different trials are overlaid). The lower panel shows a sample of the activity of the units in the recurrent network. The activity level of the recurrent units is color-coded and bounded between −1 (blue) and 1 (red). Input and output activity is normalized to the corresponding maximum value. (c) The same network shown in panel b generates an output pulse at 2 s in response to a pulse in input 2 at time zero (three traces overlaid).

Figure 2.

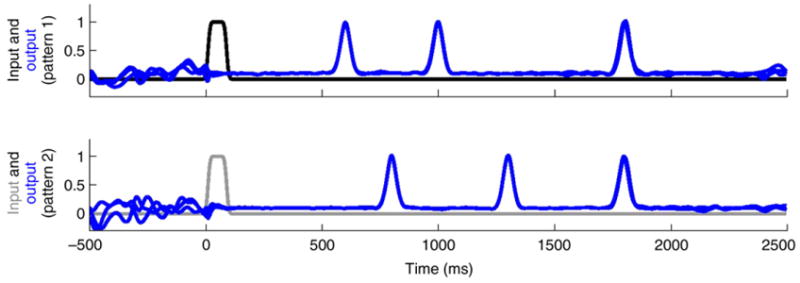
Production of two different complex temporal patterns. The same type of network as shown in Figure 1 was trained to produce two different temporal patterns, each consisting of three pulses. When pattern 1 is elicited, the output unit pulses at 600, 1000 and 1800 ms, whereas in pattern 2 the output pulses at 800, 1300 and 1800 ms. Pattern 1(2) is triggered by input 1(2). Three traces for each input are overlaid. Input and output are normalized to the corresponding maximum value. The synaptic strength factor was 1.4.

Neural correlates of timing

In vivo electrophysiology studies have revealed neural correlates of time in animals when performing tasks involving implicit or explicit timing tasks. One robust observation is that some neurons exhibit a more or less linear change in firing rate as time elapses (increasing or decreasing). Such ramping activity has been observed in different parts of the brain, including the prefrontal, parietal and motor areas [30,33,62,63]. Typically, graded firing rates that peak at the time of an anticipated response are observed. Although activity in ramping neurons correlates with time, these neurons might not be keeping track of absolute time, but might reflect temporal expectation of or preparation for a motor response, which in most tasks is linearly related to absolute time. In a study in which the delay before an expected event was drawn from a bimodal distribution, the firing rate of ramping neurons did not increase monotonically with time, but increased and decreased according to expected likelihood [64]. Thus, ramping neurons might not be telling time, but using temporal information from other areas to anticipate or react to events [5].

It has been proposed that the linear ramping of neuronal firing rate is a result of neuronal or network mechanisms [65–67]. Importantly, the population clock model based on recurrent networks with feedback can account for the experimentally observed ramping responses. Specifically, the readout units of these networks can be trained to exhibit ramping behavior. As shown in Figure 3, when the strength of the coupling within the recurrent network is relatively weak (but still self-sustaining), the activities of neurons in the population clock can themselves be positively or negatively ramping. On the other hand, with strong internal coupling (rich internal dynamics), activity in the population clock is highly variable. In both cases, however, the weights of synapses onto the readout unit can be set so that it fires in a linear manner.

Figure 3.

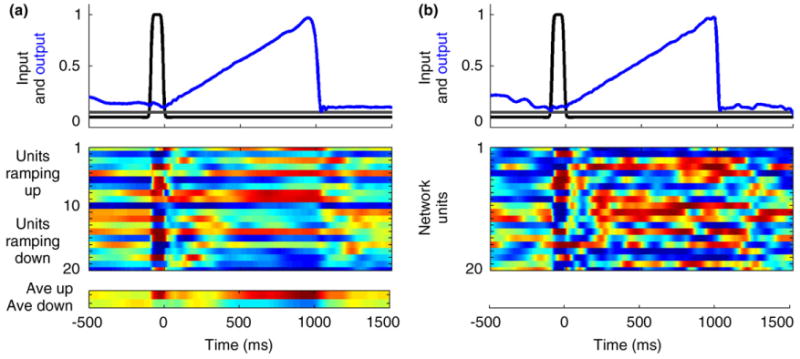
Ramping output. Dynamics or the regime in the network is governed in part by the synaptic strength factor g that scales the weights in the recurrent network. A value of g < 1 leads to decaying activity, whereas values greater than 1 make the network increasingly chaotic. (a) In this simulation, the internal synaptic strength factor was at the low end of the g>1 regime (g = 1.25) and the output unit was trained to ramp linearly from 0 to 1000 ms. In this regime, many of the neurons in the recurrent network exhibit approximately linear (graded color transitions) responses during the trained interval (raster plot shows selected units grouped according to whether they exhibit a positive or negative slope; average of ramping up and ramping down units shown below). Input and output are normalized to the corresponding maximum value. (b) When the internal synaptic coupling is increased (g = 1.5) the internal dynamics of the network becomes more complex and most recurrent units do not ramp in a linear fashion; however, the output unit can still be trained to exhibit a linear ramp. The weights of the output to recurrent units were bounded between −0.5 and 0.5 in these simulations.

In addition to linearly ramping neurons, electrophysiological studies have revealed a rich diversity of time-varying firing rate profiles, including neurons that fire at select time intervals or in a complex aperiodic manner [31,68–70]. These observations are what would be expected for a population clock. Indeed, some of these studies have shown that a linear classifier (readout unit) can be used to decode time based on the profiles of the experimentally recorded neurons, thus effectively implementing a population clock.

Concluding remarks

Population clock models propose that motor timing arises from the time-varying activity of a population of neurons. We suggest that the dynamics required for a population clock arises naturally in recurrent cortical networks as a result of the internally generated dynamics, but many critical issues regarding the control and regimes of neural dynamics in these networks remain to be resolved. Importantly, a given network can embark on different neural trajectories depending on the task at hand; this provides a powerful mechanism to generate a large number of timed motor patterns (Figures 1 and 2). Thus, in principle, different well-timed sequences of key presses on a piano can be generated by triggering different sets of inputs to the recurrent network and appropriately adjusting the weights from the recurrent units to a small set of output units.

The population clock framework falls into the category of intrinsic models, and thus many of its predictions require resolution of whether different forms of timing rely on distinct circuits. Recent psychophysical experiments have suggested that sensory timing is local, which indirectly supports the notion that sensory and motor timing are distinct [10–12], but future research must further examine this issue. Population clocks predict that the spatial and temporal components of motor patterns can be inextricably linked; once a spatiotemporal motor pattern is learned, it could be difficult to transfer the learned temporal structure to a new spatial pattern (e.g. a different sequence of finger movements). This is because both the spatial and temporal patterns are jointly encoded in the internal dynamics of the network (although population clocks could be used to code for absolute time if different external stimuli triggered a master neural trajectory). Whereas some psychophysical data are consistent with this suggestion [71,72], it remains an unresolved issue [73]. Ultimately, however, validation of the population clock model will require electrophysiological confirmation of the predicted complex neural trajectories and demonstration that modification of these trajectories alters behavioral timing.

Glossary

Dedicated models of timing

models in which timing relies on specialized and modular neural mechanisms that are primarily dedicated to temporal processing. Man-made clocks are examples of dedicated timers, as is the internal clock model of timing (Box 1).

Internal clock model

one of the first models of timing. The pulses of a central oscillator or a pacemaker are integrated by an accumulator, thus providing an explicit and linear metric of time (Box 1).

Intrinsic models of timing

models in which timing is a general and inherent ability of neural networks. In these models the same neural circuit processes temporal information and other feature dimensions of stimuli. An example of an intrinsic mechanism for timing is the state-dependent network model (Box 1).

Labeled-line model

phenomenological model in which it is assumed that different cells represent different time periods or delays. Labeled lines are often used in models that require timing but that are agnostic as to the neural mechanisms of timing.

Motor timing

production of timed motor actions or responses, ranging from a simple timed motor response to complex spatiotemporal patterns of muscle activation. Examples of motor timing include self-paced finger tapping, interval reproduction, sending a message in Morse code and playing the piano.

Population clock model

models in which a given point in time is represented by a unique spatial pattern of activity within a neural network. Distinct patterns of activity in the network unfold over time (Box 2).

Recurrently connected neural networks

networks in which the connections can form a loop; thus, activity in a single unit could indirectly feedback onto itself. Most neocortical circuits exhibit robust recurrent connectivity and many theoretical models, including state-dependent networks, rely on recurrent connectivity. Recurrent networks stand in contrast to feed-forward models such as a standard multilayer perceptron.

Sensory timing

processing or discrimination of stimuli based on temporal features. A typical sensory timing task is discrimination of the duration or interval of auditory or visual stimuli.

Spatiotemporal pattern

pattern of neural activation that unfolds both in time and space, where space refers to different neurons in a circuit.

State-dependent network model

model that proposes that cortical networks are inherently capable of processing spatial and temporal information in the range of hundreds of milliseconds as a result of state-dependent network properties imposed by ongoing activity (the active state) and time-dependent cellular and synaptic properties (the hidden state).