MECHANISMS OF INITIAL ENDPLATE FAILURE IN THE HUMAN VERTEBRAL BODY

Abstract

Endplate failure occurs frequently in osteoporotic vertebral fractures and may be related to the development of high tensile strain. To determine whether the highest tensile strains in the vertebra occur in the endplates, and whether such high tensile strains are associated with the material behavior of the intervertebral disc, we used micro-CT-based finite element analysis to assess tissue-level strains in twenty-two elderly human vertebrae (81.5 ± 9.6 years) that were compressed through simulated intervertebral discs. In each vertebra, we compared the highest tensile and compressive strains across the different compartments: endplates, cortical shell, and trabecular bone. The influence of the Poisson-type expansion of the disc on the results was determined by compressing the vertebrae a second time in which we suppressed Poisson expansion. We found that the highest tensile strains occurred within the endplates whereas the highest compressive strains occurred within the trabecular bone. The ratio of strain to assumed tissue-level yield strain was highest for the endplates, indicating that the endplates had the greatest risk of initial failure. Suppressing the Poisson expansion of the disc decreased the amount of highly tensile-strained tissue in the endplates by 79.4 ± 11.3%. These results indicate that the endplates are at the greatest risk of initial failure due to the development of high tensile strains, and that such high tensile strains are associated with the Poisson expansion of the disc. We conclude that initial failure of the vertebra is associated with high tensile strains in the endplates, which in turn are influenced by the material behavior of the disc.

1. Introduction

Osteoporotic vertebral fractures frequently involve the endplates of the vertebral body (Aebi, 2009; Brinckmann et al., 1983; Magerl et al., 1994; Moore, 2000; Perey, 1957; Wasnich, 1996). It has been suggested that the involvement of the endplates may even distinguish a vertebral fracture from a vertebral deformity (Ferrar et al., 2005). Understanding the mechanisms of endplate failure may therefore provide insight into the etiology of osteoporotic vertebral fractures.

The mechanisms underlying endplate failure remain unclear. Despite overall direct compressive loading of the vertebra by the intervertebral disc, there is evidence that appreciable levels of tensile strain can develop at the endplates (Frei et al., 2001; O'Connell et al., 2007), perhaps due to the fluid-like behavior of the intervertebral disc (Eswaran et al., 2007; Shirazi-Adl et al., 1984). The development of large tensile strain is significant biomechanically because bone tissue is weaker in tension than in compression (Bevill et al., 2009; Niebur et al., 2000; Reilly and Burstein, 1975) and thus any factors—such as the material behavior of the intervertebral disc—that contribute to the development of high tensile strain in the endplates may have an important role in vertebral fragility. However, the relative magnitude of the tensile strains in the endplates versus that of the cortical shell and trabecular centrum has never been quantified, nor has the relative magnitude of tensile and compressive strains in the vertebra been compared generally. Thus, it is not clear if the development of high tensile strains in the endplate is an important factor that might predispose the vertebral body to early failure and what role, if any, the disc may have on this. Addressing this issue, we sought to determine the location of the highest tensile strains within the vertebral body and the influence of the material behavior of the disc on such strains.

2. Materials and Methods

Study design

Since measuring tissue-level strains in the endplates, cortical shell, and trabecular bone would be very difficult using biomechanical tests, we assessed tissue-level strains by performing high-resolution, micro-CT-based finite element analysis on 22 elderly human vertebral bodies in which the vertebral bodies were virtually compressed through simulated intervertebral discs. To determine the regions within the vertebra that are likely to fail in tension and compression, we used the finite element analysis of each vertebra to identify the most highly strained tissues by type—either tension or compression—and compared the amount of highly-strained tissue of each type across the different compartments: endplates, cortical shell, and trabecular bone. Since the tissues having the highest strains with respect to the tensile and compressive yield strains are likely to fail first, we also compared the relative magnitudes of the highest tensile and compressive tissue strains across the different compartments after normalizing these strains to their respective yield strains. The influence of Poisson-type expansion of the disc on these results was determined by virtually compressing the vertebral bodies a second time in which the Poisson expansion was suppressed. The change in the amount of highly-strained tissue within each compartment after suppressing the Poisson expansion was calculated for all of the vertebral bodies.

Sample preparation and micro-CT scanning

Twenty-two human T9 whole vertebral bodies were obtained fresh-frozen from cadavers (n = 11 male; n = 11 female; age range: 53–97 years, mean±SD = 81.5±9.6 years) with no medical history of metabolic bone disorders. The posterior elements were then removed and each isolated vertebral body was micro-CT scanned using a 30 µm voxel size (Scanco 80; Scanco Medical AG, Brüttisellen, Switzerland). To reduce computational cost, the scans were coarsened to 60 µm voxel size before the hard tissue and marrow were segmented using a global threshold value (Scanco). The bone tissue in the resulting images was then compartmentalized (Figure 1) using a custom script (IDL 6.2; ITT Visual Information Solutions, Boulder, CO USA) described in detail elsewhere (Eswaran et al., 2006; Eswaran et al., 2007). Briefly, the script uses moving averages for the thickness of the cortical shell and endplates to account for the thin and porous nature of these structures and to determine the boundary between these structures and any adjacent trabeculae.

Figure 1.

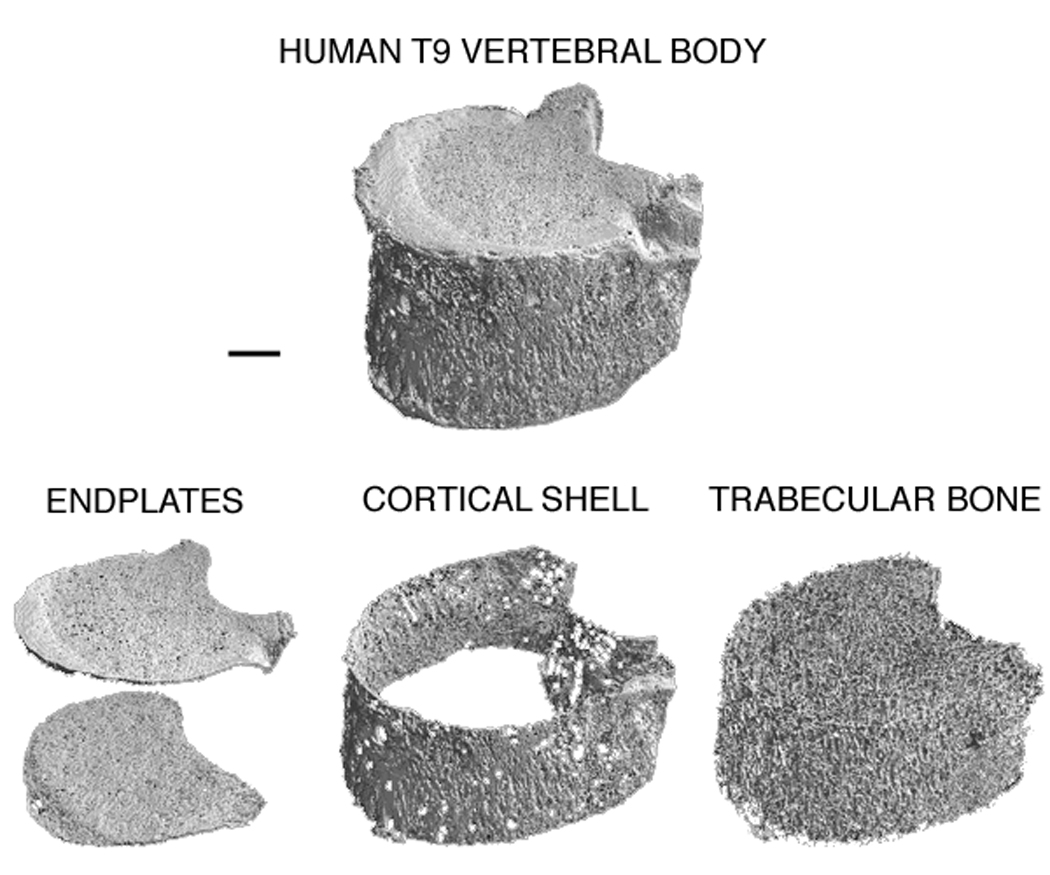
Micro-CT rendering of a human T9 vertebral body (top) compartmentalized into the endplates (bottom, left), cortical shell (bottom, center), and trabecular bone (bottom, right). Donor information: 82 year-old male. Scale bar: 5 mm.

Finite element modeling

High-resolution finite element models of each vertebral body were created using the voxel-based technique (Eswaran et al., 2007; Van Rietbergen et al., 1995). Each 60 µm-sized cubic voxel in the coarsened scans was converted into an 8-node brick element to create a finite element model of the entire vertebral body. Element size was chosen based on findings from a numerical convergence study (Eswaran et al., 2007) and was 4–15 times smaller than the thickness of the cortical shell (0.25–0.4 mm (Edwards et al., 2001; Ritzel et al., 1997; Silva et al., 1994; Vesterby et al., 1991)) and endplates (0.26–1.08 mm (Edwards et al., 2001; Silva et al., 1994; Zhao et al., 2009)), thereby exceeding the minimum ratio recommended to satisfy convergence behavior for trabecular bone (Guldberg et al., 1998; Niebur et al., 1999). Every element was tagged with a unique identifier corresponding to its compartment: endplates, cortical shell, and trabecular bone. The intervertebral discs were simulated by augmenting disc layers to the endplates in the models. Only half of the height of each disc (2.5 mm) was modeled since thoracic discs have the most uniform height (~5 mm) (Middleditch and J., 2005) and since we used a symmetry boundary condition about the disc’s mid-transverse plane (Eswaran et al., 2006; Eswaran et al., 2007).

Material properties in the finite element models were assigned based on whether the element belonged to the bone tissue within the vertebral body or the soft tissue within the discs. All bone tissue belonging to the vertebral body was given homogeneous elastic and isotropic material properties (elastic modulus of 10 GPa (Bevill et al., 2009) and Poisson’s ratio of 0.3) since the cortical shell is often described as condensed trabeculae (Mosekilde et al., 1993; Roy et al., 1999; Silva et al., 1994) and since the anisotropy of trabecular tissue has only a minor role in trabecular behavior (Kabel et al., 1999). Furthermore, these material properties were used for all vertebrae since the coefficient of variation in mean tissue mineral density—one determinant of differences in tissue elastic modulus amongst individuals—for trabecular bone is less than about 2% (Roschger et al., 2003). For the soft tissue belonging to the intervertebral disc, we assigned homogeneous elastic and isotropic material properties typical of the annulus (elastic modulus of 8 MPa (Duncan and Lotz, 1998) and Poisson’s ratio of 0.45 (Fagan et al., 2002; Kurowski and Kubo, 1986; Lin et al., 1978; Natarajan et al., 2004)) since the mean age of the cadavers was 82 years and since degenerated discs are more uniform than are healthy discs (Antoniou et al., 1996; Iatridis et al., 1997).

Loads on the vertebral bodies were simulated in the finite element models to mimic compressive loading. In all of the models, the top surface of the disc was displaced in the superior-inferior direction. The magnitude of the applied displacement was a constant percentage (1%) of the original height of the model to facilitate comparison of the results across multiple vertebrae exhibiting considerable heterogeneity in size and shape. Roller-type constraints at the mid-transverse plane of each disc were used to model the symmetry boundary conditions.

The resulting finite element models had up to 80 million elements and over 300 million degrees of freedom and required specialized software and hardware for analysis. All computations were performed using custom code—including parallel mesh partitioner and algebraic multigrid solver (Adams et al., 2004)—on an IBM Power4 supercomputer (Datastar; San Diego Supercomputing Center, San Diego, CA USA). Typical hardware requirements for a single analysis comprised 880 processors and 1800 GB total memory. The average CPU time was 115 hours.

To determine the effect of the Poisson expansion of the disc on the strains in the bone, a second finite element analysis was performed for each vertebra in which we suppressed such behavior (Poisson’s ratio of 0). We focused on this effect since our previous work indicated that the general behavior of the vertebra was sensitive to the Poisson ratio (Eswaran et al., 2007) but not to the elastic modulus (Eswaran et al., 2006). Without Poisson expansion, a disc under axial compression would not expand transversely. By contrasting values of 0.45 and 0, we simulated discs with accentuated vs. suppressed fluid-like behavior, and in that way, explored how such different behaviors could influence the tissue-level strains in the vertebra.

Outcomes

A number of outcomes from the finite element analyses were used to identify the most highly strained bone tissue in the models. The 90^th percentile limits of the maximum and minimum principal strains were first calculated for each vertebral body (Eswaran et al., 2007). Any bone element having either its maximum principal strain or minimum principal strain beyond the corresponding strain limit for that vertebra was classified as “highly-strained”. The proportion of highly-strained tissue in tension and in compression within each compartment (i.e. endplates, cortical shell, and trabecular bone) was expressed as a percentage of the total amount of highly-strained tissue in that compartment. To compare the magnitudes of the highest tensile and compressive strains across the various compartments, the 90^th percentile limits of the maximum and minimum principal strains were calculated separately for the endplates, cortical shell, and trabecular bone. To identify the tissues with the greatest risk of initial failure, the strain limits for each compartment were normalized by estimates of the effective yield strains for vertebral bone tissue (tension = 0.34%; compression = −0.69% (Bevill et al., 2009)).

Statistics

Outcomes were compared across compartments using paired t-tests with Bonferroni adjustments for multiple comparisons. The change in the amount of highly-strained tissue in tension and in compression in each compartment due to suppression of Poisson expansion of the disc was determined twofold: 1) a single-group t-test with Bonferroni adjustment to determine if the change was statistically different from zero, and 2) a paired t-test with Bonferroni adjustments to determine if the change was statistically different across compartments. All tests were taken as significant at p < 0.05.

3. Results

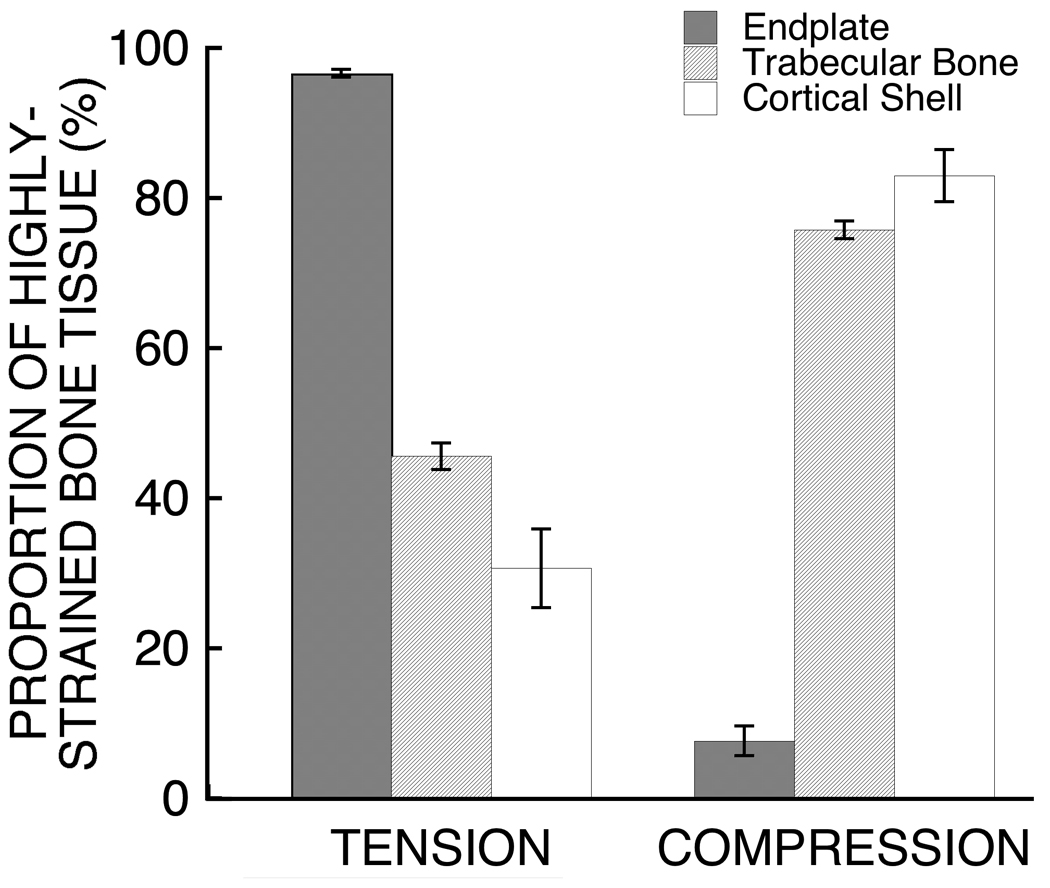
During the simulated compressive loading of the vertebral body, the endplates were more highly strained in tension than were the trabecular bone and the cortical shell, whereas the latter two were more highly strained in compression (Figure 2). Across all 22 vertebrae, an average (mean ± S.D.) of 96.6 ± 1.2% of the highly-strained tissue within the endplate was strained in tension (Figure 3), which was more than twice the proportion of highly-strained tissue in tension in the trabecular bone (45.6 ± 4.0%) and cortical shell (30.7 ± 11.8%). With respect to anatomical location, the highly strained tissue in the endplates was concentrated in the central region and comprised a larger amount of the tissue belonging to the superior endplate (27.7 ± 7.7%) than to the inferior endplate (20.8 ± 6.6%; p < 0.002 paired t-test).

Figure 2.

Mid-sagittal cutaway from a human vertebral body showing the typical distribution of highly strained tissue in tension (red) and in compression (blue) predicted by finite element analysis. The bone tissue behind the para-sagittal slice and below the superior endplate has been removed from the image for clarity.

Figure 3.

Comparison of the relative proportion of bone tissue highly strained in tension and in compression between the endplates, trabecular bone, and cortical shell. All comparisons were significantly different (p<0.0001). Error bars show 95% CI (n=22 vertebral bodies).

The bone tissue within the endplates, which had higher absolute values of tensile strains than either the bone tissue within the trabecular bone or the cortical shell, also had the greatest risk of initial failure (Table 1). The 90^th percentile compressive strain limit was higher for the bone tissue within the trabecular compartment than for the bone tissue within the other two compartments, but when the magnitude of the tensile and compressive strain limits was normalized by the assumed magnitude of the yield strains in tension and in compression, respectively, the tissue belonging to the endplates that was highly strained in tension had the greatest risk of initial failure (Table 1). Initial failure of tissue in compression was not likely in the endplates but was most likely in the trabecular bone. These trends were similar when different assumed values of the yield strains were used (tension = 0.40%; compression = −0.62% (Bevill et al., 2009)).

Table 1.

Maximum and minimum principal strain limits (90^th percentiles) for bone tissue in the endplate, trabecular bone, and cortical shell.

	Endplate	Trabecular Bone	Cortical Shell
Maximum Principal Strain
90th Percentile (μstrain)	836 ± 237 a,b	600 ± 139 b	437 ± 111
Risk of Initial Failurec	0.25 ± 0.07	0.18 ± 0.04	0.13 ± 0.03
Minimum Principal Strain
90th Percentile (μstrain)	−525 ± 126 a,b	−1085 ± 232 b	−861 ± 162
Risk of Initial Failurec	0.08 ± 0.02	0.16 ± 0.03	0.12 ± 0.02

Data given as mean ± SD (n=22 vertebral bodies).

^ap < 0.0001 vs. trabecular bone

^bp < 0.0001 vs. cortical shell

^cThe maximum and minimum principal strain limits (90^th percentiles) were normalized by the respective yield strains (tension = 0.34%; compression = −0.69% (Bevill et al., 2009)) to determine the relative risk of initial failure. Compared to a lower number, a higher number indicates a greater relative risk of initial failure. Pairwise comparisons between each of the risks of initial failure were significantly different (p < 0.0001) except for the comparison between the risk of initial failure in the cortical shell in tension and in compression.

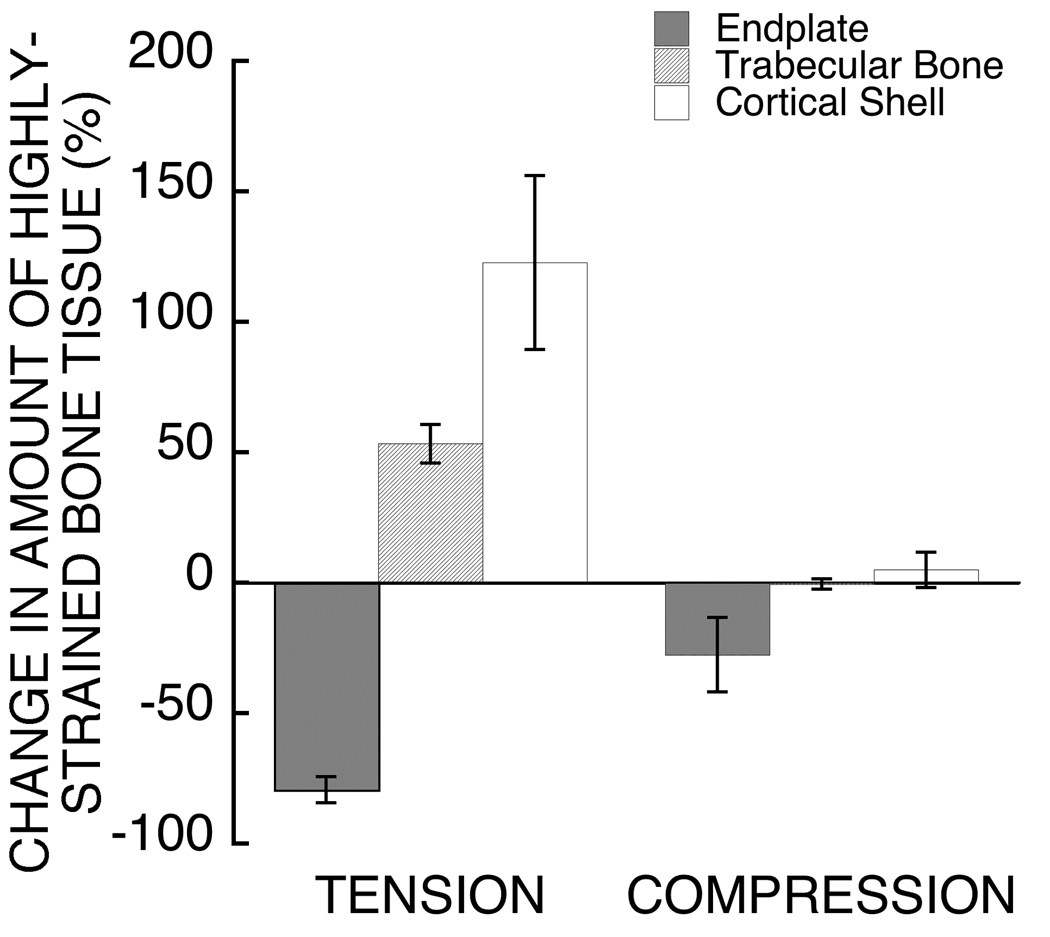
The development of these high tensile strains in the endplates was directly associated with the Poisson expansion of the intervertebral disc (Figure 4). When Poisson expansion was virtually suppressed, the amount of highly-strained endplate tissue in tension decreased by 79.4 ± 11.3% (Figure 5). Removing this behavior increased the amount of highly-strained tissue in tension belonging to the trabecular bone and cortical shell, with the effect being two-fold greater for the latter. For the endplates, suppressing the Poisson expansion of the disc reduced the total amount of highly-strained tissue more in the superior endplate (−80.6 ± 12.3%) than in the inferior endplate (−73.1 ± 15.0%; p=0.005 paired t-test).

Figure 4.

Distribution of highly strained tissue in tension (red) and in compression (blue) within the superior endplate of a human vertebral body when loaded via simulated intervertebral disc (left). Removing the Poisson expansion of the disc led to a 96% reduction in the total amount of highly-strained endplate tissue (inferior + superior) for this vertebral body (right).

Figure 5.

Comparison of the effect of suppressing the Poisson expansion of the disc on the amount of highly-strained tissue in tension and in compression between the endplates, trabecular bone, and cortical shell. The change in the amount of highly-strained tissue in tension was significantly different between the three groups (p<0.0001). The change in the amount of highly-strained tissue in compression was significantly different for the endplates only (p<0.0001 endplates vs. cortical shell and endplates vs. trabecular bone). Error bars show 95% CI (n=22 vertebral bodies).

4. Discussion

These findings support the concept that endplate failure may be an etiologic factor in osteoporotic vertebral fracture. Specifically, our findings indicate that initial failure of the vertebra is associated with the development of high tensile strains within the endplate, which in turn is influenced by the material behavior of the disc. Our previous work has shown that the general behavior of the endplates during compressive loading of the spine is sensitive to the material properties of the intervertebral disc (Eswaran et al., 2007). In cadaver experiments which observed frequent endplate failures, variations in proteoglycan content of the disc were associated (r² = 0.70) with variations in vertebral compressive strength (Hulme et al., 2007), but the link between the variations in disc properties and the mechanism of endplate or vertebral failure was unclear. Our new data provide a mechanistic link between endplate failure, initial vertebral failure, and the material behavior of the disc.

Our finding that the endplates were highly strained in tension is notable because bone tissue is weaker in tension than in compression, and because the type of tensile strains in the endplates may be more harmful than those in the other compartments. Uniaxial tension occurs in the axial trabeculae and cortices that bend under the applied compressive loads and in the transversely trabeculae that resist such bending. In contrast, a detailed analysis of the endplates revealed that biaxial tension exists in the plane of the endplate due to the Poisson expansion of the disc (Appendix A). Little is known about the failure behavior of bone tissue in biaxial tension; one hypothesis is that biaxial tension is particularly harmful because existing damage may be less able to “escape” the crack-propagating effects of this type of loading compared to uniaxial tension. Further work is recommended to understand the failure behavior of the endplates in biaxial tension and its dependence on the behavior of the intervertebral disc.

One limitation of this study is that by performing linear analyses, we could address only regions of initial failure, which may not represent the locations of final failure at the point of structural collapse of the vertebra. For example, we did not include the effects of large-deformations (Bevill et al., 2006; Stölken and Kinney, 2003), which could cause the tissue in slender trabeculae to fail before the tissue in thicker trabeculae fails (Gibson, 1985; Stölken and Kinney, 2003). Hence, the total amount and distribution of failed tissue may depend on the morphology of the bone (Fields et al., 2009; Morgan et al., 2004). Addressing this issue using nonlinear analysis would have required loading the spine segments to relatively large apparent strains (>10%) because of the highly compliant and nonlinear behavior of the disc. Given the models’ enormous size and numerical complexity, nonlinear analysis is computationally infeasible at this juncture. Thus, further work is required to extend the current findings to the structural collapse of the vertebra.

An additional limitation is that we assumed a homogeneous elastic and isotropic model for the intervertebral disc. The material behavior of the disc is complex, including material nonlinearity, time dependence, and intra- and inter-specimen heterogeneity (Iatridis et al., 1996; Pollintine et al., 2010; Wagner and Lotz, 2004). Previous finite element analyses of bone-disc complexes have accounted for some of this complexity, but have omitted inter-specimen heterogeneity and have treated the vertebra in a relatively simplistic fashion (Duncan and Lotz, 1998; Kurowski and Kubo, 1986; Natarajan et al., 2004; Shirazi-Adl et al., 1984). Here, we chose instead to model the bone in detail by using specimen-specific, high-resolution finite element models that explicitly captured the architecture of the vertebra. Our finding that the central endplates were highly strained in tension and that these tensile strains were associated with the material behavior of the disc agrees with results from more sophisticated models of the disc (Kurowski and Kubo, 1986; Shirazi-Adl et al., 1984). Furthermore, the remarkable consistency in the proportion of highly-strained endplate tissue in tension (97 ± 1.2%) across an elderly cohort exhibiting a wide variation in vertebral morphology suggests that this trend is likely to persist in the general population of elderly vertebrae. Also, our finding that the superior endplate was more vulnerable than the inferior endplate is in agreement with studies that accounted for the effects of intra- and interdiscal variations in disc behavior via direct biomechanical testing (Bay et al., 1999; Shirado et al., 1992; Zhao et al., 2009). Together, these similarities suggest that our simple disc model was sufficient for exploring general trends regarding the role of disc behavior on the mechanisms of vertebral failure. Further work is required to integrate sophisticated modeling of both the bone and the disc. Our results indicate that such analyses may provide new insight into the interaction between the bone and the disc as it pertains to vertebral strength.

The results of this study are consistent with and complementary to previous work that associated disc properties with endplate failure in the etiology of vertebral fractures (Eswaran et al., 2007; Hansson and Roos, 1981; Hulme et al., 2007; Shirado et al., 1992) and taken together, this body of work suggests disc material properties may influence vertebral strength via their effect on the development of high tensile strains in the endplates. Endplate strength is negatively influenced by the proteoglycan content within the nucleus of the disc (Hulme et al., 2007). The high concentration of proteoglycans in the nucleus of healthy discs pressurizes the central region of the disc (Adams et al., 1996; Middleditch and J., 2005). During axial loading, the pressurized nucleus directs the load to the center of the endplates (Kurowski and Kubo, 1986; Shirazi-Adl et al., 1984)—the thinnest (Zhao et al., 2009) and weakest (Grant et al., 2001) region. Complementary, our results showed that the endplates are highly strained in tension—a loading mode in which bone is biomechanically weak—and that these high tensile strains are associated with the fluid-like behavior of the intervertebral disc. Having established this, it appears reasonable to hypothesize that disc degeneration, which results in reduced water content (Iatridis et al., 1997), may well have an important influence on vertebral fracture etiology (Adams et al., 2006; Pollintine et al., 2004). Since we did not address the effects of aging or disc degeneration in this study, this motivates future work to assess real variations in disc properties—including those associated with disc degeneration—and the mechanisms of influence on vertebral strength (e.g. using micro-finite element methods validated with image-guided failure analysis (Hulme et al., 2008)).

In summary, our findings reveal two striking characteristics of the endplates that help to explain their frequent involvement in osteoporotic vertebral fractures: the endplates are at the highest risk of initial failure due to the development of high tensile strains, and the development of such high tensile strains is directly associated with the material behavior of the intervertebral disc.