Connecting instances to promote children’s relational reasoning

Abstract

The practice of learning from multiple instances seems to allow children to learn about relational structure. The experiments reported here have focused on two issues regarding relational learning from multiple instances: (1) what kind of perceptual situations foster such learning and (2) how particular object properties, such as complexity or similarity, interact with relational learning. Two kinds of perceptual situations were of interest here: simultaneous view, where instances are viewed at once, and sequential view, instances are viewed one at a time, one right after the other. We examine the influence of particular perceptual situations and object properties using two tests of relational reasoning: a common match-to-sample task (where new instances are compared to a common sample) and a variable match-to-sample task (where new instances are compared to a sample that varies on each trial). Experiments 1 and 2 indicate that simultaneous presentation of even highly dissimilar instances, one simple and one complex, effectively connects them together and improves relational generalization in both match-to-sample tasks. Experiment 3 showed simple samples are more effective than complex ones in the common match-to-sample task. However, when one instance is not used a common sample and various pairs of instances are simply compared (Experiment 4), simple and rich instances are equally effective at promoting relational learning. These results bear on our understanding of how children connect instances and how those initial connections affect learning and generalization.

Learning from multiple examples is a matter of making the right connections. The instance experienced at one time must be connected to the instance experienced at another. This connection of instances could happen externally, as when a teacher explicitly points out that they are both examples of the same concept, or this connection could happen internally, as a consequence of one instance activating or implicitly reminding the learner of a previous instance. Moreover, even after the appropriate connections are made, if learning is to be generalized, those past examples must be connected and appropriately applied to novel problems. Although connecting instances is essential to all forms of learning, it may pose special problems for learning about relationally similar instances that are superficially dissimilar and therefore difficult to connect together (e.g., the relation “same” may be instantiated in a cup-cup pairing as well as a chair-chair pairing). Appropriately, the issue of connecting instances has been especially well-studied in the laboratory in the context of children’s learning of relations, rules, and sequences (e.g., Kotovsky & Gentner, 1996; Brace, Morton, & Munakata, 2006; Bremner, Mareschal, Destrebecqz, & Cleeremans, 2007), and is the focus of the present set of studies.

The four experiments in this paper were designed to systematically examine how children effectively connect and learn from multiple instances in order to explore a broader question in developmental cognition: What aspects of the learning context impact children’s relational learning? Within that broad question, there are two specific questions addressed here: (1) How should multiple instances be presented in order to foster effective connections? and (2) What kinds of instances promote effective connections? The goal of both questions is to foster effective connecting of multiple instances. Experiments 1–2 address the first question and Experiments 3–4 address the second.

How should multiple instances be presented?

Perhaps the most obvious way to present multiple instances that should be connected together is this: simultaneous presentation, placing two instances – say a card with two chairs and a second card with two cups – side-by-side to be seen all at once. Research in relational learning has found that this presentation format does promote comparison and highlights higher order relations (Markman & Gentner, 1993; Rittle-Johnson & Star, 2007). For example, simultaneously viewing “AA” with “BB” and then “AA” with “CC” appears to promote direct comparison that highlights relational similarity (sameness), and downplays featural differences (different letters involved in the relation of sameness). This physical juxtaposition and resulting direct comparison may serve as a gateway to re-representation, altering the description of a situation in terms of the newly salient relation (e.g., sameness) that is shared by the compared entities.

However, the example above, illustrating the common structure of comparison tasks, also includes a component that involves sequential viewing: “AA” is presented with “BB” and then “AA” with “CC.” Thus a form of form of indirect comparison is also involved, one in which “BB” and “CC” are both associated with “AA” at different time points. It seems likely that the common element AA acts a memory bridge, connecting other instances of the same relation. Direct comparison involves the particular instances present in the moment but indirect comparison applies across comparison experiences. Associating different instances of a relation with one anchoring instance may allow the various instances to become related to each other even though they were never presented together.

Thus, the standard procedure for teaching relations (e.g., “AA” with “BB” and then “AA” with “CC”) appears to involve both direct comparison and indirect comparison. In order to disentangle these two processes, we must compare simultaneous viewing to sequential viewing. Simultaneous viewing can enable both direct and indirect comparison but sequential viewing can only enable indirect comparison as instances are never physically juxtaposed. Experiments 1 and 2 examine these two forms of comparison. Although the simultaneous view may be more effective than the sequential view (by promoting both direct and indirect forms of comparison), we also seek to determine the contribution of sequential viewing by including a control group, with no joint experience of multiple instances.

What kinds of instances promote effective connections?

The second question is concerned with features of the instances themselves. One object property that has been suggested to influence learning is the simplicity versus complexity of the objects used to illustrate relations. In brief, are children more likely to learn a relational rule about sameness if the examples of sameness are simple things with few features (two squares, two circles, two triangles) or if the examples are rich with many features (two penguins, two trucks, two lions)? Simplified examples may benefit learning and generalization by taking away distracting and irrelevant aspects of the component objects, enabling children to attend to relations between the objects (Rattermann, Gentner, & DeLoache, 1990). In addition, simple examples (again via the removal of irrelevant distractions) may connect to a variety of learning instances (either via direct or indirect comparison) and may foster greater generalization (Kaminski, Heckler, & Sloutsky, 2008; McNeil, Uttal, Jarvin, & Sternberg, 2009; Son, Smith, & Goldstone, 2008).

However, considerable research also suggests that rich similarities across elements in similar relational roles can aid the discovery of relational structures (Gentner & Toupin, 1986; Marzolf, DeLoache, & Kolstad, 1999; Ross, 1989). Rich object similarities may benefit the appropriate alignment of objects in parallel relational roles through corresponding surface features that correlate with the key relations. Additionally, richness can add contextual information that novices can use to meaningfully interpret relational structures (Wason & Shapiro, 1971; Son, Smith, Goldstone, & Leslie, under review). It is possible that both richness and simplicity of object properties promote connections. Because richness and simplicity are opposites, if they both foster relational learning, they might do so in different ways. Experiments 3 and 4 target this issue.

Task of Relational Reasoning: Relational Match-to-Sample

In order to investigate how types of presentation styles and types of instances affect relational reasoning, we utilized a stringent test of relational reasoning that is still easily comprehensible to preschool-aged children. This task, commonly used to assess children’s learning of relational rules, is a match-to-sample test where children match different sequences of objects that share the same relation. For example, in Kotovsky and Gentner’s (1996) relational match-to-sample task, children were introduced to cards depicting a set of three elements arranged according to a particular spatial relationship. On each trial, a child is shown a sample card showing an array of circles – little-big-little – and asked to find a match from two answer choices, circle-star-circle and star-circle-circle. The correct choice is a unique relational match to the sample, relative to the other choice. Kotovsky and Gentner found this to be a difficult task for 4 year olds, particularly when the choice required children to match relations on one dimension with relations on another, so-called cross-dimensional matches (e.g., to match a small-big-small sample with a light-dark-light choice) or when they were asked to ignore the specific values on the same dimension, so-called cross-polarity matches (e.g., matching a small-big-small sample with a big-small-big choice).

We modified this procedure to examine two ways that children could connect relationally similar instances. In the first version, the common match-to-sample task, children were asked to match to a common instance that was present across all trials. For example, if the common sample contained three squares in a small-big-small sequence, the same sample would be used with color match trials (e.g., light-dark-light) and cross polarity trials (e.g., big-small-big). The second version, the variable match-to-sample task, is similar to Kotovsky and Gentner’s (1996) original test where children were asked to match to a sample that varied across trials, presumably challenging children with a broader array of instances depicting the critical relations.

The experimental procedure has two phases. In Phase 1, which we called “training,” children are given a set of organized pre-experiences (with feedback) designed to encourage connecting relationally similar instances by aligning components with each other. The training procedure is designed to promote either direct or indirect comparison and may involve either rich or simple, similar or dissimilar instances. Then in Phase 2, called “testing,” we use Kotovsky and Gentner’s task – a series of match-to-sample trials with increasingly difficult test choices – to examine whether children can make further relational connections. The key empirical question, then, is how the pre-experiences in the training task affect performance in the Kotovsky and Gentner task. Experiments 1 and 2 keep object properties constant to examine the contributions of the simultaneous and sequential presentation of multiple instances in the training task. Experiments 3 and 4 examine how effectively simple and complex instances in training promote connections among relationally similar instances and thus success in the testing task. Finally, to examine the role of a common instance in this match-to-sample task versus one that varies trial to trial, Experiments 1 and 3 use a common sample and Experiments 2 and 4 use a varying sample.

Experiment 1

As a first step towards understanding the potential advantages of connecting instances, all children in this experiment were shown the same objects, a mixture of simple and rich, in either a sequential or simultaneous manner. In the training phase, children were trained to map a single and featurally simple sample to very different and richly detailed instances. In the testing phase, they were then tested with common match-to-sample trials where the simple samples used in training appeared on every trial. The key manipulation in the experiment concerns whether the training experience involved simultaneous versus sequential experience with the sample and matching instances. In the Simultaneous training condition, the simple and common sample for all trials was a set of 3 post-its notes (e.g., for the ABA relation this would be a small blue post-it, a large pink post-it, and small blue post-it). During training, this sample was placed below two different complex instances to indicate the relation (e.g, in the case of ABA relation below a cross-penguin-cross array and below a triangle-bear-triangle array). The Sequential training condition was identical except the elements of sample were placed directly on top of the elements of the complex instances (training sequences are illustrated in Figure 1). In this way, the sample and the relational matches in the training phase were never seen together and could only be linked indirectly. This provides a very strong test of whether indirect comparison may contribute to relational learning or whether effective comparison can only emerge from jointly perceiving relationally related instances. A third group of children received no training experience at all.

Figure 1.

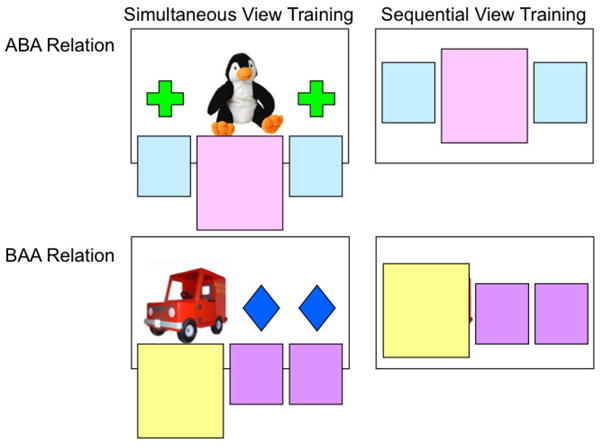
Training conditions for Experiments 1 and 2 provided either simultaneous views or sequential views of post-it samples and training instances. The control condition did not see these training cards or corresponding post-it elements at all.

Both the Simultaneous and Sequential conditions trained children with the same set of materials, a simple common sample and rich instances, but in the former there is physical juxtaposition and in the latter the children experience the instances in immediate succession. If simultaneously considering instances is critical to direct comparison and direct comparison is responsible for relational learning, then the Simultaneous training should be most effective in producing relational generalization. However, given that the physical and temporal contexts of the Simultaneous and Sequential conditions are highly similar, if indirect comparison can also foster relational learning, both training conditions should boost performance over the control condition.

Method

Participants and Design

Forty-four children from daycares in the Bloomington area, mean age of 56 months (51–68 months), were randomly assigned to one of three between-subject conditions: no-training Control (n=13), Sequential (n=15), and Simultaneous (n=16). One additional child did not complete the experiment and was excluded from the analysis for failure to meet a pre-set sample for inclusion (see below).

Materials

Training

There were four laminated training instances and two common samples presented to children in the Simultaneous and Sequential conditions. Children were trained on two relations, each instantiated in an array of three objects. There were two instances of symmetry (ABA) relation, a triangle-bear-triangle card and a cross-penguin-cross card. There were two instances of asymmetry (BAA) relation, car-diamond-diamond and boat-rectangle-rectangle. The common sample used for the ABA relations was made up of a large pink post-it flanked by small blue ones. The common sample for BAA relation cards was made up of a large yellow post-it followed by two small purple ones. Children in the Control condition did not see the training instances nor the post-it samples.

Testing

The test trials were common match-to-sample triads with a post-it sample used during training and two answer choices, which were novel instantiations of ABA and BAA (see Figure 2). To provide a strong test of the training, the test trials used only the most difficult relational matches, cross-dimension and cross-polarity, as used by Kotovsky and Gentner (1996).

Figure 2.

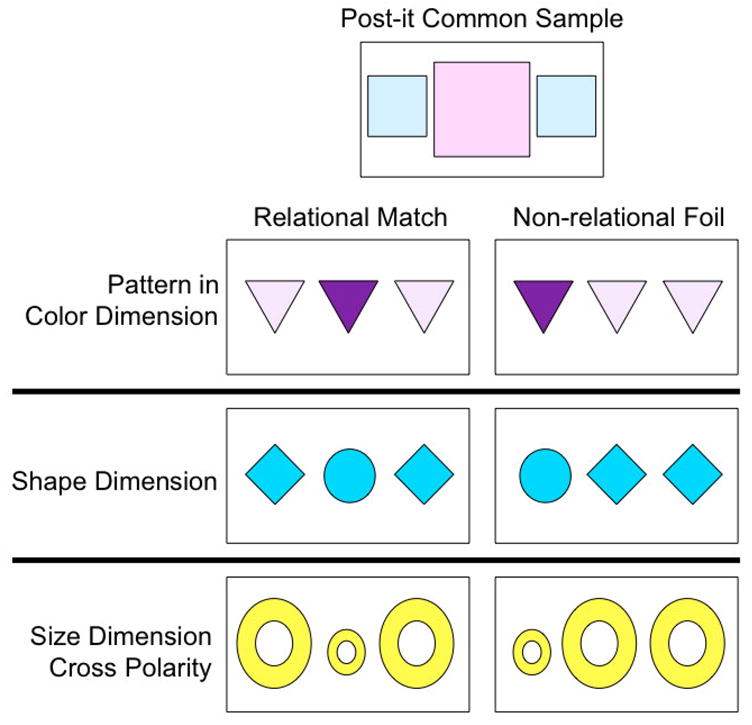
An example of the common match-to-sample trials used in Experiment 1 to test children from all three conditions (and the Simple condition in Experiment 3). The variable match-to-sample trials used in Experiment 2 and 4 were composed of the same answer choices but used a novel instance (e.g., 3 blue diamonds arranged in a small-big-small pattern) as the standard instead of the post-its.

That is, the samples always involved size patterns and different colors (small blue-big pink-small blue with for ABA or big yellow-small purple-small purple for BAA). The novel testing cards instantiated these ABA and BAA relations in new dimensions of shape (e.g., circle-diamond-circle), color shade (e.g., lavender-purple-lavender), or opposite size polarity (e.g., big-small-big). On each trial, the common sample was shown on a box and the answer choices were placed on the table in front of the participant.

Additional stimuli included familiarization triads that were used to acquaint children to the match-to-sample task. These triads had a novel sample (i.e., pentagon), an exact match and a mismatching foil (i.e., pentagon versus circle, respectively). There were also easy filler triads made up of a novel sample (i.e., two orange triangles) and two easy answer choices (i.e., two orange triangles versus one yellow triangle). These triads were designed to help encourage children during the experiment while also serving as a measure of their engagement in the task. Children were excluded from analyses if they did not answer these easy trials correctly because failure on these easy trials suggests that children did not understand the task or were not paying attention to the sample when picking an answer choice.

Procedure

In the training phase, the experimenter showed the child how to place post-its appropriately onto a training card. Children in the Simultaneous condition saw the experimenter place the post-its under each training card. Children in the Sequential condition saw the experimenter place the post-its on top of each training card. Immediately afterward, the child was given an identical training card and their own set of post-its (e.g., one large pink and two small blue ones) and children in both conditions were instructed to “put the stickers on the card just like [the experimenter] did.” This occurred four times, one for each of the four training instances. The training was always done in the same order such that the children saw two ABA instances in a row and then BAA instances in a row. Children were supposed to be given corrective feedback if they placed post-its incorrectly. However, every child in this study and the subsequent studies placed post-its correctly.

Next, children were familiarized to the match-to-sample task with the two easy familiarization triads. These were followed by a series of test and filler trials. There were six unique match-to-sample triads, half with the ABA post-its as the common sample and half with the BAA post-its as the common sample. Each triad was repeated for a total of twelve test trials. The spatial location of the relational match alternated between trials. After a block of four test trials, children received two easy filler trials. This resulted in three blocks of test trials interspersed with two sets of filler trials. Each block was either a color, shape, or opposite polarity set of triads. Children received two semi-random block orders (color-shape-polarity or shape-polarity-color).

On each test trial, the experimenter would attach the post-it samples onto a box with a slot cut out on top. The experimenter would then place two answer choices in front of the child and ask, “Which card is like this one (pointing to sample)? Pick the card like this one (pointing to sample)! Put that one in the box!” On test and filler trials, the experimenter provided neutral feedback with positive affect (e.g., “Okay! Thanks!”).

Results and Discussion

Simultaneous training, designed to maximize direct comparison, was more effective than both the Sequential training and no training at all, in promoting relational matching. This was predicted both by prior results and task analyses (as simultaneous training is likely to involve both direct and indirect comparison). A 3×3, trial-type (shape, color, opposite polarity) × training condition repeated-measures ANOVA on test trial performance revealed a significant effect of training condition, F(2, 39) = 4.12, p<.05, η²=.17. There was no effect of trial-type, F(1, 39) = .02, and no interaction, F(2, 39) = .66. Because there was no effect of trial-type, the overall percent correct out of twelve test trials are shown in Table 1. Post hoc Bonferroni-corrected t tests confirmed that Simultaneous training was more effective than Sequential training, Bonferroni critical d=.17, p<.05, and no training at all, Bonferroni critical d=.27, p<.01, in promoting relational matching. Performance in the Sequential condition did not differ significantly from that of the Control group, Bonferroni critical d=.10, n.s. Children in the Control condition chose relational matches .57 of the time (SD=.18), a rate that does not significantly differ from chance, t(12) = 1.36, however performance in the Sequential condition (M=.66, SD=.23) did differ from chance, t(13) = 2.51, p<.05, as did performance in the Simultaneous condition, (M=.84, SD=.22), t(15) = 6.30, p<.001. This suggests that indirect comparison, at least in this version of the task, contributes minimally, if at all, to children’s relational learning.

Table 1.

The overall percent correct on the relational match-to-sample trials from Experiments 1–4 are shown by training condition (in rows) and type of match-to-sample task (in columns). It should be noted that the instantiations of richness and simplicity between Experiment 3 and 4 were different. Both rich and simple samples in Experiment 3 were more dissimilar from the training instances than in Experiment 4 where rich and simple stickers were highly similar to the training instances.

	Common Match-to-Sample Task		Variable Match-to-Sample Task
	Experiment 1		Experiment 2
	Mean	St. Dev.	Mean	St. Dev.
Control	.57	.18	.52	.16
Sequential training	.66*	.23	.57	.24
Simultaneous training	. 84*	.22	.73*	.23
	Experiment 3		Experiment 4
	Mean	St. Dev.	Mean	St. Dev.
Control			.51	.19
Rich condition	67*	.16	.69*	.17
Simple condition	.82*	.16	.66*	.22

^*above chance

The greater success of children in the Simultaneous condition than the Sequential condition holds despite the critical similarity between the two: both training procedures explicitly linked the training instances to the sample by aligning elements by relational roles. However, the Sequential condition did not allow for the direct comparison of the sample (as a whole instance of the relation) with the training instance. Considerable past work has shown that simultaneous viewing is beneficial to relational or categorical learning in other domains (Loewenstein & Gentner, 2001; Namy, Smith, & Gershkoff-Stowe, 1997; this benefit does not always extend to non-relational domains, see Oakes, Kovak-Lesh, & Horst, 2009 for a recent exception), a result that is interpreted in terms of supporting the alignment of relational roles across examples through object similarities (Gentner & Namy, 1999). However, in this experiment, there were very few object similarities as children viewed highly dissimilar sets of items, but there was still a benefit of simultaneous viewing. Thus, simultaneous viewing appears crucial to the abstraction of relational roles even in the presence of many element-to-element dissimilarities.

What exactly was happening during simultaneous training that promoted relational discovery? There are several possibilities that may be working together. The alignment activity, placing post-its underneath the training elements, may have implicitly drawn attention to the relational similarity and allowing simultaneous viewing may have helped children fully appreciate the pattern. Simultaneous viewing may strengthen connections between multiple instances by giving children more time to link instances whereas in sequential training, those connections may be weaker or incomplete. Additionally, sequential viewing requires more working memory as children have to hold both instances in mind in order to compare them. Presenting instances at all at once may have freed up working memory resources for attending to the relational structure.

Experiment 2

In Experiment 1, we trained children to connect instances to samples and tested their ability to connect new instances to those trained samples. The presence of a common sample presumably minimized children’s difficulties in connecting their training experiences to the testing trials. Additionally, the common sample may have facilitated generalization across test trials as ABA trials were perfectly correlated with pink and blue post-its and BAA trials were correlated with purple and yellow post-its. Experiment 2 uses the same training as Experiment 1, but now, a new sample is presented on every unique test trial. This way, we can examine whether simultaneous viewing of instances during training can improve children’s performance on relational tests without a common sample.

Method

Participants and Design

Forty-eight children, average age 56.6 months (range 47 to 65), participated through Bloomington area daycares. There were seventeen children who served as controls, sixteen who received Sequential training, and fifteen who received Simultaneous training. Seven additional children participated in this study but did not meet the predetermined requirement of success on all the filler trials.

Materials

The training instances and post-its were identical to those used in Experiment 1. Additionally the task-training triads and filler triads were also the same. The main departure from Experiment 1 was the sample presented in the generalization tests. Instead of the post-it samples used in the training procedures, the generalization test was made up of variable match-to-sample triads with novel samples on each trial. These samples were ABA and BAA patterns made of size variations (e.g., an array of three crosses, big-small-small, see Figure 3) while the answer choices instantiated the pattern in shape (e.g., star-square-square) or color (e.g., purple-lavender-lavender). Pilot testing on the novel sample triads revealed that this test was difficult and frustrating for children so the number of unique match-to-sample triads was reduced to four, half with the ABA pattern as the sample and half with BAA. Each unique triad was repeated for a total of eight test trials. There were no opposite polarity triads in this experiment because the shape and color triads already presented a challenge.

Figure 3.

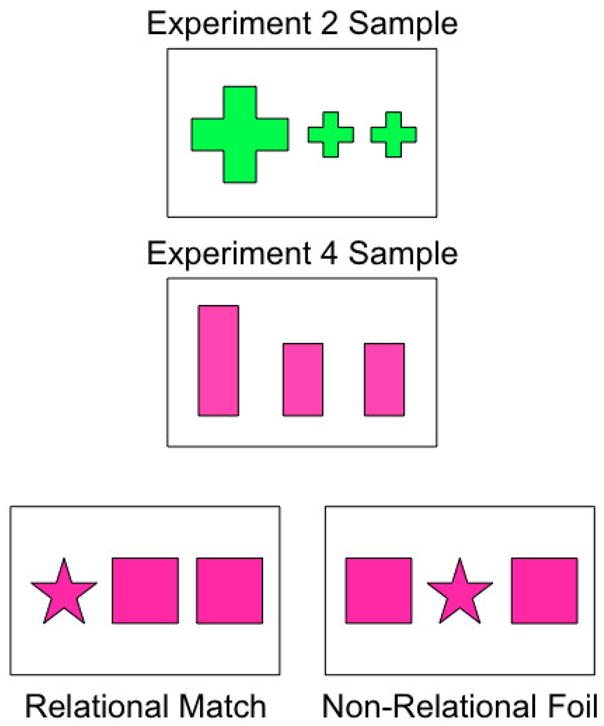
An example of a size-to-shape trial in the variable match-to-sample test. The samples were novel instances that participants never saw in training or other test trials. In Experiment 2, the sample was highly dissimilar to the answer choices. In Experiment 4, the samples were modified to be highly similar to the answer choices except that the sample instantiated the pattern in one dimension (e.g., size) and the answer choices in another dimensions (e.g., shape).

Procedure

The procedure was almost identical to that of Experiment 1. Children in the Sequential and Simultaneous conditions received post-it training before test trials. Children in the Control condition were not shown any training stimuli. Children in all three conditions were given task-training trials before moving onto the test and easy filler trials.

For each test and filler triad, children were instructed to pick the card that was most like the sample. If a child refused to pick a card (many did since these samples were highly dissimilar from the correct relational match), the experimenter told the child, “Even if it is not exactly the same, which one is most like this one (pointing to the sample)?” The spatial location of the relational match alternated between trials. As in Experiment 1, four additional easy filler triads were used to catch whether children were paying attention to the task. After every four test trials (a block), children received two filler trials. Each block was made of shape or color triads. Half the children were tested with the shape block then the color block while the other half were tested with color then shape.

Results and Discussion

Again, Simultaneous training was an effective way to promote relational generalization. A 2 (trial-type: shape, color) × 3 (training conditions) repeated-measures ANOVA of test trial performance revealed a significant effect of training condition, F(2, 38) = 3.73, p<.05, η²=.16. There was no effect of trial-type, F(1, 38) = .18, and no interaction, F(2, 38) = 2.09. The overall percent correct out of eight test trials are shown in Table 1. Post hoc analyses (Bonferroni t tests) showed a pattern of results similar to Experiment 1 albeit less pronounced. The Simultaneous condition showed significantly greater overall performance than the Control condition, Bonferroni critical d=.21, p<.05. Test performance in the Sequential condition did not exceed that of the Control condition, Bonferroni critical d=.05, n.s. Unlike Experiment 1, Simultaneous and Sequential training were not significantly different, Bonferroni critical d=.16, n.s., which suggests that pre-training had limited effects on the variable match-to-sample test. Consistent with this observation, the only group who achieved above chance performance on relational test trials was the Simultaneous condition (M=.73, SD=.23), t(12) = 3.66, p<.01. Both Experiments 1 and 2 demonstrate that side-by-side simultaneous comparison is effective for discovering relations and fostering relational generalization over the control condition. This benefit of simultaneous comparison seems particularly strong when there is a common sample during learning and testing.

There are two ways in which the common sample test may promote relational responding over the variable sample test: (1) the consistent use of the sample across test trials and (2) the familiarity of the sample in both training and testing may help children activate relevant knowledge from training at test. If the consistent and familiar presence of the common sample in Experiment 1 is important for noticing relations and connecting learning across trials, then the features of the simultaneously shown entity may not matter. Perhaps any sample, as long as it is consistently connected to other instances in a familiar and simultaneous fashion, can act as a mediator for discovering a common relation. However, it may also be the case that the post-its sets used in Experiments 1 as common instances were particularly useful because they were simplified instances of the relation to be learned.

Experiment 3

Considerable research on relational and symbolic reasoning suggests that rich details draw attention to themselves (Kaminski, Sloutsky, & Heckler, 2008; Rattermann, Gentner, & DeLoache, 1990). Rich details have been shown to make the apprehension of relational structure more difficult (McNeil et al., 2009; Uttal, Scudder, & DeLoache, 1997) and prevent children from appreciating the symbolic relation between a model and its referent (DeLoache, 1991, 1995, 2000). These issues are relevant to what items might make the best examples for discovering a relational rule. A simple sample that does not call attention to itself as an interesting object may make the common relational structure more obvious and children may use the sample more readily to connect multiple instances.

Alternatively, a rich sample with many features could be effective especially if they share many features with the instances to which they connect. High similarity between relationally similar instances draws selective attention to the common relational role (Gentner & Toupin, 1983; Holyoak & Koh, 1987). Also, if any common sample used across all trials and shown simultaneously with other instances during training is generally beneficial to relational learning, rich samples may not be detrimental. To test these ideas, Experiments 3 contrasts richly detailed samples to simple samples in the common match-to-sample task. If simultaneous viewing with a common sample is what promotes relational perception, then use of either rich or minimal samples should be benefit performance.

Method

Participants and Design

Twenty-six children, average age 58 months (range 48 to 69), participated in this experiment from daycares in Indiana. They were randomly assigned to one of two conditions: Rich Common Sample (n=14) and Simple Common Sample (n=12). One additional child participated in this study but was not included in these results (teacher reported developmental delays).

Materials and Procedure

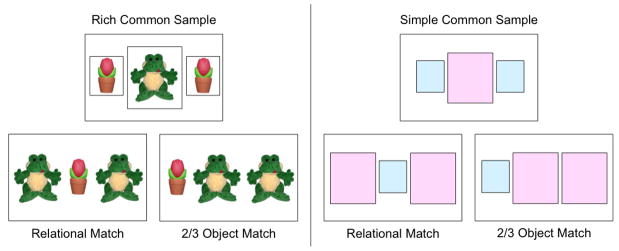
The Simple condition was a replication of Experiment 1’s Simultaneous condition in which children were trained to align simple post-it samples with learning instances. These simple post-its also served as the common samples for the generalization test triads. In the Rich condition, frogs and tulips stickers were placed beneath the ABA instances while bikes and sneakers were used with the BAA instances. These rich elements also served as samples for test triads. Children in both conditions were taught to place samples underneath the objects depicted on the training cards to provide simultaneous viewing of multiple instances.

Like Experiment 1, there were three types of blocks (shape, color shade, and opposite polarity) of four trials each for a total of twelve test trials. There were three different orders in this experiment (color-shape-polarity, shape-polarity-color, and polarity-color-shape). A departure from the other experiments was the inclusion of a fourth block made up of cross-mapping trials (shown in Figure 4). These trials were a type of opposite polarity trials, but particularly difficult because the answer choices were cross-mapped versions of the sample, made up of the same elements in different configurations. The cross-mapping trials for the Rich condition were made up of a rich sample (e.g., tulip-frog-tulip), a cross-mapped relational match (e.g., frog-tulip-frog), and a non-relational foil (e.g., tulip-frog-frog). Notice that the non-relational foil has two elements in the same position as the common sample while the relational match has no element-position matches. In order to choose the relational match, children have to value an overall relational match without any element-position matches and disregard the two element-position matches in the foil. The cross-mapping triads for the Simple condition (also shown in Figure 4) consisted of a simple sample (e.g., blue-pink-blue post-it squares), a correct relational match (e.g., pink-blue-pink), and a non-relational foil (e.g., blue-pink-pink). Once again, the foil has two element-position matches with the sample. There were four cross-mapping trials in this final block. Including the cross-mapping block, there are four blocks of test trials and two filler trials in between each block for a total of 6 filler trials.

Figure 4.

Cross mapping triads shown for the Rich and Simple conditions from Experiment 3. These rich and simple samples were used for both training and the match-to-sample test. Those in the Rich condition were shown rich samples (e.g., the tulips and frogs) while those in the Simple condition were shown simple samples (e.g., the post-its).

Results and Discussion

As shown in Table 1, the Simple samples were more effective than the Rich ones. A 4 (trial-type: shape, color, opposite polarity, cross-map) × 2 (common sample condition: Rich, Simple) repeated-measures ANOVA of test performance revealed a significant effect of common sample condition, F(1, 22) = 4.97, p<.05, η²=.18. There was no effect of trial-type, F(3, 22) = .74, and no interaction, F(3, 22) = .45. Simple common samples were more likely to foster relational generalization (M=.82, SD=.16) overall than rich common samples (M=.67, SD=.16), t(23) = 4.97, p<.05, Cohen’s d=.94. Both Simple and Rich conditions showed overall test performance significantly greater than chance, t(12) > 3.69, p<.01.

Children in the Simple condition showed better performance in every type of block, but particularly on cross-mapping trials where they were significantly more relational than the Rich condition, t(23) = 4.66, p<.05, Cohen’s d=.98. On cross-mapping trials, participants in the Simple condition made an average of 3.5 (SD=.7) relational matches out of 4 trials compared to the Rich condition’s 2.6 (SD=1.1). It is an achievement for four- and five-year-olds to be relational on these cross-mapping trials because they end up picking an answer that does not have any element-position matches over a foil that has two perfectly positioned matches. This result also fits well with past research on child and adult similarity judgments. Rattermann, Gentner, and DeLoache (1990) have found that simplifying objects allows children to overcome strong object matches for relational ones. Goldstone, Medin, and Gentner (1991) showed that even undergraduates preferred relational over featural matches when there were few overlapping features (e.g., matching XOX with TVT rather than TVX) versus when there were more overlapping features (e.g., matching XOX with TOT or TOX).

In the present context, the finding, that simpler rather than richer common samples promote learning and generalization, fits the idea of the sample functioning as a “model” of the richer instances, not just as an often-repeated familiar instance. DeLoache’s developmental work (2000) on children’s use of symbols that suggests that simple instances may be better as common samples that unify relationally similar instances, referring to (or representing) other instances rather than being interesting in their own right. By being uninteresting as objects, their most interesting feature is that they refer to something else. The advantages of simplicity for capturing a variety of instances and thus improving generalization has been widely documented from young children’s noun extensions (Son, Smith, & Goldstone, 2008) to their use of maps and math manipulatives (McNeil et al., 2009; Uttal, Scudder, & DeLoache, 1997). Even adult transfer of mathematical structure benefits from simplified or idealized learning instances (Bassok & Holyoak, 1989; Kaminski, Sloutsky, & Heckler, 2008; Sloutsky, Kaminski, & Heckler, 2005).

However, theories of comparison (Kotovsky & Gentner, 1996; Markman & Gentner, 1993) rely on a particular kind of richness to foster comparison: similarities that promote accurate local alignments and create effective connections among instances. According to the technique of progressive alignment (Gentner & Medin, 1998; Kotovsky & Gentner, 1996), learning initially with highly similar instances leads to a greater appreciation of dissimilar isomorphic instances because establishing relational correspondences causes the underlying structure to become more salient. Thus, comparing similar instances fosters the discovery of structure. Perhaps when directly compared instances are not used as common associates, their perceptual complexity does not matter. Connected rich instances may be just as effective for relational learning as simple instances when they are not functioning as common samples. Particularly when connected instances share both attributional and relational features, progressive alignment suggests that high similarity may lead to better alignment and thus more attention to relational structure during learning. If the actual richness or simplicity of the instance is only pertinent when the instance is being used as a common sample, both highly similar rich pairings and simple pairings should produce equal attention to relational structure. This issue is examined in the final experiment.

Experiment 4

Figure 5 illustrates the two main conditions for this experiment, each realizing similar instances in a different way. In what we call the Rich Similarity condition, children were trained to place stickers depicting shapes and objects richly similar to those on the training cards (i.e., the penguin and green crosses were aligned with an equally rich but different penguin and green diamonds). When the training instance had penguins, the comparison sample (the stickers) had penguins and when the training instance had bears, the sample had bears. There were many similarities to aid alignment, but the aligned stickers were specialized and not used across isomorphic learning instances. The Simple Similarity condition used stickers depicting gray silhouettes of the shapes and objects on the training card (i.e. the penguin was aligned with a gray shadow of the penguin). Again, each comparison sticker is specialized to the training instance and not used across relationally similar instances. Both the richly similar and simply similar sets support the alignment of corresponding elements. The variable match-to-sample task was used to assess the effect of rich and simple similarities when the stickers were not used as common samples across testing trials. Although Experiment 3 found that rich stickers were not as effective as simple stickers when used as common samples, Experiment 4 tests whether this finding holds true when these stickers are used only for direct comparison.

Figure 5.

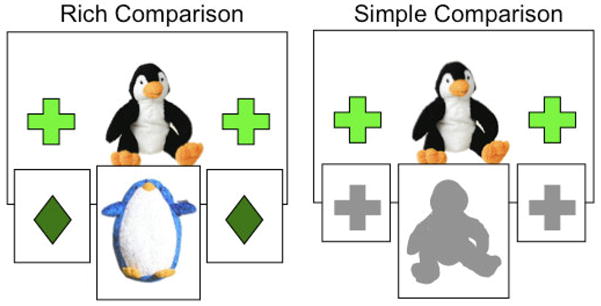
In Experiment 4, children in all conditions viewed training instances and stickers simultaneously. Those in the Rich comparison condition used a set of stickers that were richly similar to the training instance while those in the Simple condition used stickers that were simplified versions of the training elements. Each set of stickers corresponded with one of the four training instances.

Method

Participants and Design

Forty-six children, average age 59 months (range 47 to 69), participated in this experiment from daycares in Indiana. They were randomly assigned to one of three conditions: Control (n=16), Rich Similarity (n=15), and Simple Similarity (n=15). Six additional children participated in this study but were not included in these results (one was diagnosed with autism; five because they did not reach the criterion for success on the filler trials).

Materials and Procedure

Both the Rich and Simple Similarity training regimes were similar to the simultaneous training in the previous experiments. The only difference was that the colored post-it notes were replaced with stickers that were richly similar to the learning instances or simple gray silhouettes of those instances (shown in Figure 5). The Control condition had no experience with either rich or simple stickers.

Generalization tests were variable match-to-sample triads, similar to Experiment 2, using novel samples that varied on each trial. However, there was a small adjustment to these match-to-sample tests. Many children in Experiment 2 commented to experimenters that there were no correct answers because the novel samples were perceived as highly dissimilar from the answer choices. To remedy this, the triads were increased in overall similarity. For example, in size-to-shape triads (as shown in Figure 3), the novel sample varied in size (big-small-small) and answer choices varied in shape (star-square-square) but all cards shared a similar color (pink). In size-to-color triads, the cards shared similar shapes. In size-polarity triads, the cards shared similar shapes and colors. Like previous experiments, all samples depicted variations in size and answer choices varied in color, shape, and opposite polarity. These trial types were organized into three blocks of four trials. These blocks were interspersed with two easy filler trials. Children were tested with two block orders (color-shape-polarity and shape-polarity-color).

Results and Discussion

The results are shown in Table 1 and indicate when the stickers were not utilized as common samples, simple stickers were not better for comparison. The richer stickers that overlapped on many features were as effective, and indeed just slightly more effective (n.s.), than the simple stickers. A 3 (trial-type: shape, color, opposite polarity) × 3 (similarity condition: Control, Rich, Simple) repeated-measures ANOVA of test performance revealed a significant effect of condition, F(2, 39) = 3.37, p<.05, η²=.14. There was no effect of trial-type, F(2, 39) = .01, and no interaction, F(2, 39) = .94. Post hoc Bonferroni-corrected t tests confirmed that the Rich Similarity group made significantly more relational choices overall than those in the Control condition, Bonferroni critical d=.18, p<.05. The Simple Similarity was not significantly different compared to the Control condition, Bonferroni critical d=.15, n.s. The similarity conditions were not significantly different from one another, Bonferroni critical d=.03, n.s., but were both significantly above chance, t(13) > 2.72, p<.05. The performance of Control participants did not differ from chance, t(13) = .24.

Comparison with both richly and simply similar components fostered discovery of the relational rule. Another key aspect of this result is that when rich stickers are not used as a common associate with other instances, those rich stickers do not limit far generalization. A straightforward interpretation is that local similarities, whether rich or sparse, promote local alignments during learning and this may be the most critical issue for effective connections. This interpretation fits Gentner’s Structure Mapping theory (1983) and more specifically progressive alignment (Kotovsky & Gentner, 1996; Markman & Gentner, 1993). The importance of surface similarity across stickers in the same relational roles has been shown to be effective in several relational domains including children’s understanding of number (Mix, 2002), feature learning (Gentner, Loewenstein, & Hung, 2007), as well as map use (Loewenstein & Gentner, 2001).

General Discussion

These experiments were motivated by the question of how children learn about relations from multiple instances and the perceptual/presentational factors that would affect such learning. Presumably in order to learn about relations, children need to relate one isomorphic instance to another. Experiments 1 and 2 showed that simultaneous perceptual comparison was effective for helping children connect multiple instances of the same relation in a way that generalized to new instances. Simultaneous viewing was effective despite large perceptual differences between the simple samples and the complex training instances. Experiment 3 revealed that simple stickers were more effective common samples than rich stickers in promoting generalization across training and testing. But Experiment 4 showed no advantage of simple stickers, when used as just another comparison instance instead of as a common sample. Rich and simple stickers, presumably by virtue of their similarity to the learning instances, fostered relational generalization. Altogether, the results suggest that learning relational rules from instances depends on several interacting factors so in the following, we discuss the further implications of these findings.

Simultaneous versus Sequential Viewing

Without training, preschool-aged children typically find it difficult to make relational matches across sets of objects that do not share overall similarity (our control conditions as well as Hall & Waxman, 1993; Kotovsky & Gentner, 1996). The experiments reported here provided children with a short, simple training sequence, putting post-its (or stickers) underneath four training cards; critically, this brief experience helps children connect across dissimilar instances and appreciate subtle relational similarities. A surprising aspect of these results is the impact on children’s learning made by a slight difference between the Simultaneous and Sequential training. Although the same materials and similar procedures were used, the difference in perceptual opportunity affected whether the training was significantly more effective than having no training at all. This may reflect an advantage of the simultaneous view or a disadvantage of the sequential view. Simultaneous viewing may tie the two examples together more strongly or more effectively highlight the common relation in the face of irrelevant differences. Or by covering up the learning instance with post-its in the sequential training, there is an added cognitive load requiring children to hold instances in memory. Additionally, participants may have found it difficult to keep in mind the relations that fostered proper alignment in the first place. An important question for future work is to go beyond demonstrating its importance to specifying the mechanisms engaged.

Although these findings are not directly related to pedagogy and any applications to education remains to be empirically evaluated, these findings suggest that there is a potential pedagogical benefit of simultaneity. It may be best not to rely on children’s ability to remember what they have seen. By having items simultaneously present, this presentation format may change how children process and encode the items. This principle is already intuitively implemented in some classrooms. Richland, Zur, and Holyoak (2007) found that math teachers in higher performing countries (Hong Kong and Japan) are more likely to present two relationally similar examples simultaneously than teachers in the U.S.

Although there may be limits to presenting too much information at once, one of the principles of cognitive load theory (Sweller, 1994), these findings suggest that simultaneous presentation may not always be negative and overwhelming. It is important to note that Sweller, van Merrienboer, and Paas (1998), distinguishes between intrinsic, extrinsic, and germane cognitive load. Although intrinsic load is typically unavoidable because it is the nature of the material to be learned, extrinsic load can be altered by the presentation style of the material. Germane load can also be altered but it is a positive load that reflects the effort needed to construct schemas, relations, and other structural concepts. Sequential viewing may present an extrinsic load, having to remember instances, that is superfluous to the task of learning relations. Simultaneous training presents a germane load helpful for learning schema-like patterns without having to deploy additional resources for remembering the items.

Common versus Varying Samples

Perhaps relevant to these ideas, the results of the four experiments suggest a potentially important role for associating multiple instances to a common sample. Experiments 1 and 3 provided a set of instances that functioned as a common sample, associated with multiple instances. Experiments 2 and 4 provided children with varying comparison instances that did not function as a common sample. The best performances in the common match-to-sample tasks (Experiments 1 and 3) were 84% and 82%, respectively, while the best performances on the variable match-to-sample tasks (2 and 4) were 73% and 69%, respectively. Although common versus variable samples were not tested in a single experiment, this overall pattern highlights the importance of contextual similarity or some other mnemonic device that connect learning experiences separated in time.

Simple versus Complex Instances

The results of Experiments 3 and 4 suggest that it is not mere simplicity that fosters relational learning as other studies have suggested (McNeil et al., 2009; Rattermann, Gentner, & DeLoache, 1990; Son, Smith, & Goldstone, 2009). Simplicity seems particularly important for reoccuring samples and may be related to general findings that simple models help children appreciate that models point to something else rather than being unique objects in their own right (DeLoache, 2000; Uttal, Scudder, & DeLoache, 1997). One implication of our results is that it is useful to consider not only the features of learning materials but how those materials will be deployed. The value of the simple samples may not just be that they do not have many distracting and irrelevant surface properties but that they also become – across trials – concrete stand-ins (or symbols or pointers) of the common relation across diverse examples. A compelling example of this concerns judgments of same/different relations by chimpanzees (Thompson, Oden, & Boysen, 1997). In these studies, the chimpanzees are taught to label a relation with an arbitrary physical token, such as a heart-token for same (e.g., &hearts; → AA) and another token for different (e.g., # → AB). Having learned this, chimpanzees can make second-order matches, judging AA to be related to BB. Chimpanzees may do this task, not by comparing and abstracting the relation of sameness across instances, but by knowing that AA → &hearts; and BB → &hearts;. Then they can simply respond to the sameness of &hearts; and &hearts;. That is, this second-order relation (the “same” relation between “the token for same” and “the token for same”) might result from direct computations over the objects standing in for relations. Thompson and colleagues theorized that by mentally replacing AA with a heart-token and BB with a heart-token, these chimpanzees were able to re-represent this relational matching problem as a simple object-matching problem. A related set of findings fall out of Sloutsky and Robinson’s overshadowing hypothesis (Robinson & Sloutsky, 2004, 2007), where the same label can make two visual experiences more similar. Post-its, especially in the common sample task, when associated with a variety of isomorphic instances, may help children perceive, discover, and work with relations. If the reoccurring use of the common sample can enable the discovery and use of structural information, perhaps mathematical manipulatives should be used in the classroom as a familiar and common representational system (e.g., using common counters for many different situations) rather than an interesting domain of problem solving (e.g., using M&Ms one day and blocks the next day).

Another way to put the advantage of a simple symbol is this: commonly used materials that are supposed to integrate several experiences should be simple. If materials are going to be compared once, it may be fine to present complex instances. However, if materials will be compared multiple times, instructors may want to select a simple main example to compare to many other examples rather than a compelling complex one. For instance, simple counters (i.e., a set of dots) may be more effective for representing multiple word problems than rich counters (i.e., M&Ms). Simple instances have less content so they can easily represent multiple situations but students may find it hard to use M&Ms to represent computers, cities, and bears.

The same point is illustrated by arbitrary, non-iconic, and initially contentless words. Perhaps because the purpose of language is to integrate multiple experiences, language is relatively simple and detached from its content. There are several developmental findings where labeling multiple examples with a common word affects the sophistication of learning (Loewenstein & Gentner, 2005; Kotovsky & Gentner, 1996; Rattermann, Gentner, & DeLoache, 1990; Son et al., under review). By labeling several ABA instance as “even,” Kotovsky and Gentner found children were better able to attend to the pattern.

Contentless symbols acquire their meaning by familiar use and convention. Even when they start off as another instance of direct comparison, users themselves may have attended less to the non-symbolic details that are extraneous in practice. In educational practice, Lehrer and Schauble (2002) have similarly observed that first- and second-graders graphing flower growth initially include leaves and flowers to represent plants. But as their projects increasingly required more attention to plant heights and less attention to flower appearance, they replaced these iconic flower drawings simply with different colored bars to represent individual plants. The process of symbolization, or re-representation (representing something in terms of something else), seems to entail stripping away irrelevant information and simplification. Clarity and efficient encoding are probably the primary reasons for invoking re-description. The results of Experiment 3 suggest that rich samples do not clearly and efficiently represent relational construals.

Similar versus Dissimilar Comparisons

Similarity has largely been believed to be an integral part in comparison because human ability to quickly and reliably align corresponding parts is heavily influenced by similarity (Bassok, Chase, & Martin, 1998; Gentner, 1983; Gentner & Toupin, 1986; Holyoak & Thagard, 1989). However abstracting relational similarity requires going beyond merely matching up parts and studies suggest that accurate mapping does not always coincide with a useful understanding of relational structure (e.g., Novick & Holyoak, 1991; Son, Doumas, & Goldstone, in press).

If we are primarily concerned with the role of similarity in alignment, the training for the Rich condition of Experiment 3 and the training conditions in Experiment 4, putting an animal sticker below animals depicted on the training card, were the easiest mappings to make because there is a high degree of similarity (many corresponding features) between the elements and the elements on the training cards. Contrast this high similarity alignment to the training with post-its (Experiment 1, 2, and the Simple condition in Experiment 3) that have little in common with the rich objects depicted on the training cards. However, if we are concerned with the commonality derived from comparison, one might have expected that the product of a high similarity comparison may have been a narrow construal of the pattern (i.e. animals in the middle) and the product of a low similarity comparison may have been a more broad construal of the pattern (i.e. something different in the middle). Yet the obtained results reflect neither of these sets of predictions; children are able to generalize from both the high and low similarity comparisons. Future experiments are needed to understand the interaction of high and low similarity comparisons with rich and simple instances. The experiments reported here, for purposes of experimental coherence, used the same training instances and varied the samples compared with them. However, future experiments may want to compare purely rich pairs (penguins with penguins) with purely simple pairs (squares with diamonds) with mixed pairs (squares with penguins). If the key step for children in this task is effectively connecting the proper instances in the first place, a process that is aided by supporting similarities, then both purely rich and simple pairs should be more effective. However, if effective training exercises force learners to develop new construals of situations rather than simply falling back on familiar or intuitive construals (Koedinger & Aleven, 2007), giving children the challenge of finding commonalities between squares and bears, rather than the easier task of matching penguins to penguins, is the kind of training that prepares children for subsequently apprehending relational structures in novel patterns.

Conclusion: Beyond Connections

Connecting instances through comparison is powerful because it is a domain-general process that makes use of repeating regularities in the world to guide learning. The experiments reported here demonstrate a number of relevant factors that support or limit these connections, including simplicity versus complexity, a common versus varying standard, and simultaneous versus sequential examples. The results of this program of inquiry have shown a deeper story to comparison than merely being exposed to multiple examples. The particular history of interaction with multiple instances, how they are shown, which instances are repeated, and what features they share, these all play a role in how children learn about sophisticated relational structures. These subtle factors may underlie our ability to build useful and creative knowledge through a variety of initially meaningless instances.