The Gamma Slideshow: Object-Based Perceptual Cycles in a Model of the Visual Cortex

Abstract

While recent studies have shed light on the mechanisms that generate gamma (>40 Hz) oscillations, the functional role of these oscillations is still debated. Here we suggest that the purported mechanism of gamma oscillations (feedback inhibition from local interneurons), coupled with lateral connections implementing “Gestalt” principles of object integration, naturally leads to a decomposition of the visual input into object-based “perceptual cycles,” in which neuron populations representing different objects within the scene will tend to fire at successive cycles of the local gamma oscillation. We describe a simple model of V1 in which such perceptual cycles emerge automatically from the interaction between lateral excitatory connections (linking oriented cells falling along a continuous contour) and fast feedback inhibition (implementing competitive firing and gamma oscillations). Despite its extreme simplicity, the model spontaneously gives rise to perceptual cycles even when faced with natural images. The robustness of the system to parameter variation and to image complexity, together with the paucity of assumptions built in the model, support the hypothesis that perceptual cycles occur in natural vision.

Introduction

While oscillatory activity pervades the brain, its functional implications are still a matter of intense research. In particular, gamma-band oscillations (>40 Hz) have attracted significant attention since their discovery in feline visual cortex two decades ago (Eckhorn et al., 1988; Gray and Singer, 1989). Several functional roles have been suggested for gamma-band oscillations, including assisting selective attention (Niebur et al., 1993; Womelsdorf and Fries, 2007), controlling transient communication between distant regions (Fries, 2005), serving as a reference frame for temporal coding (Vanrullen et al., 2005a; Fries et al., 2007), organizing discrete items in working memory (Lisman, 2005), etc. In particular, the well-known binding-by-synchrony hypothesis posits that spatially distant neurons corresponding to a common object or concept will tend to fire together, allowing for their identification as a single representation by downstream centers (von der Malsburg, 1981; Singer, 1999). Thus gamma oscillations could support the encoding of distinct items in neural activity. Evidence for this proposal has been reported in the context of visual perception (Gray et al., 1989; Gail et al., 2000; Samonds et al., 2006), though the hypothesis is still controversial (Thiele and Stoner, 2003; Roelfsema et al., 2004; Dong et al., 2008; Leveille et al., 2010).

Recently a different role has been suggested for gamma-band oscillations, namely that of a “gatekeeper,” selecting which cells fire at each cycle, in a precise quantitative way (de Almeida et al., 2009). Gamma oscillations are thought to result from coordinated inhibitory barrages from local fast-spiking interneurons (Hasenstaub et al., 2005; Morita et al., 2008; Cardin et al., 2009). The delay between the first few pyramidal spikes, and the incoming inhibition, is relatively fixed. As a result, the proportion of cells that fire at a given cycle is not a constant fraction of all cells; rather, it was suggested that cells will fire if their level of excitation (above threshold) comes within E% of the excitation of the most excited cell. In this sense, gamma oscillations exert a strong selection, allowing only the most excited cells to fire at each cycle. This competitive aspect of gamma oscillations will play an important role in our paper.

Perceptual cycles

In this paper, we hypothesize an additional role for gamma oscillations: the segmentation of visual input into its constituent objects, over successive gamma cycles. More precisely, we suggest that, as a result of well-known connectivity patterns, distinct objects within the visual scene should be represented in neural firing at successive cycles of the gamma oscillation. Thus, the early visual cortex may spontaneously discretize the visual input into successive object-based time-slices, such that different objects within the scene will be represented in alternation over successive time-slices: at each time-slice, only the neurons representing one object (or a small number of objects) will fire. We call these successive, object-based firing epochs “perceptual cycles,” since they occur in a perceptual area, affect the perceptual input, and should have significant consequences on further processing by downstream areas of the perceptual system.

We aim to demonstrate that this apparently complex process should emerge naturally from two well-documented components of the early visual system. The first component is rapid mutual inhibition among principal cells, mediated by highly coupled interneurons, and generating iterated competition in firing. This process is thought to give rise to gamma oscillations in response to stimulation (Bartos et al., 2007; Cardin et al., 2009; de Almeida et al., 2009), and thus our perceptual cycles are also de facto gamma cycles (however, the reverse is not true, as gamma cycles by themselves do not implement any object-based segmentation, or alternation across objects). De Almeida et al. (2009) have shown how iterated, rapid mutual inhibition leads to a strong competition between principal cells, letting only the most excited cells fire at each cycle.

The second component is the set of excitatory connections between principal cells, direct or indirect, linking specifically those neurons which are likely to respond to the same object within a visual scene. These include lateral and feedback connections that implement “Gestalt” principles of object continuity (von der Heydt et al., 1984; Hess et al., 2003). In this paper, we use only contour-integrating connections, in the form of reciprocal excitatory connections between nearby cells that fall along a smooth contour (i.e., neighboring cells responding to collinear or co-circular orientations).

As a result of object-integrating excitatory connections, neurons corresponding to the same object within the visual scene will show correlated firing. By contrast, mutual competition iterated at each gamma cycle will produce negative correlation between the firing of different groups of neurons (rather than mere independence). The outcome is that neurons representing a common object tend to fire within the same cycle, while neurons representing different objects will tend to fire at different cycles. This turns gamma oscillations into actual “perceptual cycles”: different objects will tend to alternate in neural representation over successive gamma cycles.

Importantly, we are not suggesting that different objects are represented in a clean, perfectly repeating succession of isolated objects. Rather, we envision a process in which objects compete to be represented at every cycle, with only one or a few objects (those represented by the most excited neurons at that time) succeeding at every cycle. Some objects may be represented in more cycles than others if the corresponding neurons receive higher excitation; this can be caused by bottom-up biases (such as salience, closeness to the fovea, etc.), or top-down drives such as attention. For two objects of roughly equal salience, the process should lead to a relatively clean alternation (due to the negative correlation between neural groups caused by competition). For more complex images, the process should lead to more noisy sequences in which, at each cycle, a small subset of objects (different from one cycle to the next) is represented in neural firing.

A discretization of the visual input into fast, object-based perceptual cycles, even over a limited portion of the visual field, is bound to have important consequences for perceptual processing. For example, segregating the firing of neurons representing different objects should increase their saliency to downstream neurons, by reducing the noise and making it easier to identify each observed object. In addition, this segregated firing would also facilitate the learning of object features through Hebbian and anti-Hebbian learning, since it implies correlated firing of neurons responding to a same object, and anti-correlated firing of neurons responding to different objects.

To support our argument, we will build a simple computational model of the primary visual cortex that includes rapid mutual inhibition and contour-integrating lateral excitatory connections. We will show that object-based perceptual cycles emerge reliably in the system, using either simple artificial pictures or images of real scenes as input. We will demonstrate the robustness of the behavior to parameter variation. These results support the hypothesis that basic features of cortical connectivity segment the scene into its constituent objects along successive cycles of gamma frequency oscillations.

Materials and Methods

Model description

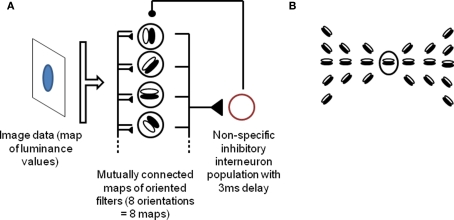
Since we want to describe a process which we suggest occurs in the early visual cortex, we implement a simple model of V1 for demonstration purposes. Our model is composed of a single layer of orientation-selective cells, representing activity in early visual areas, with lateral connections implementing contour continuation by linking neighboring neurons that respond to smooth contours (that is, neighboring neurons responding to collinear or high-radius co-circular orientations), and reciprocally connected to an inhibitory source. This model extends the model described by de Almeida et al. (2009). In order to facilitate comparisons, the organization and parameters of the system deliberately follow de Almeida et al. (2009) where applicable. The input is a time constant luminance map, with low time-varying noise added (taken at every pixel and every timestep from a (0, 1) normal distribution, and multiplied by 5% of the input range). Each cell implements a filter corresponding to oriented edge detection over a 5 × 5 window of the input picture. Each input pixel is associated with a full set of eight cells (one for each orientation), thus leading to high overlap between the receptive fields of neighboring cells. Lateral connections occur within and between the eight orientation maps, following principles of contour continuation (collinearity and high-radius co-circularity). More precisely, any principal cell is reciprocally connected, with equal weight, to cells within a 7 × 7 neighborhood that respond to orientations compatible with a smooth contour joining the two cells. The exact pattern of lateral connections for a given cell responding to a horizontal edge is shown in Figure 1. This pattern is repeated for every cell within the system, rotating orientations of target cells in accordance with the source cell's own orientation. This connection pattern is inspired from Li (1998b) and VanRullen et al. (2001). In reality, contour integration involves not just lateral connections, but also feedback from upper layers (von der Heydt et al., 1984); however we found that lateral connections were sufficient to produce the effects described in this paper. As in de Almeida et al. (2009), the source of inhibitory feedback is modeled as a single inhibitory interneuron receiving input from, and sending inhibitory output to, all pyramidal cells within the system. This simplification is justified by the wide convergence and divergence of connections between pyramidal cells and interneurons, including across columns, as well as the high coupling between interneurons created by mutual connections and electrical gap junctions (Kisvarday et al., 1997; Markram et al., 2004; Bartos et al., 2007; de Almeida et al., 2009). Thus any spike from the visual cells will generate (after a 3 ms delay) a non-specific inhibitory wave over the population. In addition, again following de Almeida et al. (2009), each neuron receives a constant background excitation current, set at the minimal level necessary to generate spiking in the absence of any input.

Figure 1.

Description of the model. (A) Outline of the model. A population of orientation-sensitive pyramidal neurons (modeled as oriented edge detectors) receives input from a map of luminance values, and sends output to a local interneuron population (modeled as a single inhibitory source). The inhibitory source discharges and sends an inhibitory potential to the pyramidal neurons, 3 ms after the first spikes, which temporarily inhibits the neurons. The iteration of this cycle leads to gamma-band oscillations and competitive firing among the pyramidal neurons (6). In addition, pyramidal cells send lateral excitatory connections to each other, implementing contour integration among the cells. (B) Pattern of lateral excitatory connections between pyramidal neurons. The central neuron is connected to all others in the picture. This pattern is repeated for all positions and orientations. Thus, any given neuron is reciprocally connected to all neurons within a 7 × 7 neighborhood that might fall along a common smooth contour with this neuron (that is, neurons selective to orientations that are collinear or co-circular with that of this neuron). The pattern is inspired from Li (1998) and VanRullen et al. (2001). See Section “Materials and Methods” for details.

Pyramidal neurons are modeled as leaky integrate-and-fire neurons, subject to excitation from the visual input (I_exc), lateral connections (I_lat) and background activity (I_min), as well as feedback inhibition (I_inhib) and after-hyperpolarization after spiking (I_ahp). The voltage V of each cell evolves according to the following differential equation:

τ * dV/dt = −(V − V_rest) + R * (I_exc + I_min + I_lat − I_inhib − I_AHP)

The parameters of the system are deliberately similar to de Almeida et al. (2009) (membrane resistance R = 33 mOhms, membrane time constant τ = 30 ms, resting potential V_rest = −65 mV, firing threshold T = −50 mV). After firing, a neuron's voltage is immediately restored to V_rest and an after-hyperpolarization current is applied (see below). In addition, the neuron is made insensitive to incoming excitation for an absolute refractory period of 2 ms. Background excitation is set at I_min = 0.5 nA.

Again following de Almeida et al. (2009), while visual stimulation is held constant (save for the added noise), inhibition and after-hyperpolarization are modeled as instantaneous rises followed by a linear decrease (inputs from lateral connections are modeled as instantaneous spikes only). After-hyperpolarization has initial amplitude A_AHP = −2 nA and time constant τ_AHP = 15 ms. Global inhibition has initial amplitude A_inhib = −20 nA and time constant τ_inhib = 3 ms.

Quantification of system behavior

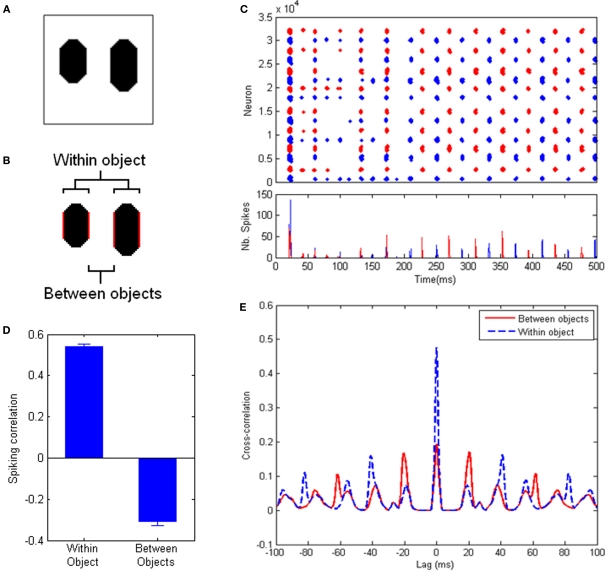
In order to objectively assess the occurrence of perceptual cycles, we use a measure based on correlation between spiking activities. First, we assign each cell in the system to the object it responds to (if any). For an image with 2 objects (Figure 2), this gives us two sets of cells, each responding to a different object. We run the system for 1000 ms of simulated time, recording spiking activity for each cell. Then we divide the record of spiking activity into successive, finite-size time bins (10 ms), thus obtaining one time-binned spiking histogram for each of the two populations. Our measure of interest is simply the correlation between these two histograms, over the course of a run (excluding time bins during which less than 10 cells fired). This measure will tend toward 1, 0 or −1, depending on whether cells from both populations tend to fire together, independently, or in alternation, respectively. A strong negative correlation indicates that cells from different objects tend to fire at different times, which implies the presence of perceptual cycles. We also use this measure to quantify population behavior within a single object, by dividing one object into its two halves and applying the above process to the populations of neurons responding to each half of the object. In this case, positive correlation will indicate a tendency of cells responding to the same object to fire within the same cycle.

Figure 2.

Experiments with a simple test picture. (A) The simple picture used for these experiments: two oblong objects with identical luminance, but different lengths, on a uniform background. (B) The reference populations used for measurements, highlighted in red. Between-objects values consider the inner edges of both objects; within-object values are obtained between the edges of each object, and the two resulting values are averaged. All measurements involve the same distance between populations. (C) (Top) Spike trains of all neurons in the system for an example run. (Bottom) Spike histogram of the same run. Neurons covering the left (resp. right) half of the image are shown in blue (resp. red). After an initial period, an oscillatory regime sets in (at ∼50 Hz frequency), with clear alternation between the populations. (D) Correlation between the spiking activities (time-binned PSTH, 10 ms time bins) of equally-spaced groups of neurons responding to the same object (left) and to different objects (right), averaged over 600 runs (error bars indicate standard error of the mean). Positive within-object correlation indicates that neurons corresponding to the same object tend to fire together; negative between-objects correlation indicates that neurons responding to different objects fire in alternation. (E) Cross-correlograms between the spike trains of equally-spaced groups of neurons responding to the same object (dashed blue line) and different objects (solid red line). Neurons coding for the same object tend to fire in phase with a period of about 40 ms. Neurons coding for different objects tend to fire in counter-phase.

To control for the possible effects of distance, we limit our populations to only the cells that code for two sides of one object and the closest side of the other object (see Figure 2B), thereby ensuring equal distance for within-object and between-objects measurements. The within-object measurement is taken over both objects and averaged.

In addition, we also calculate the auto-correlogram for the spike trains of neurons corresponding to a single object, as well as the cross-correlogram between the spike trains of neurons corresponding to distinct objects. This allows us to directly identify oscillatory behavior, including period length and phase-locking between the populations (Figure 2E).

For natural images, we adapted the previously described measure, in order to handle unpredictable object shapes while still controlling for the possible effects of distance. To this end, we first identify all cells responding to each separate object within the scene. Assuming there are n objects within the scene, this provides n populations of neurons. Cells coding for each object are obtained by selecting the cells receiving more than half maximal excitation, then manually assigning each of these cells to the object they respond to, if any (cells not responding to a well-defined object are ignored). We then randomly and automatically pick a set of “triplets” of cells; each triplet contains three cells a, b, and c, such that a and b respond to the same object, c responds to a different object, and the distances between a, b and b, c differ by less than 2 pixels. Note that cells may be picked and matched from any of the eight orientation maps indiscriminately. For each such triplet, we calculate the correlation in spiking activities between cells a and b (same object), as well as between cells b and c (different objects). Similarly to the previous measure, correlation between spiking activities is obtained by dividing the spiking record into discrete time bins (10 ms), and calculating Spearman rank correlation between the resulting time series (discarding any time bin in which none of the three cells fired). Averaged over many randomly selected triplets (100 per runs in these experiments), these provide an adequate picture of the correlation of spiking activities within and between objects, controlling for the possible effects of distance.

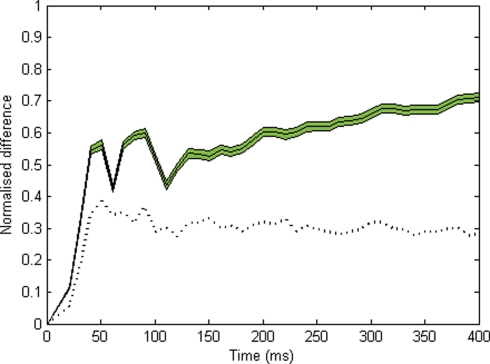
We also sought to evaluate the time course of organization within the system. First, for all successive time bins (10 ms) in each run, we obtain the proportion of all cells coding for either object that fire within a given time bin, out of all the cells that can potentially respond to this object. This gives us two time series which we may call s1(t) and s2(t), respectively. We then compute the normalized difference between s1(t) and s2(t) for every time bin, D = |s1(t) − s2(t)|/[s1(t) + s2(t)], excluding time bins in which fewer than 10 cells fired and linearly interpolating over these. This normalized difference provides a real-time estimate of the segregation between cell groups: D will be high (max. 1) if cells from different groups never fire within the same time bin. Inversely, it will fall to zero if equal proportions of cells from each group fire within a given time bin. The curve in Figure 3 shows the average of 600 runs. In order to assess significance, we use a resampling method. For every time bin, we compute the normalized difference for all 600 runs, after reassigning each cell to either object at random. Then we pick the 30th highest of all 600 values obtained for this time bin, and use this as the p = 0.05 level for this time bin (indicated by the dotted curve in Figure 3).

Figure 3.

Time course of normalized difference between the spiking activities for each object (10 ms time bins, see Materials and Methods). This difference should be zero if neurons coding for the two objects respond in synchrony, and should approach 1 if neurons for each object fire in alternation. The solid line indicates the average over 600 runs (green area: plus or minus s.e.m.). The dotted black line indicates the p = 0.05 level, obtained by randomly reassigning cells between objects, calculating the normalized PSTH difference, and taking the 30th highest value (among all 600) for each time bin. Significant segregation is observed within the first 50 ms.

Results

We implement a simple model of V1, based on the model proposed by de Almeida et al. (2009), with additional connectivity to implement contour integration. A schematic illustration of our model is provided in Figure 1 (see Material and Methods for a full description). Neurons are modeled as oriented edge detectors, organized in eight retinotopic maps (one for each of eight possible orientations from 0° to 315°). All neurons are non-specifically connected to a local interneuron population, which sends back a wave of inhibition in response to spikes from the pyramidal neurons, with a fixed delay (3 ms). This produces an iterated competition such that only the most excited pyramidal cells will be able to fire at every cycle (de Almeida et al., 2009). In addition, all pairs of neighboring neurons that fall along a smooth path are linked by reciprocal excitatory connections; the exact connection pattern is described in Figure 1B. This leads to “contour integration” among the neurons, in which neurons that represent a smooth contour in the picture will send spikes to each other, and therefore facilitate each other's firing (Li, 1998; VanRullen et al., 2001).

Results with a simple artificial picture

For our initial tests, in order to facilitate interpretation, we use a very simple artificial image in which perceptual cycles should occur prominently. Our test input is composed of two monochrome oblong objects of different sizes on a white background, as shown in Figure 2A. Using a very simple, two-color picture also makes it possible to run many experiments in a reasonable amount of time, which allows us to observe the behavior of the system over a wide range of parameters.

Figure 2 describes the results of the system with default parameter values (specified in Materials and Methods). Movies depicting the neural activity over an example run are available in Supplementary materials. Figure 2C shows the spike raster plot and spike histogram of an example run. After an initial period of self-organization, the system settles into an oscillatory pattern in which neurons responding to either object fire in alternation. In order to quantify this behavior, we use a measure based on the correlation between peri-stimulus time histograms (PSTH) within and between objects. A positive correlation between the PSTH of two neuron populations indicates that these two populations tend to fire together, while a negative correlation indicates that the two populations tend to fire at different times (see Materials and Methods). Figure 2D shows the result of this measure averaged over 600 runs, applied to two equidistant populations belonging either to the same object or to separate objects (Figure 2B). A clear signature of perceptual cycles emerges, in the form of negative correlation between the firing activities of cells responding to different objects, and positive correlation for cells responding to the same object (see Materials and Methods for a full description of the measure used). This indicates that populations of cells encoding the two objects tend to fire in alternation, that is, the scene is successfully decomposed along perceptual cycles.

Figure 2E shows the average cross-correlograms, over 600 runs, between two equidistant populations belonging either to the same object or to different objects. The cross-correlograms reveal strong oscillations in the system, with a frequency of about 50 Hz. The distribution of peaks in these cross-correlograms indicates that cells responding to the same object tend to fire mostly in phase, while cells responding to different objects tend to fire mostly in counter-phase within this oscillatory regime. Thus the emergence of perceptual cycles leads to an alternation between representations of both objects.

In order to assess the time course of the process, we use a simple segregation index (normalized difference defined as |n1 − n2|/(n1 + n2) where n1 and n2 are the normalized numbers of spikes in response to object 1 and 2, respectively – see Materials and Methods). This measure is calculated over each time bin (excluding these in which no cell or too few cells fired, and interpolating over these). Figure 3 shows the average of this measure for 600 runs, together with a p = 0.05 level obtained for each time bin by resampling under the null hypothesis (assigning each pixel to a random object, see Materials and Methods). Significant segregation occurs within the first 50 ms of activity.

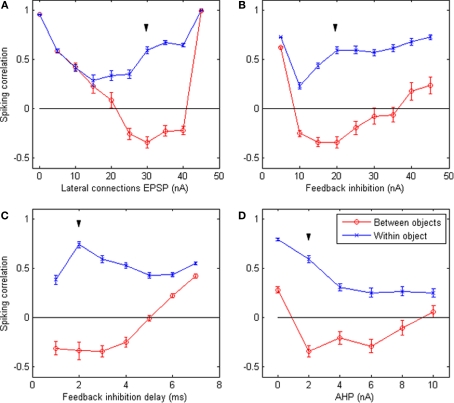
How robust are these results with regard to the choice of parameters? Figure 4 shows the results of the system when letting certain parameters vary around the default values (keeping all other parameters equal). These figures indicate that cycling behavior occurs over a sizeable range of parameter values. This suggests that the emergence of perceptual cycles is a robust phenomenon, as opposed to a fragile result highly dependent on favorable parameters. In addition, we note that perceptual cycles are eliminated when either lateral connections or feedback inhibition tend toward zero: in both cases, correlations in firing become positive for all neurons, regardless of which object they represent. This confirms that these two mechanisms (feedback inhibition enforcing competitive firing and lateral connections implementing object integration) are the two crucial requirements for the emergence of perceptual cycles in our system.

Figure 4.

Robustness of system behavior to parameter variation. Correlation between the time-binned PSTH of equally-spaced groups of neurons responding to the same object (blue crosses) and to different objects (red circles), when certain simulation parameters vary while all others remain fixed at their default values. The varying parameters are: (A) strength of EPSP carried by lateral connections; (B) peak amplitude of feedback inhibition; (C) delay between the first spike and the arrival of feedback inhibition; (D) peak amplitude of the after-hyperpolarization potential. All values are averages of 50 runs; error bars indicate s.e.m. Down arrow (▼) indicates default value. The expected behavior (positive within-object correlation, negative between-objects correlation) emerges over a wide range of parameters. Significant differences between within-object and between-objects correlations occur for an even wider range of parameters. However the behavior breaks down in the absence of lateral connections (top left) or feedback inhibition (top right), confirming that these are the crucial requirements for the emergence of perceptual cycles.

Natural images

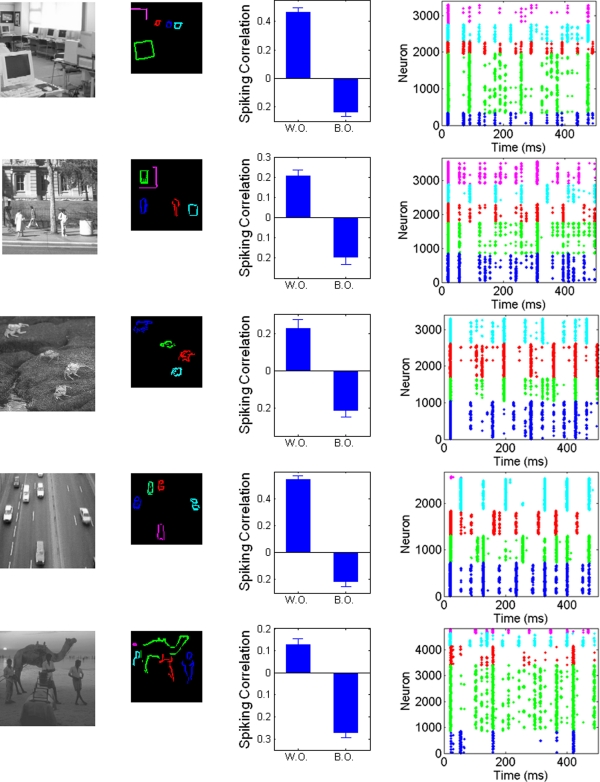
In order to provide a stronger challenge, we presented the model with a set of natural images, covering a range of different scene types (indoor, landscape, animals, etc.). These pictures were taken from the Corel database, cropped and resized to 96 × 96 pixels and converted into grayscale values (see Figure 5). The only modification of the model is that we raise the relative level of background excitation to 1 nA in order to dampen the larger dynamic range of the pictures. Figure 5 shows the resulting correlations for spiking activities between and within objects, as well as example rasterplots to illustrate the dynamics of the system. Despite the extreme simplicity of the model (in particular the absence of feedback, multi-scale processing, or special filters such as T/L detectors, etc.), the results shown in Figure 5 show that the system is still able to segregate between objects, ensuring that pixels corresponding to the same object will tend to fire together more often than pixels belonging to different objects (see also movies depicting the results of the system in Supplementary Material). While neurons not assigned to any object are not shown on the example rasterplots (since object-encoding neurons are the focus of our hypothesis), they simply fire in rhythm with the general oscillation imposed by the common inhibitory source. Unsurprisingly, the quantitative and qualitative (visual) results are clearly less pronounced than for simple pictures, indicating that the segregation is less reliable. Furthermore, results are variable between pictures. Nevertheless, the different objects are visibly segregated on visual inspection, which is numerically confirmed by the large difference between within-object and between-objects correlations in spiking activities for each image. This further confirms the robustness of the mechanism, and thus its intrinsic plausibility.

Figure 5.

Application of the system to pictures of natural scenes. First column: original pictures. Second column: neurons with activity over 50% of the maximum, assigned by hand to different objects within the scene. Third column: Correlation between PSTH within and between objects, controlling for distance. Fourth column: rasterplots for example runs, with spikes colored accordingly to the object covering the neuron's receptive field center, with the same color assignment as in second column. See Materials and Methods for details.

Discussion

Here we hypothesize that basic features of cortical organization may spontaneously segment the visual scene into its component objects, over successive cycles of local gamma oscillations. We suggest that this process should emerge naturally from the interplay between two components of cortical connectivity, namely, rapid mutual inhibition through local interneurons (generating iterated competition between neurons), and lateral and feedback connections implementing object integration. As a result, neurons responding to one object would tend to fire within the same cycle (due to object-integrating connections), while neurons responding to different objects should tend to fire at different cycles (due to iterated competition caused by feedback inhibition). We demonstrated that a simple model including very basic implementations of these mechanisms was sufficient to give rise to this process. We showed that the behavior was relatively robust to variation in parameters, and could deal with natural scenes despite the lack of advanced processing features. We expect that the strength of perceptual cycles in the model should improve as further complexity is added to the system, e.g., in the form of multi-scale processing, additional connectivity implementing other forms of object integration, border ownership, etc.

Related work

Over the last few years, there has been a resurgence in the debate over whether perception operates in a discrete or continuous manner. A discrete component for perception has been suggested from both theoretical considerations and experimental results (VanRullen and Koch, 2003; Vanrullen et al., 2005b; Freeman, 2006; Busch et al., 2009). While neural oscillations have been described as a support for encoding distinct items in memory (Lisman and Idiart, 1995), the idea that they might also support segmentation of visual input has only been recently proposed.

Lisman and Idiart have suggested a model of working memory based on “nested oscillations” (Lisman and Idiart, 1995). In this model, various items stored in working memory are individually inscribed into successive cycles of a fast (e.g., gamma) oscillation, which is itself nested into a slower (e.g., theta) oscillation. Recent evidence suggests that at least in the hippocampus, a certain sub-population of pyramidal cells exhibits properties compatible with this multiplexing, in that they maintain a preferred theta phase in the presence of gamma oscillations (Senior et al., 2008).

VanRullen and Koch (VanRullen and Koch, 2003) suggested on theoretical and empirical grounds that a similar process could occur in perceptual areas. In particular, distinct objects within the scene could be inscribed into successive cycles of a fast oscillation – corresponding to the “perceptual cycles” discussed in this paper. This fast oscillation could then be nested into a slow, globally-coherent oscillation, each cycle of which would correspond to a full “snapshot” of the scene, composed of successive perceptual cycles. Psychophysical evidence (such as ∼25 ms periodicities in reaction times – see, e.g., Latour, 1967; White and Harter, 1969; Dehaene, 1993) suggests that the fast oscillation may fall within the gamma frequency range. A similar concept has been independently proposed by Lisman (2005), as a generalization of Lisman and Idiart's model of working memory. Fries (2009) made a related, but different proposal, in which neural representations of distinct “parts of the sensory input” fire at gamma frequency, but the switching from one part to the next occurs over cycles of the slower oscillation. However, in all these proposals, the neural basis for the suggested process was only broadly alluded to.

Other authors have explored the idea of temporally segmented patterns in the neural representations of visual objects. Choe and Miikkulainen (1998) built a model in which synaptic plasticity progressively establishes synchrony between assemblies of neurons representing spatially distinct objects, whose activity would wax and wane in alternation due to lateral inhibition. Stoecker et al. (1996) showed that neurons densely connected by modulatory synapses (akin to multiplicative gap junctions) and subject to global inhibition balanced with the overall excitation level, could develop synchrony across homogenous zones of the visual input, and thus segregate into alternating representations of these zones. These proposals rely on specialized mechanisms to obtain the described effects, supporting the idea that perceptual cycles could require complex, dedicated machinery. By contrast, the main point of this paper is that segmentation and alternation between objects is expected to emerge spontaneously from basic cortical connectivity (feedback inhibition from fast-spiking interneurons, giving rise to gamma-band oscillations; and lateral-feedback connections implementing object-based correlations, such as contour integration). As we have shown, these basic mechanisms are all that is needed to generate oscillations, synchrony, competition, and (therefore) perceptual cycles.

Laurent and colleagues have studied the olfactory system of the locust extensively, showing that oscillations caused by feedback inhibition allowed for strong sparsening of odor representations. The dense, long-lasting, temporally patterned, high-firing response of antennal lobe neurons is time-sliced by local oscillations, which allows mushroom body cells to decode it into sparse, brief, almost-binary activity, presumably through coincidence detection (Laurent, 2002). This two-stage process is quite different from the one described in this paper, though it shows how oscillations based on feedback inhibition can support item-specific patterning of the perceptual input.

Our hypothesis is distinct from, but compatible with, the related hypothesis of “phase coding” or “phase tuning” at gamma frequency, which suggests that the particular phase at which a neuron fires within a given gamma cycle carries information (Hopfield, 1995; Vanrullen et al., 2005a; Fries et al., 2007; Siegel et al., 2009). Both processes rely on the same intuition, namely that the most excited neurons should fire earlier in the gamma cycle. Our own hypothesis relies on the additional observation that only a small subset of neurons (or neuron assemblies) will reach threshold early enough to fire at all before the onset of inhibition, as described by de Almeida et al. (2009). Thus, it is entirely possible (or even likely) that object-based segmentation along gamma cycles occurs concurrently with gamma phase tuning within perceptual areas.

Limitations of the model

Our system was built around a model of gamma oscillations by de Almeida et al. (2009). One of the simplifications of this model is that the inhibitory population is modeled as a single source, which receives excitatory input from (and sends inhibitory output to) all principal cells in the network. This simplification implies that the present model only captures the behavior of a local patch of cortex, constrained by the range of lateral connections and coherent gamma rhythm. Nevertheless, even a local process will have consequences on further processing by downstream neurons, in terms of increased saliency of individual objects and facilitation of Hebbian and anti-Hebbian learning. For example, a V4 neuron collects inputs from a patch of V1 with an estimated average radius of 3.8 mm, independent of eccentricity (Motter, 2009), only slightly higher than the ∼3 mm range of large basket cell inhibitory projections (Kisvarday et al., 1997). Thus, any given V4 neuron would be expected to benefit fully from the hypothesized process within its own receptive field.

It would of course be interesting to test the behavior of the model over larger distances, with individual (but coupled) interneurons. Local competitions might “tile” into each other between neighboring areas, with little long-distance correlation; alternatively, continuous phase fronts of gamma oscillations might be maintained over long distances, creating congruent competitions over relatively larger areas (Eckhorn et al., 2004). This could be the subject of further modeling work.

Our model is based on a PING model of gamma oscillations, that is, one in which gamma oscillations emerge from interactions between principal cells and local interneurons. An alternative possibility is the ING model in which interneurons generate gamma oscillations independently of local excitatory cells (Tiesinga and Sejnowski, 2009). However, a PING model does not seem to be a critical requirement for our hypothesis. Our model requires both oscillations and competitive mutual inhibition, which are both known to occur within the cortex. While a PING model is more convenient in that oscillations and competition arise from the same process of mutual inhibition, an ING model with mutual inhibition between principal cells would be expected to perform similarly. At any rate, the PING model seems to be quite compatible with the available evidence, such as the fact that gamma can result from non-periodic stimulation of the local pyramidal cells (Sohal et al., 2009), while blocking NMDA and AMPA receptors eliminates gamma even if local interneurons are induced to fire at gamma frequency (Cardin et al., 2009), or that blocking inhibition onto interneurons does not eliminate gamma (Wulff et al., 2009).

Future directions and perspectives

The process described here could readily be integrated into a larger model incorporating lower-frequency, externally generated oscillations. The interaction between the two frequencies could create a multiplexing of visual information into a fast oscillation enumerating individual objects, and a slower oscillation performing regular “sweeps” of the visual input, as suggested by VanRullen and Koch (2003) and Lisman (2005). Further studies are needed to explore the questions raised by these hypotheses, such as which frequency band (e.g., alpha, theta, delta) is a more likely candidate for the slower-frequency component.

While the mechanism discussed here produces an alternation between objects, the selection of which objects are represented in each cycle is biased by several factors: neurons receiving more excitation will clearly fire more often, and thus the corresponding objects will be represented in more cycles. This may be caused by bottom-up factors (such as salience, or foveal magnification), but also by top-down factors such as attention, presumably mediated by input from higher layers. In addition, while our simple model only includes lateral connections, object-integrating connectivity is known to involve feedback connections from higher layers (von der Heydt et al., 1984). Thus, incorporating feedback between layers in our system could greatly expand the range of effects that our model can capture.

While our system is based on a model of V1 cells, the mechanisms involved are generic features of cortical organization. Therefore, a similar process can be expected to occur in other visual areas as well. In V1, due to the small receptive fields of neurons, the process described here should apply locally to portions of the visual field. Indeed, all of our simulations can be construed as operating over a local area of the visual field rather than the entire field. By contrast, in higher areas such as V4 where receptive fields are much wider, we may expect that perceptual cycles would cover a larger portion of the scene. This process may culminate in IT, in which neurons have very large receptive fields and relatively position-invariant responses that are highly selective for complex features or even object identity, covering much of the visual input (Gross, 1992).

An important aspect of the current model is its extreme economy: very few assumptions are needed to give rise to the behavior described, and these assumptions correspond to basic, well-documented mechanisms. Furthermore, the fact that the behavior remains stable over a range of parameters, and also occurs for natural scenes, demonstrates its robustness. This suggests that the concept of perceptual cycles, far from being an outlandish claim, might actually be the default hypothesis: the existence of perceptual cycles in some form is intrinsically more likely than the opposite, given the known organization of the perceptual cortex.

Taken together, our results support the existence of a discrete component in perceptual processing, underlain by gamma oscillations and mutual excitation. These results call for confirmation from biological inquiries. It is notable that research on these subjects is currently thriving: for example, recent technical developments have refined and secured our understanding of the mechanisms of gamma oscillations, directly implicating resonant inhibition from interneuron networks in vivo (Cardin et al., 2009; Sohal et al., 2009). These developments, together with ongoing research on gamma-band synchrony (Colgin et al., 2009; Fries, 2009; Koepsell et al., 2009), may soon uncover the relevant evidence to identify causal mechanisms in a discrete component of perception.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at http://www.frontiersin.org/humanneuroscience/paper/10.3389/fnhum.2010.00205/