Use of a Reference Tissue and Blood Vessel to Measure the Arterial Input Function in DCEMRI

Abstract

Accurate measurement of the arterial input function is critical for quantitative evaluation of dynamic contrast enhanced magnetic resonance imaging data. Use of the reference tissue method to derive a local arterial input function avoided large errors associated with direct arterial measurements, but relied on literature values for K^trans and v_e. We demonstrate that accurate values of K^trans and v_e in a reference tissue can be measured by comparing contrast media concentration in a reference tissue to plasma concentrations measured directly in a local artery after the 1–2 passes of the contrast media bolus—when plasma concentration is low and can be measured accurately. The values of K^trans and v_e calculated for the reference tissue can then be used to derive a more complete arterial input function including the first pass of the contrast bolus. This new approach was demonstrated using dynamic contrast enhanced magnetic resonance imaging data from rodent hind limb. Values obtained for K^trans and v_e in muscle, and the shape and amplitude of the derived arterial input function are consistent with published results.

INTRODUCTION

Dynamic contrast enhanced magnetic resonance imaging (DCEMRI) plays an important role in clinical detection and diagnosis of cancers (1,2). The pharmacokinetic model that is often used to analyze DCEMRI data (3) requires knowledge of the arterial input function (AIF), which accounts for variations in contrast media injection, cardiac output, and vascular function (4). The AIF can be determined from a major artery (5), a predefined “population” function (6), or a reference tissue (7). However, the direct measurements from arteries are subject to significant systematic errors due to the very high contrast agent concentration at early times after injection, partial volume effects, and in-flow affects (8,9). The “population” AIF does not account for significant variability between patients and contrast media injections. To avoid these problems, “reference tissue methods” (7,10,11) were developed to infer the AIF from measurements of contrast media concentration versus time in normal tissue with known physiological properties. Reference tissue methods do not require measurements of high contrast media concentration in an artery. They provide high signal-to-noise ratio (SNR) because a large volume of relatively homogeneous normal tissue can be used, and they provide a local AIF for each subject, since a reference tissue close to the cancer can be selected. The original “reference tissue method” (7) relied on the literature values for the volume transfer constant (K^trans) and the contrast media distribution volume (v_e) as a starting point, and these may differ significantly from the true value for each experimental subject. Recently, a more accurate reference tissue method has been developed to determine a consensus AIF based on contrast media dynamics in two (10,11) or more reference tissues (12). The newer method is more robust, but accurate calculation of K^trans and v_e in the reference tissues is not guaranteed, and there is still a possibility for systematic error. The multiple reference tissue approach requires a literature value of v_e from one reference tissue to scale the AIF, and the true value for v_e may be significantly different from the literature value.

Here we introduce a new method to more accurately determine K^trans and v_e for a reference tissue, and thereafter to derive the entire AIF more accurately. The approach assumes that (i) the contrast concentration in an artery can be measured accurately by MRI after the first 1–2 passes of the contrast media bolus (about 30–60 seconds after injection in rats) when the plasma concentration of contrast media is low and changes slowly; (ii) contrast media dynamics in a reference tissue (e.g., muscle) can be accurately described by a simple physiological model, e.g., the two compartment model with or without a vascular term; (iii) contrast media concentration in plasma and in a reference tissue with modest perfusion are far from equilibrium for several minutes after injection. The latter assumption is supported by simulations based on published models for the AIF, K^trans and v_e, and is also consistent with the experimental data presented here (e.g., please see Fig. 3 and the accompanying discussion). With these assumptions, the difference between the plasma and reference tissue concentrations of contrast media over time can be analyzed to derive K^trans and v_e for the reference tissue (see “Materials and Methods” section). In the following, we refer to this new approach as the “RTPV” (reference tissue plus vessel) method. The RTPV is illustrated using preclinical DCEMRI data acquired from the hind limbs of rats.

FIG. 3.

The plots of a bi-exponential fit to the plasma concentration of contrast media as a function of time, and C_m(t) divided by v_e for (a) Case 2 and (b) Case 3 in Table 1. There was a large positive difference between the plasma and reference tissue concentrations of contrast media between ~30 s and ~1.5 min after bolus arrival, and a large negative difference between 1.5 minutes and ~7 minutes.

MATERIALS AND METHODS

This was a retrospective study, based on data acquired from Copenhagen rats with AT6.1 metastatic prostate tumors in the hind limb. However, the analysis described here uses data only from normal skeletal muscle of the hind limb. Data from the tumors was not used in the present study.

MRI Experiments

All surgical procedures were performed in accordance with the University of Chicago Institutional Animal Care and Use Committee guidelines. Animals were anesthetized using Isoflurane gas (~2%) mixed with medical air (2 L/min) and oxygen (0.2 L/min) flowing through a mask. All animals were monitored for heart rate, respiration rate, blood pressure, and temperature using an SA Instruments system (Stony Brook, NY) developed for in vivo MRI. Temperature was controlled by blowing warm air through the bore of the magnet. A 24 gauge angiocatheter was placed in the tail veins of the rats for contrast agent injection.

MRI experiments were performed on a 33 cm, horizontal bore, 4.7 Tesla scanner with a Bruker console (Bruker-Biospin, Billerica, MA) equipped with a 20 cm shielded gradient set with a maximum strength of 200 mT/m. The tumor-bearing leg was placed in a Helmholtz coil, 3.0 cm in both diameter and length. For DCEMRI experiments, the middle three slices covering the largest cross-sectional area of tumor were selected along the long axis of the leg. T₁-weighted gradient echo images (TR/TE = 40/5 msec, field of view = 40 mm × 40 mm, matrix size = 128 × 128, slice thickness = 1.0 mm, flip angle = 30°, number of averages = 1) were acquired with 5 sec temporal resolution for the first ~10 min after contrast media injection, and subsequently with ~10 sec temporal resolution for another ~10 min. There was a ~7 min gap between first and second set of DCEMRI data while other MRI data (not used in this study) were acquired. The contrast agent, Gadodiamide (OmniScan^®, GE Healthcare, Piscataway, NJ), was injected ~30 sec after the start of the acquisition at a typical dose of 0.2 mmol/kg of body weight (0.2 mL of 95.7 mg/mL of OMNISCAN in saline) over ~5 sec.

Estimation of K^trans and v_e

Contrast media concentration as a function of time [C(t)] was determined from signal intensity using a previously published method (13). Then DCEMRI data were analyzed using the following protocol to estimate K^trans and v_e for a reference tissue (skeletal muscle):

Step 1: Determine AIF

Small arteries in the leg were selected to determine plasma concentration of contrast media. The velocity of blood flow in these small vessels is much lower than in the aorta (14) and flow was primarily in the plane of the imaged slice. Therefore, in-flow effects were expected to be modest, so that contrast media concentration could be accurately measured from MRI signal intensity, after the first one or two passes of the bolus. Contrast concentration as a function of time from the vessel, C_a(t), was measured in a single candidate pixel to minimize the partial volume effects. The portion of the curve after the apparent peak (t_peak) enhancement was fitted by bi-exponential function a₀·exp(−m₀t) + a₁·exp(−m₁t), and compared with published values determined by MRI measurements of the arterial plasma contrast media concentration in rats’ tails (15). Pixels in the blood vessel were tested until a fit for C_a(t) with parameters near the previously published results were found. This insured that the selected pixel was in an artery. The acceptable ratio for “a₀/a₁” was from 1.5 to 3.0, and the acceptable ratio for “m₀/m₁” was from 28.0 to 79.0. These acceptable ratio ranges were calculated from the values listed in Table 2 of reference 15. Data from the selected pixel in the blood vessel was used for subsequent calculations. Measurements of C_a(t) were considered to be an accurate measure of the AIF at times greater than t_peak, when contrast media concentration in the artery was generally less than 1 mM, i.e., low enough to minimize $T_2^{\ast }$ effects and effects of water exchange across red cell membranes. Note that the measured t_peak is not the true peak of the arterial concentration. The true peak is generally missed due to limited temporal resolution and errors caused by high plasma concentrations of contrast media. Finally, C_a(t) was corrected using published values for the average arterial hematocrit in the rat (Hct = 0.45) (5) to define Ĉ_p(t) = C_a(t)/(1-Hct) as the plasma AIF in the leg.

Step 2: Measure C_m(t) in the Reference Tissue

The contrast media concentration as a function of time, C_m(t), was obtained from a region of interest (ROI) with 9 × 9 pixels in a portion of the leg muscle away from the tumor with relatively uniform contrast media uptake. To moderate the effect of noise, the curve was fitted using a previously published empirical mathematical model (EMM) (16), and the EMM fit was used in the remaining calculations. Specifically, the muscle curves were fitted by the following equation:

$$C_{\text{m}}(t)=A·{(1-exp(-\alpha t))}^q·exp(-\beta t)·(1+exp(-\gamma t))/2,$$

where A is the upper limit of the tracer concentration, α (min⁻¹) is the rate of uptake, β (min⁻¹) is the overall rate of washout, γ (min⁻¹) is the initial rate of washout, and q is related to the slope of uptake.

Step 3: Estimate v_e for C_m(t)

The slope of C_m(t) was close to 0 at time t ≥ ~30 min. This can be seen from the EMM parameters for the muscle curve at t ≥ ~30 min, i.e., |dC_m(t)/dt| < |Aβ|, which is a very small number. Therefore, we assumed that the interstitial and venous plasma tracer concentrations were very close to equilibrium at a late time (~30 min) after a bolus of contrast injection. Under this equilibrium condition, we have the following relation:

$${\widehat{C}}_{\text{p}}(t)=C_{\text{m}}(t)/v_{\text{e}}\to v_{\text{e}}=C_{\text{m}}(t)/{\widehat{C}}_{\text{p}}(t)\text{at}t\ge \sim 30min.$$

Step 4: To Estimate K^trans From C_m(t)

We assumed that the muscle was well approximated by the two compartment model (TCM):

$$\frac{{dC}_{\text{m}}(t)}{dt}=K^{\text{trans}}(C_{\text{p}}(t)-C_{\text{m}}(t)/v_{\text{e}}),$$ [1]

where C_p(t) is the AIF. From Eq. 1, the regional AIF [C_p(t)] can be calculated from C_m(t) in muscle, i.e.,

$$C_{\text{p}}(t)=\frac{1}{{\text{K}}^{\text{trans}}}\frac{{dC}_{\text{m}}(t)}{dt}+\frac{C_{\text{m}}(t)}{v_{\text{e}}},$$ [2]

where v_e was determined in Step 3. To estimate K^trans in muscle, K^trans values in Eq. 2 were searched between 0.001 and 0.5 min⁻¹ by using the “golden section” method to find the best fit for the measured Ĉ_p(t) for times greater than t_peak but less than 5 min. Finally, from estimated values for K^trans and v_e determined from from Steps 1–4, the complete AIF beginning at t = 0 was calculated from Eq. 2. Note that an accurate value for K^trans can be determined from Eq. 2 only if the difference between Ĉ_p(t) and C_m(t)/v_e is much greater than the noise. Therefore, the optimal reference tissue for this approach has a relatively low K^trans, so that contrast agent concentrations in the plasma and reference tissue approach equilibrium slowly.

RESULTS

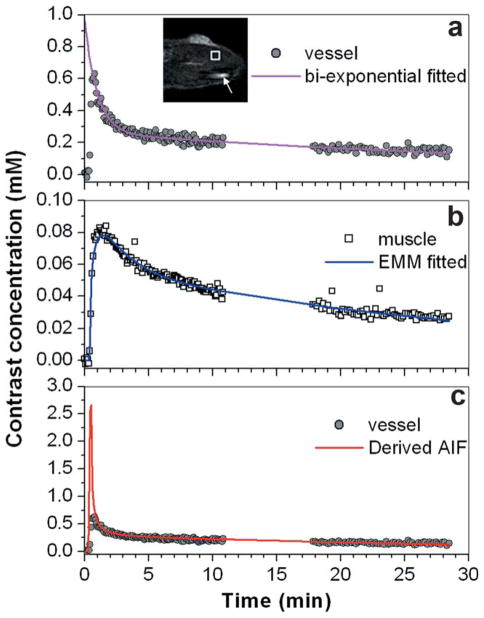
Figure 1 shows a typical image and plots of contrast media concentration in muscle and in the local artery to illustrate the steps followed for estimating K^trans and v_e in the muscle ROI. Figure 1a shows Ĉ_p(t) (gray dots) measured from the selected blood vessel pixel (indicated by an arrow in image) and the best fit bi-exponential function for times greater than t_peak (purple line). Please notice that the fitted line was extrapolated back to zero from the t_peak. Due to the ~5 sec temporal resolution and high contrast concentration at the peak of the bolus, the true peak of Ĉ_p(t) was missed and only the portion of the curve after the measured peak (t ≥ t_peak) could be accurately determined from MRI. The bi-exponential fit was excellent in spite of the gap in the data and the parameters were within the range of published results for arteries in rats. The C_m(t) (Fig. 1b open square) for the muscle ROI (indicated by square in image) was accurately fitted by the EMM (blue line). In this example, based on the EMM fit to C_m(t) and the bi-exponential fit to Ĉ_p(t), we obtained values for K^trans and v_e of 0.12 min⁻¹ and 0.19, respectively.

FIG. 1.

Illustration of the method used to estimate reference tissue K^trans and v_e: (a) A single pixel with an acceptable contrast media concentration vs. time curve (gray dots) was selected in a blood vessel (indicated by an arrow in the inset of image); the washout portion of the curve [Ĉ_p(t)] was fitted with a bi-exponential function (purple line) and extrapolated back to zero from “t_peak.” b: Contrast media concentration vs. time curve (open squares) in a muscle ROI (indicated by a square in the inset of image) was measured, and fitted with the EMM (blue line). c: The AIF was calculated from C_m(t) in the reference tissue, based on the estimated K^trans and v_e (red line) and the contrast media concentration in the blood vessel [as in (a)] (gray dots). The difference image (post contrast media injection minus preinjection) is shown in the insert with an FOV of 2 cm × 2 cm.

Figure 1c shows the complete AIF (red line) derived from using the estimated K^trans and v_e in the reference ROI. The derived AIF accurately fits the measured Ĉ_p(t) (gray dots) for times greater than t_peak. However, the derived AIF does not match the early portion of Ĉ_p(t), and has a much higher maximum amplitude.

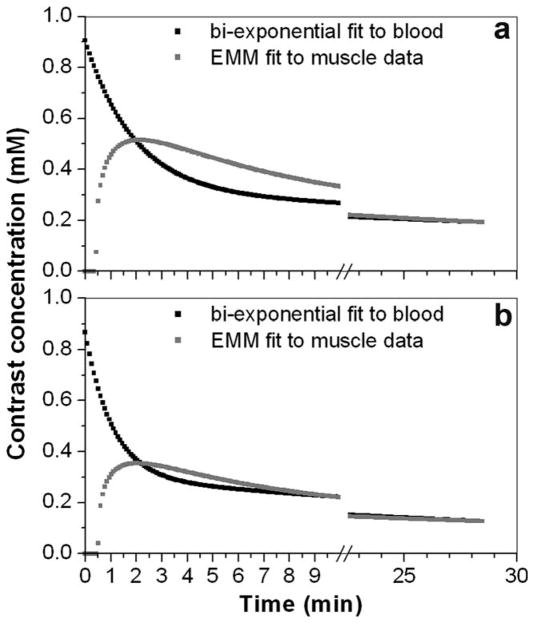
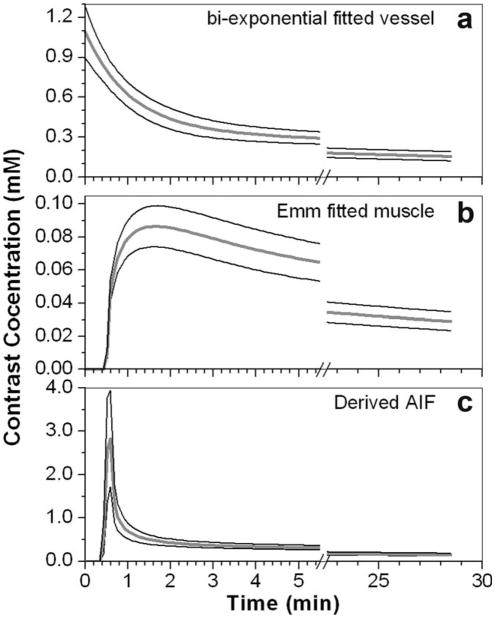
The same procedure (above) was applied to analyze data from eight experiments. The parameters for the bi-exponential fits to the Ĉ_p(t), the EMM fits to C_m(t), and estimated K^trans and v_e for muscle are given in Table 1. For the bi-exponential fits to the Ĉ_p(t) curves, the ratio of a₀/a₁ was in the range of 1.6–3.2, and ratio of m₀/m₁ was in the range of 29.0–44.0. Thus, our bi-exponential fitting parameters are within the range of previously published values (15). The directly measured average peak SNR for vessel and muscle were 41 ± 10 and 10 ± 3, respectively. The average values of K^trans and v_e for all eight cases were 0.14 ± 0.06 (min⁻¹) and 0.19 ± 0.05, respectively. Figure 2 shows average curves (thick gray lines) over eight cases for (a) bi-exponential fits to the AIF, (b) EMM fits for C_m(t), and (c) the AIF derived from the estimated K^trans and v_e using the reference tissue method. The thin black lines show the standard deviation of the distributions at each time point - demonstrating significant variability within the group. The peak amplitude of the AIF derived using the reference tissue was 2.77 ± 1.19 mM, and the peak amplitude of Ĉ_p(t) measured directly from the vessel was 0.69 ± 0.07 mM. This difference was statistically significant (P < 0.002).

Table 1.

Contrast Concentration Versus Time Curves From Vessels and for Muscle ROIs for Eight Selected MRI Experiments

Case	Bi-exponential fitted vessel curve [a0, m0; a1, m1]	EMM fitted muscle curve [A, q, α, β, γ]	Ktrans (min−1)	ve
1	[0.70, 1.04; 0.26, 0.024]	[0.12, 0.33, 0.94, 0.030, 0.46]	0.12	0.19
2	[0.59, 0.53; 0.31, 0.017]	[0.10, 0.32, 0.70, 0.021, 0.18]	0.05	0.15
3	[0.57, 0.94; 0.30, 0.030]	[0.13, 0.35, 1.02, 0.021, 0.17]	0.22	0.30
4	[1.00, 1.17; 0.31, 0.030]	[0.15, 0.49, 0.98, 0.031, 0.54]	0.18	0.23
5	[0.56, 0.67; 0.35, 0.020]	[0.15, 0.40, 1.12, 0.028, 0.59]	0.11	0.18
6	[0.90, 1.13; 0.32, 0.034]	[0.15, 0.49, 1.09, 0.037, 0.55]	0.21	0.21
7	[0.86, 0.96; 0.36, 0.033]	[0.10, 0.35, 1.02, 0.032, 0.46]	0.11	0.15
8	[0.87, 0.83; 0.42, 0.026]	[0.12, 0.33, 0.89, 0.028, 0.36]	0.08	0.14

The Bi-exponential fit for the AIF, the EMM parameters for C_m(t), and estimated K^trans and v_e are given for each case. The Bi-exponential function was defined as C_a(t) = a₀ · exp(−m₀t) + a₁ · exp(−m₁t), where a₀(mM) and m₀(min⁻¹) represent the fast component, and a₁(mM) and m₁(min⁻¹) represent the slow component. The EMM was defined as C_m(t) = A · (1−exp(−αt))^q · exp(−βt) · (1 + exp(−γt))/2, where A is in mM, q is unit-Less, and α, β, and γ is in min⁻¹

FIG. 2.

Averaged plot (thick gray line) over eight MRI experiments for: (a) the AIF measured in a blood vessel, fitted with the bi-exponential function; (b) C_m(t) fitted with the EMM; and (c) AIF derived from reference tissue. The thin black lines indicate one standard deviation above and below the average for each time point.

Figure 3 shows plots of Ĉ_p(t) and C_m(t)/v_e that were generated using typical parameters from Table 1 (Cases 2 and 3). For Case 2, the plasma concentration of contrast media is higher than the muscle concentration until ~90 seconds after bolus arrival. After the muscle and plasma curves cross, the plasma concentration drops well below muscle, because the washout of contrast from muscle (with a rate constant of ~0.3 min⁻¹) cannot keep up with the washout from plasma (with a rate constant of ~0.5 min⁻¹). For Case 3, the plasma concentration of contrast media remains above the extracellular concentration in muscle for over 2 minutes. In general in the rat hind limb, there is a 2–10 minute period when there is a significant concentration difference (positive or negative) between muscle and plasma that can be measured with adequate SNR (Fig. 3), so that K^trans can be accurately measured.

DISCUSSION

The results demonstrate that K^trans and v_e can be calculated from contrast media concentrations in a reference tissue with modest blood flow and an artery, using data acquired after the end of the first pass of the contrast agent bolus. At these times, the plasma concentration is relatively low and is changing slowly. Therefore, it can be measured accurately with high spatial resolution and SNR, if in-flow effects are minor, or accounted for. As long as the difference between concentrations of contrast media in the extracellular space of the reference tissue and the arterial plasma is significantly greater than the noise level, the reference tissue K^trans and v_e can be estimated from the change in the difference over time.

The contrast media concentration vs. time curve shapes measured directly from small arteries are similar to those obtained by McIntyre et al. (15) from rat tail arteries, and by Weidensteiner et al. (17) from rat jugular veins. However, our curves have lower amplitude; this could be due to dispersion of the AIF in the small vessels we sampled, as well as partial volume effects. The AIFs derived using the RTPV approach are similar in terms of amplitude and shape to the AIFs measured by McGrath et al. (5) in the rat left ventricle using an MRI “semi-keyhole” technique. However they are quite different from the AIFs measured by Yankeelov et al. (18) in rat aorta, based on a combination of blood sampling (at later times after injection) and MRI measurements of phase-shifts caused by the contrast agent during the first pass of the contrast agent bolus.

The AIF measured using the RTPV approach has a much larger peak value than the AIF measured directly from plasma in the same experiment. This is consistent with previous results of Yang et al.—comparing the AIF derived using the “multiple reference tissue method” with directly measured AIFs (12). The amplitude of the AIF measured directly from an artery is expected to be much lower than the true AIF because of the systematic errors associated with measurement of high concentrations of contrast media [including decreases in $T_2^{\ast }$, and effects of the relatively slow exchange of water between the cytoplasm of red blood cells and the extracellular space (19)], and inadequate temporal resolution (18).

There was considerable variability in the amplitudes and shapes of AIFs measured directly from the vessel and AIFs calculated using the reference tissue. For example, the peak amplitude of the AIFs directly measured from arteries was an average of 0.69 ± 0.07 mM, and the peak amplitude of the AIF’s derived from the reference tissue was 2.77 ± 1.19 mM. This variability in both the directly and indirectly measured AIFs demonstrates the value of measuring the AIF on a case-by-case basis. “Population” AIF’s are frequently used (20) as input to physiological models, and this approach has important benefits, but cannot account for the range of AIF’s observed experimentally.

The average K^trans (0.14 ± 0.06 min⁻¹) and v_e (0.19 ± 0.05) values for normal rat hind limb muscle reported here are close to values obtained for rat hypoglossus and masseter muscle (K^trans = 0.15 min⁻¹ and v_e = 0.2) by Yankeelov et al. (19). However, these values are much larger than rat hind flank muscle K^trans and v_e values obtained by Yankeelov et al. (18). This could be due to differences in the acquisition parameters, the shape of AIFs and the muscle groups selected for analysis. Evelhoch (21) demonstrated that contrast injection duration and image acquisition parameters significantly impact the measured kinetics of contrast media uptake and washout, and this in turn affects calculations of K^trans and v_e.

Although the K^trans and v_e values for muscle estimated using the RTPV method were within the range of literature values (22), there were significant variations across eight experiments. K^trans varied by over a factor of four, and v_e varied by more than a factor of two. This demonstrates the importance of calculating individual K^trans and v_e values for each experiment, rather than using literature values, as in the original reference tissue method (7).

In the present work, the primary assumption required by the RTPV approach was that contrast dynamics in the reference tissue are well approximated by the two-compartment model, and this assumption is well justified for muscle (7). Other models could be used for other reference tissues, including models that explicitly include the blood compartment; the only requirement is that the model reliably and accurately represents contrast media dynamics in the reference tissue.

The RTPV method eliminates systematic errors due to differences between the true K^trans and v_e and literature values. However, new sources of measurement errors are introduced. One source of error is the modest sensitivity of the reference tissue to very rapid changes in the plasma concentration of contrast media (e.g., during the first pass of the contrast agent bolus). A reference tissue with low K^trans is desirable, because it comes to equilibrium with the plasma slowly. However, this also reduces sensitivity to high frequency components of the AIF, since K^trans determines the response of tissue to changes in plasma contrast media concentration, especially during the first pass. In principle even a reference tissue with low K^trans can be used to detect high frequency components of the AIF if the SNR is very high, but low SNR and K^trans in combination will produce significant errors in the calculated AIF. The variance associated with use of a specific reference tissue and blood vessel depends on many factors including the true AIF, the K^trans and v_e of the reference tissue, the SNR, and the degree of T1-weighting. A complete treatment of sources of error will require simulations and this work is currently in progress.

The “in-flow” effects are an additional source of error. When plasma concentrations of contrast media are measured directly from the aorta, rapid flow of blood perpendicular to the imaged slice can cause large errors in the calculation of contrast media concentration (9). In the experiments discussed here, a small artery was used for concentration measurements. Flow in these smaller vessels is significantly slower than in the aorta, and in addition, the portion of each vessel selected was in the plane of the imaged slice. Therefore, in-flow effects were probably modest. The values of v_e, calculated by comparing C_m(t) to Ĉ_p(t), were within the normal range; this is an indication that the correct values for Ĉ_p(t) were measured. Nevertheless, measurements that account for in-flow effects would increase accuracy (9). In addition, in-flow effects could be decreased by acquiring 3D images from thick slabs, as opposed to the multislice protocol used here (23).

Although the relatively slow blood flow to the reference tissue is a potential weakness of the RTPV method, this problem could be avoided. Once K^trans and v_e for the “slow flow” reference tissue are known, K^trans and v_e for a reference tissue with more rapid blood flow can be calculated. This would be a special case of the double reference tissue method, the multiple reference tissue developed by Yang et al. (12), and the multiple region method of Yankeelov et al. (11), in which K^trans and v_e for the slower reference tissue would be fixed (or allowed to vary only within a small range), based on the calculations described here using the RTPV method. Then the reference tissue with high K^trans can be used to further improve AIF estimation, particularly at early times after injection.

The RTPV approach requires accurate measurement of the contrast media washout from a local artery. There may be cases where no artery is available or where partial volume effects are significant. However, in general, scans can be prescribed to include arteries of adequate size. As is always the case with reference tissue methods, it is preferable to select reference tissues that are close to the area to be studied (e.g., a tumor) so that a local AIF can be measured. However, previous work from this group demonstrated that impulse response analysis can refine any AIF so that it more accurately reflects local properties (24).

In summary, an improved reference tissue approach for measuring the AIF in DCEMRI has been demonstrated. The K^trans and v_e estimated for the muscle reference tissue were close to the literature values. The AIFs derived based on C_m(t) were close to published AIF’s for rats. The proposed method is a significant improvement relative to the original reference tissue method (7) and may offer advantages relative to later variants of the reference tissue method (11,12). The RTPV method has the potential to significantly reduce the systematic error in parameters calculated from DCEMRI data, and thus increase diagnostic accuracy and sensitivity to drug effects. Future studies with patient data and simulations will be performed to validate the technique and evaluate its limitations.