Abstract
The Binding Energy Distribution Analysis Method (BEDAM) for the computation of receptor-ligand standard binding free energies with implicit solvation is presented. The method is based on a well established statistical mechanics theory of molecular association. It is shown that, in the context of implicit solvation, the theory is homologous to the test particle method of solvation thermodynamics with the solute-solvent potential represented by the effective binding energy of the protein-ligand complex. Accordingly, in BEDAM the binding constant is computed by means of a weighted integral of the probability distribution of the binding energy obtained in the canonical ensemble in which the ligand is positioned in the binding site but the receptor and the ligand interact only with the solvent continuum. It is shown that the binding energy distribution encodes all of the physical effects of binding. The balance between binding enthalpy and entropy is seen in our formalism as a balance between favorable and unfavorable binding modes which are coupled through the normalization of the binding energy distribution function. An efficient computational protocol for the binding energy distribution based on the AGBNP2 implicit solvent model, parallel Hamiltonian replica exchange sampling and histogram reweighting is developed. Applications of the method to a set of known binders and non-binders of the L99A and L99A/M102Q mutants of T4 lysozyme receptor are illustrated. The method is able to discriminate without error binders from non-binders, and the computed standard binding free energies of the binders are found to be in good agreement with experimental measurements. Analysis of the results reveals that the binding affinities of these systems reflect the contributions from multiple conformations spanning a wide range of binding energies.
1 Introduction
Molecular recognition is an essential component for virtually all biological processes. In particular, medicinal compounds mainly act by binding to enzymes and signaling proteins thereby altering their activity. One main aim of drug discovery enterprises is to identify compounds with specific and strong affinity to their target receptors. There is a great interest therefore in the development of computer models capable of predicting accurately the strength of protein-ligand association.1 Structure-based drug discovery models seek to predict receptor-ligand binding free energies from the known or presumed structure of the corresponding complex.2 Docking and empirical scoring approaches3,4 are useful in virtual screening applications5,6 but are generally considered not suitable for quantitative binding free energy estimation.
Physical free energy models for binding,7 which are built upon realistic representations of molecular interactions and atomic motion, have the potential to achieve sufficient detail and accuracy to address finer aspects of drug development such as ligand optimization, and drug specificity, toxicity, and resistance. The computational prediction of protein-ligand binding free energies using these methods remains, however, very difficult due to inaccuracies of the potential models and limitations of conformational sampling, as well as to model uncertainties related to solution conditions, and protonation and tautomeric state assignments.8 Ongoing development efforts continue to improve the accuracy and usability of free energy models to widen their applicability in drug discovery.
Thermodynamically, the strength of the association between a ligand molecule and its target receptor is measured by the standard binding free energy.9 The statistical mechanics theory of molecular association equilibria10 is nowadays well understood and widely accepted. It provides a prescription to compute standard binding free energies from first principles. Various implementations of this theory exist some of which, such as free energy perturbation methods11–13 are suitable for estimating relative binding free energies between pairs of similar compounds. A number of methods have been proposed for computing absolute, rather than relative, standard binding free energies. Endpoint approaches compute the free energy of binding by computing the difference between the free energies of the unbound and bound states of the protein-ligand complex. Examples of this class of methods is the mining minima method,14 that attempts to exhaustively enumerate and analyze conformations of the ligand and of the complex in terms of their enthalpy and entropic components.15 Similar in spirit are MM-PBSA/GBSA methods16,17 where enthalpic changes are computed from the analysis of molecular dynamics trajectories. Free energy methods based on the double decoupling18 and potential of mean force19,20 formalisms compute absolute binding free energies by evaluating, with molecular dynamics sampling, free energy estimators along suitable thermodynamic paths connecting the unbound and bound states.21 Methods based on the latter involves physically moving the ligand in or out of the receptor, whereas double decoupling methods18,22,23 employ alchemical computational techniques to essentially decouple the ligand from the solution environment and make it appear in the receptor site.
In this paper we present a novel approach to binding free energy estimation and analysis we call the Binding Energy Distribution Analysis Method (BEDAM). One motivation for this work has been our interest in evaluating the performance of implicit solvent modelling in alchemical decoupling strategies which have been traditionally applied in the context of explicit solvation. As part of this work we have developed a formalism for the standard free energy of binding based on probability distributions of the binding energy of receptor-ligand complex conformations. We show that this formalism is useful both as an analytical tool to gain insights in the statistical thermodynamics of the binding process, as well as for forming the framework for an efficient binding free energy computational algorithm based on parallel Hamiltonian replica exchange conformational sampling and reweighting techniques.
Implicit solvent models,24 which are widely used for protein structure prediction25,26 and folding,27–29 and small molecule hydration,30,31 have also been employed in protein-ligand binding studies; for docking and scoring,32–36 for linear interaction energy modelling,37,38 and for MM-PBSA/GBSA applications as mentioned above, as well as for free energy perturbation calculations.39 We have developed the Analytical Generalized Born plus Non-Polar (AGBNP) implicit solvent model,40 which introduced a number of key innovations with respect to the treatment of electrostatic and non-polar hydration effects. Recent developments41 introduced treatment of short-range hydration interactions and improved geometric modelling to achieve a better balance between intramolecular interactions and hydration forces. Because of the parameter-free treatment of geometric estimators (Born radii and atomic surface areas), AGBNP is not only applicable to macromolecules, but also to a large variety of drug-like compounds and functional groups. AGBNP includes a model for solute-solvent van der Waals dispersion interactions which is particularly suitable for describing association equilibria42 in part because, in contrast to conventional surface area models, it is capable of describing the residual ligand-solvent van der Waals interaction energy in the associated state.43 Together with the availability of analytical gradients and other implementation features, such as multithreading parallelization, these characteristics make AGBNP particularly suitable for molecular dynamics-based modelling of protein-ligand binding.
In the context of this work the “binding energy” of a single conformation of the receptor-ligand complex is defined as the free energy gain or cost of bringing the receptor and ligand from infinite separation in solution to the their relative position and orientation in the complex without changing their internal coordinates. In this process the solvent degrees of freedom are averaged and their role is included in the binding energy in terms of the solvent potential of mean force.44 Although, in principle, this definition does not depend on whether the solvation treatment is explicit or implicit, in this work we model the solvent potential of mean force by means of an implicit solvent function. This choice is motivated not only by CPU performance, but also and much more importantly by the ability to obtain distributions of binding energies over tens of thousands of conformations of the complex, which, as shown below, can be directly employed to estimate the binding free energy. An equivalent calculation with explicit solvation would otherwise require a costly potential of mean force evaluation for each conformation of the complex.
The implicit solvent treatment also allows us to employ the binding energy as a biasing potential on which we build an efficient free energy calculation scheme based on a parallel replica exchange45 conformational sampling algorithm and histogram reweighting.46 The benefits of replica exchange sampling and multi-state reweighting techniques47 for free energy estimation has been documented in a variety of contexts47–50 including protein-ligand binding free energy estimation.51,52 In this work we use this strategy to compute binding energy distributions over a wide range of binding energies and to properly sample the variety of ligand poses that contribute to binding in the system studied here.53
The application of the BEDAM methodology is illustrated on a series of complexes of mutant forms of T4 lysozyme.54,55 The small size of the ligands and the relative simplicity of the binding sites, together with the availability of high quality structural and thermodynamic data,55,56 make these systems particularly well suited for validating computational models of protein-ligand binding.57 Extensive binding free energy calculations with explicit solvent have been conducted,58,59 which have confirmed the applicability (as well as some of the challenges23) of molecular mechanics modelling aimed at the estimation of binding free energies for this system.
2 Theory and Methods
2.1 Standard Free Energy of Binding from Binding Energy Distributions
We start from the expression of the binding constant, KAB, for the binding of ligand B to receptor A from Equation 38 in Gilson et al.18 relevant for the implicit solvation treatment of the water environment:
| (1) |
where, using the notation in Gilson et al.,18 C° is the inverse of the standard volume V0 = 1,668 Å3,
| (2) |
is the configurational partition function of the AB complex, and
| (3) |
| (4) |
are, respectively, the configurational partition functions of the ligand B and the receptor A in solution. The degrees of freedom for ZAB are the six external coordinates of the ligand (position and orientation) relative to the receptor60 which are collectively represented by the variable ζB, and the internal coordinates of the ligand and receptor which are represented by the variables xB and xA, respectively. The configurational partition functions of the ligand and receptor, ZB and ZA, extend over the internal degrees of freedom of each binding partner.
In Eqs. (2)–(4) β is 1/kBT, where kB is the Boltzmann constant and T is the absolute temperature, U is the potential energy function describing direct covalent and non-covalent intramolecular interactions as well as, for the complex, intermolecular non-covalent interactions between the ligand and the receptor. The function W represents the solvent potential of mean force44 which describes solvent-mediated interactions. In Eq. (2), J(ζB) represents the Jacobian corresponding to the external coordinates of the ligand relative to the receptor and I(ζB) is an indicator function which defines the complexed state of the system (i.e. I(ζB) = 1 within the binding site and I(ζB) = 0 outside). As discussed,18 I(ζB) can be also equivalently defined in terms of a continuous function which interpolates from values near 1 within the binding site region to values near 0 outside, which is the approach we adopt in this work. The expression for KAB given here omits symmetry numbers corrections53 and consequently the integrations in the configurational partition functions given here are meant to extend explicitly over all symmetrically equivalent conformations of the ligand.
By multiplying and dividing Eq. (1) by the quantity
| (5) |
which represents the effective volume of the binding site, it is straightforward to show that KAB can be equivalently expressed as18
| (6) |
with
| (7) |
where
| (8) |
is the effective binding energy for a given conformation of the ligand-receptor complex, and
| (9) |
is the normalized probability distribution of the ensemble of conformations of the complex in the absence of ligand-receptor interactions, including solvent-mediated interactions described by the solvent potential of mean force W.
Based on Eq. (6) the standard binding free energy can be written as
| (10) |
where the first term is interpreted as the the entropic work corresponding to the process of transferring the ligand from a solution of concentration C° to the binding site region of the complex. This term depends only on the definition of the standard state and the definition of the complex macrostate (according to the indicator function I(ζB)) and does not depend on any specific energetic property of the receptor and the ligand. The second free energy term in Eq. (10), defined as
| (11) |
represents the work for turning on interactions between the ligand and the receptor while the ligand is sequestered within the binding site region. More precisely, ΔFAB corresponds to the difference in free energy between a fictitious state (henceforth referred as the “solvated reference” state) in which the ligand and the receptor do not see each other (even though the ligand is confined within the binding site) and interact solely with the solvent continuum, and a “bound” state in which the receptor and the ligand see each other in terms of direct electrostatic and van der Waals interactions, as well as in terms of mutual desolvation effects due to the displacement of the solvent continuum from each other's environments. Note that, unlike the binding site volume term in Eq. (10), ΔFAB is independent of the definition of the standard state. As expressed by Eq. (10), the combination of the two processes of transferring the ligand in the binding site region and turning on receptor-ligand interactions is thermodynamically equivalent to the binding of the ligand to the receptor.
A useful representation for the binding constant (or equivalently for the standard binding free energy ) is obtained by writing the average 〈exp(−βu)〉0 in Eq. (6) in terms of a probability distribution density of the binding energy:
| (12) |
where p0(u), formally defined as
| (13) |
is the probability distribution for the binding energy in the solvated reference state [the same conformational ensemble specified above by Eq. (9)].
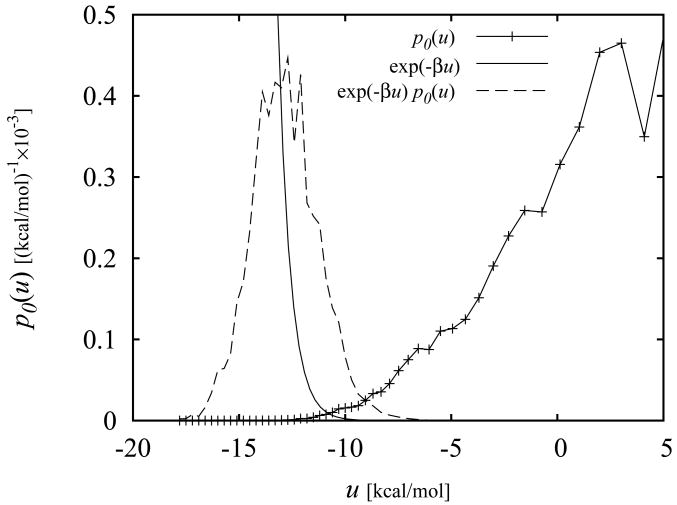
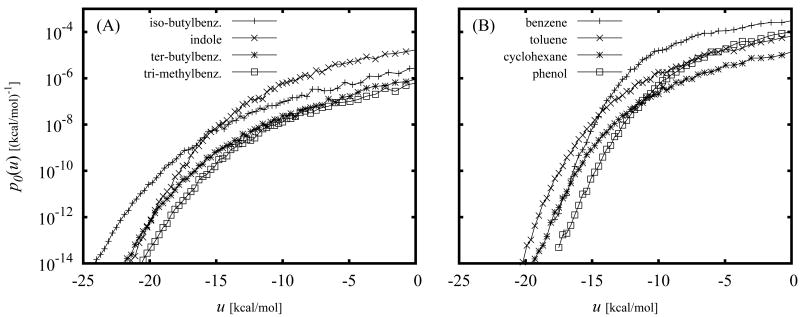
The calculated binding energy probability distribution functions p0(u) for some of the ligands of mutant T4 lysozyme discussed below are shown in Fig. 1. As illustrated in this figure, p0(u) is largest for large positive values of u with a low-probability tail extending to negative values of u. This is expected since in the absence of receptor-ligand interactions the ligand is more likely to sample conformations with unfavorable clashes between receptor and ligand atoms rather than conformations with favorable interactions with the receptor. The values of u in the extreme negative binding energy range correspond to low energy conformations of protein-ligand complexes such as those provided by X-ray crystallography and ligand docking. As illustrated in Fig. 1, while p0(u) increases with increasing u, the exp(−βu) function decreases rapidly in the same direction. In order for the integral of the product of these two functions to be finite, it is necessary for p0(u) to decrease faster than exponentially for u → – ∞. As shown below, the computed p0(u) functions in this work satisfy this asymptotic limit. In addition, the assumed normalization property imposes the requirement that p0(u) decays faster than 1/u for u → ∞.
Figure 1.
Calculated binding energy distribution p0(u) for the complex between benzene and the L99A mutant of T4 lysozyme. The curves to the left correspond to the exp(−βu) and exp(−βu)p0(u) functions (rescaled to fit within the plotting area). The integral of the latter is proportional to the binding constant [Eq. (12)].
The integral in Eq. (12) is dominated by the tail of the distribution at favorable values of u where exp(−βu) is large and p0(u) is not negligible (see Fig. 1). This however should not be taken to imply that the bulk of conformations that occur at unfavorable values of the binding energy have no effect on the resulting binding free energy. Because p0(u) is normalized, conformations at unfavorable binding energies oppose binding by increasing the magnitude of the distribution at unfavorable binding energies at the expense of the magnitude of the favorable binding energy tail of the distribution. The specific behavior of p0(u) at large u's, however, is not significant because that region of the (properly normalized) distribution makes a negligible contribution to the integral of Eq. (12). The latter is an important feature for the computational implementation of the theory because in practice, due to the sparseness of the collected samples at large binding energies, it is not feasible to estimate precisely the shape of the distribution at large values of u. Knowledge of the cumulative probability P0(u > umax) of observing any unfavorable binding energy larger than an appropriate large value umax, is sufficient to obtain accurate estimates of the binding free energies (see the section on Details of Computer Simulations below for the details on the binning procedure we have employed).
It should be noted that the formalism described above is homologous to the potential distribution theorem (PDT)61,62 of which the particle insertion method of solvation thermodynamics63 is a particular realization.64 In particle insertion the standard chemical potential of the solute, μ, is written in terms of the probability distribution p0(v) of solute-solvent interaction energies, v, corresponding to the ensemble in which the solute is not interacting with the solvent:
| (14) |
This expression, except of the term C°Vsite, is equivalent to Eqs. (6) and (12) with the solute-solvent interaction energy v replaced by the protein-ligand binding energy u. It follows that the formalism described above for the binding free energy can be regarded as a “ligand insertion” theory for protein-ligand binding, where the protein atoms and the solvent continuum play the same role as the solvent molecules in particle insertion.
A known result of particle insertion theory is a relationship between p0(v), the probability distribution of solute-solvent interaction energies in the absence of solute-solvent interactions, and p1(v), the corresponding probability distribution in the presence of solute-solvent interactions.65 In the present notation we have
| (15) |
where μ is the chemical potential. The corresponding expression linking p0(u), the probability distribution of ligand-protein binding energies for the solvated reference state, and p1(u), the probability distribution for the bound state is
| (16) |
where ΔFAB, defined by Eq. (11), is the interaction-dependent component of the standard binding free energy. It follows that p1(u) is proportional to the integrand in Eq. (12) for the binding free energy. Note however that this does not imply that the binding free energy can be computed by integration of p1(u), as obtained for example from a conventional simulation of the complex in the presence of ligand-receptor interactions. The integral of the normalized probability distribution p1(u), which is by definition unitary does not contain any information about the binding free energy. As expressed by Eq. (16), the proportionality constant between p1(u) and the integrand of Eq. (12) is related to the binding free energy, which is exactly the quantity we are seeking to compute. As discussed below, p1(u) is nevertheless a useful quantity for the analysis of the relative contributions to the binding free energy of macrostates of the complex.
2.2 The Binding Affinity Density
According to Eq. (12) the binding constant can be expressed in terms of an integral over the function
| (17) |
which can be interpreted as a measure of the contribution of the conformations of the complex with binding energy u to the binding constant. We thus call the function k(u) the binding affinity density.
Comparison of Eqs. (16) and (17) leads to the conclusion that the binding affinity density k(u) is proportional to p1(u), the binding energy probability distribution in the ligand-bound state. (The critical distinction between the two is that the integral of the latter is equal to 1 whereas the integral of the binding affinity density is equal to the binding constant.) It thus follows that the relative contributions to the binding constant of two complex macrostates one with binding energy u1 and another with binding energy u2 is simply given by their relative populations in the ligand-bound state when the interactions between the ligand and the receptor are fully turned on.
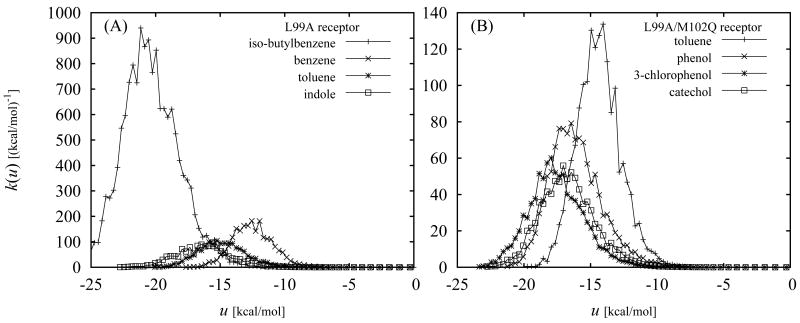
Fig. (10) shows the calculated binding affinity densities for some of the complexes studied in this work. The densities of higher magnitude and larger subtended area correspond to more tightly bound complexes. The corresponding p1(u) distributions, since by definition they all subtend the same surface area, have the same shape but with much smaller differences in magnitude across the various ligands.
Figure 10.
Binding affinity densities [Eq. (17)] for the binders of the L99A (A) and L99A/M102Q (B) receptors.
2.3 Conformational Decomposition
Given a set of macrostates i = 1,…, n of the complex, corresponding for example to different ligand poses in the receptor site, we consider the joint probability distribution p0(u, i), expressing the probability of observing the binding energy u while the complex is in macrostate i. Assuming that the set of macrostates collectively covers all possible conformations of the complex (which is always possible by including a “catch-all” macrostate), we can express p0(u) as a marginal of p0(u, i):
| (18) |
where we have introduced the conditional distribution p0(u∣i) and the population P0(i) of macrostate i in the solvated reference state, and used the relationship p0(u, i)=P0(i)p0(u∣i) between the joint and conditional distributions. By inserting Eq. (18) into Eq. (17), we have
| (19) |
where
| (20) |
represents the binding affinity density for macrostate i. In analogy with Eqs. (10) and (17) we define a macrostate-specific binding constant
| (21) |
where 〈…〉0,i represents an ensemble average in the solvated reference state limited to macrostate i. The macrostate-specific binding constant KAB(i) represents therefore the binding constant that would be measured if the conformations of the complex are limited to macrostate i. From Eqs (21) and (19), the sum of the macrostate-specific binding constants weighted by the macrostate populations P0(i) is the total binding constant:
| (22) |
The ratio P0(i)KAB(i)/KAB (reported in Fig. 11 for the systems studied here) measures the relative contribution of macrostate i to the overall binding constant. It is straightforward to show from Eqs. (21) and (16) that
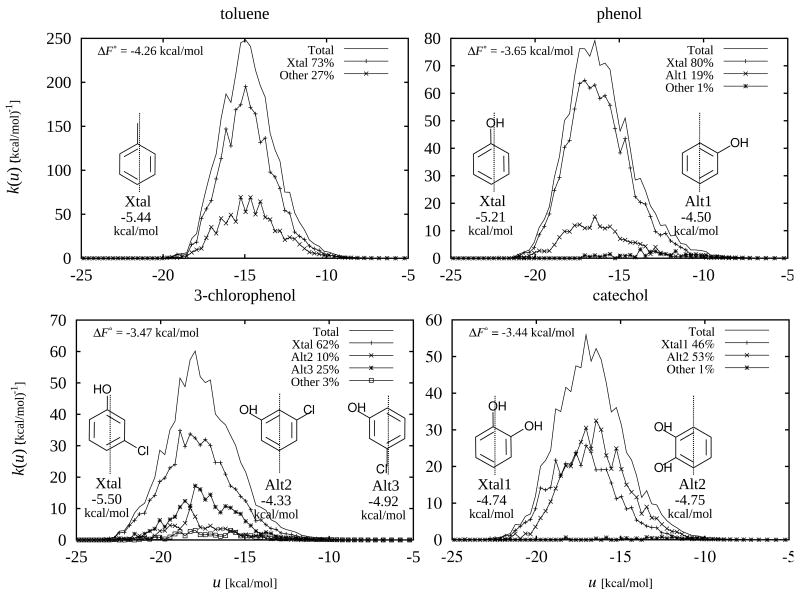
Figure 11.
Conformational decomposition of the binding affinity densities for the binders of the L99A/M102Q receptor (toluene, phenol, 3-chlorophenol, and catechol). Ligand conformational macrostates labeled “Xtal” correspond to conformations observed crystallographically, other states are labeled as “Alt”. The catch-all macrostate, which includes any conformation not included in the definition of any of the other states, is labeled as “Other”. Representative conformations of the ligand for each macrostates are schematically shown in the insets; the dotted line represents the orientation within the binding site of the crystallographic conformation. The macrostate-specific binding free energy of each macrostate from Eq. (21) is reported below the representative conformation. The binding affinity densities P0(i)ki(u) for each macrostate [Eq. (20)], weighted by the respective populations at λ = 0, are shown such that they sum to the total binding affinity density [Eq. (19)]. The relative contribution [Eq. (23)] of each macrostate to the overall binding constant is indicated as a percentage in the legend.
| (23) |
where
| (24) |
is the population of macrostate i in the bound state. In other words, this analysis shows that the relative contribution of macrostate i to the binding constant is equal to the physical population of that macrostate of the complex.
Similar to previous analysis,66 Eq. (22) expresses the fact that each conformational macrostate contributes to the total binding constant proportionally to its macrostate-specific binding constant KAB(i) weighted by the population of the macrostate in the solvated reference state measured by P0(i). Similar decompositions have also been previously employed.53 In this work (see Fig. 11) we analyze our results in terms of the relative contributions of each macrostate to the total binding constant using Eq. (23), and we also report the macrostate-specific binding free energies, from Eq. (21), for the major macrostates of the system defined as described below.
2.4 Numerical Considerations
The computation of Vsite from Eq. (5) is straightforward as it involves integration over only the six degrees of freedom ζB, which completely specify the positioning and orientation of the ligand relative to the receptor.60 For the calculations carried out in this work we adopt an analytical expression for Vsite corresponding to the particular choice for the indicator function I(ζB) (see below).
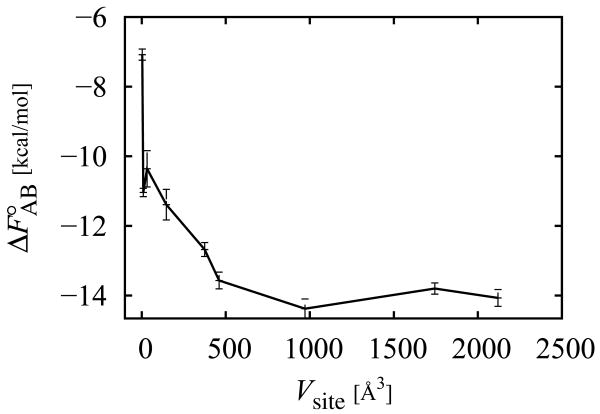
As conjectured by Gilson et al.,18 the value of the standard binding free energy estimated from Eq. (1) depends only weakly on the specific definition of the I(ζB) indicator function as long as this includes all of the important regions of the binding site volume and that the binding is sufficiently strong and specific. We have confirmed numerically this conjecture for one of the T4 lysozyme complexes system studied in this work by performing binding free energy calculations as a function of binding site volume (Fig. 2). The results indeed show that the binding free energy reaches a plateau at a binding site volume of approximately 450 Å3 and that further increases of the binding site region do not significantly alter the results. This is a consequence of the fact that the binding site volume beyond the natural dimensions of the pocket (which can be estimated as approximately 450 Å3 based on Fig. 2) only allows additional poses of the ligand that clash with receptor atoms and that, therefore, contribute only repulsive (u > 0) binding energies. It is easy to see that in this regime, as the binding site volume increases, the shape of the binding energy distribution p0(u) at favorable binding energies (u < 0) remains unchanged while its magnitude decreases due to the change of normalization, which is in turn proportional to the increase in binding site volume. It follows that the integral over the binding energy distribution in Eq. (12), of which the u < 0 range is the main contributor, decreases as 1/Vsite for sufficiently large Vsite. This dependence is exactly canceled by the C°Vsite prefactor in Eq. (12) thereby leading to the observed constancy of the binding constant with increasing binding site volume (Fig. 2).
Figure 2.
Standard binding free energy between phenol and the L99A/M102Q receptor as a function of the binding site volume. These calculations employed a simple distance-dependent dielectric model of solvation.
Increasing the binding site volume further could give the ligand access to alternative binding sites on the protein surface potentially causing changes to the computed binding constant in ways not addressed by the arguments discussed above. For an in depth discussion of the relationship between the microscopic definition of the binding constant and macroscopic observables of binding we refer the reader to the study of Mihailescu & Gilson.67
Having defined the binding site volume, the problem of computing the standard free energy of binding is reduced to the problem of evaluating ΔFAB with Eq. (11). It is apparent from Eqs. (10), (11) and (12) that, given a definition of the ligand-bound macrostate, p0(u) encodes all of the information necessary to specify the standard binding free energy of the protein-ligand complex. In principle, the calculation of p0(u) can be accomplished by brute-force collection of binding energy values from a simulation of the complex in the absence of receptor-ligand interactions (with the exception of the binding-site restraints specified by the indicator function I(ζB)). However this strategy would produce large finite sampling errors for the binding free energy through Eq. (12).68 The integral in Eq. (12) is dominated by the favorable binding energy tail of p0(u) which is rarely sampled when the ligand is not guided by the interactions with the receptor. Inaccuracies in the tail of the distribution are in turn amplified by the exp(−βu) function thereby affecting the reliability of the free energy estimate. As discussed below, biased sampling combined with the Weighted Histogram Analysis Method (WHAM)46 provides a very efficient strategy to compute p0(u) with high precision on a wide range of binding energies, leading to well converged estimates for ΔFAB from Eq. (12). The reliability of this strategy is illustrate for example in Fig. 1 which shows that p0(u) evaluated by WHAM is sufficiently well defined over the range of binding energies in which p1(u) ∝ exp(−βu)p0(u) is non-negligible.9
2.5 Binding Energy-Biased Conformational Sampling
As discussed above, straightforward binning of the binding energy values at the unbound thermodynamic end point of the binding process leads to poor estimation of the favorable binding energy tail of the binding energy distributions, which are important for the accurate computation of the binding constant. To address this problem we employ biased simulations which, collectively, are able to uniformly sample a wide range of binding energies. The results of these biased simulations are processed using WHAM to produce the unbiased binding energy distribution p0(u) that are integrated using Eq. (12) to yield the binding constant.
The biased potential energy ansatz that we employ is of the form
| (25) |
where λ is the free energy progress parameter and
| (26) |
is the effective potential energy of the complex in the absence of direct and solvent-mediated ligand-receptor interactions, and u = u(ζB, xA, xB) is the binding energy of a given conformation of the complex as defined by Eq. (8). It is easy to see from Eqs. (2)–(4), (8), and (26) that Vλ=1 corresponds to the effective potential energy of the bound complex and Vλ=0 corresponds to the state in which the receptor and ligand are not interacting. Intermediate values of λ trace an alchemical thermodynamic path connecting these two states. Multiple simulations at different values of λ are performed along this path, which collectively sample a wide range of unfavorable, intermediate and favorable binding energies which can be employed with WHAM to estimate with high precision the binding energy probability distribution at λ = 0. From Eqs. (25) and (26) it follows that the biasing potential wλ; = Vλ−V0 required in the application of the WHAM formula takes the simple form
| (27) |
That is the biasing potential is proportional to the binding energy itself. With this result, unbiased binding energy distributions are obtained by iterative application of the WHAM formula46
| (28) |
where
| (29) |
n(u) is the number of samples from all simulations with binding energy within the bin corresponding to the binding energy value u, and nλ is the total number of samples from the simulation at λ. We have confirmed that the WHAM equations as implemented are numerically capable of correctly representing the large dynamic range of probabilities necessary to describe p0(u) (see for example Fig. 8). The joint probability p0(u, i) for the conformational decomposition analysis is similarly obtained by WHAM considering the computed histograms n(u, i) corresponding to conformations of the complex in macrostate i with binding energy u. The macrostate populations P0(i) are obtained by integration of p0(u, i) over u.
Figure 8.
Favorable binding energy tails of the binding energy distributions of the L99A T4 lysozyme complexes.
2.6 Hamiltonian Replica Exchange Sampling
To enhance the sampling efficiency of ligand conformations within the receptor binding site it is useful to couple the simulations at different λ values above using an Hamiltonian parallel replica exchange scheme (HREM). In this scheme pairs of simulation replicas periodically attempt to exchange λ values through Monte Carlo (MC) λ-swapping moves. MC attempts are accepted with probability
| (30) |
with
| (31) |
where u2 and u1 are the binding energies of the pair of replicas and λ2 and λ1 are their respective λ values before the attempted exchange.
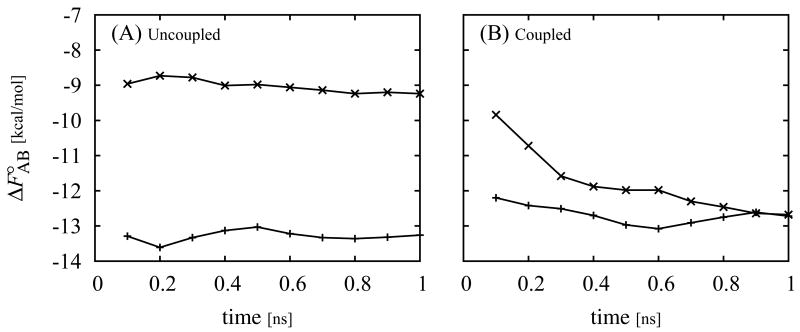
The benefit of the HREM scheme in λ space is illustrated in Fig. 3, which shows the computed binding free energies, using coupled and uncoupled simulations, of phenol bound to the L99A/M102Q mutant of T4 lysozyme as a function of simulation time. (These benchmark calculations conducted with a simple distance-dependent dielectric force field significantly overestimate the magnitude of the binding free energy of phenol but they nevertheless illustrate the advantages of HREM for this application.)
Figure 3.
Standard free energy of binding of phenol to the L99A T4 lysozyme receptor with two different starting conditions as a function of simulation time from uncoupled umbrella sampling simulations (A) and from a coupled parallel Hamiltonian replica exchange simulation (B). Plus symbols (+) correspond to simulations started from the crystallographic conformation (PDB id 1LI2) and crosses correspond (×) to simulations started from a non-crystallographic conformation in which phenol is not hydrogen bonded to Q102. These calculations employed a simple distance-dependent dielectric model of solvation.
One set of simulations was started from a conformation similar to the crystal structure and another set was started from another conformation lacking the hydrogen bond between phenol and Q102 of the receptor which is known to be critical for strong binding. We see from Fig. 3A that the uncoupled simulations started from the non-crystallographic conformation yield binding free energies less favorable than uncoupled simulations started from the crystallographic simulation. HREM instead (see Fig. 3B) yields binding free energies that converge to the same value regardless of the starting conformation. The reason for this behavior is that in the HREM scheme the ligand is less likely to become trapped in low energy conformations when the ligand interacts strongly with the receptor at λ ≃ 1. For example in the uncoupled simulation at λ = 1, which corresponds to a conventional simulation of the complex, phenol is observed to remain in the starting conformation for nearly the entire duration of the longest simulation. Kinetic trapping at large λ leads to poor convergence as shown in 3A, where the uncoupled simulation started from the non-crystallographic conformation grossly underestimates the magnitude of the binding free energy whereas the one started from the crystallographic conformations overestimates it by a small amount. In contrast, HREM does not suffer from kinetic trapping to the same extent because λ exchanges allow trapped conformations at large λ to assume smaller values of λ which facilitate transitions between different ligand conformations thanks to the weaker interactions with the receptor. By further random exchanges, these new ligand conformations can then assume again large λ values ultimately yielding more extensive conformational sampling at both small and large values of λ.
2.7 Details of Computer Simulations
The T4 lysozyme protein receptors and their respective ligands are shown in Figures 4 and 5. We considered eight ligands for each receptor (16 total), half of which are known binders and half are known non-binders.23,55,56 For each receptor, initial structures for the complex of benzene with the L99A mutant of T4 lysozyme and that of phenol bound to the L99A/M102Q mutant were prepared based on the corresponding crystal structures (PDB access codes 3DMX and 1LI2, respectively). The initial structures for all of the other complexes were prepared by superimposition of each ligand onto the conformations of either benzene or phenol. Hydrogen atoms were added and ionization states assigned assuming neutral pH. The position of Cα atoms was restrained near their crystallographic positions with a isotropic quadratic function with force constant kf = 0.6 kcal/mol/Å2, which allows for approximately a 4 Å range of motion at the simulation temperature. The other backbone atoms and protein sidechains were allowed to move freely.
Figure 4.
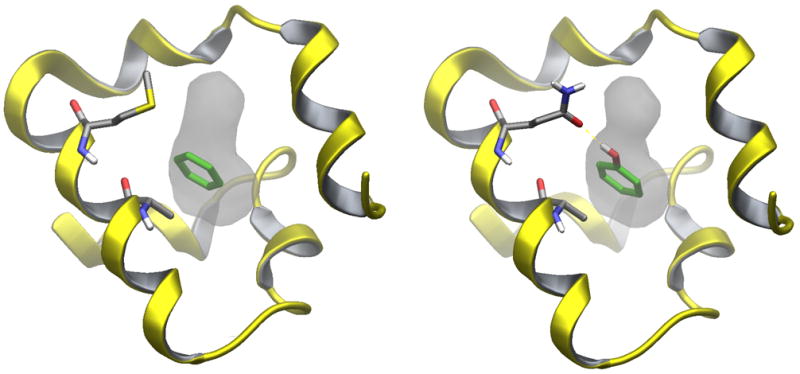
Crystal structures of the benzene-L99A (PDB id 3DMX, left) and phenol-L99A/M102Q (PDB id 1LI2, right) T4 lysozyme complexes. The A99 and M102 residues (Q102 for the L99A/M102Q receptor) are indicated. Residues 73 through 125 of T4 lysozyme are represented by the ribbon diagram. The ligand is highlighted in green. The surface surrounding the ligand represents the cavity created by the L99A and L99A/M102Q mutations.
Figure 5.
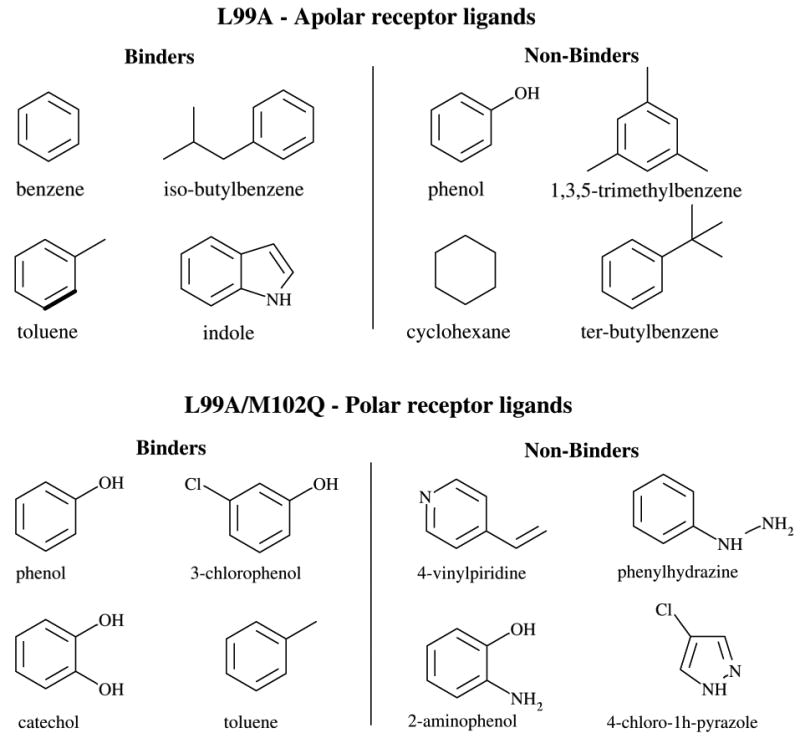
T4 lysozyme ligands investigated in this work
We employ the OPLS-AA69 force field with the AGBNP241 implicit solvent model. AGBNP2 is a recent evolution of the AGBNP implicit solvent model,40 which is based on a parameter-free analytical implementation of the pairwise descreening scheme of the generalized Born model70 for the electrostatic component, and a non-polar hydration-free energy estimator for the non-electrostatic component. Unlike traditional models based only on the solute surface-area, the non-polar term in AGBNP is the sum of two distinct estimators, one designed to mimic solute–solvent van der Waals dispersion interactions, and a second corresponding to the work required for the formation of the solute cavity in water. The AGBNP2 model includes a novel first solvation shell function to improve the balance between solute-solute and solute-solvent interactions based on the results of benchmark tests with explicit solvation. The AGBNP2 model also introduces an analytical solvent excluded volume model which improves the solute volume description by reducing the effect of spurious high-dielectric interstitial spaces present in conventional van der Waals volume representations.41
Each complex was energy minimized and thermalized at 310 K. λ-biased replica exchange molecular dynamics simulations were conducted for 2 ns with a 1.5 fs MD time step at 310 K with 12 replicas at λ =10−6, 10−5, 10−4, 10−3, 10−2, 10−1, 0.15, 0.25, 0.5, 0.75, 1, and 1.2. The parallel replica exchange calculations took approximately 30 hours per complex on 96 processor cores using a custom multithreaded version of the IMPACT program.71 Bond lengths with hydrogen atoms were constrained using SHAKE. The mass of hydrogen atoms was set to 5 amu. A 12 Å residue-based cutoff was imposed on both direct and generalized Born pair interactions. Soft-core potentials were employed for both Lennard-Jones and Coulomb interactions using a modified distance function of the form r′ = (r12 + a12)1/12 with a = 1 Å. This modified distance function limits the magnitude of non-bonded interactions at short interatomic distances that occur at small λ; it has negligible effect on the interaction energies at the interatomic distances normally encountered with full ligand-receptor interactions (for example at r = 1.5 Å, a distance typical for the shortest non-bonded interactions, the modified distance is only 0.06% larger than the actual distance).
Each replica simulates the complex with a biased potential of the form shown in Eq. (25). Using Eqs. (26) and (8) it is straightforward to show that Eq. (25) corresponds to a hybrid potential of the form
| (32) |
where U(xA) and U(xB) represent the intramolecular interactions (Lennard-Jones and Coulomb interactions) of the receptor and the ligand, and U(ζB, xA, xB) represents their mutual interactions. W(ζB, xA, xB), W(xA) and W(xB) are, respectively, the AGBNP2 hydration free energies of the complex, the receptor and the ligand. It is straightforward to implement the non-bonded component of Eq. (32) by rescaling direct receptor-ligand interactions during the simulation. The implicit solvent components are currently implemented as two separate invocations of the routines for the AGBNP2 energy and gradients, one for the complex and one for the separated receptor and ligand.
Protein-ligand binding energies of each replica were collected every 1 ps during the second half of the simulation. The replica exchange simulations yielded a total of 12, 000 binding energy samples for each ligand that were employed to compute an overall histogram n(u) of binding energies. 110 histogram bins were employed with increasing bin spacing for increasing values of u from −30 kcal/mol up to u = 80 kcal/mol. Values of u larger than this maximum were counted towards the last bin. Histograms were processed through the WHAM equation (28) with the biasing function (27) to yield the binding energy distributions p0(u). These were then integrated according to Eq. (12) to yield the standard binding free energy values for each ligand. Statistical uncertainties were computed by block bootstrap analysis23 on the set of computed binding energies using 8 samples.
The binding site indicator function was set as I(ζB) = exp[−βω(r, cosθ, ϕ)] [see Eq. (2)] where ω(r, cosθ, ϕ) is a product of flat-bottom harmonic potentials acting on the position, expressed in polar coordinates,60 of one of the atoms of the aromatic ring of each ligand with respect to the positions of the the Cα atoms of residues 88, 102, and 111 of the receptor. The distance restraint potential was centered at 6.4 Å with a 5 Å tolerance on either side (allowing unhindered distances from 1.4 Å to 11.4 Å). Distances beyond these limits were penalized by means of a quadratic function with a force constant of 3 kcal/mol/Å2. The flat-bottom harmonic restraint potential for the cosine of the angle θ between the reference ligand atom, the Cα atom of residue 88, and the Cα atom of residue 102 was centered at cos θ = 0.85 with a 0.15 tolerance on either side and a force constant of 100 kcal/mol beyond that. Finally the restraint potential for the dihedral angle defined by the three atoms above plus the Cα atom of residue 111 was centered at ϕ = 20° with a 50° tolerance on either side and a force constant of 0.1 kcal/mol/deg beyond that. The variables corresponding to the orientation of the ligand with respect to the receptor were not restrained; they contribute 8π2 to the integral in Eq. (5) - thereby canceling out the same quantity in the denominator of Eq. (5). According to this definition of I(ζB), the volume of the binding site Vsite [Eq. (5)] was measured to be 469.2 Å3 corresponding to a value for −kBT ln C°Vsite in Eq. (10) of approximately 0.75 kcal/mol. This value, which is the same for all ligands, is added to the value of the computed ΔFAB for each ligand to yield the standard binding free energies reported in Table 1.
Table 1.
Experimental and calculated standard binding free energies and corresponding ligand rankings.
| Molecule | ΔF°(expt)a,b | ΔF°(calc)a | Rank(expt) | Rank(calc) |
|---|---|---|---|---|
| L99A Apolar Cavity | ||||
| iso-butylbenzene | -6.51c | -5.21±0.06 | 1 | 1 |
| toluene | -5.52c | -3.80±0.05 | 2 | 3 |
| benzene | -5.19c | -4.01±0.04 | 3 | 2 |
| indole | -4.89c | -3.75±0.02 | 4 | 4 |
| ter-butylbenzene | >-2.7d | -2.93±0.03 | 5 | |
| cyclohexane | >-2.7d | -2.21±0.05 | 6 | |
| 1,3,5-trimethylbenzene | >-2.7d | -1.68±0.05 | 7 | |
| phenol | >-2.7d | -1.40±0.03 | 8 | |
| L99A/M102Q Polar Cavity | ||||
| 3-chlorophenol | -5.51e | -3.47±0.05 | 1 | 3 |
| phenol | -5.23e | -3.65±0.04 | 2 | 2 |
| toluene | -4.93e | -4.26±0.06 | 3 | 1 |
| catechol | -4.16e | -3.44±0.04 | 4 | 4 |
| 4-vinylpiridine | >-2.7e | -2.38±0.02 | 5 | |
| 4-chloro-1h-pyrazole | >-2.7e | -1.60±0.03 | 6 | |
| 2-aminophenol | >-2.7e | -0.70±0.05 | 7 | |
| phenylhydrazine | >-2.7e | 2.63±0.05 | 8 | |
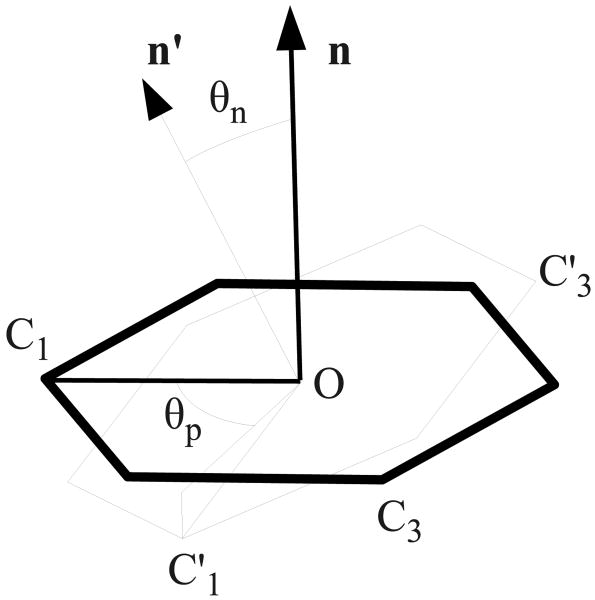
The macrostates of the complex for the conformational decomposition analysis have been defined in terms of the orientation of the ligand with respect to a reference orientation (based typically on the crystallographic structure). The central binding site cavities of the two receptors which contain the aromatic ring of the ligand (Fig. 4) are wide and flat allowing basically only two possible kinds of motion of the ligand: rotation within the plane of the ring and a 180 degrees flip of the plane of the ring. These motions are captured, respectively, by the pitch angle θn between the normals to the ring planes of the reference and given conformation of the ligand, and the in-plane rotation angle θp between the given and reference axes going through a chosen atom of the ring (Fig. 6).
Figure 6.
Diagram depicting the definition of the pitch angle θn and in-plane rotation angle θp used in the conformational decomposition analysis. The hexagon in thick lines represents the aromatic ring of the reference pose, C1 and C3 are two atoms of the ring, O is the centroid of the heavy atoms of the ring, and n is the normal to the plane of the ring (the plane defined by O, C1, and C3). C′1, C′3, and n′ are the corresponding quantities for the ring of the given pose. θn is defined as the angle between n and n′ and θp is defined as the angle between the OC1 segment and the projection of the OC′1 segment onto the plane of the ring of the reference pose.
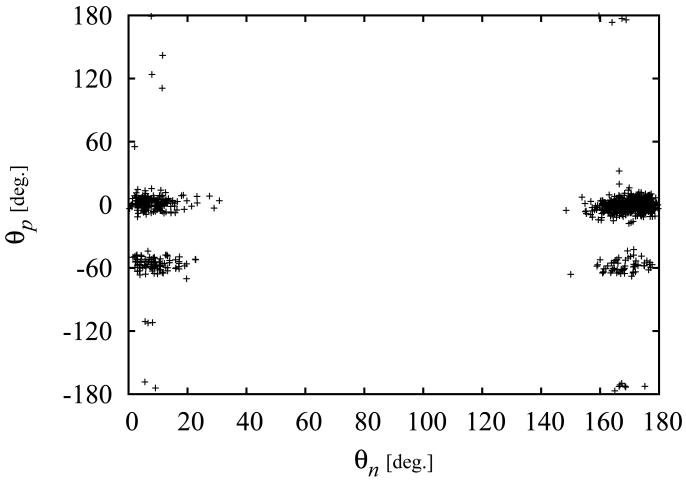
Macrostate boundaries are selected from the distribution of samples of (θn, θp) pairs collected from the HREM replica at λ = 1. A representative example is given in Fig. 7 for phenol bound to the L99A/M102Q receptor. Two macrostates can be identified, one corresponding to the crystallographic pose with θp = 0° ± 30°, and another less populated macrostate with θp = −60° ± 30°. In this case, given the C2 symmetry of phenol, the θn angles near 0° and 180° correspond to the same state. The difference in the number of samples between the left and right sides of Figure 7 can be used, after taking into account statistical fluctuations, as a measure of convergence of the HREM conformational sampling protocol. For molecules lacking C2 symmetry, such as 3-chlorophenol, the θn angle is used to distinguish conformations with substituents oriented on opposite sides of the ring. For all ligands the definition of the macrostates used a range of 30° on either side of a central value of the in-plane θp rotation angle identified similarly as for phenol above. For molecules possessing C2 symmetry, the ranges of the pitch angle θn included the intervals θn < 30° and θn > 150°. For other molecules the range for θn includes only one of the two intervals depending on the macrostate.
Figure 7.
Samples of pitch and in-plane rotational angles pairs (θn, θp) for phenol bound to the L99A/M102Q T4 lysozyme receptor.
3 Results
The computed binding energy distributions obtained from the BEDAM calculations are shown in Figs. 1, 8, and 9. The corresponding standard binding free energies from Eq. (12) for the L99A and L99A/M102Q mutants of T4 lysozyme are presented in Table 1 for the ligands listed in Fig. 5. We see that the ligand rankings based on the computed binding free energies distinguish without errors the binders from the non-binders as determined experimentally. For example the model correctly predicts that toluene binds to both the L99A and L99A/M102Q receptors while phenol binds only to the L99A/M102Q receptor. More subtle trends are also reproduced. Iso-butylbenzene is correctly predicted as the best binder to the L99A receptor while the binding of the relatively similar ter-butylbenzene is correctly predicted to be much weaker. Cyclohexane is correctly predicted as a non-binder of the L99A receptor distinguishing it from benzene, which is a binder. The related catechol and 2-aminophenol are correctly differentiated as a binder and non-binder, respectively, to the L99A/M102Q receptor.
Figure 9.
Favorable binding energy tails of the binding energy distributions of the L99A/M102Q T4 lysozyme complexes.
The method correctly reproduced the ranking of the best binder (iso-butylbenzene) and the weakest binder (indole) of the L99A receptor, whereas the rankings of the two intermediate binders, benzene and toluene, are reversed relative to the experiments. The order of the rankings of the binders to the L99A/M102Q receptor are not as accurate relative to the experiments. Toluene is predicted to be the best binder for the L99A/M102Q receptor whereas 3-chlorophenol is known to be the best binder in this set.
The computed standard binding free energies all underestimate the experimental binding affinities. For the L99A receptor the amount of underestimation is approximately 1.2 kcal/mol for most of the binders. Relative binding free energies are in good agreement with the experiments. Larger variations in accuracy are observed for the L99A/M102Q receptor binders with toluene having the smallest discrepancy (approximately 0.7 kcal/mol) while larger discrepancies are observed for the polar compounds (up to approximately 2 kcal/mol for 3-chlorophenol).
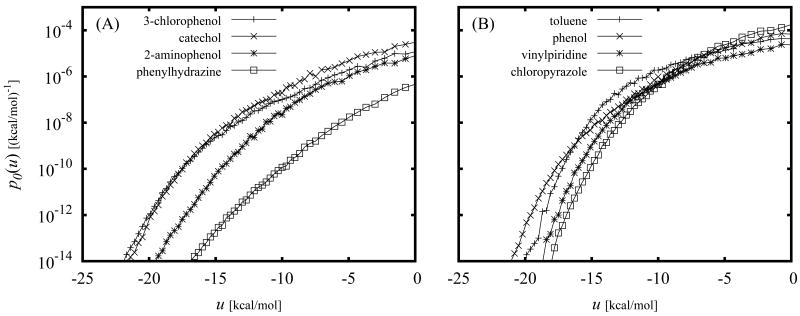
The binding energy distributions provide insights into the binding thermodynamics of these complexes. Figures 8 and 9 show, in logarithmic scale, the details of the low binding energy tails of the computed binding energy distributions for the L99A and L99A/M102Q complexes, respectively. As discussed above, this region of the distributions provide nearly all of the contribution to the binding affinity. It can be clearly seen from these results that the p0(u) distributions decay with decreasing binding energy faster than exponential (that is faster than linear in the log scale) as required by the theory. The ligands for each receptor can be roughly divided in two groups based on the shape of the tails of the distributions. The first group (Figures 8A and 9A) is composed of relatively larger and multiply-substituted ligands characterized by slower-varying tails with larger probabilities at low binding energies (u < −15 kcal/mol). The second group of complexes (Figures 8B and 9B) is composed of more compact ligands characterized by higher probabilities at intermediate binding energies (−15 < u < 0 kcal/mol) which decay rapidly with decreasing binding energy.
The computed binding affinity densities k(u) [Eq. (17)] for the four binders to each receptor are shown in Fig. 10. k(u) measures the contribution of conformations with binding energy u to the binding constant. In these figures curves of larger magnitude correspond to the stronger binders. The range of binding energies over which k(u) is significant gives an indication of the energetics of the conformations of the complex that contribute to binding. For example it is evident from these curves that the conformations that contribute to iso-butylbenzene binding to the L99A receptor tend to have more favorable binding energies than those of benzene (approximately 7 kcal/mol less favorable on average, see Fig. 10).
Figure 11 summarizes the conformational decomposition analysis for the L99A/M102Q complexes of the four binders toluene, phenol, 3-chlorophenol, and catechol. Each panel in this figure shows the macrostate binding affinity densities, ki(u) from Eq. (20), for the major macrostates of the ligand identified using the pitch and in-plane rotation angles θn and θp as described in Section 2.7. The figure legend reports the fraction of the binding constant attributed to each macrostate from Eq. (23), which, as shown above, is also the value of the population of that macrostate in the physical complex at λ = 1. Also reported in this figure are the macrostate-specific binding free energies ΔF°(i) of each macrostate computed from Eq. (21).
4 Discussion
The accuracy of the standard binding free energies of the T4 lysozyme complexes obtained from BEDAM (Table 1) are comparable to the corresponding results obtained through double-decoupling calculations with explicit solvation.23,53,58,59,72 The method correctly discriminates the binders from the non-binders for the set of compounds we have examined. As pointed out above the values of the BEDAM binding free energy estimates are systematically smaller in magnitude than the experiments. The fact that for most complexes the estimates for the L99A receptor are offset by a constant amount suggests that the systematic error is due in part to over-hydration of the apo receptor rather than to other effects, such as ligand-receptor interactions or ligand hydration, which are dependent on ligand size and ligand composition. The ligand-free L99A hydrophobic cavity is not occupied by water molecules.73 Our implicit solvent model, however, assumes that the cavity is filled with high dielectric and does not sufficiently penalize hydration sites within hydrophobic enclosures. We suspect that the hydration free energy for the unbound L99A receptor is overly stabilizing, thereby disfavoring binding.
The data for the polar L99A/M102Q receptor suggests a more complex origin for the errors in computed affinities. The calculated binding free energy of toluene to the L99A/M102Q receptor (Table 1) is in better agreement with the experiment (0.7 kcal/mol difference) than for the L99A receptor. This indicates that the model error originating from the over-hydration of the apo L99A/M102Q receptor is smaller than for the apo L99A receptor, conceivably because the former is simply more hydrated.55 The remainder of the errors for the L99A/M102Q receptor ligands vary from ligand to ligand and are probably due to overly weak ligand-receptor interactions since AGBNP2 hydration free energies generally do not appear to systematically overestimate hydration free energies of small molecules.41 Incomplete sampling of ligand and receptor conformations can also be a source of errors. We observed, for example, particularly slow convergence of the binding free energy of 3-chlorophenol probably due to the multiple, and nearly degenerate, ligand poses for this ligand (see below and Figure 11).
The magnitude and shape of the low binding energy tail of the binding energy probability distributions p0(u) presented in Figures 8 and 9 aid in the rationalization of the trends observed in the binding free energies. In general, higher probabilities in this range of binding energies is reflected in more favorable binding free energies. For example in Fig. 8A the curves for the two binders, iso-butylbenzene and indole, lie well above those for the two non-binders, ter-butylbenzene and tri-methylbenzene. In addition, because of the exponential weighting in the integral for the binding constant [Eq. (12)], low binding energies have a larger effect on the binding affinity than intermediate binding energies. This explains in part why, for example, toluene and phenol bind the L99A/M102Q receptor better than 4-vinylpiridine and 4-chloro-1h-pyrazole (Fig. 9B).
The 16 ligands we have investigated can be classified in two groups based on the shape of their binding energy distributions. Bulkier ligands (Figs. 8A and 9A) correspond to binding energy distributions that extend to lower binding energies and that tend to have smaller probabilities at intermediate binding energies than those of more compact ligands (Figs. 8B and 9B). This behavior is consistent with the interpretation that larger ligands are capable of forming stronger interactions with the receptor but only in specific poses that occur with low probability. Conversely, small ligands can achieve favorable binding affinity by means of larger numbers of conformations with intermediate binding energies. The role of these two modes of binding can also be seen by comparing the distributions of related ligands. For example the distributions for benzene and toluene (Fig. 8B), which bind the L99A receptor with similar affinity, reveal that the the addition of a methyl group substituent has a small effect on the binding affinity because the gain in the strength of ligand-receptor interactions (u < −15 kcal/mol) is almost completely counterbalanced by the loss of probability density at intermediate binding energies (−15 < u < 0 kcal/mol), which is explained by the fewer alternative ways for toluene to properly fit into the binding site compared to benzene.
The distributions also help explain differences in binding affinities between related ligands with distributions of similar shape. For example the shapes of the distributions for catechol, a binder for the L99A/M102Q receptor, and 2-aminophenol, a non-binder, are very similar (Fig. 9A), indicating a similar pattern of interactions for the two ligands. The probability tail for catechol, however, is down-shifted by about 2 kcal/mol, an amount that mirrors the difference between their binding free energies (Table 1). These results suggest that the lower binding affinity of 2-aminophenol is energetic in origin. Analysis of the binding energy terms [Eq. (8)] indeed indicates that the two ligands differ mainly in the desolvation free energy term which opposes binding of 2-aminophenol by approximately 2 kcal/mol more than catechol. Analogously, the binding energy distributions of phenol bound to the L99A and L99A/M102Q receptors are similar in shape (Figs.8B and 9B) with the one for the L99A/M102Q receptor down-shifted by approximately 4 kcal/mol relative to the other. This energy shift, caused by the hydrogen bonding interaction between phenol and Q102, is responsible for the better affinity of phenol for the L99A/M102Q receptor compared to the L99A receptor.
Some of the computed binding affinity densities [k(u), from Eq. (17)] are shown in Fig. 10. These functions measure the contribution of conformations with binding energy u to the binding constants, given by the areas under the curves. We see from these figures that the range of binding energies that contribute to binding varies significantly from one ligand to another. For example the binding affinity density for iso-butylbenzene is significant for binding energies around −20 kcal/mol (Fig. 10A) whereas k(u) for benzene is significant only for much less favorable binding energies (approximately 7 kcal/mol less favorable on average). In contrast, the difference of the binding free energies between these two ligands is much smaller (about 1.2 kcal/mol, Table 1). The reason for this is that, although iso-butylbenzene can form strong interactions with the receptor, it can do so with low probability (from Fig. 8A at u ≃ −20 kcal/mol p0(u) ≃ 10−11 kcal/mol−1). In contrast, benzene achieves favorable binding by means of more numerous conformations of moderate binding energies; for instance, at u ≃ −13 kcal/mol the probability density for benzene is approximately p0(u) ≃ 10−6 kcal/mol−1 (Fig. 8B), a value 5 orders of magnitude greater than for iso-butylbenzene above.
These probabilistic effects, which oppose binding, can be quantified by the residual between the binding free energy and the average binding energy 〈u〉1 = 〈V1−V0〉1 at λ = 1. This quantity can be expressed as the sum of the the conformational entropy loss, , 15 and the reorganization energy, ΔEreorg, upon binding given by
| (33) |
and
| (34) |
where ΔEAB = 〈V1〉1 − 〈V0〉0 is the effective enthalpy of binding and Vλ, given by Eq. (25), is the λ-dependent effective potential. Using the computed binding free energy values from Table 1 and the average binding energy values from Table 2 we obtain values for of 15.2 kcal/mol for iso-butylbenzene, compared to only 8.5 kcal/mol for benzene. The large difference between these residuals indicates that iso-butylbenzene, in addition to losing more conformational entropy than benzene, also induces significantly more receptor strain. Indeed we observed that in the λ = 1 trajectory of the complex with iso-butylbenzene that the V111 residue together with helix F of the receptor are shifted away from the binding pocket compared to the complex with benzene. The positioning of these elements in the simulation of the complex with iso-butylbenzene is similar to the corresponding crystal structure73 except for the rotameric state of V111 which remains in the starting apo configuration instead of adopting the one seen in the crystal structure. Explicit modelling of this conformational change has been shown to improve the agreement with the experimental binding free energies.59
Table 2.
Lowest and average binding energies and corresponding ligand rankings.
| Molecule | Rank(calc)a | min(u)b | min(u)-rankc | 〈u〉1d | 〈u〉1-ranke |
|---|---|---|---|---|---|
| L99A Apolar Cavity | |||||
| iso-butylbenzene | 1 | -27.3 | 1 | -20.4 | 1 |
| benzene | 2 | -17.8 | 7 | -12.5 | 7 |
| toluene | 3 | -20.2 | 5 | -14.8 | 5 |
| indole | 4 | -22.9 | 4 | -16.3 | 4 |
| ter-butylbenzene | 5 | -24.7 | 2 | -18.4 | 2 |
| cyclohexane | 6 | -19.6 | 6 | -14.1 | 6 |
| 1,3,5-trimethylbenzene | 7 | -22.9 | 3 | -16.8 | 3 |
| phenol | 8 | -17.5 | 8 | -11.7 | 8 |
| Rank order CC:f | 0.36 | 0.36 | |||
| L99A/M102Q Polar Cavity | |||||
| toluene | 1 | -20.0 | 6 | -14.8 | 6 |
| phenol | 2 | -21.4 | 5 | -16.1 | 3 |
| 3-chlorophenol | 3 | -23.5 | 2 | -17.6 | 1 |
| catechol | 4 | -22.9 | 3 | -16.7 | 2 |
| 4-vinylpiridine | 5 | -18.7 | 7 | -13.6 | 7 |
| 4-chloro-1h-pyrazole | 6 | -18.7 | 8 | -12.4 | 8 |
| 2-aminophenol | 7 | -22.9 | 4 | -15.0 | 5 |
| phenylhydrazine | 8 | -26.2 | 1 | -15.7 | 4 |
| Rank order CC:f | -0.21 | 0.38 | |||
Ligand rankings based on the calculated binding free energies (from Table 1).
Lowest binding energy found over the conformations sampled from the HREM simulation.
Ligand rankings based on lowest binding energy values.
Average binding energy at λ = 1.
Ligand rankings based on average binding energy values.
Rank order correlation coefficients between lowest/average binding energy rankings (4th and 6th column, respectively) and binding free energy rankings (2nd column).
We see from the computed k(u) functions (Fig. 10) that, as expected, the contribution from conformations with unfavorable binding energies (u > 0) is negligible. (This is true for both binders and non-binders although only the binding affinity densities of binders are shown in Fig. 10.) Interestingly, this analysis shows that conformations with very favorable binding energies also contribute little to binding. For example the smallest binding energy we observed for phenol bound to the L99A/M102Q receptor is −21.4 kcal/mol. However as the binding affinity density for phenol shows (Fig. 10B), conformations with binding energies in this low range provide a negligible contribution to the binding constant. This is because they occur with insufficient probability in the bound complex to make a difference. Consequently, it is apparent that for an accurate computation of the binding constant it is not necessary to sample binding energies well below values that are frequently found for the complex at room temperature.
Another notable and common feature of the binding affinity densities we obtained (Fig. 10) is their relatively large widths, indicating that conformations with a wide range of binding energies are contributing to binding. For example we see (Fig. 10A) that the binding affinity of iso-butylbenzene is the result of appreciable contributions from conformations with binding energies in a 10 kcal/mol range from −25 to −15 kcal/mol. In addition, conformational decomposition analysis (see discussion below and Figure 11), shows that in this system energetic heterogeneity is accompanied by extensive conformational heterogeneity.
The conformational decomposition analysis of the binding affinity densities (summarized in Fig. 11 for the L99A/M102Q complexes) illustrates the wide range of ligand poses that give rise to the calculated binding free energies, even for these simple ligands with very few internal degrees of freedom. We see that in none of the cases examined is all of the binding affinity due to a single macrostate of the complex. In the case of catechol two distinct poses contribute equally to the binding affinity and therefore missing one of them would underestimate the binding constant by a factor of 2. Phenol presents a less extreme case in which 80% of the affinity is accounted for by the macrostate corresponding to the crystallographic pose. For toluene and 3-chlorophenol a variety of ligand poses contribute appreciably to binding in addition to the crystallographic pose. Because, as noted above, the relative contributions to binding of ligand macrostates are equal to their relative populations at λ = 1, information about these contributions can in principle be obtained from a conventional simulation of the complex. As previously noted,53 however, due to kinetic trapping it is challenging in practice to achieve equilibrium between conformational macrostates without resorting to enhanced sampling strategies, like for example HREM.
The conformational decomposition analysis yields macrostate-specific standard binding free energies, ΔF°(i) [Eq. (21)], which correspond to the binding free energies that would be measured if ligand conformations were restricted to within specific macrostates. Macrostate-specific binding free energies have been previously introduced to compute standard binding free energies from multiple free energy calculations each focused on a single macrostate.53,66 The macrostate-specific binding free energies for the binders of the L99A/M102Q receptor computed in this work are reported in Fig. 11. Notably, the magnitudes of macrostate-specific binding free energies often exceed that of the total binding free energy. For example the binding free energy for the crystallographic macrostate of phenol is −5.21 kcal/mol compared to the total computed standard binding free energy of −3.65 kcal/mol. This is due to the fact that macrostate-specific binding free energies ignore the entropic loss due to the many other orientations of the ligand in solution which can not form favorable interactions with the receptor. These effects are encoded in the populations, P0(i), of ligand macrostates in solution that, when properly combined in Eq. (22) with their respective macrostate-specific binding constants, yield the total binding constant.
The energetic and conformational heterogeneities we observed for the complexes studied in this work (Figs. 10 and 11) illustrate why it is difficult to correlate the properties of a single conformation of the complex to the binding affinity The binding affinity originates from multiple and diverse conformations whose contributions depend on the balance between their binding energy and their probability of occurrence. In addition, we note that empirical scoring functions for binding74 are often applied to energetically optimized conformations that do not necessarily contribute significantly to binding. To illustrate this point we show in Table 2 the ligand rankings for each receptor based on the most favorable binding energies observed in the simulations together with their correlations with the free energy rankings. We see that there is very little correlation in this system between the lowest binding energies and the binding free energies, particularly for the L99A/M102Q receptor for which phenylhydrazine (the poorest binder) is predicted to be the best binder based on the lowest binding energy. The average binding energies collected at λ = 1 (which correspond for example to the binding energy term of the single-trajectory MM-PBSA method75) are somewhat better correlated with the binding free energies (Table 2).
Similar to docking and scoring approaches,2 BEDAM is based on computing receptor-ligand interaction energies. Rather than doing so on a single or few selected ligand poses, however, in BEDAM the probability distributions of binding energies are collected from thousands of conformations drawn from canonical conformational ensembles computed with physical models of molecular interactions. The latter feature is in common with endpoint approaches, such us MM-PB/GBSA76 and mining minima methods,14 which employ separate models for the binding enthalpy and binding entropy. In contrast, BEDAM is essentially a binding free energy model that, as discussed, in principle includes all enthalpic and entropic effects through the p0(u) binding energy distribution.
BEDAM bears some relationship to both potential of mean force and double decoupling methods for computing standard binding free energies.8,18,21 Since they share the same statistical mechanics foundation [i.e. Eq. (1)], in principle BEDAM yields equivalent results to these methods (to the extent that the implicit solvent models reflect the solvent potential of mean as accurately as explicit solvation). Potential of mean force methods obtain the binding free energy by computing the free energy profile for transferring the ligand from solution to the binding site region. Similarly, the binding energy considered by BEDAM for each conformation of the complex represents the change in potential of mean force (with implicit solvation) for moving the ligand from the solution to a particular position and orientation in the binding site at fixed receptor and ligand conformations. Conformational, translational, and rotational entropic contributions are included in BEDAM by means of the exponential averaging [Eq. (12)] of the binding energies over all possible conformations and positioning of the ligand relative to the receptor. Potential of mean force methods capture the same contributions by means of a thermodynamic cycle involving restraining and releasing steps.20
Similar to double decoupling strategies,8,18 BEDAM is based on an alchemical transformation to link the bound and unbound states of the complex. There are, however, conceptual and methodological differences between BEDAM and double decoupling strategies. BEDAM is based on binding energy values computed with implicit solvation whereas double decoupling has been employed so far only with explicit solvation. The implicit solvent representation in BEDAM makes it possible to compute binding energy distributions that, as illustrated above, represent receptor-ligand complex fingerprints which are useful for the analysis of binding interactions and their conformational decomposition. On the operational side, BEDAM involves only one simulation leg rather than two (one for the unbound ligand and one for the complex) with double decoupling. This feature is potentially advantageous for more rapid convergence of the binding free energies of highly polar and charged ligands, which, in double decoupling and endpoint approaches, are the result of a nearly complete cancellation between the large free energies of the solvated and bound states.20 Because binding energies are averaged over a single simulation, BEDAM results will be less sensitive to statistical errors. Care should be taken, however, to achieve the correct balance between interatomic and hydration interactions for charged groups with implicit solvation.41
Other notable operational differences between BEDAM and double decoupling approaches, as commonly implemented,23,77 involve the free energy computational protocol and the treatment of restraints. In double decoupling the free energy of turning off the interactions of the ligand from its environment is conducted in a series of steps, or windows, evaluated independently or sequentially by second generation FEP free energy estimators.65,78 In BEDAM instead the binding free energy is computed through the binding energy distribution using a strategy based on Hamiltonian replica exchange (HREM) umbrella sampling and histogram reweighting (WHAM). In potential of mean force and double decoupling implementations the thermodynamic path connecting the bound and unbound states is commonly divided into a series of intermediate steps involving imposition and removal of conformational restraints and the separate decoupling and re-coupling of electrostatic, van der Waals, and steric interactions.77 In BEDAM no conformational restraints are imposed other than those pertinent to the definition of the bound complex as prescribed by the theory. In addition, in this work we have not found it necessary to decouple electrostatic interactions separately from other interactions. This is due in part to the fact that BEDAM interactions are not completely turned on or off. Rather, as λ goes from 0 to 1, ligand-solvent interactions are smoothly replaced by ligand-receptor interactions. Similarly, the sampling efficiency gained by Hamiltonian replica exchange partly explains the ability of BEDAM to reach reasonable convergence in the simple systems considered here without imposing tight restraints or subdividing the calculation across multiple conformational states.53,66
One of the key features of BEDAM is the close match between the underlying theory and its numerical implementation. Indeed, the HREM umbrella sampling and WHAM protocols are particularly well suited for the computation of binding energy distributions on which BEDAM is based. HREM in λ space allows for the rapid equilibration between stable conformations of the complex, which provide the energetic driving force for binding, and for efficient coverage of the families of conformations not as suitable for binding, which provide the entropic cost of association. HREM MD trajectories are not limited to a single λ-step, rather they can explore the whole range of the thermodynamic path thereby enhancing conformational sampling and mixing. At the same time, conformational sampling is focused in the binding site region thereby avoiding spending computing time to sample uninteresting regions of conformational space that do not contribute to the binding free energy. The ladder of λ values for HREM can be chosen so that uniform coverage of the range of binding energies important for binding is achieved.
The WHAM reweighting procedure applies naturally to the computation of the binding energy distribution at λ = 0 from the binding energy values extracted from the HREM trajectories. Through WHAM, each sample contributes to the overall free energy result and not only to the λ value at which it was collected. Furthermore, the dynamic range of binding energy probabilities that can be robustly probed with this method can be very large, thereby enhancing the reliability of the binding free energies computed from it. This is because the relative precision of the computed binding energy distribution p0(u) depends mainly on the number of samples collected at binding energy u, rather than the value of p0(u) itself. The Multistate Bennett Acceptance Ratio method (MBAR),47 which does not require binning, could be equivalently used in BEDAM to compute the binding free energy by reweighting. However the computation of the binding energy distributions p0(u) and p1(u), which are useful analytical tools, require binning. Another strategy that could prove convenient in cases where the extreme favorable binding energy tail of p0(u) is difficult to sample, is to adopt a parametric model for p0(u) whose parameters are optimized from the collected samples by means of inference analysis.9 Future work will address these potential enhancements for BEDAM.
5 Conclusions
We have presented the Binding Energy Distribution Analysis Method (BEDAM) for the calculation of protein-ligand standard free energies of binding with implicit solvation. We have shown that the theory underlying the method is homologous to the test particle insertion method of solvation thermodynamics with the solute-solvent potential replaced by the effective binding energy of the protein-ligand complex. Accordingly, in BEDAM the binding constant is computed by means of a Boltzmann-weighted integral [Eq. (12)] of the probability distribution of the binding energy obtained in the canonical ensemble in which the ligand, while positioned in the binding site, is embedded in the solvent continuum and does not interact with receptor atoms. We have shown that the binding energy distribution encodes all of the physical effects of binding and that its analysis yields useful insights into energetic and entropic contributions to binding. We have also shown how joint probability distributions can be constructed to perform the conformational decomposition of the computed binding affinity.
We developed an efficient computational protocol for the binding energy distribution based on the AGBNP2 implicit solvent model, parallel Hamiltonian replica exchange sampling and histogram reweighting. We have shown that the sampling of ligand conformations is such that the results are independent of the starting conformation of the complex. We have also confirmed that the results are converged with respect to the definition of the binding site volume. Illustrative results are reported for a set of known binders and non-binders of the L99A and L99A/M102Q mutants of T4 lysozyme receptor. The method is found to be able to correctly discriminate the known binders from the known non-binders. The computed standard binding free energies of the binders are found to be in reasonably good agreement with reported calorimetric measurements. The conformational decomposition analysis of the results reveals that the binding affinities of these systems reflect contributions from multiple binding modes spanning a wide range of binding energies.
Despite the positive results for the T4 lysozyme model system, further work will be needed to apply the BEDAM method to more complex targets. Systems of pharmaceutical interest often involve larger and more flexible ligands as well as more flexible receptors than those studied here. Ligand and receptor reorganization make important contributions to the binding affinity,8,79–82 and, although these effects are implicitly included in the theory, they are only partially accounted for by the BEDAM conformational sampling protocol as currently implemented. The HREM conformational sampling algorithm developed here is quite successful in sampling a variety of receptor-ligand poses but it is expected to be less useful for ergodic sampling at physiological temperature of the internal degrees of freedom of some ligands.83 Similarly, the current conformational sampling methodology has not been designed to extensively sample receptor conformations. While acceptable for the relatively rigid receptors investigated in this study, this limitation will pose a significant challenge for the application of the method to other kinds of receptors. To address these issues we are currently exploring the applicability of methods based on the combination of Hamiltonian and temperature replica exchange to enhance conformational sampling. The robustness of implicit solvent modelling is also of concern for the general applicability of the method. The two major challenges are probably the accurate modelling of charged groups and the treatment of structural water molecules.84 Further tests of the method will likely offer useful insights into the improvement of the representation of the solvent for these applications.
Acknowledgments
We are grateful to Dr. Michael K. Gilson for critically reviewing the manuscript and elucidating some aspects of the theory. We are also grateful to three anonymous reviewers for helpful suggestions and insights. This work has been supported in part by a research grant from the National Institute of Health (GM30580). The calculations reported in this work have been performed at the BioMaPS High Performance Computing Center at Rutgers University funded in part by the NIH shared instrumentation grant no. 1 S10 RR022375.
References
- 1.Jorgensen WL. Science. 2004;303:1813–1818. doi: 10.1126/science.1096361. [DOI] [PubMed] [Google Scholar]
- 2.Guvench O, MacKerell AD. Curr Opin Struct Biol. 2009;19:56–61. doi: 10.1016/j.sbi.2008.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brooijmans N, Kuntz ID. Annu Rev Biophys Biomol Struct. 2003;32:335–373. doi: 10.1146/annurev.biophys.32.110601.142532. [DOI] [PubMed] [Google Scholar]
- 4.McInnes C. Curr Opin Chem Biol. 2007;11:494–502. doi: 10.1016/j.cbpa.2007.08.033. [DOI] [PubMed] [Google Scholar]
- 5.Shoichet BK. Nature. 2004;432:862–865. doi: 10.1038/nature03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhou Z, Felts AK, Friesner RA, Levy RM. J Chem Inf Model. 2007;47:1599–1608. doi: 10.1021/ci7000346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gilson MK, Zhou HX. Annu Rev Biophys Biomol Struct. 2007;36:21–42. doi: 10.1146/annurev.biophys.36.040306.132550. [DOI] [PubMed] [Google Scholar]
- 8.Mobley DL, Dill KA. Structure. 2009;17:489–498. doi: 10.1016/j.str.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chipot C, Andrew Pohorille, editors. Free Energy Calculations Theory and Applications in Chemistry and Biology. Springer; Berlin Heidelberg: 2007. (Springer Series in Chemical Physics). [Google Scholar]
- 10.Zhou HX, Gilson MK. Chem Rev. 2009;109:4092–4107. doi: 10.1021/cr800551w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tembe BL, McCammon JA. Computers & Chemistry. 1984;8:281. [Google Scholar]
- 12.Shirts M, Mobley D, Chodera J. Ann Rep Comput Chem. 2007;3:41–59. [Google Scholar]
- 13.Jorgensen WL, Thomas LL. J Chem Theory Comput. 2008;4:869–876. doi: 10.1021/ct800011m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chang CE, Gilson MK. J Am Chem Soc. 2004;126:13156–13164. doi: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- 15.Chang CA, Chen W, Gilson MK. Proc Natl Acad Sci USA. 2007;104:1534–1539. doi: 10.1073/pnas.0610494104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE. Acc Chem Res. 2000;33:889–897. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- 17.Chong LT, Pitera JW, Swope WC, Pande VS. J Mol Graph Model. 2009;27:978–982. doi: 10.1016/j.jmgm.2008.12.006. [DOI] [PubMed] [Google Scholar]
- 18.Gilson MK, Given JA, Bush BL, McCammon JA. Biophys J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lee MS, Olson MA. Biophys J. 2006;90:864–877. doi: 10.1529/biophysj.105.071589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Woo HJ, Roux B. Proc Natl Acad Sci USA. 2005;102:6825–6830. doi: 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Deng Y, Roux B. J Phys Chem B. 2009;113:2234–2246. doi: 10.1021/jp807701h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hermans J, Subramaniam S. Isr J Chem. 1986;27:225–227. [Google Scholar]
- 23.Boyce SE, Mobley DL, Rocklin GJ, Graves AP, Dill KA, Shoichet BK. J Mol Biol. 2009;394:747–763. doi: 10.1016/j.jmb.2009.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chen J, Brooks C, Khandogin J. Curr Opin Struct Biol. 2008;18:140–148. doi: 10.1016/j.sbi.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Felts AK, Gallicchio E, Chekmarev D, Paris KA, Friesner RA, Levy RM. J Chem Theory Comput. 2008;4:855–868. doi: 10.1021/ct800051k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang Y. Curr Opin Struct Biol. 2009;19:145–155. doi: 10.1016/j.sbi.2009.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Scheraga HA, Khalili M, Liwo A. Annu Rev Phys Chem. 2007;58:57–83. doi: 10.1146/annurev.physchem.58.032806.104614. [DOI] [PubMed] [Google Scholar]
- 28.Felts AK, Harano Y, Gallicchio E, Levy RM. Proteins: Struct, Funct, Bioinf. 2004;56:310–321. doi: 10.1002/prot.20104. [DOI] [PubMed] [Google Scholar]
- 29.Felts A, Andrec M, Gallicchio E, Levy R. Water and Biomolecules - Physical Chemistry of Life Phenomena. Springer Science; 2008. [Google Scholar]
- 30.Gallicchio E, Zhang LY, Levy RM. J Comp Chem. 2002;23:517–529. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 31.Mobley D, Chodera J, Dill K. J Phys Chem B. 2008;112:938–946. doi: 10.1021/jp0764384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shoichet BK, Leach AR, Kuntz ID. Proteins. 1999;34:4–16. doi: 10.1002/(sici)1097-0134(19990101)34:1<4::aid-prot2>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 33.Majeux N, Scarsi M, Apostolakis J, Ehrhardt C, Caflisch A. Proteins. 1999;37:88–105. [PubMed] [Google Scholar]
- 34.Maple JR, Cao Y, Damm W, Halgren TA, Kaminski GA, Zhang LY, Friesner RA. J Chem Theory Comput. 2005;1:694–715. doi: 10.1021/ct049855i. [DOI] [PubMed] [Google Scholar]
- 35.Huang N, Kalyanaraman C, Irwin JJ, Jacobson MP. J Chem Inf Model. 2006;46:243–253. doi: 10.1021/ci0502855. [DOI] [PubMed] [Google Scholar]
- 36.Naim M, Bhat S, Rankin KN, Dennis S, Chowdhury SF, Siddiqi I, Drabik P, Sulea T, Bayly CI, Jakalian A, Purisima EO. J Chem Inf Model. 2007;47:122–133. doi: 10.1021/ci600406v. [DOI] [PubMed] [Google Scholar]
- 37.Carlsson J, Andér M, Nervall M, Åqvist J. J Phys Chem B. 2006;110:12034–12041. doi: 10.1021/jp056929t. [DOI] [PubMed] [Google Scholar]
- 38.Su Y, Gallicchio E, Das K, Arnold E, Levy R. J Chem Theory Comput. 2007;3:256–277. doi: 10.1021/ct600258e. [DOI] [PubMed] [Google Scholar]
- 39.Michel J, Essex JW. J Med Chem. 2008;51:6654–6664. doi: 10.1021/jm800524s. [DOI] [PubMed] [Google Scholar]
- 40.Gallicchio E, Levy R. J Comp Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 41.Gallicchio E, Paris K, Levy RM. J Chem Theory Comput. 2009;5:2544–2564. doi: 10.1021/ct900234u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Su Y, Gallicchio E. Biophys Chem. 2004;109:251–260. doi: 10.1016/j.bpc.2003.11.007. [DOI] [PubMed] [Google Scholar]
- 43.Levy RM, Zhang LY, Gallicchio E, Felts AK. J Am Chem Soc. 2003;125:9523–9530. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 44.Roux B, Simonson T. Biophys Chem. 1999;78:1–20. doi: 10.1016/s0301-4622(98)00226-9. [DOI] [PubMed] [Google Scholar]
- 45.Sugita Y, Okamoto Y. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- 46.Gallicchio E, Andrec M, Felts AK, Levy RM. J Phys Chem B. 2005;109:6722–6731. doi: 10.1021/jp045294f. [DOI] [PubMed] [Google Scholar]
- 47.Shirts MR, Chodera JD. J Chem Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sugita Y, Kitao A, Okamoto Y. J Chem Phys. 2000;113:6042–6051. [Google Scholar]
- 49.Rick SW. J Chem Theory Comput. 2006;2:939–946. doi: 10.1021/ct050207o. [DOI] [PubMed] [Google Scholar]
- 50.Hritz J, Oostenbrink C. J Chem Phys. 2008;128:144121. doi: 10.1063/1.2888998. [DOI] [PubMed] [Google Scholar]
- 51.Woods CJ, Essex JW, King MA. J Phys Chem B. 2003;107:13703–13710. [Google Scholar]
- 52.Jiang W, Hodoscek M, Roux B. J Chem Theory Comput. 2009;5:2583–2588. doi: 10.1021/ct900223z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mobley DL, Chodera JD, Dill KA. J Chem Phys. 2006;125:084902. doi: 10.1063/1.2221683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Eriksson AE, Baase WA, Wozniak JA, Matthews BW. Nature. 1992;355:371–373. doi: 10.1038/355371a0. [DOI] [PubMed] [Google Scholar]
- 55.Wei BQ, Baase WA, Weaver LH, Matthews BW, Shoichet BK. J Mol Biol. 2002;322:339–355. doi: 10.1016/s0022-2836(02)00777-5. [DOI] [PubMed] [Google Scholar]
- 56.Morton A, Baase WA, Matthews BW. Biochemistry. 1995;34:8564–8575. doi: 10.1021/bi00027a006. [DOI] [PubMed] [Google Scholar]
- 57.Graves AP, Brenk R, Shoichet BK. J Med Chem. 2005;48:3714–3728. doi: 10.1021/jm0491187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Deng Y, Roux B. J Chem Theory Comput. 2006;2:1255–1273. doi: 10.1021/ct060037v. [DOI] [PubMed] [Google Scholar]
- 59.Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA. J Mol Biol. 2007;371:1118–1134. doi: 10.1016/j.jmb.2007.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Boresch S, Tettinger F, Leitgeb M, Karplus M. J Phys Chem B. 2003;107:9535–9551. [Google Scholar]
- 61.Widom B. J Phys Chem. 1982;86:869–872. [Google Scholar]
- 62.Beck TL, Paulaitis ME, Pratt LR. The Potential Distribution Theorem and Models of Molecular Solutions. Cambridge University Press; New York: 2006. [Google Scholar]
- 63.Pohorille A, Pratt LR. J Am Chem Soc. 1990;112:5066–5074. doi: 10.1021/ja00169a011. [DOI] [PubMed] [Google Scholar]
- 64.Widom B. J Chem Phys. 1963;39:2808–2812. [Google Scholar]
- 65.Lu N, Singh JK, Kofke DA. J Chem Phys. 2003;118:2977–2984. [Google Scholar]
- 66.Jayachandran G, Shirts MR, Park S, Pande VS. J Chem Phys. 2006;125:084901. doi: 10.1063/1.2221680. [DOI] [PubMed] [Google Scholar]
- 67.Mihailescu M, Gilson MK. Biophys J. 2004;87:23–36. doi: 10.1529/biophysj.103.031682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lu N, Kofke DA. J Chem Phys. 2001;114:7303–7311. [Google Scholar]
- 69.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. J Phys Chem B. 2001;105:6474–6487. [Google Scholar]
- 70.Feig M, Brooks C. Curr Op Struct Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 71.Banks J, et al. J Comp Chem. 2005;26:1752–1780. doi: 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Mobley DL, Chodera JD, Dill KA. J Chem Theory Comput. 2007;3:1231–1235. doi: 10.1021/ct700032n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Morton A, Matthews BW. Biochemistry. 1995;34:8576–8588. doi: 10.1021/bi00027a007. [DOI] [PubMed] [Google Scholar]
- 74.Eldridge MD, Murray CW, Auton TR, Paolini GV, Mee RP. J Comput Aided Mol Des. 1997;11:425–445. doi: 10.1023/a:1007996124545. [DOI] [PubMed] [Google Scholar]
- 75.Brown SP, Muchmore SW. J Chem Inf Model. 2007;47:1493–1503. doi: 10.1021/ci700041j. [DOI] [PubMed] [Google Scholar]
- 76.Simonson T, Archontis G, Karplus M. Acc Chem Res. 2002;35:430–437. doi: 10.1021/ar010030m. [DOI] [PubMed] [Google Scholar]
- 77.Wang J, Deng Y, Roux B. Biophys J. 2006;91:2798–2814. doi: 10.1529/biophysj.106.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Shirts MR, Bair E, Hooker G, Pande VS. Phys Rev Lett. 2003;91:140601. doi: 10.1103/PhysRevLett.91.140601. [DOI] [PubMed] [Google Scholar]
- 79.Sherman W, Day T, Jacobson MP, Friesner RA, Farid R. J Med Chem. 2006;49:534–553. doi: 10.1021/jm050540c. [DOI] [PubMed] [Google Scholar]
- 80.Yang CY, Sun H, Chen J, Nikolovska-Coleska Z, Wang S. J Am Chem Soc. 2009;131:13709–13721. doi: 10.1021/ja9039373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.DeLorbe JE, Clements JH, Teresk MG, Benfield AP, Plake HR, Millspaugh LE, Martin SF. J Am Chem Soc. 2009;131:16758–16770. doi: 10.1021/ja904698q. [DOI] [PubMed] [Google Scholar]
- 82.Lapelosa M, Arnold GF, Gallicchio E, Arnold E, Levy RM. J Mol Biol. 2010;397:752–766. doi: 10.1016/j.jmb.2010.01.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Okumura H, Gallicchio E, Levy RM. J Comput Chem. 2010;31:1357–1367. doi: 10.1002/jcc.21419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Abel R, Young T, Farid R, Berne BJ, Friesner RA. J Am Chem Soc. 2008;130:2817–2831. doi: 10.1021/ja0771033. [DOI] [PMC free article] [PubMed] [Google Scholar]