Abstract
We develop a new principal components analysis (PCA) type dimension reduction method for binary data. Different from the standard PCA which is defined on the observed data, the proposed PCA is defined on the logit transform of the success probabilities of the binary observations. Sparsity is introduced to the principal component (PC) loading vectors for enhanced interpretability and more stable extraction of the principal components. Our sparse PCA is formulated as solving an optimization problem with a criterion function motivated from penalized Bernoulli likelihood. A Majorization-Minimization algorithm is developed to efficiently solve the optimization problem. The effectiveness of the proposed sparse logistic PCA method is illustrated by application to a single nucleotide polymorphism data set and a simulation study.
Keywords and phrases: Binary data, Dimension reduction, MM algorithm, LASSO, PCA, Regularization, Sparsity
1. Introduction
Principal components analysis (PCA) is a widely used method for dimensionality reduction, feature extraction and visualization of multivariate data. Several sparse PCA methods have recently been introduced to improve the standard PCA (e.g., Jolliffe et al., 2003; Zou et al., 2006; Shen and Huang, 2008). By requiring the principal component loading vectors to be sparse, sparse PCA methods yield PCs that are more easily interpretable. Sparsity also regularizes the extraction of PCs and thus makes the extraction more stable. Such stability is much desired when the dimension is high, especially in the so-called high-dimension low-sample-size settings. As extensions of the standard PCA, however, these sparse PCA methods are mostly suitable to variables of continuous type, they are not generally appropriate for other data types such as binary data or counts. Although the basic objective of PCA, or its sparse version, can be achieved regardless of the nature of the original variable, it is true that variances and covariances have especial relevance for multivariate Gaussian variables, and that linear functions of binary variables are less readily interpretable than linear functions of continuous variables (Jolliffe, 2002). The goal of this paper is to develop a sparse PCA method for binary data.
There are two commonly used definitions of PCA that give rise to the same result. PCA can be defined by finding the orthogonal projection of the data onto a low dimensional linear subspace such that the variance of the projected data is maximized (Hotelling, 1933). Alternatively, PCA can also be defined by finding the linear projection that minimizes the mean squared distance between the data points and their projections (Pearson, 1901). Shen and Huang (2008) developed their sparse PCA method following the viewpoint of Pearson. Suppose y1, … ,yn ∈ ℝd are the n data points and consider a k-dimensional (k < d) linear manifold spanned by a bases b̃1, … , b̃k with a shift vector μ. According to Pearson, the PCA minimizes the following reconstruction error
| (1.1) |
subject to the constraint that A = (aij) has orthonormal columns. Usually the variables presented in yi are scaled so that they have the same order of magnitude. Note that (1.1) is a least squares regression if aik ’s were known. In light of this connection to regression and borrowing idea from LASSO (Tibshirani, 1996), Shen and Huang (2008) proposed to add an L1 penalty ∥b̃1∥1+…+∥b̃k∥1 to the reconstruction error (1.1) to obtain sparse loading vectors b̃1, … , b̃k. Since the reconstruction error (1.1) can be viewed as the negative log likelihood up to a constant for the Gaussian distributions with mean vectors θi = μ+ai1 b̃1 +…+aikb̃k for i = 1, … , n and identity covariance, the method of Shen and Huang can be interpreted as a penalized likelihood approach for sparse PCA. The key idea of the current paper is to replace the Gaussian likelihood by the Bernoulli likelihood where θi will be the logit transform of the success probabilities. We refer to the proposed PCA method as sparse logistic PCA. The relationship of the proposed sparse logistic PCA to the sparse PCA of Shen and Huang is analogous to the relationship between logistic and linear LASSO regression.
We develop an iterative weighted least squares algorithm to perform the proposed sparse logistic PCA. Since the log Bernoulli likelihood is not quadratic and the L1 penalty function is non-differentiable, the optimization problem defining the sparse logistic PCA is not straightforward to solve. Our algorithm applies the general idea of optimization transfer or Majorization-Minimization (MM) algorithm (Lange et al., 2000; Hunter and Lange, 2004). By iteratively replacing the complex objective function with suitably defined quadratic surrogates, each step of our algorithm solves a weighted least squares problem and has closed form. The algorithm is easy to implement and guaranteed at each iteration to improve the penalized PCA log-likelihood. We show that the same MM algorithm is applicable when there are missing data. We also develop a method for choosing the penalty parameters and for choosing the number of important principal components. PCA of binary data using Bernoulli likelihood has previously been studied by Collins et al. (2001), Schein et al. (2003), and de Leeuw (2006), but none of these works considered sparse loading vectors. As we demonstrate using simulation and real data, sparsity can enhance interpretation of results and improve the stability and accuracy of the extracted principal components.
Other approaches of sparse PCA are not as easily extendible to binary data. Jolliffe et al. (2003) modified the defining maximum variance problem of the standard PCA by applying an L1-norm constraint on the PC loading vectors to obtain PCA with sparse loadings. Its use of sample variance makes it unappealing for binary data. Zou et al. (2006) rewrote PCA as a regression-type optimization problem and then applied the LASSO penalty (Tibshirani, 1996) to obtain sparse loadings. However, since the data appear both as regressors and responses in their regression-type problem, the connection of their approach to penalized likelihood is not as natural as Shen and Huang (2008).
The rest of this article is organized as follows. In Section 2, we introduce the optimization problem that yields the sparse logistic PCA and provide methods for tuning parameter selection. Section 3 applies the sparse logistic PCA to a single nucleotide polymorphism data set and compares it with the non-sparse version of logistic PCA. Section 4 presents a Majorization-Minimization algorithm for efficient computation of the sparse logistic PCA and Section 5 discusses how to handle missing data. Results of a simulation study are given in Section 6. Section 7 concludes the paper with some discussion. An appendix contains proofs of theorems.
2. Sparse Logistic PCA with Penalized Likelihood
2.1. Penalized Bernoulli Likelihood
Consider the n×d binary data matrix Y = (yij) each row of which represents a vector of observations from binary variables. We assume that entries of Y are realizations of mutually independent random variables and that yij follows the Bernoulli distribution with success probability πij. Let θij = log{πij/(1−πij)} be the logit transformation of πij. Define the inverse logit transformation π(θ) = {1+exp(−θ)}−1. Then the success probabilities can be represented using the canonical parameters as πij = π(θij). The individual data generating probability becomes
with qij = 2yij − 1 since π(−θ) = 1 − π(θ). This representation leads to the compact form of the log likelihood as
| (2.1) |
Note that the Bernoulli distributions are in the exponential family and θij are the corresponding canonical parameters.
To build a probabilistic model for principal components analysis of binary data, the d-dimensional canonical parameter vectors θi = (θi1, … , θid)T are constrained to reside in a low dimensional manifold of ℝd with the dimensionality k. (The choice of k will be discussed later in Section 2.3.) Specifically, we assume that, for some vectors μ, b̃1, … , b̃k ∈ ℝd, the vector of canonical parameters satisfies θi = μ + ai1 b̃1 + … + aik b̃k for i = 1,…, n. We call b̃1, … ,b̃k the principal component loading vectors and the coefficients ai = (ai1, … , aik)T the principal component scores (PC scores) for the ith observation. Geometrically, the vectors of canonical parameters θi are projected onto the k-dimensional manifold which is the affine subspace spanned by k PC loading vectors and translated by the intercept vector μ. In matrix form, the canonical parameter matrix Θ = (θij) = (θ1, … , θn)T is represented as
| (2.2) |
where A = (a1, … , an)T is the n × k principal component score matrix and B = (b̃1, … ,b̃k) is the p × k principal component loading matrix. For identifiability purpose, we require that A have orthonormal columns.
We target a method that can produce a sparse loading matrix, a loading matrix with many zero elements. A sparse loading matrix implies variable selection in principal components analysis, since each principal component only involves those variables corresponding to the nonzero elements of the loading vector. We propose to perform variable selection using the penalized likelihood with a sparsity inducing penalty. Let denote the jth row of B. Then (2.2) implies that where μj is the jth element of μ. The log likelihood can be written as
| (2.3) |
If ai were observable, (2.3) is the log likelihood for d logistic regressions
This connection with logistic regression suggests use of the L1 penalty to get a sparse loading matrix, as in the LASSO regression (Tibshirani, 1996).
Specifically, consider the penalty
| (2.4) |
where λl are regularization parameters whose selection will be discussed later. We obtain sparse principal components by maximizing the following penalized log likelihood
| (2.5) |
subject to the constraint that A has orthonormal columns. Note that B enters the likelihood together with A through ABT and so B can be arbitrarily small by just increasing the magnitude of A and not changing the likelihood. The orthonormal constraint on A prevents elements of A becoming arbitrary large and thus validates our use of the L1 penalty on B.
The sparse principal components can be equivalently formulated as minimizing the following criterion function
| (2.6) |
subject to the constraint that A has orthonormal columns. In (2.6), the negative log likelihood can be interpreted as a loss function and the L1 penalties increase the loss for nonzero elements of B according to their magnitude. This penalized loss interpretation is also appealing in the sense that the independent Bernoulli trials assumption for obtaining the likelihood (2.3) need not be a realistic representation of actual data generating process but rather a device for generating a suitable loss function. Since the L1 penalties regularize the loss minimization, the sparse logistic PCA is sometimes also referred to as the regularized logistic PCA. We shall focus on the minimization problem (2.6) for the rest of the paper. A computational algorithm for solving the minimization problem is presented in Section 4.
The effectiveness of the proposed sparse logistic PCA is illustrated in Figure 1 using a rank-one model (i.e., k = 1). While the sparse logistic PCA can recover the original loading vector well, the nonregularized logistic PCA gives more noisy results. A systematic simulation study is reported in Section 6.
Fig 1.
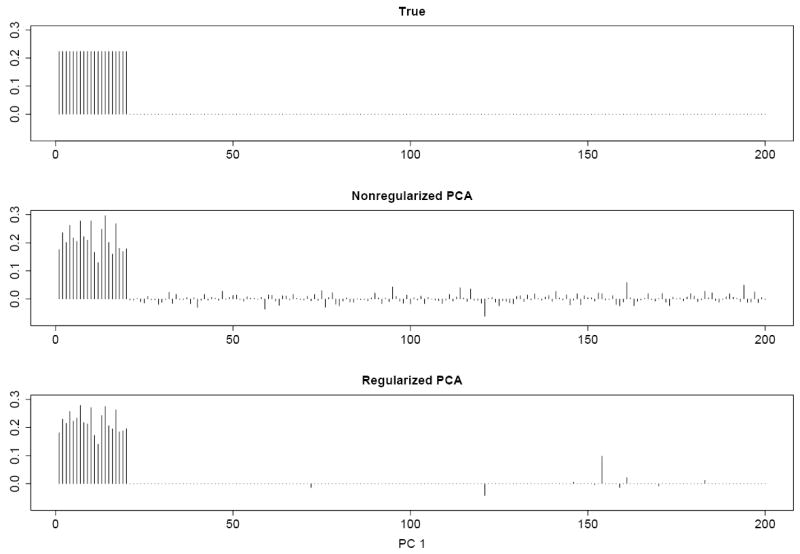
A simulated data set with n = 100, d = 200, and k = 1. Top, middle and bottom panels show respectively the true loadings, loadings from the nonregularized logistic PCA and from the regularized logistic PCA. The penalty parameter is selected using the BIC.
2.2. Choosing the penalty parameters
Although different penalty parameters can be used for different PC loading vectors for maximal flexibility of the methodology, we consider using only a single penalty parameter λ for all PC loadings. This simplification substantially reduces the computation time, especially when k is large. Note that a larger value of λ will lead to a smaller number of nonzeros in the loading matrix B and reduced model complexity, but the reduced model complexity is usually associated with less good fit of the model. To compromise the goodness-of-fit and model complexity, for fixed k, we choose λ by minimizing the following BIC criterion
| (2.7) |
where m(λ) is a measure of the degrees of freedom. Note that Zou et al. (2007) showed that the number of nonzero coefficients is an unbiased estimate of the degrees of freedom for the LASSO regression. The degrees of freedom m(λ) used in (2.7) is defined as m(λ) = d + nk + ∣B(λ)∣, where d is the length of the vector μ, nk is the total number of elements of A, and ∣B(λ)∣ is the cardinality of the index set B(λ) of the nonzero loadings in B when the penalty parameter is λ. We use a grid search to find the optimal λ that minimizes the BIC.
2.3. Determining the dimensionality of the subspace
The BIC criterion defined in (2.7) can also be used to select a suitable “k”. A two-dimensional grid search can be used to find the minimizer of the BIC with respect to both k and λ. To expedite computation, we implement the following strategy: First fix k at a reasonable large value and select a good λ, then using this λ we refine the choice of k and, finally, we refine λ with the refined k. When optimizing with respect to λ, a coarse grid can be used in the first step and a finer grid in the second step. Our simulation study showed that this strategy works reasonably well (see Section 6.3).
Remark 1
In classical multivariate analysis, the percentage of total variance explained by the principal components provides an intuitive measure that can be used for subjectively choosing the appropriate number of principal components. Zou et al. (2006) and Shen and Huang (2008) extended it to sparse PCA by modifying the definition of variance explained by the PCs. Since there is no clear definition of total variance for the binary data, extension of the notion of “percentage of variance explained” to logistic PCA is an interesting but unsolved problem.
3. Application to single nucleotide polymorphism data
Association studies based on high-throughput single nucleotide polymorphism (SNP) data (Brookes, 1999; Kwok et al., 1996) have become a popular way to detect genomic regions associated with human complex disease. A SNP is a single base pair position in genomic DNA at which the sequence (alleles) variation occurs between members of a species, wherein the least frequent allele has an abundance of 1% or greater. A crucial issue in association studies is population stratification detection (Hao et al., 2004) which is to determine whether a population is homogeneous or has hidden structures within it. With the presence of population stratification, the naive case-control approach not accounting for this factor would yield biased results (Ewens and Spielman, 1995) and, therefore, draw inaccurate scientific conclusions. See Liang and Kelemen (2008) for an extensive discussion of statistical methods and difficulties for SNP data analysis.
The proposed sparse logistic PCA method can be used for population stratification detection. For the purpose of demonstration, we use the SNP data set available in the International HapMap project (The International HapMap Consortium, 2005). It consists of 3 different ethnic populations of 90 Caucasians (Utah residents with ancestry from northern and western Europe; CEO), 90 Africans (Yoruba in Ibadan, Nigeria; YRI) and 90 Asians (45 Han Chinese in Beijing, China; CHB and 45 Japanese in Tokyo, Japan; JPT). Our task is to detect this three-subpopulation structure using the SNP data on the 270 subjects. At many SNP locations, heterozygosity distribution and allele frequency are known to be different among populations and could confound the effect of the risk of disease. To account for this factor, Serre et al. (2008) selected 1,536 SNPs with the similar heterozygosity distribution and allele frequency. The locations of these SNPs cover all the chromosomes except for the sex-determining chromosome. Among these 1,536 SNPs, 1,392 are shared by three ethnic groups, which are used in our analysis. We coded 0 for the most prevalent homogeneous base pair (wild-type) and 1 for others (mutant), resulting in a 270 × 1392 binary matrix. This data matrix has 2.37% missing entries.
We applied the sparse logistic PCA to this SNP data set to explore variability among high dimensional SNP variables, using the computation algorithm given in Sections 4 and 5 below. The method described in Section 2.3 was used for model selection. Specifically, we initially fixed the reduced dimension to k = 30 and chose the penalty parameter λ among the rough grid of 0, 1.5−18, 1.5−17, … , 1.5−10 using the BIC criterion defined in Section 2.3. Given the selected λ = 1.5−16, the dimension k was refined by minimizing the BIC, giving k = 10. Finally, with k = 10, we refined λ by searching over the grid 0, 0.0005, 0.0010, 0.0015, … , 0.0100, resulting in λ = 0.0015. As a comparison, we also applied the nonregularized logistic PCA to the data, which corresponds to λ = 0 in our general formulation of regularized logistic PCA.
To examine which principal components represent the variability associated with three racial groups, we used a F-test where scores for each fixed PC is regressed on the group dummy variables. For the sparse logistic PCA, only the first two PCs were highly significant with both p-values less than 0.0001 and the remaining eight PCs were not significant with large p-values (0.7681, 0.9109, 0.4764, 0.5523, 0.3376, 0.5415, 0.4480, 0.6441 for the third to the tenth PCs respectively). This result suggests that the sparse logistic PCA can effectively compress the racial group information into two leading PCs. Similar compression was not achieved by the nonregularized logistic PCA; the F-test was significant for all the first ten PCs with p-values <0.0001, <0.0001, 0.0002, 0.0001, <0.0001, <0.0001, <0.0001, 0.0028, <0.0001, and 0.0299 respectively.
Pairwise scatterplots were used to check clustering of subjects using the PC scores. Figure 2 shows the scatterplots of first 2 PC scores with and without regularization. The three ethnic groups are clearly separated by the regularized PCA but not by the nonregularized PCA. To verify that the group separation obtained is not because of luck, we permuted observations for each SNP and applied the sparse logistic PCA to the permuted data set; no clear clustering showed up in the PC scores.
Fig 2.
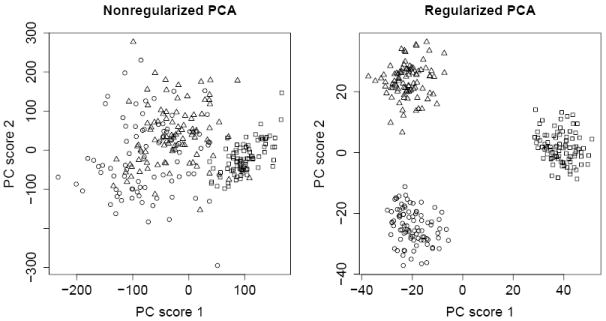
The scatterplots of the first two PC scores from the nonregularized (left) and regularized logistic PCA. Circle, rectangle and triangle represent Caucasian, African and Asian population respectively.
The proposed sparse PCA method allows directly identifying the SNPs that contribute to the group separation. The selected model has 790 and 658 nonzero loadings (representing the SNPs) respectively for the first 2 PCs, among which 509 SNPs are shared. Therefore, 939 SNPs involved in the first 2 PC directions are claimed to be associated with the ethnic group effect. Our result suggests that the population stratification factor should be taken into consideration at these 939 SNP locations in the subsequent study of the association between SNPs and the disease phenotype to avoid biased conclusion. Although in light of our simulation results, some selected SNPs could be false positives, we believe that a large proportion of the selected SNPs are relevant in differentiation among the three racial groups, because the studied SNPs were delicately selected to represent the most genetic diversity of the whole genome (Serre et al., 2008) and the genetic differentiation is the greatest when defined on a continental basis, which is the case for our comparison between Caucasian, Asian, and African (Risch et al., 2002).
We further compared the regularized and nonregularized logistic PCA by assessing the variability of the probability estimates using the parametric bootstrap. For each method, we generated 100 bootstrapped data sets of binary matrices; each binary matrix has entries that are independently drawn from the Bernoulli distribution with success probability π̂ij for the (i, j)-th entry, where π̂ij is the estimated probability. We then applied the method to these bootstrapped data sets to obtain 100 bootstrapped probabilities for each (i, j) combination and to construct a 90% variability interval using the 5% and 95% quantiles of the bootstrapped probabilities. These 90% variability intervals were plotted against the ordered π̂ij to form a variability envelop. The variability envelop for the regularized PCA is narrower than that for the nonregularized PCA, indicating that regularization indeed reduces the variability of the probability estimates (Figure 3).
Fig 3.
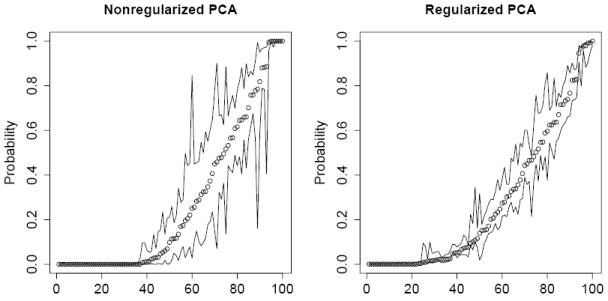
The SNP data: 90% bootstrap variability envelope (showed as lines) of the probability estimates, using 100 randomly selected SNPs. Circles are the estimated probabilities π̂ij from the SNP data. Results are based on 100 bootstrap samples.
Our working model for the logistic PCA specified by (2.1) and (2.2) assumes that, conditional on the principal component scores, the observations are independent. Since there exists spatial dependency among SNPs, one may concerns about the validity of our analysis results if the dependence is strong. In our data set, the 1,536 SNPs were selected from the whole genome to capture most of the genetic diversity in population considering factors of physical distances, allele frequencies, and linkage disequilibrium patterns. The selected SNPs are sufficiently well separated within each chromosome so that they can be representative of the whole genome (Serre et al. 2007). Therefore we expect that the spatial dependency in this data set should not be too serious to invalidate our results. To address this issue empirically, we first computed Pearson’s residuals after fitting the models for the nonregularized and regularized logistic PCA, then calculated pairwise correlations of these Pearson’s residuals for all SNP pairs for each chromosome. Figure 4 shows the histogram of the pairwise correlations for each model. For both models, most pairwise correlations are close to zero, indicating that the SNPs are weakly correlated. We noticed that there exists a very small proportion of SNP pairs that are highly correlated. Examination of the physical locations revealed that those highly correlated SNP pairs consist of SNPs in close vicinity, indicating the imperfection of the initial SNP selection process.
Fig 4.
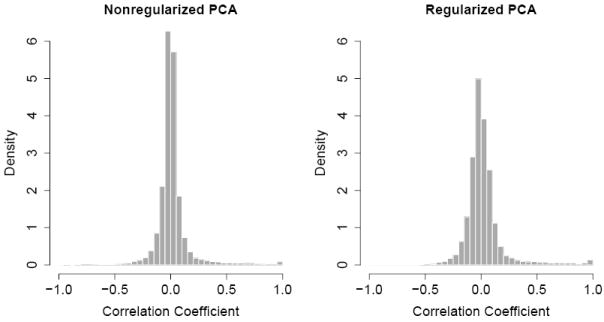
Histograms of pairwise correlations of Pearson’s residuals from nonregularized (left) and regularized (right) logistic PCA
4. Computational algorithm
We develop a majorization-minimization (MM) algorithm for minimizing (2.6), which iteratively minimizes a suitably defined quadratic upper bound of (2.6). Instead of directly dealing with the non-quadratic log likelihood and the non-differentiable sparsity inducing L1 penalty, the MM algorithm sequentially optimizes a quadratic surrogate objective function. A function g(x∣y) is said to majorize a function f(x) at y if
In the geometrical view, the function surface g(x∣y) lies above the function f(x) and is tangent to it at the point y so g(x∣y) becomes an upper bound of f(x). To minimize f(x), the MM algorithm starts from an initial guess x(0) of x, and iteratively minimizes g(x∣x(m)) until convergence, where x(m) is the estimate of x at the mth iteration. The MM algorithm decreases the objective function in each step and is guaranteed to converge to a local minimum of f(x). When applying the MM algorithm, the majorizing function g(x∣y) is chosen such that it is easier to minimize than the original objective function f(x). See Hunter and Lange (2004) for an introductory description of the MM algorithm.
To find a suitable majorizing function of (2.6), we treat the log likelihood term and the penalty term separately. For the log likelihood term, note that, for a given point y,
| (4.1) |
| (4.2) |
and the equalities hold when x = y (Jaakkola and Jordan, 2000; de Leeuw, 2006). These inequalities provide quadratic upper bounds for the negative log inverse logit function at the tangent point y. We refer to the former bound as the tight bound, and the latter bound as the uniform bound since its curvature does not change with y. We pursue here the MM algorithm by using the uniform bound and leave the discussion of using the tight bound to the supplementary materials. Use of the tight bound usually leads to less number of iterations of the algorithm but longer computation time because of the complexity involved in computing the bound. For the penalty term, the inequality
| (4.3) |
gives an upper bound for ∣x∣ and the equality holds when x = y (Hunter and Li, 2005). Application of (4.2) and (4.3) yields a suitable majorizing function of (2.6) and thus an MM algorithm.
Now we present details of the MM algorithm via the uniform bound. Let Θ(m) be the estimate of Θ obtained in the mth step of the algorithm, with the entries . By completing the square, the uniform bound (4.2) can be rewritten as
| (4.4) |
Substituting x and y with qijθij and respectively in (4.4) and noticing that qij = ±1, we obtain
| (4.5) |
where and
| (4.6) |
The superscript m of and indicates the dependence on Θ(m). Summing over all i, j of (4.5) and ignoring a constant term that does not depend on unknown parameters, we obtain the following quadratic upper bound of the negative log-likelihood
| (4.7) |
On the other hand, (4.3) implies that the penalty Pλ(B) has the following quadratic upper bound
| (4.8) |
Combining (4.7) and (4.8) yields the following quadratic upper bound (up to a constant) of the criterion function S(μ, A, B) defined in (2.6):
| (4.9) |
where is a diagonal matrix with diagonal elements for l = 1,…, k.
Theorem 4.1
Up to a constant that depends on μ(m), A(m), and B(m) but not on μ, A, and B, the function g(μ, A, B∣μ(m), A(m), B(m)) defined in (4.9) majorizes S(μ, A, B) at (μ(m), A(m), B(m)).
Let (μ(m), A(m), B(m)), m = 1, 2,…, be a sequence obtained by iteratively minimizing the majorizing function. Then S(μ(m), A(m), B(m)) decreases as m gets larger and it converges to a local minimum of S(μ, A, B) as m goes to infinity.
The majorizing function given in (4.9) is quadratic in each of μ, A, and B when the other two are fixed and thus alternating minimization of (4.9) with respect to μ, A, and B has closed-form solutions, which are given below. We now drop the superscript in for notational convenience. Recall that is a constant. For fixed A and B, set , the optimal μ̂j is given by
| (4.10) |
This leads to a simple matrix formula , which is obtained by taking the column means of .
To update A and B for fixed μ, set or in matrix form, . Denote the ith row vector of X* as For fixed μ and B, the ith row of A is updated by minimizing with respect to ai the sum of squares , which has a closed form solution
| (4.11) |
or  = X*B(BTB)−1 in matrix form. The columns of updated A can be made orthonormal by using the QR decomposition. Denote the jth column vector of X* as . For fixed μ and A, the jth row of B is updated by solving the ridge regression problem that minimizes with respect to bj the penalized sum of squares
which has a closed form solution
| (4.12) |
Since, during the iteration, A is made orthonormal, AT A becomes the identity matrix of size k. Therefore, since the matrices to be inverted are diagonal matrices, b̂j can be obtained by component-wise shrinkage
where ãl is the lth column of A.
The MM algorithm will alternate between (4.10), (4.11), and (4.12) until convergence. The details are summarized in Algorithm 1. In this algorithm, k, the number of columns of A and B, should be specified in advance. Different from the sequential extraction approach of Shen and Huang (2008), the matrices A and B obtained after applying Algorithm 1 depends on the value of k, but the results are reasonably stable when k is large enough. See Section 2.3 for discussion on choice of k. We use random initial values for μ, A and B. As any nonlinear optimization algorithms, our algorithm is not guaranteed to converge to a global minimum. We can follow the common practice to random start the algorithm several times and find the best solution. Our experience is that the algorithm with different initial values usually converges to the same solution (within the precision specified by the convergence criterion).
Algorithm 1 Sparse Logistic PCA Algorithm I
Initialize with Set m = 1.
Compute using (4.6) and set .
Set with . Update μ using .
Set X(m+1)* = X(m) − 1n ⊗ μ(m+1)T.
Update A by A(m+1) = X(m+1)*B(m)(B(m)TB(m))−1. Compute the QR decomposition A(m+1) = QR and then replace A(m+1) by Q.
- Set . Update B by where
Repeat steps 2 through 6 with m replaced by m + 1 until convergence.
Remark 2
The orthogonalization in Step 5 of Algorithm 1 does not change the decent property of the MM algorithm. Let A(m+1) be the optimizer before orthogonalization. Then S(A(m+1), B(m)) ≤ S(A(m), B(m)), where, for simplicity, μ is omitted from the objective function S. Let A(m+1) = Ã(m+1) R be the QR decomposition of A(m+1) and let B̃(m) = B(m) RT. Then Ã(m+1) B̃(m)T = A(m+1) B(m)T and so S(Ã(m+1), B̃(m)) = S(A(m+1), B(m)). Consequently, S(Ã(m+1), B̃(m)) ≤ S(A(m), B(m)).
5. Handling Missing Data
Missing data are commonly encountered in real applications. In this section, we extend our sparse logistic PCA method to cases when missing data are present.
Let N = {(i, j)∣yij is not observed} denote the index set for missing values. The sparse logistic PCA minimizes the following criterion function
| (5.1) |
where
| (5.2) |
can be interpreted as the observed data log likelihood for model (2.2). Similar to the non-missing data case, direct minimization of (5.1) is not straight-forward because the log likelihood term is not quadratic and the penalty term is non-differentiable. Direct minimization of (5.1) is also complicated by the fact that the summation in the definition of the observed data log likelihood is not over a rectangular region. Again, we develop an iterative MM algorithm to solve the optimization problem. The strategy is to fill in the missing data with the fitted values based on the current parameter estimates, then proceed with the algorithm that assumes complete data, and iterate until convergence.
Define the working variables
| (5.3) |
where is defined in (4.6). Let
| (5.4) |
where are diagonal matrices with diagonal elements for l = 1,…,k. The following result extends Theorem 4.1 to the missing data case. The proof is given in the Appendix.
Theorem 5.1
Up to a constant that depends on μ(m), A(m), and B(m) but not on μ, A, and B, the function h(μ, A, B∣μ(m),A(m), B(m)) defined in (5.4) majorizes T(μ, A, B) at (μ(m), A(m), B(m)).
Let (μ(m),A(m), B(m)), m = 1, 2,…, be a sequence obtained by iteratively minimizing the majorizing function. Then T(μ(m), A(m), B(m)) decreases as m gets larger and it converges to a local minimum of T(μ, A, B) as m goes to infinity.
Note that the majorizing functions given in (5.4) have the same form as those given in (4.9) except that in (4.9) is changed to in (5.4). Thus the computation algorithm developed in Section 4 is readily applicable in the missing data case with a simple replacement of by . The working variable in (5.4) is easily understood: It is the same as the non-missing data case if yij is observable; otherwise, it is an imputed θij value based on the reduced rank model (2.2) and the current guess of μ, A, and B.
6. Simulation Study
In this section we demonstrate our sparse logistic PCA method using a simulation study. The method worked well in various settings that we tested, but here we only report results in a challenging case that the number of variables d is bigger than the sample size n.
6.1. The signal-to-noise ratio
To facilitate setting up simulation studies, we introduce a notion of signal-to-noise ratio for logistic PCA. In our logistic PCA model, the entries of the n × d data matrix are independent Bernoulli random variables with success probability πij = {1 + exp(−θij)}−1 for the (i, j)-th cell. The matrix of canonical parameters Θ = (θij) has a reduced rank representation Θ = 1 ⊗ μT + ABT , where A is a n × k matrix of PC scores and B is a sparse d × k PC loading matrix. In our simulation study, elements of the l-th column of A are independent draws from from a zero-mean Gaussian distribution with variance , 1≤ l ≤k. The variance measures the signal level of the l-th PC. We set up the PC variances relative to a suitably defined baseline noise level.
We define a baseline noise level for fixed n, d, and k as follows. First we create a binary data matrix by generating n × d independent binary variables from Bernoulli distribution with the success probability 1/2. These binary variables are understood to come from the pure noise since they are generated without having any structure on the success probabilities. Then, we conduct a k-component logistic PCA without regularization and compute the average of the sample variances of the obtained k PC scores, which is denoted as . We repeat the above process of generating “pure noise” binary data matrices a large number of times (for example, 100) and take the mean of computed from these matrices as the baseline noise level.
With the notion of baseline noise level, we define the signal-to-noise ratio (SNR) for a PC as
| (6.1) |
In our simulation study, we first compute the baseline noise level for a given combination of n, d, and k, then use the above formula to specify the variances of PC scores based on the fixed values of SNR.
6.2. Simulation setup
We set the intrinsic dimension to be k = 2 and the number of rows of the data matrix to be n = 100. We varied the number of variables d and the signal-to-noise ratio SNR. We considered three choices of d: d = 200, d = 500, and d = 1000. The scores of the l-th PC were randomly drawn from the distribution with · (baseline noise level), where SNRl is the SNR for the l-th PC. We considered two settings of SNR: (3, 2) and (5, 3). For example, when the SNR is (3, 2), the variance of the first PC is 3 times the baseline noise level and the variance of the second PC is 2 times the baseline noise level. We construct two sparse PC loading vectors as follows: Let bj1 and bj2 denote correspondingly the components of the first and the second PC loading vectors. We let bj1 = 1 for j = 1,…, 20, bj2 = 1 for j = 21,…,40, and the rest of bjl are all taken to be 0. The mean vector μ was set to be a vector of zeros.
6.3. Simulation results
Logistic PCA with and without sparsity inducing regularization was conducted on 100 simulated data sets for each setting. When applying the sparse logistic PCA algorithm, three choice of k was considered: k is fixed at the true value (k = 2), at a moderately large value (k = 30), and selected using the BIC. The penalty parameter was selected using the method described in Section 2.2.
To measure the closeness of the estimated PC loading matrix B̂ and the true loading matrix B, we use the principal angle between spaces spanned by B̂ and B. The principal angle measures the maximum angle between any two vectors on the spaces generated by the columns of B̂ and B. More precisely, it is defined by cos−1(ρ)×180/π, where ρ is the minimum eigenvalue of the matrix , where QB̂ and QB are orthogonal basis matrices obtained by the QR decomposition of matrices B̂ and B, respectively (Golub and van Loan, 1996).
The mean and standard deviation of principal angles for logistic PCA with and without regularization are presented in Table 1. Since smaller principal angles indicate better estimates of the PC loading matrix, the sparsity inducing regularization has a clear benefit — it can substantially reduce the principal angles. The benefit is even more profound when the number of PCs used in the program (k = 30) is larger than the true number that was used to generate the data (k = 2). The performance of sparse logistic PCA with selected k is similar to that when k is fixed at the true value. Frequencies of the selected k from 100 simulation data sets in each settings of Table 1 are shown in Table 2. When d = 200, the BIC finds well the true k = 2 but, as d gets larger, there is a trend that a slightly larger k is selected. The performance of using BIC to select k is considered as quite good, given that the sample size is only 100.
Table 1.
The results of logistic PCA with and without sparsity inducing regularization, based on 100 simulated data sets for each setting. The reported values are the mean (standard error) of the principal angle (°) between the estimated and the true PC loading matrices.
| d | SNR | k = 2 | k = 30 | selected k |
|---|---|---|---|---|
| 200 | SNR=(3, 2) | |||
| nonregularized | 12.532 (0.115) | 35.725 (0.177) | – | |
| regularized | 5.860 (0.123) | 10.125 (0.324) | 5.816 (0.125) | |
| SNR=(5, 3) | ||||
| nonregularized | 11.913 (0.122) | 36.350 (0.189) | – | |
| regularized | 5.803 (0.128) | 9.843 (0.321) | 5.769 (0.127) | |
| 500 | SNR=(3, 2) | |||
| nonregularized | 10.890 (0.095) | 31.884 (0.188) | – | |
| regularized | 4.731 (0.115) | 9.413 (0.282) | 4.690 (0.101) | |
| SNR=(5, 3) | ||||
| nonregularized | 10.166 (0.095) | 31.941 (0.193) | – | |
| regularized | 4.729 (0.121) | 9.242 (0.252) | 4.544 (0.119) | |
| 1000 | SNR=(3, 2) | |||
| nonregularized | 12.018 (0.167) | 36.040 (0.181) | – | |
| regularized | 7.015 (0.486) | 11.807 (0.433) | 4.534 (0.141) | |
| SNR=(5, 3) | ||||
| nonregularized | 11.370 (0.156) | 36.144 (0.180) | – | |
| regularized | 6.767 (0.474) | 10.825 (0.475) | 4.196 (0.127) |
Table 2.
Frequencies of the selected k using the BIC.
| selected k |
||||||||
|---|---|---|---|---|---|---|---|---|
| d | SNR | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 200 | (3, 2) | 0 | 95 | 5 | 0 | 0 | 0 | 0 |
| (5, 3) | 0 | 96 | 4 | 0 | 0 | 0 | 0 | |
| 500 | (3, 2) | 1 | 58 | 37 | 4 | 0 | 0 | 0 |
| (5, 3) | 0 | 60 | 36 | 3 | 1 | 0 | 0 | |
| 1000 | (3, 2) | 3 | 34 | 36 | 15 | 10 | 1 | 1 |
| (5, 3) | 2 | 31 | 47 | 15 | 4 | 1 | 0 | |
A useful feature of the sparse logistic PCA is its ability to select relevant variables when estimating the PC loading vectors. A zero loading of a variable on a PC means that the corresponding variable is not used when forming that PC, and a nonzero loading indicates a useful variable. Our experience with simulated data shows that nonzero loadings can almost always be identified by the method, but some identified nonzero loadings may correspond to irrelevant variables, cases of false positives. Table 3 presents the percentages of false positives for various settings reported in Table 1. When d is 500 or 1000, the percentages of false positives are low, all below 20%. But when d is 200, the percentages of false positives are between 40% and 50%, suggesting a big room for improvement in variable selection.
Table 3.
The results of logistic PCA with sparsity inducing regularization, based on 100 simulated data sets for each setting in Table 1. The reported values are the mean (standard error) of the percentages of false positives. The description of results is in the text.
| d | SNR | k = 2 | k = 30 | selected k |
|---|---|---|---|---|
| 200 | (3, 2) | 45.05 (1.54) | 41.51 (1.39) | 44.94 (1.51) |
| (5, 3) | 48.16 (1.63) | 40.53 (1.36) | 48.26 (1.63) | |
| 500 | (3, 2) | 14.83 (0.74) | 18.91 (0.51) | 16.70 (0.72) |
| (5, 3) | 16.06 (0.68) | 18.78 (0.42) | 16.93 (0.68) | |
| 1000 | (3, 2) | 10.87 (0.75) | 12.80 (0.73) | 10.13 (0.60) |
| (5, 3) | 10.89 (0.70) | 12.86 (0.73) | 9.26 (0.50) |
7. Discussion and Extension
In this paper we propose a sparse PCA method for analyzing binary data by maximizing a penalized Bernoulli likelihood. The sparsity inducing L1 penalty is used to acquire simple principal components for the sake of easy interpretation and stable estimation. The MM algorithm developed for implementation of our method provides a unified solution for dealing with i) the non-quadratic likelihood, ii) the non-differentiable penalty function; iii) presence of missing data. Although the theoretical derivation is not straightforward, the steps of the algorithm are very simple — they are (weighted) penalized least squares with closed-form expressions.
We have focused on the logit link so far, but other link function can also be used. In particular, a slight modification of the proposed method can handle the probit link, where the success probabilities with Φ(·) being the cdf of the standard Gaussian distribution. The log likelihood function (2.3) of the reduced rank model is changed to
| (7.1) |
Instead of using the majorization in (4.2), we apply the following upper bound to majorize the negative log likelihood
| (7.2) |
where ϕ(·) is the Gaussian density (Böhning, 1999; de Leeuw, 2006). Algorithm 1 still applies with appropriate changes to the definitions of the weights and the working variables .
Our method can also be extended in a straightforward way to handle composite data which consisting of both binary and continuous variables. While the binary variables are modeled with Bernoulli distributions, the continuous variables can be modeled with Gaussian distributions. Including some continuous variables corresponds to adding some negative Gaussian log likelihood terms to the log likelihood expression (2.3). Since the Gaussian log likelihood is quadratic, it blends in easily with the quadratic majorization used for the logistic PCA. Specifically, if the j-th variable is of continuous type, we assume yij ~ N (θij, σ2) with θij satisfying (2.2), and simply let and when forming the majorizing function (4.9). The residual variance σ2 of fitting the continuous variables can be estimated using the residual sum of squares. Taking into account the fact that different weighting schemes are used for the binary variables and the continuous variables in the majorizing function, a slight modification of Algorithm 2 presented in the supplementary materials can be used for computation.
Supplementary Material
Acknowledgments
We would like to thank Editor Michael Stein, an Associate Editor, and two referees for helpful comments. We would also like to thank Lan Zhou for help in improving the writing of the paper.
APPENDIX A: APPENDIX
A.1. Proof of Theorem 4.1
We prove the results for both the tight and the uniform bound case. Applications of (4.1) and (4.2) yield the following majorizing functions of the negative log likelihood −l(μ, A, B):
for the tight bound, and
for the uniform bound. Note that
for qij = ±1. By completing the squares and using the definitions of and , these majorizing functions can be rewritten as
On the other hand, application of (4.3) yields the following majorizing function of Pλ(B):
Since the majorization relation between functions is closed under the formation of sums, −l̃+nP̃λ(B∣B(m)) majorizes S(μ, A, B) at (μ(m), A(m), B(m)) Noticing that −l̃+nP̃λ(B∣B(m)) equals g(μ, A, B∣μ(m), A(m), B(m)) up to a constant independent of (μ, A, B), we complete the proof of part (i). Part (ii) of the theorem follows from the general property of the MM algorithm (Hunter and Lange, 2004).
A.2. Proof of Theorem 5.1
Note that the objective function to be minimized is the summation of two terms – the log likelihood term and the penalty term. Because the majorization property is closed under function summation, we deal with the two terms separately. We can find a majorization function of the penalty term as in Theorem 4.1. To find a majorization function of the log likelihood term, we apply the argument in the standard EM algorithm for handling missing data (Dempster et al., 1977). The complete data log likelihood is
Its conditional expectation given the observed data and the current guess of the parameter values is
| (A.1) |
where Yo denote the observed data. By the standard EM theory,
| (A.2) |
majorizes −lobs(μ,A,B) at (μ(m),A(m),B(m)), that is, −l̃obs(μ,A,B) ≥ −lobs(μ,A,B), and the equality holds when (μ,A,B) = (μ(m),A(m),B(m)).
Now we find a quadratic majorizing function of −l̃obs(μ,A,B), which in turn majorizes −lobs(μ,A,B) because of the transitivity of the majorization relation. We need only to find a quadratic majorization function of −Q(μ,A,B∣μ(m),A(m),B(m)) since it is the only term in the definition (A.2) of −l̃obs(μ,A,B) that depends on the unknown parameters. According to (A.1), −Q(μ,A,B∣μ(m),A(m),B(m)) can be decomposed into two terms, one corresponding to observed data, the other corresponding to the missing data. The former term can been treated as in the proof of Theorem 4.1. When (i, j) ∉ N, −log π(qijθij) is majorized by , up to a constant. To treat the latter term, note that, when (i, j) ∈ N,
using the fact that the missing data are independent of the observed data, and that 1 − π(θ) = π(−θ). Then, by applying the inequalities (4.1) and (4.2) and using the definition of , we obtain that
where Cm is a constant independent of μ, A, and B. Combining the above results, we see that −Q(μ,A,B∣μ(m),A(m),B(m)) is up to a constant majorized by , where equals if (i, j) ∉ N, and if (i, j) ∈ N. The proof of Part (i) is thus complete. Part (ii) of the theorem follows from the general result of the MM algorithm.
Footnotes
SUPPLEMENTARY MATERIAL Supplement A: The MM algorithm for sparse logistic PCA using the tight bound (http://www.e-publications.org/ims/support/download/filename-to-be-specified). Development of the MM algorithm using the tight majorizing bound. Numerical comparison with the MM algorithm using the uniform bound.
Contributor Information
Seokho Lee, Department of Biostatistics, Harvard School of Public Health, Boston, MA 02115, USA, seokhol@hsph.harvard.edu.
Jianhua Z. Huang, Department of Statistics, Texas A&M University, College Station, TX 77843-3143, USA, jianhua@stat.tamu.edu.
Jianhua Hu, Department of Biostatistics, Division of Quantitative Sciences, University of Texas M.D. Anderson Cancer Center, Houston, TX 77030-4009, USA, jhu@mdanderson.org.
References
- 1.Böhning D. The lower bound method in probit regression. Computational Statistics and Data Analysis. 1999;30:13–17. [Google Scholar]
- 2.Brookes AJ. Review: The essence of SNPs. Gene. 1999;234:177–186. doi: 10.1016/s0378-1119(99)00219-x. [DOI] [PubMed] [Google Scholar]
- 3.Collins M, Dasgupta S, Schapire RE. A generalization of principal component analysis to the exponential family. Advanced in Neural Information Processing System. 2001;14 [Google Scholar]
- 4.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B. 1977;39:1–38. with Discussion. [Google Scholar]
- 5.de Leeuw J. Principal component analysis of binary data by iterated singular value decomposition. Computational Statistics and Data Analysis. 2006;50:21–39. [Google Scholar]
- 6.Ewens WJ, Spielman RS. The transmission/disequilibrium test: history, subdivision, and admixture. The American Journal of Human Genetics. 1995;57:455–464. [PMC free article] [PubMed] [Google Scholar]
- 7.Golub G, van Loan C. Matrix Computations. 3. The Johns Hopkins University Press; 1996. [Google Scholar]
- 8.Hao K, Li C, Rosenow C, Wong WH. Detect and adjust for population stratification in population-based association study using genomic control markers: an application of Affymetrix Genechip® Human Mapping 10K array. European Journal of Human Genetics. 2004;12:1001–1006. doi: 10.1038/sj.ejhg.5201273. [DOI] [PubMed] [Google Scholar]
- 9.Hotelling H. Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology. 1933;24:417–441. [Google Scholar]
- 10.Hunter DR, Lange K. A tutorial on MM algorithms. The American Statistician. 2004;58:30–37. [Google Scholar]
- 11.Hunter DR, Li R. Variable selection using MM algorithms. The Annals of Statistics. 2005;33:1617–1642. doi: 10.1214/009053605000000200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.The Internationa HapMap Consortium. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jaakkola TS, Jordan MI. Bayesian parameter estimation via variational methods. Statistics and Computing. 2000;10:25–37. [Google Scholar]
- 14.Jolliffe IT, Trendafilov M, Uddine M. A modified principal component technique based on the LASSO. Journal of Computational and Graphical Statistics. 2003;12:531–547. [Google Scholar]
- 15.Jolliffe IT. Principal Component Analysis. Springer; 2002. [Google Scholar]
- 16.Kwok PY, Deng Q, Zakeri H, Taylor SL, Nickerson DA. Increasing the information content of STS-based genome maps: Identifying polymorphisms in mapped STSs. Genomics. 1996;31:123–126. doi: 10.1006/geno.1996.0019. [DOI] [PubMed] [Google Scholar]
- 17.Lange K, Hunter DR, Yang I. Optimization transfer using surrogate objective functions. Journal of Computational and Graphical Statistics. 2000;9:1–20. with discussion. [Google Scholar]
- 18.Liang Y, Kelemen A. Statistical advances and challenges for analyzing correlated high dimensional SNP data in genomic study for complex diseases. Statistics Surveys. 2008;2:43–60. [Google Scholar]
- 19.Pearson K. On lines and planes of closest fit to systems of points in space. The London, Edinburgh and Dublin Pholosophical Magazine and Journal of Science, Sixth Series. 1901;2:559–572. [Google Scholar]
- 20.Risch N, Burchard E, Ziv E, Tang H. Categorization of humans in biomedical research: genes, race and disease. Genome Biology. 2002;3(7) doi: 10.1186/gb-2002-3-7-comment2007. comment 2007.1-2007.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Serre D, Montpetit A, Paré G, Engert JG, Yusuf S, Keavney B, Hudson KJ, Anand S. Correction of population stratification in large multi-ethnic association studies. PLoS ONE. 2008;2(1):e1382. doi: 10.1371/journal.pone.0001382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schein AI, Saul LK, Ungar LH. A generalized linear model for principal component analysis of binary data. Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics. 2003:14–21. [Google Scholar]
- 23.Shen H, Huang JZ. Sparse principal component analysis via regularized low rank matrix approximation. Journal of Multivariate Analysis. 2008;99:1015–1034. [Google Scholar]
- 24.Tibshirani RJ. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, B. 1996;58:267–288. [Google Scholar]
- 25.Zou H, Hastie TJ, Tibshirani RJ. Sparse principal component analysis. Journal of Computational and Graphical Statistics. 2006;15:265–286. [Google Scholar]
- 26.Zou H, Hastie TJ, Tibshirani RJ. On the “Degrees of Freedom” of the LASSO. Annals of Statistics. 2007;35:2173–2192. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


