Regional species pools control community saturation in lake phytoplankton

Abstract

Recent research has highlighted that positive biodiversity–ecosystem functioning relationships hold for all groups of organisms, including microbes. Yet, we still lack understanding regarding the drivers of microbial diversity, in particular, whether diversity of microbial communities is a matter of local factors, or whether metacommunities are of similar importance to what is known from higher organisms. Here, we explore the driving forces behind spatial variability in lake phytoplankton diversity in Fennoscandia. While phytoplankton biovolume is best predicted by local phosphorus concentrations, phytoplankton diversity (measured as genus richness, G) only showed weak correlations with local concentrations of total phosphorus. By estimating spatial averages of total phosphorus concentrations on various scales from an independent, spatially representative lake survey, we found that close to 70 per cent of the variability in local phytoplankton diversity can be explained by regionally averaged phosphorus concentrations on a scale between 100 and 400 km. Thus, the data strongly indicate the existence of metacommunities on this scale. Furthermore, we show a strong dependency between lake productivity and spatial community turnover. Thus, regional productivity affects beta-diversity by controlling spatial community turnover, resulting in scale-dependent productivity-diversity relationships. As an illustration of the interaction between local and regional processes in shaping microbial diversity, our results offer both empirical support and a plausible mechanism for the existence of common scaling rules in both the macrobial and the microbial worlds. We argue that awareness of regional species pools in phytoplankton and other unicellular organisms may critically improve our understanding of ecosystems and their susceptibility to anthropogenic stressors.

1. Introduction

Phytoplankton comprises the unicellular, photosynthetic organisms populating the surface waters of the lakes and oceans. They drive the bulk of primary production in most aquatic ecosystems and contribute 50 per cent to the global assimilation of organic carbon (Falkowski et al. 1998). A recent analysis has revealed that phytoplankton primary production does not only depend on the availability of limiting resources (light and nutrients). Compiling a large dataset from lakes and coastal systems, Ptacnik et al. (2008) showed that phytoplankton primary production is linked to diversity in ways similar to what has been previously shown for higher organisms (Hooper et al. 2005). Both the magnitude and the predictability of resource use efficiency, measured as the biomass yield per unit limiting nutrient, increase with the diversity of the community (Ptacnik et al. 2008).

In spite of its importance for the global carbon cycle and ecosystem services such as aquatic food production, our knowledge regarding the drivers of phytoplankton diversity is very limited. Research addressing the drivers of phytoplankton taxon richness has hitherto focused on the importance of local drivers (e.g. disturbance intervals Sommer et al. (1993); chaotic oscillations Huisman & Weissing (1999); system size Smith et al. (2005)), while processes on the regional level have received rather little attention.

For higher plants and metazoa, it has been shown previously that local species richness cannot be understood from local environmental conditions alone. Research focusing on higher organisms (metazoa) has revealed that the number of species found at a given site does not only depend on the local environment, but also on the number of surrounding sites with similar characteristics (Leibold et al. 2004). Species found in a given habitat (e.g. plants in a meadow) are part of populations of connected habitats, which span wider geographical areas (e.g. all meadows with similar characteristics within the dispersal range of the plant in question). Such regional communities are commonly referred to as ‘metacommunities’ (Leibold et al. 2004). According to metacommunity theory, the number of species present at a given site does not only reflect local environmental conditions, but also the connectivity to adjacent sites.

A fundamental aspect of metacommunity theory is the existence of dispersal limitation. For example, experiments with terrestrial plant communities showed that local species richness of natural communities increases once seed dispersal is increased (Turnbull et al. 2000). Thus, the number of taxa present at a given site reflects steady-state colonization–extinction dynamics (Vandvik & Goldberg 2006).

Highly mobile organisms are generally expected to have metacommunities spanning larger spatial scales than less mobile organisms (Jenkins et al. 2007). The relative importance of local versus regional environmental factors in controlling local species richness thus depends, among others, on the dispersal rate (= mobility) of the species in question. There is a long-standing tenet in microbial ecology that organisms less than 1 mm are not dispersal limited, which is corroborated by the fact that many protistan morpho-species are found on all continents (Finlay 2002; Fenchel & Finlay 2004). Their apparently high dispersal rate has been the basis for assuming that dispersal limitation is irrelevant for structuring microbial communities, so that the species composition of microbial communities will never be undersaturated (Finlay 2002).

If there are regional metacommunities in microbes, they should be detectable through spatial autocorrelation among local communities. A number of studies have recently tried to evaluate whether regional species pools matter in diversity of unicellular organisms (review in Martiny et al. (2006)). Most of those studies have analysed spatial turnover of community composition (as opposed to species richness), and often found local variables to dominate over regional ones (e.g. Van der Gucht et al. (2007)). However, two recent studies analysing the spatial structure of species richness in communities of benthic lake diatoms reported considerable large-scale variation, pointing at the existence of regional species pools (Telford et al. 2006; Vyverman et al. 2007).

Lakes are suitable for testing metacommunity hypotheses since they represent clearly defined systems and can be regarded as ‘inverted islands on the land’ (Turner 1999). Lakes may differ considerably in environmental parameters in spite of close proximity. Especially, the concentration of total phosphorus (TP) is a key parameter in temperate lakes. TP often represents the primary limiting factor for primary production in such systems (Vollenweider 1989). Moreover, even in systems that are not primarily phosphorus limited, productivity usually scales with TP (Elser et al. 2007).

Here, we test for the existence of regional species pools in lakes across Fennoscandia. We do so by assessing the relative importance of local versus regional environments as predictors of local genus richness. We focus on the effect of phosphorus, while taking other potential environmental drivers into account. The study is supplemented by a detailed analysis of spatial patterns of both phytoplankton genus richness and environmental parameters. Finally, we analyse how productivity (=TP) affects spatial turnover (beta-diversity) as well as size of regional species pools (gamma-diversity).

2. Material and methods

(a). Phytoplankton data and local environmental parameters

The phytoplankton dataset (set A) was compiled from various monitoring programmes carried out between 1988 and 2003 (Moe et al. 2008). In order to limit the influence of seasonal dynamics, we selected observations from July and August (except for analysis of beta-diversity, see below). Phytoplankton data plus a number of physical and chemical parameters were measured on the same sample using standard methods (Moe et al. 2008). Abundances and biovolumes of phytoplankton species and genera were estimated using the Utermöhl method (Utermöhl 1958). As a proxy for phytoplankton diversity, we use genus richness (G), which should be more robust to differences in skill and effort among the individual phytoplankton analysts. However, G and species richness are highly correlated in this dataset (r² = 0.95). Acidified lakes (pH < 6) and high-altitude lakes (more than 300 m above sea level) were excluded, resulting in a final dataset of 477 lakes. Many lakes in this dataset have multiple observations. To avoid over-sampling bias, we averaged G and environmental variables from all available summer samples for each lake, while we used a mild weighting by the square root of number of observations in the regression analyses. TP was ln-transformed in all analyses. In the remainder of the text, we refer to the TP measured at a site where a phytoplankton sample was taken from as local TP (L-TP).

(b). Analysis of beta-diversity

Here, we used data from one constrained geographical area (southeast Norway), where enough data from one season were available. The analysis was based on 126 samples collected from 52 lakes from July to September 1988. We tested the effect of L-TP on turnover by predicting dissimilarity among lake pairs from their average L-TP. Distance in L-TP (delta L-TP), spatial distance between lake pairs and time interval between samplings were considered as potential covariables. The analysis was performed as multiple regression on distance matrices (MRM; Lichstein (2006)) with resampling (n = 1000). In each draw, we selected exactly one sample from each lake (=52). This allowed us to use multiple observations per site, while excluding temporal turnover within lakes from the analysis at the same time. Coefficients, confidence intervals and significance levels were then derived from the bootstrapped parameter estimates (Fox 2002). MRM was performed using the ecodist package in R (Goslee & Urban 2007).

Temporal community turnover per lake was calculated separately for each lake in this data as outlined in Ptacnik et al. (2008), with temporal turnover being standardized by ln(time interval), hence giving the daily turnover.

(c). Phytoplankton gamma-diversity

Genus accumulation curves were calculated across lakes as an approximation of regional gamma-diversity. Estimates of average gamma-diversity as function of sample size were obtained by calculating the total genus richness in a given number of lakes randomly drawn from a given region, and repeating this procedure 50 times for each region and sample size to obtain robust estimates of mean richness and its standard deviations. Lakes with multiple observations were used only once per draw.

(d). Regional environmental parameters

The lake survey data (set B) were compiled in a coordinated effort by the Fennoscandian countries in 1995 (Henriksen et al. 1998). In Finland, Norway and Sweden, 4800 randomly selected lakes were each sampled once by hydroplane for a number of standard parameters. Lakes in set A and set B were sampled independently from each other, and less than 5 per cent of lakes are common to both datasets. Since set B consists from randomly chosen lakes, it also contains a small number of eutrophicated lakes, which appear as outliers in a density distribution (electronic supplementary material, figure S1). Since these extreme values would have an over proportional impact on regionally averaged TP, we decided to exclude the upper 5 percentile from set B. Since average TP increases from west to east, we did not merely remove the upper 5 percentile from the entire dataset, but selected this percentile from a quantile regression of TP along the longitudinal gradient (electronic supplementary material, figure S1). This resulted in a more normal distribution of TP concentrations in set B, as expected for a spatially representative dataset (electronic supplementary material, figure S1).

Regional estimates for TP (R-TP) were calculated using distance-weighted interpolation (DWI). DWI was preferred over kriging since DWI allows weighting of observations depending on their proximity to the position of interest (Babak & Deutsch 2009). Moreover, in contrast to kriging, we did not intend to estimate L-TP from nearest neighbours. Instead, R-TP should reflect a regionally averaged parameter, integrating TP in space around a given geographical location. We first generated a regular grid (0.2 × 0.2 degree) of lake TP concentrations across Fennoscandia by spatial interpolation of ln(TP) from the selected lakes in set B (function interp in the akima package R Development Core Team (2009)). R-TP were then calculated for every lake in set A from all grid points falling within a critical distance (D_c; 50 ≤ D_c ≤ 600 km) around this lake using DWI with (1 − d_s)² as weight, where d_s is the distance between a given lake in set A and a given grid point, standardized by D_c (0 ≤ d_s ≤ 1). Preliminary analysis showed that R-TP, calculated with the squared distance as weights, gave best results as a predictor of G among a number of possible distance weights tested (1/d_s, 1 − d_s, 1 − ln(d_s), no weights). With increasing D_c, the number of grid points contributing to the estimated R-TP increases, hence the precision of R-TP increases with increasing D_c. In order to exclude this sample-size effect when comparing different D_c, we repeatedly sampled 50 grid points with replacement from all points falling within D_c (n = 500). For each D_c and each lake in set A, this resulted in 100 estimates of R-TP. For each D_c, we performed 100 linear regressions of the form G = a + b (R-TP), giving a robust estimate of the goodness of fit (r²) for a given D_c (electronic supplementary material, figure S2). L-TP and R-TP are significantly correlated (Spearman's ρ = 0.54, p < 0.01), but L-TP contains a high degree of site-to-site variation (electronic supplementary material, figure S3).

To test for a potential effect of environmental heterogeneity, we calculated the spatial variability of TP based on the ln(TP) grid outlined above. For all locations in set A, environmental variability was calculated as the standard deviation of ln(TP), applying a critical distance of 150 km.

Regional temperature estimates were calculated by the same distance weighing as outlined above for R-TP (D_c = 150 km). Regional temperature estimates were based on a 0.5 × 0.5 degree grid of summer air temperature averaged over the period 1975–2000 (Mitchell & Jones 2005).

Lake density was taken from the global lakes and wetland database (GLWDB; Lehner & Döll (2004)), which comprises all lakes with a surface area ≥0.1 km². For every lake with phytoplankton data (set A), we selected all lakes from the GLWDB falling within a critical distance around this lake (D_c = 150 km). Lake density was calculated as the weighted sum of the log-transformed lake surface areas within D_c, applying the same distance weighing as outlined above. We used the weighted sum of log-transformed surface areas instead of merely the number of lakes, since the total number of phytoplankton taxa present in a system has been found to scale with the log-transformed surface area in both lakes and marine systems (Smith et al. 2005).

(e). Spatial autocorrelation and PCNM eigenvector maps

Patterns of spatial autocorrelation in G and other variables were illustrated using Moran's I, a measure of spatial autocorrelation (e.g. Fortin & Dale (2005)) calculated for discrete distance classes using the function correlog in R-package ncf (Bjørnstad et al. 1999). Confidence intervals were obtained by 100 bootstrap samples per distance class (sampling without replacement).

We generated principal coordinates of neighbour matrices (PCNM) for the geographical locations of lakes in set A in order to estimate the degree of variation in G that can be attributed to regular spatial patterns (Dray et al. 2006). PCNM eigenvectors were calculated using the PCNM package in R. PCNM variables significantly explaining spatial structure in the response variable were identified by forward selection using function forward.sel from R-package packfor Monti & Legendre (2009) (packages PCNM and packfor are available at https://r-forge.r-project.org/R/?group_id=195). All statistical analyses were done in R (R Development Core Team 2009).

3. Results

(a). Spatial patterns of phytoplankton genus richness and major environmental parameters in Fennoscandia

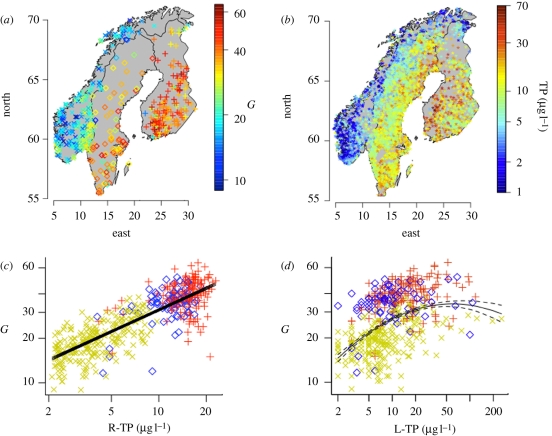
Phytoplankton alpha-diversity, measured as average genus richness (G) per lake, shows a longitudinal gradient across Fennoscandia, with a minimum in south-western Norway, and a maximum in southern Finland (figure 1a). TP concentrations from a representative lake survey in the area (figure 1b) show a similar large-scale pattern, which becomes particularly evident when plotting G and TP from the representative dataset along the longitudinal gradient (electronic supplementary material, figure S3). Longitudinal gradients are also seen in summer air temperature and lake density (electronic supplementary material, figure S3).

Figure 1.

(a,b) Regional patterns of (a) phytoplankton genus richness and (b) concentrations of total phosphorus. Note that the data shown in (a,b) comes from two different sampling programmes. Dots represent locations of lakes where samples were taken. Colour codes give (a) mean genus richness per lake G, and (b) total phosphorus concentration. (c,d) Genus richness (G) versus R-TP; r² = 0.69 (c) and (d) L-TP; r² = 0.23. G and TP log-transformed. See table 1 for summary statistics. Cross symbol, Norway; diamond symbol, Sweden; and plus symbol, Finland.

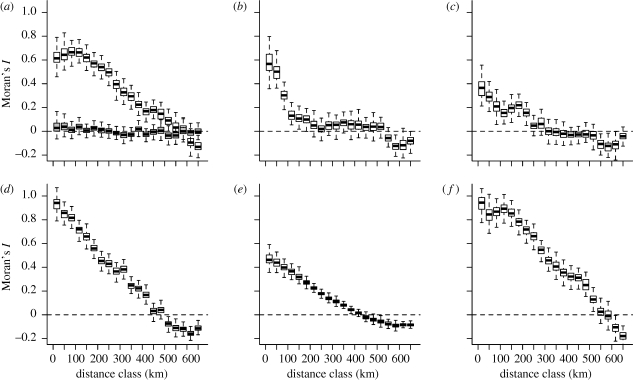
Spatial correlograms show that G varies at relatively broad scales with Moran's I being positive for distance classes up to 500 km, while other environmental parameters, including L-TP, lake mean depth and TP concentrations from the representative lake survey are all self-similar at smaller scales (figure 2). Only average summer air temperatures, taken from a 0.5 × 0.5 degree grid, as well as regionally averaged R-TP concentrations, are self-similar at comparable scales (figure 2).

Figure 2.

Spatial autocorrelation for G and a number of environmental parameters. Shown is Moran's I for discrete distance classes (x-axis, in km). (a–c) Variables sampled at the level of individual lakes in set A. (a) Moran's I for G plus for the residuals of a regression predicting G from regional parameters (grey). (b) L-TP; (c) log(mean depth). (d) Air temperature (0.5 × 0.5 degree grid), (e) TP from a representative lake survey (set B) and (f) regionally averaged TP (=R-TP).

(b). Predicting genus richness

G shows a weak, hump-shaped correlation with the local phosphorus concentrations (L-TP), i.e. with the TP concentration measured in the same lake where the phytoplankton sample was taken from (r² = 0.19 and 0.23 for the linear and quadratic model; figure 1c and table 1). When TP is estimated on a regional level, based on the representative lake survey (set B, figure 1b), G shows a strong, consistently linear relationship with those R-TP (figure 1d), even though the lakes used for estimating R-TP come from a completely independent dataset. When R-TP is calculated for a range of spatial scales, R-TP estimated within a radius of 100–200 km around a given lake gives the best fit (electronic supplementary material, figure S2) and explains 69 per cent of phytoplankton G in Fennoscandia (table 1). In contrast to G, phytoplankton biovolume is best predicted by L-TP (electronic supplementary material, figure S4), supporting the general assumption that L-TP is the major determinant of phytoplankton biomass in lakes (e.g. Vollenweider (1989)).

Table 1.

Performance of local and regional factors as predictors of G. (Given are the t-values together with the adjusted r² for linear regressions predicting G as functions of local and/or regional parameters. R-TP, regional temperature (Tr) and lake density (LD) correspond to a critical distance of 150 km. For L-TP and pH, the squared terms (L-TP², pH²) were included as well. L-TP, surface area (SA) and mean depth (MD) all were ln-transformed in the analysis. Alt, altitude. Terms in the full model (last line) were selected using the Bayesian information criterion Johnson & Omland (2004), while no selection was applied in the other models. All models and terms were highly significant (p < 0.001) except for LD in model 4 (p = 0.02), pH² in model 7 (p = 0.001) as well as log(mean depth) in model 8 (p = 0.04). n = 477. Detailed statistics for the full model are given in electronic supplementary material, table S1, together with a comparison of the relative importance of all predictors.)

	regional			local
	R-TP	Tr	LD	L-TP	L-TP2	pH	pH2	SA	MD	Alt	adj r2
(1)	32.7										0.69
(2)		21									0.47
(3)			14								0.30
(4)	18	4.6	2.9								0.71
(5)				10.7							0.19
(6)				7.5	−4.9						0.23
(7)				4.4	−3.6	3.5	−3.3	10.6	−11.5	−4.5	0.50
(8)	14	2.6	3.6	n.s.	n.s.	4.3	−4.2	n.s.	−2.8	−3.5	0.73

Regional estimates of summer air temperature and lake density (electronic supplementary material, figure S3) both show significant relationships with G, but the correlations are weaker than for R-TP (r² = 0.47 and 0.30, respectively; table 1). A combined model of all regional variables explains 71 per cent of the variation in G (table 1). These regional variables capture apparently the bulk of the spatial structure seen in G, since there is very low autocorrelation in the residuals of this regression model (figure 2a). Further regional environmental parameters (precipitation, alkalinity, spatial variability of TP) gave only marginal correlations with G (not shown). Finally, using a stepwise selection of variables, we built a least parsimonious model from all available regional and local variables. This full model explained 73 per cent of the total variation in G, with R-TP remaining the outstanding predictor (electronic supplementary material, table S1).

We used PCNM eigenvectors (§2e) to quantify the amount of variation in G, that can be explained by spatial structure. Forward selection gave a set of 24 PCNM eigenvectors. Most of them were of low order, i.e. represented spatial structure at broader scales (Dray et al. 2006). These eigenvectors explained in total 74 per cent of the variation in G. Hence, the three regional predictors identified above (R-TP, summer temperature and lake density) explained almost all spatial pattern seen in G (71%).

(c). Patterns of beta- and gamma-diversity

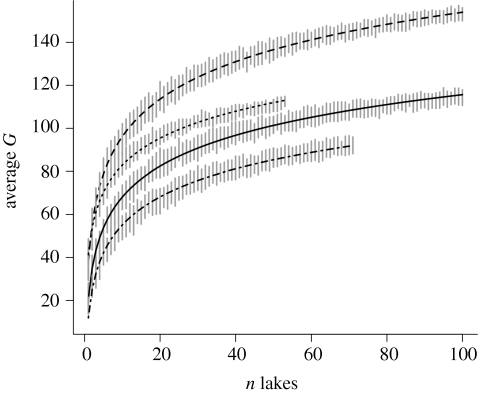
We estimated genus richness accumulation curves in four regions of southern Fennoscandia from up to 100 randomly sampled lakes within each region (figure 3). The division into regions followed natural borders (major mountain ridges or barriers such as the Baltic Sea) and was constrained by availability of data (highest in southern Fennoscandia). This estimate of gamma-diversity shows a longitudinal gradient, with the smallest pool size seen in southwestern Norway, and largest pools in southern Finland. The pattern indicates that the longitudinal gradient seen in alpha-diversity (G, above) is mirrored by a longitudinal gradient in species pool size.

Figure 3.

Average number of genera (from ×50 resampling) found in a given number of lakes in four different regions in southern Fennoscandia (less than 63° north). Vertical bars give ×2 s.d. The curves were fitted to the model G = a + b × ln(n lakes). The analysis was constrained by the total number of lakes with phytoplankton data in the corresponding regions. Dashed line, south Finland; dotted line, south Sweden; solid line, southeast Norway; dashed dotted line, southwest Norway.

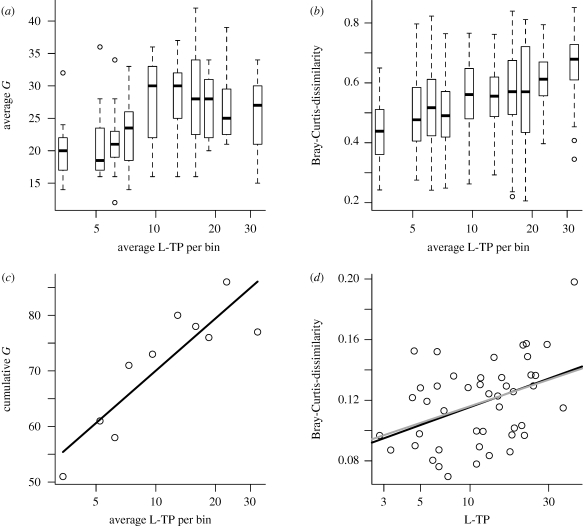
We have shown earlier that temporal community turnover increases strongly with productivity (L-TP Ptacnik et al. (2008)). We test here whether this implies an increase in spatial turnover (i.e. beta-diversity) with L-TP, since a positive relationship between productivity and beta-diversity could explain a positive relationship between regional productivity and gamma-diversity (Steiner & Leibold 2004). In order not to confound the effect of productivity-driven turnover with those of spatial scale or time interval between samplings, we performed the analysis within one spatially constrained area (southeast Norway), where sufficient data was available from one season to make the analysis meaningful. We analysed the role of productivity for spatial turnover in a bootstrapped multiple regression analysis where compositional dissimilarity among random pairs of lakes was predicted from their average L-TP (§2b). The difference in L-TP among lake pairs (delta L-TP) was considered as covariable, together with spatial and temporal distance. The analysis revealed highly significant effects of both average and delta L-TP (table 2), pointing at a twofold effect of productivity on turnover. The delta L-TP effect confirms earlier studies showing that communities in productive lakes are different from those in unproductive lakes (e.g. Ptacnik et al. (2009)), while the effect of average L-TP implies that communities become increasingly dissimilar as L-TP increases. Moreover, in spite of the limited spatial extension, the analysis revealed a significant effect of space, but no effect for time interval between samplings (but note that turnover within lakes was excluded from this analysis). Figure 4 illustrates how temporal and spatial turnover translate into a scale-dependent productivity–diversity relationship among lakes of southeast Norway.

Table 2.

Coefficients (+s.d.) from a multiple linear regression predicting spatial turnover (=beta-diversity) among random lake pairs in southeast Norway. (Coefficients and standard deviation were estimated from 1000 bootstrap replications. Significance levels refer to the probability of a coefficient being either positive or negative. r² = 0.39. Data from southeast Norway. Note the limited temporal (July–September 1988) and spatial extension (median and maximum distance 84 and 225 km) of this subset.)

intercept	average L-TP ln(µg l−1)	delta L-TP ln(µg l−1)	spatial distance sqrt (km)	time interval sqrt (days)
0.28 (0.04)	0.080 (0.012)	0.093 (0.009)	0.007 (0.001)	0.001 (0.002)
p < 0.001	p < 0.001	p < 0.001	p = 0.058	p = 0.24

Figure 4.

(a) Alpha-, (b) beta- and (c) gamma-diversity estimated for distinct L-TP bands in lakes of southeast Norway (L-TP in µg l⁻¹). A linear fit is shown in (c) (cumulative G = 39 + 14 ln(L-TP); r² = 0.75, p < 0.001). (d) Temporal (=daily) community turnover. Every dot represents one lake in 1988 in southeast Norway. The black line gives a linear fit (T = 0.08 + 0.017 ln(L-TP); p = 0.005, r² = 0.15), which is very similar to the trend seen in the pooled data of Fennoscandia (grey line; Ptacnik et al. (2008)).

4. Discussion

There is a risk of overestimating the significance of spatially correlated predictors in regression analysis of spatially correlated data (Lennon 2000). In our analysis, the regional predictors (R-TP, air temperature and lake density) resolve virtually all spatial variation in phytoplankton genus richness. Since residuals have negligible autocorrelation (figure 2a), this analysis should not be biased as pointed out by Diniz–Filho et al. (2003). It should also be noted that the problems formulated in Lennon (2000) apply especially to regional data sampled from continuous systems, where range size of the organisms may exceed the spatial resolution of the grid. In our study, every grid point represents a distinct system (a lake), implying that spatial autocorrelation in G does not reflect pseudo-replication in space but spatial processes that affect community dynamics at the regional scale.

(a). Local versus regional control of phytoplankton diversity

Phytoplankton taxon richness can apparently not be predicted from the local environment alone, as seen from the patterns in Fennoscandia. On the contrary, G exhibited a high degree of spatial autocorrelation and was strongly correlated with regional patterns of TP and temperature. Both parameters are linked to primary production. The data thus point at the existence of regional phytoplankton species pools, which can be predicted from regionally averaged productivity.

(b). Scale-dependent productivity–diversity relationships

G shows a weak, unimodal relationship with L-TP, but a strong linear one with regional productivity (R-TP, temperature). Such scale-dependent productivity–diversity relationships are known from communities of higher organisms (Chase & Leibold 2002; Steiner & Leibold 2004), but are novel in the reign of microbes. Especially, studies on pond communities have repeatedly found unimodal productivity–diversity relationships on the local level, while monotonic positive correlations were found on the landscape level (Mittelbach et al. 2001; Chase & Leibold 2002; Chase & Ryberg 2004).

Scale-dependent productivity–diversity relationships require a positive correlation between productivity and dissimilarity among sites. Chase & Leibold (2002) have identified three possible mechanisms leading to such scale-dependent relationships. (H1) A positive correlation between mean productivity and environmental variability; (H2) increasing number of alternative stable states with increasing productivity; or (H3) compositional turnover among sites increases with increasing productivity. There seems to be little support for H1 and H2. Variability in geography and geology is low in central Finland, where highest G was observed, while the topographical variability of especially southern Norway is rather high. In agreement with this, spatial variability of TP tends to decrease towards the east, as seen by a weak albeit significant negative correlation between the standard deviation of regional averages of TP and longitude (Spearman's ρ = −0.25, p < 0.01). Likewise, while lakes may exhibit alternative stable states at the system level (e.g. dominance of macrophytes versus phytoplankton; Scheffer (1990)), we are unaware of well-documented alternative equilibria within the phytoplankton. On the contrary, there is considerable support that chaotic oscillations are a common feature of microbial communities even in the absence of environmental fluctuations (e.g. Huisman & Weissing (1999)). With regard to H3, we have shown earlier that temporal community turnover increases strongly with productivity (Ptacnik et al. 2008). The high temporal turnover seen in productive lakes implies high spatial community turnover among productive lakes (figure 4). As a result, the total number of taxa present within an area at a given time increases with the average productivity of the lakes in the area.

Since phytoplankton biovolume in a particular lake is mainly determined by L-TP (electronic supplementary material, figure S4), the total amount of propagules dispersing from a lake will always be a function of its productivity (times surface area). Thus, by affecting both diversity as well as quantity of propagules, productivity has a twofold effect on dispersal.

(c). Metacommunity scaling

According to our results, phytoplankton metacommunities integrate richness of local communities across environmental gradients on the scale of several 100s of kilometres (figure 2). Little is known about quantitative dispersal rates in microbes, but existing data indicate that they can be highly variable (Jenkins et al. 2007; Chrisostomou et al. 2009). Experiments with zooplankton have shown that insects and water birds may be important in long-range dispersal of aquatic invertebrates (greater than 10 km; Havel & Shurin (2004)). Conversely, Jenkins & Underwood (1998) have shown that transport by wind and rain is rather inefficient for spreading rotifer propagules. Moreover, in contrast to intuition, a compilation of available data revealed that cell size is only weakly correlated with dispersal rate in unicellular organisms (Jenkins et al. 2007). The scaling identified here must therefore be regarded as an average dispersal range, emerging from a diverse group of unicellular organisms.

(d). Instrinsic versus extrinsic drivers of plankton diversity

Numerous empirical and theoretical studies have addressed the question how species-rich phytoplankton communities can persist in the presence of only a few limiting resources (‘paradox of the plankton’ (Hutchinson 1961; Huisman & Weissing 1999)). In the light of the data presented here, it appears surprising how little attention has been given to extrinsic factors (dispersal) as opposed to pure intrinsic factors (system dynamics). Our study suggests that the high phytoplankton diversity observed in natural systems cannot be explained solely by local dynamics. Rather, species richness in a given lake is obviously strongly linked to metacommunity dynamics and dispersal from adjacent habitats. Predictive models of phytoplankton diversity may profit from taking regional attributes such as those reported here and elsewhere (e.g. Vyverman et al. (2007)) into account.

The detection of regional scale patterns will always depend upon the strength of the underlying environmental gradient(s). If we based our analysis solely on data from Finland, the relationship between G and R-TP could hardly be detected, since regional-level productivity is high throughout Finland (figure 1b,c). Likewise, in contrast to Vyverman et al. (2007), we found only a weak relationship with lake density, presumably because lake density is generally high across Fennoscandia (electronic supplementary material, figure S5). It is therefore important to consider the length of environmental gradients when trying to evaluate the existence of regional species pools.

Prevailing regional control of species richness has previously been reported for various higher organisms in both terrestrial and aquatic environments (examples in Cornell & Karlson (1997). From that, Cornell & Karlson (1997) concluded that local dynamics have rather secondary effects on local community assemblage. However, there is little doubt that local dynamics are very important in shaping plankton communities. For example, Shurin Shurin (2000) showed experimentally that community assemblage in pond zooplankton is dominated by local dynamics. At the same time, Shurin et al. (2000) found a linear relationship between regional and local richness in lake zooplankton. They concluded that zooplankton is ecologically saturated at the local level with regard to the respective regional species pool, while regional pools may be historically unsaturated. In agreement with Shurin et al. (2000), local sorting is also indicated in our data by the constrained distribution of genera with respect to L-TP (figure 4c). Likewise, Ptacnik et al. (2009) found that local community composition (but not richness) correlates strongly with L-TP in lakes of Norway. From that, it appears that regional control of richness does not contradict strong local sorting. Rather, local richness reflects the dynamic local colonization–extinction equilibrium. With increasing dispersal (i.e. increasing size of regional species pools), a balance is reached at a higher level, but ultimately, it is the local dynamics that select taxa from the regional pool.

Effective local sorting results in a high correspondence between the local environment and community composition, making phytoplankton a widely used indicator for water quality monitoring (see references in Ptacnik et al. (2009)). However, if the local environment has a stronger effect on local composition than on local richness, this has important implications to what extent regional pools can be recognized by spatial analysis of community composition. In this respect, it is worthwhile noticing that evidence for the existence of regional species pools in microalgae has come so far mainly from studies analysing richness patterns (this study; Telford et al. 2006; Vyverman et al. 2007).

Strong local sorting should not be mistaken as an indication for ecological saturation. Rather, the existence of metacommunities in phytoplankton lends much support to empirical studies linking phytoplankton resource use and community stability to the diversity of local communities (Ptacnik et al. 2008; Striebel et al. 2009), since local diversity is subject to both local and regional processes. In other words, the necessary diversity for maintaining ecosystem processes cannot be supported by the local species pool alone (this study; Telford et al. 2006; Vyverman et al. 2007). Regional factors affecting metacommunity dynamics (e.g. climate, connectivity, regional productivity) might therefore have profound effects on a system's susceptibility to pollution, etc. Our results indicate that the regional perspective holds promise for a better understanding of plankton dynamics. Future studies should test whether the frequency of events such as harmful algal blooms are related to regional species pool size, and whether the adaptability of systems to environmental change can be linked to the size and dynamics of regional species pools.

Our findings add to the emerging view that general spatial scaling rules apply for all organisms, including microbes (Green & Bohannan 2006). The frequent claim that dispersal limitation does not affect microbial diversity owing to their high dispersal rates apparently oversees the equally high extinction rates in microbial communities. Fast dispersal of micro-organisms may certainly explain the cosmopolitan distribution of numerous protist morpho-species. However, on the local level, maintenance of high diversity in microbial communities also depends on having species-rich habitats within proximate distance.