Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Jun 21.
Published in final edited form as: Phys Med Biol. 2010 May 28;55(12):3535–3544. doi: 10.1088/0031-9155/55/12/017

The Impact of 3D Volume-of-Interest Definition on Accuracy and Precision of Activity Estimation in Quantitative SPECT and Planar Processing Methods

Bin He 1, Eric C Frey 2
PMCID: PMC2992950  NIHMSID: NIHMS253348  PMID: 20508323

Abstract

Accurate and precise estimation of organ activities is essential for treatment planning in targeted radionuclide therapy. We have previously evaluated the impact of processing methodology, statistical noise, and variability in activity distribution and anatomy on the accuracy and precision of organ activity estimates obtained with quantitative SPECT (QSPECT), and planar (QPlanar) processing. Another important effect impacting the accuracy and precision of organ activity estimates is accuracy of and variability in the definition of organ regions of interest (ROI) or volumes of interest (VOI). The goal of this work was thus to systematically study the effects of VOI definition on the reliability of activity estimates. To this end, we performed Monte Carlo simulation studies using randomly perturbed and shifted VOIs to assess the impact on organ activity estimations. The 3D NCAT phantom was used with activities that modeled clinically observed 111In ibritumomab tiuxetan distributions. In order to study the errors resulting from misdefinitions due to manual segmentation errors, VOIs of the liver and left kidney were first manually defined. Each control point was then randomly perturbed to one of the nearest or next-nearest voxels in the same transaxial plane in three ways: with no, inward or outward directional bias, resulting in random perturbation, erosion or dilation, respectively of the VOIs. In order to study the errors resulting from the misregistration of VOIs, as would happen, e.g., in the case where the VOIs were defined using a misregistered anatomical image, the reconstructed SPECT images or projections were shifted by amounts ranging from −1 to 1 voxels in increments of 0.1 voxels in both the transaxial and axial directions. The activity estimates from the shifted reconstructions or projections were compared to those from the originals, and average errors were computed for the QSPECT and QPlanar methods, respectively. For misregistration, errors in organ activity estimations were linear in the shift for both the QSPECT and QPlanar methods. QPlanar was less sensitive to object definition perturbations than QSPECT, especially for dilation and erosion cases. Up to one voxel misregistration or misdefinition resulted in up to 8% error in organ activity estimates, with the largest errors for small or low-uptake organs. Both types of VOI definition errors produced larger errors in activity estimates for a small and low uptake organ (i.e. −7.5% to 5.3% for left kidney) than for a large and high uptake organ (i.e. −2.9% to 2.1% for liver). We observed that misregistration generally had larger effects than misdefinition, with errors ranging from −16% to 8.5%. The different imaging methods evaluated responded differently to the errors from misregistration and misdefinition. We found that QSPECT was more sensitive to misdefinition errors, but less sensitive to misregistration errors, as compared to the QPlanar method. Thus, sensitivity to VOI definition errors should be an important criterion in evaluating quantitative imaging methods.

1. INTRODUCTIONS

Accurate and precise estimation of organ activity is essential for targeted radionuclide therapy treatment planning (Siegel et al., 1984; Clarke et al., 1999; Koral et al., 2002; Delpon et al., 2003; Wong et al., 2006). Since there is no clinically practical direct measurement method available, noninvasive quantitative imaging techniques are widely used. A number of quantitative imaging methods for in vivo organ activity estimation have been developed and used. The conventional planar (CPlanar) imaging method is such a method and variants of it are widely used in many clinical trails. This method is based on geometric mean attenuation compensation using conjugate view scintillation camera whole body scans (Thomas et al., 1976). However, there are limitations in this method that make accurate and precise quantification very difficult. These include overlap of an organ’s projections with those of other organs and background regions, scatter and attenuation in the patient, scatter and septal penetration in the collimator, partial volume effects, and statistical noise (Norrgren et al., 2003). We have previously developed two processing methods, quantitative SPECT (QSPECT) and planar (QPlanar), which provide comprehensive compensation for all these degrading effects (He et al., 2005; He and Frey, 2006). We have evaluated them in terms of accuracy and noise precision of organ activity estimates using experimental and simulated phantoms. We further evaluated these methods in terms of the impact of statistical noise (He et al., 2008) and variation in activity distribution and anatomy on the accuracy of residence time estimates (He et al., 2009).

However, the accuracy and precision of these methods also depends on the accuracy of and variability in the definition of the 2D regions of interest (ROIs), for CPlanar, or 3D volumes of interest (VOIs), QSPECT and QPlanar, used in the quantification process. Limited studies have been performed investigating the effect of VOI misdefinition on the accuracy and precision of organ activity estimates. Most of the studies were focused on the tumor VOI definitions by manual, semi-auto, or auto thresholding in PET (Erdi et al., 1997; Daisne et al., 2003; Biehl et al., 2006; Jentzen et al., 2007). The goal of this work was to systematically study the effects of VOI definition errors on the accuracy and precision of organ activity estimates. We assumed that the VOIs were defined manually using a combination of SPECT and CT images. Two types of VOI errors were evaluated. The first type, termed misdefinition, is due to errors in the delineation of organ VOIs on the CT or SPECT images. A second type is due to the misregistration of SPECT and CT images. In this case, we assume that the VOIs were first defined on anatomical images (e.g., a CT image) and then applied to reconstructed SPECT images for activity estimation. Thus, any misregistration of the CT and SPECT images results in misregistration of the VOIs with the true organ VOI.

2. METHODS

A. Digital Phantom and Simulation

The 3D NCAT phantom (Segars, 2001) was used to provide a realistic and flexible model of human anatomy and physiology. The concentrations of activities in the major organs (heart, lungs, liver, kidneys, spleen, bone marrow, and blood vessels) were determined based on average organ uptakes from 6 clinical 111In ibritumomab tiuxetan studies. These concentrations were estimated using SPECT/CT scans 24 hours after injection (Frey et al., 2006). The uptake in the lungs was non-uniform since activity in airways was set to zero.

A modified version of the SimSET/Photon History Generator Monte Carlo code (Harrison et al., 1993) combined with an angular response function (ARF) based simulation of the interactions in the collimator and detector (Song et al., 2005) was used to simulate the projection data. The ARF method is based on full simulations of the collimator-detector point response function obtained using MCNP (Briesmeister, 1997) and has been previously validated (Du et al., 2002; He et al., 2005; Wang et al., 2002).

The simulations were performed using parameters appropriate for a GE Discovery VH/Hawkeye SPECT/CT system with a 2.54 cm thick crystal and an MEGP collimator. The intrinsic resolution of the gamma camera was assumed to be 0.4 cm. Both 111In photopeaks (171 keV and 245 keV) were simulated with the appropriate abundances. Low-noise projection images were generated in 128 transaxial and 170 axial projection bins at 120 views over 360° using a 0.442 cm projection bin size. No additional Poisson noise was added to the simulated low-noise projections as the focus of this work was to study the effects of definition.

B. Quantitative Imaging Methods

The QSPECT reconstructions were performed using the iterative ordered-subsets expectation-maximization (OS-EM) algorithm (Hudson and Larkin, 1994). Attenuation, scatter, and the collimator-detector response function (CDRF) were modeled during the iterative process using a rotation-based projector (Frey et al., 1993; Zeng et al., 1994). The true abundance weighted average of the phantom attenuation maps for the 171 and 245 keV photons emitted by 111In was used in the reconstruction. Scatter was modeled using the effective source scatter estimation (ESSE) method (Frey and Tsui, 1996). The CDRF was estimated by Monte Carlo simulation of point sources at various distances from the face of the collimator including propagation of photons in the collimator and detector. A detailed description of the QSPECT method can be found in (He et al., 2005).

To address some of the practical limitations of the QSPECT method (i.e., long scan and processing times, and limited field of view) and theoretical limitations of CPlanar (i.e., limited applicability of geometric mean and overlap problem) methods, we have previously developed the QPlanar processing method (He and Frey, 2006). This method uses an iterative ML-EM algorithm to estimate the organ activities directly from two conjugate view planar projections using 3D organ VOIs and the following estimation procedure. In the estimation procedure, the activity inside each organ’s VOI is assumed to be uniform. The background is modeled as one (in this work) or more VOIs, each having uniform activity concentration distributions. The projection of each separate organ VOI (normalized to have unit total intensity) is estimated using a model-based projector that includes the same models of the image degrading factors as used in the QSPECT reconstructions (i.e., it modeled attenuation, scatter, and the full collimator-detector response). The measured projection is assumed to be a linear combination of these organ VOI projections. Since the noise in the measured projections is Poisson distributed, we used the Poisson ML-EM algorithm to estimate the scale factors for each VOI’s projections; these scale factors then represent the total activity in that organ. A major difference between this method and 3D SPECT reconstruction is that only a small number of parameters (i.e., the number of VOIs) are estimated, and thus they can be estimated quite effectively from only 2 projection views. More details about the QPlanar method can be found in (He and Frey, 2006).

C. Misdefinition Study

In the clinical studies, VOIs are often defined manually using a stack of polygonal ROIs drawn on each slice. The process of defining the vertices of these ROIs is imprecise and can affect the accuracy of organ activity quantitation. The nature and size of these errors depends on the skill, experience and training of the operator. We investigated the case where the operator had no bias, bias toward larger VOIs, or bias toward smaller VOIs; in all of these cases we modeled the errors at each vertex as random variables, as described below.

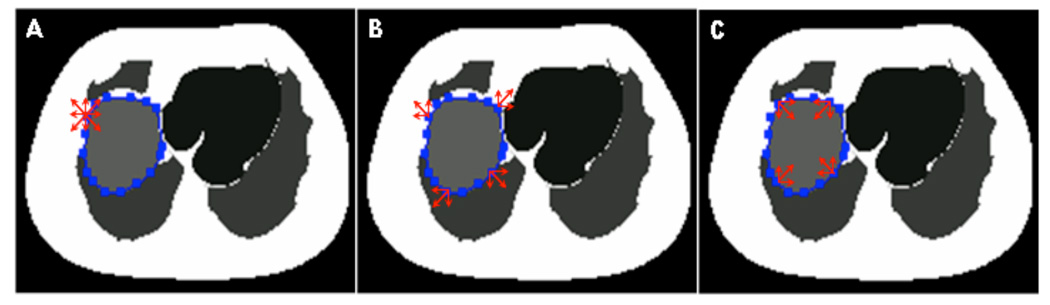
In order to study the impact of these types of errors on the activity estimates, we simulated random perturbations of the VOIs as follows. VOIs of the liver (representing a large organ) and the left kidney (representing a small organ) were first manually defined using the phantom images to try to delineate the organ as exactly as possible. As illustrated in Figure 1, each VOI was defined as a stack of 2D ROIs on each slice. Each 2D ROI was a polygon with all the control points (vertices) manually defined by operators. We did not use the exact definitions of the two organ VOIs from the phantom configuration because we wanted to simulate the manual process used clinically. To study misdefinition errors, we randomly moved each control point defining the VOI on each slice to one of the nearest neighbor voxels in three different ways to investigate three models of VOI definition errors, as shown in the Figure 1. In the first strategy (referred to as Random), the movement direction was unbiased: each control point had a one fourth chance of remaining stationary, a one eighth chance of being be moved up, down, left or right 1 voxel, and a one sixteenth chance of being moved northeast, northwest, southeast or southwest. These probabilities model a 2D normal distribution with zero mean and a standard deviation of 0.85 voxels. In the second strategy (referred to as Dilation), each control point also had a one fourth chance of remaining stationary, and a one fourth chance of being moved 1 voxel in one of the three directions toward the outside of the VOI. This simulated an operator biased toward defining larger VOIs. The third strategy (referred to as Erosion) is the opposite of the second strategy, and simulated an operator who tends to define smaller VOIs.

Figure 1.

Figure 1

Open in a new tab

Three different misdefinition cases: A. Random, each control point can randomly move to 8 directions to the nearest or next-nearest neighbor; B. Dilation, each control point only randomly moves to one of the four outward directions; C. Erosion, each control point only randomly moves to one of the four inward directions.

We repeated these processes to generate 20 realizations of the randomly perturbed VOIs for each strategy (Random, Dilation and Erosion) and organ (liver and left kidney). These perturbed VOIs were then used in the quantification process for both the QSPECT and QPlanar methods. For QSPECT, organ activity was computed by summing voxel values inside the perturbed VOI; for QPlanar, the perturbed VOI was used in the QPlanar estimation process. The mean and standard deviation of percent differences in activity estimates (compared to the estimates using original VOIs) were then calculated for all three strategies and both organs.

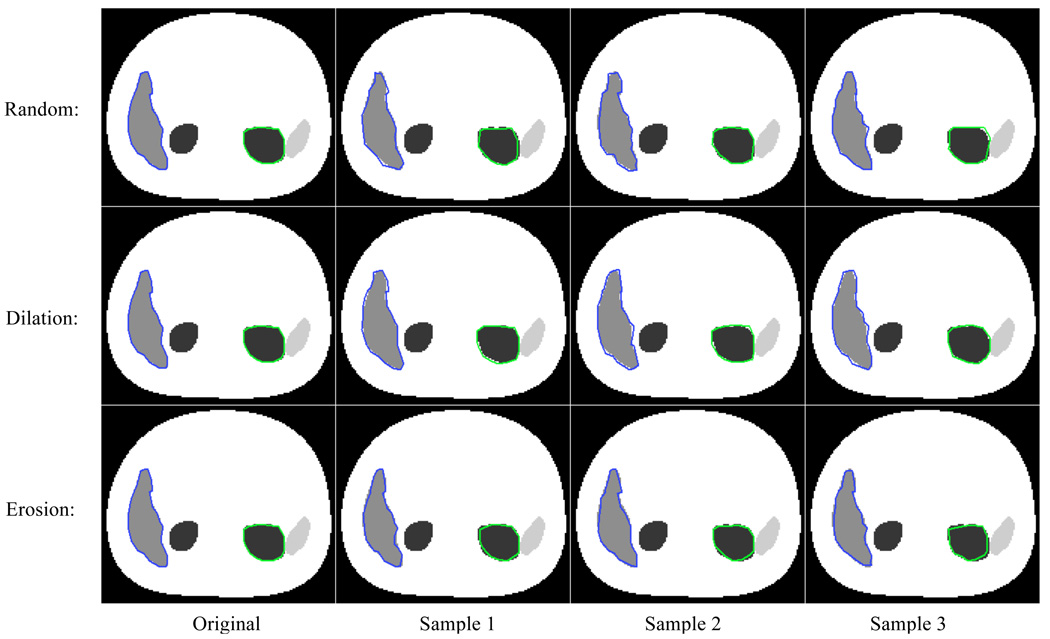
Figure 2 shows a few sample slices of the perturbed VOIs along with the original manually defined VOIs.

Figure 2.

Figure 2

Open in a new tab

Sample slices of perturbed VOIs. The first column is the original manually defined VOIs. The second to fourth columns are three samples of perturbed VOIs for three different misdefinition strategies: random (first row), dilation (second row), and erosion (third row).

D. Misregistration Study

Since SPECT images provide relatively poor anatomical information, one common way of defining 3D VOIs is to define them using registered anatomical images (e.g., CT/MRI) and then to transfer the VOIs to the functional images (e.g., SPECT/PET) to estimate organ activities. Thus, if the functional and anatomical images are misregistered, this can introduce errors in organ activity estimates. In order to study this type of VOI definition error, for the QSPECT method, we shifted the reconstructed SPECT images from −1 to 1 voxels (0.1 voxels per step) in three directions: the left or right lateral (x), anterior or posterior (y), and two axial (z) directions. The original (unshifted) VOIs were used as the reference to calculate the errors introduced by the shifting. For the QPlanar method, we shifted the anterior and posterior planar images from −1 to 1 voxel (0.1 voxel increments) in both left-right lateral (x) and inferior-superior (z) directions. Then we used the non-shifted templates calculated using the original VOIs to estimate organ activities from the shifted projections. For the anterior-posterior (y) direction, we shifted the attenuation and region maps from −1 to 1 voxels and used those maps to calculate the misregistered templates. This models the case where the VOIs are defined in a CT image which is misregistered with the planar images in the y direction (i.e. the table moved up or down between CT and planar scans). This results in errors in the templates due the distance dependence of the collimator-detector response. The percent differences in activity estimates (compared to the estimates using original VOIs) as a function of the shifts were then calculated for all organs.

3. RESULTS

Table 1 shows the relative errors and standard deviation of errors in organ activity estimates calculated from 20 sets of randomly perturbed VOIs for all three perturbation strategies and for both the liver and left kidney. For all three of the perturbation strategies, but especially for Dilation and Erosion, QPlanar was less sensitive to the misdefinition of VOIs than QSPECT. This was probably because the misdefinition of the VOI affects the organ projection used in the ML-EM estimation. The estimation algorithm adjusts the scale factor (i.e., the organ activity) to match the projection of the misdefined organ to the measured projection data. Since the size of the misdefinitions was small, the shape change of the organ projections was small, and there was thus little change in the estimated scale factor. On the other hand, for QSPECT, the misdefinition of VOIs directly influenced the number of voxels counted inside the organs, and thus directly affected the activity estimate. The standard deviations of the percent errors calculated from 20 sets of random perturbations were small compared to the percent errors. This indicates that the errors were dependent on the probability model for the perturbations, but relatively insensitive to the details of the perturbations. As expected, for the small organs like the kidneys, misdefinition had a larger impact than for larger organs such as liver, especially for the QSPECT method.

Table 1.

The percent error and standard deviation of error in organ activity estimates calculated from 20 sets of random perturbed VOIs

Methods \ Organs Liver Left Kidney
Random QSPECT −0.33±0.05 % −1.24±0.38 %
QPlanar 0.27±0.13 % 0.42±0.06 %
Dilation QSPECT 2.06±0.05 % 5.27±0.15 %
QPlanar −0.50±0.09 % 0.08±0.04 %
Erosion QSPECT −2.85±0.06 % −7.52±0.19 %
QPlanar 0.80±0.09 % 0.76±0.04 %
Open in a new tab

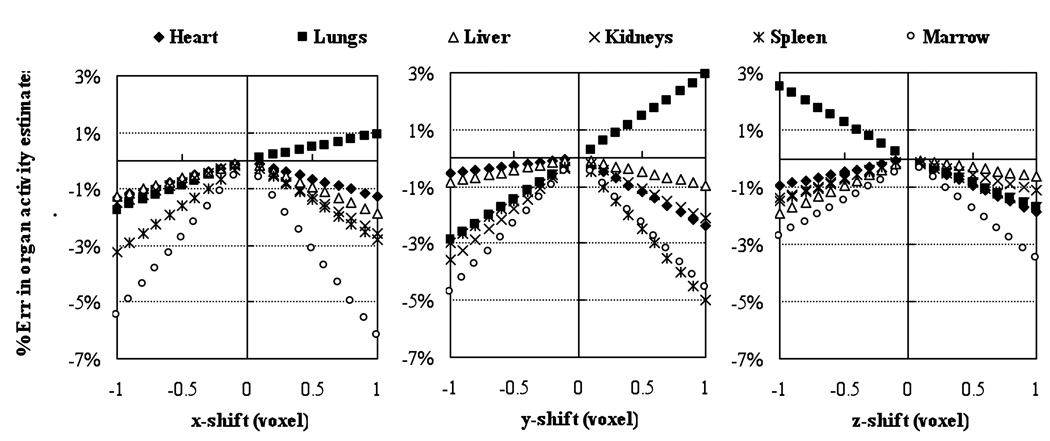
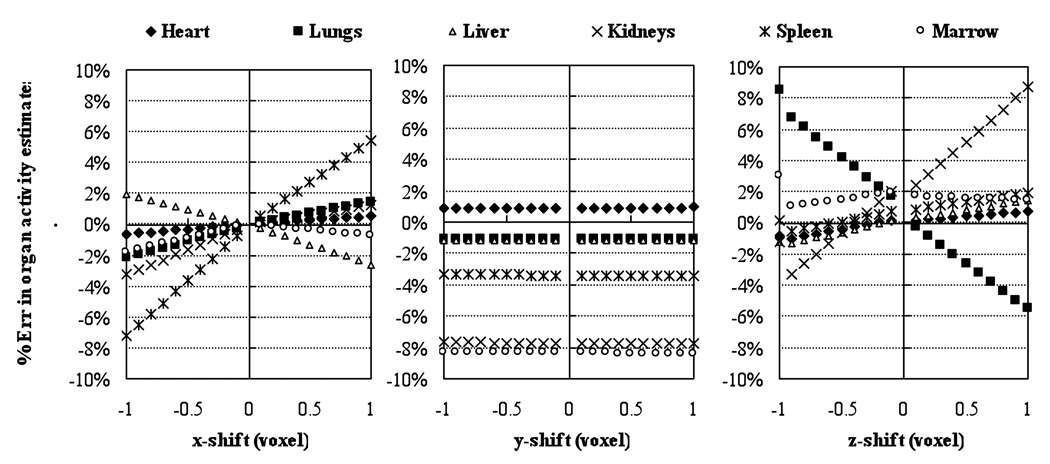
Figures 3 and 4 show the results of the misregistration studies where VOIs were shifted by amounts ranging from −1 to 1 voxels for the QSPECT and QPlanar methods. As expected, the misregistration of VOIs and projection data had a larger impact for small organs (such as the kidneys) and low uptake organs close to high uptake ones (such lungs). For the QSPECT method, the misregistration produced errors in organ activities that were proportional to the VOI shift, at least for the range of shifts studied. For all the organs except the lungs, the errors were underestimates. This is because, for the shifts studied, for all the organs except the lungs the regions adjacent to the organs had lower activity than the organ itself. However, for the lungs, the heart and liver had higher activities and were directly adjacent to the lungs. For the QPlanar method, the results were more complicated because of the interposition of the estimation process between VOI errors and activity estimate errors. For most organs, the errors were slightly larger than those for the QSPECT method. This indicates that the QPlanar method is slightly more sensitive to misregistration errors than the QSPECT method. In addition, the errors due to misregistration were generally larger than those due to misdefinition. For a 1 voxel misregistration, the errors were as large as −16% (for the kidneys), and 2% for a larger, high-uptake organs like the liver.

Figure 3.

Figure 3

Open in a new tab

Percent errors in organ activity estimates introduced by shifting VOIs from −1 to 1 voxels in both left-right lateral (x), anterior-posterior (y) and superior-inferior (z) directions for the QSPECT method.

Figure 4.

Figure 4

Open in a new tab

Percent errors in organ activity estimates introduced by shifting VOIs from −1 to 1 voxels in both left-right lateral (x), anterior-posterior (y) and superior-inferior (z) direction for the QPlanar method.

The mis-registration errors for QPlanar shown in Figure 4 was linear with the shift over the range −1 to 1 voxels. However, this is not necessary to be true. There should be no error for zero shifts in all these cases since it is the baseline for calculating. For example, the errors in bone marrow estimates most likely would be negative for any shift since the attenuation of other tissues is always less than the attenuation of bones. The errors for positive and negative shifts would not necessary to be symmetrical if the organ is not symmetrical. For the y shift, since the VOIs were still registered to the attenuation maps, the only changesd in the templates would be the resolutionwere due to the change of distance to two detectorsdue to differences in the distances from the two detectors to the object, which affects the amount of blurring of the templates by the collimator-detector response; there was no physical misalignment of the projection of the regions as was the case for the other directions. As a result, the errors from shifts in the anterior-posterior direction were small. It had larger effect on the organs (e.g. kidneys and marrow) that are not symmetrical in y direction.

4. DISCUSSION

As a result of the model used for VOI definition errors, these studies may not predict the kind and magnitude of errors that a human observer would make; it would have been more realistic to study errors by having a number of operators draw a number of VOIs. However, such a study would have also been much more difficult to perform and would have represented only the errors for one particular sample of observers. Nevertheless, we believe that the misdefinition method used shed light on the trends and magnitudes of errors in activity estimates resulting from errors in VOI definition. In addition, they provide information about the relative impact of VOI definition errors on the QPlanar and QSPECT processing methods and the level of care on the part of operators that is required in order to achieve a desired accuracy and precision.

Another limitation of this work is that it studied only rigid misregistration up to 1 voxel in three directions and not the more general case of nonrigid misregistration. This model is appropriate to represent misregistration of SPECT and CT images obtained on a SPECT/CT camera without perfect registration. However, it does not reflect errors due to misregistration of SPECT and CT images where there was patient movement between the studies. We did not attempt to develop a realistic model for and systematically study non-rigid misregistration, and addressing this problem in full generality remains a task for future work.

Despite the above limitations, some clinically relevant conclusions can be drawn. This work demonstrated that misregistration generally had a larger impact on the estimation than misdefinition. Thus it is critical that CT images used to define VOIs and SPECT images to which the VOIs are applied should be registered to each other with an accuracy of better than 1 voxel. The increase in variability introduced by misdefinition was generally small. However, errors introduced by consistently defining larger or smaller regions were, especially for small organs, non-negligible compared to other sources of error. From these data we conclude that it is important that operators try to minimize both misregistration and systematic misdefinition errors when quantifying organ uptakes. Although the use of hybrid SPECT/CT systems with careful attention to quality control should reduce misregistration errors, the possibility of patient movement between the SPECT and CT scans indicates the need for postacquisition evaluation of the registration.

5. CONCLUSIONS

This work studied the impact of misregistration and misdefinition of VOIs on activity estimates for the QSPECT and QPlanar processing methods. Both types of VOI definition errors produced larger errors in activity estimates for a small and low uptake organs (i.e. −7.5% to 5.3% for the left kidney) than for a large and high uptake organ (i.e. −2.9% to 2.1 for the liver). We observed that misregistration generally had larger effects than misdefinition, with errors ranging from −16% to 8.5%. The different imaging methods evaluated responded differently to the errors from misregistration and misdefinition. We found that QSPECT was more sensitive to misdefinition errors but less sensitive to misregistration errors as compared to the QPlanar method. This was true for all directions except along the projection direction for the planar projections where QPlanar was very insensitive to misregistration. Thus, sensitivity to VOI definition errors should be an important criterion in evaluating quantitative imaging methods.

ACKNOWLEDGMENTS

The majority of this work was performed at the Johns Hopkins Medical Institutions. This work was supported by the National Institutes of Health (NIH) under Grant R01-CA109234.

Footnotes

DISCLOSURE

The reconstruction code used in this work has been licensed to GE Healthcare for inclusion in a commercial product. Under separate licensing agreements between the General Electric Company and the Johns Hopkins University and the University of North Carolina at Chapel Hill and GE Healthcare, Dr. Frey is entitled to a share of royalty received by the universities on sales of products described in this article. The terms of this arrangement are being managed by the Johns Hopkins University in accordance with its conflict of interest policies.

REFERENCES

  1. Biehl KJ, Kong F-M, Dehdashti F, Jin J-Y, Mutic S, El Naqa I, Siegel BA, Bradley JD. 18F-FDG PET Definition of Gross Tumor Volume for Radiotherapy of Non-Small Cell Lung Cancer: Is a Single Standardized Uptake Value Threshold Approach Appropriate? J. Nucl. Med. 2006;47:1808–1812. [PubMed] [Google Scholar]
  2. Briesmeister JF. A Genral Monte Carlo N-Particle Transport Code. Versioin 4B LA-12625-M. 1997 [Google Scholar]
  3. Clarke KG, Odom-Maryon TL, Williams LE, Liu A, Lopatin G, Chou J, Farino GM, Raubitschek AA, Wong JYC. Intrapatient consistency of imaging biodistributions and their application to predicting therapeutic doses in a phase I clinical study of 90Y-based radioimmunotherapy. Med. Phys. 1999;26:799–809. doi: 10.1118/1.598588. [DOI] [PubMed] [Google Scholar]
  4. Daisne JF, Sibomana M, Bol A, Doumont T, Lonneux M, Gregoire V. Tri-dimensional automatic segmentation of PET volumes based on measured source-to-background ratios: influence of reconstruction algorithms. Radiother Oncol. 2003;69:247–250. doi: 10.1016/s0167-8140(03)00270-6. [DOI] [PubMed] [Google Scholar]
  5. Delpon G, Ferrer L, Lisbona A, Bardies M. Impact of Scatter and Attenuation Corrections for Iodine-131 Two-Dimensional Quantitative Imaging in Patients. Cancer Biother. Radiopharm. 2003;18:191–199. doi: 10.1089/108497803765036355. [DOI] [PubMed] [Google Scholar]
  6. Du Y, Frey EC, Wang WT, Tocharoenchai C, Baird WH, Tsui BMW. Combination of MCNP and SimSET for Monte Carlo simulation of SPECT with medium- and high-energy photons. IEEE Trans. Nucl. Sci. 2002;49:668–674. [Google Scholar]
  7. Erdi YE, Mawlawi O, Larson SM, Imbriaco M, Yeung H, Finn R, Humm JL. Segmentation of lung lesion volume by adaptive positron emission tomography image thresholding. Cancer. 1997;80:2505–2509. doi: 10.1002/(sici)1097-0142(19971215)80:12+<2505::aid-cncr24>3.3.co;2-b. [DOI] [PubMed] [Google Scholar]
  8. Frey EC, He B, Sgouros G, Flinn IW, Wahl RL. Development and validation of an organ residence time estimation method for high dose Y-90 ibritumomab tiuxetan therapy. Eur. J. Nucl. Med. Mol. Imaging. 2006;33:S103-S. [Google Scholar]
  9. Frey EC, Ju ZW, Tsui BMW. A Fast Projector-Backprojector Pair Modeling the Asymmetric, Spatially Varying Scatter Response Function for Scatter Compensation in Spect Imaging. IEEE Trans. Nucl. Sci. 1993;40:1192–1197. [Google Scholar]
  10. Frey EC, Tsui BMW. A new method for modeling the spatially-variant, object-dependent scatter response function in SPECT. IEEE Nucl. Sci. Symp. 1996;2:1082–1086. [Google Scholar]
  11. Harrison RL, Haynor DR, Gillispie SB, Vannoy SD, Kaplan MS, Lewellen TK. A Public-Domain Simulation System for Emission Tomography - Photon Tracking through Heterogeneous Attenuation Using Importance Sampling. J. Nucl. Med. 1993;34:P60. [Google Scholar]
  12. He B, Du Y, Segars WP, Wahl RL, Sgouros G, Jacene H, Frey EC. Evaluation of quantitative imaging methods for organ activity and residence time estimation using a population of phantoms having realistic variations in anatomy and uptake. Med. Phys. 2009;36:612–619. doi: 10.1118/1.3063156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. He B, Du Y, Song XY, Segars WP, Frey EC. A Monte Carlo and physical phantom evaluation of quantitative In-111SPECT. Phys. Med. Biol. 2005;50:4169–4185. doi: 10.1088/0031-9155/50/17/018. [DOI] [PubMed] [Google Scholar]
  14. He B, Frey EC. Comparison of conventional, model-based quantitative planar, and quantitative SPECT image processing methods for organ activity estimation using In-111 agents. Phys. Med. Biol. 2006;51:3967–3981. doi: 10.1088/0031-9155/51/16/006. [DOI] [PubMed] [Google Scholar]
  15. He B, Wahl RL, Du Y, Sgouros G, Jacene H, Flinn I, Frey EC. Comparison of residence time estimation methods for radioimmunotherapy dosimetry and treatment planning - Monte Carlo simulation studies. IEEE Trans. Med. Imaging. 2008;27:521–530. doi: 10.1109/TMI.2007.908131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hudson HM, Larkin RS. Accelerated Image-Reconstruction Using Ordered Subsets of Projection Data. IEEE Trans. Med. Imaging. 1994;13:601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
  17. Jentzen W, Freudenberg L, Eising EG, Heinze M, Brandau W, Bockisch A. Segmentation of PET volumes by iterative image thresholding. J. Nucl. Med. 2007;48:108–114. [PubMed] [Google Scholar]
  18. Koral KF, Francis IR, Kroll S, Zasadny KR, Kaminski MS, Wahl RL. Volume reduction versus radiation dose for tumors in previously untreated lymphoma patients who received iodine-131 tositumomab therapy - Conjugate views compared with a hybrid method. Cancer. 2002;94:1258–1263. doi: 10.1002/cncr.10294. [DOI] [PubMed] [Google Scholar]
  19. Norrgren K, Svegborn SL, Areberg J, Mattsson S. Accuracy of the Quantification of Organ Activity from Planar Gamma Camera Images. Cancer Biother. Radiopharm. 2003;18:125–131. doi: 10.1089/108497803321269403. [DOI] [PubMed] [Google Scholar]
  20. Segars WP. Ph. D. Dissertation. University of North Carolina; 2001. Development of a new dynamic NURBS-based cardiac-torso (NCAT) phantom. [Google Scholar]
  21. Siegel JA, Harpen MD, Paul Lee W, Verma RC, Greenfield MA. Quantitative differences between the thyroid uptake of 123I and 99mTc. Eur. J. Nucl. Med. Mol. Imaging. 1984;9:494–498. doi: 10.1007/BF00263252. [DOI] [PubMed] [Google Scholar]
  22. Song X, Segars WP, Du Y, Tsui BMW, Frey EC. Fast modelling of the collimator-detector response in Monte Carlo simulation of SPECT imaging using the angular response function. Phys. Med. Biol. 2005;50:1791–1804. doi: 10.1088/0031-9155/50/8/011. [DOI] [PubMed] [Google Scholar]
  23. Thomas SR, Maxon HR, Kereiakes JG. In vivo quantitation of lesion radioactivity using external counting methods. Med. Phys. 1976;3:253–255. doi: 10.1118/1.594287. [DOI] [PubMed] [Google Scholar]
  24. Wang WT, Frey EC, Tsui BMW, Tocharoenchai C, Baird WH. Parameterization of Pb X-ray contamination in simultaneous Tl-201 and Tc-99m dual-isotope imaging. IEEE Trans. Nucl. Sci. 2002;49:680–692. [Google Scholar]
  25. Wong JYC, Chu DZ, Williams LE, Liu A, Zhan J, Yamauchi DM, Wilczynski S, Wu AM, Yazaki PJ, Shively JE, Leong L, Raubitschek AA. A Phase I Trial of 90Y-DOTA-Anti-CEA Chimeric T84.66 (cT84.66) Radioimmunotherapy in Patients with Metastatic CEA-Producing Malignancies. Cancer Biother. Radiopharm. 2006;21:88–100. doi: 10.1089/cbr.2006.21.88. [DOI] [PubMed] [Google Scholar]
  26. Zeng GL, Hsieh YL, Gullberg GT. A Rotating and Warping Projector Backprojector for Fan-Beam and Cone-Beam Iterative Algorithm. IEEE Trans. Nucl. Sci. 1994;41:2807–2811. [Google Scholar]

RESOURCES