An Optimum Method for Pulsed High Intensity Focused Ultrasound Treatment of Large Volumes using the InSightec ExAblate® 2000

Abstract

Pulsed high intensity focused ultrasound (pHIFU) is a method for delivering ultrasound to tissue while avoiding high temperatures. The technique has been suggested for non-destructively enhancing local uptake of drugs. Side effects include thermal necrosis, therefore, realtime monitoring of tissue temperature is advantageous. This paper outlines a method for improving the treatment effciency of (pHIFU) using the MR image guided InSightec ExAblate® 2000, an ultrasound system integrated into a whole body human MRI scanner with the ability to measure temperature at the treatment location in near real-time. Thermal measurements obtained during treatment of a tissue phantom were used to determine appropriate heating parameters, and compared to in vivo treatment of rabbit muscle. Optimization of the treatment procedure and ultrasound transducer steering patterns was then conducted with the goal of minimizing treatment time while avoiding overheating. The optimization was performed on the basis of approximate solutions to the standard bioheat equation. The commercial system software of the Exablate® system was modified to assist in this optimization. Depending on the size of the treatment volume, the presented results demonstrate that it is possible to use the technique described to cut treatment times significantly, up to one third of that required by the current standard treatment cycle.

1. Introduction

The advent of MR thermal imaging has resulted in a boost of interest in the use of focused ultrasound as a means of image guided therapy for deep tissues and tumors. Focused ultrasound is a technology whereby ultrasound energy from a large transducer (or transducer array) is concentrated into a very small volume, where it deposits significant thermal and strain energy in the tissue. This design results in tissue hyperthermia, thermal damage, radiation force induced displacements and acoustic streaming. Ultrasonic cavitation is also possible depending on the local properties of the tissue (ter Haar 2007). The ability to monitor the precise location of an ongoing treatment using near real-time thermal and anatomical imaging has led to a growing acceptance that the technology is both safe and efficacious. In the United States, the ExAblate® 2000 system (InSightec Inc, Haifa, Israel) has been approved for focused ultrasound thermal ablation of uterine fibroids (Hesley et al. 2008, McDannold et al. 2006). Currently, the ExAblate® system is undergoing clinical trials for other ablative thermal therapies, such as palliation of bone cancer metastasis, and modified versions are being tested for prostate, breast and brain tumor ablation in various parts of the world. (InSightec, Inc. 2010).

An interesting nonablative application for this system is drug delivery. Pulsed high intensity focused ultrasound (pHIFU) treatment has been promoted as a means of non-destructively enhancing the local uptake of drugs. It has been shown that a treatment regimen employing short duty-cycle pulses can improve the concentration of large molecular weight drugs and agents while avoiding significant heating and thermal tissue damage (Bednarski et al. 1997, Dittmar et al. 2005, Frenkel, Etherington, Greene, Quijano, Xie, Hunter, Dromi & Li 2006, Frenkel & Li 2006, Frenkel, Oberoi, Stone, Park, Deng, Wood, Neeman, Horne & Li 2006, O’Neill et al. 2009). One major challenge to the practical use of pHIFU technology is efficiency. A typical application of pHIFU has consisted of 100 or more pulses, at 5 % duty cycle and 1 Hz repetition rate, for each focal spot placed on a grid of 2 mm separation (O’Neill et al. 2009, Hancock et al. 2009). Thus, treatment of a single focal spot requires almost 2 minutes of treatment time, compared to approximately 20 s for thermal ablation. While the importance of these particular treatment parameters are still debatable, there are compelling reasons to believe that they reflect important physical properties of the tissue. Specifically, the number of pulses determines the total deposition of mechanical and thermal energy in the focal region, and likely cannot be significantly reduced without an increase in duty cycle. The 50 ms pulse length is thought to be close to optimal; as it appears to be the characteristic time it takes for tissue to approach a maximum of displacement. Increasing the pulse length beyond 50 ms will thus result in more thermal energy deposition, but not in any additional strain energy (O’Neill et al. 2009). The remaining 950 ms is required for diffusion of the thermal energy to occur and prevents the temperature from reaching much beyond 5 °C above ambient (O’Neill et al. 2009). The duty cycle and repetition rate thus control the balance between mechanical and thermal energy deposition, and cannot be significantly altered without impacting the treatment. At 100 seconds per focal spot, and a spot size of only a few mm³, treating a volume of any significance requires an inordinate amount of time and becomes prohibitive for future clinical applications. For example, using the parameters given the time required for treatment alone (excluding patient preparation, initial imaging and treatment planning) is almost 60 minutes/cc of tissue. Therefore, it is highly desirable to develop a treatment scheme that would allow the tissue cooling time to be used to treat elsewhere, without compromising the pulse length or temperature requirements. Our approach to fulfill this requirement consists of moving the transducer in between treatments, thereby depositing heat in one location while allowing other locations to cool simultaneously. This approach can only be successful if the two locations are sufficiently separated for treatments of different zones not to interfere with each other. The ExAblate® 2000 system can be steered using some combination of electronic and mechanical steering. The electronic steering is much faster than the mechanical steering, however, it has a much more limited range. The goal of this study was to develop steering patterns for the transducer of the ExAblate® system and a theory for optimizing treatment parameters so as to safely minimize overall treatment time. The feedback necessary to conduct this optimization is an accurate measurement of the temperature rise in space and time caused by treatment of a local (electronic steering only) zone. These temperature measurements were performed using dedicated magnetic resonance imaging (MRI) pulse sequences that take advantage of the temperature dependence of the phase of the proton spins. Comparable temperature measurements were made during treatments of a tissue phantom and in vivo in rabbit muscle. Having established its relevance, a more extensive data set was then collected in the phantom rather than in vivo or ex vivo tissue, and used to determine parameters for optimization. This approach allowed us to avoid the phase changes that take place in tissue as protein denatures, and therefore explore a broader region of the parameter space. Once the local heating profile was established as a function of the acoustic treatment parameters, we were able to design a treatment plan to maximize the overall duty cycle without overheating.

2. Materials and Methods

2.1. MR-guided focused ultrasound system

The FDA-approved ExAblate® 2000 MR guided focused ultrasound device from InSightec, Inc. was adopted for all procedures. A typical design using a transducer with 1.0 MHz center frequency, f-number (ratio of focal length to diameter) of one, will result in an ellipsoidal acoustic focal spot size with −3 dB diameter approximately 2 mm and length 10 mm. The acoustic energy flux in this region can be on the order of 10³W/cm². Anatomical imaging and temperature monitoring is done with a GE 3.0T HDxT magnetic resonance scanner using a breast coil provided by InSightec. The first series of the image acquisition consisted of a three-plane localizer (sagittal, coronal and axial orientation, 256 × 128 acquisition matrix interpolated to 256 × 256, pixel spacing 1.7 mm×1.7 mm, slice thickness 7 mm) to ensure the target was oriented correctly with respect to the position of the transducer. In a second series, T2-weighted images were acquired (fast spin echo, echo time (TE) of 120 ms, repetition rate (TR) of 3400 ms, acquisition matrix 512×256 interpolated to 512×512, pixel spacing 0.47 mm×0.47 mm, field-of-view (FOV) 240 mm, slice thickness 2 mm, echo train length 22). These images were used for treatment planning, and to ensure good acoustic coupling(achieved by a thin film of degassed water in combination ultrasound gel), defined as the absence of air bubbles at the transducer window/tissue or phantom interface. Coupling is also assessed with the ExAblate® system using ultrasound reflection as a matter of routine with each sonication. Prior to sonication, a very short pulse is sent and received by selected elements of the therapeutic transducer and the reflected energy is displayed on the screen in mV². The coupling is considered a problem if the reflected energy exceeds 1.6 mV². The total ultrasound exposure during this test is approximately 0.01 J.

During treatment, a coronal slice intersecting the treatment region was continuously scanned using a fast gradient echo sequence (TE=7.8 ms, TR=38 ms, slice thickness 3 mm, FOV 220 mm × 220 mm, acquisition, matrix 128 × 128, pixel spacing 0.86 mm × 0.86 mm) by choosing an appropriate number of phases. The acquisition time for one temperature measurement (i.e. time of acquiring one slice) ranged from 3 s to 9 s and was adjusted by modifying the number of averages (NEX) acquired. During long sonication periods, i.e. 15 minutes or longer, reducing the total number of MRI images acquired became necessary to avoid overloading the post-processing capabilities of the ExAblate® system. Magnitude and phase images were automatically reconstructed. Temperature maps calculated from these images by the ExAblate® system were used in the further analysis. The method of MR thermometry employed by the ExAblate® system is based on the small changes of the proton resonance frequency (PRF) in water (i.e. soft tissue) that occur as a function of temperature. This linear relationship between PRF and temperature is used to compute the relative change in temperature of the tissue and display the corresponding thermal images (Ishihara et al. 1995). Each image is compared to a baseline (cold) image acquired just prior to the sonication and the corresponding phase differences are computed and displayed as thermal maps of the region of interest. An increase in signal intensity in these phase-difference images over time represents an increase in temperature. The system can detect temperature changes as small as 1 °C with a standard deviation of 0.3 °C (mean error) in 3.0 T. The relative temperature increase is added to an operator determined baseline temperature, typically 37 °C , and then used to compute the thermal dose (time equivalent at 43 °C) received by the tissue according to Sapareto & Dewey (1984). The accumulated volume of tissue to have reached the ‘threshold for necrosis’ as defined by the system appears as an overlay on the anatomical T2-weighted planning images. As well, temperature evolution over time is displayed in real time for the (current) hottest voxel as well as for the 9 voxels centered on the hottest voxel.

In order to operate effectively for pulsed mode HIFU, the ExAblate® control system had to be modified somewhat from the clinical configuration. A non-FDA approved research version of the ExAblate® software was adapted for use in pulsed mode. Pulsed-mode operation was introduced by integrating an external pulser (33220A Waveform Generator, Agilent Inc., Santa Clara CA) to provide a gating signal with the desired pulse width and repetition rate. The pulse width of 50 ms was kept constant, while the repetition rate was varied to arrive at duty cycles ranging from 5 % to 100 %. The ExAblate® system software for cavitation detection was found to be insufficient to adequately capture short pulses (<200 ms) and therefore, to ensure consistent cavitation detection, the backscattered ultrasound signal from each pulse was fed into an external spectrum analyzer (E5071C Network Analyzer, Agilent Inc., Santa Clara CA) triggered by the external gating signal, and the resulting spectrum was stored for analysis. The ultrasound signal used for this purpose was the same as that measured by the ExAblate® system, and has already been passed through a low pass filter (−60 dB for frequencies greater than 0.9 MHz) to suppress the fundamental signal. A cavitation-free signal was considered to be one where the half harmonic had less than half the amplitude of the suppressed fundamental. This is similar to the criteria used by InSightec for the same purpose. Once tested, it was found that cavitation was easily avoided at the low powers used in this optimization study, provided the coupling was free of trapped air. In a further adjustment, the basic motion system was modified to allow repetitive, sequential treatment of operator defined points separated by mechanical movements. This step allows the operator to bypass/streamline the following steps that are normally required by the clinical system between treatment zones: 1) accept last treatment, 3) wait for cool-down, 3) select next point, 4) start next sonication.

2.2. Tissue and Phantom measurements

Sonication tests were carried out both in vivo and in a tissue phantom using the ExAblate® 2000. In vivo heating profiles were used to ensure the behavior of the phantom was sufficiently representative despite the lack of perfusion. The bulk of the tests were then carried out on the phantom. Five in vivo sonications were done in the thigh muscle (either side) of three female New Zealand White rabbits, each between 3 and 4 kg in weight. All animals were handled according to a protocol approved by the Animal Care and Use Committee of the Methodist Hospital Research Institute. Following sedation, the thigh to be treated was shaved and treated with a depilatory cream. The shaved leg was placed in a shallow pool of degassed water on a gel pad above the acoustic window of the ultrasound transducer. Degassed water also coupled the ultrasound from the transducer into the gel pad. The gel pad was located at the center of a breast coil provided by InSightec, Inc., which was used to acquire MR images as described above. The thermal maps were used as study data and to ensure the targeted regions were sufficiently distant from major blood vessels and bones. Most of the additional data used in the study was obtained from a tissue phantom substitute for live animals. The tissue phantom used was the standard sound absorbing solid gel supplied for daily quality assurance (DQA) purposes by InSightec, Inc., Model TXS-100 from ATS Laboratories, Inc.(Bridgeport, CT). This DQA phantom is a slightly tapered cylinder approximately four inches (10.2 cm) in diameter and five inches (12.7 cm) tall. The manufacturer provided documentation lists the acoustic absorption as 0.503 dB/cm/MHz and the speed of sound at 1538 m/s. The thermal properties were not given. The phantom was placed on the gel pad at the center of the breast coil in the same manner as described above for the in vivo experiments. MR thermometry was used to obtain temperature maps during treatment as described in the previous section. Treatments in rabbit muscle tested the heat build-up and dissipation during single sonications. These results were compared with phantom heating (see below). The phantom was then sonicated using a much wider range of pulse numbers, acoustic powers, duty cycles, steering patterns and ultrasound frequencies, including duty cycles of up to 100 %, which would quickly cause thermal ablation in tissue. The heat build-up in the treatment zone (see figure 1) was measured by MR thermometry under various electronic steering patterns, all designed to treat focal spots on a two millimeter grid in either one or two passes, with a total of 100 pulses per spot. The heated region for a single focal spot sonication was defined as the zone achieving at least one degree Celsius above ambient following a complete sonication (100 pulses). The size of this region during in vivo treatment was estimated by drawing oval ROI’s on 5 thermal images captured immediately following sonication of a single focal spot and finding the average diameter. Presumably, a second treatment spot anywhere within this region would see at least some additional rise in temperature due to heat carried over from the first spot unless sufficient time was given to allow all residual heat to dissipate. Temperature maps during treatment of spots placed at the outer limits of electronic steering were used to test this hypothesis to the best of our ability (mechanical steering being too slow to be useful in this case).

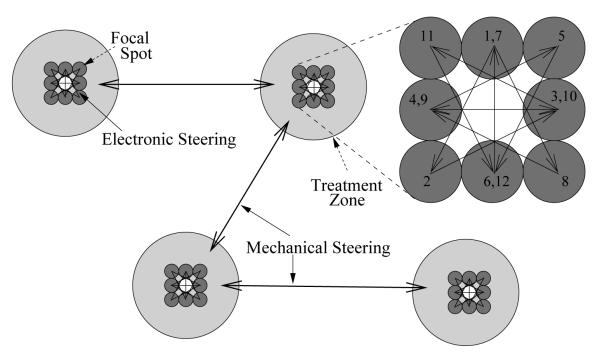
Figure 1.

Treatment of multiple independent zones using electronic plus mechanical steering. The proposed design for optimal treatment is as follows. Individual focal spots within each treatment zone are consecutively treated in the order shown via fast electronic steering (inset, upper right). When the peak temperature in a given treatment zone reaches a pre-determined level, mechanical steering is used to move to a new treatment location at some distance. Continued treatment of the first zone occurs only after the temperature there has returned to ambient. Cycling through all treatment zones continues until each focal spot has received the full allotment of HIFU pulses.

2.3. Extraction of model parameters

For optimization with combined mechanical and electronic steering, a treatment zone with a spot pattern consisting of eight spots was selected. The spot on the central axis of the transducer was left out to avoid excessive thermal dose (figure 1). Each of the focal spots was pulsed repetitively in a star-shaped pattern to spread out the heat deposition as much as possible with electronic steering. The peak temperature during each such treatment was measured as a function of time and machine duty cycle, maintaining a constant pulse length of 50 ms, for duty cycles ranging from 5 % to 100 %. Curves of the maximum temperature in the treatment zone versus time during heating are presumed to take the form:

$$T\left(t\right)=AP\mathit{dc}(1-\exp (-\alpha t\left)\right)$$ (1)

where A in °C/W and α in Hz depend on the ultrasound beam parameters and tissue properties, but are, to first order, independent of duty cycle, dc, peak acoustic power, P, time and temperature. T here and in subsequent expressions is the temperature rise above ambient. A is proportional to the acoustic absorption and is therefore dependent on ultrasound frequency and, through nonlinear second order effects, on acoustic power. Both A and α are related to temperature due to the thermal dependence of the tissue properties. This expression may be theoretically deduced as follows. The Pennes bioheat equation can be written (Wissler 1998):

$$c_v\stackrel{.}{T}(\overrightarrow{x},t)=-k{\nabla }^{2}T(\overrightarrow{x},t)-\omega T(\overrightarrow{x},t)+Q(\overrightarrow{x},t).$$ (2)

Here c_v is the volumetric heat capacity of the tissue, k is the thermal conductivity, and ω is the rate of heat exchange to the blood. $Q(\overrightarrow{x},t)$ is the spatial and temporal deposition of heat from the acoustic beam, and may be written exactly as $2\stackrel{‒}{\alpha }I(\overrightarrow{x},t)∕c$, where $I(\overrightarrow{x},t)$ is the intensity of the acoustic beam, which is proportional to the instantaneous acoustic power P, $\stackrel{‒}{\alpha }$ is the acoustic absorption, and c the speed of sound. Since we are only interested in the slow dynamics (temperature changes measured every 3–10 s), we can average over the fast pulsing and steering, and rewrite

$$Q(\overrightarrow{x},t)\approx AP\mathit{dc}\varphi \left(\overrightarrow{x}\right),$$ (3)

where $\varphi \left(\overrightarrow{x}\right)$ is a function of space only, accounting for the steering pattern, and φ(0) = 1 at the center of the pattern. Let us also write $T(\overrightarrow{x},t)$ in separable form as $T\left(t\right)\rho \left(\overrightarrow{x}\right)$. The bioheat equation then becomes:

$$c_v\rho \left(\overrightarrow{x}\right)\stackrel{.}{T}\left(t\right)=-kT\left(t\right){\nabla }^2\rho \left(\overrightarrow{x}\right)-\omega T\left(t\right)\rho \left(\overrightarrow{x}\right)+AP\mathit{dc}\varphi \left(\overrightarrow{x}\right).$$ (4)

If we can write:

$$\rho \left(\overrightarrow{x}\right)=\varphi \left(\overrightarrow{x}\right)$$ (5)

and

$${\nabla }^2\varphi \left(\overrightarrow{x}\right)\approx \frac{C}{R^2}\varphi \left(\overrightarrow{x}\right),$$ (6)

with R² as the thermal zone radius and C a constant, then we recognize T(t) is the temperature at the center of the heated zone, and the bioheat equation reduces further to:

$$\stackrel{.}{T}\left(t\right)=-\alpha T\left(t\right)+AP\mathit{dc}.$$ (7)

with α = [Ck/R² + ω]/c_v. The exact solution to this equation gives (1) as the peak temperature at the center of the treatment spot.

For each combination of acoustic power and frequency, temperature vs. time data was imported into R (R Development Core Team 2007), where a non-linear least squares fit of the form:

$$\frac{\left(T\right(t;\mathit{dc})+T_0)}{T_m}\approx 1$$ (8)

was used to find A, α, and the intercept T₀, where T_m are the measured data and T(t, dc) is calculated from (1). The form of the equation used here helps to weight the lower values and stabilize the intercept T₀ near the baseline temperature.

2.4. Treatment optimization

Once A and α for a particular combination of ultrasound power and frequency were known, the scanning parameters can be optimized for maximum treatment efficiency. The pHIFU treatment paradigm determines the following constraints: 1) maximum allowable local temperature, T_z; 2) fixed number of pulses, N, at each focal spot given a fixed number, m, of focal spots in a treatment zone; 3) maximum number, M, of accessible treatment zone in any given volume; 4) finite time, t_q, to move from one treatment zone to another (see table 1). Using the basic heating equation, (1), and its associated cooling equation:

$$T\left(t\right)=T_0\exp (-\alpha t),$$ (9)

we are able to determine the optimum set of motion and treatment parameters to accomplish these goals in the minimum time. In (9), T₀ is the initial temperature at which the cooling portion of the cycle begins. In this manner, the machine duty cycle, dc, and number of pulses per focal spot, n_z, that will maximize the net duty cycle, DC_N, while maintaining a low local duty cycle, DC_z (table 1) can be determined.

Table 1.

List of parameters and variables.

Label	Definition (typical value)
Constraints
Tmax	maximum allowable temperature (5.25 °C)
Tz	desired peak temperature in a treatment zone (5 °C)
tp	pulse length (period = tp/dc) (50 ms)
M	number of treatment zones (4-6)
m	number of focal spots per treatment zone (8)
tq	time of mechanical motion (30 s); q = tq/tp
N	total number of pulses per focal spot (100)
Variables & Symbols
T	temperature
dc	device duty cycle
DCz	local ‘treatment zone’ duty cycle
DCN	net duty cycle
nz	pulses per focal spot in a single pass
n	pulse number, from 0 to N
theat = mnztp/dc	time spent treating (heating) a single treatment zone
tM = M (mnztp/dc + tq)	time required to treat M treatment zones
tcool = tM – theat	time between treatments of a single treatment zone
Δ	increase in Tmax over Tz: $\Delta =\frac{T_{\max }-T_z}{T_z}$

From the diagram (figure 1) and definitions, one can write:

$${\mathit{DC}}_z=\frac{\prime \text{on}\prime \text{time for one zone}}{\text{total time}}=\frac{t_{\text{heat}}\mathit{dc}}{M(t_{\text{heat}}+t_q)}=\frac{\mathit{dc}}{M\left(1+\frac{q\mathit{dc}}{n_{z}m}\right)},$$ (10)

using dc/t_p as the repetition rate and q × t_p as the time required to move from one treatment zone to the next. The overall duty cycle that we need to maximize is:

$${\mathit{DC}}_N=\frac{{}^{\prime }\text{on}^{\prime }\text{time for all zones}}{\text{total time}}=M{\mathit{DC}}_z=\frac{\mathit{dc}}{\left(1+\frac{q\mathit{dc}}{n_{z}m}\right)}$$ (11)

It is possible to use (11) directly for constant dc, n_z, and a given M by picking t_q to maintain a sufficiently low average local duty cycle. In that case, n_z must be fixed from the constraint on T_z and (1) following treatment of a single treatment zone:

$$T_z=AP\mathit{dc}(1-\exp (-\alpha t_{\text{heat}}\left)\right)\Rightarrow t_{\text{heat}}=-\ln \left(1-\frac{T_z}{AP\mathit{dc}}\right),$$ (12)

from which n_z = t_heat dc/(m t_p). The total number of treatment cycles, that is, the number of times each of the M treatment zones must be treated so that each focal spot receives N pulses, is just N/n_z. Knowing n_z, we can then insist that the treatment zone duty cycle, DC_z remain at or below some empirically ‘safe’ value, for example, 5 %, which is known to give a less than 5 °C rise in temperature at N = 100. This then provides a constraint on t_q from (10): t_q ≥ t_heat dc ((M DC_z)⁻¹ – dc⁻¹), and DC_N = MDC_z. This approach could work for duty cycles and pulse numbers that do not deviate much from known safe values, however could give problems if it were applied to some new situation. The problem is that it leaves no room for consideration of a possible build-up of heat from one treatment cycle to the next, and the final temperature may overshoot the target, particularly if the total number of pulses is increased beyond 100.

More generally, we can insist on an additional condition to prevent the final temperature from rising above a certain level for any given number of total pulses. The local cooling after each local heating cycle may be approximated by (9), where T₀ is the peak temperature following the n_zth cycle and α is the same parameter as in the heating equation. The total number of heating and cooling cycles in each treatment zone required to achieve N total pulses may be written: S = N/n_z ≈ t_total/t_M, where t_M = t_heat + t_cool is the time required for a single pass through all M treatment zones, and t_total is the total time required for a complete treatment of N pulses per focal spot. The max temperature reached following S cycles may be approximated as:

$$T_{\max }=T_z\sum _{k=0}^{S-1}\exp (-k\alpha t_M).$$ (13)

This may be deduced as follows. T_z is, by definition and design, the peak temperature in a zone that has just been treated for the first time. As the treatment moves to other zones, the temperature falls according to (9) through the cooling period, t_cool, when it forms the new baseline temperature for the next heating period. This works mainly because the sharp, high, and rapidly falling temperature peak created during treatment zone heating has been reduced to a broad, low, slowly decreasing temperature elevation by the time even one other treatment zone has been treated. T_z is a new peak applied on top of this new baseline, however, the baseline continues to drop towards ambient throughout the heating period. By the end of the second heating period, therefore, the peak temperature is approximately T_z exp (−αt_M) + T_z. Extending this through S cycles results in (13). T_max here may be conveniently constrained by insisting that:

$$T_{\max }\le T_z(1+\Delta ),$$ (14)

where the local zone temperature rise during a single cycle, T_z is fixed, and the fractional rise in temperature from the first to last cycle, Δ, is also limited.

Using the sum of the geometric series (for S > 1) this implies:

$$\Delta \ge \sum _{k=1}^{S-1}\exp (-k\alpha t_M)=\frac{\exp (-\alpha t_M)-\exp (-\alpha (S\left)t_M\right)}{1-\exp (-\alpha t_M)}.$$ (15)

Substituting S = 2 and isolating in terms of t_M, we have exp (−αt_M) ≤ Δ. For S → ∞, exp (−αt_M) ≤ Δ/(1 + Δ). These form the small and large bounds for this expression, and for small Δ, they become nearly equivalent.

3. Results

3.1. Tissue and Phantom Heating

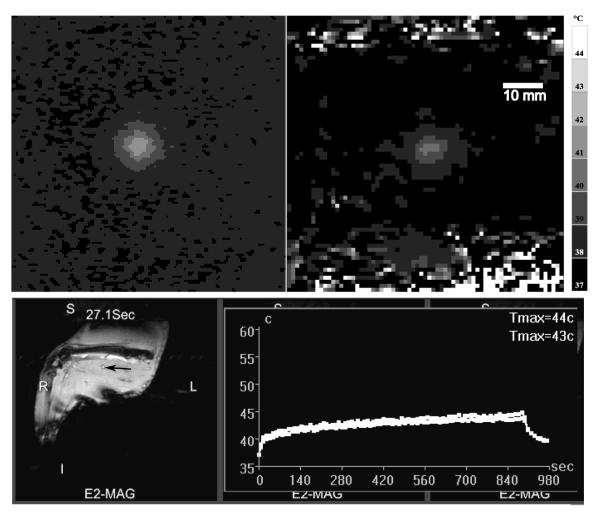
The average diameter of a single-sonication heated zone in rabbit thigh muscle was found, using the method described in section 2.2, to be 18 ± 2 mm, much broader than the 6 mm range of electronic steering available to the ExAblate® 2000 (figure 2, upper right). The heated zone in the phantom was 15 ± 1 mm (figure 2, upper left). A standard treatment of a multi-spot zone in rabbit muscle using electronic steering (m = 9 spots treated consecutively in one pass, 100 pulses per spot, 5 % duty cycle, 2 mm grid separation) was found to result in a monotonic increasing temperature rise over the entire treatment of 900 s (figure 2, lower right) and a smooth spatial temperature. This result can only be explained as a continuous thermal buildup coming from the entire collection of focal spots. Similar results were found in the phantom. The actual electronic steering pattern had little discernible impact on the peak temperatures ultimately measured in the region, although increasing the distance between focal spots did have an effect. The peak temperature rise measured during treatment of a 4-point square pattern was reduced from 7 °C above ambient to 6 and 5 °C above ambient in a tissue phantom during treatment at 40 W, 5 % duty cycle with spot separation of 2, 4, and 6 mm, respectively. To get a full grid then requires multiple treatments to fill the gaps, which, if done without an extended cool down period, again results in virtually the same final temperature.

Figure 2.

Upper: Comparison between representative temperature maps following 100 pulses at 40 W acoustic power and 5 % duty cycle, 50 ms pulse width in tissue phantom (left) and rabbit thigh muscle (right). Lower: Temperature over time (right) collected in real-time during a standard pHIFU heating of a multiple focal spot (m = 9, N = 100, dc = 5 %) treatment zone in rabbit muscle. T2-weighted images were used to place the treatment spot (arrow, left image). Thermal maps are acquired centered on the region of treatment, and the peak temperature plotted in real time (right). These curves are the temperature evolution of the hottest voxel (upper, Tmax=44 °C) or a 9 voxel average centered on the hottest voxel (lower, Tmax=43 °C). Detailed image acquisition parameters are given in section 2.1.

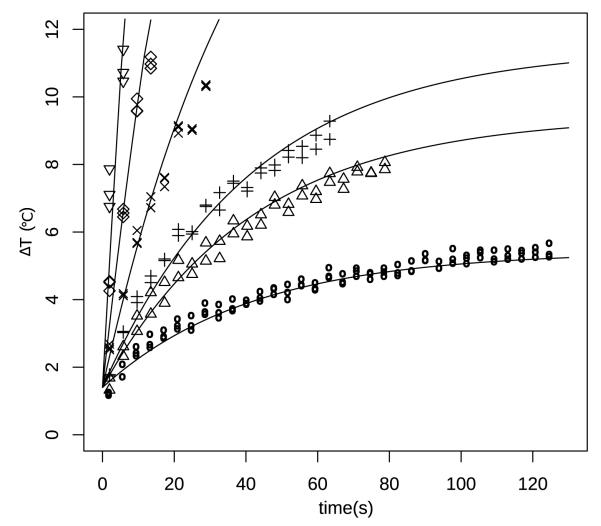
To optimize the treatment with the addition of mechanical motion, thermal parameters are needed to predict treatment zone heating. The least squares fitting of phantom heating curves are shown in table 2 and figure 3. While A varies somewhat with the changing acoustic beam parameters, α is dependent only on the material properties. All the fitted parameters were highly significant with R² > 0.80. The excellent fit justifies the use of the simple expression (1).

Table 2.

Known and fitted parameters from least squares fit of (1) to curves of peak temperature over time.

Frequency (MHz)	Acoustic Power (W)	A (°C/W)	α (×10−3/s)	T0 (°C)	R2	degrees of freedom
1.0	20	1.31 ± 0.06	37 ± 3	1.27 ± 0.04	0.89	149
1.0	40	1.50 ± 0.08	22 ± 2	1.79 ± 0.07	0.83	193
1.3	20	2.30 ± 0.05	26 ± 1	1.21 ± 0.03	0.92	263
1.3	40	2.00 ± 0.05	24 ± 1	1.40 ± 0.04	0.94	214

Figure 3.

Representative curve fitting to temperature rise over time in tissue phantom treated at 1.3 MHz center frequency, 40 W peak acoustic power. Duty cycles from lowest to highest: 5 % (○), 10 % (△), 12.5 % (+), 25 % (×), 50 % (◇), 100 % (▽).

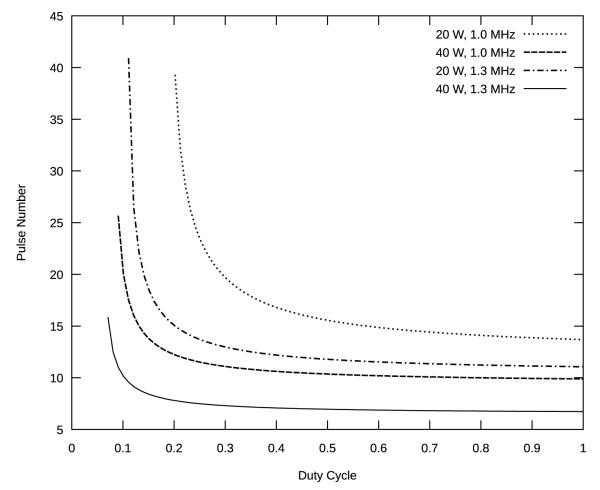
Figure 4 shows the number of pulses required to raise the temperature of a given treatment zone by 5 °C, as a function of duty cycle, based on the parameters of table 2.

Figure 4.

Number of pulses required to raise the temperature to 5 °C, as function of machine duty cycle, based on (12) with t_p = 50 ms, m = 8. Curves are calculated based on fit parameters from Table 2. Although the curves are continuous, the results are used by rounding down to the nearest whole number.

3.2. Treatment Optimization

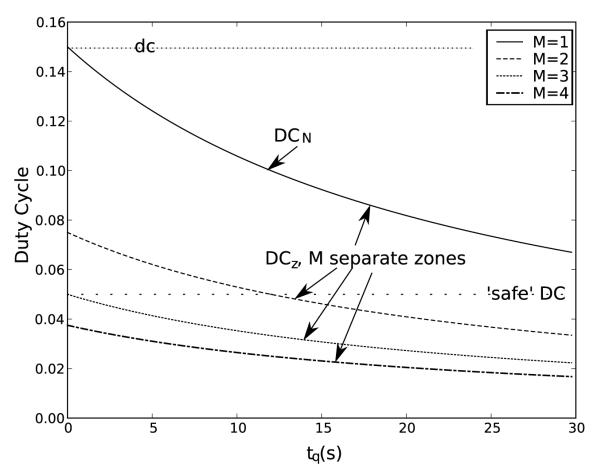
Empirical results consistently show that maintaining a local duty cycle below 5 %, with an average 95 s of local cooling for every 100 pulses, will result in a peak increase in temperature of about 5 °C at 40 W peak acoustic power. Using (11) with t_p = 50 ms, m = 8, dc = 0.15 ⇒ n_z = 8 (from figure 4, T_z = 5 °C, 40 W, 1.3 MHz), we can plot DC_N vs. delay time t_q. (see figure 5). The result demonstrates that by jumping between just two zones (M = 2) with a delay of ≈ 12 s, the local duty cycle is DC_z < 5 %, while the net duty cycle is DC_N > 10 %, inferring that it is possible to safely treat those two zones in half the time that would be required if the zones were treated independently. It is not possible, based on this analysis, to be certain the temperature will stay below T_z.

Figure 5.

Analysis of duty cycles for various delay times and numbers of treatment zones. Even with significant delay times, there may be a clear advantage to combining electronic and mechanical steering, particularly if we want to maintain a relatively low duty cycle. Here t_p = 50 ms, m = 8, dc = 0.15, n_z = 8.

More accurately, by placing constraints on both T_z and Δ in (15), the time that must be spent on heating and cooling each zone can be found:

$$t_M\ge \max \left\{-{\alpha }^{-1}\ln \left(\frac{\Delta }{1-\Delta }\right),2(t_q+t_{\text{heat}})\right\}.$$ (16)

The first of these conditions comes from solving the conservative S → ∞ form of (15) for t_M. The second condition is the minimum time required to steer and treat the minimum number of two zones. Based on (1),

$$t_{\text{heat}}=-{\alpha }^{-1}\ln \left(1-\frac{T_z}{AP\mathit{dc}}\right),$$ (17)

therefore:

$$t_{\text{cool}}\ge t_M-t_{\text{heat}},$$ (18)

where t_M and t_heat come from (16) and (17) respectively. The local duty cycle is:

$${\mathit{DC}}_z=\mathit{dc}\frac{t_{\text{heat}}}{t_M}.$$ (19)

The number of zones one can hope to treat at one time is:

$$M=\min \left\{\frac{t_{\text{cool}}}{t_{\text{heat}}+t_q},M_{\max }\right\}$$ (20)

and the net overall duty cycle is:

$${\mathit{DC}}_N=M\times {\mathit{DC}}_z=\mathit{dc}\times \min \left\{\frac{t_M-t_{\text{heat}}}{t_{\text{heat}}+t_q},M_{\max }\right\}\times \frac{t_{\text{heat}}}{t_M}.$$ (21)

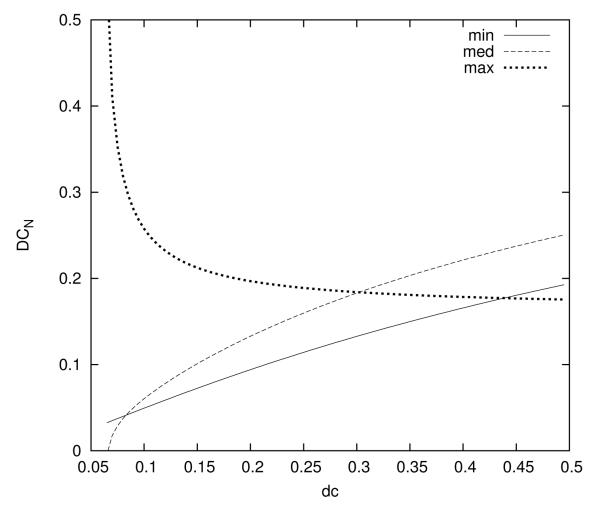
Here, M_max is set by the practical limits on the number of available “distant” locations in a tissue volume. The global duty cycle is constrained on the lower end by the max of t_M, on the upper end by the min of M (figure 6).

Figure 6.

Three expressions determine the net duty cycle, DC_N, as a function of machine duty cycle, dc. The treatment parameters are 1.3 MHz, 40 W peak acoustic power, 50 ms pulse length, maximum of 8 simultaneous treatment zones, and peak temperature around 5.25 °C. The transition from one treatment zone to the next was assumed to be 5 s. The net duty cycle is bounded from below by “min”, which is related to the transition time, and from above by “max”, which is determined by the number of treatment zones. In between, it follows the curve of “med”, which is determined by the heating constraint. The maximum net duty cycle of almost 20 % is achieved by using a machine duty cycle of 30 %.

Given constraints T_z = 5 °C, Δ = 0.05 (T_max = 5.25 °C), t_q = 5 s, t_p = 50 ms, N ≈ 100, and M_max = 8 available treatment sites, using A and α from the phantom study with 40 W and 1.3 MHz, the optimization theory predicts that DC_N is a maximum when the machine duty cycle is dc = 30 % (see figure 6). Applying (1) and (9), t_heat ≤ 9.65 s and t_M ≥ 126.9 s. With m = 8 focal spots per treatment zone, n_z = 7 pulses per focal spot will fit these requirements (t_heat = mn_zt_p/dc), and M = 7 treatment zones from (20). With S = 14 cycles of the treatment zones, there are N = 98 pulses per spot. The result, from (10) and (11), is a net duty cycle of 19.5 %, and a peak temperature increase of approximately 5.14 °C. Thus treatment under these conditions is about 4 times faster than could be achieved without optimization.

4. Discussion

In this study, we have developed an optimization procedure of pHIFU treatments for the ExAblate® 2000 system. The optimization has been developed in respect to safety considerations concerning tissue heating. The goal of this research is to enable an efficient means of treating large tumors with pHIFU while using feedback from MR thermometry to prevent tissue burning. Our results demonstrate that it is not sufficient to assume there will be no overlap of heating from neighboring focal spots, even if the distance between those spots is rather greater than the acoustic beam width. The spot width produced for a single sonication appears to be significantly larger than a theoretical estimate might suggest (Chung et al. 1999). This may be attributed in part to scattering of the ultrasonic beam off intervening tissue structures, but we believe it merits further investigation. Experimentally, our results appear very much in line with those of Gorny et al. (2006), who found average full-width, half-maximum diameters of single sonication spots to be 4.7 ± 0.3 mm, although with somewhat different parameters. In our case, the thermal buildup from neighboring focal spots in a small treatment zone was found to be significant over time, and could easily result in inhomogeneous heating, overheating, and thermal injury. Electronic steering alone was not found to reduce the heating rate significantly, and there appeared to be an unavoidable build-up of heat in the treatment zone regardless of the electronic steering pattern. This fact severely limits the rate at which small volumes may be treated without incurring thermal injury. Our optimization therefore involved a strategy to overcome the physical limitations imposed by slow tissue cooling for treatment of large volumes. We developed a method that allows treatment of multiple regions, making better use of treatment duty cycle while avoiding overheating. It involves fast electronic cycling between neighboring focal spots within a treatment zone combined with slow mechanical movements between distant treatment zones. This allows thermal dissipation while making best use of the speed of electronic steering. Cycling through the multiple treatment zones continues until all spots have received the required number of pulses. We were able to demonstrate that our method considerably reduces the time required for treatment of large tissue volumes.

To make use of the thermal measurements for optimization, we employed a simple theory of heating and cooling, expressed in (1) and (9). In the derivation of (1), two major assumptions are made, expressed as (3) and (6). Clearly, for this theory to work, the spatial heat deposition must rapidly assume a fairly smooth sinusoidal profile at the center of the treatment zone. In the case of a single treatment spot, this is a reasonable approximation to the more exact expression in O’Neill et al. (2009). For our problem here, however, with multiple distributed focal spots, it is not at all clear that (3) and particularly (6) will hold near the center of the treatment zone. Ultimately, the only justification for using (1) is that it adequately fits the empirical data, as indeed it does, evidenced in figure 3. We did not show an explicit derivation of (9), rather it was simply assumed that the heat would continue to dissipate at the same rate. In general, as time passes, this assumption becomes less accurate, particularly in the phantom with no perfusion. However, maintaining this simple form allows us to make use of an analytical solution. A compromise might be to use a different rate for cooling, which could be empirically justified by fitting the cooling portion of the cycle to (9).

The optimization results obtained here were based mainly on phantom thermal measurements. It is important to note that without the minimal animal data displayed, it would be difficult to accept the applicability of (1) and (9) beyond a phantom model having no perfusion. In fact, the animal results in this study preceded the phantom studies, and first demonstrated to us that, at least in bulk muscle, heating from neighboring focal spots is very significant and perfusion is not very significant when it comes to pHIFU treatment. These two facts are what made the phantom heating study both necessary and possible.

Even given the muscle results, with different tissues having different thermal and acoustic properties, one could question how well these results translate to a clinical setting. As demonstrated in the lower part of figure 2, it is possible to measure in vivo heating curves analogous to the phantom curves in figure 3. The main added difficulties compared to phantom studies lie in getting accurate thermal maps while working within the more limited range of temperatures that can be tolerated by tissues. These issues may contribute to additional variability in the parameters A and α, but for low pHIFU temperatures, would be unlikely to result in significant additional risk during an optimized treatment. At higher temperatures, on the other hand, this variability may indeed be a problem, and must be carefully addressed for each new tissue treated.

The results shown here are specifically applicable to the ExAblate® 2000, and potentially other systems with limited electronic steering, whether MRI guided or not. With increased electronic steering, other alternative strategies may be used. For example, with a large enough volume, a treatment involving quasi random jumping between distant focal spots would likely result in a more homogeneous temperature and thermal dose distribution than our approach. In principle, this could also be done with mechanical steering as well, provided the system is able to move rapidly enough.

5. Conclusion

There exists a physical limit to the rate at which one can apply pHIFU to small volumes without the risk of additional thermal buildup. Efficient treatment of large volumes is possible, but requires large movements, on the order of several centimeters in order to be implemented. In the ExAblate® 2000 system, this requires mechanical movements as well as electronic steering. Because the mechanical movements are much slower than electronic steering in this system, we developed a theory for optimally combining the rapid electronic steering movements with slow mechanical motions to effectively treat large volumes while maintaining a low peak temperature.