3D Forward and Back-Projection for X-Ray CT Using Separable Footprints

Abstract

Iterative methods for 3D image reconstruction have the potential to improve image quality over conventional filtered back projection (FBP) in X-ray computed tomography (CT). However, the computation burden of 3D cone-beam forward and back-projectors is one of the greatest challenges facing practical adoption of iterative methods for X-ray CT. Moreover, projector accuracy is also important for iterative methods. This paper describes two new separable footprint (SF) projector methods that approximate the voxel footprint functions as 2D separable functions. Because of the separability of these footprint functions, calculating their integrals over a detector cell is greatly simplified and can be implemented efficiently. The SF-TR projector uses trapezoid functions in the transaxial direction and rectangular functions in the axial direction, whereas the SF-TT projector uses trapezoid functions in both directions. Simulations and experiments showed that both SF projector methods are more accurate than the distance-driven (DD) projector, which is a current state-of-the-art method in the field. The SF-TT projector is more accurate than the SF-TR projector for rays associated with large cone angles. The SF-TR projector has similar computation speed with the DD projector and the SF-TT projector is about two times slower.

I. introduction

Iterative statistical methods for 3D tomographic image reconstruction [1]-[3] offer numerous advantages such as the potential for improved image quality and reduced dose, as compared to the conventional methods such as filtered back-projection (FBP) [4]. They are based on models for measurement statistics and physics, and can easily incorporate prior information, the system geometry and the detector response.

The main disadvantage of statistical reconstruction methods is the longer computation time of iterative algorithms that are usually required to minimize certain cost functions. For most iterative reconstruction methods, each iteration requires one forward projection and one back-projection, where the forward projection is roughly a discretized evaluation of the Radon transform, and the back-projector is the adjoint of the forward projector. These operations are the primary computational bottleneck in iterative reconstruction methods, particularly in 3D image reconstruction. Forward projector methods are also useful for making digitally rendered radiographs (DRR) [5], [6].

Traditional forward and back-projectors compute the intersection lengths between each tomographic ray and each image basis function. Many methods for accelerating this process have been proposed, e.g., [7]-[13]. Due to the finite size of detector cells, averaging the intersection lengths over each detector cell is considered to be a more precise modeling [14]-[19]. Mathematically, it is akin to computing the convolution of the footprint of each basis function and some detector blur, such as a 2D rectangular function.

Any projector method must account for the geometry of the imaging system. Cone-beam geometries are needed for axial and helical cone-beam X-ray computed tomography (CT). In 3D parallel-beam geometry projection space, there are four independent indices (u, v, φ, θ). The ray direction is specified by (φ, θ) where φ and θ denote the azimuthal and polar angle of the ray respectively and (u, v) denote the local coordinates on a 2D area detector. In contrast, axial cone-beam projection space is characterized by three independent indices (s, t, β) and two distance parameters (D_s0, D_0d), where β denotes the angle of the source point counter-clockwise from the y axis, (s, t) denote the detector coordinates, D_s0 denotes the source to rotation center distance and D_0d denotes the isocenter to detector distance. (See Fig. 1). The axial cone-beam geometry is a special case of helical cone-beam geometry with zero helical pitch.

Fig. 1.

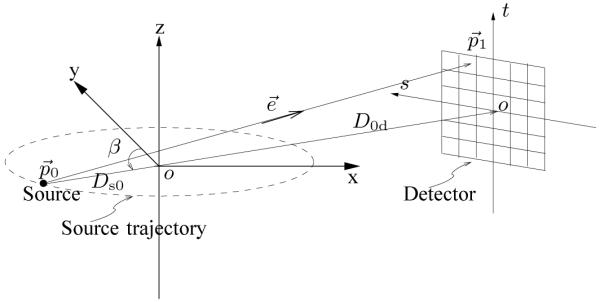
Axial cone-beam flat-detector geometry.

The divergence of tomographic rays in the cone-beam geometry causes depth-dependent magnification of image basis functions, i.e., voxels close to the X-ray source cast larger shadows on the detector than voxels close to the detector. This complication does not appear in the parallel-beam geometry. Therefore, many existing projection and back-projection methods designed for 3D parallel-beam geometry [16]-[18], [20], [21] are not directly suitable for cone-beam geometry.

A variety of projection methods for 3D cone-beam geometries have been proposed [5], [14], [15], [22]-[25]. All methods provide some compromise between computational complexity and accuracy. Among these, spherically symmetric basis functions (blobs) [15], [22] have many advantages over simple cubic voxels or other basis functions for the image representation, e.g., their appearance is independent of the viewing angle. However, evaluating integrals of their footprint functions is computationally intensive. Ziegler et al. [15] stored these integrals in a lookup-table. If optimized blobs are used and high accuracy is desired, the computation of forward and back-projection is still expensive due to loading a large table and the fact that blobs intersect many more tomographic rays than voxels.

Rectification techniques [24] were introduced to accelerate the computation of cone-beam forward and backward projections. Riddell et al. [24] resampled the original data to planes that are aligned with two of the reconstructed volume main axes, so that the original cone-beam geometry can be replaced by a simpler geometry that involves only a succession of plane magnifications. In iterative methods, resampled measurements can simplify forward and back-projection each iteration. However, resampling involves interpolation that may slightly decrease spatial resolution. Another drawback of this method is that the usual assumption of statistical independence of the original projection data samples no longer holds after rectification, since interpolation introduces statistical correlations.

The distance-driven (DD) projector [14] is a current state-of-the-art method. It maps the horizontal and vertical boundaries of the image voxels and detector cells onto a common plane such as xz or yz plane, approximating their shapes by rectangles. (This step is akin to rectification). It calculates the lengths of overlap along the x (or y) direction and along the z direction, and then multiplies them to get the area of overlap. The DD projector has the largest errors for azimuthal angles of the X-ray source that are around odd multiples of π/4, because the transaxial footprint is approximately triangular rather than rectangular at those angles.

This paper describes two new approaches for 3D forward and back-projection that we call the separable footprint (SF) projectors: the SF-TR [26] and SF-TT [27] projector. They approximate the voxel footprint functions as 2D separable functions. This approximation is reasonable for typical axial or helical cone-beam CT geometries. The separability of these footprint functions greatly simplifies the calculation of their integrals over a detector cell and allows efficient implementation of the SF projectors. The SF-TR projector uses trapezoid functions in the transaxial direction and rectangular functions in the axial direction, whereas the SF-TT projector uses trapezoid functions in both directions. It is accurate to use rectangle approximation in the axial direction for cone-beam geometries with small cone angles (< 2°) such as the multi-slice detector geometries, and to use trapezoid approximation for CT systems with larger cone angles (> 10°) such as flat-panel detector geometries.

Our studies showed that both SF projector methods are more accurate than the distance-driven (DD) projector. In particular, the SF methods reduce the errors around odd multiples of π/4 seen with DD. The SF-TT projector is more accurate than the SF-TR projector for voxels associated with large cone angles. The SF-TR projector has similar computation speed with the DD projector and the SF-TT projector is about 2 times slower.

To balance computation and accuracy, one may combine the SF-TR and SF-TT projector, that is, to use the SF-TR projector for voxels associated with small cone angles such as voxels near the plane of the X-ray source where the rectangle approximation is adequate, and use the SF-TT projector for voxels associated with larger cone angles.

The organization of this paper is as follows. Section II reviews the cone-beam geometry and projection, describes the cone-beam 3D system model. and presents the analytical formula of cone-beam projections of voxel basis functions. Section III introduces the SF projectors and contrasts the SF projectors with DD projector. Section IV gives simulation results, including accuracy and speed comparison between the SF-TR, SF-TT and DD projector as stand-alone modules and within iterative reconstruction. Finally, conclusions are presented in Section V.

II. cone-beam projection

A. Cone-Beam Geometry

For simplicity of presentation, we focus on the flat-detector axial cone-beam geometry (see Fig. 1). The methods generalize easily to arc detectors and helical geometries.

The source lies on points on a circle of radius D_s0 centered at the rotation center on the z = 0 plane. The source position ${\overrightarrow{p}}_0$ can be parameterized as follows:

$${\overrightarrow{p}}_0=\left(\begin{array}{c}\hfill -D_{s0}\sin \beta \hfill \\ \hfill D_{s0}\cos \beta \hfill \\ \hfill 0\hfill \end{array}\right),$$ (1)

where D_s0 is the source to rotation center distance and β denotes the angle of the source point counter-clockwise from the y axis. For simplicity, we present the case of an ideal point source of X-rays. To partially account for non-ideal X-ray sources, one can modify the footprint function in (20) and (26) below.

Let (s, t) denote the local coordinates on the 2D detector plane, where the s-axis is perpendicular to the z-axis, and the t-axis is parallel to the z-axis. A point on the 2D detector can be expressed as

$${\overrightarrow{p}}_1=\left(\begin{array}{c}\hfill s\cos \beta +D_{0d}\sin \beta \hfill \\ \hfill s\sin \beta -D_{0d}\cos \beta \hfill \\ \hfill t\hfill \end{array}\right),$$ (2)

where D_0d = D_sd − D_s0 is the isocenter to detector distance. The direction vector of a ray from ${\overrightarrow{p}}_0$ to ${\overrightarrow{p}}_1$ can then be expressed as

$$\overrightarrow{e}=\frac{{\overrightarrow{p}}_1-{\overrightarrow{p}}_0}{\parallel {\overrightarrow{p}}_1-{\overrightarrow{p}}_0\parallel }=\left(\begin{array}{c}\hfill \sin \phi \cos \theta \hfill \\ \hfill -\cos \phi \cos \theta \hfill \\ \hfill \sin \theta \hfill \end{array}\right)$$ (3)

where

$$\gamma =\gamma \left(s\right)\triangleq \text{arctan}\left(\frac{s}{D_{sd}}\right)$$ (4)

$$\phi =\phi (s,\beta )\triangleq \gamma \left(s\right)+\beta$$ (5)

$$\theta =\theta (s,t)\triangleq -\text{arctan}\left(\frac{t}{\sqrt{s^2+D_{sd}^2}}\right)$$ (6)

and φ and θ denote the azimuthal and polar angle of the ray from ${\overrightarrow{p}}_0$ to ${\overrightarrow{p}}_1$ respectively.

The cone-beam projections of a 3D object $f\left(\overrightarrow{\mathrm{X}}\right)$, where $\overrightarrow{\mathrm{X}}=(x,y,z)$, are given by

$$p(s,t;\beta )={\int }_{\mathcal{L}(s,t,\beta )}f\left(\overrightarrow{x}\right)dl,$$ (7)

where the integral is along the line segment:

$$\begin{array}{cc}\hfill \mathcal{L}(s,t,\beta )=& \{{\overrightarrow{p}}_0+l\overrightarrow{e}:l\in [0,L_p]\}\hfill \\ \hfill L_p\triangleq & \sqrt{D_{sd}^2+s^2+t^2}\hfill \end{array}$$ (8)

For a point $\overrightarrow{\mathrm{X}}=(x,y,z)$ between the source and detector, the projected s coordinate of it is

$$\tau (\beta ;x,y)=D_{sd}\frac{{\tau }_p(\beta ;x,y)}{d_s(\beta ;x,y)}$$ (9)

where

$$\begin{array}{cc}\hfill {\tau }_p\triangleq & x\cos \beta +y\sin \beta ,\hfill \\ \hfill d_s\triangleq & D_{s0}-{\tau }_{\perp }(\beta ;x,y),\hfill \\ \hfill {\tau }_{\perp }\triangleq & -x\sin \beta +y\cos \beta \hfill \end{array}$$ (10)

The projected t coordinate is

$$t(\beta ;x,y,z)=z\frac{D_{sd}}{d_s(\beta ;x,y)}$$ (11)

The azimuthal and polar angles of the ray connecting the source and $\overrightarrow{\mathrm{X}}$ are

$$\phi (\beta ;x,y)=\beta +\text{arctan}\left(\frac{{\tau }_p(\beta ;x,y)}{d_s(\beta ;x,y)}\right)$$ (12)

$$\theta (\beta ;x,y)=-\text{arctan}\left(\frac{z}{\sqrt{{\tau }_p^2+d_s^2}}\right)$$ (13)

B. Cone-Beam 3D System Model

In the practice of iterative image reconstruction, rather than operating on a continuous object $f\left(\overrightarrow{\mathrm{X}}\right)$, we forward project a discretized object represented by a common basis function ${\beta }_0\left(\overrightarrow{\mathrm{X}}\right)$ superimposed on a N₁ × N₂ × N₃ Cartesian grid as follows:

$$f\left(\overrightarrow{x}\right)=\sum _{\overrightarrow{n}}f\left[\overrightarrow{n}\right]{\beta }_0\left((\overrightarrow{x}-\overrightarrow{c}\left[\overrightarrow{n}\right])\oslash \overrightarrow{\Delta }\right)$$ (14)

where the sum is over the N₁×N₂×N₃ lattice that is estimated and $\overrightarrow{c}\left[\overrightarrow{n}\right]=({\mathrm{c}}_1\left[\overrightarrow{n}\right],{\mathrm{c}}_2\left[\overrightarrow{n}\right],{\mathrm{c}}_3\left[\overrightarrow{n}\right])$ denotes the center of the $\overrightarrow{n}\mathrm{th}$ basis function and $\overrightarrow{n}=(n_1,n_2,n_3)\in {\mathbb{Z}}^3$. The grid spacing is $\overrightarrow{\Delta }=({\Delta }_1,{\Delta }_2,{\Delta }_3)$, and ⊘ denotes element-wise division. We consider the case Δ₁ = ±Δ₂ hereafter, but we allow Δ₁ ≠ Δ₃, because voxels are often not cubic.

Most projection/back-projection methods use a linear model that ignores the ”exponential edge gradient effect” caused by the nonlinearity of Beer’s law [28], [29]. We adopt the same type of approximation here. Assume that the detector blur h(s, t) is shift invariant, independent of β, and acts only along the s and t coordinates. Then the ideal noiseless projections satisfy

$${\stackrel{‒}{y}}_{\beta }[s_k,t_l]=\int \int h(s_k-s,t_l-t)p(s,t;\beta )dsdt,$$ (15)

where p(s, t; β) is the 3D projection of $f\left(\overrightarrow{\mathrm{X}}\right)$ given by (7), and (s_k, t_l) denotes the center of detector cell specified by indices (k, l). The methods we present are applicable to arbitrary samples (s_k, t_l), but for simplicity of presentation and implementation we focus on the case of uniformly spaced samples:

$$\begin{array}{cc}\hfill s_k=& (k-w_s){\Delta }_s,k=0,\dots ,N_s-1,\hfill \\ \hfill t_l=& (l-w_t){\Delta }_T,l=0,\dots ,N_t-1,\hfill \\ \hfill w_s=& (N_s-1)∕2+c_s,\hfill \\ \hfill w_t=& (N_t-1)∕2+c_t,\hfill \end{array}$$ (16)

where Δ_S and Δ_T denote the sample spacing in s and t respectively. The user-selectable parameters c_s and c_t denote offsets for the detector, e.g., c_s = 1/4 corresponds to a quarter detector offset [30], [31].

Substituting the basis expansion model (14) for the object into (15) and using (7) leads to the linear model

$${\stackrel{‒}{y}}_{\beta }[s_k,t_l]=\sum _{\overrightarrow{n}}a\beta [s_k,t_l;\overrightarrow{n}]f\left(\overrightarrow{n}\right),$$ (17)

where the elements of system matrix A are samples of the following cone-beam projection of a single basis function centered at $\overrightarrow{c}\left[\overrightarrow{n}\right]$:

$$a_{\beta }[s_k,t_l;\overrightarrow{n}]=F(s_k,t_l;\beta ;\overrightarrow{n})$$ (18)

where the “blurred footprint” function is

$$F(s_k,t_l;\beta ;\overrightarrow{n})\triangleq \int \int h(s_k-s,t_l-t)q(s,t;\beta ;\overrightarrow{n})dsdt,$$ (19)

and $q(s,t;\beta ;\overrightarrow{n})$ denotes the cone-beam footprint of basis function ${\beta }_0\left((\overrightarrow{\mathrm{X}}-\overrightarrow{c}\left[\overrightarrow{n}\right])\oslash \overrightarrow{\Delta }\right)$, i.e.,

$$q(s,t;\beta ;\overrightarrow{n})={\int }_{\mathcal{L}(s,t,\beta )}{\beta }_0\left((\overrightarrow{x}-\overrightarrow{c}\left[\overrightarrow{n}\right])\oslash \overrightarrow{\Delta }\right)dl.$$ (20)

Computing the footprint of the voxel is also known as “splatting” [32].

The goal of forward projectors is to compute (17) rapidly but accurately. Although the system matrix A is sparse, it is impractical to precompute and store even the nonzero system matrix values for the problem sizes of interest in cone-beam CT, so practical methods (including our proposed approach) essentially compute those values on the fly.

We focus on a simple separable model for the detector blur

$$h(s,t)=\frac{1}{r_s{r}_t}\text{rect}\left(\frac{s}{r_s}\right)\text{rect}\left(\frac{t}{r_t}\right)$$ (21)

where r_s and r_t denote the width along s and t respectively. This model accounts for the finite size of the detector elements. Note that r_s and r_t can differ from the sample spacing s_k − s_k−1 and t_l − t_l−1 to account for detector gaps.

C. Footprints of Voxel Basis Functions

We focus on cubic voxel basis functions hereafter, but one could derive analytical formulas for footprints of other basis functions. The cubic voxel basis function is given by,

$$\begin{array}{cc}\hfill {\beta }_0\left(\overrightarrow{x}\right)=& \text{rect}\left(x\right)\text{rect}\left(y\right)\text{rect}\left(z\right)\hfill \\ \hfill =& 1_{\{\mid x\mid \le 1∕2\}}{1}_{\{\mid y\mid \le 1∕2\}}{1}_{\{\mid z\mid \le 1∕2\}}\hfill \end{array}$$ (22)

where $1_{\{\cdot \}}$ denotes the indicator function.

Substituting (22) into (20), the analytical formula for the cone-beam projection footprint of the $\overrightarrow{n}\text{th}$ basis function is:

$$\begin{array}{cc}\hfill q(s,t;\beta ;\overrightarrow{n})=& {\int }_0^{L_p}{\beta }_0\left(({\overrightarrow{p}}_0+l\overrightarrow{e}-\overrightarrow{c}\left[\overrightarrow{n}\right])\oslash \overrightarrow{\Delta }\right)dl\hfill \\ \hfill =& {\int }_0^{L_p}{1}_{\{\mid d_1+l{e}_1\mid \le {\Delta }_1∕2\}}{1}_{\{\mid d_2+l{e}_2\mid \le {\Delta }_2∕2\}}{1}_{\{\mid d_3+l{e}_3\mid \le {\Delta }_3∕2\}}dl\hfill \\ \hfill =& a_1\cdot a_{}\cdot a_3\cdot {[l_{max}-l_{min}]}_{+},\hfill \end{array}$$ (23)

where $\overrightarrow{e}=(e_1,e_2,e_3)$ was defined in (3), ${\left[x\right]}_{+}\triangleq \max (x,0)$ and

$$\begin{array}{cc}\hfill \overrightarrow{d}\triangleq & {\overrightarrow{p}}_0-\overrightarrow{c}\left[\overrightarrow{n}\right]=(d_1,d_2,d_3),\hfill \\ \hfill a_1=& \{\begin{array}{cc}{1}_{\{\mid d_1\mid \le {\Delta }_1∕2\}};\hfill & \sin \phi =0\hfill \\ 1;\hfill & \sin \phi \ne 0,\hfill \end{array}\phantom{\}}\hfill \\ \hfill a_2=& \{\begin{array}{cc}{1}_{\{\mid d_2\mid \le {\Delta }_2∕2\}};\hfill & \cos \phi =0\hfill \\ 1;\hfill & \sin \phi \ne 0,\hfill \end{array}\phantom{\}}\hfill \\ \hfill a_3=& \{\begin{array}{cc}{1}_{\{\mid d_3\mid \le {\Delta }_3∕2\}};\hfill & \sin \theta =0\hfill \\ 1;\hfill & \sin \theta \ne 0,\hfill \end{array}\phantom{\}}\hfill \\ \hfill l_{max}=& \text{min}\left\{L_p,l_{+}^1,l_{+}^2,l_{+}^3\right\},\hfill \\ \hfill l_{min}=& \text{max}\left\{0,l_{-}^1,l_{-}^2,l_{-}^3\right\},\hfill \\ \hfill l_{+}^i=& \{\begin{array}{cc}\text{max}\left\{\frac{{\overrightarrow{\Delta }}_i∕2-d_i}{e_i},\frac{-{\overrightarrow{\Delta }}_i∕2-d_i}{e_i}\right\},;\hfill & e_i\ne 0\hfill \\ \alpha ;\hfill & e_i=0\hfill \end{array}\phantom{\}}\hfill \\ \hfill l_{-}^i=& \{\begin{array}{cc}\text{min}\left\{\frac{{\overrightarrow{\Delta }}_i∕2-d_i}{e_i},\frac{-{\overrightarrow{\Delta }}_i∕2-d_i}{e_i}\right\},;\hfill & e_i\ne 0\hfill \\ -\alpha ;\hfill & e_i=0,\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (24)

For typical cone-beam geometries, polar angles θ of rays are much smaller than 90°, so there is no need to consider the case of cosθ = 0. Combining (18), (19) and (23) yields the “ideal” projector for cubic voxels in cone-beam CT.

III. separable footprint (SF) projector

It would be expensive to exactly compute the true footprint (23) and the “blurred footprint” (19) for the voxel basis function on the fly, so appropriate approximations of the “blurred footprint” (19) are needed to simplify the double integral calculation.

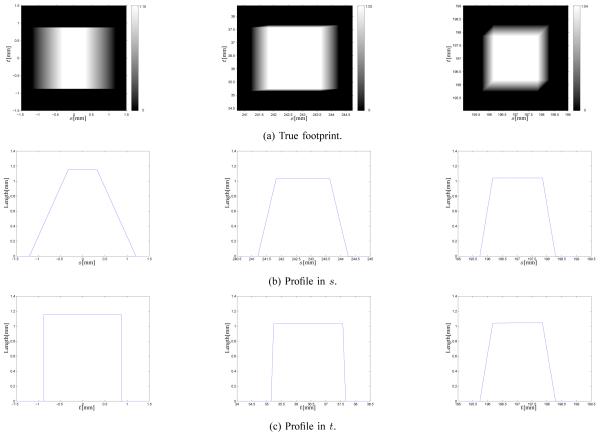
To explore alternatives, we simulated a flat-detector cone-beam geometry with D_s0 = 541 mm and D_sd = 949 mm. We computed cone-beam projections of voxels analytically using (23) at sample locations (nΔ_S, mΔ_T) where Δ_S = Δ_T = 0.001 mm and $n,m\in \mathbb{Z}$. The left column of Fig. 2 shows the exact footprint function and its profiles for a voxel with Δ₁ = Δ₂ = Δ₃ = 1 mm centered at the origin when β = 30°. The center column of Fig. 2 shows those of a voxel centered at (100, 150, 15) mm when β = 0°. The azimuthal and polar angle of the ray connecting the source and this voxel center are 14.3° and 2.1° respectively. The cone angle of a typical 64-slice cone-beam CT geometry is about 2°. The right column of Fig. 2 shows those of a voxel centered at (93, 93, 93) mm when β = 0°. The azimuthal and polar angle of the ray connecting the source and this voxel center are 11.7° and 11.5° respectively. The cone angle of a typical cone-beam CT geometry with 40 × 40 cm² flat-panel detector is about 12°. The first two true footprints look like 2D separable functions. The third footprint is approximately separable except for small areas at the upper left and lower right corner.

Fig. 2.

Exact footprint functions $q(s,t;\beta ;\overrightarrow{n})$ and their profiles for 1mm³ voxels centered at the origin (left), (100, 150, 15) mm (center) and (93, 93, 93) mm (right).

Inspired by shapes of the true footprints (see Fig. 2), we approximate them as follows,

$$q(s,t;\beta ;\overrightarrow{n})\approx q_{ap}(s,t;\beta ;\overrightarrow{n})\triangleq l(s,t;\beta ;\overrightarrow{n})q_{sf}(s,t;\beta ;\overrightarrow{n})$$ (25)

where $q_{\mathrm{sf}}(s,t;\beta ;\overrightarrow{n})$ denotes a 2D separable function with unit maximum amplitude,

$$q_{sf}(s,t;\beta ;\overrightarrow{n})\triangleq q_1(s,\beta ;\overrightarrow{n})q_2(t;\beta ;\overrightarrow{n}),$$ (26)

where $q_1(s;\beta ;\overrightarrow{n})$ and $q_2(t;\beta ;\overrightarrow{n})$ denote the approximating functions in s and t respectively. In (25), $l(s,t;\beta ;\overrightarrow{n})$ denotes the “amplitude” of $q_{\mathrm{sf}}(s,t;\beta ;\overrightarrow{n})$.

For small basis functions and narrow blurs h(s, t), the angles of rays within each detector cell that intersect each basis function are very similar, so $l(s,t;\beta ;\overrightarrow{n})$ is much smoother than h(s, t) and $q(s,t;\beta ;\overrightarrow{n})$. Substituting (25) into (19) leads to

$$\begin{array}{cc}\hfill F(s,t;\beta ;\overrightarrow{n})\approx & F_{sf}(s,t;\beta ;\overrightarrow{n})\hfill \\ \hfill \triangleq & h(s,t)\ast \ast \left[l(s,t;\beta ;\overrightarrow{n})q_{sf}(s,t;\beta ;\overrightarrow{n})\right]\hfill \\ \hfill \approx & l(s,t;\beta ;\overrightarrow{n})[h(s,t)\ast \ast q_{sf}(s,t;\beta ;\overrightarrow{n})],\hfill \end{array}$$ (27)

where the inequality uses the fact that $l(s,t;\beta ;\overrightarrow{n})$ is approximately a constant over each detector cell. The value $l(s_k,t_l;\beta ;\overrightarrow{n})$ denotes this constant for detector cell (s_k, t_l), and * denotes 2D convolution

If the detector blur is also modeled as separable, i.e.,

$$h(s,t)=h_1\left(s\right)h_2\left(t\right),$$ (28)

then the blurred footprint functions (27) have the following separable approximation:

$$F_{sf}(s_k,t_l;\beta ;\overrightarrow{n})=l(s_k,t_l;\beta ;\overrightarrow{n})F_1(s_k;\beta ;\overrightarrow{n})F_2(t_l;\beta ;\overrightarrow{n}),$$ (29)

where

$$\begin{array}{cc}\hfill F_1(s_k;\beta ;\overrightarrow{n})& \triangleq \int h_1(s_k-s)q_1(s;\beta ;\overrightarrow{n})ds\hfill \\ \hfill F_2(t_l;\beta ;\overrightarrow{n})& \triangleq \int h_2(t_l-t)q_2(t;\beta ;\overrightarrow{n})dt.\hfill \end{array}$$ (30)

A. Amplitude Approximation Methods

One natural choice for the amplitude function l(·) is the following voxel-dependent factor that we call the A3 method:

$$l(s_k,t_l;\beta ;\overrightarrow{n})=l_3(\beta ;\overrightarrow{n})\triangleq l_{{\phi }_0}\cdot l_{{\theta }_0}$$ (31)

where

$$l_{{\phi }_0}\triangleq \frac{{\Delta }_1}{\max \left\{\mid \cos \left({\phi }_0\right)\mid ,\mid \sin \left({\phi }_0\right)\mid \right\}}$$ (32)

$${l_{\theta }}_0\triangleq \frac{1}{\mid \cos \left({\theta }_0\right)\mid },$$ (33)

where ${\phi }_0={\phi }_0(\beta ,\overrightarrow{n})$ and ${\theta }_0={\theta }_0(\beta ,\overrightarrow{n})$ denote the azimuthal and polar angles of the ray connecting the source and center of the $\overrightarrow{n}\mathrm{th}$ voxel. They can be computed by (12) and (13). Since this voxel-dependent amplitude depends on angles (θ₀, φ₀) and β, the approximated footprint $q_{\mathrm{ap}}(s,t;\beta ;\overrightarrow{n})$ is separable with respect to s and t too. However, the dependence on voxel centers $\overrightarrow{c}\left[\overrightarrow{n}\right]$ requires expensive computation. One must compute N₁ × N₂ × N₃ × N_β different l_θ0 values and N₁ × N₂ × N_β different l_φ0 values, where N_β denotes the number of projection views. In addition, computing l_θ0 and l_φ0 for each voxel at each projection view involves either trigonometric operations (cos, sin and tan⁻¹) or square and square root operations to directly evaluate cos and sin.

To accelerate computation of the SF projector, we propose a voxel-ray-dependent amplitude named the A2 method:

$$l_2(s_k,t_l;\beta ;\overrightarrow{n})\triangleq l_{{\phi }_0}\cdot l_{\theta (s_k,t_l)}$$ (34)

$$l_{\theta (s_k,t_l)}\triangleq \frac{1}{\mid \cos \left(\theta (s_k,t_l)\right)\mid },$$ (35)

where θ(s_k, t_l) given in (6) is the polar angle of the ray connecting the source and detector center (s_k, t_l). There are many fewer tomographic rays (N_s × N_t) than voxels in a 3D image (N₁ × N₂ × N₃) and θ(s_k, t_l) does not depend on β for flat detector geometries (see (6)), so using (34) saves substantial computation versus (31).

We also investigated a ray-dependent amplitude named the A1 method:

$$l_1(s_k,t_l;\beta )\triangleq l_{\phi (s_k;\beta )}\cdot l_{\theta }(s_k,t_l)$$ (36)

$$l_{\phi (s_k;\beta )}\triangleq \frac{{\Delta }_1}{\max \left\{\mid \cos \left(\phi (s_k;\beta )\right)\mid ,\mid \sin \left(\phi (s_k;\beta )\right)\mid \right\}},$$ (37)

where φ(s_k; β) given in (5) is the azimuthal angle of the ray connecting the source and detector cell center (s_k, t_l). For each β, there are N_s different l_φ(sk;β) for the A1 method and N₁ × N₂ different l_φ0 for the A2 method.

These amplitude methods are similar to Joseph’s method [8] where the triangular footprint function is scaled by 1/max(| cos φ|, | sin φ|) for 2D fan-beam geometry. All three methods have similar accuracies, but the A3 method is much slower than the other two (see Section IV-A). Thus we do not recommend using the A3 amplitude in the SF projector method. Hereafter, we refer to (29) with either (34) or (36) as “the SF method”.

B. SF Projector with Trapezoid/Rectangle Function (SF-TR)

Inspired by the shapes of the true footprints associated with small cone angles (see the first two columns of Fig. 2), we approximate them as 2D separable functions with trapezoid functions in the transaxial direction and rectangular functions in the axial direction. This approximation is reasonable for typical multi-slice cone-beam geometries, where the azimuthal angles φ of rays cover the entire 360° range since the X-ray source rotates around the z axis, whereas the polar angles θ of rays are small (less than 2°) since the cone angle is small.

The approximating function in the s direction is

$$\begin{array}{cc}\hfill q_1(s;\beta ;\overrightarrow{n})\triangleq & \mathrm{trap}(s;{\tau }_0,{\tau }_1,{\tau }_2,{\tau }_3)\hfill \\ \hfill =& \{\begin{array}{cc}\frac{s-{\tau }_0}{{\tau }_1-{\tau }_0},\hfill & {\tau }_0<s<{\tau }_1\hfill \\ 1,\hfill & {\tau }_1\le s\le {\tau }_2\hfill \\ \frac{{\tau }_3-s}{{\tau }_3-{\tau }_2},\hfill & {\tau }_2<s<{\tau }_3\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},\hfill \end{array}$$ (38)

where τ₀, τ₁, τ₂ and τ₃ denote vertices of the trapezoid function that we choose to match the exact locations of those of the true footprint function in the s direction. They are the projected s coodinates of four corner points located at $({\mathrm{c}}_1\left[\overrightarrow{n}\right]\pm {\Delta }_1∕2,{\mathrm{c}}_2\left[\overrightarrow{n}\right]\pm {\Delta }_2∕2)$ for all z.

The approximating function in the t direction is

$$q_2(t;\beta ;\overrightarrow{n})\triangleq \mathrm{rect}\left(\frac{t-t_0}{w_{t0}}\right),$$ (39)

where

$$\begin{array}{cc}\hfill t_0\triangleq & \frac{t_{+}+t_{-}}{2},\hfill \\ \hfill w_{t0}\triangleq & t_{+}-t_{-},\hfill \end{array}$$ (40)

where t₊ and t₋ denote the boundaries of the rectangular function which we choose to be the projected t coordinates of the two endpoints of the axial midline of the voxel. Those endpoints are located at $\overrightarrow{c}\left[\overrightarrow{n}\right]\pm (0,0,{\Delta }_3∕2)$. Given β and a point $\overrightarrow{\mathrm{X}}=(x,y,z)$, the projected s and t coordinate of this point can be computed by (9) and (11). Since the boundaries of the separable function are determined by the projections of boundaries of the voxel basis function under the cone-beam geometry, the depth-dependent magnification is accurately modeled.

The blurred footprint functions (30) of this SF-TR projector are

$$F_1(s_k;\beta ;\overrightarrow{n})=\frac{1}{r_{\mathrm{s}}}\gamma (s_k-\frac{r_{\mathrm{s}}}{2},s_k+\frac{r_s}{2}),$$ (41)

and

$$F_2(t_l;\beta ;\overrightarrow{n})=\frac{1}{r_{\text{t}}}{[\text{min}(t_l+\frac{r_{\text{t}}}{2},t_{+})-\text{max}(t_l-\frac{r_{\text{t}}}{2},t_{-})]}_{+},$$ (42)

where

$$\begin{array}{cc}\hfill \gamma (s_1,s_2)\triangleq & {\int }_{s_1}^{s_2}\text{trap}(s;{\tau }_0;{\tau }_1;{\tau }_2;{\tau }_3)d_s\hfill \\ \hfill =& {\gamma }_1(\text{max}(s_1,{\tau }_0),\text{min}(s_2,{\tau }_1))\hfill \\ \hfill & +{\gamma }_2(\text{max}(s_1,{\tau }_1),\text{min}(s_2,{\tau }_2))\hfill \\ \hfill & +{\gamma }_3(\text{max}(s_1,{\tau }_2),\text{min}(s_2,{\tau }_3)),\hfill \\ \hfill {\gamma }_1(b_1,b_2)\triangleq & \frac{1}{2({\tau }_1-{\tau }_0)}[{(b_2-{\tau }_0)}^2-{(b_1-{\tau }_0)}^2]1_{\{b_2>b_1\}},\hfill \\ \hfill {\gamma }_2(b_1,b_2)\triangleq & (b_2-b_1)1_{\{b_2>b_1\}},\hfill \\ \hfill {\gamma }_3(b_1,b_2)\triangleq & \frac{1}{2({\tau }_3-{\tau }_2)}[{(b_1-{\tau }_3)}^2-{(b_2-{\tau }_3)}^2]1_{\{b_2>b_1\}}.\hfill \end{array}$$ (43)

C. SF Projector with Trapezoid/Trapezoid Function (SF-TT)

Inspired by the shape of true footprint of a voxel associated with large cone angles (see the last column of Fig. 2), we approximate it as a 2D separable function with trapezoid functions in both the transaxial and axial direction. This trapezoid approximation in axial direction is reasonable for cone-beam geometries with large cone angles (> 10°) such as flat-panel detector geometries.

Along s, the SF-TT projector uses the same trapezoid approximation as the SF-TR projector. The trapezoid footprint and the blurred footprint are given in (38) and (41).

The approximated footprint function in t is

$$q_2(t;\beta ;\overrightarrow{n})\triangleq \text{trap}(t;{\xi }_0,{\xi }_1,{\xi }_2,{\xi }_3),$$ (44)

where ξ₀, ξ₁, ξ₂ and ξ₃ denote vertices of the trapezoid function. ξ₀ and ξ₁ are the smallest and largest one of the projected t coordinates of the lower four corners of the $\overrightarrow{n}\mathrm{th}$ voxel located at $({\mathrm{c}}_1\left[\overrightarrow{n}\right]\pm {\Delta }_1∕2,{\mathrm{c}}_2\left[\overrightarrow{n}\right]\pm {\Delta }_2∕2,{\mathrm{c}}_3\left[\overrightarrow{n}\right]-{\Delta }_3∕2)$, and ξ₂ and ξ₃ are the smallest and largest one of the projected t coordinates of the upper four corners located at $({\mathrm{c}}_1\left[\overrightarrow{n}\right]\pm {\Delta }_1∕2,{\mathrm{c}}_2\left[\overrightarrow{n}\right]\pm {\Delta }_2∕2,{\mathrm{c}}_3\left[\overrightarrow{n}\right]+{\Delta }_3∕2)$. The blurred footprint function in t is

$$F_2(t_1;\beta ;\overrightarrow{n})=\frac{1}{r_{\text{t}}}\gamma (t_1-\frac{r_{\text{t}}}{2},t_l+\frac{r_{\text{t}}}{2}),$$ (45)

where γ is given in (43).

By choosing the vertices of the approximating footprints to match the projections of the voxel boundaries, the approximation adapts to the relative positions of the source, voxels and detector, as true footprints do. Take a voxel centered at the origin as an example. Its axial footprint is approximately a rectangular function (see the left figure in the third row of Fig. 2), instead of a trapezoid function. For this voxel trap(t; ξ₀, ξ₁, ξ₂, ξ₃) is almost a rectangle because ξ₀ ≈ ξ₁ and ξ₂ ≈ ξ₃ because ξ₀, ξ₁, ξ₂ and ξ₃ are the projected t coordinates of four axial boundaries of this voxel.

D. Implementation of SF Projector

We use the system matrix model (18) with the separable footprint approach (29) for both forward and back projection, which ensures that the SF forward and back projector are exact adjoint operators of each other.

Table I summaries the SF-TR projector with the A1 amplitude method (SF-TR-A1) and with the A2 method (SF-TR-A2) for a given projection view angle β. Implementating the SF-TT projector with these two amplitude methods is similar. Implementation of the back-projector is similar, except for scaling the projections at the beginning instead of the end. The key to efficient implementation of this method is to make the inner loop over z (or equivalently over t_l) [33], because the values of $F_1(S_k;\beta ;\overrightarrow{n})$ are independent of z and t_l so they are precomputed prior to that loop. Because (11) is linear in z, the first value of t_± for a given (x, y) position can be computed prior to the inner loop over z, and subsequent values can be computed by simple incremental updates, cf. [34]. Thus only simple arithmetic operations and conditionals are needed for evaluating $F_2(t_l;\beta ;\overrightarrow{n})$ in that inner loop; all trigonometric computations occur outside that loop. Note that this separable footprint approach does not appear to be particularly advantageous for 2D fan-beam forward and backprojection because computing the transaxial footprint $F_1(s_k;\beta ;\overrightarrow{n})$ requires trigonometric operations. The compute efficiency here comes from the simple rectangular footprint approximation in the axial direction. More computation is needed for the SF-TT method because it uses trapezoids in the axial direction instead rectangles.

TABLE I.

Pseudo-code for the SF-TR forward projector with the A1 amplitude method (SF-TR-A1) and the A2 method (SF-TR-A2)

• Initialize projection view array to zero, i.e., ${\stackrel{‒}{y}}_{\beta }[s_k,t_l]=0$ for  k = 0, … , Ns − 1 and l = 0, … , Nt − 1

• For each row n1 = 0, 1, … , N1 − 1 of $f\left[\overrightarrow{n}\right]$:

1) For each column n2 = 0, 1, … , N2 − 1:

a) Compute trapezoid vertices τ0, τ1, τ2, τ3 in (38) using    (9).

b) Determine indices (sk values) of detector cells that    intersect [τ0, τ3], i.e. $\{k:[s_k-\frac{r_s}{2},s_k+\frac{r_s}{2}]\cap [{\tau }_0,{\tau }_3]\ne \varnothing \}$.

c) Compute transaxial footprint $F_1(s_k;\beta ;\overrightarrow{n})$ using (41)    and (43) for all these sk values and store them.

d) Compute $l_{{\phi }_0}$ using (32) (SF-TR-A2 only)

e) For each slice n3 = 0, 1, … , N3 − 1:

i) Determine indices (tl values) of detector cells that     intersect [t−, t+], i.e., $\{l:[t_1-\frac{r_t}{2},t_l+\frac{r_t}{2}]\cap [t_{-},t_{+}]\ne \varnothing \}$.

ii) For each tl value:

A) Compute $F_2(t_l;\beta ;\overrightarrow{n})$ using (42).

B) For each sk value:

– Compute projection       $p(s_k,t_l;\beta ;\overrightarrow{n})$ where $p=f\left[\overrightarrow{n}\right]F_1(s_k;\beta ;\overrightarrow{n})F_2(t_l;\beta ;\overrightarrow{n})$ for SF-       TR-A1,       $p=f\left[\overrightarrow{n}\right]l_{{\phi }_0}{F}_1(s_k;\beta ;\overrightarrow{n})F_2(t_l;\beta ;\overrightarrow{n})$ for       SF-TR-A2.

– Update projection view ${\stackrel{‒}{y}}_{\beta }[s_k,t_l]\pm p$.

• Scale all the projection view by l1(sk, tl; β) using (36) for  SF-TR-A1 or by lθ(sk, tl) using (35) for SF-TR-A2.

The implementation of amplitude $l(s_k,t_l;\beta ;\overrightarrow{n})$ in (29) for the A1 and A2 methods are different. For the A1 method, for each β the amplitude l₁(s_k, t_l; β) is implemented by scaling projections outside the loop over voxels since it depends on detector cells only. For the A2 method, we implemented the two terms $\left(l_{{\phi }_0}\text{and}{l}_{\theta (s_k,t_l)}\right)$ of $l_2(s_k,t_1;\beta ;\overrightarrow{n})$ separately. We scaled the projections by l_θ(sk,tl) outside of the loop over voxels and computed l_φ0 outside the inner loop over z since it does not depend on z.

The SF methods require O(N⁴) operations for forward/back projection of a N³ volume to/from N³ samples of the cone-beam projections. There exist O(N³ log N) methods for back-projection [35]-[37]. However, those algorithms may not capture the distance-dependent effect of detector blur incorporated in the model (18). In 2D one can use the Fourier Slice Theorem to develop O(N² log N) methods [38], but it is unclear how to generalize those to 3D axial and helical CT efficiently.

E. SF Compared with DD

The DD method essentially approximates the voxel footprints using rectangles in both directions on a common plane such as xz or yz plane. It also uses the separable and shift-invariant detector blur (21) on the detector plane. However, the approximated separable detector blurs on the common plane based on the mapped boundaries of original detector blurs are no longer shift invariant. This appears to prevent using the inner loop over s_k that aids efficiency of the SF methods.

IV. results

To evaluate our proposed SF-TR and ST-TT projectors, we compared them with the DD projector, a current start-of-the-art method. We compared their accuracy and speed as single modules and within iterative reconstruction methods.

A. Forward and Back-Projector as Single Modules

We simulated an axial cone-beam flat-detector X-ray CT system with a detector size of N_s × N_t = 512 × 512 cells spaced by Δ_S = Δ_T = 1 mm with N_β = 984 angles over 360°. The source to detector distance D_sd is 949 mm, and the source to rotation center distance D_s0 is 541 mm. We included a rectangular detector response (21) with r_s = Δ_S and r_t = Δ_T.

We implemented the SF-TR and SF-TT projector in an ANSI C routine. The DD projector was provided by De Man et al., also implemented as ANSI C too. All used single precision. For both the SF methods and the DD method we used POSIX threads to parallelize the operations. For the forward projector each thread works on different projection views, whereas for the back projector each thread works on different image rows (n₂).

1) Maximum Errors of Forward Projectors

We define the maximum error as

$$e(\beta ;\overrightarrow{n})=\underset{s,t\in R}{\text{max}}\mid F(s,t;\beta ;\overrightarrow{n})-F_{\text{ap}}(s,t;\beta ;\overrightarrow{n})\mid ,$$ (46)

where F_ap is any of the approximate blurred footprints by the SF-TR, SF-TT and DD methods. We generated the true blurred footprint $F(s,t;\beta ;\overrightarrow{n})$ in (19) by linearly averaging 1000 × 1000 analytical line integrals of rays sampled over each detector cell. We computed the line integral of each ray by the exact method described in (23).

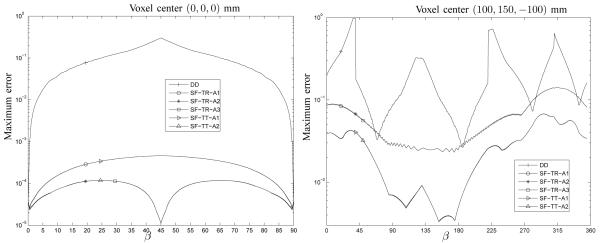
We compared the maximum errors of these forward projectors for a voxel with Δ₁ = Δ₂ = Δ₃ = 1mm centered at the origin. Since the voxel is centered at the origins of all axes, we choose N_β = 180 angles over only 90° rotation. Fig. 3 shows the errors on a logarithmic scale. We compared the proposed three amplitude methods by combining them with the SF-TR projector. The errors of the A1 method are slightly larger than those of the A2 and A3 method; the biggest difference, at β = 45°, is only 3.4×10⁻⁴. The error curves of the A2 and A3 methods overlap with each other. For the SF-TT projector, we plotted only the A1 and A2 methods because the combination of the SF-TT projector and A3 method is computationally much slower but only slightly improves accuracy. For the same amplitude method, the error curves of the SF-TR and SF-TT method overlap. The reason is that the rectangular and trapezoid approximation are very similar for a voxel centered at the origin of z axis. All the SF methods have smaller errors than the DD method, i.e., the maximum error of the DD projector is about 652 times larger than the proposed SF methods with the A1 amplitude, and 2.6 × 10³ times larger than the SF methods with the A2 amplitude when β = 45°.

Fig. 3.

Maximum error comparison between the forward DD, SF-TR and SF-TT projector for a voxel centered at the origin (left) and a voxel centered at (100, 150, −100) mm (right).

Fig. 3 also compares the maximum errors of these forward projectors for a voxel centered at (100, 150, −100) mm. We choose N_β = 720 angles over 360° β rotation. The error curves of the SF-TR projector with three amplitude methods overlap and the curves of the SF-TT projector with the A1 and A2 amplitude methods overlap with each other, demonstrating again that these three amplitude methods have similar accuracies. For voxels associated with large cone angles, the SF-TT projector is more accurate than the SF-TR projector. The maximum errors of the DD and SF-TR projector are about 13 and 3 times of that of the SF-TT projector respectively.

2) Speed of Forward and Back-Projectors

We compared computation times of the DD, SF-TR and SF-TT forward and backward projectors using an image with a size of N₁ = 512, N₂ = 512, N₃ = 128 and a spacing of Δ₁ = Δ₂ = Δ₃ = 0.5 mm in the x, y, z direction respectively. We evaluated the elapsed time using the average of 5 projector runs on a 8-core Sun Fire X2270 server with 2.66 GHz Xeon X5500 processors. Because of the “hyperthreading” of these Nehalem cores, we used 16 POSIX threads. (We found that using 16 threads reduced computation time by only about 10% compared to using 8 threads.)

Table II summarizes the computation times. For the SF-TR projector, the A1 and A2 amplitude methods have similar speed, but the A3 method is about 50% slower. The computation times of the SF-TR and DD projector are about the same, whereas the SF-TT projector is about 2 times slower. Although execution times depend on code implementation, we expect SF-TR and DD to have fairly similar compute times because the inner loop over z involves similar simple arithmetic operations for both methods.

TABLE II.

Speed comparison of DD, SF-TR and SF-TT forward and back projectors

Projectors	DD	SF-TR-A1	SF-TR-A2	SF-TR-A3	SF-TT-A1	SF-TT-A2
Forward time (seconds)	46	35	35	59	91	91
Backward time (seconds)	49	44	45	63	92	93

B. Forward and Back-projectors within Iterative Reconstruction

We compared the DD and SF projectors (SF-TR and SF-TT) with the A1 and A2 amplitude methods within iterative image reconstructions. The results of A1 and A2 methods were visually the same. For simplicity, we present the results of SF projectors with the A1 method.

1) SF-TR vs. DD

In many cases, the region of interest (ROI) needed for diagnosis is much smaller than the scanner field of view (FOV). ROI reconstruction can save computation time and memory. Ziegler et al. [39] proposed the following approach for iterative reconstruction of a ROI.

1. Iterative reconstruction of the whole FOV, yielding an initial estimate ${\widehat{x}}_{\mathrm{FOV}}$ of x_FOV which is the vector of basis coefficients of the object $f\left(\overrightarrow{\mathrm{X}}\right),i.e.,f\left[\overrightarrow{n}\right]$ in (14).

2. Define ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{m}}={\widehat{x}}_{\mathrm{FOV}}\cdot \mathrm{m}$ where m = (m₁, … , m_p) with 0 ≤ m_j ≤ 1 (j = 1, … , p) is a mask vector setting the estimated object, inside the ROI to zero and providing a smooth transition from the ROI to the remaining voxels.

3. Compute ${\mathbf{p}}_{out}=\mathbf{A}{\widehat{x}}_{\mathrm{FOV}}^{\mathrm{m}}$ which is the forward projection of the masked object ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{m}}$.

4. Compute the projection of ROI, p_roi = y − p_out where y is the measured data.

5. Iterative reconstruction of the ROI only from p_roi. Due to the transition zone, the region of this reconstruction needs to be extended slightly from the predetermined ROI.

This method requires accurate forward and back projectors. Errors in step 2, where re-projection of the masked image is computed, can greatly affect the results of subsequent iterative ROI reconstruction. Moreover, for general iterative image reconstruction, even small approximation errors might accumulate after many iterations. We evaluated the accuracy of our proposed SF-TR projector and the DD projector in this iterative ROI reconstruction method.

We simulated the geometry of a GE LightSpeed X-ray CT system with an arc detector of 888 detector channels for 64 slices (N_s = 888, N_t = 64) by N_β = 984 views over 360°. The size of each detector cell was Δ_S × Δ_T = 1.0239 × 1.0964mm². The source to detector distance was D_sd = 949.075mm, and the source to rotation center distance was D_s0 = 541mm. We included a quarter detector offset in the s direction to reduce aliasing.

We used a modified 3D Shepp-Logan digital phantom that has ellipsoids centered at the z = 0 plane to evaluate the projectors. The brain-size field of view (FOV) was 250×250×40mm³, sampled into 256 × 256 × 64 voxels with a coarse resolution of 0.9766 × 0.9766 × 0.6250mm³.

We simulated noiseless cone-beam projection measurements from the Shepp-Logan phantom by linearly averaging 8 × 8 analytical rays [40, p. 104] sampled across each detector cell. Noiseless data is used because we want to focus on projector accuracy. We scaled the line integrals by a chosen factor to set their maximum value to about 5.

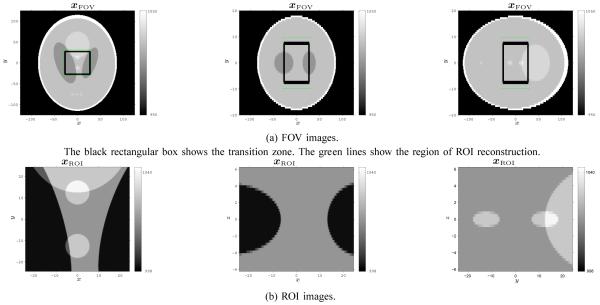
We chose a ROI centered at the rotation center that covered about 48.8 × 48.8 × 12.5mm³ (50 × 50 × 20 voxels with the coarse resolution). The transition zone surrounds the ROI, and covers about 13.7 × 13.7 × 5mm³ (14 × 14 × 8 voxels with the coarse resolution). To construct masked images ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{m}}$, we removed the ROI and smoothly weighted the voxels corresponding to the transition zone by a 3D separable Gaussian function. Fig. 4 shows different views of x_FOV with the transition zone superimposed on it in the first row.

Fig. 4.

Shepp-Logan digital phantoms in Hounsfield units. The first, second and third columns show axial, coronal and sagittal views respectively.

We implemented iterative image reconstruction of the entire FOV with these two projector/backprojector methods. We ran 300 iterations of the conjugate gradient algorithm, initialized with reconstruction by the FDK method [4], for the following penalized weighted least-squares cost function with an edge-preserving penalty function (PWLS-CG):

$$\Phi \left(x_{FOV}\right)=\sum _t{w}_i\frac{1}{2}{(y_i-{\left[A{x}_{FOV}\right]}_i)}^2+\beta R\left(x_{FOV}\right)$$ (47)

$$R\left(x_{FOV}\right)=\sum _k\psi \left({\left[C{x}_{FOV}\right]}_k\right),$$ (48)

where y_i is the negative log of the measured cone-beam projection, w_i values are statistical weighting factors, A is the system matrix, C is a differencing matrix and Ψ(t) is the potential function. We used the hyperbola:

$$\psi \left(t\right)=\frac{{\delta }^2}{3}\left(\sqrt{1+3{\left(\frac{t}{\delta }\right)}^2}-1\right).$$ (49)

For this simulation, we used w_i = exp(−y_i), β = 4 and δ = 5 Hounsfield units (HU).

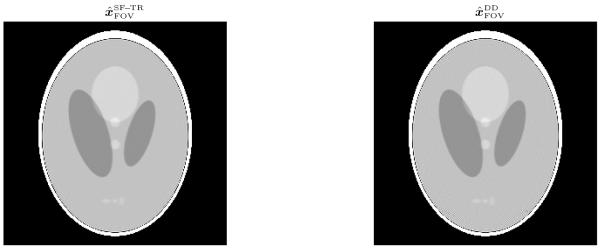
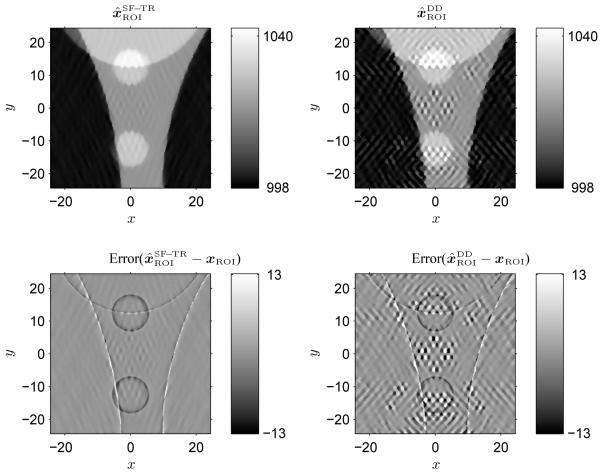
Fig. 5 shows axial views of the reconstructed images ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{SF}-\mathrm{TR}}$ and ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{DD}}$ by the iterative method (PWLS-CG) using the SF-TR and DD method respectively. We computed the maximum error, ${\max }_j\mid {\widehat{x}}_j-x_j\mid$, and root-mean-square (RMS) error, $\sqrt{\frac{1}{N}{\sum }_{j=1}^N({\widehat{x}}_j-x_j)}$. The maximum and RMS errors of ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{SF}-\mathrm{TR}}$ and ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{DD}}$ are close because the errors are dominated by the axial cone-beam artifacts due to the poor sampling (not truncation) at the off-axis slices, but the DD method causes artifacts that are obvious around the top and bottom areas. Similar artifacts of the DD method were reported in [41]. This figure illustrates that the SF method improves image quality for full FOV reconstruction with large basis functions (coarse resolution).

Fig. 5.

Axial views of FOV images ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{SF}-\mathrm{TR}}$ and ${\widehat{x}}_{\mathrm{FOV}}^{\mathrm{DD}}$ reconstructed by the iterative method (PWLS-CG) using the SF and DD method respectively. Left: SF-TR projector; Right: DD projector.

We applied the PWLS-CG iterative method mentioned above with β = 1 and δ = 1HU to reconstruct estimated ROI images ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{SF}-\mathrm{TR}}$ and ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{DD}}$ of 256 × 256 × 64 voxels with a fine resolution of 0.2441×0.2441×0.3125mm³. The domains of ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{SF}-\mathrm{TR}}$ and ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{DD}}$ covered the ROI and transition zone (see Fig. 4). For this image geometry, we also generated a Shepp-Logan reference image x_ROI from the same ellipsoid parameters used to generate x_FOV. Fig. 4 shows different views of x_ROI in the second row. The fine sampling of x_ROI is 1/4 and 1/2 of the coarse sampling of x_FOV in the transaxial and axial direction respectively, and has a size of 200 × 200 × 40.

Fig. 6 shows the axial view of reconstructed images ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{SF}-\mathrm{TR}}$ and ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{DD}}$ by the iterative method (PWLS-CG) using the SF-TR and DD projector. The maximum errors are 20 HU and 105 HU for the SF and DD method respectively and the RMS errors are 1.6 HU and 2.8 HU. The SF-TR projector provides lower artifact levels than the DD projector. The rectangle approximation in the transaxial direction of the DD method resulted in larger errors in the reprojection step and caused more errors when resolution changed from coarse to fine. The rectangle approximation basically blurs corners of image voxels, and the level of blur varies for different image voxel sizes.

Fig. 6.

Axial views of ROI images ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{SF}-\mathrm{TR}}$ and ${\widehat{x}}_{\mathrm{ROI}}^{\mathrm{DD}}$ reconstructed by the iterative method (PWLS-CG) using the SF-TR and DD method respectively. Left: SF-TR projector; Right: DD projector.

We also reconstructed full FOV images (not shown) at a fine resolution, i.e., 1024 × 1024 × 128 voxels with a spacing of 0.2441 × 0.2442 × 0.3125mm³. There were no apparent artifacts in both reconstructed images using the SF-TR and DD method and the maximum and RMS errors were similar. It seems that the aliasing artifacts in the reconstruction by the DD method were removed by fine sampling [42], [43]. For smaller transaxial voxel sizes, the difference between the rectangular (DD method) and trapezoid (SF-TR) approximation becomes less visible.

2) SF-TR vs. SF-TT

We compared the SF-TR and SF-TT projectors by reconstructing an image under an axial cone-beam CT system with largest cone angle of 15° or so using these two methods [27]. We expected to see differences in some off-axis slices of the reconstructed images because the trapezoid approximation of the SF-TT method is more realistic than the rectangle approximation of the SF-TR method especially for voxels far away from the origin. Nevertheless, we did not see obvious visual difference, and the maximum and RMS errors were similar. It appears that the axial cone-beam artifacts due to poor sampling (not truncation) at the off-axis slices dominate other effects in the reconstructed images, such as the errors caused by rectangle approximation. Further research will evaluate these two projectors within iterative reconstruction methods under other CT geometries where the off-axis sampling is better, such as helical scans, yet where the cone angle is large enough to differentiate the SF-TR and SF-TT method .

V. conclusion

We presented two new 3D forward and back projector for X-ray CT: SF-TR and SF-TT. Simulation results have shown that the SF-TR projector is more accurate with similar computation speed than the DD projector, and the SF-TT projector is more accurate but computationally slower than the SF-TR projector. The DD projector is particularly favorable relative to other previously published projectors in terms of the balance between speed and accuracy. The SF-TR method uses trapezoid functions in the transaxial direction and rectangular functions in the axial direction, while the SF-TT method uses trapezoid functions in both directions. The rectangular approximation in the axial direction is adequate for CT systems with small cone angles, such as the multi-slice geometries. The trapezoid approximation is more realistic for geometries with large cone angles, such as the flat-panel detector geometries. To balance accuracy and computation, we recommend to combine the SF-TR and SF-TT method, which is to use the SF-TR projector for voxels corresponding to small cone angles and to use the SF-TT projector for voxels corresponding to larger cone angles.

The model and simulations here considered an ideal point source. For a finite sized X-ray source there would be more blur and it is possible that the differences between the SF and DD methods would be smaller.

Approximating the footprint functions as 2D separable functions is the key contribution of this approach. Since the separability greatly simplifies the calculation of integrals of the footprint functions, using more accurate functions in the transaxial and axial direction is possible without complicating significantly the calculations.

The computational efficiency of the SF methods rely on the assumption that the vertical (t) axis of the detector plane is parallel to the rotation axis. If the detector plane is slightly rotated then slight interpolation would be needed to resample onto coordinates that are parallel to the rotation axis.

Although we focused on voxel basis functions in this paper, the idea of 2D separable footprint approximation could also be applied to other basis functions with separability in the axial and transaxial directions, with appropriate choices of functions.

Further research will address the implementation of the SF projector based on graphics processing unit (GPU) programming techniques [6], [44] to improve the speed.