Effects of degraded sensory input on memory for speech: Behavioral data and a test of biologically constrained computational models

Abstract

Poor hearing acuity reduces memory for spoken words, even when the words are presented with enough clarity for correct recognition. An "effortful hypothesis" suggests that the perceptual effort needed for recognition draws from resources that would otherwise be available for encoding the word in memory. To assess this hypothesis, we conducted a behavioral task requiring immediate free recall of word-lists, some of which contained an acoustically masked word that was just above perceptual threshold. Results show that masking a word reduces the recall of that word and words prior to it, as well as weakening the linking associations between the masked and prior words. In contrast, recall probabilities of words following the masked word are not affected. To account for this effect we conducted computational simulations testing two classes of models: associative linking models and short-term memory buffer models. Only a model that integrated both contextual linking and buffer components matched all of the effects of masking observed in our behavioral data. In this Linking-Buffer model, the masked word disrupts a short-term memory buffer, causing associative links of words in the buffer to be weakened, affecting memory for the masked word and the word prior to it, while allowing links of words following the masked word to be spared. We suggest that these data account for the so-called "effortful hypothesis", where distorted input has a detrimental impact on prior information stored in short-term memory.

Introduction

When speech is heard in a degraded form – whether due to reduced hearing acuity, poor articulation on the part of the speaker, or the presence of background noise – words can be missed or misidentified, resulting in poor comprehension or recall accuracy. However, a degraded neural trace due to a degraded sensory stimulus does not explain all performance deficits, since impaired memory can result even when words are correctly identified. Some years ago, Rabbitt (1968) demonstrated that when clearly presented words are followed by partially masked words, recall of those words, but also recall of the prior, non-masked, words is reduced. Rabbitt proposed what may be called an effortfulness hypothesis: the suggestion that perceptual effort required to identify degraded speech, even when successful, might draw resources that would otherwise have been available to effectively store what had been heard in memory (Rabbitt, 1968, 1991; for supporting data see also McCoy, Tun, Cox, Colangelo, Stewart, & Wingfield, 2005; Murphy, Craik, Li & Schneider, 2000). We had two goals in the present paper. First, we wished to determine the effects of acoustic masking of a single word in a word-list on its recall, and potentially, on the recall of the words surrounding it. Our second goal was to use these data to test several biologically constrained computational models to account for these behavioral effects.

Based on the above-cited work we expect that partially noise-masking a single word in a word-list at a masking level that makes its perception possible, but difficult, will decrease recall accuracy for this degraded word. We also expect to see the asymmetry first reported by Rabbitt (1968); that recall will also be reduced for words preceding masked words but not following them. In a previous paper we offered a preliminary model based on a principle of reduced neural activity among cells responsive to a partially degraded word during its presentation (Miller & Wingfield, 2010). In vitro data describing synaptic changes suggest that such reduced activity would lead to a reduction in synaptic plasticity (Bi & Poo, 2001; Sjostrom, Turrigiano & Nelson, 2001; Pfister & Gerstner, 2006; Erickson, Maramara, & Lisman, 2009).

The simulations we reported showed that, compared to control conditions, this reduced plasticity would diminish recall probability of a degraded word and also recall of its non-degraded neighbors (Miller & Wingfield, 2010). This would imply a weakening of an associative link between the masked and neighboring words. That is, if the linkage between words ordinarily facilitates recall, then reduced recall of the masked word will consequently reduce the chance of recall of a non-masked neighbor via the link from masked word. This would be true even when the level of acoustic masking allows the word to be correctly identified, albeit with perceptual effort. Interestingly, the simulations reported in Miller and Wingfield (2010) suggested that one would see a reduction in recall probability of words both directly preceding and directly following the difficult-to-identify word. This question of the symmetry or asymmetry of the effect is of special interest, and motivated the behavioral experiment we now describe.

EXPERIMENTAL METHOD

Participants

Thirty-two university undergraduate and graduate students, ages 18 to 25, participated in this study (24 females). All participants met a criterion of normal hearing based on pure tone thresholds in the speech range and speech reception thresholds (Hall & Muller, 1997). All spoke English as their first language.

Materials

Preparation of the stimuli began with construction of 30 lists of 7 two-syllable words drawn randomly without repetition from the Toronto Word Pool (Friendly, Franklin, Hoffman, & Rubin, 1982). The words were normalized to ensure even loudness across words and word-lists and were prepared for presentation at a rate of one word per 1500 ms at a uniform loudness level of 40 dB HL. For each word-list we constructed two conditions: experimental and control.

In the experimental condition concurrent multi-talker babble was time-locked to one of the words in the 7-item list, either in the 3rd, 4th or 5th position within the list. The amplitude of the babble was adjusted to 38 dB, producing a signal-to-noise ratio (SNR) of +2 dB. Through preliminary studies it was determined that this level of masking would make the masked word perceptually difficult, although identifiable in most cases. To smooth the transition between the non-masked words and the masked word the babble was ramped up for 200 ms preceding the masked word and dampened for 200 ms following it (Heinreich, Schneider & Craik, 2008). To reduce the contrast between masked and non-masked words and protect against an isolation effect (Fabiani & Donchin 1995), the remaining six words in the lists were heard with a low level of babble (32 dB; SNR = +8 dB). This same low-level babble was also present in the control condition. The average number of words recalled in the control condition was consistent with prior literature on recall accuracy for spoken word lists presented at a 1.5 second rate (Baddeley et al., 1975; Cowan, 2000).

Procedure

Each participant heard all 30 word-lists, 15 in the experimental condition and 15 in the control condition. Stimuli were presented in a mixed-list design so that the participant would not know in advance whether a particular list would be in the control or experimental condition, or - if the latter - which of the three positions would be masked. The position of the words in the lists and the order of presentation of lists were varied across participants.

Stimuli were presented binaurally over earphones in a sound-isolated testing room. Participants were instructed to listen to each list as it was presented, and as soon as it was ended, to recall as many of the words in the just-heard list as possible. Participants were told they were free to recall the lists in any order the words came to mind.

Intelligibility Check

On completion of the experiment, participants were presented with each stimulus word in isolation as heard when masked (SNR = +2). Instructions were simply to identify the word as soon as it was heard. Recognition accuracy averaged 88.8 % (SD = 1.42), confirming that the masked words were generally identifiable, although perceptually difficult. Our goal was to find a level that would engage perceptual effort, whether or not this effort was successful.

RESULTS

Recall as a function of Serial Position

Table 1 gives recall accuracy according to the position of words in the presented lists for the control condition (top row), in which none of the words was masked, and for the experimental condition when the masked word occurred in the 3^rd, 4^th, or 5^th list position. Inspection of Table 1 suggests a trend across the three masked positions for both the masked word and word prior to the masked word to be less frequently recalled than words in the same positions in the control condition.

Table 1.

Recall accuracy by list position for separated conditions.

		Serial Position in List
		1	2	3	4	5	6	7
Masked Position	Control	.72 ± .03	.64 ± .04	.64 ± .04	.56 ± .04	.63 ± .03	.68 ± .04	.82 ± .03
	3	.64 ± .06	.53 ± .05	.50 ± .05	.58 ± .06	.62 ± .05	.70 ± .06	.84 ± .06
	4	.73 ± .07	.67 ± .06	.60 ± .07	.50 ± .06	.67 ± .06	.76 ± .07	.93 ± .07
	5	.75 ± .07	.60 ± .05	.52 ± .06	.51 ± .06	.58 ± .06	.65 ± .05	.79 ± .05

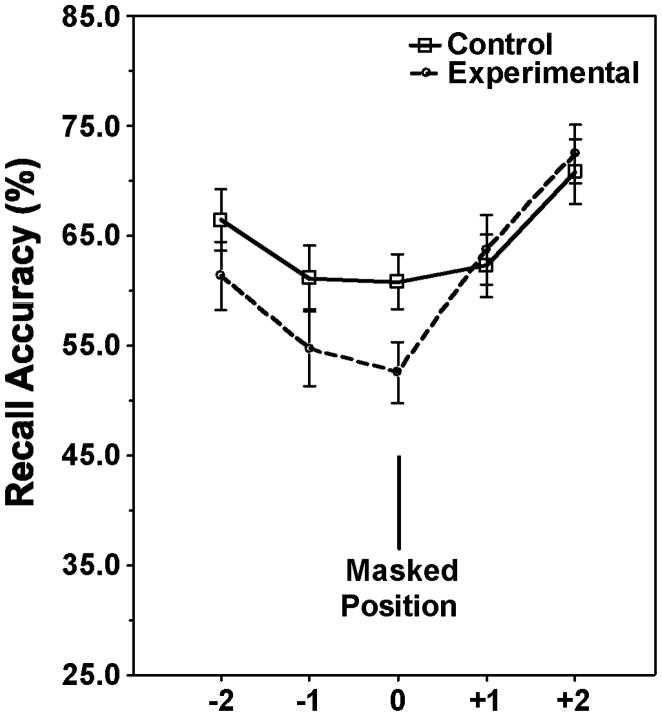
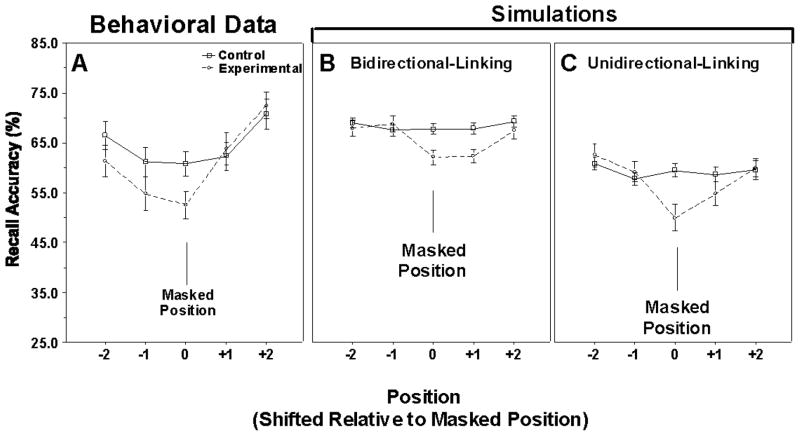
To assess the significance of this trend we collapsed the data across the three masked positions and represented the results in terms of word position relative to the masked word. This is depicted in Figure 1. The point on the abscissa labeled “0” represents the masked position, “−1” refers to the word that was presented directly prior to the masked word and “+1” refers to the word presented directly following the masked word. The points labeled “−2” and “+2” show the effects on the two words before and two words after the masked word. The solid line shows the data for the control condition and the broken line shows the results for the experimental condition.

Figure 1.

Percentage of words correctly recalled for masked words and for the two words before and two words after the masked words in the experimental condition. Recall accuracy also shown for words in the same list positions in the control condition where none of the words was masked. Error bars represent one standard error.

The appearance in Figure 1 that a masked word is recalled significantly less often than a word presented in the same position without masking (control condition) was confirmed by a t-test (t(31) = 3.68, p < .001). Of particular interest was a significant difference between recall accuracy for the word occurring directly prior to the masked word (−1) in the experimental list and its counterpart in the control list (t(31) = 2.39, p < .05). There was also a non-significant tendency for the word occurring two positions before the masked word (−2) to have reduced recall as compared to words in the same position in the control lists (t(31) = 1.83, p = .07). As can be seen in Figure 1, masking a word to make it perceptually difficult had no effect on the words that followed it in the list, in either the +1 or +2 positions.

The finding depicted in Figure 1 that masking disrupts memory for the masked word itself and for the word presented prior to the masked word, could arise by three distinct means, none of which are necessarily mutually exclusive: (1) The probability of being recalled first could be reduced for masked words or words prior to the masked word; (2) The probability of “following a link” to the masked word or a word preceding the masked word from a neighboring word could be reduced compared to the control; (3) When a transition is not to a neighboring word, but jumps to elsewhere in the list, that jump could avoid the masked word or the word directly preceding the masked word. We investigate these three possibilities in the following sections in which we decompose the serial position curve in terms of output order, sequencing and accuracy (Howard & Kahana, 1999; Kahana, 1996; Kahana, Howard, Zaromb & Wingfield, 2002).

Probability of First Recall

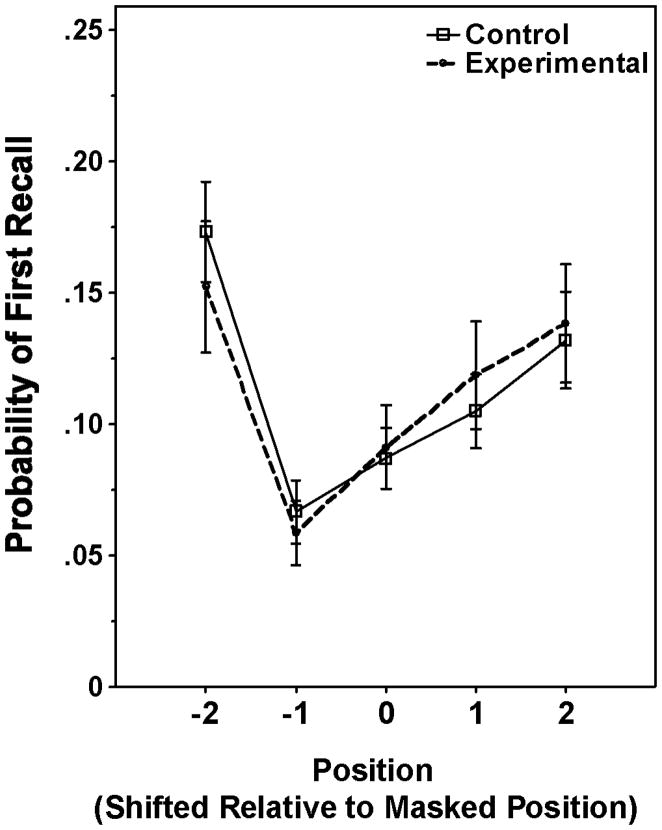
A change in where participants begin their recall (the probability of first recall; PFR) in the experimental condition relative to the control condition could account for changes in the overall probability of recall. For example, if recall more often began after the masked word in the experimental lists, then given the propensity for forward recall, the masked word and earlier words would be recalled less often. In general, a change in PFR could thus lead to changes in overall recall probabilities in the absence of compensating changes in transition probabilities.

Table 2 gives the probability of first recall for the control condition and when the 3rd, 4^th or 5^th word was masked in the experimental condition. These were calculated by tallying the number of times the first word recalled came from a certain serial position in the presented word list, and then dividing by the number of lists. The similarity in PFR curves for the experimental and control conditions can be seen in Figure 2, where the probability of first recall of words is plotted relative to the position of the masked word collapsed across individual masked positions. As can be seen, participants tended to begin their recall with words earlier in the list, both in control and experimental conditions. This similarity was reflected in the absence of an interaction between condition and position (F(2,36) < 1).

Table 2.

Probability of first recall by list position for separated conditions

		Serial Position in List
		1	2	3	4	5	6	7
Masked Position	Control	.40 ± .05	.06 ± .01	.06 ± .01	.08 ± .03	.12 ± .02	.11 ± .02	.17 ± .04
	3	.35 ± .06	.03 ± .01	.05 ± .02	.14 ± .04	.14 ± .03	.10 ± .03	.15 ± .04
	4	.35 ± .06	.05 ± .02	.09 ± .03	.10 ± .02	.12 ± .04	.14 ± .04	.19 ± .05
	5	. 47 ± .08	. 06 ± .02	. 06 ± .03	.05± .02	. 12 ± .03	. 09 ± .03	. 13 ± .03

Figure 2.

Percentage of trials on which subjects initiated recall (probability of first recall) beginning with masked words (0 on the abscissa) or with the two words before or after the masked words in the experimental condition. Probability of first recall also shown for words in the same list positions in the control condition where none of the words was masked. Error bars represent one standard error.

Lag-Conditional Response Probability (lag-CRP) analysis

The conditional response probability concerns itself with the probability of recalling an item in terms of the distance (lag) between the items in the presented list. The lag-CRP is obtained by combining the transitional data (shown in the next section) for all pairs of words separated by the same lag within a list. For example, the CRP for a lag of “+1” is a weighted mean (weighted by number of possible transitions) of the transition probabilities from word 1 to 2, from word 2 to 3, from word 3 to 4 and so on. Thus the lag-CRP for a given value of Lag is the sum of transitions taken by a participant from all words X to words Y =X+Lag, divided by the sum of all possible transitions from words X to Y=X+Lag. Note that the number of possible transitions from X to Y is limited for two reasons. First, Y may have been already recalled and subjects usually will not repeat words already recalled. Therefore, word Y would not be available for recall. Second, the position Y may not exist, either because X+Lag < 1 or X+Lag > 7.

Previous work has shown a tendency for participants to recall successive words in a forward manner as well as words occurring from a nearby serial position (Howard & Kahana, 1999; Kahana, 1996). This tendency indicates that the associative process is not symmetric, favoring forward associations over backward associations. For example, if a list had contained the subsequence “orchid, mustard, pillow” and a participant recalled mustard, the word pillow (with a lag of +1) has the highest probability of being recalled next. This influence of contiguity on retrieval transitions defines the lag-recency effect.

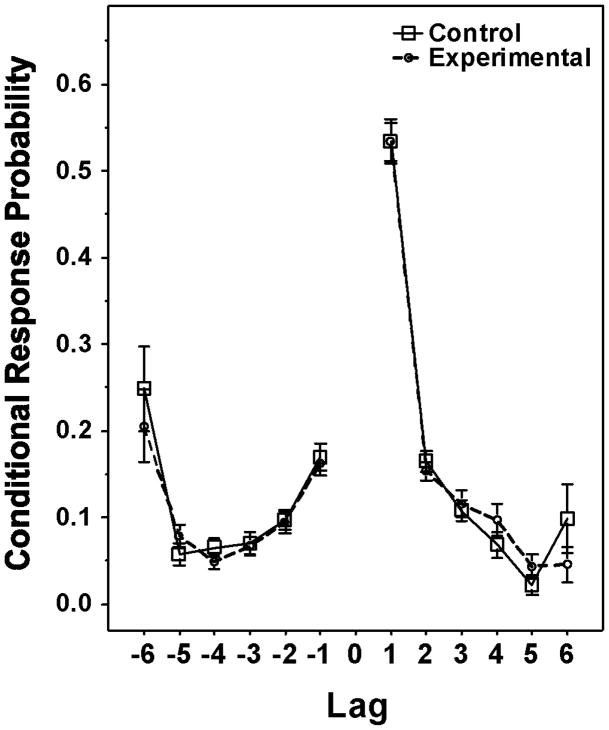
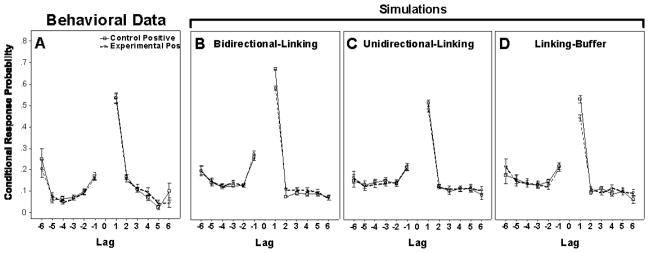
As seen by the serial position curves in Figure 1, masking affects recall of the masked word and the word heard immediately before the masked word. But does masking disrupt the order of recall? To answer this question, we plot the lag-CRP curves for the experimental and control conditions in Figure 3. We emphasize that CRP is defined as probability of recall when a word in such a position can be recalled, such that low CRP to transition to distant words within a list (lag of +/− 5) is not because there are fewer opportunities for these transitions within a short list. Rather, it reflects the participants’ tendency to make transitions to nearby serial positions. The increased CRP for a lag of −6 indicates that, following recall of the seventh and final word, subjects have a strong tendency to next recall the first list word if it has not been already recalled. Others have observed similar non-monotonic effects in lag-CRP curves (Farrell & Lewandowsky, 2008; Howard et al., 2009). As can be seen in Figure 3, our masking manipulation did not disrupt the tendency for successively recalled words to come from nearby serial positions, nor the non-monotonic increase for a lag of −6.

Figure 3.

Lag-CRP functions: after recalling a particular word from a word-list (0 on the abscissa), the probability that the next word recalled will be the one that immediately preceded it (−1 on the abscissa) or immediately followed it (+1 on the abscissa), or that had occurred two through 6 words prior to or following the recalled word. Data are shown for the experimental and control conditions. Error bars represent one standard error.

Transition probabilities reveal changes in forward temporal associations

As demonstrated in Figure 3, there was no significant consequence of masking on the lag-CRP curves. As noted, the lag-CRP is a transition probability that is averaged over all positions in the original list. The question might be raised, however, whether the serial position of a word relative to the masked word has an effect on individual transition probabilities between words.

For this analysis the transition probability from position X to position Y was calculated as the percentage of times the word in position Y was recalled immediately following recall of the word in position X, out of all the times when the word in position Y was available (because it was not already recalled) for next recall. Table 3 contains the complete set of transition probabilities for the control list. Each entry corresponds to the transition probability from a word just recalled (given by the column number), to the next word recalled (given by the row number), when that subsequent word was available for recall.

Table 3.

Transition Probabilities: Control Condition

	To 1	To 2	To 3	To 4	To 5	To 6	To 7
From 1	-	.61 ± .03	.12 ± .02	.06 ± .01	.05 ± .01	.02 ± .01	.04 ± .01
From 2	.24 ± .04	-	.53 ± .03	.14 ± .02	.12 ± .02	.05 ± .01	.02 ± .01
From 3	.13 ± .03	.16 ± .03	-	.43 ± .03	.18 ± .03	.12 ± .02	.10 ± .02
From 4	.15 ± .03	.10 ± .02	.15 ± .03	-	.41 ± .03	.18 ± .03	.11 ± .02
From 5	.07 ± .02	.05 ± .02	.06 ± .02	.09 ± .02	-	.56 ± .03	.23 ± .03
From 6	.05 ± .01	.05 ± .01	.08 ± .02	.06 ± .02	.19 ± .03	-	.76 ± .03
From 7	.25 ± .03	.08 ± .02	.12 ± .02	.10 ± .02	.18 ± .03	.30 ± .03	-

The effect of masking can be enumerated by calculating the changes in these transition probabilities for each position of the masked word. We show these changes in Tables 4, 5, 6 for each of the three masked positions in the experimental lists. Given the large number (42) of possible transitions per condition, no individual changes were significant with a Bonferroni correction. Neglecting the correction, but using a slightly more stringent criterion of p < .01 for significance, the single transition from position 2 to 3 was reduced when position 5 was masked.

Table 4.

Transitional Probability Change from Control for Masked Position 3

	To 1	To 2	To 3	To 4	To 5	To 6	To 7
From 1	-	−.05 ± .06	.04 ± .04	.07 ± .03	.01 ± .03	.01 ± .02	−.01 ± .03
From 2	.03 ± .10	-	−.14 ± .07	.02 ± .05	−.01 ± .05	.01 ± .03	−.02 ± .02
From 3	−.10 ± .06	−.04 ± .06	-	.03 ± .07	.04 ± .06	.01 ± .05	.02 ± .05
From 4	−.04 ± .06	−.09 ± .04	−.03 ± .05	-	−.01 ± .07	.05 ± .06	.03 ± .05
From 5	−.01 ± .03	.01 ± .03	.03 ± .03	.05 ± .04	-	.09 ± .06	−.06 ± .06
From 6	.00 ± .03	−.01 ± .03	−.01 ± .03	−.06 ± .03	−.07 ± .06	-	.07 ± .05
From 7	.02 ± .05	.01 ± .03	−.05 ± .04	−.00 ± .04	.05 ± .05	−.04 ± .07	-

Table 5.

Transitional Probability Change from Control for Masked Position 4

	To 1	To 2	To 3	To 4	To 5	To 6	To 7
From 1	-	.03 ± .05	−.06 ± .04	.02 ± .03	−.02 ± .03	−.01 ± .02	−.01 ± .03
From 2	−.09 ± .08	-	−.07 ± .06	−.06 ± .04	.02 ± .04	.07 ± .03	.02 ± .02
From 3	−.04 ± .06	.03 ± .06	−	−.02 ± .06	−.05 ± .05	−.05 ± .05	.08 ± .05
From 4	−.06 ± .06	−.07 ± .05	−.02 ± .06	-	.06 ± .07	−.08 ± .06	.04 ± .05
From 5	.06 ± .04	−.00 ± .03	.06 ± .03	−.04 ± .04	-	.08 ± .06	−.03 ± .06
From 6	.06 ± .03	−.03 ± .02	−.04 ± .03	−.01 ± .03	−.01 ± .06	-	.10 ± .05
From 7	−.00 ± .05	−.03 ± .03	−.06 ± .03	−.04 ± .03	.09 ± .05	.06 ± .06	-

Table 6.

Transitional Probability Change from Control for Masked Position 5

	To 1	To 2	To 3	To 4	To 5	To 6	To 7
From 1	-	−.08 ± .05	.01 ± .04	.04 ± .03	−.01 ± .03	.01 ± .02	−.02 ± .02
From 2	−.11 ± .10	-	−.18 ± .06	.06 ± .05	.07 ± .05	.03 ± .03	.06 ± .03
From 3	−.01 ± .07	.02 ± .06	-	−.10 ± .07	−.02 ± .05	−.06 ± .05	.04 ± .05
From 4	−.02 ± .06	.05 ± .05	−.01 ± .06	-	−.12 ± .07	−.01 ± .06	.02 ± .05
From 5	−.01 ± .04	−.04 ± .03	.03 ± .03	.04 ± .04	-	.00 ± .07	−.00 ± .06
From 6	.06 ± .03	−.04 ± .03	−.04 ± .03	.00 ± .03	.03 ± .06	-	−.05 ± .06
From 7	.02 ± .06	−.01 ± .03	−.03 ± .04	.01 ± .04	−.07 ± .05	−.02 ± .06	-

There is a more general trend for masking to reduce forward transition probabilities between consecutive words (i.e. transitions that contribute to the +1 lag-CRP) prior to the masked word and to the masked word itself. These are the transition probabilities highlighted in bold in Tables 4, 5, 6. There is also a trend for transition probabilities between later words to increase, which is observable in the forward transition probabilities (lag of +1) that appear immediately above the diagonal in the lower rows of Tables 4–6. Thus, the question is whether position in the list of successive words relative to masked word impacts the individual transition probabilities with a lag of +1.

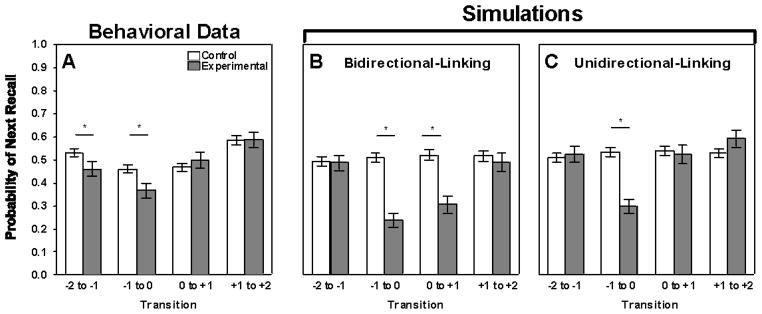
The results of this analysis are shown in Figure 4, where the data have been collapsed across masked positions and probabilities of next recall are shown relative to the masked position (position “0”).

Figure 4.

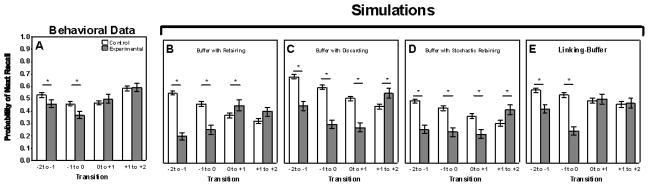
Linking associations: the probability of recalling in order the word immediately following the masked word (0 to +1), the following two words in sequence (+1 to +2), or the sequences prior to the masked word. Data shown for the experimental and control conditions. Error bars represent one standard error.

As can be seen in Figure 4, there were significant differences between transitions occurring within the control lists (white bars) and experimental lists (filled bars). The probability of recalling the masked word following recall of the prior word (transition from −1 to 0) is reduced compared to control lists (p <.05). Moreover, the presence of the masked word significantly lowered the forward transition probability between the two words before the masked word (transition from −2 to −1; p < .05). It can also be seen, however, that there are no corresponding differences for the transitions to the words following the masked words (0 to +1 and +1 to +2). This latter result shows that masking can asymmetrically affect links between words that are not masked. Most important, these results suggest that the diminished recall of words prior to the masked words is not solely due to the reduced recall of the masked word.

In an additional analysis we determined that there was no significant difference between control and experimental conditions for backward transitions between neighboring words (i.e. transitions that contribute to the −1 lag-CRP) even when aligning words relative to the masked position (2-tailed Binomial test, p>0.5, all positions). Similarly, transitions between nonconsecutive words, either to the masked word or to any other word, were not significantly different from the control, indicated by the absence of condition effect (F(2,36) < 1) and absence of an interaction between position and condition (F(2,36) < 1).

Effects of Serial versus Free Recall Strategies

As we saw in Table 2 the probability of first recall across participants was greatest for the initial word in the list. However, we assessed whether a subset of our participants were responsible for this PFR primacy effect by tending to recall in serial order even though this was not required by the instructions (Ward et al., in press). Indeed, when separating PFR data in control lists by participant, we found a bimodal distribution: 15 of 33 subjects initiated recall with the first word on 20% or fewer trials, but 7 subjects initiated recall with the first word on 80% or more of trials. The question might thus be raised whether participants who showed a serial recall strategy might yield different results than those who recalled in a non-serial order (“free recall”).

To answer this question we separated the subjects into two groups, a “free recall” group containing 20 subjects and a “serial recall” group containing 13 subjects, who respectively initiated recall with the first word on fewer than 50% of control trials or more than 50% of control trials. The serial recall group had a significantly higher likelihood (p < .05) of transition from the first list-word to the second, compared to the free recall group, indicating the group’s tendency to recall in serial order. We repeated the previous analyses for the two groups separately and present the results in Figure 5.

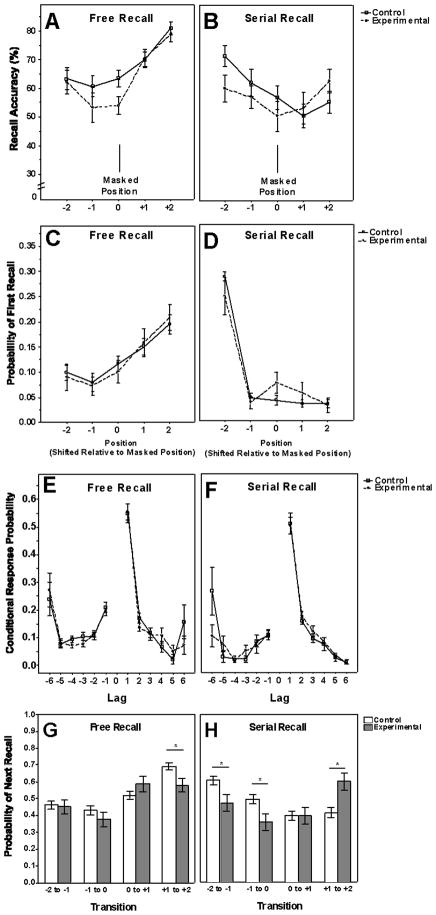
Figure 5.

Mean recall accuracy for the masked word and for the two words before and after the masked word (A), probability of first recall (C), lag-CRP functions (E), and linking associations (G) for subgroup of subjects using a free recall strategy. Figures B, D, F, and H show same data for subgroup of subjects using a serial recall strategy. Data shown in each case for experimental and control conditions. Error bars represent one standard error.

Figures 5A and 5B show that those who chose a free recall or serial recall strategy produced differences in the shapes of the recall functions. Most notably, there is a stronger recency effect for the free recall group, and a tendency to recall position +2 more often in the experimental condition than control. One also sees that the free recall group had an overall higher level of accuracy collapsed across all positions than the serial recall group (p < .05) both in the control condition (70% versus 62% correct) and the experimental condition (69% versus 61% correct). One should be cautious in interpreting these differences, however, because the data are drawn from only a smaller subset of the full subject numbers. Most important for our present interests, however, both groups show the overall group tendency of reduced recall for the masked word relative to the control, and for the one word (Figure 5A) or two words (Figure 5B) prior to the masked word.

The PFR curves plotted in Figures 5C and 5D show a large primacy effect for the serial recall group and a large recency effect for the free recall group, which was observable in the overall accuracy data noted above. However, it is seen that masking does not affect the probability of first recall significantly for either group, although there is a non-significant trend (p=0.11) for the serial recall group to initiate recall with the masked word. Consistent with other studies (Golomb, Peelle, Addis, Kahana, & Wingfield, 2008) Figures 5E and 5F demonstrate similar lag-CRP curves for the two recall strategies. Most important, however, there was no significant effect of masking for either group. Transitions from a word to the prior word (lag of −1), however, were more likely for the free recall group than for the serial recall group, with this observation unaffected by masking.

Forward transition probabilities presented in Figures 5G and 5H show the greatest difference between the two recall strategies. In the free recall group (Figure 5G) the presence of a masked word reduced the forward transition probability for +1 to +2 relative to the control condition (p <.05). In contrast, masking increased the same forward transition probability for the serial recall group (p <.05). The significant reduction in transition probabilities from −2 to −1, and from −1 to 0 relative to the control condition seen in Figure 4 was also clearly seen in the data of the serial recall group shown in Figure 5H (p < .05 for both transitions). As can be seen in Figure 5G this was not the case for the free recall group (p = .81 for −2 to −1 and p = .25 for −1 to 0).

DISCUSSION OF BEHAVIORAL RESULTS

The experimental data confirm the previously cited expectation that degrading the clarity of words by acoustic masking would significantly reduce the likelihood of recalling both the masked word and the word directly prior to it (Rabbitt, 1968). One question is whether the associations between words are affected by a masked word. To answer this question we calculated the transition probability for pairs of successive words in recall as a way of estimating the strength of a linking association between them. This analysis showed that the existence of a masked word significantly lowered the likelihood of a transition from the prior word to the masked word, suggesting that masking interferes with this link. This finding that a masked word in the list interferes with the linking association between the non-masked words prior the masked word is consistent with the notion that a disruption in temporal associations may underlie the frequently-cited effortfulness hypothesis.

The present findings also confirm that perceptual difficulty in identifying a masked word in a word-list has an asymmetric effect on encoding and retrieval of words prior to the perceptually difficult word. Although participants understood that they could recall the lists in any order, many chose a strategy of initiating recall with the first word in the list. Indeed, recent work (Ward et al., 2010) suggests that if our lists were slightly shorter, then serial recall would be the norm. We saw a strong propensity for the subjects who initiated recall with the first word to recall in forward order, thus one could expect diminished recall of words following a disrupting masked word. These subjects, however, showed reduced recall and preferential disruption of linking associations for words prior to the masked word. The directionality of the asymmetric effect of masking a list-word to make its identification more difficult is thus a generalizable one that was not a consequence of recall order. It is also the case that the asymmetric effect is unlikely to be due to simple backward masking, since the timescale of word presentation in our experiment (1500 ms per stimulus) is more than an order of magnitude longer than typical timescales between auditory stimuli (<50 ms) when backward masking is observed (Gehr & Sommers, 1999).

In the remainder of the paper we examine several computational models as possible accounts for these data.

INTRODUCTION TO THE MODELS

The experimental data showed that masking a single word within a word-list led to an asymmetric decrease in memory for the masked word and for the word prior to the masked word. In this section we test these data against two classes of current models of word encoding and retrieval: associative linking models (Howard and Kahana, 1999; Sederberg et al., 2008; Polyn et al., 2009) and short-term memory buffer models (Jensen et al., 1996; Page & Norris, 1998; Burgess & Hitch, 1998; Baddeley, 2000; Becker & Lim, 2003; Davelaar et al., 2005; Rudner & Rönnberg, 2008; Farrell & Lewandosky, 2008). In this report, we do not address models whereby the ability to recall an item depends on its distinctiveness from other items (Brown et al., 2008) but focus on how associations between items relate to their successive recall.

Both Associative Linking models and Buffer models have nuanced variations in the literature. For our purposes we conducted simulations using an empirical version of each, including two versions of the consequences of masking on an Associative Linking model (Bidirectional Linking, Unidirectional Linking) and three versions of the consequences of masking on a Buffer model (Buffer with Retaining, Buffer with Discarding, Buffer with Stochastic Retaining). Our final test was represented by a hybrid Linking-Buffer model that combines features of the two. In all cases we drew the model parameters from the control data and asked, in each case, how masking a word would alter these parameters to produce the behavioral data as observed in the previous section.

Associative Linking Models

In Associative Linking Models the underlying mechanism of list recall is via links between words. These links could be associations with temporal or contextual activity in the brain, or directly between the words themselves. The quintessential associative linking model is the Temporal Context Model (TCM), which posits that words in a list are associated with each other via their associations to a gradually changing context (Howard & Kahana, 1999; Sederberg et al., 2008). The activation of a word, either in listening or recall, causes a change in context, which during recall activates words heard in a similar context. These contextual associations, according to TCM, give rise to the contiguity effects (the tendency to recall neighboring items together) that are observed in recall.

We first present simulations examining two versions of the recall consequences of acoustic masking of a list item using an Associative Linking Model. Our focus in both cases is on models that are biologically plausible (Miller & Wingfield, 2010). In a Bidirectional-Linking model we assume that masking a single word during list presentation reduces the associated neural activity and results in less synaptic strengthening, both when the cells with low activity are postsynaptic and presynaptic. Thus links both to and from masked words are weaker than those between nonmasked words in a control list. In a Unidirectional-Linking model we assume - in line with in vitro measurements of long-term synaptic plasticity (Pfister & Gerstner, 2006) - that the level of synaptic strengthening depends on postsynaptic firing rate alone. Thus, in the Unidirectional-Linking Model links to masked words are weakened, but links from masked words to nonmasked words are unaffected.

Short-Term Buffer Models

Unlike TCM, Buffer models account for the contiguity effects in recall using a short-term memory buffer (Davelaar et al., 2005; Farrell & Lewandosky, 2008), as well offering an account for the traditional bow-shaped curve when one plots probability of recall as a function of input serial position (Glanzer & Cunitz, 1966; Murdock, 1962). According to Buffer Models, as words are heard they enter a short-term limited capacity buffer. The connections between words that are coactive in the buffer are incrementally strengthened, resulting in the contiguity effect. Words can also be consolidated from the buffer into long-term memory, which accounts for primacy effects in serial position curves (better recall for items early in the list relative to items in the middle of the list). By the same token, the most recently heard words are still refreshed in the buffer, resulting in the traditionally observed better recall for items at the end of the list than those in pre-recency positions (Crowder, 1976).

We tested three versions of disruption of mnemonic activity by masking in a Buffer model, as predictors of the experimentally demonstrated effects of word-masking on recall. The Buffer Model differs from the Associative Linking model in that it requires words to be retained in a short-term memory buffer in order to be linked (Jensen et al., 1996; Burgess & Hitch, 1998). In line with an “effortful hypothesis,” the Buffer Model assumes that the extra cognitive effort required for a subject to perceptually identify a masked word increases the probability of disruption of the short-term memory buffer. It also assumes that upon buffer disruption, all words present in the memory buffer are lost from it, leaving it empty. The Buffer Model with Discarding assumes that such disruption prevents the disrupting word from entering the buffer. The Buffer Model with Retaining assumes that disruption of the buffer precedes the disrupting word entering the buffer, so the disrupting word becomes the first word in an otherwise empty buffer. The Buffer Model with Stochastic Retaining allows the disruptive word to enter an empty buffer probabilistically.

Linking-Buffer Model

In addition to the above models, we developed a hybrid, Linking-Buffer Model that combines the Unidirectional-Linking model and the Buffer Model with Retaining. In this model, words are first linked with a strength that depends on stimulus quality during word presentation, but the presence of words in a buffer significantly increases their probability of successive recall. Thus in the Linking-Buffer Model, the masking of a word has two consequences: (1) links to the masked word are weakened; and (2) buffer disruption by the masked word can produce an asymmetric effect, indirectly weakening links only between prior words.

Recall in Models

Based on the data for the control condition, for all models we implemented the rule that recall of one word causes a high probability of recalling the following linked word, or to a lesser extent, the prior linked word. We use the term “strength” of the link to denote the magnitude of the conditional probability of recall of a word immediately following its neighbor. For this presentation, we did not simulate the specific synaptic strengths and neural activity upon which such recall would depend (see Miller & Wingfield, 2010). Second, the probability of first recall is fixed for all models to match the behavioral data, as we focused this study on how masking affects recall, and as we saw, the probability of first recall was unaffected by masking. In addition, within all models, if recall of a word does not cause either of its linked neighbors to be subsequently recalled, then either recall jumps to any available word with equal probability, or recall terminates with a fixed probability.

Results of the simulations were analyzed in the same manner as the behavioral data, with the same number of experimental and control lists and with the masked words varying in position. To forecast the results, our simulations show that only the Linking-Buffer Model is able to reproduce all the characteristic effects of masking on the behavioral data. Most notably, it yields asymmetric affects on recall of a word prior to the masked word, but not on the words that follow.

SIMULATION PROCEDURES

For all simulation methods the behavioral data for probability of first recall is enforced as a constraint so that all models match the behavioral data in this measurement. The probability of first recall (FR) of the n^th item, P_FR(n), is approximated from the behavioral data as follows: P_FR(1) = 0.4, : P_FR (2) = 0.05, : P_FR (3) = 0.1, P_FR (4) = 0.1, P_FR (5) = 0.1, P_FR (6) = 0.1, P_FR (7) = 0.15.

In these simulations the word for first recall is randomly chosen, weighted by the respective P_FR values. Given recall of one word in the list, recall of a neighboring word follows if the relevant link is intact; that is, if a neighboring word is available for a logically possible recall and not recalled previously. Probability of an intact link varies according to condition and according to the model, as specified below. In cases where the link is intact to both the prior and following word, then one direction is chosen at random in control lists with a 4 to 1 ratio favoring forward recall to match behavioral data. When no intact link to a neighboring word exists or the word has already been recalled, then either recall ends with a given probability, which we denote as P_break (P_break = 0.25 for linking models, or P_break = 0.3 for buffer models–values that produce consistency with the behavioral total recall probabilities), or a word is selected at random from all available positions in the list and the process of recall via links can be continued.

In all models, we simulate recall of 32 sets of 15 control trials and 15 masked trials, equally divided across masked positions 3, 4, and 5 for lists of length 7. Parameters are chosen to match overall recall probabilities and conditional response probabilities of nearest neighbors averaged across positions and trials.

Associative Linking Models: Linking between all neighboring words

Bidirectional-Linking Model: Masking symmetrically weakens links between neighbors

Constraints are placed on this model in the following manner: (1) Links in the forward (F) direction between neighboring non-masked (N) words are intact with probability P_NNF=0.4, and in the reverse (R) direction with probability, P_NNR=0.1. Links can be intact only if the neighboring words have not been previously recalled; (2) Links from non-masked (N) words to masked (M) words are intact with one fourth of the probability of that between non-masked words, thus in the forward (F) direction P_NMF = 0.1, and in the reverse (R) direction P_NMR = 0.025; (3) Conversely, forward (F) and reverse (R) links from masked (M) to non-masked (N) words are intact with the same probability as from non-masked to masked words (P_MNF = P_NMF = 0.1, P_MNR = P_NMR = 0.025); (4) In cases where links in both directions are intact, the direction is chosen randomly, weighted by the probability of an intact link; (5) In the case of no neighboring words with intact links, the probability of terminating recall is P_break=0.25. Otherwise a new word is probabilistically selected from those not yet recalled, with a weight favoring the first and last word by a factor of 2.5 (in accordance with behavioral data); (6) Recall of a trial ends when either all words are recalled, or a break that finishes recall is selected.

Unidirectional-Linking Model: Masking weakens links to the masked word but not from the masked word

The Unidirectional-Linking Model is identical to the Bidirectional-Linking Model, with the exception that the probability of an intact link from a masked word to neighboring non-masked words is identical to that of an intact link between two non-masked words (P_MNF = P_NNF =0.4, P_MNR = P_NNR =0.1).

Buffer-only Models: Linking between neighboring words coactive in buffer only, with buffer disruption by masking

The Buffer-only Models differ conceptually from The Bidirectional-Linking Model and Unidirectional-Linking Model, which assume that the activity of perceiving a word leads to plasticity between coactive cells. In the Buffer-only Models, only those neighboring words that are stored in a short-term memory buffer can become linked together. The Buffer-only Models then test the effects of an “effortful hypothesis” by assuming that while adding a word to the buffer can lead to buffer disruption in control conditions, a masked word in the list greatly increases the probability of disruption of the short-term memory buffer. Consequentially, by disrupting the existing buffer, the masked word can affect links between earlier words, even when both of the earlier words were non-masked. Importantly, words that enter the buffer after the masked word are not affected.

The Buffer Models have two stages: first the encoding stage, which allows linking of words within the buffer, followed by a recall stage, which proceeds in the same manner as the Unidirectional-Linking Model (though with altered probabilities). We elaborate below.

Encoding in Buffer Models

This aspect of the buffer models is constrained in the following manner: (1) During listening, words are added successively to the buffer, unless the buffer is designated as full – a probability that begins at P_Full(0) = 0 and increases by 0.15 following the addition of each successive word (producing a maximum capacity of 7 words); (2) The buffer can be disrupted (D) or emptied with a probability of P_D = 0.1 whenever a word is added to it, and with a probability of P_MD = 0.8 when a masked (M) word is heard (hence the buffer only survives with a probability of (1–0.8)*(1–0.1)=0.18 when a masked word is both heard and added to the buffer). Note that when the buffer is designated as full no new words are added and the buffer is not disrupted. This is essential to allow the simulation of the common experimental observation of recall of the first two or three words of the list in sequence, without recall of the entire list in sequence; (3) If the buffer is disrupted, all prior words are removed. With a probability that varies across Buffer Models, either the current word or the subsequent word becomes the first word in the fresh buffer; (4) Only neighboring words present within an intact buffer at the end of a list are designated as linked.

Recall in Buffer Models

This aspect of the model is constrained in the following manner: (1) Forward links between non-masked words are intact with probability P_NNF =1.0, and reverse links with probability P_NNR =0.25; (2) In cases with two intact links, recall of the following word is chosen with a probability of 0.8 (and the prior word with a probability of 0.2); (3) In the case of no neighboring words with intact links, the probability of finishing recall is P_break=0.3, otherwise a new word is selected by chance from those not recalled; (4) Recall of a trial ends when either all words are recalled, or a break finishing recall is randomly selected. Each of the Buffer Model versions varies in the following ways:

Buffer Model with Discarding

Upon buffer disruption the disrupting word, in particular the masked word, is never allowed to enter the buffer, so that all links to the disrupting word are reduced. This ensures diminished recall of a disrupting (e.g., masked) word.

Buffer Model with Retaining

Upon buffer disruption the disrupting word, in particular the masked word, is always allowed to enter an empty buffer, so that any link from a masked word to the following word do not differ from the control, as seen in the behavioral data.

Buffer Model with Stochastic Retaining

Upon buffer disruption the disrupting word, in particular the masked word, enters a fresh buffer with 50% probability.

Linking-Buffer Model: linking within and outside the buffer

The Linking-Buffer Model is based on a combination of the Buffer Model with Retaining (where a disrupting word enters a new buffer) and the Unidirectional-Linking Model (linking with unidirectional weakening by masking) with parameters altered to maintain consistency with overall recall probabilities. We assume that subsequent recall of a neighboring word can arise by two parallel routes: either due to their temporal proximity and overlap of corresponding activity during presentation as in the Unidirectional-Linking Model, or due to their coactivity in a short-term memory buffer as in the Buffer Model with Retaining. These parallel mechanisms produce separate probabilities of following a link. Only if neither produces a successful following of the link is that link not followed. If both a forward and backward link can be successfully followed then selection is according to the arithmetic mean of the selection probabilities of the two models. These two selection probabilities are identical except when the prior or following word is masked.

Parameters for the Linking-Buffer Model, which combines in parallel two mechanisms of retrieval, are identical to those of the Buffer Model with Retaining for the buffer mechanism, and match those of the Unidirectional-Linking Model, except for the following reductions in all linking probabilities: P_MNF = P_NNF =0.2; P_MNR = P_NNR =0.05; P_NMF =0.05; P_NMR =0.0125 for associations independent of the buffer.

MODEL RESULTS

Linking Models

Serial Position Effects

Panel A in Figure 6 reproduces the experimental results seen in Figure 1 for recall accuracy of masked words and for the two words before and after the masked words relative to words in the same positions in the control condition where no words received special masking. Panels B and C respectively show the simulation results for the Bidirectional-Linking Model and the Unidirectional-Linking Model, where linking can occur between all neighboring words, but masking of a word interferes with links to and from the masked word. It can be seen for both the Bidirectional- and Unidirectional-Linking Models that recall of masked words is significantly reduced compared to words in the same position in control lists (t(31) = 2.96, p <.01 and t(31) = 2.80, p< .01 respectively). The simulation results for the Bidirectional-Linking Model show that the masked word most strongly affects recall of the word following it (t(31) = 2.98, p <.01). The underlying reason for this is that recall in forward order dominates over recall in reverse order. Simulation results for the Unidirectional-Linking Model, where only links to the masked word are weakened, show all neighboring words to be unaffected compared to the control condition.

Figure 6.

Behavioral data from Figure 1 showing mean recall accuracy for the masked words and for the two words before and after the masked words (A), simulation results using a Bidirectional-Linking Model (B) and a Unidirectional-Linking Model (C).

Lag-Recency Effects

Figure 7 compares the lag-CRP data produced by the model simulations with the behavioral results from Figure 3 shown in Panel A. One can see qualitatively similar lag-CRP curves for both Bidirectional-Linking (Panel B) and Unidirectional-Linking (Panel C) models because the models are designed to favor recall via the linking of one word to a neighboring word and to favor forward recall in order to match the experimental data. Because we wish to assess the effect of masking on links between neighbors, simulated links for all models are between neighboring words only. As a consequence of this the models do not reproduce the gradual declines in CRP for words that differ by greater than one serial position. Masking significantly reduces the CRP for a lag of “+1” compared to the control condition in the Bidirectional-Linking model (p <.001) but not for the Unidirectional-Linking Model.

Figure 7.

Behavioral lag-CRP functions from Figure 3(A), simulation results for this metric using a Bidirectional-Linking Model (B), a Unidirectional-Linking Model (C) and a Linking-Buffer Model (D).

Forward Recall Associations

Panel A in Figure 8 reproduces the behavioral data from Figure 4 for comparison with the model simulations. In the Bidirectional-Linking Model (Panel B), where links to and from the masked word are weakened, one sees that recall of the word before the masked word is less likely to produce successive recall of the masked word (transition from -1 to 0) compared to similarly positioned words in control lists (p <.001). However, following successful recall of the masked word the model shows a reduced probability of recalling the word directly after the masked word (p <.001). This effect is not seen in the experimental data in Panel A. Moreover, unlike the experimental data, the successive recall probability is unaffected for the words prior to the masked word.

Figure 8.

Behavioral linking associations from Figure 4(A), simulation results using a Bidirectional-Linking Model (B) and a Unidirectional-Linking Model (C).

Panel C in Figure 8 shows the results for the Unidirectional-Linking Model, where links to the masked word are weakened. Here masking reduces the forward transition probability to the masked word (p <.001, two-tailed Binomial), but no other transitions are significantly affected.

Buffer-only models

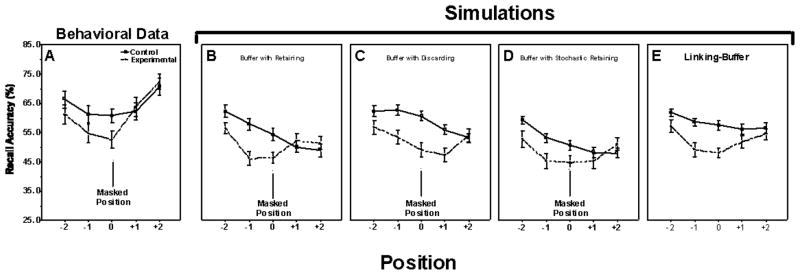
Serial Position Effects

For the Buffer-only Models, preferential recall of neighboring words only arises if the successive words remain in the buffer, and the presence of the masked word increases the likelihood of buffer disruption. Figure 9 demonstrates that simulations driven by the buffer-only models can reproduce many key features of the behavioral data, though not all within a single model. The Buffer Model with Retaining (Figure 9, Panel B) is particularly successful, as it demonstrates reduced recall of the masked word (t(31) = 3.11 , p <.01), the prior word (t(31) = 3.81, p <.001), and marginally, two words prior (t(31)=2.02, p = .052) relative to the same positions in a control list, while recall of other words is not significantly different from the control. However, the Buffer Model with Retaining stipulates that when the masked word disrupts the buffer, it enters a fresh buffer. Consequently, the reduced recall probability of the masked word is only because of the greater reduced recall of the prior word and the absence of links between the two words. Thus, unlike the experimental data, the Buffer Model with Retaining produces a larger decrease in recall of the word prior to the masked word than of the masked word itself. Intriguingly, such a substantial effect of masking on words prior to the masked word, compared to the masked word itself, is seen for the serial recall group of subjects shown in Figure 5B.

Figure 9.

Behavioral data from Figure 1 showing mean recall accuracy for the masked words and for the two words before and after the masked words (A), simulation results using a Buffer with Retaining Model (B), a Buffer with Discarding Model (C), a Buffer with Stochastic Retaining Model (D) and a Linking-Buffer Model (E).

In the Buffer Model with Discarding (Panel C in Figure 9), when the masked word disrupts the buffer it does not enter the buffer. As a result, the simulation shows the recall probability of the masked word to be the most affected (t(31) = 4.20, p <.001), and the prior word also significantly less often recalled relative to the same position in the control list (t(31) = 3.30, p = .01). However, in contrast to the experimental data, the probability of recall of the word following the masked word is also affected, (t(31) = 3.65, p <.001).

We wished to see if a version of a buffer-only model can simultaneously reproduce the two observed experimental results: (1) masking has the greatest negative impact on recall of the masked word, and (2) for the word directly following the masked word, neither recall nor forward association is significantly reduced compared to the control. Results for the Buffer Model with Stochastic Retaining, shown in Panel D of Figure 9, indicate that the model is unable to account for such features of the behavioral data. As we increase the probability of retaining a disruptive masked word in a fresh buffer (simultaneously increasing its recall probability), the word following the masked word approaches the control condition recall probability. Before the following word reaches control levels, however, recall probability of the masked word surpasses recall of the word prior to the masked word. Recall of the prior word therefore becomes the most affected by masking in contrast with the experimental data. Thus, in buffer-only models there is a trade-off between the masked word being recalled too often and recall of the word following being insufficient.

In the simulation results for the Buffer Model with Stochastic Retaining shown in Panel D of Figure 9, for which the probability is 50% for retaining and 50% for discarding of a disruptive masked word, one sees a statistically marginal effect of the masked word being less often recalled than the control (t(31) = 2.00, p = .054), whereas the prior word, and two words prior, are significantly affected (t(31) = 2.53, p <.05 and t(31) = 2.27, p <.05, respectively).

Lag-Recency Effects

All three versions of a buffer-only model produce lag-recency curves that are essentially identical to each other (data not shown) and to the lag-recency curve produced by the Linking-Buffer Model to be described.

Forward Recall Associations

Like the behavioral data, the Buffer Model with Retaining shown in Panel B of Figure 10 diminishes forward associations between the prior word and the masked word (p <.001, two-tailed Binomial test) and even more strongly between the two prior words (p <.001). Moreover, a rebound is observed in the form of a marginal increase in the association from the masked word to the following word (p = 0.057) and the two following words (p = 0.08). This is so because they often both enter a fresh new buffer. Such a rebound was hinted at in the experimental data shown in Figure 4A.

Figure 10.

Behavioral Linking Associations from Figure 4(A), simulation results using a Buffer with Retaining Model (B), a Buffer with Discarding Model (C), a Buffer with Stochastic Retaining Model (D) and a Linking-Buffer Model (E).

The incompatibility between the Buffer Model with Discarding and the experimental data is further evinced in Panel C of Figure 10. Although the model produces a reduced forward association between the prior word and masked word (p <.001, two-tailed Binomial) and between the two prior words (p <.001), in contrast with the experimental data shown in Panel A of Figure 10 this model also produces a strong reduction in the forward association from the masked word to the following compared to the control (p <.001). The reduced probability of recall of the following word seen in Panel C of Figure 9 thus arises because of the predominance of forward recall, combined with the low likelihood of an association between the masked word and following word since the two are rarely in the buffer together.

Panel D in Figure 10 shows that the Buffer Model with Stochastic Discarding produces a significant reduction in forward association from a prior word to the masked word (“−1 to 0”, p <.001, two-tailed Binomial). Unlike the experimental data, however, the effect is stronger between prior words (transition from −2 to −1; p <.001). Also unlike the experimental data, there is a significant impact of masking on the association between the masked and the following word (transition from 0 to +1; p <.01), while there is a rebound of an increase in the forward temporal association between the two words following the masked word (transition from +1 to +2; p = .01). Such a rebound matches the observed data for the serial recall subgroup that was seen in Figure 5F.

Linking-Buffer Model

Serial Position Effects

By contrast to the Linking Models, the addition of a buffer in the Linking-Buffer Model (Panel E of Figure 9) produces an asymmetric effect of the masked word on recall of prior words on the list. Indeed, not only is the probability of recall of the masked word lower than similarly positioned control words (t(31) = 3.09, p <.01), but the probability of recall of the prior word is also lower, relative to comparably positioned words in control lists, (t(31) = 2.47, p <.05). As with the experimental data, recall probabilities of words that follow the masked word are not significantly affected in the simulations of the Linking-Buffer Model.

Lag-Recency Effects

The lag-recency curve produced by the Linking-Buffer Model (Panel D of Figure 7) is similar to those for the two Linking Models and, as noted previously, essentially identical to those for the three Buffer Models.

Forward Recall Associations

For the Linking-Buffer Model (Panel E in Figure 10) the presence of a masked word reduced the probability of successive recall of prior non-masked words (transition from -2 to −1) in accordance with the experimental data. In these simulations the masked word disrupts the preexisting short-term memory buffer, removing prior pairs of words from the buffer that would otherwise be linked. The effect is to reduce forward linking to the masked word compared to control lists (p <.001, two-tailed Binomial) and from the word two-back to one-back from the masked word (p <.001, two-tailed Binomial).

DISCUSSION OF SIMULATIONS

Our simulation results show that Linking Association Models alone, in which the effect of masking acts solely to disrupt associative links between the masked word and neighboring words, cannot account for the experimentally observed asymmetry of the effects of word-masking on recall. Such a result is unsurprising, since in both Bidirectional- and Unidirectional-Linking models the weakening of links due to masking is temporally symmetric, while the high likelihood of recall in forward order leads to an adverse effect of masking on recall of later words. A model for free recall based solely on temporal context has been shown to be effective in describing word-list recall for clearly presented stimuli (Howard & Kahana, 1999; Kahana, 1996; Sederberg et al., 2008), to include generalizing to results for older adults with mnemonic deficits (Golomb et al., 2008; Kahana et al., 2002; Wingfield & Kahana, 2002). We could envision no form of a model based solely on the linking associations between words, whether direct links or linking via associations with context, however, in which perceptually degrading a stimulus word could unilaterally diminish the linking associations between prior, unmasked words.

Buffer models in word-list recall make historical contact with early hypotheses that included the notion of a short-term memory buffer as an account for the superior recall of items in later serial positions within a word-list (Crowder, 1976; Glanzer & Cunitz, 1966; Murdock, 1962). It should be noted in this regard that a short-term memory buffer is computationally indistinguishable from ongoing verbal rehearsal, such that our results may indicate that the extra effort needed to hear a masked word disrupts the rehearsal of prior words, rather than disrupting their presence in a short-term memory buffer. This former possibility was in fact the one assumed by Rabbitt (1968) in his initial demonstration of the phenomenon. We instantiated three versions of general buffer models as potential accounts for the effects of degrading a stimulus word on recall of that word and words prior to it. As we observed, although the simulations based on pure Buffer Models produce an effect on linking associations with a prior word, the effects on recall do not entirely match the experimental data.

The Buffer Model with Retaining comes very close to reproducing the results of the behavioral experiment. In this simulation the masked word enters a fresh buffers and the associations from the masked word to later words were as good as, or better, than for the control condition where none of the words receive special masking. Further, buffer disruption by the masked word ensures a weakening of associations between prior words, and from the prior words to the masked word, producing poorer overall recall for prior words. Moreover, recall of a buffer-disrupting masked word is reduced compared to a word in the same position in the control condition even though according to the model the masked word enters a fresh new buffer. The reason this is so is because recall is dominated by forward associations. The Buffer Model with Retaining only differs from the behavioral data in that words prior to the masked word are more strongly affected by masking than the masked word itself.

In the Buffer Model with Discarding, the disrupting masked word remains absent from a new buffer, such that any link from the masked word to the following word is absent, reducing the forward temporal association to the word following the masked word. This was not seen in the behavioral data. This mismatch with the complete set of experimental data is also seen with the final buffer-only version tested, the Buffer Model with Stochastic Retaining, in which the disruptive masked word is allowed to enter a fresh buffer probabilistically. The interesting qualitative similarity with the data from the subgroup of subjects who appear to have used a serial recall strategy suggests the need for future work in which a specific contrast is created between serial versus free recall (Golomb, 2008)

In contrast with Associative Linking and Buffer Models alone, the Linking-Buffer Model is the most successful in reproducing the experimental results. This hybrid model, that combines the Buffer Model with Retaining, and the Unidirectional-Linking Model as two parallel mechanisms for recall, yields the poorer recall of the masked word relative to a word in the same serial position in the control condition, reduced recall for the word prior to the masked word relative to a word in the same position in a control list, and no effect on recall of words following the masked word as seen in the experimental data.

GENERAL DISCUSSION

Our simulations demonstrate that reduced recall of non-masked words preceding a masked word in a list of unrelated words arises from disruption of a short-term memory buffer. In principle, reduced recall of a masked word could lead to reduced recall of neighboring words, simply because the masked word became a broken link in a chain of recall. If recall were predominantly in reverse order, then the masked word, acting as a broken link, would preferentially diminish recall of prior words. However, subjects tend to recall more frequently in forward order than reverse order. Moreover, our behavioral data show that the associative link between two non-masked words is diminished by the masking of a subsequent word. This, in conjunction with the absence of reduced recall for words following a masked word, shows that a degraded stimulus, in this case due to masking, preferentially affects prior words in memory rather than later words. With this we affirm the asymmetric effect of degrading a spoken word on recall of prior words as first reported by Rabbitt (1968).

Using simulations, we address two biologically plausible effects of a masked stimulus on word encoding and retrieval. In one scenario, we assume that the reduced signal-to-noise ratio pertaining to a masked word produces weaker word-specific neural activity prior to word-identification. That is, while neural activity following word identification is independent of prior stimulus quality, the transient activity during the hearing of a word depends strongly on stimulus quality. We showed in prior work (Miller & Wingfield, 2010) that since synaptic strengthening increases with firing rates of the connected neurons (Sjostrom, Turrigiano & Nelson, 2001; Pfister & Gerstner, 2006; Erickson, Maramara, & Lisman, 2009), if the synaptic strengthening is necessary for recall, then recall probability depends on neural inputs and thus on stimulus quality. The Linking Models in this paper are based on such assumptions, whereby the stimulus-dependence of activity during word identification determines the strength of association with ongoing contextual activity, and thus the probability of recall of one word prompting recall of a neighboring word. While these models can explain reduced recall of the masked word, within this framework we can see no possibility for diminished neural activity during the identification of a masked word to affect the conditional probability for successive recall of prior words heard in the clear. In Linking Models, the necessary synapses for producing consecutive recall of prior words have already been strengthened and cannot be affected by a later masked word.

In our second scenario we assume that, in accordance with the effortful hypothesis, the extra cognitive effort required for a subject to hear a masked word increases the probability of disruption of a short-term memory buffer that ordinarily aids word recall. Since such disruption of a memory buffer can affect only prior words, the Buffer Models reproduce the temporal asymmetry found in the behavioral data. At the neural level, disruption of a buffer by masking could mean that an attention-based modulation of neural spiking is necessary to maintain mnemonic activity in a group of cells, and that such a modulating signal is lost when attention is refocused on deciphering a masked word. Alternatively, the neurons involved in maintaining the short-term memory buffer could be in a neural area in which cells are recruited when a word is difficult to identify, in which case their prior mnemonic activity is lost via reallocation of their circuitry.

The behavioral constraints are best simulated by the Linking-Buffer Model, which combines the two effects of masking described here: words retained in a short-term memory buffer, which is disrupted by masking, have stronger links; while some stimulus-dependent linking arises between words during identification prior to their entry in the buffer. Thus, these data support the effortful hypothesis, the argument that the extra effort required to perceive an indistinctly presented word can disrupt ongoing memory processes (McCoy et al., 2005; Murphy et al., 2000; Rabbitt, 1991). The work we report here represents the first attempt to offer a computational model to account for this effect.