Comparison of viable cell concentration estimation methods for a mammalian cell cultivation process

Abstract

Various mechanistic and black-box models were applied for on-line estimations of viable cell concentrations in fed-batch cultivation processes for CHO cells. Data from six fed-batch cultivation experiments were used to identify the underlying models and further six independent data sets were used to determine the performance of the estimators. The performances were quantified by means of the root mean square error (RMSE) between the estimates and the corresponding off-line measured validation data sets. It is shown that even simple techniques based on empirical and linear model approaches provide a fairly good on-line estimation performance. Best results with respect to the validation data sets were obtained with hybrid models, multivariate linear regression technique and support vector regression. Hybrid models provide additional important information about the specific cellular growth rates during the cultivation.

Introduction

Suspension cultures of mammalian cells are used to produce many of the current blockbuster proteins (Walsh 2006). Chinese Hamster Ovary (CHO) cells are the workhorses of industrial glycoprotein production (Chu and Robinson 2001; Hossler et al. 2009).

With respect to safety and efficacy, production of drugs is one of the tightest regulated fields. This leads to many activities in risk-based developments, change traceability or integrated validation concepts. New processes must be designed in such a way that product quality can be guaranteed by controlling measures performed during the running process and not by tests performed later on at the finished product. Recent regulatory pressure, performed by FDA/EMEA in their PAT initiative (FDA 2004), forces manufacturers to improve process performance by on-line monitoring and control. One of the central variables to be monitored during the very product formation process is the concentration X_V of the viable cells.

Many of the new processes are operated in fed-batch mode (Wlashin and Hu 2006) because of its operational simplicity, reliability and flexibility for implementation in multipurpose facilities (Bibila and Robinson 1995). In these processes, the mass of protein m_P produced within the cultivation time interval [0, t] can be described by

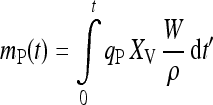1

where W is the mass or size and ρ the density of the liquid culture, X_V the viable cell concentration and q_P the specific product formation rate. At a given culture size W, the viable biomass concentration X_V, which is a function of time, must be kept on a high level (high cell density cultivation) as long as possible in order to achieve a high amount of product. Longevity alone is not sufficient for a well performing process, the specific product formation rate q_P, i.e., the cells’ performance in producing the desired product, must also be kept as high as possible over the entire time interval as required by the integral in Eq. 1.

In a production process, it is not desired to push m_p to any possible high value, good manufacturing practice aims in a high reproducibility of the entire production process. These demands require to continuously monitor the key variables (Schügerl 2001). For many cultures, particularly those where the specific MAb secretion rate remains constant, increases in the culture longevity directly translate into an increase in the final antibody yield (Bibila and Robinson 1995). Hence, the most prominent measurement quantity is the active biomass concentration or viable cell number density X_V.

Several direct measurement devices have been proposed and used to measure the cell number density (Konstantinov et al. 1992; Behrendt et al. 1994; Ducommun et al. 2001; Brinkmann et al. 2002; Joeris et al. 2002; Cannizzaro et al. 2003; Shah et al. 2006). There are several disadvantages of using such for on-line measurements of viable cell densities in production scale bioreactors. Most cannot distinguish between viable growing cells and those which are no longer active. Also, they usually require sophisticated equipment which is not easy to validate and maintain in a GMP environment. Generally, at production bioreactors for animal cell cultures, the number of measurement devices is usually kept as low as possible in order to avoid contamination risks and to reduce efforts of sensor validation.

Indirect measurements using on-line measurements which are already available do not suffer from these disadvantages (Eyer and Heinzle 1996; Junker and Wang 2006; Teixeira et al. 2009). However, indirect biomass estimators need models that relate other measurements to the viable cell count. Presently, a sound physically based description of the relationship between growth, productivity and measurable nutrient concentrations is not available for mammalian cells in culture (Wlaschin and Hu 2006). Hence, simple modeling and correlation techniques must be used. In this way the volume ratios of off-gas components, base addition rates, as well as of pH and pO₂ measurements which are already installed at most production reactors can be related to the viable cell number. Off-gas measurements do not pose an enhanced risk of contamination and can be performed with well established measurement devices that are in use for many decades in biotechnology.

In this paper we focus on those techniques at the example of a CHO culture.

Experimental set up

CHO-S cells purchased from Invitrogen (Karlsruhe), were cultured in a stirred tank fermenter (Biostat B, B.Braun Biotech, Melsungen) on a 2-L-scale.

The cells were grown in a glutamine limited fed-batch mode. As the serum-free base medium, HyQ SFM4CHO-Utility from HyClone, (Logan, Utah, USA) was used. It contains 3 g/L glucose and is void of glutamine. All glutamine was separately fed to the reactor after inoculation. As the cell line is auxotroph with respect to hypoxanthine and thymidine, the medium was supplemented with 10 mL/L HT-Supplement (Gibco 50×, Invitrogen, Karlsruhe). Two separate feeds were used. The concentration of glutamine in the first feed solution was 20 mM. At 75 h the old 20 mM glutamine feed reservoir was replaced by a new one with the same glutamine concentration (20 mL of a 200 mM glutamine stock solution) but with additional 50 mL MEM (Minimal Essential Medium) vitamins (Cat#: N11-002, PAA, Pasching, Austria) and 130 mL water to yield a final volume of 200 mL. The second feed solution contained 83 mM glucose supplemented with 50 mL MEM essential and 50 mL non-essential amino acids (Cat#: M11-002, Cat#: M11-003, PAA, Pasching, Austria), 250 mg/L myo-inositol and 15 mg/L biotin, 3 mL HT-supplement and 97 mL 1.5× concentrated HyQ SFM4CHO-Utility medium to yield a final volume of 200 mL. It was started at 75 h. Both exponential feeding rate profiles were calculated to achieve a constant specific growth rate of μ = 0.02 h⁻¹. During cultivation the feed stocks were stored on ice.

Important to state estimation of cell cultures considered in this paper is that the cultures were tightly controlled with respect to temperature, pH and pO₂. These quantities were controlled independently of each other by separate front end PID controllers using 1 M NaOH for pH correction and stirrer speed for pO₂. The total consumption of NaOH for pH correction was taken as an on-line variable, referred to as “Base” and was used in the estimation procedures.

The ambient conditions were constant at 37 °C, pH 7.15, 20% pO₂ and 0.1 L/min air. Until 91 h the culture was aerated via its headspace and was then switched to air dispersion using a ring sparger. The stirrer speed was allowed to be varied in the range of 60–400 rpm.

Glucose and lactate concentrations were determined with the biochemistry analyzer YSI 2700 SELECT (Yellow Springs Instruments, Yellow Springs, Ohio, USA), glutamine and ammonium with R-Biopharm test kits (10139092035, 11112732035, R-Biopharm, Darmstadt).

The culture mass W was measured by means of a Sartorius balance (BP34, Sartorius, Göttingen). The culture density ρ is assumed to be 1 kg/L throughout the cultivation.

Viable and total cell concentrations, as well as cell and debris sizes were measured off-line by an automated cell counter (CASY TT, Roche Innovatis AG, Mannheim). The sample can be directly injected to the measurement device.

Volume fractions of the gas components, particularly O₂ and CO₂, in the reactor’s vent line were measured with a standard quadrupole mass spectrometer (Balzers QMA 200, Balzers, Liechtenstein). In order to increase accuracy, the volume fractions were additionally measured in the gas supply line. For that purpose a 2-way valve was installed to periodically multiplex between input and output and gauge gas measurements. In the inlet line to the ionization chamber of the mass spectrometer an aperture was installed. From the O₂ and CO₂ measurements the oxygen uptake rate (OUR) and carbon dioxide production rate (CPR) were determined employing well known equations (Oeggerli et al. 1994).

Soft sensing methods

Most work was published about biomass estimates from microbial cultures. Zabriskie and Humphrey (1978) started the development with an estimator based on a material balance on oxygen and a kinetic model for molecular oxygen utilization. Jenzsch et al. (2006) compared many different data-driven approaches for biomass estimation in E.coli cultures. Dorresteijn et al. (1996) determined the biomass activity in animal cell cultures from on-line measured oxygen uptake rate and the lactic acid production. From an industrial production perspective, one primarily needs estimates from data that can be measured routinely on-line with well established validated devices at production reactors. Here, soft-sensing methods based on signals for the on-line variables: Base, tOUR (tOUR = OUR·W) and tCPR (tCPR = CPR·W), already mentioned in experimental part of the paper, were investigated.

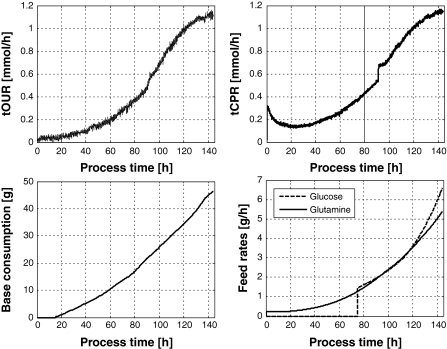
In Fig. 1 typical on-line measured signals of the variables tOUR, tCTR, base consumption and the feed rates from open-loop-controlled fed-batch process are shown. Some disturbances appear during the determination of the respiration rates. Upon switching from headspace aeration to gas sparging at 91 h the tCTR signal rises temporarily as additional CO₂ appears in the headspace from the rising bubbles while there is still CO₂ from headspace aeration. Due to the low aeration rate the gas composition in the headspace changes rather slowly. Only 4 h after the switch the signal gets back on track. Another effect is stripping of CO₂ by the headspace aeration at the beginning of the process. This results from the 4 mM NaHCO₃, the medium initially contained. When these discontinuities occur at the same time to nearly the same extent both in the training as well in the validation data, it is not supposed to play an important role with respect to the cell estimation techniques discussed in this paper. For the Luedeking/Piret model type (Luedeking and Piret 1959) this distortion in tCTR has some but a small impact on cell growth rate within the 4 h time interval.

Fig. 1.

Typical data records from a CHO cell culture performed in the experimental setup described above

Simple model-based approach

In microbial cultures, a simple model-based approach proved to be well performing. It is based on a Luedeking/Piret type of model equation relating the biomass and the on-line measurable uptake or production rates of oxygen, carbon dioxide or base consumptions.

For the absolute or total oxygen uptake rate tOUR such a relationship reads

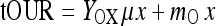2

Y_ox is the oxygen mass consumed per biomass formed, m_o the maintenance coefficient. With the definition of the biomass formation rate dx/dt = μ·x we get

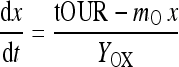3

This is a simple ordinary differential equation in the viable cell count x. When the parameters Y_ox and m_o of Eq. 2 and the initial value of biomass x are known, then Eq. 3 can be solved time-stepwise using the actual on-line measurement values of tOUR at each on-line sampling time t. With the time increments dt usually appearing for the on-line measurements in commonly taken process control systems, a simple Euler approach can be taken to compute the viable cell count estimate x_i at each sampling time t_i:

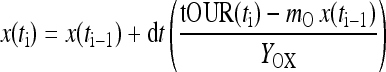4

The parameters Y_ox and m_o can be determined from nonlinear fits of Eq. 3 to measurement data of the biomass x versus the total oxygen uptake rate tOUR. The success of such an approach can be quantified by means of the root mean square error between the off-line measured viable cell counts and the estimates.

The same approach can alternatively be formulated in terms of the carbon dioxide production rate and the base consumption. These expressions read:

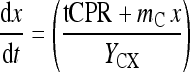5

and

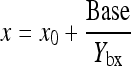6

These simple Luedeking/Piret and linear approaches using a single measurement signal is not really satisfactory. However, when we take a weighted average (w.a.) of the estimates from all three versions (Eqs. 3, 5, 6) using the reciprocal root mean square error (RMSE) values as weights (Eq. 8), then the overall estimate becomes much better.

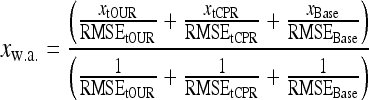7

Linear regression techniques

FDA’s process analytical technology (PAT) initiative (FDA 2004) has led a major industry-wide effort to utilize multivariate data acquisition and analysis tools, modern process analyzers or process analytical chemistry tools, process and endpoint monitoring and control tools, and continuous improvement and knowledge management tools (Gunther et al. 2008).

A most simple black-box approach to multivariate data analysis is multiple linear regression, where the three input signals, the total rates used in the previous section are related by a linear equation

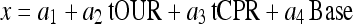8

This is an equation with 4 unknown coefficients that can simply be fitted to the process data by means of least square methods and standard software programs, e.g. MATLAB’s “regress”.

As compared with the simple model-aided approach, the results of such estimation is quite promising, however, they can be improved when cumulative data are used instead of the total rate signals. In the cumulative signals random noise is largely repressed.

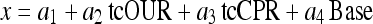9

For a linear approach, this estimator depicts a remarkably good fit.

Principal component analysis (PCA) is a technique that analyses the correlation structure between many interrelated process variables. As it is particularly mentioned in the PAT recommendations of the FDA, this technique is discussed in many recently published papers starting with FDA (2004). Its main advantage used in many applications of high-dimensional data spaces is its capability to reduce the dimension of the data space to be analyzed in detail.

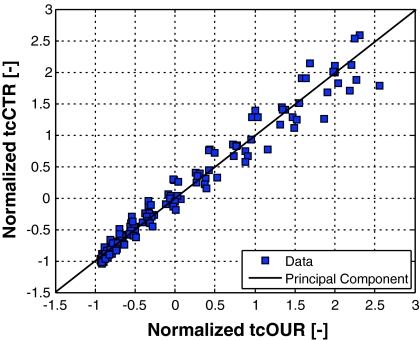
When applied to on-line measured tcOUR and tcCPR data from CHO cultures as shown in Fig. 2, the first principal component depicts a nearly perfect linear relationship between the two components.

Fig. 2.

Simplest PCA analysis of normalized tcOUR and tcCPR signals measured at CHO fed-batch cultures. Symbols represent the measurement data, the line the first principal component

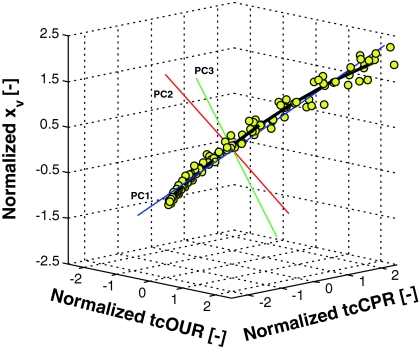
When, however, the cell number x is plotted as the third dimension on the tcOUR-tcCPR-plane, a nonlinear data cloud appears as shown in Fig. 3. The three straight lines in Fig. 3 are the principal axes. It is evident that the first principal axis (blue line) is no longer a good approximation of the three-dimensional data and a reduction in the data dimension does not make sense in this case.

Fig. 3.

Normalized cell count as a function of normalized tcOUR and tcCPR from the same experiments as those depicted in Fig. 2. All three principal axes are plotted into the data cloud (straight lines). The curve through the data (symbols) depicts the quadratic extension of the linear approach described in the text

Nonlinear regression techniques

The nonlinear character of the relationship between the variables becomes clear when one looks at a correlation plot. Figure 3 depicts a bended data bundle. In applications where the data clouds depict a nonlinear form, the nonlinearity with respect to the variables involved can often well be handled with an approach that is quadratic in its input variables. This can be formulated by adding quadratic terms to Eq. 9 resulting in a cumulative multiple polynomial regression

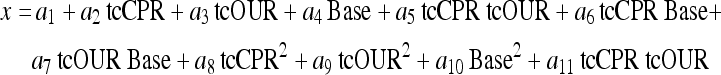10

This expression is nonlinear with respect to the basic process variables but linear in the unknown coefficients a_i. The nonlinear terms, the cross term tcOUR tcCPR and the quadratic-terms tcOUR² and tcCPR² can directly be derived from the tcOUR and tcCPR data. They can thus be considered auxiliary variables with known values.

In order to determine the unknowns, we are thus in the same situation as with multiple linear regression already discussed. Hence, least square methods and the multiple linear regression routines from the standard numerical packages such as MATLAB, MathCat, Excel, etc. can be applied to find the parameters.

Simple feed-forward artificial neural networks

Artificial neural networks are known to be universal representations of multiple nonlinear relationships. Very simple versions of artificial neural networks (ANN) can be used to replace traditional engineering correlations. Hornik et al. (1989) proved that a feed-forward neural network with a single hidden layer of sigmoidal nodes depicts universal approximation properties.

When such an ANN is used as estimator for the cell density from off-gas measurements, improvements can be obtained as compared with the linear estimates. Again, the same input data vector Dat_in = [tcOUR, tcCPR, Base] is used in this case. Additionally, a bias node fixed to the constant value 1 was employed. A single hidden layer with 4 nodes was applied and the single output layer node is the viable cell count.

Support vector regression

An up-to-date approach to data classification and nonlinear regression is the support vector machines (SVM) and support vector regression (SVR) technique (Drucker et al. 1997). It is based on kernel-based transformations. Its performance is comparable to artificial neural networks; however, the fitting procedures are simpler and more reproducible. Ready-to-use software for implementation of support vector regression techniques is freely available on various machine learning portals. In our experimental investigations we used the well known public software library LIBSVM (Chang and Lin 2001). For training of ν-SVR models, the user must choose some important parameters that influence the performance of the ν-SVR model. In order to get a satisfactory model, these parameters need to be selected properly. It is important to choose the right kernel functions, define the cost of errors and the width of the error-insensitive tube. Radial basis function kernels were used in this application. The parameters of the kernels (Gaussian kernel, γ = 0.5), the values of the cost function (C = 100) and the width of the error-insensitive tube (ε = 0.5) was obtained using a trial-and-error procedure.

Hybrid model

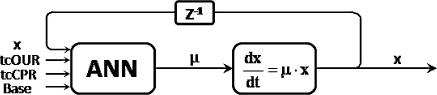
Further improvements can be expected when the pure black-box approach taken in an ANN is complemented with hard knowledge in form of a mass balance equation (Simutis et al. 1997). Such a hybrid approach is depicted in Fig. 4. While the biomass balance is a well known equation, the kinetic expression is less well known. Hence, where enough measurement data are available, the kinetics can be represented in a data-driven way. Here the kinetics in a dynamic mode for biomass estimation is formulated by means of an artificial neural network.

Fig. 4.

Hybrid estimator composed of a mass balance for biomass x and an ANN for the specific growth rate μ. While the mass balance equation is known, the kinetic expression is mechanistically less well known and thus replaced by a data driven expression

Note that this ANN is completely different to that used in the previous chapter. Its inputs are the same variables as already mentioned for the simple feed-forward ANN. But its output is the specific biomass growth rate μ. This specific growth rate is the input variable for the viable biomass balance equation. The viable biomass (cell count), the solution of the balance equation is fed back to the input of the ANN.

As we do not have direct measurement data for the specific biomass growth rate which could be used to fit the model parameters of the network (network training to obtain the weight coefficients), the sensitivity approach (Schubert et al. 1994) was employed to train the network. For this purpose, the measurement data for the input variables of the ANN and the initial value of the cell count must be provided.

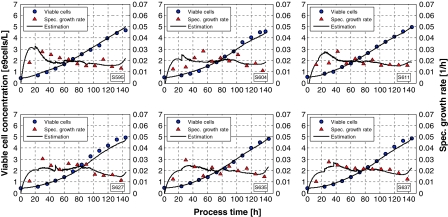
Typical results are depicted in 1. The data taken to identify the model parameters, here the weights of the artificial neural network are the same training data sets used to identify the previous models.

It is important to note that without biomass, where we only need the initial value, all other input values to the model are on-line available. Hence the model is not only a proper dynamic process model but also a model that can be used for biomass estimation with the extension, as compared to the simple ANN, that the specific biomass growth rate is simultaneously estimated.

Note, the data were taken from fed-batch experiments, where an exponential feed rate F(t) was used corresponding to a specific biomass growth rate of μ_set = 0.02 h⁻¹. The growth is glutamine limited, the maximal specific growth rate of the cells is about μ_max = 0.04 h⁻¹.

Results

To evaluate the various estimation approaches 6 fermentation runs were used for parameter identification and 6 completely independently measured data sets for validation of the methods. The performance of each method is quantified by means of the RMSE value for viable cell concentration (X = x/W).

The general result is that all techniques investigated depict acceptable results when the measurement data are undisturbed. However, there are differences with respect to the estimation precision. The best result with respect to the validation sets was obtained with the hybrid model approach, the worst, where the RMSE is about three times larger by an estimation of the biomass from the tCPR data. All results are compiled in Table 1.

Table 1.

Summary of the proposed estimation techniques and their corresponding RMSE for training and validation data

Estimation technique	RMSE of training data (e9cells/L)	RMSE of validation data (e9cells/L)
Hybrid model	0.16	0.154
Cumulative multiple linear (Eq. 9)	0.20	0.158
Support vector regression	0.19	0.162
Feed-forward ANN	0.16	0.175
Model based w.a. (Eq. 7)	0.17	0.185
Base related (Eq. 6)	0.28	0.188
Cumulative multiple polynomial (Eq. 10)	0.14	0.197
Multiple linear (Eq. 8)	0.22	0.209
tOUR related (Eq. 3)	0.45	0.407
tCPR related (Eq. 5)	0.38	0.430

In the table, the RMSE value is given independently for the training data and for the validation data. These are different, for the training data they were computed from the differences between the off-line measured data used to fit the various model parameters and the computed values. For the validation data they were computed as differences between the measured data and the values computed with the already trained estimator. In order to judge the various estimators the latter value is important (obtained with the validation data). With respect to the training data the ranking of the methods would be different.

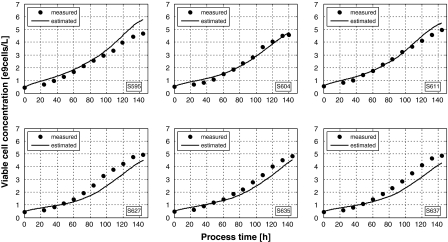
In order to allow an even better judgment, the estimated biomass can be plotted together with the off-line data as a function of time. To cut a long story short, only the worst and the best estimates are shown in the following graphs (Fig. 5).

Fig. 5.

Biomass estimates by the hybrid model sketched in Fig. 4. The network weights were identified with the same data as taken in the previous examples. The symbols are the off-line measured cell concentrations (circles) and calculated specific growth rates (triangles), the lines the on-line estimates

Even with the estimator that led to the worst result a quite good estimation quality was obtained as can be seen here:

The quality of estimation based on Luedeking/Piret (Fig. 6) varies in different cultivation phases. This causes changes in yield coefficients which are not considered in this form of equations. This marching on technique is better in the beginning where it starts with concrete measurment data. Later, the error becomes obviously larger.

Fig. 6.

Luedeking/Piret-type approach using total carbon dioxide production rate data tCPR to estimate the viable cell concentration (Eq. 8). The symbols are the off-line measured cell concentrations, the lines are the estimates computed

Generally the methods presented here deliver very good results although they are based on simple well established measurement techniques that can be installed at every production fermenter as well. No sophisticated measurement devices requiring skilled personnel to keep it working are necessary. These techniques do not pose any risk with respect to contamination to the culture as the measurements are installed in the vent line. To our experience, the quite expensive mass spectrometers can be replaced by new developments in off gas analysis techniques which are much less expensive.

The proposed method delivers representative values for the entire culture and not local measurements. These estimators were designed for monitoring and control of cultivation processes which require stable and robust estimates.

The method was developed for real cultures using common feeding strategies and validated against process data. Other feeding strategies could be tested and the estimators could be adapted, however, these investigations would require additional expensive experiments away from the common procedure in industry to validate the results.

Conclusion

Data presented show a comparison of several techniques for on-line biomass estimation. The choice of the techniques was made from an industrial perspective: The techniques are immediately applicable in production plants as the required measurement can all be performed with well established measurement devices. Most information is to be expected from off-gas measurements, i.e. the oxygen and carbon dioxide gas volume fractions in the bioreactor vent line.

It thus makes sense to monitor cell culture processes with modern techniques of off-gas analysis as it allows to compute reliable on-line estimates of key process quantities: viable cell count x and its actual growth rate. In case of distortions, the base related model aided support still gives values which are quite accurate. i.e. in case that a feed-back control is based on the off-gas data the process can be kept running when there are problems with the primary data signals.

As with experiences from microbial biomass estimations (Jenzsch et al. 2006), stable estimates with respect to the validation sets can be obtained with multiple linear regression technique and simple feed-forward artificial neural networks with a single hidden layer. Support vector regression also leads to good results. When one is not interested in the specific growth rate estimates, which are automatically delivered with the hybrid model approach, then these approaches are the methods of choice.

Best results were obtained with hybrid models. Hybrid models, however, require more complicated identification procedures; but provide estimates on biomass and its current specific growth rate.

The polynomial regression estimator (Eq. 9) identified using least square method led to the best result with respect to the training data (see Table 1, RMSE = 0.14°e9cells/L). However, because of its large number of parameters the estimator has an insufficient generalization capacity. In other words, it tends to overfitting. Consequently the quality of estimation with respect to the validation data sets is even lower than that of the linear estimator. Artificial neural networks also have a lot of parameters; therefore, the trainings procedure of the ANNs must be carried out very carefully using special cross-validation mechanisms that avoid overfitting.

Abbreviations

μ

Specific growth rate (h⁻¹)

q_P

Specific product formation rate (g e9cells⁻¹ h⁻¹)

X

Cell concentration (e9cells L⁻¹)

X_V

Viable cell concentration (e9cells L⁻¹)

x

Cells count (e9cells)

m_P

Mass of product (g)

W

Culture weight (kg)

ρ

Culture density (kg L⁻¹)

t

Process time (h)

OUR

Oxygen uptake rate (mmol kg⁻¹ h⁻¹)

CPR

Carbon dioxide production rate (mmol kg⁻¹ h⁻¹)

tOUR

Total oxygen uptake rate (mmol h⁻¹)

tCPR

Total carbon dioxide production rate (mmol h⁻¹)

tcOUR

Total cumulative O₂ uptake rate (mmol)

tcCPR

Total cumulative CO₂ production rate (mmol)

Base

Consumed Base (g, kg)

Y_OX

Yield O₂/Cells, Y_OX = 10.34 (mmol e9cells⁻¹)

Y_CX

Yield CO₂/Cells, Y_CX = 11.37 (mmol e9cells⁻¹)

m_O

Maintenance for O₂, m_O = 0.001 (mmol e9cells⁻¹ h⁻¹)

m_C

Maintenance for CO₂, m_C = 0.001 (mmol e9cells⁻¹ h⁻¹)

Y_bX

Yield Base consumption/Cells Ybx = 9.0e-3 (kg e9cells⁻¹)

RMSE

Root mean square error (e9cells kg⁻¹)

w.a.

Weighted average of Base, tOUR, tCPR related models