Analysis of the willow root system by electrical impedance spectroscopy

Abstract

Information on plant roots is increasingly needed for understanding and managing plants under various environmental conditions, including climate change. Several methods have been developed to study fine roots but they are either destructive or cumbersome, or may not be suitable for studies of fine root functionality. Electrical impedance, resistance, and capacitance have been proposed as possible non-destructive measures for studying roots. Their use is limited by a lack of knowledge concerning the electrical circuit of the system. Electrical impedance spectroscopy (EIS) was used for hydroponically raised willows (Salix schwerinii) to estimate the root system size. The impedance spectra were investigated in three experimental set-ups and the corresponding appropriate lumped models were formulated. The fit of the proposed lumped models with the measured impedance spectra data was good. The model parameters were correlated with the contact area of the roots and/or stems raised in the hydroponic solution. The EIS method proved a useful non-destructive method for assessing root surface area. This work may be considered to be a new methodological contribution to understanding root systems and their functions in a non-destructive manner.

Introduction

The main functions of tree roots consist of anchorage, and uptake of water and nutrients and their transport with metabolites between roots and shoots. Due to their wide distribution, roots also play a key role in the water and carbon balance of the forest ecosystem. As a consequence, knowledge of the growth and activity of the root system is increasingly needed to understand the function of trees and the management of forests in a changing environment. This requires particular attention to be paid to fine roots which function in symbiosis with mycorrhizal hyphae and in water and nutrient uptake, and which therefore affect the overall vitality and growth of trees. In spite of the decisive role played by roots, for technical reasons studies in this particular area are relatively sparse compared with studies devoted to shoots. Several methods have been developed for studying fine roots (biomass, growth, and longevity), but they are either destructive or cumbersome, or may not be suitable for studies of fine root functionality. Therefore, a major challenge exists to develop new non-destructive methods for studying tree roots in situ.

In recent years efforts have been made to develop electrical impedance spectroscopy (EIS) to study the root system (Ozier-Lafontaine and Bajazet, 2005; Repo et al., 2005). Previously, EIS had been used to investigate the properties of plant, animal, and human tissues (Tiitta et al., 1999; Altmann et al., 2004; Bayford, 2006; Grimnes and Martinsen, 2008). In plants, the method has also been used to reveal the responses of detached plant tissues to cold acclimation, freeze–thaw and heat injury, and exposure to elevated ozone and carbon dioxide (Zhang et al., 1992; Zhang and Willison, 1993; Repo et al., 1994, 2000, 2004; Ryyppö et al., 1998).

In the course of several studies, single-frequency alternating current was applied in order to assess the capacitance or resistance of the root system, since those attributes were assumed to provide a measurement of the active root surface area (Walker, 1965; Chloupek, 1972, 1977; Dalton, 1995; Preston et al., 2004; Aubrecht et al., 2006; Čermák et al., 2006; McBride et al., 2008). A form of single-frequency (128 Hz) measurement, the earth impedance method, was introduced to estimate the absorbing root surface area in the field (Aubrecht et al., 2006; Čermák et al., 2006). The impedance was related to the basal area over a large range of stem diameters, which was further assumed to be related to the absorbing root surface area (Čermák et al., 2006). Based on the single-frequency measurements, equivalent models were formulated using resistors in the case of willow cuttings with their root system raised in hydroponic systems (Cao et al., 2010). In that particular study it was found that the resistance decreased in relation to an increase in the contact surface area of roots using the solution. The resistance depended strongly on the area of the stem in contact with the solution, which, however, tended to cause a bias in the evaluation of the root surface area. The single-frequency approach provides a simplified view of the overall equivalent model of the system because it does not consider multiple resistances and capacitances in the circuitry.

In the EIS approach, a wide frequency range is used to measure an impedance spectrum that is comprised of real and imaginary parts. An equivalent circuit model (lumped or distributed) is then formulated for the system and the model parameters are estimated by means of the complex non-linear least squares (CNLS) curve-fitting program (Macdonald, 1992; Barsoukov and Macdonald, 2005). In order to understand the details of the electrical current pathways and to devise a reasonable interpretation of the equivalent circuit elements, it is necessary to split the circuitry under consideration into parts and then to analyse each part in detail, as has been done previously by Dalton (1995) and Ozier-Lafontaine and Bajazet (2005). The proposed models took into account the electrode–soil interface, root medium, roots, stem, and electrode–stem interface, each of which was represented by a parallel circuit of resistance and capacitance (R//C) and all R//C circuits in series. Further studies were suggested for analysis of the significant components in the circuitry independently; that is, the electrode–soil interface, soil, root, stem, and stem–electrode interface.

The aim of this study was to develop equivalent circuits for willow roots grown in hydroponic solution and then to analyse the circuit elements using the EIS approach. The hydroponic cultivation method was used to standardize the role of the growing substrate. The EIS was carried out in three experimental set-ups: (i) both stem and root in the solution; (ii) root in the solution; and (iii) stem in the solution. Lumped models were formulated for each situation, and the model parameters were correlated with the area of contact of roots and stem with the solution. It was hypothesized that the root system size could be evaluated using the EIS method with the aid of an appropriate equivalent circuit model.

Materials and methods

Willow cuttings (Salix schwerinii) were collected in June 2009 from a plantation in Siikasalmi (62°30′ N, 29°30′ E) in eastern Finland, and stored in water containers in a cold room (4 °C). Eighteen cuttings (18–20 mm in diameter, 250 mm in length) were cultivated for 14 d in containers (500 mm×390 mm×250 mm) of aerated tap water in a greenhouse with the following conditions: photosynthetic photon flux density (PAR) 320 μmol s⁻¹ m⁻², photoperiod 18/6 h (day/night), and relative humidity 80%. The cuttings were embedded half way up in the water solution by using floating pads. The water was changed at 3 d or 4 d intervals. After 14 d of growth, the tap water was replaced by a nutrient solution with conductivity of 54.2 μScm⁻¹ (10 mg N in 1.0 l of water with macro- and micronutrients; Riddoch et al., 1991) for the impedance spectra measurements. The specimens were moved within the same containers from the greenhouse to the laboratory to start electrical impedance measurements on the following day.

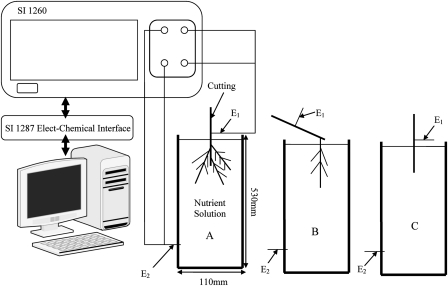
The electrical impedance spectra (Wessel diagram) were measured using an impedance gain-phase analyser (SI1260, Solartron, Farnborough, Hampshire, UK) at 31 frequencies between 60 Hz and 60 kHz. For the impedance spectra, one Ag electrode (0.5 mm in diameter) was inserted in the middle position of the stem above the solution. This position was kept the same throughout the measurements. To maintain an even electric field distribution in the solution, another Ag electrode was placed at the bottom of the narrow solution container (Fig. 1). The electrodes were connected with coaxial cables to the analyser. The input voltage level of the sinusoidal signal was 0.1 V (rms). The effect of the system function (including the solution, polarization on the surface of the solution electrode, and noise from the surroundings) was eliminated by measuring the impedance spectrum of the solution without the plant, and then subtracting it from the impedance spectrum with the plant.

Fig. 1.

Diagram of the experimental set-ups for the measurement of the impedance spectra of willows. (A) The stem with the whole root system in the solution (‘Stem and root’). (B) A single root in the solution (‘Root’). (C) The stem only in the solution (‘Stem’). E₁ and E₂ refer to the Ag electrodes.

The impedance spectra were measured in three experimental set-ups. (A) All of the roots, along with the cutting, were immersed in the solution (‘Stem and root’) (Fig. 1A). (B) One light-coloured and non-wounded root of each cutting was immersed in the solution (‘Root’) (Fig. 1B). The other roots were kept away from the circuitry by means of a plastic film. (C) The roots were dissected and only a part of the stem was immersed in the solution (‘Stem’) (Fig. 1C). The immersion depth of the stem was the same in each measurement set-up.

After the impedance spectra were measured, the roots were dissected and scanned (Epson Expression 1640XL, Epson America, Inc., USA) so that the contact surface area of the roots with the solution could be assessed (WinRhizo, Régent Instruments Inc., Québec, Canada). The base diameter and the immersion depth of the cuttings were recorded to obtain the contact area of the stems with the solution in both an axial (longitudinal) and a radial (cross-sectional) direction.

Models

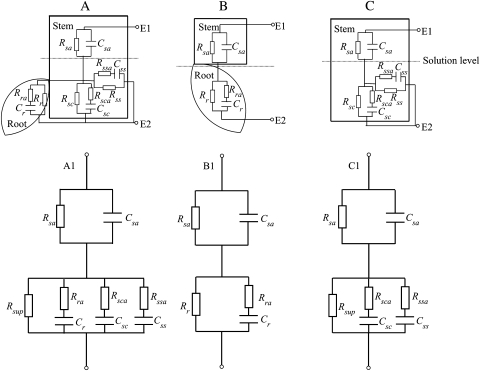
According to the measured impedance spectra and prior knowledge of the physicochemical properties and the equivalent circuit models for different components in the experimental set-ups (Zhang and Willison, 1991; Repo and Zhang, 1993; Dalton, 1995; Barsoukov and Macdonald, 2005; Ozier-Lafontaine and Bajazet, 2005; Cao et al., 2010), a lumped model was formulated for each set-up (Fig. 2A–C) and then simplified for parallel resistors in circuits A and C (Fig. 2A1–C1).

Fig. 2.

The detailed electrical models (A, B, and C) and the corresponding simplified models (A1, B1, and C1) for willow in the three experimental set-ups (see Fig. 1). R_sa and C_sa, the resistance and capacitance of the stem above the solution level; R_ss and C_ss, the resistance and capacitance of the longitudinal interface of the stem with the solution; R_sc and C_sc, the resistance and capacitance of the cross-sectional interface of the stem with the solution; R_r and C_r, the resistance and capacitance of the interface of roots with the solution; R_ssa, R_sca, and R_ra, the auxiliary resistances for the bulk resistance properties of the surface of the stem, the cross-section of the stem, and the root immersed in the solution, respectively. The superposition resistance, R_sup, combines the effects of the parallel interface resistances of stem (C) and roots (A) with the solution. E₁ and E₂ refer to the electrodes.

In the model for the whole root system immersed in the solution together with the stem, the stem above and below the solution surface was considered in addition to the root (Fig. 2A, A1). One R//C circuit represents the stem above the solution, being composed of resistance R_sa and capacitance C_sa. Three R//C circuits consider the axial and radial current pathways between the stem, the roots, and the solution. Capacitances C_ss, C_sc, and C_r represent the longitudinal and cross-sectional interface area of the stem with the solution and the interface of roots with the solution, respectively. The superposition resistance R_sup combines the effects of the parallel interface resistances of stem and roots with the solution, i.e. the longitudinal (R_ss) and cross-sectional (R_sc) interface of the stem and the interface of the roots (R_r) (Fig. 2A1). In addition, R_ssa, R_sca, and R_ra are termed auxiliary resistances; they consider the bulk properties of the stem in the radial and axial direction and the properties of roots, respectively.

The model for a single root in the solution is composed of two R//C circuits in series (Fig. 2B, B1). One R//C circuit represents the stem above the solution, being composed of resistance R_sa and capacitance C_sa (compare Fig. 2A and A1). Another R//C circuit represents the root immersed in the solution, being composed of three components. Resistance R_r and capacitance C_r represent the interface of root with the solution. Auxiliary resistance R_ra considers the bulk resistance property of the root (compare Fig. 2A and A1).

In the case of only the stem in the solution (Fig. 2C, C1), the situation was similar to that found in the case of the stem with the roots in the solution (Fig. 2A, A1) with no extension circuit for the roots in the solution. R_sa and C_sa represent the electrical properties of the stem above the solution surface level as in the above models (Fig. 2A1, B1). The capacitances C_ss and C_sc refer to the longitudinal and cross-sectional interfacial layers of the stem in contact with the solution, respectively. The superposition resistance R_sup represents two parallel interface resistances of the stem, i.e. the longitudinal (R_ss) and the cross-sectional (R_sc) interface of the stem in contact with the solution (Fig. 2C1). R_ssa and R_sca represent the auxiliary resistance, and they are considered to be the bulk resistance properties of the stem in a radial and an axial direction for the immersed part of the stem.

The parameters of the equivalent circuits were estimated using a free CNLS curve-fitting program (LEVM Version 8.09, J. R. Macdonald, http://www.jrossmacdonald.com).

The regression module of SPSS software (ver. 15.0, SPSS Inc., IL, USA) was used to test the relationships between the lumped model parameters with the longitudinal and cross-sectional stem surface area and the root surface area.

Results

Impedance spectra and model evaluations

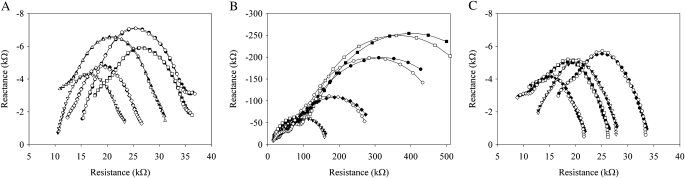
According to the impedance spectra of the three experimental set-ups, the magnitude of real and imaginary parts of the root in contact with the solution >10 times higher (Fig. 3B) than that of stem and roots in contact with the solution (Fig. 3A), or only the stem in contact with the solution (Fig. 3C). The magnitude of the real and imaginary parts of the impedance spectra in three experimental set-ups changed depending on the contact area of the specimens with the solution (Fig. 3). The fit of the proposed lumped models with the impedance spectra data in the three experimental set-ups (see Fig. 2) was good (Fig. 3). The estimated relative standard deviations (ERSDs) of the parameters were <10%, except for the capacitance C_sa of the stem and roots in the solution (Fig. 1A, Table 1).

Fig. 3.

Examples of the impedance spectra of the three experimental set-ups in the solution (filled symbols) and the best fit of the lumped model (open symbols) (see Figs 1, 2). (A) The stem with the whole root system in the solution (‘Stem and root’). (B) A single root in the solution (‘Root’). (C) The stem only in the solution (‘Stem’). In each curve, referring to different plants with different sizes of roots and stem, the frequency increases from right (60 Hz) to left (63 kHz).

Table 1.

Examples of the best-fit lumped model parameter estimates, standard deviations (SDs), and estimated relative standard deviations (ERSDs) for three experimental set-ups in the solution (see Figs 1–3)

		Rsa (kΩ)	Csa (nF)	Rssa (kΩ)	Css (nF)	Rsca (kΩ)	Csc (nF)	Rra (kΩ)	Cr (nF)	Rsup (kΩ)
A. Stem and root	Estimate	2.3	780.5	60.2	0.37	23.6	0.07	115.8	0.98	23.5
	SD	0.09	68.9	1.5	0.02	0.56	0.001	5.6	0.03	0.08
	ERSD (%)	3.9	8.8	2.5	5.4	2.4	1.4	4.8	3.1	0.3
B. Root	Estimate	59.5	0.18					21.4	1.5	406.0
	SD	1.6	0.008					1.1	0.04	10.0
	ERSD (%)	2.7	4.4					5.1	2.7	2.5
C. Stem	Estimate	3.4	103.4	48.8	0.61	47.0	0.08			24.4
	SD	0.15	11.5	1.0	0.016	1.0	0.005			0.16
	ERSD (%)	4.4	11.1	2.0	2.6	2.1	6.3			0.7

EIS parameters in relation to morphology

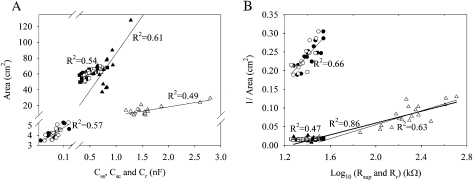
The EIS parameters were related to the contact area of the specimens with the solution. In the set-up with stem and roots in the solution (see Figs 1A, 2A), the interfacial capacitances C_ss, C_sc, and C_r, referring to the longitudinal and cross-sectional interface of stem and to the interface of roots with the solution, increased linearly with the increase in the surface area (Fig. 4A, Table 2). The logarithmic superposition resistance R_sup had positive linear relationships with the reciprocal of the longitudinal stem surface area and with the stem cross-sectional area in the solution (Fig. 4B, Table 2). The relationship between the superposition resistance R_sup and the root surface area in contact with the solution was low (R²=0.09) (Fig. 4B, Table 2). For the root in contact with the solution only (see Figs 1B, 2B), the parameters referring to the root–solution interface, i.e. interfacial capacitance C_r and resistance R_r, were dependent on the root surface area. Capacitance C_r increased linearly (Fig. 4A, Table 2), whereas the logarithmic resistance R_r positively increased with an increase in the reciprocal of root surface area (Fig. 4B, Table 2). There was no difference between the set-ups with ‘Stem’ and ‘Stem and roots’ in contact with the solution (see Figs 1C, 2C) with respect to the relationship between the interfacial capacitances C_ss and C_sc and the superposition resistance R_sup with the longitudinal and cross-sectional area of the stems (Fig. 4, Table 2).

Fig. 4.

Relationships between the lumped model parameters, i.e. interfacial capacitances (A) and superposition resistance and interfacial root resistance (B), with the contact area of stem and root with the solution of willows in three experimental set-ups: ‘Stem and root’ (filled squares, circles, and triangles), ‘Root’ (open triangle), and ‘Stem’ (open squares and circles) (see Fig. 1, 2). Squares, circles, and triangles refer to the longitudinal (C_ss and R_sup) and cross-sectional interface (C_sc and R_sup) of stem and to the interface of roots (C_r, R_r, and R_sup) with the solution, respectively. The detailed regression results can be seen in Table 2.

Table 2.

Regressions between interfacial capacitances, resistance, and superposition resistance with the longitudinal and cross-sectional interfacial area of stem and with the interfacial area of roots in the solution used in the three experiment set-ups (see Fig. 4)

Dependent variable (y)	Independent variable (x)	Regression	Symbols in Fig. 4
Stem longitudinal area	Css (pooled data from set-ups A and C)	y=30.08x+45.05	Filled and open squares
		R2=0.54
	log10Rsup (pooled data from set-ups A and C)	1/y=0.015x–0.003	Filled and open squares
		R2=0.47
Stem cross-sectional area	Csc (pooled data from set-ups A and C)	y=23.62x+2.42	Filled and open circles
		R2=0.57
	log10Rsup (pooled data from set-ups A and C)	1/y=0.34x–0.23	Filled and open circles
		R2=0.66
Root surface area	Cr (data from set-up A)	y=10.93x–3.60	Filled triangles
		R2=0.61
	log10Rsup (data from set-up A)	1/y=0.023x–0.05	Filled triangles
		R2=0.09
	Cr (data from set-up B)	y=94.05x–8.16	Open triangles
		R2=0.49
	log10Rr (data from set-up B)	1/y=0.108x–0.17	Open triangles
		R2=0.63
	log10 (Rr+Rsup) (pooled data from set-ups A and B)	1/y=0.079x–0.098	Filled and open triangles
		R2=0.86

Several common parameters exist in the models for the different set-ups (Fig. 2A1, B1, C1). Hence, it is reasonable to compare those parameters in the different independent measurements with different set-ups. Based on the mean values, most of the parameters for the ‘Stem and root’ (see Figs 1A, 2A, A1) and for the ‘Stem’ (see Figs 1C, 2C, C1) were close to each other (Table 3). The parameters also bore a similar relationship to the contact area of the stem (Fig. 4A, Table 3). When the single root (‘Root’) was in the solution then the parameter estimates for the stem (R_sa, C_sa) differed from the corresponding values in the other two set-ups (compare Fig. 1B with 1A, C, respectively) (Table 3). The auxiliary parameter estimate referring to the properties of root (R_ra) was lower for the ‘Root’ than for the ‘Stem and root’. The interfacial resistance of the ‘Root’ (R_r) (see Fig. 2B) was much higher than the superposition resistance (R_sup) for the set-up ‘Stem and roots’ (Fig. 2A). However, the slope for the interfacial root capacitance (C_r) with the root surface area was clearly different for the ‘Root’ in comparison with the ‘Stem and root’ (Fig. 4A, Table 2). According to the pooled data, the logarithmic superposition resistance (R_sup) in the set-up ‘Stem and root’ and the interfacial resistance of the single root (R_r) in the set-up ‘Root’ were correlated strongly with the reciprocal of the contact area of roots in the solution (Fig 4B, Table 2).

Table 3.

The mean lumped model parameters (standard deviation in parentheses) for stem and roots of willow cuttings in the three experimental set-ups (Figs 1, 2) (n=15)

Set-up	Rsa (kΩ)	Csa (nF)	Rssa (kΩ)	Css (nF)	Rsca (kΩ)	Csc (nF)	Rra (kΩ)	Cr (nF)	Rsup or Rr (kΩ)
A. Stem and root	2.9 (0.9)	459 (248)	49 (12)	0.4 (0.2)	33 (23)	0.07 (0.01)	122 (46)	0.8 (0.2)	27 (5)
B. Root	55 (40)	0.3 (0.2)					22 (10)	1.4 (0.5)	200 (127)
C. Stem	3.3 (0.6)	109 (30)	50 (12)	0.6 (0.1)	33 (18)	0.08 (0.02)			24 (4)

In the right-hand column R_SUP refers to set-ups A and C, and R_r to set-up B.

Discussion

The aim of the present study was to develop the EIS method for estimating root system size non-destructively. The investigation focused on developing an equivalent circuit model for willow roots cultivated in a hydroponic solution. The impedance spectra were obtained from three experimental set-ups, i.e. stem and roots, root, and stem immersed in the solution (see Figs 1, 2). The lumped models were formulated for each condition, and the measured impedance spectra data were analysed with regard to the corresponding models. High correlations were found for some electrical parameters, referring to the interfacial parts of stem and roots, with the contact surface area of the respective organs in the solution.

The lumped models were formulated for the roots and stems of willows in the three experimental set-ups, and they resulted in a good fit with the measured data (parameter ERSD values <10%). In previous EIS studies of plants, two kinds of electrical models, i.e. distributed (DCE) and lumped, have been used (Dalton, 1995; Repo et al., 2000, 2002, 2004; Ozier-Lafontaine and Bajazet, 2005). The lumped models, consisting of a limited number of ideal resistors and capacitors, have been used for uniform tissues such as potato tubers, carrot roots, and apple fruits (Zhang and Willison, 1991). The lumped models are assumed to describe the biological structure of specimens in more detail than the distributed models. Hence, their use is preferred to the DCE models, where the sample is modelled by means of a mathematical expression. While the DCE model, with a smaller number of parameters than the lumped model, may result in a mathematically good fit, the detailed equivalent model and the biological interpretation of the parameters may remain unknown.

Although lumped models have advantages, their formulation is not unambiguous. For a given impedance spectrum data set there exists more than one equivalent circuit that may result in a good fit, and it is necessary to select the model that provides the best and most realistic representation of the sample (Ozier-Lafontaine and Bajazet, 2005). The choice should be based on the simplicity and consistency of the system's properties and also on whether the circuit elements are connected in series or in parallel (Barsoukov and Macdonald, 2005; Ozier-Lafontaine and Bajazet, 2005). In this study, the lumped models were formulated for the three experimental set-ups on the basis of these principles and previous studies on roots (Zhang and Willison, 1991; Repo and Zhang, 1993; Dalton, 1995; Barsoukov and Macdonald, 2005; Ozier-Lafontaine and Bajazet, 2005; Cao et al., 2010).

The lumped models described well the role played by roots and stems and their interfaces with the cultivation solution, while the influence of the solution was eliminated. In addition, certain lumped model parameters (C_ss, C_sc, C_r, and R_sup) that were common to the different set-ups correlated highly with the contact area of roots and the stem in the solution, thus suggesting plausible models. In previous root studies, lumped models consisting of parallel R//C elements in series were used to present the soil–root interface and the root and stem continuum without measuring the various components separately (Dalton, 1995; Ozier-Lafontaine and Bajazet, 2005). In the present study, however, these components were analysed independently and thus it was possible to propose a new connection of these circuit elements (Fig. 2). Hence, it can be concluded that the proposed lumped model provides a more reasonable interpretation of the plant and growing medium than previous lumped models.

With regard to the assessment of root size by the EIS, the interfacial root capacitance (C_r) was linearly correlated with the contact area of the root in the solution in both the ‘Root’ and the ‘Stem and root’ set-up (Fig. 4A, Table 2). Due to the larger root surface area in the ‘Stem and root’ than in the ‘Root’ set-up, the root–solution interfacial capacitance (C_r) should be higher for the former than for the latter, and the relationship with the root surface area should be the same. The root–solution interfacial capacitance (C_r) was not, however, higher for the former than for the latter, and the slope for these two relationships was different. As a consequence, there seemed to be some interaction of the root and stem in the set-up ‘Stem and root’. The difference in the slopes for the various interfacial capacitances, i.e. C_ss, C_sc, and C_r, with the respective areas are due to different electrochemical properties on the surfaces of the stem and root (Table 2). It can be concluded that the regression line for ‘Stem and root’ would provide a more realistic assessment of the root size in a real situation (roots with cuttings in soil/solution) than if the regression line for the ‘Root’ were to be used.

Due to the strong overlapping effect of the stem with regard to the roots in the ‘Stem and root’ set-up and the parallel connection of the interfacial resistances of stem (longitudinal R_ss and cross-sectional R_sc) and root (R_r) (the stem resistance being smaller than the root resistance), the logarithmic superposition resistance (R_sup) had only a low correlation with the reciprocal contact area of the roots (R²=0.09) (Fig. 4B, Table 2). This is further supported by the mean R_sup that was approximately the same for ‘Stem and root’ and ‘Stem’, but both were roughly 10-fold lower than R_r for ‘Root’ (Table 3). This result is consistent with a previous study conducted at a single low frequency where the impedance strongly correlated with the contact area of the stem in the solution, but not with the root surface area in the solution (Cao et al., 2010). It can be concluded that current goes preferably to the solution through the stem–solution interface and thus tends to bypass the root system. Under such conditions, the assessment of root size by root resistance is liable to be less accurate than an assessment made with regard to root capacitance. This, in turn, tends to agree with previous studies where the capacitance method was applied more widely in the assessment of root size (Chloupek, 1972, 1977; Dalton, 1995; van Beem et al., 1998; Preston et al., 2004; Rajkai et al., 2005; McBride et al., 2008) than was the resistance method (Aubrecht et al., 2006; Čermák et al., 2006).

When the data for the superposition (R_sup) in the ‘Stem and root’ set-up and the interfacial resistance of the single root (R_r) in the ‘Root’ set-up were pooled, a high correlation was found between the reciprocal of the root surface area and the logarithm of the superposition resistance (R_sup and R_r) (Fig 4B, Table 2). This differs from the result for the pooled data of the root–solution interfacial capacitance (C_r) of those two set-ups. The difference is probably due to the decisive role played by the interfacial stem resistance in the superposition resistance (R_sup). The superposition resistance (R_sup) included root resistance, as had been proposed (Fig. 2). However, it can be concluded that it is possible to estimate root size by the resistance method if the measurement is similar to that found in the ‘Root’ set-up.

The cut surface area of the stem formed an open end through the phloem and xylem to provide the solution to the problem posed in this study. This surface was expected to provide a high passage of current between the stem and the solution (compare Fig. 3A–C). In consequence, it was included in the corresponding circuit models (Fig. 2B1, C1). However, for seed-originated plants no such open ends exist. In future studies with different species and growing substrates, this part of the circuit needs to be verified and the model revised accordingly.

In conclusion, the EIS approach employing the lumped model provided an improved method for studying roots and their function as compared with the single frequency approach. With regard to the estimation of the root size of hydroponically raised willows, root capacitance proved a more useful parameter than did root resistance. The latter would be useful if the effect of the stem in contact with the growing substrate could be eliminated. Further studies of the EIS are needed with soil as the growing substrate, with different contrasts in the resistivity between roots and growing medium, with verification of the method using seed-grown plants under laboratory and field conditions, and also by taking into account the role played by mycorrhizas.

Glossary

Abbreviations

C_r

root–solution interfacial capacitance

C_sa

capacitance of stem above solution level

C_sc

stem–solution cross-sectional interfacial capacitance

C_ss

stem–solution longitudinal interfacial capacitance

DCE

distributed circuit element

E₁

electrode 1

E₂

electrode 2

EIS

electrical impedance spectroscopy

ERSD

estimated relative standard deviation

IS

impedance spectrum

R_r

root–solution interface resistance

R_ra

auxiliary resistance of root

R_sa

resistance of stem above solution level

R_sc

stem–solution cross-sectional interfacial resistance

R_sca

auxiliary resistance of cross-sectional direction of stem

R_ss

stem–solution longitudinal interfacial resistance

R_ssa

auxiliary resistance of longitudinal direction of stem

R_sup

superposition resistance