Abstract
In many muscles, the tendinous structures include both an extramuscular free tendon as well as a sheet-like aponeurosis. In both free tendons and aponeuroses the collagen fascicles are oriented primarily longitudinally, along the muscle's line of action. It is generally assumed that this axis represents the direction of loading for these structures. This assumption is well founded for free tendons, but aponeuroses undergo a more complex loading regime. Unlike free tendons, aponeuroses surround a substantial portion of the muscle belly and are therefore loaded both parallel (longitudinal) and perpendicular (transverse) to a muscle's line of action when contracting muscles bulge to maintain a constant volume. Given this biaxial loading pattern, it is critical to understand the mechanical properties of aponeuroses in both the longitudinal and transverse directions. In this study, we use uniaxial testing of isolated tissue samples from the aponeurosis of the lateral gastrocnemius of wild turkeys to determine mechanical properties of samples loaded longitudinally (along the muscle's line of action) and transversely (orthogonal to the line of action). We find that the aponeurosis has a significantly higher Young's modulus in the longitudinal than in the transverse direction. Our results also show that aponeuroses can behave as efficient springs in both the longitudinal and transverse directions, losing little energy to hysteresis. We also test the failure properties of aponeuroses to quantify the likely safety factor with which these structures operate during muscular force production. These results provide an essential foundation for understanding the mechanical function of aponeuroses as biaxially loaded biological springs.
Introduction
The mechanical behavior of tendon as a spring-like biological material has been shown to play an important role in minimizing the energetic cost of muscle-powered movements (Cavagna et al. 1977; Alexander 1984; Biewener and Baudinette 1995; Roberts et al. 1997). Stretching of tendons in response to an applied load stores elastic energy, which can be recovered upon unloading. As simple springs, tendons’ capacity for storage and recovery of elastic energy is in large part determined by their stiffness as well as by the efficiency with which they return stored mechanical energy (resilience).
The characterization of tendons as simple linear springs arises from both their uniform structural properties as well as their simple loading regimes. Tendons consist of highly organized bundles of collagen, oriented primarily along a muscle's line of action (Elliott 1965). The loading regime of most tendons is largely limited to the longitudinal direction. The simple structural properties and mechanical behavior of tendons have motivated a number of studies linking the mechanical properties of tendons to their locomotory function (Bennett et al. 1986; Shadwick 1990; Pollock and Shadwick 1994).
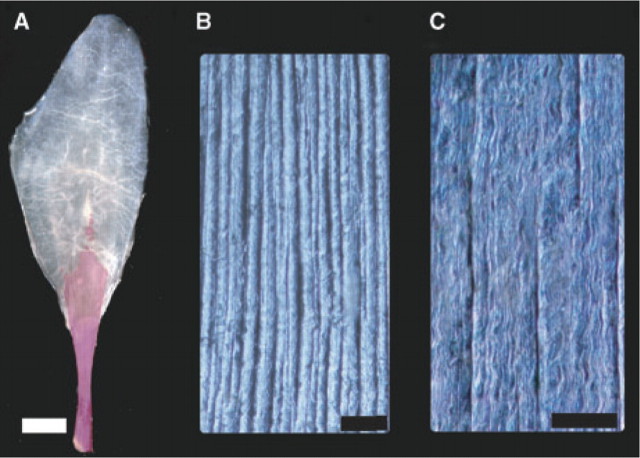
Series elastic structures in muscles are not limited to the extramuscular free tendon. In fact, most muscles with a long free tendon also have a sheet-like aponeurosis that serves as a broad tendinous insertion for muscle fibers. Similar to free tendons, aponeuroses consist of collagen fascicles that are oriented primarily longitudinally (Fig. 1). Given that free tendons and aponeuroses are contiguous and share similar structural properties it is commonly assumed that they are functionally similar.
Fig. 1.
Morphology and collagen architecture of the LG aponeurosis of wild turkeys. (A) Cleared and stained aponeurosis showing the alizarine stained calcified free tendon (red) as well as the aponeurosis. (B) and (C) Images of collagen fascicles of the aponeurosis visualized by oblique contrast microscopy. The primary orientation of collagen fascicles is parallel to the muscle's line of action (longitudinal). The same specimen is shown at two different magnifications. The scale bars correspond to (A) 1 cm, (B) 1 mm, and (C) 300 μm.
An important feature distinguishing aponeuroses from tendons is that unlike free tendons, aponeuroses can cover a substantial portion of a muscle's surface. This arrangement may subject aponeuroses to a more complex loading regime than that of tendons. Since muscles are constant-volume structures (Baskin and Paolini 1967), any shortening along the muscle's line of action will require expansion of the muscle in directions orthogonal to the line of action (Savalberg et al. 2001; Azizi et al. 2008). The close association of aponeuroses with the muscle belly suggests that any changes in shape that occur in a contracting muscle should also stretch the aponeurosis in the transverse direction, perpendicular to the muscle's line of action. Therefore, unlike free tendons aponeuroses may be subject to strains along multiple axes. A few previous studies have, in fact, observed a pattern of biaxial strain in aponeuroses during muscular force production (Scott and Loeb 1995; van Donkelaar et al. 1999). This biaxial loading pattern may have important implications for how this sheet-like biological material functions in a contracting muscle. To our knowledge, however, the mechanical properties of aponeuroses along directions orthogonal to a muscle's line of action have not been investigated.
In this study, we compare the mechanical properties of the aponeurosis of the turkey lateral gastrocnemius (LG) in the longitudinal and transverse directions. We use uniaxial material tests of the tissue oriented either longitudinally (parallel to the orientation of collagen fascicles) or transversely (perpendicular to the orientation of the collagen fascicles) to quantify the tissue's Young's modulus and resilience, as well as the stress and strain at which the tissue fails. Hypotheses posed in this study are informed in large part by the structural properties of the tissue (Fig. 1). We hypothesize that aponeuroses are significantly more compliant when stretched in the transverse direction (perpendicular to the collagen orientation) compared to the longitudinal direction. Expected differences in loads and compliance between the longitudinal and transverse directions lead us to also predict significant differences in the failure properties of the two directions. Aponeuroses are likely subject to lower loads in the transverse direction compared to the longitudinal and therefore we hypothesize that the tissue will fail at a lower stress in the transverse direction. We also hypothesize that strain at failure will be higher in the transverse direction due to its greater compliance.
Materials and methods
Superficial aponeuroses of LG muscles were extracted from nine frozen cadavers of wild turkeys, Meleagris gallopavo. In selected specimens, the aponeuroses were cleared and stained and used for examination of the tissue's collagen structure. In this preparation, muscle attached to LG aponeuroses was first macerated in a trypsin solution. The tissue was stained for calcified regions using an alizarine stain and then cleared using stepwise treatment in glycerine/KOH mixtures. Whole, cleared, and stained aponeuroses were photographed and then cut into small sections for examination under an oblique contrast microscope.
Samples from seven aponeuroses were isolated and used for materials testing. The muscle fascicles attached to the aponeurosis were physically removed using blunt dissection. The epimysium on the superficial surface of the aponeurosis was also removed using fine forceps. Care was taken to prevent any puncture or damage to the aponeurosis during the isolation process. Once isolated, each aponeurosis was cut into longitudinal and transverse strips using a custom built punch-die. The visible orientation of collagen fascicles was used as a guide to ensure that the aponeurosis strips were oriented properly. The aponeurosis tapers and thins at the edges of the tissue. Therefore, samples were taken from the center of the aponeurosis to avoid the tapering edges. The strips cut from the aponeurosis were thicker at the ends than in the middle (dog-bone-shaped), which provided greater surface for clamping. This shape also reduced errors associated with uneven clamping and ensured that the tissue would fail in the middle rather than at the clamps. Three ink markers were placed on the surface of each aponeurosis strip. The tissues were kept moist during the isolation and testing process using physiological saline.
Mechanical testing of samples was performed using an MTS MiniBionix II materials testing instrument (MTS Corp., MN, USA). Each sample was placed in custom-made clamps covered with 600-grit emery cloth. Prior to tests, the tissue was slowly stretched at 0.5 mm steps until force began to develop in the tissue. The development of force in the tissue could be resolved at approximately 0.1 N. The length at which each subsequent length step resulted in an increase in force was defined as the tissue's resting length (Lo). Once the resting length was set, the tissue was driven through a series of three cyclical tests and one ramp extension. Each cyclical test extended the tissue sinusoidally by 1%, 2%, or 4% of Lo for the longitudinal samples and 2%, 4%, or 8% of Lo for the transverse samples. Each cyclical test consisted of five identical loading cycles performed at a frequency of 1 Hz. The magnitude of tissue extension (i.e. the amplitude of the sine waves) during the cyclical tests was based on strain data measured from the same aponeurosis during active muscle contractions (Azizi, unpublished data). The range of strain values used here encompassed the strain values reported in previous studies (Scott and Loeb 1995; van Donkelaar et al. 1999). Following the three cyclical tests, each sample was stretched at a constant rate (1%/s) until mechanical failure. For each test instantaneous force and clamp displacements were recorded for future analysis. All mechanical tests were performed at room temperature (∼21–23°C).
Each test was recorded using high-speed video (Photron Fastcam 1024, Photron Inc. San Diego, CA). A single camera was oriented to image the surface of the sample during all tests. High-speed video was used to track three ink markers on the surface of the tissue (Fig. 2). Surface marker positions and tissue dimensions were analyzed using a centroid tracker function in MATLAB (v. 7.0, Mathworks Inc., MA, USA). The script found the center of the marker and was therefore insensitive to changes in the shape of the marker resulting from tissue stretch. The distance between surface markers was used to quantify tissue strain during tests. The use of markers rather than the displacements measured by the MTS allowed us to avoid the potential error associated with slipping at the interface between the tissue and the clamp. Although the use of marker tracking allowed us to measure the true strains in the tissue, tests with significant slipping at the clamp were discarded because the length changes were smaller than the prescribed strains. One potential source of error associated with tracking of external markers is the potential for sliding of tissue across the thickness of the structure. This would result in a mismatch between the actual length change of the tissue and the length change observed at the surface. The thinness of the aponeurosis likely reduces such errors. Under conditions in which we were confident there was little clamp slipping, we found good agreement between length changes measured from surface markers and length changes recorded by the materials testing machine.
Fig. 2.
Materials testing of aponeuroses. (A), (B), and (C) show three frames from a high-speed video sequence captured during failure tests. Three markers placed on the surface of the tissue were used to calculate strains. Grids with 2 mm spacing placed on the tissue clamps were used to calibrate the images. The LED light attached to the stationary clamp was used to synchronize force data gathered from the MTS with strain data measured from the video sequences.
Changes in length measured between surface markers were converted to strains and used to quantify the tissue's Young's modulus for cyclical tests and the strain at failure for failure tests. High-speed video collection was synchronized with MTS data using an LED in the field of view, which was triggered by a square wave pulse recorded as an auxiliary wave in the MTS. High-speed video was recorded at 125 frames per second.
Prior to mechanical testing, the dimensions of each sample were recorded and the tissue was weighed. The dimensions and the weight of the tissue were used to calculate the thickness of the specimen, using a volumetric calculation. The thickness of the tissue was calculated using a tendon density of 1.12 g/cm3 (Ker 1981). Samples used in the study had an average thickness of 225 μm (± 37 μm). Cross-sectional area of the sample was calculated from the sample's thickness and width. Cross-sectional areas were then used to convert forces (N) to stresses (MPa).
Data from materials tests of isolated aponeuroses were analyzed using Igor Pro software (Wavemetrics, Lake Oswego, OR, USA). For cyclical tests, little variation was observed in the force profile among the five cycles of each test. However, the first cycle occasionally resulted in a slightly lower force, which likely resulted from tissue settling within the clamps. As a result, the first and last two loading cycles were discarded and only the third cycle was analyzed. Tissue strain measured from the video was plotted against tissue stress measured from the MTS. The slope of the extension portion of the loading cycle was used to quantify the Young's modulus. Linear regressions were fitted to data at lengths beyond the “toe region” where stress–strain data followed a linear path. The linear region was identified by plotting the instantaneous Young's modulus as a function of strain and identifying the strain region over which the tissue reached a constant modulus. Data from all samples were used to calculate the average Young's modulus for the longitudinal and transverse directions. Cyclical loading tests were also used to calculate the tissue's resilience (elastic efficiency). The resilience of the aponeurosis was defined as the ratio of the energy (mechanical work) recovered during unloading to the energy (mechanical work) stored during the loading phase of a cycle. Thus, resilience represents the proportion of energy that was not lost to hysteresis and which can be recovered upon unloading. The work associated with the loading and unloading phase of each trial was calculated using the area under the instantaneous mechanical power curves. The stress and strain at mechanical failure were quantified by plotting the stress versus strain (measured from the video) of the tissue during ramp extensions. A rapid drop in force was used to indicate mechanical failure of the tissue. The stress and strain just prior to this drop in force were recorded as the stress and strain at failure.
A one-way ANOVA was performed to compare the stress and strain at failure during tests performed in the transverse and longitudinal directions. The Young's modulus and resilience of the tissue in the longitudinal and transverse directions were compared using a nested ANOVA where tissue orientation was the main effect and the strain associated with each test (i.e. 1%, 2%, or 4%) was used as a nested factor. All tests were performed using JMP (v 5.0) software (SAS Inc., NC, USA).
Results
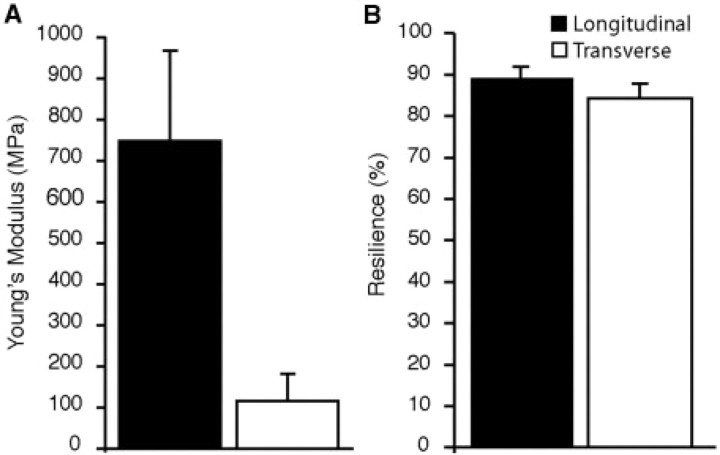
Oblique contrast microscopy revealed that the collagen architecture within the aponeurosis was similar to that of tendons, with fascicles oriented primarily longitudinally along the muscle's line of action (Fig. 1B and C). As predicted from the orientation of the collagen fascicles, we find that the aponeurosis was much stiffer in the longitudinal than in the transverse direction (P < 0.0001; Figs 3A and 4A). The mean Young's modulus for data pooled across all trials was found to be 744.39 ± 219 MPa (mean ± SD) for the longitudinal direction (n = 18) and 115.65 ± 66.48 MPa for the transverse direction (n = 17) (Fig. 4A). We found that within a given tissue orientation, the amplitude of the loading cycle (i.e. 1%, 2%, or 4%) had no significant effect on the measured Young's modulus (P = 0.699).
Fig. 3.
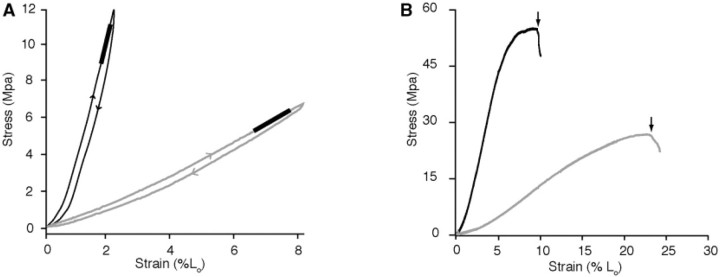
Sample stress–strain plots from (A) cyclical loading and (B) failure tests. (A) Stress–strain curves of cyclical loading tests used to characterize the elastic modulus and the resilience of samples oriented in the longitudinal (black) and transverse (gray) directions. The linear region of the extension portion of each curves is fit by linear regression (thick line), the slope of which is used to characterize the tissue's Young's modulus. Note the difference in stiffness between the longitudinal and transverse directions. The plotted loops also show the energy dissipated during the cycle, which can be quantified as the area within each loop. (B) Stress–strain plots of samples oriented in the longitudinal (black) and transverse (gray) directions stretched until failure. Arrows indicate the stress and strain at which the tissue failed. The plots show that tissue samples oriented in the transverse direction fail at a lower stress and higher strain than in the longitudinal direction.
Fig. 4.
A comparison of the mechanical properties in the longitudinal and transverse directions during cyclical loading. (A) The elastic modulus is significantly greater in the longitudinal direction (P < 0.0001). (B) The aponeurosis behaves as an efficient spring in both the longitudinal and transverse directions, with slightly greater resilience in the longitudinal direction (P = 0.005). Error bars are the standard deviations of the mean.
Tissue resilience, calculated as the proportion of the energy recovered within a loading cycle, was high in both the transverse and longitudinal directions (Fig. 4B). However, resilience differed significantly between the longitudinal and transverse directions (P = 0.005). The average resilience for data pooled across all trials was found to be 88.9% ± 3.1% for the longitudinal direction (n = 18) and 84.3% ± 3.6% for the transverse direction (Fig. 4B) (n = 17). We also found that within a given tissue orientation, the amplitude of the loading cycle (i.e. 1%, 2%, or 4%) had no significant effect on resilience (P = 0.399).
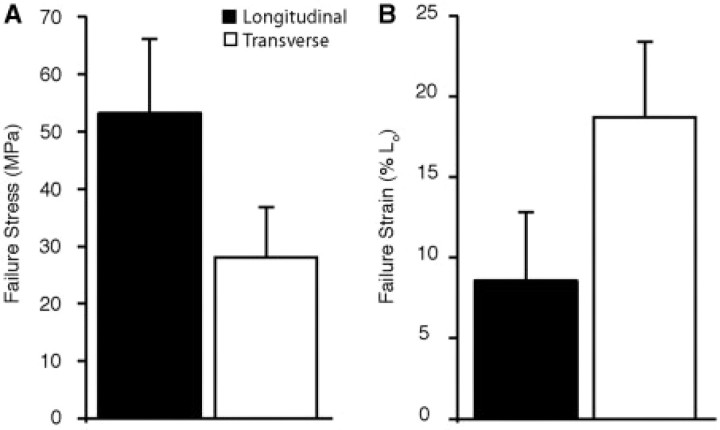
Failure tests revealed significant differences in both the stress and strain at failure for the two tissue orientations. The aponeurosis failed at a significantly higher stress in the longitudinal than in the transverse direction (P = 0.0005). The mean failure stresses were 53.19 ± 12.89 MPa for the longitudinal (n = 10) and 28.12 ± 8.69 MPa for the transverse (n = 7) directions (Fig. 5A). Although the aponeurosis failed at lower stresses in the transverse direction, we found that it could be stretched to much longer greater lengths before failure (P = 0.0006). The mean strain at failure was 8.58% ± 4.22% for the longitudinal direction and 18.71% ± 4.67% for the transverse directions (Fig. 5B).
Fig 5.
A comparison of the failure properties in the longitudinal and transverse directions. Samples oriented transversely fail at significantly higher (A) strains (P = 0.0005) and lower (B) stresses (P = 0.0006) compared to those oriented in the longitudinal direction. Error bars are the standard deviations of the mean.
Discussion
In many muscles, aponeuroses function as the insertion site of muscle fibers and therefore cover a substantial portion of the muscle belly. As a result, aponeuroses strain along multiple axes (Scott and Loeb 1995). The results of the present study provide the first measurements of the mechanical properties of aponeuroses along multiple orientations. The mechanical properties measured here are consistent with the collagen architecture of aponeuroses which, like free tendons, consist of a longitudinal array of collagen fascicles (Fig. 1). Aponeuroses were significantly stiffer and failed at higher stresses when stretched in the longitudinal direction compared to the transverse direction. Although the uniaxial mechanical properties cannot simulate the complex biaxial loading of the tissue that likely occurs in vivo, these data are an important first step in understanding the significance of biaxial loading in these ubiquitous structures.
Numerous studies have quantified the material properties of free tendons, given their important locomotory function and their tractability for materials testing. Previous studies have reported Young's modulus values measured for isolated tendons ranging from 600 MPa to 2000 MPa (e.g. Ker 1981; Shadwick 1990; Pollock and Shadwick 1994; Wren et al. 2001). The Young's modulus for the combined series elastic structures has also been estimated by means of fixed-end muscle contractions, where shortening of contracting muscle fibers is used to measure the extension of the free tendon and aponeurosis (Ito et al. 1998; Maganaris and Paul 1999; Buchanan and Marsh 2001). These studies report values ranging from 338 to 1200 MPa. A recent study quantified in vivo longitudinal stiffness in human triceps surae aponeurosis, using ultrasonography and estimated that the elastic modulus ranges from 1048 to 1474 MPa (Magnusson et al. 2001). Using uniaxial materials tests, we found the average elastic modulus of the turkey LG aponeurosis to be 744 MPa in the longitudinal direction. This value is within the range of elastic moduli reported in previous studies.
Aponeuroses can function as efficient springs in both longitudinal and transverse directions. The effectiveness of tendons as locomotor springs is in part due to the fact that very little energy is dissipated during a loading cycle. Most estimates suggest that upon unloading, tendons lose less than 10% of the energy stored during loading (Bennett et al. 1986). Our results suggest that aponeuroses function with similar resilience, particularly in the longitudinal direction (Fig. 4B). The turkey gastrocnemius aponeurosis operates with somewhat lower resilience in the transverse direction but still only lose 15% of the mechanical energy stored in this direction. Aponeuroses can be considered efficient springs in both the transverse and longitudinal directions when compared to other biological material such as passive muscle, which can dissipate nearly 40% of the energy stored per loading cycle (Meyhofer and Daniel 1990).
Although the spring-like behavior of the aponeurosis in the longitudinal direction can be attributed to the observed arrangement of collagen fascicles, it is unclear what structures are responsible for the spring-like behavior of the aponeurosis in the transverse direction. The observed transverse stiffness and resilience suggest that some fibers must also be oriented in this direction. Several structural features of the aponeurosis may act to resist tension in the transverse direction. First, some collagen fascicles interdigitate, such that collagen fibers from one fascicle converge with an adjacent fascicle (e.g. Fig. 1C; Fallon et al. 2002). This convergence could resist tensile loads when the tissue is loaded perpendicular to the orientation of collagen fascicles. Additionally, in tendons interfascicular spaces are composed of cross-fibered collagen arrays (the epitenon) that also likely resist transverse loads (Gotoh et al. 1997; Kannus 2000). Given the relatively low transverse modulus it may be that such structural features, although modest compared to the primary array of collagen fascicles, may be sufficient to resist relatively small transverse loads. Recent evidence suggests that there is little transmission of force between adjacent tendon fascicles loaded longitudinally (Haraldsson et al. 2008). Manual manipulation of the aponeuroses, however, suggests that fascicles are much more difficult to tease apart, compared to free tendons. It is possible that interfascicular connections are more robust in aponeuroses given that they are subject to biaxial strains.
Considering in vivo function
The role of elastic energy storage in minimizing the energetic cost of running in wild turkeys has been previously investigated (Roberts et al. 1997). Specifically, measurements of force and length in the LG have shown that much of the energy or work associated with each running step is stored and subsequently recovered from elastic structures (Roberts et al. 1997). The tendons of turkey LG are unusual in that a substantial portion of the free tendon is calcified (Fig. 1A). Not surprisingly, the calcified portion of the tendon has been shown to be much stiffer than soft tendons and likely lacks the compliance to contribute significantly to elastic energy storage (Bennett and Stafford 1988). The presence of tendon calcification in this system suggests that the aponeurosis of the LG may play a significant role in storing elastic energy.
When isolated tissues are stretched to failure we find that the aponeurosis fails at approximately 8.6% strain in the longitudinal direction and 18.7% strain in the transverse direction (Fig. 5B). These data on failure properties can be compared to estimates of in vivo biaxial strains to calculate the safety factor with which this aponeurosis operates during locomotion. When the turkey LG contracts with maximum isometric force, the aponeurosis stretches by 2.5% in the longitudinal direction and 8% in the transverse direction (Azizi, unpublished data). Therefore, we estimate that at maximum isometric force, aponeuroses function with a safety factor of 3.4 in the longitudinal direction and 2.3 in the transverse direction.
It is not surprising that aponeuroses function with a higher safety factor in the longitudinal direction compared to the transverse direction. Given that the longitudinal direction is in line with the muscle's line of action, any instabilities in running strides may result in rapid stretches of the muscle tendon in this direction, thereby absorbing energy and decelerating the body (Daley and Biewener 2006). It may therefore be critical to operate with a relatively high safety factor given the exposure of the tissue to a potentially wide range of longitudinal stresses. In contrast, the transverse direction is likely loaded by the forces associated with the expansion of the muscle resulting from fiber shortening. Therefore, the transverse direction may operate with a lower safety factor given the highly predictable stresses to which it is exposed.
Our estimate of safety factor in the longitudinal direction is well within the range of values determined for free tendons (West et al. 2004; Biewener 2005). It is important to note, however, that the strains at failure reported here were measured during uniaxial loading and that biaxial loading may decrease the reported safety factors. It is also important to recognize that failure stress and strain data from isolated tissues should be considered estimates at the lower limit given the potential for the development of artificial concentrations of stress in such preparations (Ker 2007).
Conclusions
This study reveals the nature of anisotropy in aponeuroses. Aponeuroses are significantly stiffer when stretched along the muscle's line of action, parallel to the primary trajectory of collagen fascicles. Aponeuroses operate with safety factors that are similar to those previously documented for free tendons. Aponeuroses are efficient springs when loaded in either the transverse or longitudinal directions. These findings suggest that aponeuroses are well suited for the biaxial strain patterns they likely undergo during muscular force production. The biaxial nature of aponeurosis loading may have important, yet unexplained, implications for the mechanical performance of muscle-tendon units during locomotion.
Acknowledgments
The authors thank Brooke Swanson and Mason Dean for organizing the stimulating symposium “Biomaterials: Properties, Variation, and Evolution”. We thank the Society for Integrative and Comparative Biology (SICB), Divisions of Comparative Physiology and Biochemistry (DCPB), and Vertebrate Morphology (DVM), Air Force Office of Scientific Research (AFOSR), and National Science Foundation (NSF) for funding the symposium. We thank Beth Brainerd for providing access to the materials testing system. This work was supported by the National Institute of Health (NIH) grant F32AR 054246 to E.A. and AR055295 to T.J.R., NSF grant 0642428 to T.J.R., and the W. M. Keck Foundation.
References
- Alexander RMcN. Elastic energy stores in running vertebrates. Am Zool. 1984;24:85–94. [Google Scholar]
- Azizi E, Brainerd EL, Roberts TJ. Variable gearing in pennate muscles. Proc Natl Acad Sci USA. 2008;105:1745–50. doi: 10.1073/pnas.0709212105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baskin RJ, Paolini PJ. Volume change and pressure development in muscle during contraction. Am J Physiol. 1967;213:1025–30. doi: 10.1152/ajplegacy.1967.213.4.1025. [DOI] [PubMed] [Google Scholar]
- Bennett MB, Ker RF, Dimery NJ, Alexander RM. Mechanical properties of various mammalian tendons. J Zool. 1986;209:537–48. [Google Scholar]
- Bennett MB, Stafford JA. Tensile properties of calcified and uncalcified avian tendons. J Zool. 1988;214:343–51. [Google Scholar]
- Biewener AA. Biomechanical consequences of scaling. J Exp Biol. 2005;208:1665–76. doi: 10.1242/jeb.01520. [DOI] [PubMed] [Google Scholar]
- Biewener AA, Baudinette RV. In vivo muscle force and elastic energy-storage during steady-speed hopping of tammar wallabies (Macropus eugenii) J Exp Biol. 1995;198:1829–41. doi: 10.1242/jeb.198.9.1829. [DOI] [PubMed] [Google Scholar]
- Buchanan CI, Marsh RL. Effects of long-term exercise on the biomechanical properties of the Achilles tendon of guinea fowl. J App Physiol. 2001;90:164–71. doi: 10.1152/jappl.2001.90.1.164. [DOI] [PubMed] [Google Scholar]
- Cavagna GA, Heglund NC, Taylor CR. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am J Physiol Regul, Integr Comp Physiol. 1977;233:243–61. doi: 10.1152/ajpregu.1977.233.5.R243. [DOI] [PubMed] [Google Scholar]
- Daley MA, Biewener AA. Running over rough terrain reveals limb control for intrinsic stability. Proc Natl Acad Sci USA. 2006;103:15681–86. doi: 10.1073/pnas.0601473103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliot DH. Structure and function of mammalian tendon. Biol Rev. 1965;40:392–421. doi: 10.1111/j.1469-185x.1965.tb00808.x. [DOI] [PubMed] [Google Scholar]
- Fallon J, Blevins FT, Vogel K, Trotter J. Functional morphology of the supraspinatus tendon. J Orthop Res. 2002;20:920–6. doi: 10.1016/S0736-0266(02)00023-2. [DOI] [PubMed] [Google Scholar]
- Gotoh T, Murashige N, Yamashita K. Ultrastructural observations on the tendon sheath of the rat tail. J Electron Microsc. 1997;46:247–52. doi: 10.1093/oxfordjournals.jmicro.a023516. [DOI] [PubMed] [Google Scholar]
- Haraldsson BT, Aagaard P, Qvortrup K, Bojsen-Moller J, Krogsgaard M, Koskinen S, Kjaer M, Magnusson SP. Lateral force transmission between human tendon fascicles. Matrix Biol. 2008;27:86–95. doi: 10.1016/j.matbio.2007.09.001. [DOI] [PubMed] [Google Scholar]
- Ito L, Kawakami Y, Ichinose Y, Fukashiro S, Fukunaga T. Nonisometric behavior of fascicles during isometric contractions of a human muscle. J App Physiol. 1998;85:1230–35. doi: 10.1152/jappl.1998.85.4.1230. [DOI] [PubMed] [Google Scholar]
- Kannus P. Structure of the tendon connective tissue. Scand J Med Sci Sports. 2000;6:312–20. doi: 10.1034/j.1600-0838.2000.010006312.x. [DOI] [PubMed] [Google Scholar]
- Ker RF. Dynamic tensile properties of the plantaris tendon of sheep (Ovis aries) J Exp Biol. 1981;93:283–302. doi: 10.1242/jeb.93.1.283. [DOI] [PubMed] [Google Scholar]
- Ker RF. Mechanics of tendon, from an engineering perspective. Int J Fatigue. 2007;29:1001–9. [Google Scholar]
- Maganaris CN, Paul JP. In vivo human tendon mechanical properties. J Physiol. 1999;521:307–13. doi: 10.1111/j.1469-7793.1999.00307.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maganaris CN, Paul JP. In vivo human tendinous tissue stretch upon maximum muscle force generation. J Biomech. 2000;33:1453–9. doi: 10.1016/s0021-9290(00)00099-3. [DOI] [PubMed] [Google Scholar]
- Magnusson SP, Aagaard P, Rosager S, Dyhre-Poulsen P, Kjaer M. Load-displacement properties of the human triceps surae aponeurosis in vivo. J Physiol-London. 2001;531:277–88. doi: 10.1111/j.1469-7793.2001.0277j.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyhofer E, Daniel T. Dynamic mechanical properties of extensor muscle cells of the shrimp Pandalus danae – Cell design for escape locomotion. J Exp Biol. 1990;151:435–52. [Google Scholar]
- Pollock CM, Shadwick RE. Allometry of muscle, tendon, and elastic energy-storage capacity in mammals. Am J Physiol. 1994;266:R1022–31. doi: 10.1152/ajpregu.1994.266.3.R1022. [DOI] [PubMed] [Google Scholar]
- Roberts TJ, Marsh RL, Weyand PG, Taylor CR. Muscular force in running turkeys: the economy of minimizing work. Science. 1997;275:1113–5. doi: 10.1126/science.275.5303.1113. [DOI] [PubMed] [Google Scholar]
- Savalberg HM, Willems PJB, Baan GC, Huijing PA. Deformation and three-dimensional displacement of fibers in isometrically contracting rat plantaris muscles. J Morphol. 2001;250:89–99. doi: 10.1002/jmor.1061. [DOI] [PubMed] [Google Scholar]
- Scott SH, Loeb GE. Mechanical properties of aponeurosis and tendon of the cat soleus muscle during whole-muscle isometric contractions. J Morphol. 1995;224:73–86. doi: 10.1002/jmor.1052240109. [DOI] [PubMed] [Google Scholar]
- Shadwick RE. Elastic energy-storage in tendons – mechanical differences related to function and age. J App Physiol. 1990;68:1033–40. doi: 10.1152/jappl.1990.68.3.1033. [DOI] [PubMed] [Google Scholar]
- van Donkelaar CC, Willems PJB, Muijtjens AMM, Drost MR. Skeletal muscle transverse strain during isometric contraction at different lengths. J Biomech. 1999;32:755–62. doi: 10.1016/s0021-9290(99)00073-1. [DOI] [PubMed] [Google Scholar]
- West JR, Juncosa N, Galloway MT, Boivin GP, Butler DL. Characterization of in vivo Achilles tendon forces in rabbits during treadmill locomotion at varying speeds and inclinations. J Biomech. 2004;37:1647–53. doi: 10.1016/j.jbiomech.2004.02.019. [DOI] [PubMed] [Google Scholar]
- Wren TAL, Yerby SA, Beaupre GS, Carter DR. Mechanical properties of the human Achilles tendon. Clinic Biomech. 2001;16:245–51. doi: 10.1016/s0268-0033(00)00089-9. [DOI] [PubMed] [Google Scholar]