Displacement of particles in microfluidics by laser-generated tandem bubbles

Abstract

The dynamic interaction between laser-generated tandem bubble and individual polystyrene particles of 2 and 10 μm in diameter is studied in a microfluidic channel (25 μm height) by high-speed imaging and particle image velocimetry. The asymmetric collapse of the tandem bubble produces a pair of microjets and associated long-lasting vortices that can propel a single particle to a maximum velocity of 1.4 m∕s in 30 μs after the bubble collapse with a resultant directional displacement up to 60 μm in 150 μs. This method may be useful for high-throughput cell sorting in microfluidic devices.

Microfluidic platforms for single cell manipulation and sorting¹ have unique advantages over traditional droplet-based fluorescence-activated cell sorters² because only small amounts of samples are used in an enclosed microchannel, resulting in high yield with a rapid processing time and the potential for multifunctional integrations on a disposable chip. Cell sorting in microfluidic systems³ often requires the use of a variety of microswitching devices constructed based on electrokinetic or magnetic switching, reversible thermal polymer switches, dielectrophoretic forces, pneumatic valves, and bubble-induced fluid flow.⁴ However, maintaining cell viability while achieving a fast switching time still remains a challenge. Recently, single cavitation bubbles have been demonstrated to provide a reproducible and efficient means for creating small-scale transient flows⁵ with high-speed microjets⁶ and shear stresses⁷ that can alter the local flow field within a time frame of microseconds.⁸

In this letter, we describe a technique for directional translation of single micro-objects utilizing the high-speed microjet and vortices from laser-generated tandem bubble. This method may be used to provide convenient and precisely controlled microswitches in microfluidic systems for high-throughput and efficient cell sorting.

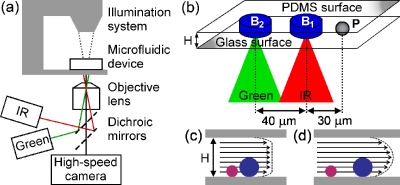
The dynamic interaction between laser-generated tandem bubble and a spherical particle is investigated in a microfluidic device, made of poly-dimethylsiloxane (PDMS) (Dow Corning, Sylgard 184) cured on a customized silicon master mold (Stanford Microfluidic Foundry). The PDMS and glass were bonded using oxygen plasma treatment (Emitech, K-1050X) to form a microchannel with a height H=25 μm. Spherical polystyrene particles of two different diameters (Duke Scientific, R0200, d_P=2 μm and Thermo Scientific, 100243–10, d_P=10.8 μm, ρ_P=1.05 g∕cm³) were centrifuged and resuspended in 0.4% trypan blue saline solution (Sigma-Aldrich, T8154) of ρ_F=1 g∕cm³. The assembled microchip was clamped onto a rotating slide holder (Prior Scientific, H22ROTS) and placed on an inverted optical microscope (Zeiss, Axio Observer D1) [Fig. 1a]. Directional flow in the microchannel was produced by the coupled oscillation and resultant microjets and vortices from laser-generated tandem bubble (52.8±1.6 μm in maximum bubble diameter).⁶ The two laser pulses were offset in time by 4 μs and focused through a micro-objective (Zeiss, 63× LD Plan Neofluar) onto two foci separated by 40 μm [Fig. 1b].

Figure 1.

(a) Experimental setup for producing directional particle displacement in a microfluidic channel using laser-generated tandem bubble. (b) A single particle was aligned along the axis of the tandem bubble. The infrared and green lasers (with corresponding foci separated by 40 μm) were focused in the channel (H=25 μm) at a stand-off distance of 30 μm from the particle. [(c) and (d)] Schematic diagrams of the fluid flow profile progression over time in the microfluidic channel with particles of two different sizes. The drag force acting on a particle in the flow field is related to H∕d_p and time for (c) uniform flow when t⪡τ_transient and (d) parabolic flow when t⪢τ_transient.

In the experiment, a particle near the central axis of the microchannel was selected and aligned to a stand-off distance about 30 μm from the proximal bubble origin [Fig. 1b]. As previously shown,⁹ the effect of channel height on the flow induced by the explosive expansion of a laser-induced bubble can be related to the diffusive growth of the viscous boundary layer inside the microchannel and the approximate transient time is given by:

$${\tau }_{\text{transient}}=\frac{H^2}{{3.44}^2{\nu }_F},$$ (1)

where ν_F=0.9×10⁻⁶ m² s⁻¹ is the kinematic viscosity of the fluid at 25 °C. In the early stage when time t⪡τ_transient (≈60 μs), the flow can be considered two-dimensional and the velocity profile is approximately uniform except near the channel wall [Fig. 1c].¹⁰ As time progresses (t⪢τ_transient), the velocity profile is transformed into a parabolic profile by the viscous forces [Fig. 1d].^{10, 11} Considering an external flow of velocity u_F≈1 m∕s around a single particle inside the microchannel, the particle acceleration will depend on several parameters, including the proximity of the particle to the boundary, particle rotational speed, and the Reynolds number.^{11, 12} At Re_P=d_pu_F∕ν_F∼10, Stokes’ law can be utilized to determine the approximate upper limit of the particle acceleration time constant which is proportional to the square of the particle diameter,¹³

$${\tau }_{\text{drag}}=\frac{d_P^2}{18{\nu }_F}\frac{{\rho }_P}{{\rho }_F}.$$ (2)

Particle motion and laser-induced bubble dynamics were captured by using a color high-speed camera (Vision Research, Phantom v7.3, 1 μs exposure) and an ultrahigh-speed camera (DRS Hadland, Imacon 200, 50 ns exposure), illuminated by a fiber coupled xenon flash lamp (Dyna-Lite, ML-1000, 200 μs duration). Precise triggering between the cameras, the flash lamp, and the lasers was achieved using two digital delay generators (Berkley Nucleonics, 2-channel BNC 565, 8-channel BNC 565). Based on the acquired high-speed images, particle kinematics (displacement, velocity, and acceleration) produced by either a single or tandem bubble was calculated.

Figure 2 shows high-speed images of the transient interaction between a 10 μm particle and a laser-generated single bubble or tandem bubble. Using a single bubble [see B₁, Fig. 2a], the particle was propelled outward from the laser focus by the initial bubble expansion (t=0–3 μs) and subsequently pulled back as the bubble began to collapse (t=4–7 μs). Interestingly, the 2 μm particle has a slightly larger negative net displacement (−4.3±0.4 μm) compared to the 10 μm particle (−3.5±1.5 μm). However, both particles experienced a negative net displacement moving inward toward the origin of B₁.

Figure 2.

High-speed images of the dynamic bubble-particle interaction, vortex flow field, and particle displacement produced by laser-generated single or tandem bubble: (a) a 10 μm particle at a 30 μm stand-off distance is negatively displaced by the oscillation of a single bubble, (b) dynamics of tandem bubble with directional formation of microjets (J₁ and J₂), and their interaction with a 10 μm particle at a 30 μm stand-off distance. The 10 μm particle is directionally accelerated and negatively displaced by the tandem bubble during the initial 11 μs, (c) the formation of two pairs of vortices produced by the tandem bubble over a time period of 150 μs, and (d) the positive displacement of a 10 μm particle by the interaction with the tandem bubble long after the bubble collapse. Laser foci and initial particle position are shown with solid horizontal lines.

Using tandem bubble [Fig. 2b], the particle was initially pushed away by the radial flow produced by the expansion of B₁ (t=0–4 μs), which is similar to the single bubble case. However, the second bubble (B₂), generated 4 μs later, intensifies the asymmetric collapse of B₁ by the formation of the first microjet (J₁) and consequently reverses the direction of the particle movement shortly afterwards (t=5–11 μs). Furthermore, the asymmetric collapse of B₂ led to the formation of the second microjet (J₂) in the opposite direction (t=9 μs). Thereafter, two pairs of vortices, visualized by particle image velocimetry, were generated and lasted for over 150 μs [Fig. 2c]. The vortex formation was absent in laser-induced single bubble oscillation.⁶ As shown in Fig. 2c, each vortex spanned an area approximately 50 μm in diameter and gradually drifted away from each other with decreasing rotational speed. At t=100 μs, the maximum fluid velocity was approximately 0.1 m∕s, which matches well with the velocity of a single 2 μm particle observed at this time [see Fig. 3b]. Figure 2d shows the trajectory of a 10 μm particle propelled by the tandem bubble, captured using a 15 μs interframe time. Because of the formation of the long-lasting vortices, the tandem bubble can sustain the particle movement over a long period (∼150 μs) far exceeding the collapse time of an individual bubble (∼8 μs), resulting in a significant particle net displacement away from the origin of B₁.

Figure 3.

Particle displacement and velocity induced by laser-generated tandem or single bubble: (a) 10 μm (squares) and 2 μm (triangles) particle displacement curves after interaction with either the tandem bubble (filled) or single bubble (open); and (b) average velocity curves of the 10 μm (squares) and 2 μm (triangles) particles after being directionally propelled by a laser-induced tandem bubble of antiphase, compared to in-phase (circles). The initial position is shown with a dashed horizontal line at 30 μm.

The particle trajectory and net displacement are directly related to the particle size and bubble dynamics. Figure 3a shows the average displacements of different particles produced by either the laser-generated tandem bubble or a single bubble. During the initial phase (t⪡τ_transient) when the flow has an approximately uniform velocity profile inside the microchannel, the 2 and 10 μm particles show similar trends in positive and negative displacements. However, later on after the flow field is transitioned into a parabolic profile (t⪢τ_transient) there is a progressive separation between the displacements of the two particles. Driven by the antiphase tandem bubble, the 2 μm particle is propelled to a final displacement of 32±6 μm (mean±standard deviation, n=10) compared to 60±6 μm (n=10) for the 10 μm particle. In contrast, tandem bubble oscillating in-phase [see Fig. 3b] produces a net negative particle displacement similar to that produced by the single bubble-particle interaction.

The average velocities of the 2 and 10 μm particles show a similar temporal profile, with both curves reaching the maximum velocity at about 30 μs [Fig. 3b]. Although the initial acceleration is faster for the 2 μm particle, its maximum velocity (0.8 m∕s) is less than the corresponding value (1.4 m∕s) for the 10 μm particle. Moreover, the derived maximum acceleration values are 50 km∕s² (t=10 μs) and 80 km∕s² (t=20 μs) for the 2 μm and 10 μm particles, respectively [Fig. 3b, inset]. The maximum inertial force, estimated by the product of particle acceleration and mass, on the 10 μm particle is ∼100 nN, which far exceeds the drag force acting on rolling cells,¹¹ indicating that this method could be useful for propelling cells in suspension.

The differences observed between 2 and 10 μm particle kinematics can be attributed to the drag force and the establishment of the parabolic velocity profile within the microchannel. In the early phase $\left(t<{\tau }_{\text{drag}}\approx 0.7d_P^2∕H^2{\tau }_{\text{transient}}\right)$ when the particle is accelerated by a quasi two-dimensional expansion flow with an approximately uniform velocity profile [Fig. 1c], a 10 μm particle will remain inert (τ_drag=6 μs) long after a 2 μm particle has begun to move (τ_drag=0.3 μs). Because of its shorter response time (less than the bubble collapse time), the 2 μm particle can achieve a greater negative velocity than the 10 μm particle [Fig. 3b]. In the later phase (t>τ_transient⪢τ_drag), when a parabolic velocity profile has been fully developed, the 2 μm particle is convected by a slower mean velocity near the boundary than the 10 μm particle [Fig. 1d]. Consequently, a smaller net displacement is produced for the 2 μm particle compared to that for the 10 μm particle. The same principle is employed in hydrodynamic chromatography.¹⁴

In this work, we have demonstrated a method for directional particle displacement and acceleration in a microfluidic channel by laser-generated tandem bubble. Although an initial negative displacement is induced by the collapse of the tandem bubble for both the 2 and 10 μm particles, a final positive displacement is produced by the directional microjet and resultant long-lasting vortex flow, which propels the particles for up to 60 μm in about 150 μs. Suspended cells would most likely mimic the translational motion of the 10 μm particles, indicating that this technique has the potential to be utilized in high-throughput microfluidic systems for cell sorting.