Determination of spin compartment in Arterial Spin Labeling MRI

Abstract

A major difference between Arterial-Spin-Labeling (ASL) MRI and gold-standard radiotracer blood flow methods is that the compartment localization of the labeled spins in the ASL image is often ambiguous, which may affect the quantification of cerebral blood flow (CBF). In this study, we aim to probe whether the spins are located in the vascular system or tissue by using T2 of the ASL signal as a marker. We combined two recently developed techniques, Pseudo-Continuous Arterial Spin Labeling (PCASL) and T2-Relaxation-Under-Spin-Tagging (TRUST), to determine the T2 of the labeled spins at multiple post-labeling delay times. Our data suggest that the labeled spins first showed the T2 of arterial blood followed by gradually approaching and stabilizing at the tissue T2. The T2 values did not decrease further toward the venous T2. By fitting the experimental data to a two-compartment model, we estimated gray matter CBF, arterial transit time, and tissue transit time to be 74.0±10.7 ml/100g/min (mean±SD, N=10), 938±156 ms, and 1901±181 ms, respectively. The arterial blood volume was calculated to be 1.18 ±0.21 ml/100g. A post-labeling delay time of 2 seconds is sufficient to allow the spins to completely enter the tissue space for gray matter, but not for white matter.

Introduction

The ultimate goal of Arterial Spin Labeling (ASL) MRI is to replace the ¹⁵O-PET technique as the standard method for cerebral blood flow (CBF) measurement. However, unlike PET which specifically measures the labeled water molecules that have been exchanged into tissue (1–2), the signal origin of ASL is more ambiguous. Often, we do not know whether the measured signal (in the difference image) is in the vascular spaces or tissue. This may cause uncertainty in the quantification of CBF as well as difficulty in direct comparison with more established methods (3).

A number of studies have used multi-delay ASL experiments to obtain information on how long it takes for the labeled blood to reach the imaging slices (3–8), often referred to as arterial transit time (δ_a). However, this method does not distinguish between labeled water molecules in vessels or tissue, therefore providing little information as to the compartment localization of the spins. Another method employed crusher gradients to partially suppress vessel contribution to the ASL signal (9–13). However, the efficacy of these gradients to dephase vessel signals is highly variable and is dependent on the vessel orientation and the cutoff velocity.

In the present study, we aim to distinguish spin compartments based on their transverse relaxation time. Water spins in different compartments have characteristic T2 values and at 3T arterial, venous and tissue T2 are approximately 160 ms (at a hematocrit of 42 ± 4%) (14), 50 ms (at an oxygenation level of 60%) (14) and 90 ms (15), respectively. Therefore, we can use the T2 value of the labeled spins to probe whether the detected ASL signal is located in artery, vein, or tissue, and investigate how the spin compartment localization changes with post-labeling delay time. In this work, we combined two recently developed MRI techniques, Pseudo-Continuous Arterial Spin Labeling (PCASL) (16–18) and T2-Relaxation-Under-Spin-Tagging (TRUST) MRI (19), to determine the T2 of the labeled spins in ASL. Experimental data were fitted to a two-compartment model to obtain arterial transit time, tissue transit time and CBF. The results were compared to those from a standard single-compartment model.

Methods

TRUST-PCASL pulse sequence

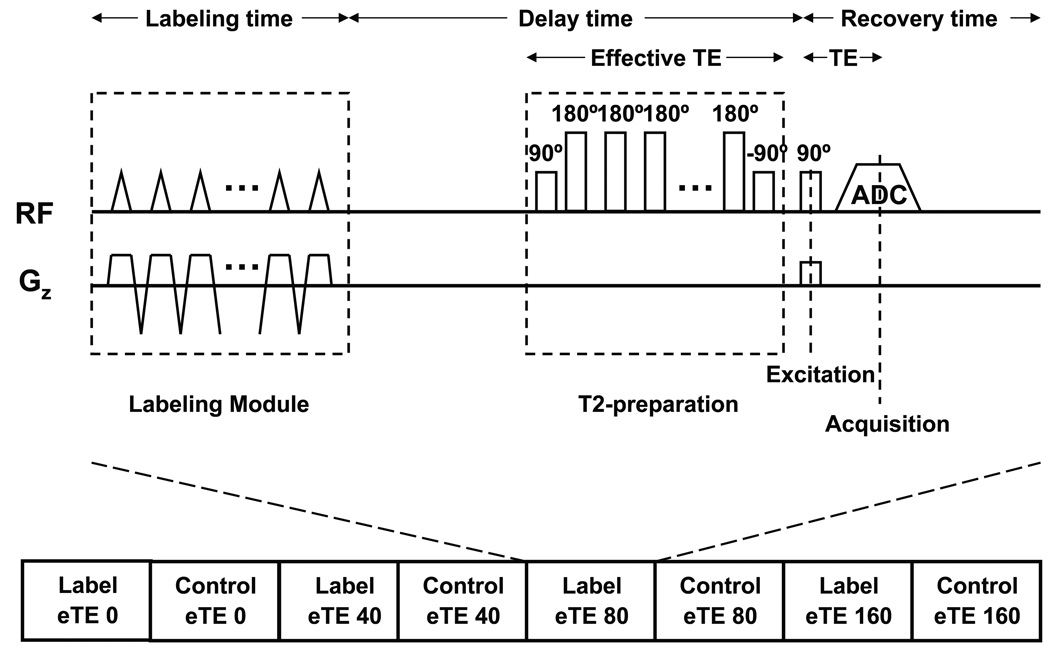
The TRUST-PCASL sequence was based on the PCASL technique (16–18,20) but a series of non-slice-selective T2-preparation pulses were inserted before the slice-selective excitation pulse to modulate the T2-weighting (Fig. 1). A complete sequence for TRUST-PCASL MRI consists of labeled and control scans acquired at different T2-weightings (Fig. 1). The subtraction of the control and labeled images yields the ASL signal. The monoexponential fitting of the ASL signal as a function of the T2-preparation duration (termed effective TE, eTE) then gives the T2 value of the labeled spins. A similar technique has previously been used to measure venous T2 and oxygenation level (19). The non-slice-selective T2 preparation is critical to ensure that the measured T2 value is insensitive to the flow velocity, which could cause an underestimation when using a conventional multi-echo T2 sequence (21). Two schemes were applied to minimize the imperfection in the T2-prep pulses: 1) Composite pulses were used, i.e. 90_x180_y90_x for the 180 pulses. 2) The signs of the 180 pulses were arranged in a MLEV pattern (e.g. 1 1 −1 −1 etc) (22). For each component in the composite pulses, a block pulse was used with a duration of 1.1 ms (for 90°).

Fig. 1.

Schematic diagram of the TRUST-PCASL sequence. The sequence consists of interleaved acquisitions of label and control scans. For each scan, after a train of RF pulses which provide the pseudo-continuous flow driven inversion, a series of non-slice-selective T2-preparation pulses are inserted before the slice-selective excitation pulse to modulate the T2-weighting, the duration of which is denoted by eTE. The subtraction of the control and labeled images yields the ASL signal.

MRI experiment

The experiments were performed on a 3T MRI system (Philips Medical Systems, Best, The Netherlands). The protocol was approved by UT Southwestern Medical Center’s Institutional Review Board and informed written consent was obtained from each participant. A total of ten healthy subjects (5 men and 5 women, 27.7 ± 5.9 years of age) participated in this study. For each subject, four TRUST-PCASL MRI scans were performed with post-labeling delay times (w) of 200, 850, 1525 and 2000 ms. The shortest delay time was chosen to be 200 ms to allow sufficient time for the T2-preparation module to be played out. The longest delay time was chosen to be 2000 ms to obtain a compromise between the range of coverage and SNR. The other delay times were chosen to have approximately equal intervals. The order of the scans was pseudo-randomized across subjects. The body coil was used for RF transmission and an eight-channel sensitivity encoding (SENSE) head coil was used for receiving. Foam padding was used to stabilize the head and minimize motion. The blood labeling position was chosen to be 84 mm below the anterior-commissure (AC) posterior-commissure (PC) line, based on a previous study (23). The imaging slice consisted of a single axial slice positioned at 10 mm above the AC-PC line. A single-slice mode was employed because the use of T2-preparation pulses precluded a multi-slice acquisition. The scan used four eTE times: 0 ms, 40 ms, 80 ms, and 160 ms, corresponding to 0, 4, 8, and 16 refocusing pulses in the T2 preparation module (τ_CPMG = 10 ms; Carr-Purcell-Meiboom-Gill [CPMG]). Other sequence parameters were: single-shot echo-planar imaging (EPI), voxel size = 3×3×10 mm³, field-of-view (FOV) = 240×240×10 mm³, echo time (TE) = 14 ms, SENSE factor 2.5, 16 averages, total labeling duration (τ) = 1650 ms, labeling pulse duration = 0.5 ms, labeling pulse flip angle = 18°, pause between labeling pulses = 0.5 ms, and recovery time after image acquisition = 787 ms. The duration of the scans varied according to the post-labeling delay times and was 5.6, 7.0, 8.5 and 9.5 minutes for delays of 200, 850, 1525 and 2000 ms, respectively.

To assess whether the transit times and CBF are different for slices at a different location, seven of the ten subjects were recruited back for a second session, in which the scan protocol was identical to that in the first session except that the imaging slice was positioned at a more distal location (40 mm above the AC-PC line).

Data analysis

The data were processed using in-house MATLAB (Mathworks, Natick, MA) scripts and standard image processing software. The images with the same delay time and TE were realigned using a 2D realignment script in SPM2 (University College London, UK). The images at different TEs and delay times were co-registered using FSL’s function FLIRT (FMRIB Software Library, Oxford University, UK). The MR signal at equilibrium magnetization, M₀, was obtained from manual ROI drawing of the thalamus in the control image and by accounting for T₁ relaxation, M₀ = M_thal/(1−exp(−TR/T_1,thal)), when assuming T_1,thal = 0.986 s (15). We chose to draw the ROIs in the thalamus because it is gray matter and the structure thickness is sufficient for manual drawing (cortical gray matter can be very thin). Pairwise subtraction was then performed for the control and label images to obtain CBF-weighted images for each eTE and post-labeling delay time. The imaging slice was segmented into regions-of-interest (ROIs) corresponding to large vessels, gray matter, and white matter. To delineate gray and white matter, histogram of the CBF-weighted image at 1525 ms was investigated and the peak of the histogram (0.5%) was used as the cutoff for gray/white matter masks. For the delineation of large vessel ROI, histogram of the CBF-weighted images at 200 ms was used. Since the arterial vessels occupy less than 2% of the total volume, the voxels in the top 2% of the histogram were included in the vessel ROI.

Raw signals in each ROI were spatially averaged. Signal-to-noise ratio (SNR) of the ROI data was calculated for each post-labeling delay time and TE. The SNR was calculated as the mean of the signal time course (with 16 points) divided by the standard deviation of the time course followed by multiplication of $\sqrt{16}=4$. The ROI data were fitted to the function ΔM(eTE)=ΔM(0)·exp(−eTE/T₂) to yield the amplitude of the ASL signal, ΔM(0), and the T2 value of the signal (19). Monte Carlo simulations were also performed to assess the bias in the fitted parameters using SNR values matching the experimental data. The simulations were carried out for each delay time and 100,000 trials were conducted for each simulation.

Two-compartment perfusion model and data fitting

To obtain a theoretical understanding of the experimental data and to explore the possibility of fitting the data to a model, we used a two-compartment perfusion model that was first proposed by Alsop and Detre (3) and modified by Wang et al (24). The conceptual framework of the model is illustrated in Fig. 2. The magnetically labeled water spins (shown in gray) first arrive at the arterial vessels in the imaging voxels, the time of which is termed the arterial transit time (δ_a). The spins then travel within the imaging voxel to arrive at the tissue compartment, the time of which is termed the tissue transit time (δ). At any time-point, the exact location of the labeled bolus is dependent upon an imaging parameter, post-labeling delay time (w). The labeled bolus experiences different T2 in vessel and tissue compartments. Under this framework, for any set of physiologic parameters CBF (f), δ_a, and δ, we can calculate the expected ASL signal, ΔM, as a function of TE and w, which are the measured signals in the TRUST-PCASL experiments. The details of the derivation are similar to those in Wang et al. 2002 (24). The final result of the derivation is that the signal can be written as:

$$\mathrm{\Delta }M(\mathit{\text{eTE}})=\mathrm{\Delta }{M}_a(\mathit{\text{eTE}})+\mathrm{\Delta }{M}_t(\mathit{\text{eTE}})$$ [1]

where ΔM_a is the ASL signal in the arterial compartment, given by

$$\begin{array}{cc}\hfill \mathrm{\Delta }{M}_a(\mathit{\text{eTE}})=\{2\alpha \frac{{\mathit{\text{fM}}}_0}{\lambda }{T}_{1a}[\text{exp}\left(\frac{\text{min}(\delta a-w,0)-\delta a}{T_{1a}}\right)-\text{exp}(-\frac{\text{min}(w+\tau ,\delta )}{T_{1a}}\left)\right]·\text{exp}(-\frac{\mathit{\text{eTE}}}{T_{2,a}})\hfill & \hfill ,w\le \delta \hfill \\ \hfill 0\hfill & \hfill ,w>\delta \hfill \end{array}$$ [2]

and ΔM_t is the ASL signal in the tissue compartment, given by

$$\begin{array}{cc}\hfill 0\hfill & \hfill ,w+\tau <\delta \hfill \\ \hfill \mathrm{\Delta }{M}_t(\mathit{\text{eTE}})=\{2\alpha \frac{{\mathit{\text{fM}}}_0}{\lambda }{T}_{1\mathit{\text{app}}}\text{exp}(-\frac{\delta }{T_{1a}})\left[\text{exp}\right(\frac{\text{min}(\delta -w,0)}{T_{1\mathit{\text{app}}}})-\text{exp}(\frac{(\delta -w-\tau )}{T_{1\mathit{\text{app}}}}\left)\right]·\text{exp}(-\frac{\mathit{\text{eTE}}}{T_{2,t}})\hfill & \hfill ,w+\tau \ge \delta \hfill \end{array}$$ [3]

where 1 / T_1app = 1 / T₁ + f / λ. α is the labeling efficiency (0.86, (23)); λ is the blood-brain partition coefficient (0.98 mL/g for gray matter) (25–27); T₁ is the brain tissue T₁ (1.165 s for gray matter) (15); T_1a is the T₁ of arterial blood (1.664 s) (28).

Fig. 2.

Illustration of the two-compartment perfusion model for PCASL. The labeled spins are shown by the gray areas. The box indicates the imaged voxel which consists of vessels and tissue. T_2,a and T_2,t are the transverse relaxation times. δ_a and δ are the time it takes for the labeled spin to reach the arterial and tissue compartments, respectively. τ and w are imaging parameters indicating the labeling duration and post-labeling delay, respectively.

By fitting the experimental data to the two-compartment model, we can obtain an estimation of CBF, δ_a, and δ. The fitting was based on minimizing the mean square error between experimental and model ΔM(0) and T2 (at 4 delay times and a total of 8 experimental points). Because of the fact that ΔM(0) and T2 have different units and our finding that the ΔM(0) curve is primarily determined by CBF and δ_a whereas the T2 curve is primarily affected by δ, an iterative, two-step fitting method was used. Each iteration consisted of two steps. In the first step, δ was fixed at a constant value and the ΔM(0) data were used to fit for CBF and δ_a using a non-linear fitting routine (nlinfit.m) in MATLAB. In the second step, CBF and δ_a were fixed at the values obtained from the first step and the T2 data were used to fit for δ, again using the non-linear fitting routine. Then the iteration was repeated until the differences between the fitted CBF, δ_a, and δ values in the present iteration and those in the previous iteration were less than a threshold value, at which point the results were considered converged. The threshold values were 0.1 ml/100g/min, 0.001ms and 0.001ms for CBF, δ_a, and δ, respectively.

Robust analysis was conducted for the model fitting. To assess whether the choice of initial values would result in the algorithm to fall into local minima and affect the fitting outcomes, each model fitting was conducted 1331 times with a large range of initial values (40 to 140 ml/100g/min at 10 ml/100g/min interval for CBF, 0.5 to 1.5 ms at 0.1 ms interval for δ_a, 1 to 3 ms at 0.2 ms interval for δ). When more than one set of parameters were obtained from the fittings (i.e. there exist local minima), the parameter set with the smallest residual error will be used as the final outcome. To further assess whether such a procedure can identify the true parameter values, Monte Carlo simulations were performed in which the group averaged parameter set was used to generate a noise-free dataset. Noise was then added to generate the simulated dataset, which was processed with the procedure described above to obtain the estimated parameters. The noise level was based on the experimental datasets. The simulation was performed 500 times, and the mean and the standard deviation of the estimated parameters were calculated.

Arterial blood volume, V_a, was also calculated from the fitted parameters by V_a = f·(δ − δ_a) (3).

The results from the two-compartment model fitting was compared to that of single-compartment model (3). Statistical analyses were conducted using student t tests and a P value of less than 0.05 was considered significant.

Results

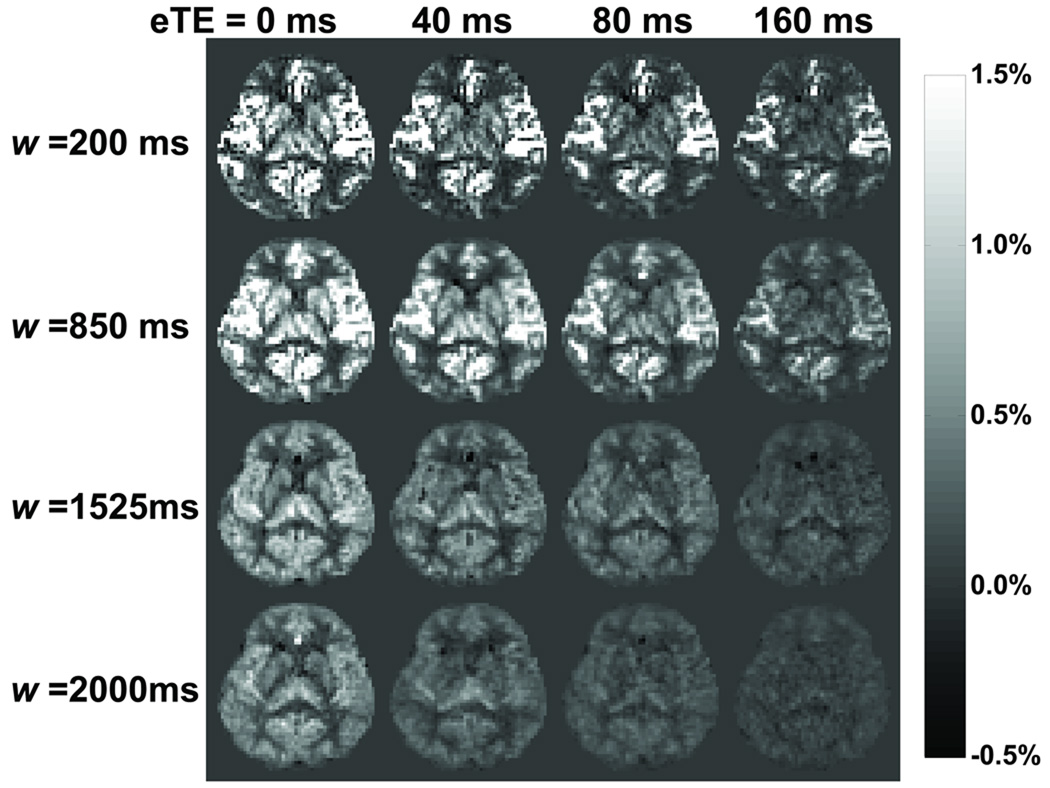
A representative set of the TRUST-PCASL images (control–label) are displayed in Fig. 3. The image intensity decreases as eTE increases due to T2 relaxation. The overall image intensity also decreases at longer delay time due to T1 relaxation, but becomes more uniform as the labeled blood enters the brain tissue from the arterial vessels.

Fig. 3.

CBF-weighted images (control-label) from a representative subject. The images were acquired with post labeling delays from 200 to 2000 ms and effective echo times from 0 to 160 ms. The scale bar indicates ΔM/M₀ (%).

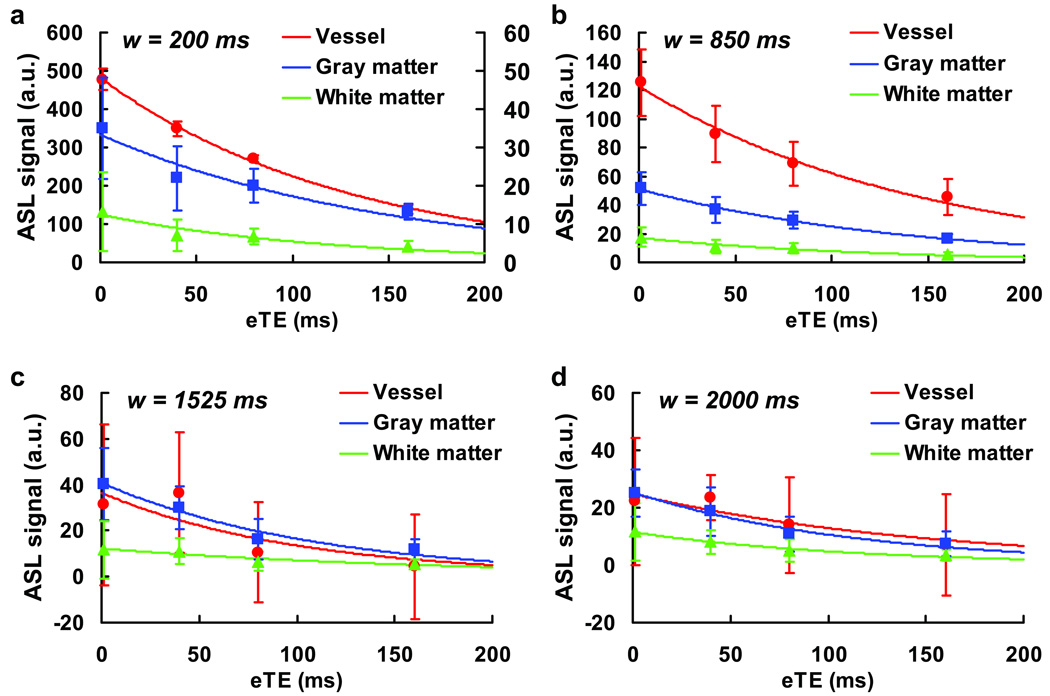
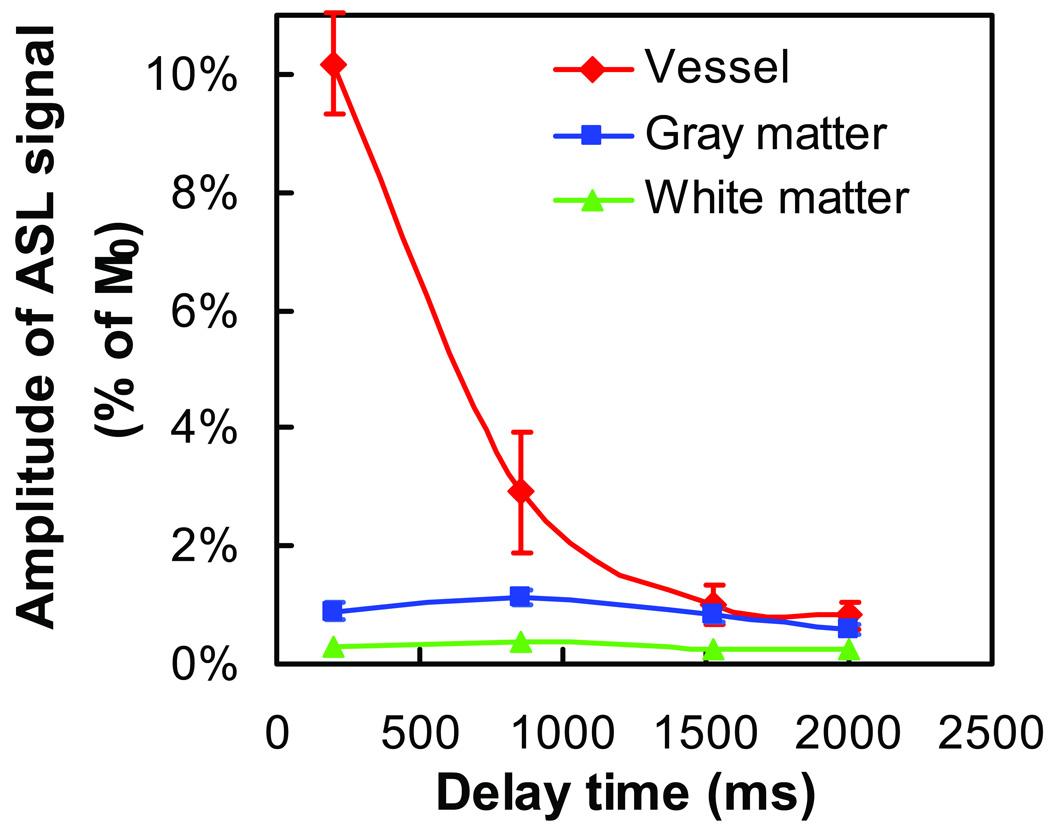
The ROIs corresponding to gray matter, white matter and vessels contained 797 ± 146 (mean ± SD, N=10), 482 ± 134, and 46 ± 18 voxels, respectively. Table 1 summarizes SNR of these ROIs at different delay times and eTEs. Figure 4 shows the T2 fitting results from a representative subject. Figure 5 shows the ASL signal intensity, ΔM(0), as a function of post-labeling delay time for each of the ROIs. Signals from voxels containing large vessels decay rapidly with delay time as the labeled spins pass through the vessels, while signals from regions containing predominantly gray matter or white matter decay more slowly, consistent with previous reports (3). The white matter signal intensity is significantly lower (P<0.001) than that of gray matter, but the values were greater than zero for all subjects at all delay times.

Table 1.

ASL signal-to-noise ratio (SNR) in ROIs containing gray, white matter and vessels (mean ± SD, N = 10).

Gray Matter
	eTE = 0 ms	eTE = 0 ms	eTE = 80 ms	eTE = 160 ms
w = 200 ms	14.8 ± 4.1	20.2 ± 4.9	29.1 ± 10.4	26.3 ± 6.1
w = 850 ms	20.9 ± 3.3	25.0 ± 8.6	29.0 ± 7.7	29.1 ± 6.6
w = 1525 ms	19.7 ± 9.6	15.3 ± 4.7	15.3 ± 5.2	12.4 ± 3.0
w = 2000 ms	11.0 ± 2.5	11.8 ± 3.2	10.3 ± 2.8	10.0 ± 2.6
White Matter
	eTE = 0 ms	eTE = 40 ms	eTE = 80 ms	eTE = 160 ms
w = 200 ms	6.4 ± 1.7	10.0 ± 2.7	14.6 ± 5.9	14.8 ± 5.5
w = 850 ms	9.0 ± 1.8	15.7 ± 6.0	15.0 ± 5.7	16.8 ± 3.9
w = 1525 ms	6.2 ± 3.4	9.9 ± 2.7	10.7 ± 2.3	10.4 ± 1.7
w = 2000 ms	5.7 ± 1.8	7.8 ± 1.4	7.1 ± 1.8	7.5 ± 1.1
Vessel
	eTE = 1 ms	eTE = 40 ms	eTE = 80 ms	eTE = 160 ms
w = 200 ms	58.8 ± 22.8	67.0 ± 23.0	61.7 ± 26.2	38.1 ± 21.2
w = 850 ms	13.2 ± 5.3	12.2 ± 4.9	13.7 ± 6.2	8.6 ± 4.6
w = 1525 ms	6.6 ± 4.1	5.1 ± 3.0	5.5 ± 4.5	2.0 ± 1.6
w = 2000 ms	4.6 ± 2.0	5.0 ± 3.3	2.7 ± 2.2	1.5 ± 1.3

Fig. 4.

An example of the mono-exponential fitting of the ROI data. The symbols and curves indicate the experimental data and the fitting, respectively. Error bars indicate standard deviations of the signals over the ROI. The plots are for the four delay times of 200 ms, 850 ms, 1525 ms and 2000 ms from the subject shown in Fig. 3. The fitting for the vessel ROI is not good at longer delay times (1525 ms and 2000 ms) due to lower SNR as shown in Table 1.

Fig. 5.

Amplitude of ASL signal in ROIs containing vessels (red), gray matter (blue) and white matter (green). The error bars indicate the standard deviations across the subjects. Note that the error bars for gray and white matters are very small.

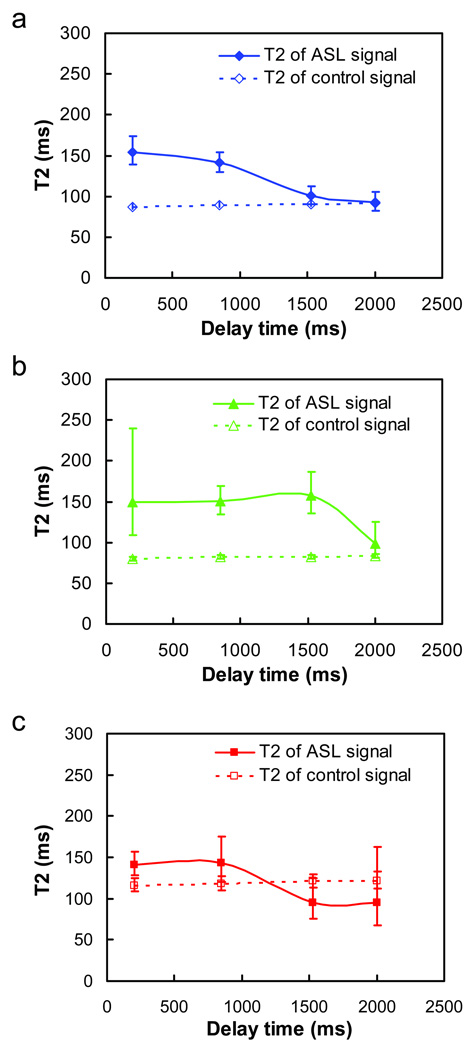
Figure 6 shows the estimated T2 of ASL signal (control–label) at different delay times for each ROI. For comparison, the T2 of the control signal is plotted as dashed lines. The gray matter ASL T2 (solid line in Fig. 6a) has a high value at delay times of 200 ms, but decreases gradually at longer delay times (P = 0.04 for w = 200 ms vs. w = 850 ms; P<0.001 for w = 850 ms vs. w = 1525 ms). Considering that the T2 of arterial blood is approximately 152 ms (at hematocrit of 42%) (14) and tissue T2 is about 90 ms (15), this pattern suggests that the labeled spins were primarily in arterial vessels at the 200 ms delay and enter the tissue compartment at longer delay times. Comparing the ASL signal T2 and control signal T2, the ASL curve appears to gradually approach the control curve. At w = 2000 ms, there was virtually no difference between these T2 values (P = 0.85), suggesting that all labeled spins have reached tissue.

Fig. 6.

T2 of ASL signal (solid line) and control signal (dashed line) for gray matter (a), white matter (b), and vessel ROIs (c). The error bars indicate the standard deviations across the subjects. Note that the white matter T2 at delay time of 200ms had a large error bar because the ASL signal intensity was low.

In contrast, the ASL T2 curve of the white matter ROI (solid line in Fig. 6b) has a different pattern. There were no differences among T2 values at delay times of 200 ms, 850 ms and 1525 ms (P>0.48) and the values were all close to the arterial blood T2, suggesting that most of the labeled spins are still in the arterial compartment at those delay times. At delay time of 2000 ms, on the other hand, the white matter T2 started to show a significant decrease (P < 0.001). However, the values of the ASL T2 (98.7 ± 22.2 ms) were still slightly higher (P = 0.026) than that of the control T2 (83.0 ± 2.5 ms), suggesting that some labeled spins may be located in the arterial vessels even at this delay time.

The voxels in the vessel ROIs are expected to consist of considerable arterial vessels, but may also contain some gray and white matter. Consequently, the ASL signal contribution is dependent on the delay time. At delay time of 200 ms, the ASL signal is expected to originate predominantly from arterial vessels (as can be seen from the red curve Fig. 5). Thus the T2 value is expected to reflect arterial T2. At long delay times, the labeled spins should have passed through the vessels and the signals are expected to originate from gray matter. Thus both the amplitude (Fig. 5) and the T2 (Fig. 6c) of the ASL signal are comparable to the respective gray matter ROI values. The T2 value at delay time of 850 ms appears to be an average of gray matter ROI and arterial blood.

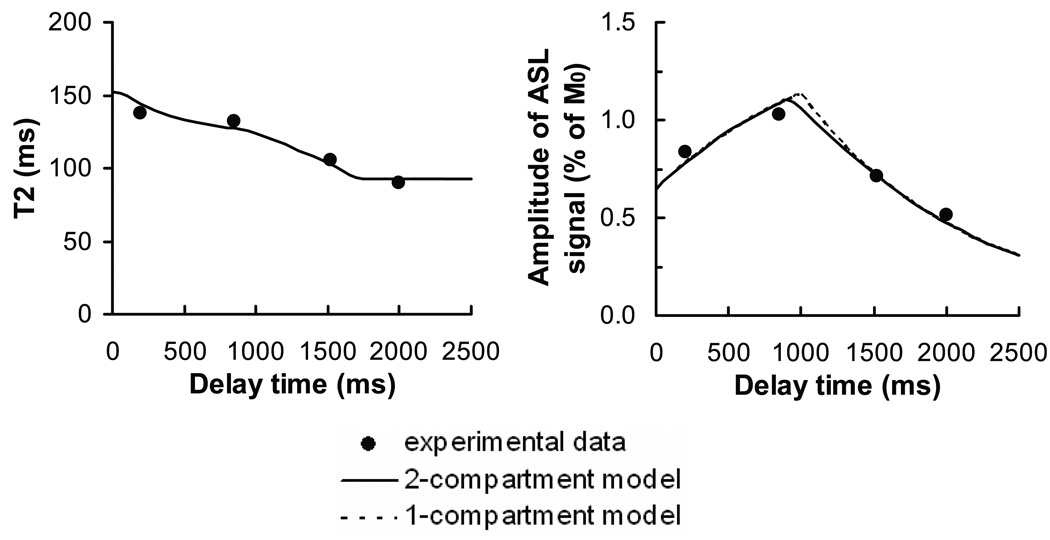
The gray matter ASL signal amplitude and T2 were fitted to the two-compartment model for each subject (Fig. 7). Model fitting was not performed for vessel and white matter ROIs because the perfusion model is not applicable for blood vessels and the low ASL signal in white matter precluded the possibility of reliable fitting. The estimated gray matter CBF, arterial transit time, and tissue transit time were 74.0 ± 10.7 ml/100g/min, 938 ± 156 ms, and 1901 ± 181 ms, respectively. The calculated arterial blood volume, V_a, was 1.18 ± 0.21 ml/100g. The ASL signal amplitude was also fitted to a standard one-compartment model, and CBF and arterial transit time were found to be 92.2 ± 12.2 ml/100g/min and 1024 ± 143 ms, respectively. Notably, CBF from the one-compartment fitting was 18 ± 3 % greater than that from the two-compartment model.

Fig. 7.

Fitting of experimental data to the perfusion models in a representative subject. Both two-compartment (solid curves) and one-compartment (dashed curves) models were tested. For the two-compartment model, the procedure was conducted in two steps in which spin T2 (left) and ASL signal amplitude (right) were separately fitted (see Methods for details). The T2 curve was primarily affected by the tissue transit time whereas the amplitude curve was predominantly determined by CBF and the arterial transit time. The one-compartment model fitting only used the amplitude data in accordance with previous reports.

Robust analysis of the model fitting revealed that different initial values may result in different fitted parameters. For the ten subjects we studied, three yielded one set, six yielded two sets and one yielded three sets of parameter values. Monte Carlo simulations suggested that the estimated CBF, arterial transit time, and tissue transit time could be 0.0 ± 3.1 ml/100g/min, 2 ± 43 ms, and 8 ± 136 ms from the true values.

The re-scan of seven subjects at a distal slice yielded CBF, arterial transit time, and tissue transit time of 68.2 ± 5.8 ml/100g/min (N = 7), 949 ± 164 ms, and 2065 ± 200 ms, respectively. These values were not significantly different from those of the proximal slice in the same sub-group of subjects (paired t tests, P > 0.13).

Discussion

In the present work, a TRUST-PCASL MRI technique was used to measure the CPMG-T2 of labeled spins in ASL. This method allowed the assessment of spin localization at the time of image acquisition because different compartments in the voxel have characteristic T2 values. Furthermore, by fitting the experimental data to a two-compartment perfusion model, we were able to obtain an estimation of the arterial transit time, tissue transit time, and CBF. Importantly, while a number of studies in the literature have assessed the arterial transit time, few have considered the tissue transit time, which is an important parameter in perfusion kinetics and may affect the quantification of CBF.

Our data showed an expected pattern that the labeled spins first showed the T2 of arterial blood followed by gradually approaching and stabilizing at the tissue T2 (Fig. 6). The T2 values did not decrease further toward the venous T2, which appears to suggest that virtually all blood spins are exchanged to tissue when transiting through capillary beds and very few remained in the vessel to enter the vein. This is to be expected considering the large volume ratio between tissue and capillary (> 50:1). Comparing gray and white matters, the tissue transit time for white matter appears to be longer. Specifically, at a post-labeling delay time of 1525 ms, the labeled spins in white matter still had a T2 value characteristic of arterial blood. We also note that, at delay time of 200 ms, the T2 values in the vessel ROIs (141.1 ± 14.1 ms) were found to be slightly lower (P = 0.08) than those in the gray matter ROIs (154.4 ± 17.4 ms). This may be associated with hematocrit differences, as it is known that hematocrit in microvessels is about 85% of that in macrovessels (29). An alternative possibility is that some of the perfusion spins in the gray matter are located in the CSF space, which has a longer T2.

Previous studies on arterial transit time of continuous ASL methods showed a relatively large range, e.g. Alsop et al. (~600 ms) (3), Ye et al. (~500 ms) (9), Gonzalez-At et al. (651–1200 ms) (5), Mildner et al. (~1600 ms) (8), possibly because of differences in the gap between labeling and imaging locations. The arterial transit time obtained in this study (938 ± 156 ms, mean ± SD) was within this general range. Other studies have used pulsed ASL at multiple delay times and the observed arterial transit time tended to be lower due to a smaller gap between the labeling slab and the imaging slice (6–7). For estimation of tissue transit time, bipolar crusher gradients have been used to separate the vessel and tissue compartments in ASL (8–12,24). Depending on the labeling location and cutoff velocity, the values ranged from 940 ms to 1930 ms. The tissue transit time observed in the present study (1901 ± 181 ms) is in the high end of this range. Our findings are also in reasonable agreement with knowledge of blood flow velocities in cerebral vessels. Using a vascular architecture model developed by Piechnick and colleagues (30), one can divide vessel length by velocity to calculate the time it takes for the blood to travel through each vascular segment. It was found that it takes approximately 1.07 s to transit from major arteries to intracortical arterioles, and another 0.88 s to reach capillary.

Previous studies have used various techniques to determine the arterial cerebral blood volume (aCBV). Methods using crusher gradients reported values of 0.93 ± 0.06 ml/100 ml (11), whereas those based on magnetization transfer found values of 1.0 ± 0.3 ml/100g, which were comparable with aCBV measured with MR contrast agent (1.1 ± 0.5 ml/100 g) (31). A recent study based on inflow VASO found slightly higher values (1.61 ± 0.20 ml/100 ml) (32). The arterial blood volume obtained in the present study (1.18 ± 0.21 ml/100g) is within the range of these previous reports and is also consistent with the notion that aCBV is 20–30% of the total CBV (around 5 ml/100g) (33).

Typical CBF reported in the literature is approximately 60 ml/100g/min for the gray matter, but the values varied considerably across studies with a range from 38 ml/100g/min (11) to 98 ml/100g/min (26). These discrepancies may be attributed to differences in measurement techniques (34), spatial resolutions (34), and ROI selection criteria (7). The CBF values obtained in the present study (74.0 ± 10.7 ml/100g/min) are in the higher half of this range. We attributed this to three possible reasons. Our ROI definition was based on histograms of ASL signals and only voxels that have an ASL signal of greater than 0.5% were included in the gray matter ROI, which may have missed gray matter voxels with relatively low CBF values. In addition, the pulse sequence used in the present study did not include a crusher gradient which may result in an over-estimation. Thirdly, CBF may also be over-estimated due to potential errors in the transit time fitting.

T2 or T2* values of ASL have been studied previously to account for fast transverse decay of capillary signals (35). A recent study by Wells and colleagues has further investigated the T2 values of ASL signals in intracellular and extracellular spaces in a rat model (36). The previous studies have used a standard multi-echo approach to estimate T2, whereas the present study used a non-slice-selective T2 preparation method. The T2 preparation method may be critical for accurate estimation of T2 in arterial blood because rapid movement of the flowing spins will cause an additional signal delay with echo time (21). The relatively low arterial T2 (60–80 ms at 2.35 Tesla) observed in Wells et al. may be associated with this contribution (36).

Knowledge of transit times could be important in the quantification of CBF from ASL signal. Previous studies have demonstrated the relevance of arterial transit time in flow quantification (3,37). Our study showed that the tissue transit time is also important and that the standard one-compartment model, which only considered arterial transit time, could overestimate the CBF by about 18% when compared to the two-compartment model. The reason for this overestimation is that the labeling effect decays at a slower rate in the blood (due to longer T1), thus gives a larger apparent signal.

ASL is based on signal subtraction between control and label images, and the difference is typically only 1–2% of the control signal. With additional T2 weighting as employed in the present study, the signal is expected to be even smaller. To assess whether our experimental data would allow a reliable T2 estimation, we quantified SNR of our data for each post-labeling delay time and each TE. It was found that SNR at the single voxel level was too low for T2 fitting. On the other hand, ROIs containing several hundred voxels have relatively high SNR values (Table 1) and were the focus of our data processing. Monte Carlo simulations suggested that the ROI data can yield a T2 estimation with an uncertainty of ±10 ms and ±20 ms for gray and white matter, respectively. Due to the nature of non-linear fitting, a systematic bias may also be present in fitted parameters, but this was estimated to be less than 4 ms for our experimental SNR.

The present technique could be improved in a number of aspects. The scan duration of the current protocol is approximately 40 minutes. This may be acceptable for a technical study focusing on ASL methodology, but is not practical for clinical studies. A possible solution is to conduct the experiment at only one delay time which at least allows for the assessment of the ASL signal T2 in addition to the ASL signal amplitude. A second technical limitation is that the experiment could only be conducted using single-slice acquisition because multi-slice acquisition will interfere with the T2-preparation. Additionally, the signal at equilibrium magnetization, M₀, was determined from a thalamus region and used for the entire image. Therefore, inhomogeneities in B₁ excitation profile and in transverse relaxation time (T2*) can result in bias in the CBF estimation. A B₁ map and a T₂* map would be helpful in reducing these errors. Also, the tissue segmentation procedures used in this study were based on the CBF weighted images themselves, thus the ROI delineation criteria may have biased the CBF values. In future studies, a separate T1 or T2 weighted scan should be included. It should also be noted that the transit times determined in the present study are applicable for continuous or pseudo-continuous ASL methods. Such parameters for the pulse ASL methods should be determined in separate studies. We expect that similar T2-prepration schemes could be used and the accuracy of the fitting may be higher than the continuous method because one can sample both the ascending and the descending phases of the curve. Finally, the two step fitting algorithm may fall into local minima, causing the fitting outcome to be dependent on the initial values. An improved fitting algorithm is desirable to reduce the fitting errors.

Conclusion

A TRUST-PCASL technique was employed to probe the localization of the labeled spins inside the imaging voxel. The results demonstrated that the labeled spins spent considerable time traveling inside the voxel before eventually entering the tissue space. A post-labeling time delay of 2 seconds appears to be sufficient to allow the spins to completely enter the tissue space for gray matter, but not for white matter. CBF values may be overestimated if the tissue transit time is not accounted for.