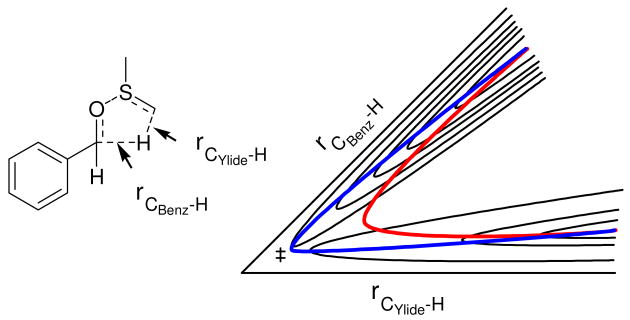
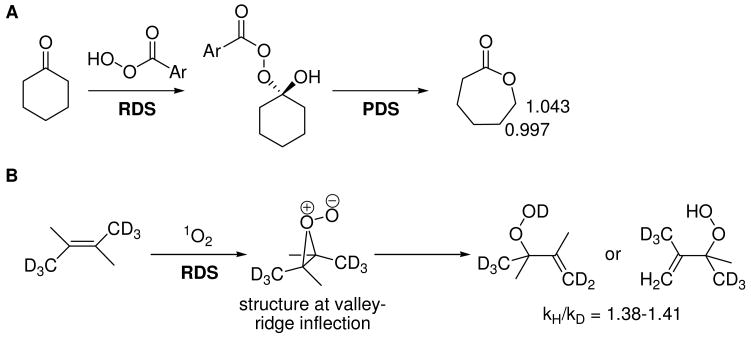
Abstract
Deprotonation of the alkoxysulfonium intermediate has been shown to be rate-determining in the Swern oxidation of benzyl alcohol. Directly following this rate-determining step is the intramolecular syn-β-elimination of the ylide. In the present study, intramolecular 2H kinetic isotope effects (KIEs) are used to gain insight into this syn-β-elimination step. As a result of the stereogenic sulfur center in the ylide intermediate, two diastereomeric transition states (endo-TS1 and exo-TS1) must be assumed to contribute to the intramolecular KIE. The intramolecular 2H KIE determined at -78 °C is 2.82 ± 0.06. Attempts to reproduce this measurement computationally using transition state theory and a Bell tunneling correction yielded a value (1.58) far below that determined experimentally. Computational analysis is complicated by the existence of two distinct transition structures owing to the stereogenic center. Two extremes of Curtin-Hammett kinetics are explored using energies, vibrational frequencies, and moments of inertia from computed transition structures. Neither Curtin-Hammett scenario can reproduce the observed KIE to any acceptable degree of fidelity. Evidence based upon previous kinetics measurements and calculations upon a model system suggest that the stereogenic sulfur center is not likely to undergo inversion to a significant degree at the temperatures at which the Swern oxidation is performed here. Proceeding under the assumption of no stereoinversion at the sulfur center, calculations predict a nearly linear Arrhenius plot for the KIE – even with the inclusion of a 1-dimensional tunneling correction. By contrast, the experimentally-determined temperature dependence shows a significant concave upward curvature indicative of the influence of tunneling. Notably, KIEs measured in CCl4, CHCl3, CH2Cl2, dichloroethane, and chlorobenzene at -23 °C showed little variance. This finding discounted the possible influence from dynamical effects due to incomplete vibrational relaxation. An ad hoc amplification of the imaginary frequencies corresponding to the first order saddle points corresponding to endo-TS1 and exo-TS1 allowed us to reproduce the experimental temperature dependence of the KIE using only two adjustable parameters applied to a kinetic scenario that involves four isotopomeric transition states. The cumulative data and computational modeling strongly suggest that, even though the intramolecular 2H KIE observed in these experiments is small, this reaction requires a multi-dimensional description of the tunneling phenomenon to accurately reproduce experimental trends.
Introduction
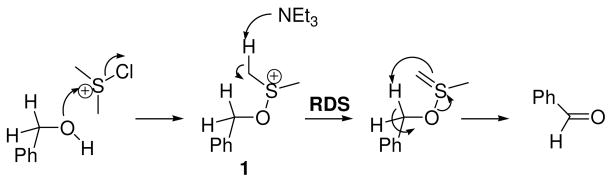
The Swern oxidation is one of the most useful methods for the conversion of primary and secondary alcohols to aldehydes and ketones, respectively.1-3 Excellent mechanistic work by Swern and others has yielded a cogent mechanistic model (Scheme 1) for this oxidation.4-10 The rate-determining step, under standard conditions is the deprotonation of 1 to yield the ylide. The following step, an intramolecular syn-β-elimination, is perhaps the most interesting elementary reaction step in the mechanism for the Swern oxidation.
Scheme 1.
Consensus mechansism for the Swern and related oxidations.
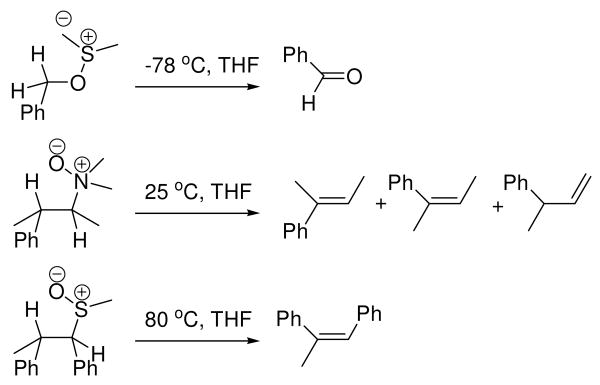
The β-elimination step, which liberates dimethyl sulfide and the product aldehyde (in the oxidation of 1° alcohols), involves the participation of six electrons in a cyclic array. This aspect raises a number of important questions: 1) Why is the syn-β-elimination in the Swern oxidation significantly more facile than other syn-β-eliminations that proceed by 5-membered transition states (Scheme 2)? 2) How important is tunneling to this reaction step? 3) Is the 5-membered transition state aromatic? The challenge of answering these questions is exacerbated by the fact that the rate-determining deprotonation precedes the step of interest.9 This precludes measurements of substituent and solvent effects upon rate as a means to probing charge distribution in the transition state, which could otherwise lend insight into the question of an aromatic transition state. Bach, Kwart, and others have performed kinetic isotope effect (KIE) measurements upon other syn-β-eliminations.11-23 These studies raise questions of how transition state geometry affects the facility of tunneling and raise the possibility that traditional hydrogen tunneling models are inappropriate for some of these systems. In a related vein, pericyclic reactions that involve hydrogen transfer have also required the invocation of tunneling models that explicitly treat more than one dimension quantum mechanically. Exploration of the temperature dependence of the intermolecular 2H KIE can lend insight into the importance and nature of hydrogen tunneling. However, measurements of intermolecular KIEs as a function of temperature do not report upon the syn-β-elimination. To circumvent these limitations, we have utilized intramolecular 2H KIEs to serve as a point of contact with values computed from transition structure models.
Scheme 2.
Intramolecular syn-β-eliminations with 5-membered transition states.
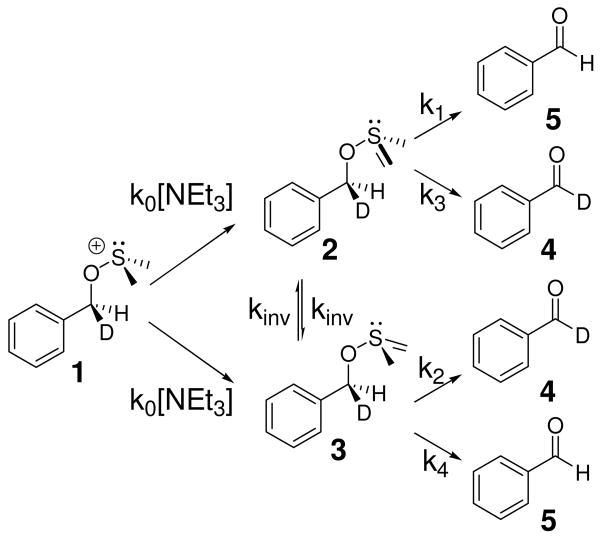
Intramolecular KIEs have traditionally been employed in systems where the competing positions are equivalent by symmetry.24 -26 The presence of a chiral sulfur center in the ylide makes the benzylic positions diastereotopic and therefore inequivalent. This situation does not preclude the use of intramolecular KIEs, but computational treatments must take the four energetically distinct transition states and their enantiomers into account. As a result, the experimentally determined KIE is a composite of rate constants k1-k4 (Scheme 3).
Scheme 3.
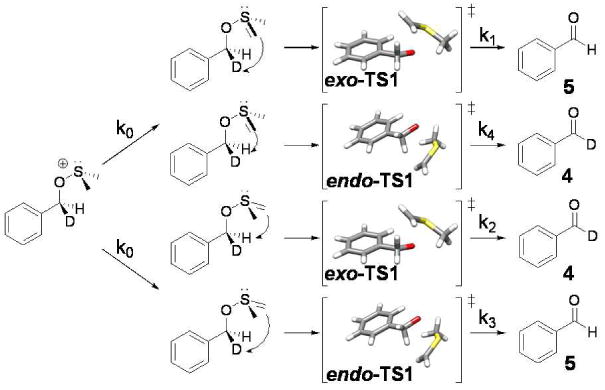
Competing reactions that yield the intramolecular 2H KIEs measured here.
Questions of stereochemical inversion at the sulfur center further complicate the expression of the observed KIE in terms of rate constants k1-k4. Fortunately, these difficulties can be overcome using both theory and experiment in concert. In this paper, we present measurements of the intramolecular 2H KIE for the Swern oxidation of d1-benzyl alcohol as a function of temperature and as a function of solvent. From these measurements and complementary computational efforts, we attempt to elucidate intriguing aspects of the detailed mechanism of the syn-β-elimination step of the Swern reaction.
Results and Discussion
Experimental Intramolecular 2H KIE
The Swern oxidation is typically performed at -60 °C. We found that the reaction proceeded to completion at -78 °C in under one hour after addition of triethylamine. Measurement of the ratios of d-benzaldehyde [4] to benzaldehyde [5] resulting from oxidation at -78 °C yielded an intramolecular 2H KIE of 2.82 ± 0.06. In considering what this measurement means in terms of the factors that contribute to its magnitude, it is useful to consider the intrinsic meaning of traditional intramolecular KIEs. Two excellent examples of the application of intramolecular KIEs are represented in mechanistic studies of the singlet oxygen ene reaction and the Baeyer-Villiger oxidation. In an early example of the power of intramolecular KIEs Grdina, et al. reported a very elegant study of the singlet oxygen ene reaction. Using isotopomers of d6-tetramethylethylene as mechanistic probes, they provided evidence that suggested the formation of a symmetric perepoxide intermediate during the rate-determining step.24 This result was at variance with early computational work by Goddard, et al., who found that the perepoxide possessed too much potential energy to be a viable intermediate within the reaction pathway for the reaction.27 Recently, Singleton, et al. resolved this discrepancy by measuring intramolecular 13C KIEs and computing the potential energy surface using high-level ab initio methods in conjunction with density functional theory.25 Their findings interpret the intramolecular KIEs as arising from the presence of a valley-ridge inflection instead of a stable perepoxide intermediate. Structurally, the valley-ridge inflection found in this study does resemble the putative perepoxide. In an application of intermolecular and intramolecular 2H and 13C KIEs, Singleton and Szymanski provided evidence for rate-limiting addition of peroxyacid to the cyclohexanone followed by product-determining migration.26 Intramolecular 2H KIEs in the Swern oxidation would be simple to interpret if the sulfur center were planar in 2 and 3 (making them equivalent). In such a situation, the observed intramolecular 2H KIE would simply be the ratio of the 1°-KIE to the 2°-KIE at the benzylic position.
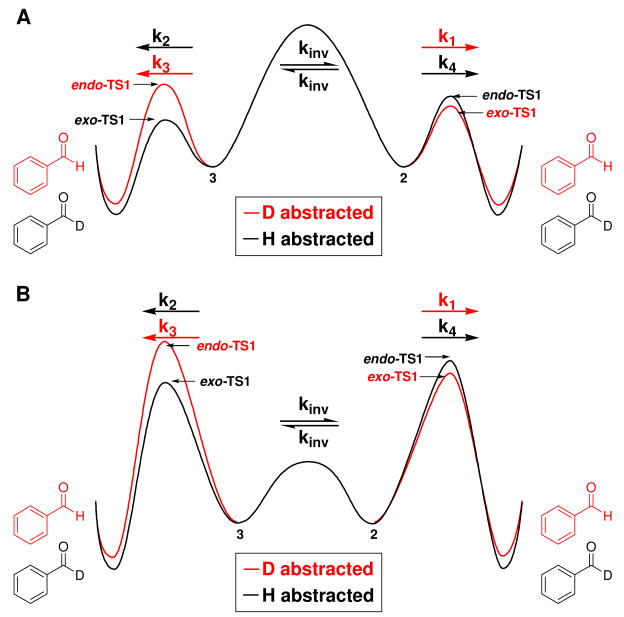
The Swern oxidation poses additional challenges regarding the interpretation of the observed experimental intramolecular KIEs. Because of the stereogenic sulfur center present in the ylide, abstraction of the pro-S and pro-R benzylic hydrogen atoms represent distinct first order saddle points on the potential energy surface for this reaction. These two transition structures can be classified as endo-TS1 and exo-TS1 (Figures 2A and 2B, respectively). If the energy difference between the exo-TS1 and endo-TS1 were substantially larger than the energy differences that give rise to the primary 2H KIE, then no intramolecular KIE would be observed. Abstraction of the pro-S or pro-R positions would be mandated by the stereochemistry of the sulfur ylide. As can be seen in Table 1, the two competing transition structures do indeed have similar structural and energetic properties. As a consequence, the effect of isotopic substitution upon the relative free energies of reaction manifest themselves in the observed KIE.
Figure 2.
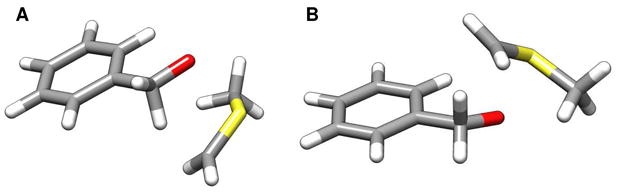
Two distinct first-order saddle points for the syn-β-elimination step investigated here computed with B3LYP/6-31+G(d,p): A) endo-TS1 and B) exo-TS1.
Table 1.
Structural and energetic metrics of the endo-TS1 and exo-TS1 transition structures.
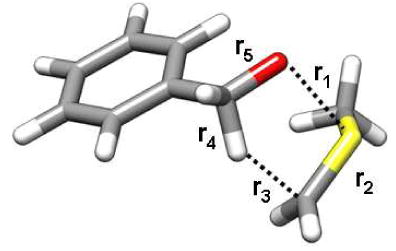 | |||||||
|---|---|---|---|---|---|---|---|
| r1 (Å) | r2 (Å) | r3 (Å) | r4 (Å) | r5 (Å) |
iv‡ (cm-1) |
Erela | |
| endo-TS1 | 2.241 | 1.657 | 1.816 | 1.189 | 1.337 | -390 | 0.5 |
| exo-TS1 | 2.225 | 1.656 | 1.802 | 1.189 | 1.335 | -367 | 0.0 |
Relative computed gas phase [B3LYP/6-31+G(d,p)] energies in kcal/mol.
As a first approximation of the magnitude of isotope effects that one might expect, it is instructive to compute the ratio of the primary and secondary 2H KIEs for both the endo-TS1 and exo-TS1 structures. These ratios are 2.19 and 2.26, respectively. These values contain a tunnel correction computed using the first term of the Bell28 expression and a frequency scaling factor of 0.9806.29 The computed ratios deviate quite strongly from the measured intramolecular KIE. In considering the effects that both transition states have upon the observed KIE, it is instructive to consider two limiting Curtin-Hammett kinetic regimes (Scheme 4).30 The first kinetic scheme (Figure 3A) we employ assumes forbidden stereoinversion for the sulfur ylides (2 and 3). The other limiting case is facile stereoinversion at the sulfur center for 2 and 3 (Figure 3B).
Scheme 4.
Kinetic scheme employed for testing the two limiting Curtin-Hammett scenarios.
Figure 3.
Limiting Curtin-Hammett scenarios: A) forbidden stereoinversion and B) facile stereoinversion of ylides 2 and 3.
| (1) |
| (2) |
Under the assumption of facile stereoinversion of the sulfur center in 2 and 3 (kinv≫k1-k4), the ratio of d-benzaldehyde to benzaldehyde is given by eq. 1. The computed intramolecular 2H KIE under this assumption is 2.21 which is substantially smaller than the experimentally-determined value. Under the assumption of forbidden stereoinversion, the intramolecular KIE is given by eq. 2. The computed intramolecular 2H KIE under this assumption is 1.58, which is egregiously lower than the experimentally-determined value. It would be a reasonable hypothesis to assume that these results imply that stereoinversion of the sulfur ylide is, in fact, quite facile in the Swern oxidation and that tunneling beyond what might be computed using a simple 1-dimensional correction might be the cause of disagreements between the experimental and calculated KIEs. Such a supposition, if it were true, would seem contradictory to the expectation that chiral sulfur ylides are conformationally stable. An early measurement of the rate constant for stereoinversion of stabilized sulfure ylides found that the rate constant for the stereoinversion of 6 is 3.52 × 10-5 s-1 at 25 °C in dichloromethane.31 Temperature dependence of the rate constant for inversion yielded an enthalpy of activation of 23.3 kcal/mol. A similar measurement for the unstabilized ylide derived from Eastman's sulfonium salt yields an enthalpic barrier of 28.0 kcal/mol.32 Other measurements of sulfur ylide inversion barriers have yielded similar values.33 Calculations of the potential energy differences between the ground state of 7 and the transition structure for stereoinversion yielded a similar value of 36.3 kcal/mol. Estimates of the inversion barriers for these two ylides suggest that the barrier for inversion between 2 and 3 is high enough to prohibit any substantial stereoinversion at any of the temperatures explored in the present study.
Experimental data from other researchers and computatonal data collected in the present study suggest that interconversion between 2 and 3 is likely to be attenuated to such a degree that would allow it to be ignored. It is surprising, then, that the forbidden stereoinversion yields a computed KIE that deviates so strongly from the experimentally-determined value. Several possible reasons for this disagreement are plausible. First, it is conceivable that the energy difference between endo-TS1 and exo-TS1 is not estimated accurately by the B3LYP34 functional when paired with the 6-31+G(d,p)35 basis set. Secondly, though the syn-β-elimination step studied here appears to be pericyclic (vide infra), it may be that a proper solvent model would change the frequencies corresponding to the transition structures in such a way that the intramolecular KIE is more exalted. A third possibility is that dynamical effects that are not included in our semiclassical transition state theory treatment are operative. A fourth possiblity is that the effects of hydrogen tunneling upon the KIE in this reaction step are not amenable to a simple Bell correction. Below, we will systematically explore these possibilities.
The B3LYP functional has proven to be very good at reproducing frequencies.36 In fact, the vast majority of KIE calculations, which rely heavily upon accurate force constant estimates, utilize the B3LYP functional.37 Computing intramolecular KIEs here requires that accurate estimates of the relative energies of the saddle points are obtained. The B3LYP functional has proven only moderately useful in the prediction of barrier heights in pericyclic reactions. However, the problem treated here is less exacting than the calculation of barrier heights. Instead, we are computing the relative electronic energies of the first order saddle points represented by endo-TS1 and exo-TS1. Because these two transition structures are the same in kind and differ only conformationally, it is likely that relative energy calculations are reasonably accurate. In other words, it is likely that the errors inherent in estimating the electronic energies of the two transition states are of similar origin and magnitude. As a consequence, calculations of the differences in energy between these two structures are likely to benefit from canellation of error. It is worthwhile, though, to explore the degree to which the computed KIE under the assumption of forbidden stereoinversion varies as a function of the difference between Eendo-TS1 and Eexo-TS1 (Figure 4). The maximum intramolecular KIE under the assumption of forbidden inversion is 2.20, and this value obtains when Eendo-TS1 and Eexo-TS1 are equivalent. The intramolecular KIE under the assumption of facile inversion is nearly invariant to the energy difference between the two competing transition structures. This situation obtains because the ratio of primary to secondary 2H KIEs for both endo-TS1 and exo-TS1 are nearly equivalent (k2/k1≈k4/k3). Thus, it appears that changing the relative electronic energies of the two distinct transition structures cannot produce a computed KIE as large as the experimentally-determined value.
Figure 4.
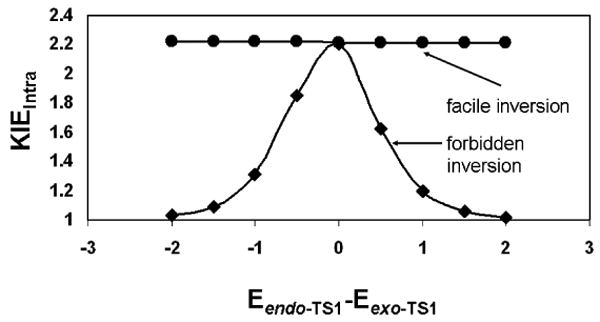
Dependence of the computed intramolecular KIE upon the difference in electronic energies (kcal/mol) of endo-TS1 and exo-TS1.
Another consideration in our discussion of disparities between computed versus measured intramolecular 2H KIEs is the validity of utilizing density functional theory to treat the present system. The endo-TS1 structure places the S-Me group somewhat near the face of the phenyl ring in the substrate. Dispersion interactions, which are mediated by electron correlation, are not reproduced by the hybrid B3LYP functional. Inclusion of dispersion interactions may be expected to alter the differences between Eendo-TS1 and Eexo-TS1 relative to what is found using B3LYP. This consideration is raised in light of Figure 4, which illustrates that the difference between Eendo-TS1 and Eexo-TS1 can have profound effects upon the computed KIE. In fact, using Grimme's B97D38 functional with a dispersion correction alters the energy difference between endo-TS1 and exo-TS1 such that the endo-TS1 becomes slightly lower in potential energy than exo-TS1. However, the change is not substantial, and the overall effect is a lowering of the expected intramolecular KIE under the assumption of no stereoinversion at the sulfur center to 1.47 (versus 1.52 for B3LYP) in the gas phase. Calculations involving a polarizable continuum model for CH2Cl2 yield 1.42 using the B97D functional and 1.63 using the B3LYP functional. In summary, it appears that dispersion forces do affect the relative energies corresponding to the two energetically distinct transition structures but do not appreciably affect the computed intramolecular 2H KIE.
Solvent Effects upon Intramolecular KIEs
Another possible cause of disagreement between experiment and theory is the use of gas phase calculations to model reactions occurring in solution. If there is considerable charge build-up or attenuation at the transition states, it might be that optimization of the transition structures in the presence of a continuum model would yield transition structures that differ substantially from those optimized in the gas phase. Figure 5 shows overlays of the endo-TS1 and exo-TS1 structures optimized in the presence of a dielectric continuum model of dichloromethane and in the gas phase. For these calculations, the IEFPCM model was employed.39 A discrete sphere was employed for the transferred hydrogen atom. Table 2 shows how structural and energetic elements within the two transition structures are altered.
Figure 5.
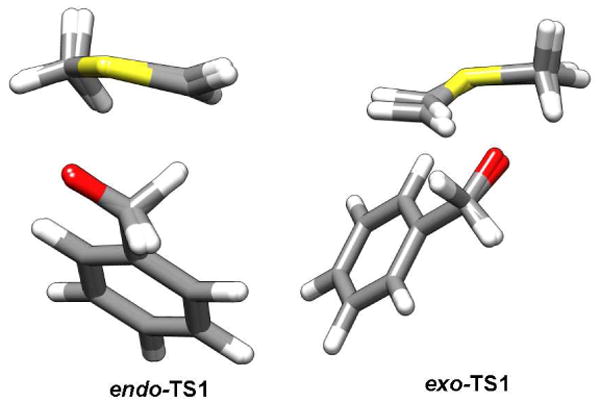
Overlays of endo-TS1 and exo-TS1 structures computed in the gas phase and optimized using a polarizable continuum with a dielectric constant corresponding to dichloromethane.
Table 2.
Structural and energetic metrics of the endo-TS1 and exo-TS1 transition structures optimized within a polarizable continuum model of CH2Cl2. Structural parameters correspond to those shown in Table 1.
| r1 (Å) | r2 (Å) | r3 (Å) | r4 (Å) | r5 (Å) |
iν‡ (cm-1) |
Erela | |
|---|---|---|---|---|---|---|---|
| endo-TS1 | 2.296 | 1.649 | 1.864 | 1.174 | 1.343 | -286 | 0.4 |
| exo-TS1 | 2.273 | 1.649 | 1.866 | 1.175 | 1.345 | -272 | 0.0 |
Relative computed gas phase [B3LYP/6-31+G(d,p)] energies in kcal/mol.
There are three main alterations that are induced by optimization using a polarizable continuum model. Structurally, it appears that the only bond that changes appreciably is the S–O bond, which becomes longer due to dielectric screening of the positive charge upon sulfur and the negative charge upon oxygen. Perhaps the most substantial change can be seen in the imaginary frequencies. The presence of a polarizable continuum reduces the imaginary frequencies of both endo-TS1 and exo-TS1 transition structures by approximately 100 cm-1. Finally, the energies of the two transition structures become closer by a small amount. Given the substantially smaller magnitude of the imaginary frequencies for transition structures optimized within a polarizable continuum as compared to gas phase frequencies, it seems reasonable to expect the absolute magnitude of the computed KIE to decrease. In fact, the intramolecular 2H KIE decreases to 1.89 under the facile stereoinversion scenario. This diminished value results from the attenuation of the ratio of the primary and secondary 2H KIEs in both transition structures to 1.72 and 1.85 for exo-TS1 and endo-TS1, respectively. Due to a smaller difference in electronic energy between the both endo-TS1 and exo-TS1 transition structures, the intramolecular 2H KIE increases to 1.63 under the forbidden stereoinversion scenario. This value, while higher than the value of 1.58 computed using gas phase calculations, is still quite distant from the experimental value of 2.82. Analysis of the charge distribution using natural population analysis40 offers another means of understanding the effects of the polarizable continuum upon endo-TS1 and exo-TS1 transition structures. Table 3 shows the partial charges upon the five atoms undergoing substantial bonding changes in gas phase and polarizable continuum structures. The only atoms whose charges are altered substantially by the presence of a polarizable continuum in both transition structures are the oxygen atom and the hydrogen-abstracting carbon atom. The screening effect of the dielectric allows for the development of greater negative charge with concomitant lengthening of the S–O bond. Effectively, the transition state is later due to this change, but this effect is not propagated into the nascent and breaking bonds to the transferred hydrogen atom. In summary, the data provided by the PCM calculations suggest that disparities between calculation and experiment cannot be rectified by including electrostatic solvent effects in the calculations.
Table 3.
Comparison of charges obtained from natural population analysis on the component atoms of the 5-membered endo-TS1 and exo-TS1 transition structures optimized in the gas phase and using a polarizable continuum model of CH2Cl2.
| Gas Phase Structures | |||||
|---|---|---|---|---|---|
| CBenzyl | H | CDMS | S | O | |
| endo-TS1 | -0.090 | 0.204 | -0.803 | 0.719 | -0.685 |
| exo-TS1 | -0.090 | 0.206 | -0.807 | 0.724 | -0.689 |
| Polarizable Continuum (CH2Cl2) Structures | |||||
| CBenzyl | H | CDMS | S | O | |
| endo-TS1 | -0.097 | 0.203 | -0.766 | 0.720 | -0.737 |
| exo-TS1 | -0.100 | 0.206 | -0.774 | 0.726 | -0.737 |
A third possible hypothesis for the observed deviations of experimental numbers from transition state theory calculations is dynamical corner-cutting.41,42 Conceptually, this could arise in the following way: The rate-limiting step precedes the syn-β-elimination step being studied here. The ylide produced from the rate-limiting step could retain vibrational energy in crossing the dividing surface between the ylide and the products. One result of changing the geometry at which most reaction flux occurs will change the manner in which isotopic labeling affects the rate. Some recent studies on small molecule gas phase hydrogen abstractions have shown that both primary and secondary kinetic isotope effects can deviate strongly from transition state theory predictions - largely as a result of dynamical avoidance of the first order saddle point.43,44 Perhaps the best way to test this hypothesis is to perform intramolecular KIE measurements in solvents that have different effects upon vibrational relaxation lifetimes. The physical properties of a solvent such as the dielectric constant, dipole moment, and vibrational density of states can drastically affect the rate of vibrational relaxation in solutions. Solvents with the smallest degree of coupling to the reacting species should yield results that deviate most strongly from transition state theory. Solvents with a high density of states should facilitate vibrational relaxation in going from the transition state for deprotonation to the ylide intermediate.
Table 4 shows the intramolecular KIEs measured in different chlorinated solvents. We performed 5 replicates of measurements in both CH2Cl2 and CCl4 based on the knowledge that the dipole moments, dielectric constants, and vibrational densities of states of these two solvents are very different. We performed these experiments at -23 °C, which is the freezing point of carbon tetrachloride, the solvent with the highest freezing point of the solvents tested. We found that, while there was some difference in intramolecular KIEs measured in dichloromethane and carbon tetrachloride, the differences were not substantial. To explore solvent effects further, we then measured intramolecular 2H KIEs once in dichloroethane, chlorobenzene, and chloroform. The intramolecular 2H KIE measured in chlorobenzene was close to the average value determined in carbon tetrachloride. This is surprising given the marked difference between the two solvents in terms of dipole moment and vibrational density of states. By contrast, chloroform and dichloromethane yielded different intramolecular 2H KIEs but have similar dielectric constants and dipole moments. In total, it became apparent that solvent effects upon the experimental intramolecular 2H KIE appear to be small and yield no observable trend.
Table 4.
Intramolecular 2H KIEs measured at -23 °C as a function of solvent, computed KIEs under assumptions of no stereoinversion and facile stereoinversion, and ratios of primary to secondary 2H KIEs for the two distinct transition structures.
| CH2Cl2 | CCl4 | PhCl | C2H4Cl4 | CHCl3 | |
|---|---|---|---|---|---|
| ε | 8.9 | 2.2 | 5.6 | 10.1 | 4.7 |
| μ | 1.14 | 0.00 | 1.54 | 1.80 | 1.15 |
| 2H KIE (Expt.) | 2.08 ± 0.07 | 2.17 ± 0.04 | 2.14 | 2.08 | 1.98 |
| 2H KIE (no inversion) | 1.53 | 1.51 | 1.41 | 1.52 | 1.52 |
| 2H KIE (inversion) | 1.65 | 1.81 | 1.68 | 1.64 | 1.70 |
| (1°/2°) KIE (endo-TS1) | 1.62 | 1.75 | 1.64 | 1.61 | 1.67 |
| (1°/2°) KIE (exo-TS1) | 1.72 | 1.86 | 1.74 | 1.71 | 1.76 |
It is useful to question whether one should expect a solvent effect within the array of solvents employed in the measurements reported in Table 4. To answer this question, one should consider the ways in which solvent differences might impact the observed KIEs. Solvent dipole moment or dielectric constant could certainly be expected to perturb transition structure; however, this perturbation does not appear to be substantial, given that polarizable continuum models do not predict substantial differences among the solvents in ratios of primary to secondary 2H KIEs for the endo-TS1 and exo-TS1 transition structures. As these values ultimately largely determine the observed intramolecular 2H KIE, it could be expected that dipole moment and dielectric constant should not yield distinct differences among KIEs measured in these solvents.
The question inherent to understanding potential dynamical differences among the solvents can be related to other researchers' measurements of vibrational relaxation in chlorinated solvents. Measurements of vibrational relaxation of the carbonyl chromaphore in tungsten hexacarbonyl in CCl4 and CHCl3 show very different behaviors between the two solvents.45 In fact, the temperature dependence of the vibrational lifetimes of the carbonyl chromaphore is opposite for CCl4, where the relaxation time decreases with increasing temperature, compared to CHCl3, where the relaxation time increases with increasing temperature. Similarly, in another study, the vibrational lifetimes of the carbonyl chromaphore in ethyl trichloroacetate were shown to differ by a factor of two between the two solvents.46 Given the fundamentally different way in which these solvents facilitate vibrational relaxation, it seems reasonable to have expected a much larger solvent effect upon the intramolecular 2H KIE if inefficient vibrational relaxation were responsible for the substantial differences between measured and computed KIEs.
Temperature Dependence of Intramolecular KIEs
KIEs are among the most successful experimental diagnostics for hydrogen tunneling phenomena.47,48 Perhaps one of the most often employed metrics for the importance of tunneling to hydrogen transfer is the magnitude of the primary 2H KIE. The maximum primary 2H KIE to be expected from semiclassical transition state theory is approximately kH/kD = 7 at 25 °C. When this value is extrapolated to -78 °C under the assumption that the isotope effect largely results from isotopic perturbation of ΔH‡, a value of 19 is obtained. While the intramolecular KIEs reported here are not fully expressed primary 2H KIEs, the kinetic expressions for the observed intramolecular 2H KIE measured here can be expanded into expressions that are dominated by primary 2H KIE factors. Eq. 3 is the expression for the intramolecular KIE under the assumption of facile inversion, and eq. 4 is the same expression under the assumption of no stereoinversion. The kH,H factors are rate constants corresponding to the perprotiated transition structures.
| (3) |
| (4) |
The measured intramolecular KIE reported here (2.82 ± 0.07) is an order of magnitude smaller than the semiclassical maximum extrapolated to -78 °C. Based on the magnitude of the intramolecular KIE alone, there is no reason to believe that tunneling is contributing substantially to the observed KIE. Furthermore, the reduced masses for the imaginary modes in the transition structures for the syn-β-elimination involved in the oxidation of benzyl alcohol are 4.39 for exo-TS1 and 3.62 for endo-TS1. By contrast, most hydrogen transfer reactions have reduced masses near unity. Neither the magnitude of the observed intramolecular KIE nor the computed reduced mass corresponding to the imaginary mode in the computed transition structures suggest that tunneling should be responsible for the disagreement between the computed and measured intramolecular KIEs reported here.
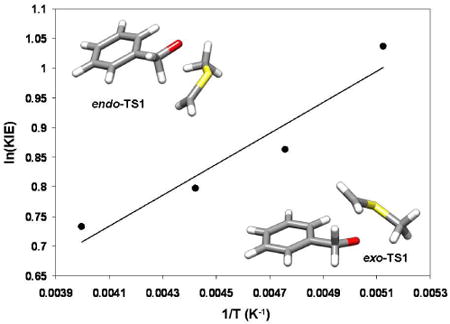
The temperature dependence of primary 2H KIEs is also frequently used as a diagnostic for the importance of tunneling to the magnitude of the observed KIE. 28,47,49,50 Curvature in plots of ln(1°-KIE) vs. 1/T is indicative of tunneling having a significant effect upon the observed KIE. Based upon previous work, it is quite reasonable to expect tunneling to affect the primary 2H KIEs to a greater degree than secondary 2H KIEs.51,52 Given that eqs. 3 and 4 are dominated by factors that effectively resemble the ratio of a primary to a secondary 2H KIE, one would expect a plot of ln(KIEIntra) vs. 1/T to be significantly curved if tunneling factored into the observed intramolecular 2H KIE significantly. Of course, one possible origin of the minute curvature observed in the Arrhenius plot could be the composite nature of the expressions for the intramolecular KIE (eqs. 1 and 2). To gain insight into how one might expect the expressions in eqs. 1 and 2 to depend upon temperature, we constructed Arrhenius plots of the computed composite expressions for the natural logarithm of the intramolecular 2H KIE versus inverse temperature. As a point of comparison, we also plotted the natural logarithms of the ratios of the primary to secondary 2H KIEs for both endo-TS1 and exo-TS1 versus inverse temperature as these ratios are component parts of the expressions shown in eqs. 3 and 4 (Figure 6). The ratio of primary to secondary KIEs for the two transition structures have a very small upward curvature. This is not surprising, given that there is a tunneling correction applied to these KIE calculations. What is surprising is that the Bell tunneling correction is nearly the same for transfer of H and D in the endo-TS1 (Qt,H = 1.171; Qt,D = 1.170) and exo-TS1 (Qt,H = 1.188; Qt,D = 1.187) transition structures optimized in a polarizable continuum model for dichloromethane. The same trend is present in gas phase calculations and in other polarizable continuum model solvents and appears to be a general feature of transition structures for the Swern oxidation. Presumably because of the composite nature of eqs. 3 and 4 upon individual KIE ratios, computed expectations of the intramolecular KIE under assumptions of facile inversion and forbidden inversion have a slight downward curvature.
Figure 6.
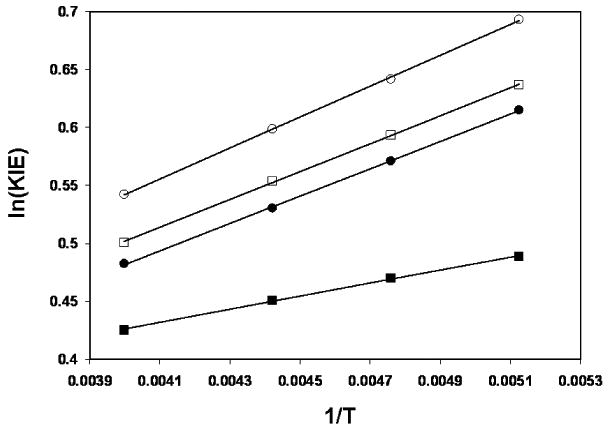
Arrhenius plots of the computed expressions for the intramolecular 2H KIE as given by eqs. 1 (open squares) and 2 (closed squares) and the ratios of primary to secondary 2H KIEs for both endo-TS1 (closed circles) and exo-TS1 (open circles). Black lines are linear fits to each set of data.
Having exhausted all viable hypotheses excepting that the primary KIE is exalted beyond what is computed using semiclassical transition state theory augmented with a 1-dimensional tunnel correction, we explored the temperature dependence of the intramolecular 2H KIE (Table 5; Figure 7). We also attempted to compute the KIE under the assumption of no inversion by amplifying the magnitudes of ν‡ corresponding to deuterium transfer (k1 and k3) by a factor of 2.3 and ν‡ corresponding to protium transfer (k2 and k4) by a factor of 2.6. While this is an ad hoc correction, it is satisfying that, by using only two adjustable parameters, we can reproduce the temperature dependence of a complex kinetic expression that involves four transition states.
Table 5.
Intramolecular 2H KIEs measured in dichloromethane as a function of temperature, computed KIEs under assumptions of no stereoinversion and facile stereoinversion, and ratios of primary to secondary 2H KIEs for the two distinct transition structures. All structures used to compute KIEs were optimized in the presence of a polarizable continuum model for dichloromethane.
| -78 °C | -63 °C | -47 °C | -23 °C | |
|---|---|---|---|---|
| 2H KIE (Expt.) | 2.82 ± 0.06 | 2.37 ± 0.05 | 2.22 ± 0.02 | 2.08 ± 0.07 |
| 2H KIE (Sim.)a | 2.76 | 2.44 | 2.23 | 2.04 |
| 2H KIE (no inversion) | 1.63 | 1.60 | 1.57 | 1.53 |
| 2H KIE (inversion) | 1.89 | 1.81 | 1.74 | 1.65 |
| (1°/2°) KIE (endo-TS1) | 1.85 | 1.77 | 1.70 | 1.62 |
| (1°/2°) KIE (exo-TS1) | 2.00 | 1.90 | 1.82 | 1.72 |
Computed intramolecular KIE under the assumption of no stereoinversion at the stereogenic sulfur center with amplification factors of 2.3 and 2.6 for the imaginary frequencies corresponding to deuterium abstraction (k1 and k3) and protium abstraction (k2 and k4), respectively.
Figure 7.
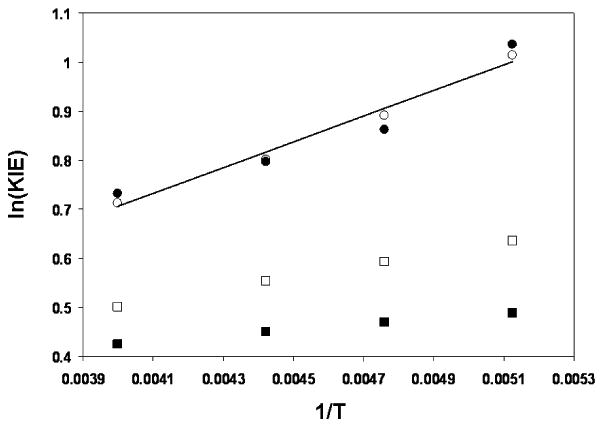
Arrhenius plots of the experimentally-determined intramolecular 2H KIE (closed circles), computed KIEs given by eqs. 1 (open squares) and 2 (closed squares) and KIEs computed from eq. 2 employing static multipliers of 2.3 and 2.6 for the imaginary frequencies corresponding to deuterium and protium transfer (open circles). The black line is a linear fit to the experimental KIE measurements.
Fitting the experimental data shown in Figure 7 to the Arrhenius equation yields AH/AD = 0.71 and DEa-HEa = 0.52 kcal/mol. If we consider these parameters to largely reflect the primary 2H KIE, then one might say that the isotope effect upon the Arrhenius prefactor, AH/AD, is close to what is normally accepted as a lower limit for evidence of tunneling.53 The difference in Ea for the two isotopes is well within what might be expected owing only to differences in zero-point energy. As Kreevoy has pointed out, this is an overly simplistic view. Tunneling is no more exotic than zero-point energy, as both of these effects are merely results of wave/particle duality.54 More to the point of mechanistic inquiry is the question of whether semiclassical transition state theory is a suitable model. In other words, is it sufficient to include quantum effects arising from zero-point energy only and to assume that tunneling has only a negligible effect upon observables such as rates or KIEs? Assuming that the transition structures presented here are ample representations of the average geometry of the transition state ensemble, it seems evident that semiclassical transition state theory fails to reproduce the temperature dependence of the intramolecular 2H KIE measured here. The question then becomes one of whether tunneling is best represented as occuring along the minimum energy path or whether the average tunneling path might be expected to deviate from this path.
How can the ad hoc imaginary frequency amplification discussed above be understood conceptually? Frequency amplification can be thought of as an effective reduction in the reduced mass, an increase in the force constant magnitude, or some combination thereof.55 As such, this simple correction reproduces in a curve-fitting fashion what might be expected from tunneling corrections that take into account deviations from the minimum energy path. In what has often been called corner-cutting tunneling (Figure. 8), the pathway that describes the average trajectory for protium transfer deviates from that which describes deuterium transfer. In particular, the critical configuration for transfer of the two isotopes differs in such a way that protium tunneling occurs at greater donor/acceptor distances than deuterium tunneling. Likewise, the tunneling pathway for protium proceeds under regions of greater potential energy than those corresponding to deuterium transfer. These two dominant characteristics of corner-cutting tunneling directly affect what might be thought of as an effective imaginary frequency corresponding to the point on the potential energy surface at which the tunneling pathways cross from the reactant portion of the surface to the products region.
Figure 8.
Pictorial representation of corner-cutting tunneling. The blue path represents the minimum energy path, while the red path denotes a representative corner-cutting tunneling pathway.
Comparison with Other Reactions
In addition to the Cope elimination13,15,18,21,22 and sulfoxide elimination13,23, the Wittig modification of the Hofmann elimination11,12,17 has been shown to proceed via 5-membered syn-β-elimation in many cases. Kwart has argued for a similar transition state in the base-promoted thermolyses of nitrates; however, this argument was based entirely upon the magnitude of the primary 2H KIE exhibited.56 How do intramolecular 2H KIEs in these systems compare with the syn-β-elimation step in the Swern oxidation?
The Cope elimination has been studied using intramolecular 2H KIEs and computational methods. Bach, et al. report transition structures for the Cope elimination of butylamine oxide that are similar in kind to the endo-TS1 and exo-TS2 structures reported here. These small model systems were optimized using MP2 theory with the 6-31G* basis set.21 These transition structures yield primary 2H KIEs of 3.37 at 120 °C including a 1-dimensional Wigner tunneling correction.57 Komaromi and Tronchet computed primary 2H KIEs for the Cope elimination of ethylamine oxide also using MP2 theory but with a slightly larger basis set, 6-31G**.22 They report a computed primary 2H KIE of 2.56 at 125 °C not including a tunnel correction. Unfortunately, they do not report imaginary frequencies for the reaction coordinate at the transition state as a function of isotope, so estimation of the Wigner or Bell tunneling correction is precluded. However, applying the same tunnel correction used in the study by Bach, et al., the primary 2H value is elevated to 2.97. Bach and Braden performed a very elegant measurement of both the primary and secondary intramolecular 2H KIEs using of intramolecular 2H KIEs in the Cope elimination of 8.18 They report a primary and secondary 2H KIE of 2.23 and 1.22, respectively at 120 °C. Extrapolated to -78 °C, these values are 5.03 and 1.49, respectively. Kwart and Brechbiel report a measurement for the intramolecular KIE as ‘kH/kD = 2.778’ for the Cope elimination of 9 at 120 °C.15 Extrapolated to -78 °C, this value becomes 7.833. The value measured by Kwart and Brechbiel is actually the ratio of primary to secondary 2H KIEs. In a system where the secondary 2H KIE might be expected to be normal and substantial, this implies a sizable primary KIE. In any course, it can be seen that the extrapolated KIEs are well in excess of those measured here.
Thermolyses of sulfoxides to yield an alkene and sulfenic acid are quite analogous to the syn-β-elimination step in the Swern oxidation. Kwart and coworkers have investigated this reaction by performing intramolecular 2H KIE measurements14 on 10 and intermolecular 2H KIE measurements13 using 11 and d9-11 as competing reactants. Unfortunately, no mention is made of how the measured KIE is corrected for elimination from the ethyl substituent in the competition between 11 and d9-11. If reported intermolecular KIEs do not have this reaction pathway factored into the result, the net effect would be that the actual KIE would be larger than the one measured by monitoring the disappearance of 11 and d9-11 versus an internal standard. In perhaps a more appropriate system for the exploration of intermolecular isotope effects, Yoshimura, et al. measured KIEs using 12 and d3-12 as competing reactants.18 Intermolecular KIEs measurements upon 11 and 12 yielded values of 5.4 at 112 °C and 5.15 at 80 °C, respectively. KIEs estimated from computed transition structures produced values that were approximately 20% too small in each case; however, the computed KIEs did not include any correction for tunneling. An intramolecular KIE of 3.17 at 130 °C was reported for the thermolysis of 10.14 The intramolecular KIE measured via the conversion of 10, however, is more complex than the competition between two pathways that differ only in the position of the isotopic label. This system shares the complexity inherent to the syn-β-elimination step in the Swern oxidation. Four rate constants are likely to play a role in the thermolysis of 10 as well. It is worth noting that the only system for which the computed 2H KIEs of Cubbage, et al.23 agree with experiment are those for which ethyl phenyl sulfoxide is used as a model for 2-d1-heptyl phenyl sulfoxide. It is not our intention to question the choice of ethyl as a substitute for heptyl. Instead, it is important to point out that agreement is likely spurious for the following reasons. The calculations do not include tunneling or relevant diastereomeric transition states. This is, to some degree, reflected in the fact that the computed KIE at higher temperatures is larger than the measured value and smaller than the measured value at lower temperatures. If tunneling were responsible for differences in experiment and theory, one might reasonably expect computed and measured values to converge asymptotically at higher temperatures barring substantial contributions from variational effects. In spite of the difficulties associated with obtaining reliable interpretations of the physical processes giving rise to KIEs measured in sulfoxide eliminations, it can at least be surmised that the primary KIEs in sulfoxide eliminations are of far greater magnitude at high temperatures (ca. 100 °C) than those contributing to the intramolecular KIEs in the Swern oxidation at low temperatures.
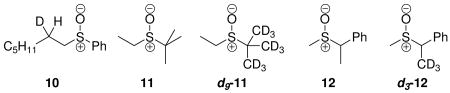
The Wittig modification on the Hofmann elimination has been found to proceed by at least two mechanisms. One is the E2 pathway which directly involves the base in the rate-limiting step. The other mechanism involves deprotonation to form a nitrogen ylide followed by rate-limiting syn-β-elimination. Bach and coworkers have examined this reaction in cyclooctylammonium salts using a number of strong bases to create the ylide.11,12,20 Primary 2H KIEs typically vary between 1.47 and 2.07 for eliminations leading to Z-cyclooctene using KNH2 in liquid ammonia (-33 °C). Extrapolated to -78 °C, these limits become 1.61 to 2.45. The corresponding limits for eliminations leading to E-cyclooctene are 2.53 and 5.89. Reactions that utilize alkyllithiums as the base (at 25 °C) yield primary 2H KIEs of between 1.26 and 1.52. Extrapolated to -78 °C, these values become 1.42 to 1.90. Gas phase calculations of the primary KIE upon a simple model system yield estimates of kH/kD = 1.69 at -33 °C and 1.53 at 25 °C.21 These estimates include a Wigner tunneling correction but are still on the low end of the distribution of measured values. Unfortunately, the temperature dependence of this isotope effect was not investigated. It is worth noting that this system does exhibit vanishingly small primary 2H KIEs. It is likely that these values are even smaller than the primary 2H KIEs that are inherent in the intramolecular KIE measurements reported here. The principle difference between the transition structure models computed for the Wittig modification of the Hofmann elimination and the Cope elimination is the degree of hydrogenic motion involved in the normal mode corresponding to the imaginary frequency. In this regard, the former reaction exhibits a noteworthy similarity to the syn-β-elimination step in the Swern oxidation. This seems to point to a scenario in the former reaction whereby the donor and acceptor atoms are moving together in concert with hydrogen transfer.
Results for the Wittig modification of the Hofmann elimination serve as a bridge to a pericyclic reaction in which multi-dimensional tunneling has been implicated. More than four decades ago Roth and Konig measured the primary deuterium KIE for the [1,5] sigmatropic rearrangement of 1,3-pentadiene (5.1 at 200 °C).58 The surprisingly large value of this KIE at an elevated temperature led theorists to develop numerous models capable of reproducing this measurement. Some forty years later, Doering and Zhao explored the temperature dependence of the [1,5] sigmatropic rearrangement in a compound that possesses an conformationally rigid s-cis conformation of the double bonds involved in the rearrangement.59 Surprisingly, Doering and Zhao found that the temperature dependence of the primary 2H KIE produced a linear Arrhenius plot. In early theoretical work, Liu, et al. found that small curvature tunneling corrections were essential to reproducing the KIE measured by Roth and Konig.60 In recent work, Shelton, et al. have reproduced the temperature dependence observed by Doering and Zhao and have found that multi-dimensional tunneling is, in fact, important to reproducing the temperature dependence of the KIE.61 Curvature in the Arrhenius plot of the intramolecular 2H KIE measured in the Swern oxidation (Figure 7) is obvious and substantial. There are points at which the physical behavior of the [1,5] sigmatropic rearrangement and the syn-β-elimination in the Swern oxidation diverge. Phenomenologically, the [1,5] sigmatropic rearrangement has a substantially larger primary 2H KIE. In terms of the physical origins that give rise to these differences, it seems likely that the reduced mass for the [1,5] sigmatropic is much smaller than that for the syn-β-elimination. Perhaps the best correspondence in the literature at this time is the Wittig modification to the Hofmann elimination. Unfortunately, the temperature dependence of the primary KIE for this reaction has not yet been determined.
Transition State Aromaticity and the β-Elimination
Given the cyclic 6-electron transition states inherent to 5-membered syn-β-elimination transition states, it is worthwhile to consider which aspects lead to aromaticity in the transition state. We have employed the Nuclear-Independent Chemical Shift (NICS) method developed by Schleyer and co-workers to analyze the transition states for the syn-β-elimination step in the Swern oxidation and the intramolecular elimination of sulfoxides (see Scheme 2).62,63 Stable aromatic rings are present in each structure to provide a NICS value against which the NICS value at the center of the 5-membered transition state may be compared (Figure 9). Here, we have utilized the GIAO formalism for computing NICS values for the bystander aromatic ring and the geometric center of the active atoms in the 5-membered transition structures.64 In order to compare the transition structures for the Swern oxidation to other reactions, we attempted to control for as many factors as possible. The sulfoxide thermolysis shown below allows direct computational comparison with a reaction that may plausibly described as pseudopericyclic.23,65 Geometrically, the transition
Figure 9.
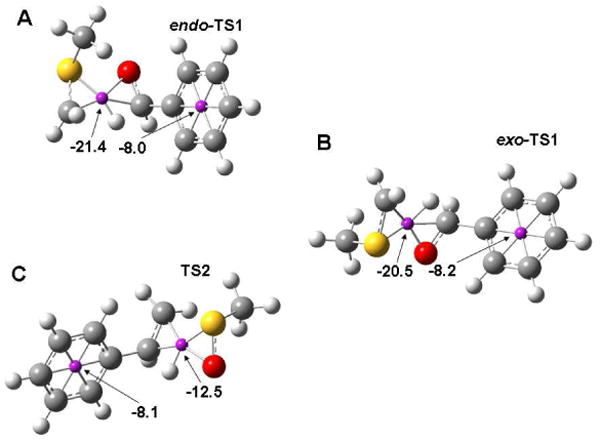
NICS values for the A. endo-TS1, B. exo-TS1, and C. sulfoxide elimination (TS2) transition structures computed using B3LYP/6-31+G(d,p).
structure for the thermolysis (TS2) shown in Figure 9 is similar to exo-TS1. The NICS value for sulfoxide thermolysis is of substantially smaller magnitude than those for the syn-β-elimination step in the Swern oxidation but still might be classified as having substantial aromatic character. Cubbage, et al. attribute the behavior observed in sulfoxide eliminations to the fact that the sulfur-oxygen bond in sulfoxides is best represented as a single bond that is shortened due to coulombic attraction between the positively-charged sulfur atom and the negatively-charged oxygen atom.23 By contrast, the ylide S–C double bond in both 2 and 3 changes by less than 0.001 A upon changing from optimizations in the gas phase to those including a polarizable continuum. This leads to the conclusion that the ylides 2 and 3 are best represented as possessing an S–C double bond versus the alternative single-bonded resonance structure. Natural bond orbital66 (NBO) calculations support our assertion that ylides 2 and 3 are best represented by their double-bonded resonance structure. In contrast, NBO calculations of the model sulfoxide shown above yield only one occupied orbital connecting the sulfur and oxygen atoms. In conjunction with NICS values shown in Figure 9, these observations suggest that the syn-β-elimination step in the Swern oxidation is pericyclic.
Other well-studied pericylic reactions involving hydrogen transfer offer a point of comparison with the NICS values reported in Figure 9. The [1,5] sigmatropic hydrogen shift that occurs upon heating (Z)-1,3-pentadiene has served as a previous comparison to the syn-β-elimination step in the Swern oxidation. This reaction has been well studied computationally, and has served as an exemplum in early discussions of aromatic transition states.67 The NICS value computed at the geometric center of the six-membered transition structure for this reaction optimized at B3LYP/6-311+G(d,p) is -16.6.68 This NICS value is smaller in magnitude than that found for the pericyclic hydrogen transfer explored here but is well in excess of that computed for the sulfoxide elimination shown in Figure 9C. The transition structure for the prototypical ene reaction between propene and ethylene yields a NICS value of -24.4 in a structure optimized using the B3LYP functional in conjunction with the 6-311+G(d,p) basis set.69 The transition structures for these two inconically pericyclic reactions yield NICS values that bracket those computed for both endo-TS1, and exo-TS1 structures, while they well exceed the NICS value computed for the transition structure for sulfoxide elimination. These comparisons further suggest that the syn-β-elimination step in the Swern oxidation is pericyclic, yielding some insight into why this fundamental reaction step is so facile.
Concluding Comments
In the study presented here we have attempted to convey several notions. First, the use of intramolecular KIEs as a mechanistic probe is not limited to systems that exhibit symmetry. Computational analysis of the intramolecular KIE becomes more complicated in asymmetric systems because of the influence that relative barrier heights can have upon the observed value. However, if the transition structures that give rise to the observed KIE are similar in nature, then computed relative barrier heights should be more reliable than the estimation of an isolated barrier height or the comparison of barrier heights for two disparate reactions. Secondly, we have provided compelling evidence for multi-dimensional tunneling in a reaction that does not exhibit a 2H KIE of large magnitude. Finally, we have attempted to understand the facility with which the syn-β-elimination in the Swern oxidation occurs. It appears that this fundamental reaction step is likely to proceed via an aromatic transition state. Furthermore, in comparison to sulfoxide elimination, it appears that the non-zwitterionic resonance forms for the ylides 2 and 3 best represent the reactivity of these species.
Here, we provide reliable experimental measurements of the intramolecular 2H KIE for the Swern oxidation of benzyl alcohol. We have also attempted to understand the fundamental reactivity of ylides 2 and 3 as a function of temperature and solvent. Our measurements provide an entry into further understanding of hydrogen transfer phenomena, multidimensional tunneling, and aromatic transition states involving hydrogen transfer. Study of the syn-β-elimination in the Swern oxidation provides a point of comparison with the few existing mechanistic studies of other syn-β-eliminations and other reactions with aromatic transition states that involve hydrogen transfer. We hope that these measurements will stimulate theoreticians to undertake more detailed studies of the phenomena reported here.
Experimental Section
Intramolecular 2H KIEs
The substrate for this study, d1-benzyl alcohol, was synthesized by reducing benzaldehyde with NaBD4 in ethanol (see Supporting Information). Two series of intramolecular 2H KIE measurements were performed. One series explored the temperature dependence of the intramolecular 2H KIE. The other explored the effect of solvent upon the intramolecular 2H KIE at -23 °C. The choice of temperature was necessitated by the melting temperature of CCl4. Intramolecular 2H KIEs are reported as the ratio of d-benzaldehyde to benzaldehyde as determined by quantitative 1H NMR using calibrated 90° pulse widths and delays of 5 × T1. Longitudinal relaxation times were determined using an inversion recovery experiment. The intramolecular 2H KIE is computed from the integrations of the aromatic peaks and the aldehyde peaks. The ratio of d-benzaldehyde to benzaldehyde was corrected for contamination of the d1-benzyl alcohol substrates with perprotiated substrate using quantitative 1H NMR spectra of the d1-benzyl alcohol substrates. Swern oxidations of d1-benzyl alcohol at -78 °C, -63 °C, -47 °C, and -23 °C were performed using a dry ice/acetone bath and the melting transitions of CHCl3, m-xylene, and CCl4 as thermostating mechanisms, respectively. It should be noted here that no evidence of the Pummerer rearrangement product was observed at any of the temperatures explored. Five replicates of each experiment were performed. The effect of solvent upon the intramolecular 2H KIE was explored by performing the Swern oxidation of d1-benzyl alcohol in chlorobenzene, dichloroethane, CHCl3, CH2Cl2, and CCl4. Five replicates were performed for CH2Cl2 and CCl4, and one measurement was taken for the other three solvents. Detailed experimental procedures are provided in the Supporting Information.
Calculation of KIEs
The syn-β-elimination step that converts the diasteromeric ylides (2 and 3) to a mixture of d-benzaldehyde (4) and benzaldehyde (5) has eight transition states that exist as four enantiomeric pairs. The intramolecular 2H KIE measured in the current study is simply the ratio of 4 to 5 in the product. Here, we compute the anticipated 2H KIE under two limiting assumptions. The first assumption is rapid inversion of the stereogenic sulfur center in 1. Eq. 1 shows how the ratio of 4 to 5 is determined in terms of operative rate constants under this assumption. Eq. 5 illustrates how this expression can be decomposed into an expression in terms of single rate constant ratios. The second limiting regime is that under which the barrier for inversion at the stereogenic sulfur center prohibits inversion on the timescale of the syn-β-elimination step. Under this assumption, the ratio of 4 to 5 is given by eq. 2. Eq. 6 is an expression of the KIE in terms of rate constant ratios which allows for the calculation of the KIE from computed transition structures. Derivations of eqs. 1-6 are provided in the Supporting Information.
| (5) |
| (6) |
Because the rate constant ratios, k1/k2 and k3/k4, reflect isotopomeric ratios, they can be computed by employing the Redlich-Teller product rule (eq. 7).70 Because k2 and k3 (and k1 and k4) correspond to structurally and energetically distinct transition states, the ratios, k2/k3 and k4/k1 must be computed using the ratios of the full expression for the molecular partition function pertaining to the relevant transition states (eq. 8). Because the reactants involved in the rate constant ratio expressions are the same or diastereomeric by virtue of isotopic substitution in all cases, only partition functions for the transition states need to be considered. Vibrational partition function ratios of reactants are found to be very near unity for isotopic diastereomers of the ylides. All structures used to compute rate constant ratios were optimized using the B3LYP34 functional in conjunction with the 6-31+G(d,p)35 basis set. Frequency calculations were performed at the same level of theory and used the same basis set. For all rate constant ratio calculations, a 1-dimensional Bell tunneling correction was applied (eq. 9).
| (7) |
| (8) |
| (9) |
Supplementary Material
Figure 1.
Use of intramolecular KIEs in the A) Baeyer-Villiger reaction (Ref. 26) and the B) singlet oxygen ene reaction (2H KIEs: see Ref. 24; 13C KIEs: see Ref. 25).
Acknowledgments
MPM thanks the NIGMS (GM87706-01) for financial support. This research was also supported in part by the National Science Foundation through TeraGrid resources provided by PSC. MPM thanks Charles Perrin (UCSD) and David F. Kelley (UCM) for useful discussions and Michael Colvin (UCM) for the use of his Linux cluster.
Footnotes
Supporting Information Available: Details of the experimental and computational methods, derivations of eqs. 1-6, and Cartesian coordinates for all computed structures. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Mancuso AJ, Swern D. Synthesis. 1981:165–185. [Google Scholar]
- 2.Tidwell TT. Organic Reactions. 1990;39:297–572. [Google Scholar]
- 3.Tidwell TT. Synthesis. 1990:857–870. [Google Scholar]
- 4.Albright JD, Goldman L. J Am Chem Soc. 1965;87:4214–4216. [Google Scholar]
- 5.Omura K, Swern D. Tetrahedron. 1978;34:1651–1660. [Google Scholar]
- 6.Pfitzner KE, Moffat JG. J Am Chem Soc. 1965;87:5661–5670. [Google Scholar]
- 7.Fenselau AH, Moffat JG. J Am Chem Soc. 1966;88:1762–1765. [Google Scholar]
- 8.Mancuso AJ, Huang SL, Swern D. J Org Chem. 1978;43:2480–2482. [Google Scholar]
- 9.Marx M, Tidwell TT. J Org Chem. 1984;49:788–793. [Google Scholar]
- 10.Isaacs NS, Laila AH. J Phys Org Chem. 1991;4:639–642. [Google Scholar]
- 11.Bach RD, Andrzejewski D. J Am Chem Soc. 1971;93:7118–7120. [Google Scholar]
- 12.Bach RD, Bair KW, Andrzejewski D. J Am Chem Soc. 1972;94:8608–8610. [Google Scholar]
- 13.Janssen JWAM, Kwart H. J Org Chem. 1977;42:1530–1533. [Google Scholar]
- 14.Kwart H, George TJ, Louw R, Ultee W. J Am Chem Soc. 1978;100:3927–3928. [Google Scholar]
- 15.Kwart H, Brechbiel M. J Am Chem Soc. 1981;103:4650–4652. [Google Scholar]
- 16.Kwart H, George TJ, Horgan AG, Lin YT. J Org Chem. 1981;46:5143–5147. [Google Scholar]
- 17.Kwart H, Brechbiel M. J Am Chem Soc. 1981;103:4650–4652. [Google Scholar]
- 18.Yoshimura T, Tsukurimichi E, Iizuka Y, Mizuno H, Isaji H, Shimasaki C. Bull Chem Soc Jpn. 1989;62:1891–1899. [Google Scholar]
- 19.Bach RD, Braden ML. J Org Chem. 1991;56:7194–7195. [Google Scholar]
- 20.Bach RD, Knight JW, Braden ML. J Am Chem Soc. 1991;113:4712–4714. [Google Scholar]
- 21.Bach RD, Gonzalez C, Andres JL, Schlegal HB. J Org Chem. 1995;60:4653–4656. [Google Scholar]
- 22.Komaromi I, Tronchet JMJ. J Phys Chem A. 1997;101:3554–3560. [Google Scholar]
- 23.Cubbage JW, Guo Y, McCulla RD, Jenks WS. J Org Chem. 2001;66:8722–8736. doi: 10.1021/jo0160625. [DOI] [PubMed] [Google Scholar]
- 24.Grdina MB, Orfanopoulos M, Stephenson LM. J Am Chem Soc. 1979;101:3111–3112. [Google Scholar]
- 25.Singleton DA, Hang C, Szymanski MJ, Meyer MP, Leach AG, Kuwata KT, Chen JS, Greer A, Foote CS, Houk KN. J Am Chem Soc. 2003;125:1319–1328. doi: 10.1021/ja027225p. [DOI] [PubMed] [Google Scholar]
- 26.Singleton DA, Szymanski MJ. J Am Chem Soc. 1999;121:9455–9456. [Google Scholar]
- 27.Harding LB, Goddard WA., III J Am Chem Soc. 1977;99:4520–4523. [Google Scholar]
- 28.Bell RP. The Tunnel Effect in Chemistry. New York: Chapman and Hall; 1980. [Google Scholar]
- 29.Irikura KK, Johnson RD, III, Kacker RN. J Phys Chem A. 2005;109:8430–8437. doi: 10.1021/jp052793n. [DOI] [PubMed] [Google Scholar]
- 30.Seeman JL. Chem Rev. 1983;83:83–134. [Google Scholar]
- 31.Darwish D, Tomlinson RL. J Am Chem Soc. 1968;90:5938–5939. [Google Scholar]
- 32.Roush DM, Heathcock CH. J Am Chem Soc. 1977;99:2337–2338. [Google Scholar]
- 33.Scartazzini R, Mislow K. Tetrahedron Lett. 1967:2719–2722. [Google Scholar]
- 34.a) Becke AD. J Chem Phys. 1993;98:5648–5652. [Google Scholar]; b) Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. J Phys Chem. 1994;98:11623–11627. [Google Scholar]
- 35.Francl MM, Pietro WJ, Hehre WJ, Binkley JS, DeFrees DJ, Pople JA, Gordon MS. J Chem Phys. 1982;77:3654–3665. [Google Scholar]
- 36.Salomon O, Reiher M, Hess BA. J Chem Phys. 2002;117:4729–4737. [Google Scholar]
- 37.A few examples: Beno BR, Houk KN, Singleton DA. J Am Chem Soc. 1996;118:9984–9985.Meyer MP, DelMonte AJ, Singleton DA. J Am Chem Soc. 1999;121:10865–10874.. c) Christian, C. F.; Takeya, T.; Szymanski, M. J.; Singleton, D. A. Saettel NJ, Wiest O, Singleton DA, Meyer MP. J Am Chem Soc. 2002;124:11552–11559. doi: 10.1021/ja026924z.Stafford SE, Meyer MP. Tetrahedron Lett. 2009;50:3027–3030.Saavedra J, Stafford SE, Meyer MP. Tetrahedron Lett. 2009;50:1324–1327.Zhu H, Clemente FR, Houk KN, Meyer MP. J Am Chem Soc. 2009;131:1632–1633. doi: 10.1021/ja806672y.
- 38.Grimme S. J Comp Chem. 2006;27:1787–99. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- 39.Tomasi J, Mennucci B, Cammi R. Chem Rev. 2005;105:2999–3094. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 40.Reed AE, Weinstock RB, Weinhold F. J Chem Phys. 1985;83:735–746. [Google Scholar]
- 41.Parr CA, Polanyi JC, Wong WH. J Chem Phys. 1973;58:5–20. [Google Scholar]
- 42.Hartke B, Manz J. J Am Chem Soc. 1988;110:3063–3068. [Google Scholar]
- 43.Marinkovic M, Gruber-Stadtler M, Nicovich JM, Soller R, Mülhäuser M, Wine PH, Bache-Andreassen L, Nielsen CJ. J Phys Chem A. 2008;112:12416–12429. doi: 10.1021/jp807609d. [DOI] [PubMed] [Google Scholar]
- 44.Gruber-Stadtler M, Mülhäuser M, Sellevaåg SR, Nielsen CJ. J Phys Chem A. 2008;112:9–22. doi: 10.1021/jp0753833. [DOI] [PubMed] [Google Scholar]
- 45.Moore P, Tokmakoff A, Keyes T, Fayer MD. J Chem Phys. 1995;103:3325–3334. [Google Scholar]
- 46.Navarro R, Hernanz A, Bratu I. J Chem Soc, Faraday Trans. 1994;90:2325–2330. [Google Scholar]
- 47.Reviews: Kohen A, Klinman JP. Chem Biol. 1999;6:R191–R198. doi: 10.1016/s1074-5521(99)80058-1.Kohen A. Prog React Kinetics Mech. 2003;28:119–156.Pu J, Gao J, Truhlar DG. Chem Rev. 2006;106:3140–3169. doi: 10.1021/cr050308e.Caldin EF. Chem Rev. 1969;69:135–156.Nagel ZD, Klinman JP. Chem Rev. 2006;106:3095–3118. doi: 10.1021/cr050301x.Gunay A, Theopold KH. Chem Rev. 2010;110:1060–1081. doi: 10.1021/cr900269x.German ED, Sheintuch M. J Phys Chem. 2010;114:3089–3097.Hammes-Schiffer S. Acc Chem Res. 2006;39:93–100. doi: 10.1021/ar040199a.Kohen A, Klinman J. P Acc Chem Res. 1998;31:397–404..
- 48.Recent examples: Wang Z, Kohen A. J Am Chem Soc. 2010 doi: 10.1021/ja103010b., ASAP. Edwards SJ, Soudackov AV, Hammes-Schiffer S. J Phys Chem B. 2010;114:6653–6660. doi: 10.1021/jp100133p.Cho J, Woo J, Nam W. J Am Chem Soc. 2010;132:5958–5959. doi: 10.1021/ja1015926.Panay AJ, Fitzpatrick PF. J Am Chem Soc. 2010;132:5584–5585. doi: 10.1021/ja101563t.McCusker KP, Klinman JP. J Am Chem Soc. 2010;132:5114–5120. doi: 10.1021/ja909416z.Yoon M, Song H, Håkansson K, Marsh ENG. Biochemistry. 2010;49:3168–3173. doi: 10.1021/bi1001695.Finnegan S, Agniswamy J, Weber IT, Gadda G. Biochemistry. 2010;49:2952–2961. doi: 10.1021/bi902048c.Fukuzumi S, Kobayashi T, Suenobu T. J Am Chem Soc. 2010;132:1496–1497. doi: 10.1021/ja910349w.
- 49.Limbach HH, Lopez JM, Kohen A. Phil Trans R Soc B. 2006;361:1399–1415. doi: 10.1098/rstb.2006.1872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kwart H. Acc Chem Res. 1982;15:401–408. [Google Scholar]
- 51.Rickert K, Klinman JP. Biochemistry. 1999;38:12218–12228. doi: 10.1021/bi990834y. [DOI] [PubMed] [Google Scholar]
- 52.Ostović D, Roberts RMG, Kreevoy MM. J Am Chem Soc. 1983;105:7629–7631. [Google Scholar]
- 53.Schneider ME, Stern MJ. J Am Chem Soc. 1972;94:1517–1522. [Google Scholar]
- 54.Kim Y, Kreevoy MM. J Am Chem Soc. 1992;114:7116–7123. [Google Scholar]
- 55.Truhlar DG. J Phys Chem A. 2003;107:4006–4007. [Google Scholar]
- 56.Kwart H, George TJ, Horgan AG, Lin YT. J Org Chem. 1981;46:5143–5147. [Google Scholar]
- 57.Wigner E. Trans Faraday Soc. 1938;34:29–41. [Google Scholar]
- 58.Roth WR, Konig J. Liebigs Ann Chem. 1966;699:24–32. doi: 10.1002/jlac.19666990103. [DOI] [PubMed] [Google Scholar]
- 59.Doering WvE, Zhao X. J Am Chem Soc. 2006;128:9080–9085. doi: 10.1021/ja057377v. [DOI] [PubMed] [Google Scholar]
- 60.Liu YP, Lynch GC, Truong TN, Lu DH, Truhlar DG, Garrett BC. J Am Chem Soc. 1993;115:2408–2415. [Google Scholar]
- 61.Shelton GR, Hrovat DA, Borden WT. J Am Chem Soc. 2007;129:164–168. doi: 10.1021/ja0664279. [DOI] [PubMed] [Google Scholar]
- 62.von Ragué Schleyer P, Maerker C, Dransfeld A, Jiao H, van Eikema Hommes NJR. J Am Chem Soc. 1996;118:6317–6318. doi: 10.1021/ja960582d. [DOI] [PubMed] [Google Scholar]
- 63.Chen Z, Wannere CS, Corminboeuf C, Puchta R, von Ragué Schleyer P. Chem Rev. 2005;105:3842–3888. doi: 10.1021/cr030088+. [DOI] [PubMed] [Google Scholar]
- 64.Wolinski K, Hilton JF, Pulay P. J Am Chem Soc. 1990;112:8251–8260. [Google Scholar]
- 65.Ross JA, Seiders RP, Lemal DM. J Am Chem Soc. 1976;98:4325–4327. [Google Scholar]
- 66.Reed AE, Curtiss LA, Weinhold F. Chem Rev. 1988;88:899–926. [Google Scholar]
- 67.Woodward RB, Hoffmann R. Angew Chem Int Ed. 1969;8:781–932. [Google Scholar]
- 68.Jiao H, von Rague Schleyer P. J Phys Org Chem. 1998;11:655–662. [Google Scholar]
- 69.Manojkumar TK. J Mol Struct (THEOCHEM) 2009;909:96–101. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.