Why Urea Eliminates Ammonia Rather Than Hydrolyzes in Aqueous Solution

Abstract

A joint QM/MM and ab initio study on the decomposition of urea in the gas phase and in aqueous solution is reported. Numerous possible mechanisms of intramolecular decomposition and hydrolysis have been explored; intramolecular NH₃-elimination assisted by a water molecule is found to have the lowest activation energy. The solvent effects were elucidated using the TIP4P explicit water model with free energy perturbation (FEP) calculations in conjunction with QM/MM Monte Carlo simulations. The explicit representation of the solvent was found to be essential for detailed resolution of the mechanism, identification of the rate-determining step, and evaluation of the barrier. The assisting water molecule acts as a hydrogen shuttle for the first step of the elimination reaction. The forming zwitterionic intermediate, H₃NCONH, participates in 8–9 hydrogen bonds with water molecules. Its decomposition is found to be the rate-limiting step, and the overall free energy of activation for the decomposition of urea in water is computed to be ca. 37 kcal/mol; the barrier for hydrolysis by an addition/elimination mechanism is found to be ca. 40 kcal/mol. The differences in the electronic structure of the transition states of the NH₃-elimination and hydrolysis were examined via natural bond order analysis. Destruction of urea’s resonance stabilization during hydrolysis via an addition/elimination mechanism, and its preservation in the rearrangement to the H₃NCONH intermediate were identified as important factors in determining the preferred reaction route.

Introduction

The decomposition of urea is an important process in Nature. Many pathogens are associated with the activity of ureolytic bacteria, and the efficiency of soil nitrogen fertilization with urea is severely decreased by urease activity. The reaction by which urea decomposes has been studied extensively over the past century.^1–31 In aqueous solution, urea decomposition yields cyanate and ammonium ions, (NH₂)₂CO → CNO⁻ + NH₄⁺. An elimination mechanism appears to be operative. Cyanate ion further readily undergoes conversion to CO₂ and ammonia.^1–4

In contrast, when catalyzed by ureases, urea is generally believed to undergo hydrolysis rather than ammonia elimination.^4–18 The products of hydrolytic decomposition have been reported to be either HCO₃⁻ and NH₄⁺ or ammonium carbamate depending on the buffer system.¹⁹ These products are most readily rationalized to arise from an addition-elimination sequence. It has also been established that ureases are among the most proficient enzymes.^20–22

Activation energies for urea decomposition in water at different pH have been obtained experimentally.^1,4,23,24 For neutral pH, the reported activation energy varies from 28.4 to 32.4 kcal/mol.^1,24,25 The carbon isotope effect for this reaction was also investigated.²⁶ A kinetic study by Lynn concluded that, in alkaline media, the activation energy was ca. 22 kcal/mol,⁴ while Laider and Hoare compared the ΔG^‡ for both the acid- and enzyme-catalyzed hydrolysis of urea.^27,28 There also have been numerous theoretical investigations of the decomposition of urea and related systems.^{15–17,29–31} A B3LYP study on cluster models of the active site of ureases was carried out recently.¹⁵ Models of various resting states of the active site were modeled and investigated, and mono- and bidentate modes of urea coordination were considered. Estiu and Merz¹⁷ tested different mechanisms of urea decomposition in the gas phase and in solution modeled by the isodensity continuum polarizable model (ICPM). The preferred pathway had an activation barrier of 23 kcal/mol and featured H₂O-mediated H-transfer between the two amino groups, which was followed by facile NH₃-elimination.¹⁷ In a comparative B3LYP/6-31G* study of the hydrolytic decomposition of esters, amides, and urea, the authors proposed an active role for a water molecule in proton-shuttling in the gas-phase reaction.²⁹ However, in aqueous solution modeled by the polarizable continuum model (PCM), the activation energy for the process without the participation of a water molecule was found to be lower.²⁹ Assisting water molecules in the neutral hydrolysis of ethyl acetate were also considered to be important in the B3LYP/6-31G* study by Yamabe et al.³⁰ In addition, Lopez et al. studied the alkaline hydrolysis of amides, and identified the cleavage of the C-N bond as the rate-limiting step.³¹

This work addresses decomposition of urea in neutral aqueous solution, which is most relevant as the reference point for biological processes. A joint ab initio and QM/MM study on alternative reaction pathways was carried out, and preferred routes for the hydrolytic and ammonia-eliminative processes were identified. The explicit role of solvent in the reactions was elucidated through QM/MM Monte Carlo (MC) simulations including hundreds of water molecules and extensive sampling for the solutes and solvent. In addition, an extensive chemical bonding analysis was performed for the key-species on the decomposition paths. This permitted analysis of the changes in resonance stabilization for the competing hydrolysis and intramolecular elimination pathways and clearer understanding of the preference in solution for urea to eliminate ammonia rather than undergo hydrolysis.

Computational Methods

Initial potential energy surface (PES) scanning was done using the PDDG/PM3 (PDDG) semiempirical molecular orbital (SMO) method,³² which has been extensively validated for gas-phase structures and energetics, and it has yielded excellent results in QM/MM/MC studies for numerous S_N2, addition, and elimination reactions in solution.33 SMO methods such as AM1^34a and PM3^34b have also performed well in prior studies of proton-transfer reactions.³⁵ Additional scanning of the PESs was performed with inclusion of solvation represented by the generalized Born/surface area (GB/SA) model and the all-atom OPLS force field.³⁶ Specifically, the PDDG calculations produced CM3 atomic charges,³⁷ which were scaled by a factor of 1.07 and used for assessing free energies of solvation via the GB/SA method.^36c The preliminary activation energies and the initial guess for the geometries of transition structures and intermediates were thus obtained.

Free-energy perturbation (FEP) calculations were carried out in the context of Metropolis Monte Carlo (MC) simulations in the NPT ensemble at 25 °C and 1 atm. In these QM/MM calculations, the energy of the solute was computed using PDDG for every attempted move of the solute, i.e., every 100 configurations. The solvent was represented with the TIP4P water model.³⁸ For the solute in explicit water, CM3 charges scaled by a factor of 1.14, which minimizes the error for free energies of hydration,³⁹ were used to calculate the electrostatic portion of the solute-solvent interaction energy. The intermolecular interactions were truncated with cutoffs at 10 Å based on distances between non-hydrogen atoms. The systems consisted of the reacting molecules, e.g., urea and zero to two water molecules treated quantum mechanically, plus 395 TIP4P water molecules in a rectangular periodic cell. Each FEP window entailed 2.5 × 10⁶ configurations of equilibration followed by 5.0 × 10⁶ configurations of averaging. When a distance was used as a reaction coordinate, the increment between windows was 0.04 Å for general scanning and 0.02 Å for refinement near stationary points. For angles as reaction coordinates, the corresponding increments were 9.0° and 3.6°.

The identified transition structures, intermediates, initial complexes and products of the reactions having the lowest activation energies were further considered with higher level quantum calculations. A hybrid DFT method, namely B3LYP^40–42 with a polarized split-valence basis set (6-311++G**),^43,44 was used to obtain refined geometries, energies, and vibrational frequencies. Free energies of hydration were again estimated for the DFT and MP2/6-311++G**/ICPM¹⁷ structures with GB/SA calculations using CM1A charges scaled by 1.07.^36c The complete active space self-consistent field (CASSCF(8,8)/6-311++G**)^45–50 method was employed to explore the nature of the wavefunction for some species, and to check the appropriateness of the single-determinant methods. For the analysis of electronic structure, the Natural Bond Order method^51–55 at the B3LYP/6-311++G** level was employed. BOSS 4.6⁵⁶ was used for the MM, MC, FEP and QM/MM calculations, MOPAC 6.0⁵⁷ was used for some additional SMO calculations, and Gaussian 03⁵⁸ was used for the DFT and ab initio calculations.

Mechanisms of the decomposition of urea

Despite urea’s status as a simple molecule and its decomposition as an extremely important process in biology, controversy still exists regarding the mechanism of its decomposition. Intramolecular rearrangement leading to the release of NH₃ or hydrolysis is possible, and these reactions may occur with or without the assistance of additional water molecules. Furthermore, there are several feasible routes for the NH₃-elimination. Though the role of bulk water for such reactions can be envisioned to be significant, computational studies with explicit inclusion of large numbers of water molecules in QM/MM simulations have not been reported previously for these reactions. Therefore, the present broad study was undertaken for the competing reaction pathways in the gas phase, with GB/SA hydration, and with explicit representation of hundreds of water molecules in the MC simulations.

Intramolecular Elimination

The simplest unimolecular pathway involves hydrogen-transfer from one NH₂-group to the other, followed by cleavage of the C-N bond and NH₃ elimination. The process yields isocyanic acid, which has been experimentally observed as a product of urea decomposition.^1–4

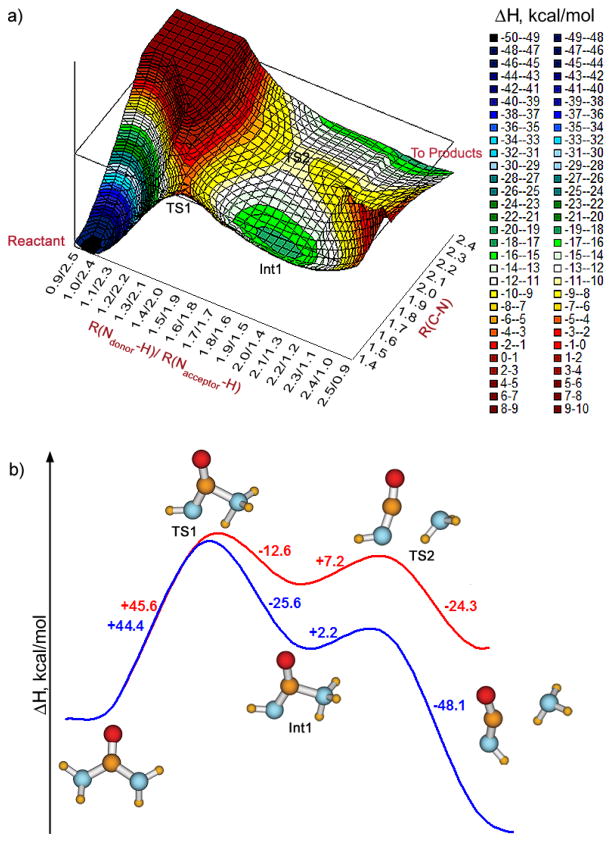
A 2-D projection of the PDDG PES was obtained using two reaction coordinates, the length of the breaking C-N bond and a coordinate representing the hydrogen transfer (Figure 1a). The choice for the latter required some investigation. If just the length of the breaking N-H bond was used, a discontinuous drop in energy occurs corresponding to sudden formation of the new N-H bond. This suggested that the proper reaction coordinate should include the simultaneous change of both N-H distances. An additional surface was built with the two N-H distances being reaction coordinates, and R(C-N) fixed at 1.5 Å, as expected from the TS found in preliminary investigations. The minimum energy path had the sum of the R(N-H)s approximately constant at 2.4 Å. Thus, the second reaction coordinate was chosen as shown in Figure 1a: an increase of R(N_donor-H) was accompanied by a decrease of R(N_acceptor-H), with the sum of the two distances set at 2.4 Å. The scanning revealed that the PES contained the initial minimum (urea), two transition states (TS1 and TS2) interceded by one intermediate (Int1), and it showed the final descent toward the well of the products. The PES-projection built in the same manner for the reaction in solution (PDDG in conjunction with GB/SA) has the same features (TS1, Int1, TS2). Higher precision (smaller grid) runs were subsequently carried out around the stationary points on the PESs, and their gas-phase structures were further refined with standard geometry optimizations. Having determined the PDDG stationary points and energies, schematic reaction profiles were constructed (Figure 1b). This exemplifies the typical computational approach. For some reactions, several projections of the PES for different reaction steps had to be built, and then the results were combined in a single plot for the reaction profile. Details of constructing the PESs for the other cases are omitted, and only the resulting reaction profiles are shown.

Figure 1.

(a) Projection of the gas phase PDDG PES for the unimolecular elimination of ammonia on the two reaction-coordinates, the difference of the two N-H distances, and R(C-N). (b) PDDG reaction profile for urea decomposition via elimination of ammonia in the gas phase (red curve) and including GB/SA hydration (blue curve).

One may see that, in the gas phase, the proton transfer is the first and the rate-limiting step. In transition structure TS1, the transferring hydrogen is closer to the acceptor N, and the cleaving C-N bond lengthens by only ca. 0.1 Å. The barrier for the process is 45.6 kcal/mol from the PDDG calculations. The zwitterion Int1 then arises in which the hydrogen has completed the transfer, but the C-N bond has not yet cleaved. This intermediate undergoes a subsequent low-barrier (7.2 kcal/mol) decomposition releasing NH₃ and HNCO. In solution, proton transfer then yields NH₄⁺ and NCO⁻. This final step is not shown in the reaction profile; however, it was simulated using one assisting QM water molecule in the rectangular periodic box of TIP4P water. In this case, the process was found to involve sequential proton transfer from HNCO to water to ammonia with a barrier of only 3.5 kcal/mol.

Upon inclusion of GB/SA hydration, the reaction profile remains qualitatively the same (blue curve, Figure 1b). The transition state TS1 is very similar in structure to the one in the gas phase with R(C-N) = 1.55 Å. However, the structure of the zwitterion Int1 is sensitive to solvation. In the gas phase, the C-NH₃ bond is elongated to 1.87 Å from the PDDG calculations, while it is 1.50 Å including GB/SA hydration. The corresponding dipole moments are 4.2 and 8.0 D, so the zwitterionic character is much enhanced in solution. The PDDG barrier height of 44.4 kcal/mol agrees closely with the value of 46 kcal/mol obtained by Elstiu and Merz using MP2/6-311++G**/ICPM.¹⁷ The second barrier, corresponding to the decomposition of Int1, is computed to be even smaller than in the gas phase (2.2 kcal/mol), and the overall reaction is much more exothermic. The consensus, computed barrier height of 44–46 kcal/mol for the rate-limiting step of the unimolecular decomposition in continuum models for water significantly exceeds the experimental range of 28.4 to 32.4 kcal/mol.^1,24,25 Alternative routes with lower barriers are found below, so it is likely that the decomposition of urea in water does not follow the unimolecular mechanism.

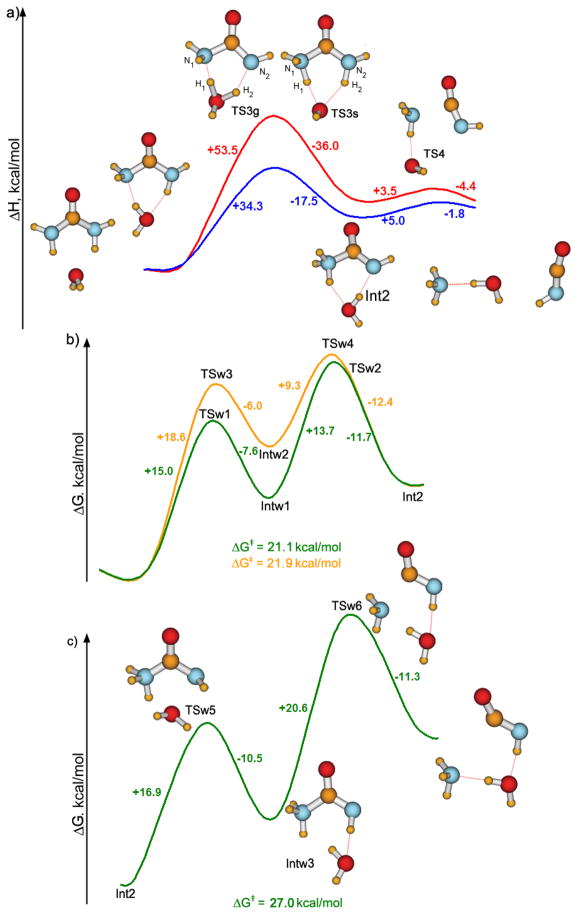
Figure 2 contains the PDDG results for an alternative mechanism in which a water molecule serves as a relay by deprotonating one NH₂ group and protonating the other. The projection of the PES on the coordinates corresponding to the two H-transfers was plotted; the resulting reaction profile is shown in Figure 2a. Both C-N distances were optimized at each point and neither C-N bond broke during the H-transfers. The gas-phase reaction involves an initial rearrangement of the urea-H₂O complex from the most stable conformation to the one with the water molecule oriented for the H-transfers (see Figure 2a). For the double H-transfer in the gas phase, two alternative pathways were found with PDDG. The more favorable one is shown in Figure 2a. The transition structure TS3g has the proton-donor NH₂ almost fully deprotonated (R(N₂-H₂) =1.86 Å, R(O-H₂) =1.20 Å), while the other NH₂ group is intact, though rotated, and R(O-H₁) =1.12 Å and (N₁-H₁) =1.57 Å. TS3g is structurally close to a complex of H₃O⁺ and the urea anion, H₂NCONH⁻. The barrier of this reaction was computed to be 53.3 kcal/mol with PDDG. The second pathway (not shown) involved a more concerted double H-transfer and has a slightly higher activation energy of 54.3 kcal/mol. The reaction path continues to the intermediate Int2 in Figure 2a, in which the H-transfer is complete and the water molecule is restored. The C-NH₃ distance in this zwitterion is slightly elongated to 1.51 Å. The next step of the reaction, NH₃ elimination, is predicted to have a barrier of only 3.5 kcal/mol.

Figure 2.

Reaction pathway for urea decomposition via elimination of ammonia with one H₂O assisting the H-shuttling: (a) PDDG results for the gas-phase reaction (red curve) and with GB/SA hydration (blue curve); QM/MM/FEP reaction profiles (b) for the first step of the reaction (TS structures are shown in Figure 3), and (c) for the final NH₃ departure.

When the GB/SA hydration is added, the pathway remains similar; only the order of the two H-transfers changed leading to TS3s. TS3s is geometrically close to a complex of OH⁻ and N-protonated urea (R(N₁-H) =1.16 Å, R(O-H₁) =1.58 Å, R(N₂-H₂) =1.03 Å, R(O-H₂) =1.98 Å). The activation energy for this rate-determining step in GB/SA solution, 34.3 kcal/mol, is much lower than in the gas phase.

Then, the effect of explicit hydration was assessed via QM/MM/FEP calculations in TIP4P water; urea and the one bridging water molecule were treated quantum mechanically. For the double H-move, the two reaction coordinates were perturbed in ranges defined by the gas-phase calculations. Figure 2b contains the FEP-generated profile for the first step of the reaction, reactants → Int2. The reaction path in explicit water is more complex. Basically, the bulk hydration stabilizes the ion-pair-like transition states TS3g and TS3s from Figure 2a such that they become intermediates, and the second proton transfer to yield the zwitterion Int2 becomes rate-determining. There are two routes with different orders of the two H-moves: (1) reactant → TSw1 → Intw1 (complex of OH⁻ and N-protonated urea) → TSw2 → Int2, and (2) reactant → TSw3 → Intw2 (complex of H₃O+ and deprotonated urea) → TSw4 → Int2 (Figure 2b). The overall activation barriers are also reduced from the GB/SA result, and they are similar for the two routes, 21.9 kcal/mol and 21.1 kcal/mol (Figure 2b). From the QM/MM simulations, the zwitterion Int2 is 9.4 kcal/mol higher in free energy than the reactant, urea, in water.

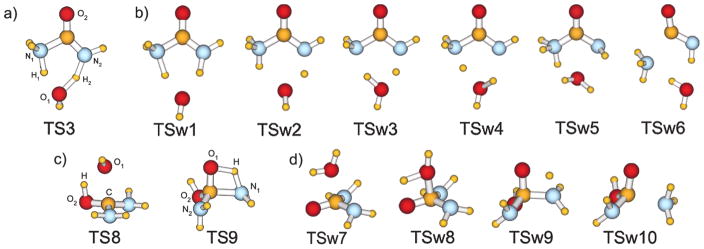
Ab initio calculations for the reaction yielding the zwitterion Int2 were also performed (Table 1). To evaluate the nature of the wavefunctions for the found stationary points on the PES, single-point CASSCF(8,8)/6-311++G** calculations were performed using the B3LYP/6-311++G** geometries optimized structures. The Hartree-Fock configuration was found to be highly-dominant in the CAS-expansions, justifying the application of the single-determinant methods. Computed geometrical parameters for TS3, TSw1, TSw2, TSw3, and TSw4 are summarized in Table 1, and their structures are illustrated in Figure 3. It is again noteworthy that the gas phase calculations and continuum solvent models only predict the existence of one transition state, TS3, between the reactants and Int2, while the QM/MM simulations find two (Figure 2b). In the B3LYP/6-311++G** structure of TS3, H₁ is closer to N₁ than to the oxygen atom of H₂O, and H₂ is approximately half-way between N₂ and O (Figure 3a). The only imaginary frequency corresponds to the double proton-shuttling between N₁ and O, and N₂ and O in an antiparallel fashion. From the absolute values of the total energy, and the entropy of the reactants and the transition state obtained in the frequency calculations, ΔE^‡₀, ΔH^‡, ΔG^‡, and ΔG^‡_solution = ΔG^‡ + ΔΔG_hydation were computed at 25 °C for the first step of the reaction (Table 2). The free-energy of activation in solution is similar from the present QM/MM and the prior MP2/ICPM calculations,¹⁷ though the transition structures differ in the details of the H-transfer to the assisting water molecule (TSw2 and TS3).

TABLE 1.

Calculated Geometrical Parameters of the Transition States for the First Step of the Intramolecular Decomposition Route (Figure 2)

Geometrical parameter, Å	PDDG	PDDG GB/SA	B3LYP/6-311++G**	MP2/6-311++G** ICPMa	QM/MM MC/FEP
	TS3				TSw1	TSw2	TSw3	TSw4
R(N1-H1)	1.48	1.16	1.15	1.01	1.26	1.02	1.58	1.28
R(O-H1)	1.12	1.44	1.40	1.94	1.34	1.58	1.02	1.32
R(N2-H2)	1.50	1.04	1.27	1.99	0.98	1.30	1.38	1.62
R(O-H2)	1.10	1.56	1.23	0.96	1.62	1.30	1.22	0.98
R(C-N1)	1.51	1.50	1.57		1.50	1.51	1.47	1.51
R(C-N2)	1.36	1.40	1.31		1.48	1.42	1.42	1.41

^aResults from Ref. 17.

Figure 3.

Structures of the TSs on the decomposition paths of urea: NH₃-elimination (a) in the gas phase (B3LYP/6-311++G**), and (b) in solution (snapshots from the MC/FEP simulations); addition-elimination hydrolysis (c) in the gas phase (B3LYP/6-311++G**), and (d) in solution (snapshots from the MC/FEP simulations).

TABLE 2.

Energetics for the First Step of the Decomposition of Urea Assisted by One Water Molecule Leading to the H₃NCONH Zwitterion (Int2)

	PDDG	PDDG GB/SA	QM/MM MC/FEP	B3LYP/6-311++G**	MP2/6-311++G** ICPMd
ΔE‡ (ZPE-corrected), kcal/mol	53.3b			27.3	24.6
ΔE‡0= ΔE‡ + ΔEthermala				23.2
ΔH‡ = ΔE‡ + ΔnRT, kcal/mol				23.2
ΔG‡ = ΔH‡ − TΔ S, kcal/mol				26.6	24.9
ΔG‡solution = ΔG‡ + ΔΔGsolvation		34.2b,c	21.1	26.4c	23.1

^aE_thermal = E_vibtational + E_rotational + E_{translational}.

^bVibrational frequencies were not calculated at the PDDG level.

^cThe values include the ΔG of hydration obtained from the GB/SA model.

^dResults from Ref. 17.

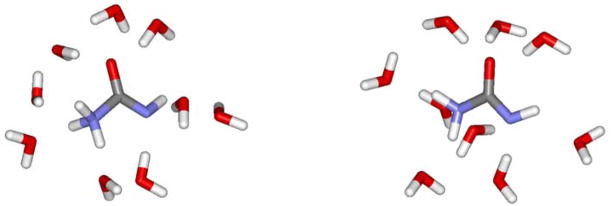
The energetics for the second step, loss of NH₃ from Int2, change dramatically, when the solvent is treated explicitly. Direct elimination by breaking the C-N bond has a barrier greater than 40 kcal/mol from the QM/MM/FEP calculations, so it appears that the solvent stabilization of the zwitterion is not represented well by the GB/SA calculations. As shown in Figure 4, the zwitterion participates in 8 or 9 hydrogen bonds with water molecules; the four NH bonds serve as hydrogen bond donors, and the oxygen and formally anionic nitrogen accept three and two hydrogen bonds, respectively. Disruption of this network on progressing towards the neutral products, ammonia plus isocyanic acid, is certainly expected to be much more costly than suggested by the continuum model. Thus, multiple alternative pathways were investigated.

Figure 4.

Two views of a snapshot from a QM/MM simulation of the H₃NCONH zwitterion in TIP4P water just showing the nine hydrogen-bonded water molecules.

The route that was found with the lowest activation barrier is illustrated in Figure 2c. This pathway begins with conversion of the cis (CONH) form of Int2 to the trans alternative, which is arranged for anti-periplanar elimination of NH₃. The barrier of this step is 16.9 kcal/mol, and the trans conformer is 6.4 kcal/mol less stable than the cis. The C-N bond can then cleave with a barrier of 20.6 kcal/mol to yield isocyanic acid and ammonia, and subsequent proton transfer to provide cyanate and ammonium ions is assumed. Thus, the elimination follows the pathway urea → cis-H₃NCONH → trans-H₃NCONH → OCNH + NH₃. The barrier from the cis-zwitterion (Int2) to the products by this route is 27.0 kcal/mol, and the overall barrier starting from urea is ca. 37 kcal/mol, which is somewhat higher than the experimental range of 28.4 to 32.4 kcal/mol.^1,24,25 Notably, the elimination of ammonia from the trans-zwitterion turns out to be the rate-determining step. In fact, this was proposed previously by Williams and Jencks,⁵⁹ who detected the H₃NCONH zwitterion in their kinetic experiments and suggested that its decomposition is rate-limiting.

Among the alternative routes for the ammonia elimination, direct elimination from trans-NH₃CONH was considered without the assistance of a water molecule, but with NH to NH₃ transfer to yield NH₄⁺ + NCO⁻. The MC/FEP barrier for this route is 22.9 kcal/mol or 29.3 kcal/mol with inclusion of the cis-trans rearrangement. Thus, this possibility is competitive and the final ionization may be simultaneous with the ammonia elimination. Similar NH₃-elimination from the cis form of the zwitterion was also considered, but the cis-trans isomerization of the zwitterion occurred spontaneously, and the elimination barrier was 34.5 kcal/mol. Additional mechanisms with an initial protonation or deprotonation of urea or the zwitterion by water can also be imagined. However, they seem unlikely since the rate of the uncatalyzed decomposition of urea in water is known to be insensitive to pH in the range 2 to 12,^3,60,61 and, within this range, the products of the decomposition are invariant, ammonia and isocyanic acid. At pH over 12, the rate of the reaction increases, and at pH below 2, the reaction rate decreases.^3,61 Thus, the onset of alternative ionic mechanisms is likely in these extremes. At low pH, protonation of urea on oxygen is expected,^62–64 and decomposition by elimination or addition-elimination routes can still be envisaged.

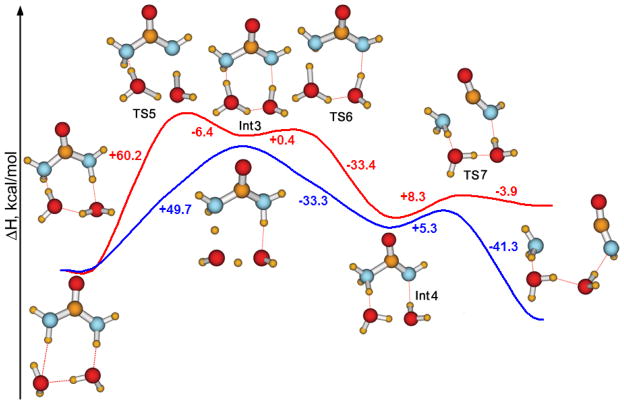
For the neutral pH process, another possibility that was explored incorporated two water molecules in the formation of Int2. Figure 5 illustrates the lowest-barrier pathway that was found for the gas phase reaction. Inclusion of the second water molecule did not facilitate the process; the barrier for the gas phase reaction increased to 60.2 kcal/mol (Figure 5, red curve). The system goes through a transition state, TS5, and a metastable intermediate, Int3, then crosses a barrier of only 0.4 kcal/mol (TS6), forms the zwitterion (Int4), and finally loses ammonia. In GB/SA solution, this becomes a two-step reaction omitting Int3 (Figure 5, blue curve). Though the barrier for the process in solution decreased significantly in comparison with the gas phase (49.7 kcal/mol), it is still higher than that for the reaction with only one assisting water molecule.

Figure 5.

Reaction pathway for urea decomposition via elimination of ammonia in the gas phase with two water molecules assisting the hydrogen shuttling. PDDG results with (blue curve) and without (red curve) GB/SA hydration.

A final mechanism, which was previously considered,¹⁷ consists of tautomerization of urea to the iminol form, hydrogen transfer from the NH to NH₂, and elimination to ammonia and cyanic acid. The activation energy for the tautomerization is computed here to be 39.8 kcal/mol in the gas phase (PDDG), and 44.3 kcal/mol with GB/SA hydration. Furthermore, the second hydrogen transfer is found to have a barrier of 56.2 kcal/mol (PDDG) in the gas phase, and 49.6 kcal/mol with GB/SA hydration. Quantitatively similar results were obtained from the previous MP2/6-311++G** calculations.¹⁷ The high computed barriers for the process are inconsistent with the experimental data, and the consensus is that this mechanism is not competitive.

In conclusion, the lowest-energy path for the elimination of ammonia from urea in water that was found with the present QM/MM/FEP approach involves intramolecular hydrogen transfer with one assisting water molecule to form the H₃NCONH zwitterion, and subsequent rate-determining elimination of ammonia. The computed mechanism of the reaction changes significantly upon inclusion of hundreds of explicit water molecules and MC sampling (Figure 2). Though there is agreement that the elimination occurs with particular assistance of one water molecule, the prior continuum-based calculations did not find the zwitterion as an intermediate, and only a single transition state was reported with a structure similar to Int2, which leads without an additional barrier to the products.¹⁷ For transformations in aqueous solution of highly polar species, capable of participating in multiple hydrogen bonds (Figure 4), it can not be expected that continuum-based treatments even with inclusion of a few explicit water molecules can lead to an accurate description of the energetics. Even with the present explicit inclusion of hundreds of water molecules, complicating factors remain including the numerous possible reaction paths involving alternative sequences of hydrogen transfers, the mixed QM/MM representation, the level of the QM calculations, and the lack of treatment of quantum effects.

Hydrolytic decomposition

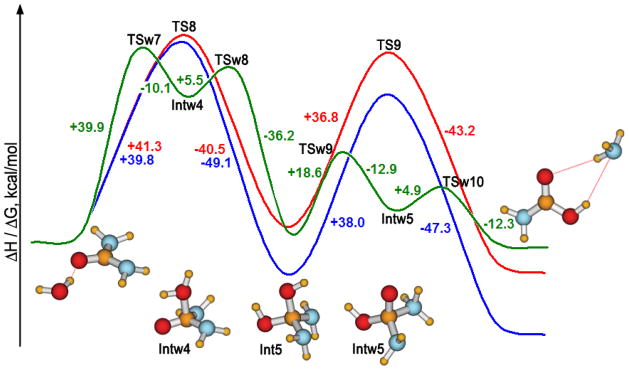
Hydrolysis is an alternative reaction path for urea. The consensus is that it is less facile; however, establishment of the activation barrier for the process is central to assessing the catalytic efficiency of urease enzymes.^17,21 The uncatalyzed hydrolysis reaction is expected to proceed through an addition-elimination mechanism. Nucleophilic attack of a water molecule on the carbonyl carbon and protonation of the carbonyl oxygen occur in the first step. In the resultant tetrahedral intermediate, a hydrogen then transfers from a hydroxyl group to an amino group, and the corresponding C-N bond cleaves releasing ammonia and carbamic acid. Figure 6 shows the computed reaction profiles for the hydrolysis in the gas phase, with inclusion of GB/SA hydration, and in explicit TIP4P water. Table 3 summarizes calculated molecular parameters for the transition states, and their structures are shown in Figure 3.

Figure 6.

Hydrolysis of urea. Enthalpy profiles: red – in the gas phase (PDDG), blue - in implicit solvent (PDDG + GB/SA). In green, the free energy profile from the QM/MM/FEP simulations in explicit TIP4P water. TS structures are shown in Figure 3.

TABLE 3.

Calculated Geometrical Parameters of the Transition States for the Addition/Elimination Mechanism (Figure 6)

Geometrical Parameter, Å	PDDG	PDDG GB/SA	B3LYP/6-311++G**	MP2/6-311++G** ICPM	QM/MM MC/FEP
	TS8				TSw7	TSw8
R(C-O1)	1.55	1.47	2.05	2.01a	1.82	1.42
R(O2-H)	1.52	1.50	1.04	1.06a	1.74	1.48
R(O1-H)	1.18	1.20	1.53	1.40a	0.96	1.22
	TS9				TSw9	TSw10
R(C-N1)	1.62	1.53	1.58	1.61	1.56	2.00
R(O1-H)	1.40	1.44	1.30	1.35	1.32
R(N1-H)	1.20	1.16	1.26	1.21	1.28

^aResults from Ref. 17.

The nucleophilic attack is rate-determining in all media: in the gas phase, ΔH^‡ = 41.3 kcal/mol; it is lowered slightly to 39.8 kcal/mol upon inclusion of the GB/SA hydration; and ΔG^‡ from the QM/MM/FEP calculations in explicit water is 39.9 kcal/mol. These activation barriers are about 6 kcal/mol lower than from the MP2/ICPM and DFT + GB/SA results (Table 4). Notably, the magnitude of the barrier for the first step of hydrolysis is rather insensitive to the solvent representation, suggesting little differential hydration for the process. However, in explicit water, the nucleophilic attack and protonation of the carbonyl oxygen are not concerted; the sequence is urea → TSw7 → Intw4 → TSw8 → Int5 (Figure 6), whereas the gas-phase and GB/SA calculations reveal only one transition state for this step.

TABLE 4.

Energetics for Urea Hydrolysis by the Addition/Elimination Mechanism

	PDDG	PDDG GB/SA	QM/MM MC/FEP	B3LYP/6-311++G**	MP2/6-311++G** ICPM
	First Step
ΔE‡ (ZPE-corrected), kcal/mol	41.3b			50.5	53.5d
ΔE‡0 = ΔE‡ + ΔEthermala				48.0
ΔH‡ = ΔE‡ + ΔnRT, kcal/mol				48.6
ΔG‡ = ΔE‡ − TΔS, kcal/mol				49.0	51.2d
ΔG‡solution = ΔG‡ + ΔΔGsolvation		39.8b,c	39.9	45.0c	46.8d
	Second Step
ΔE‡ (ZPE-corrected), kcal/mol	36.8b			31.8	23.2
ΔE‡0 = ΔE‡ + ΔEthermala				27.8
ΔH‡ = ΔE‡ + ΔnRT, kcal/mol				27.2
ΔG‡ = ΔE‡ − TΔS, kcal/mol				26.9	24.1
ΔG‡solution = ΔG‡ + ΔΔGsolvation		38.0b,c	18.6	25.6c	23.3

^aE_thermal = E_vibtational + E_rotational + E_{translational}.

^bVibrational frequencies were not calculated at the PDDG level.

^cThe values include the ΔG of hydration obtained from the GB/SA model.

^dResults from Ref. 17.

The reaction then continues with the decomposition of the tetrahedral intermediate (Int5). In the gas phase and in the implicit solvent, it is a single-step process with activation enthalpies of 36.8 and 38.0 kcal/mol, respectively. In explicit water, a hydrogen first transfers from an OH to NH₂ group (Int5 → TSw9 → Intw5) resulting in formation of the zwitterionic intermediate Intw5. Then, crossing a small barrier of 4.9 kcal/mol (TSw10), ammonia is eliminated. The reaction would be completed by the protonation of ammonia and deprotonation of carbamic acid. The overall barrier for the second step of the hydrolysis is greatly reduced in explicit water to 18.6 kcal/mol.

The resulting free energy of activation for hydrolysis from the QM/MM/FEP calculations (ca. 40 kcal/mol) is higher than that for the ammonia elimination (ca. 37 kcal/mol). In both cases, these values exceed the experimental estimates by 6–10 kcal/mol.²¹ However, there is consensus that elimination is favored over hydrolysis, and the corresponding rate ratios of 150 from the present QM/MM/FEP calculations and 54 from the experimental data at 298 K are in reasonable accord.²¹ In contrast, the ΔG^‡ results from the prior MP2/ICPM-based computational study were in good accord with experimental data for the elimination process, but predicted a higher barrier for hydrolysis by 28 kcal/mol.¹⁷ This difference is far too large and led to the serious overestimation of the catalytic proficiency of urease.²¹ It is apparent from Figures 2 and 6 that the results for reaction surfaces are changed significantly in going from continuum hydration to the QM/MM/FEP model with inclusion of hundreds of explicit water molecules. Additional intermediates and transition states arise with the more realistic description of hydrogen bonding between the reacting system and water molecules. In particular, zwitterionic intermediates such as Int2 (Figure 4) are stabilized.

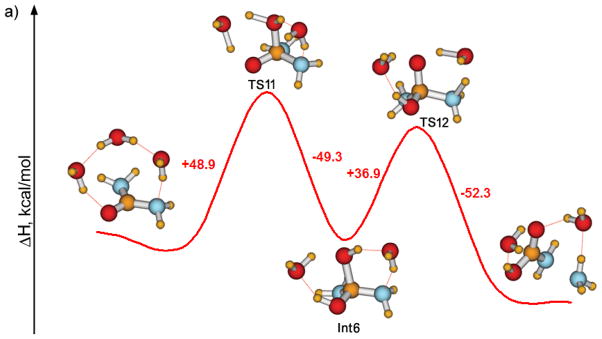
The reaction route for the gas phase hydrolysis in the presence of two assisting water molecules, which participate in the proton-transfers, was also considered (Figure 7). The activation energy changed little from the prior results (Figure 6), which again shows that the barrier for the addition step happens to be relatively insensitive to the details of the hydration model.

Figure 7.

Hydrolysis of urea in the gas phase assisted by two water molecules (PDDG results).

Evolution of the Resonance Stabilization in Urea

Urea is known to be stabilized by resonance.^22,65 Hence, in addition to solvent effects, it is interesting to examine the evolution of the resonance in urea during ammonia elimination and hydrolysis. Such an analysis may lead to further insight on the origins of the mechanistic preference. A NBO analysis at the B3LYP/6-311++G** level for urea and transition states on the corresponding PESs was carried out (Table 5).

TABLE 5. Results of the Natural Bond Order Analysis (B3LYP/6-311++G**).

TABLE 5.1. Urea

Bond orbital	Population	Atom	Natural charge
π(C-O)	1.654	O	−0.647
σ (C-N1)	1.822	C	+0.784
σ (C-N2)	1.822	N	−0.841
LP(N1)	1.828
LP(N2)	1.828
LP1(O)	1.978
LP2(O)	1.853
Donor Orbital	Acceptor Orbital	E(2), kcal/mol	E(i) – E(j), a. u.	Fij, a. u.
LP(N1)	π* (C-O)	40.53	0.32	0.106
LP(N2)	π* (C-O)	40.53	0.32	0.106
LP2(O)	σ* (C-N1)	24.20	0.67	0.115
LP2(O)	σ* (C-N2)	24.20	0.67	0.115

Urea

Two major resonance-effects are present in urea (Table 5.1). Prominent electron-density donation from the lone-pair of the nitrogen atoms (n_N) to the antibonding π*_C=O has been previously examined,⁶⁵ and the NBO confirms this effect. The second-order perturbation theory contribution to the stabilization energy is 40.5 kcal/mol per n_N. Due to this π-resonance, the nitrogen atoms in urea approach sp²-hydridzation; the sum of the H-N-H and the two H-N-C angles is 348°. An additional resonance effect consists of two n_O→ σ*_C-N donations yielding two times 24.2 kcal/mol of stabilization. This results in a π_C=O bond order of 0.827, bond orders of 0.911 for the σ(C-N) bonds, and reduced populations for the lone-pairs, n_N and n_O.

TS3

The NBO-analysis was done for the B3LYP/6-311++G** gas-phase geometry of TS3 (Table 5.2). Despite structural perturbations occurring in urea when transformed to TS3, no major changes happen in the electronic structure of the N₂CO-skeleton. The π_C=O bond-order decreases only to a minor degree, and both σ_C-N localized orbitals are still highly populated. Expectedly, when n_N1 accepts the hydrogen in TS3, it stops contributing to the π-resonance. However, the n_N2 → π*_C=O donation for the N-atom losing the hydrogen now brings 102.2 kcal/mol of stabilization energy, which in fact is greater than that from both n_N → π*_C=O donations in urea (2 times 40.5 kcal/mol). The n_O → σ*_C-N portion of the resonance, although misbalanced due to the symmetry changes, is also enhanced to a total of 60.9 kcal/mol versus 48.4 kcal/mol in urea. The energy correction from n_O → σ*_C-N1 for the C-N bond preparing to cleave is now substantially larger. Therefore, TS3 is even more resonance-stabilized than urea, which lowers the energy of TS3, and promotes the NH₃-elimination route.

TABLE 5.2.

TS3^a

Bond orbital	Population	Atom	Natural charge
π(C-O2)	1.592	O2	−0.639
σ (C-N1)	1.825	C	+0.777
σ (C-N2)	1.943	N1	−0.821
σ (N1-H1)	1.826	N2	−0.858
σ (N2-H2)	1.722	O1	−1.041
LP(N1)	0.000
LP(N2)	1.590
LP1(O2)	1.994
LP2(O2)	1.812
LP1(O1)	1.846
LP2(O1)	1.731
LP3(O1)	1.994
Donor Orbital	Acceptor Orbital	E(2), kcal/mol	E(i) – E(j), a. u.	Fij, a. u.
LP(N2)	π* (C-O2)	102.18	0.23	0.137
LP2(O2)	σ* (C-N1)	44.13	0.45	0.126
LP2(O2)	σ* (C-N2)	16.78	0.80	0.107
LP1(O1)	σ* (N1-H1)	68.79	0.60	0.181
LP2(O1)	σ* (N2-H2)	146.05	0.77	0.125

^aN₁ is a proton-acceptor; N₂ is a proton-donor; O₁ belongs to H₂O; O₂ is the carbonyl oxygen.

TS8

Table 5.3 summarizes NBO results for TS8 corresponding to the nucleophilic attack in the hydrolysis mechanism. TS8 is closer to the tetrahedral intermediate, Int5, than to urea in terms of its geometry and electronic structure. The disruption of the resonance in TS8 is dramatic. The new σ_C-O1 bond to the nucleophile has undergone a majority of its formation; the corresponding localized orbital is populated by 1.58 electrons. The protonation of the carbonyl is nearly complete (1.84 electrons populate σ_O2-H), and the neucleophilic O-atom possesses almost two full lone-pairs. The carbonyl π_C=O bond is completely destroyed, and much of the π-electron density is pushed onto the N-C-N part of the molecule. There is also a major electron-density exchange between the substrate and the forming C-O bond. The initial resonance stabilization found in urea is completely lost in TS8. Therefore, TS8 is much higher in energy than TS3. The identified electronic effects clearly contribute to the preference for elimination (Figure 2) over hydrolysis (Figure 6) for the uncatalyzed decomposition of urea.

TABLE 5.3.

TS8^a

Bond orbital	Population	Atom	Natural charge
σ(C-O2)	1.948	O2	−0.747
π(C-O2)	0.000	O1	−1.086
σ(C-O1)	1.581	C	+0.843
σ (C-N1)	1.909	N1	−0.776
σ (C-N2)	1.578	N2	−0.787
π (C-N2)	1.724
σ(O2 -H)	1.838
LP(N1)	1.722
LP(N2)	0.000
LP1(O2)	1.973
LP2(O2)	1.915
LP1(O1)	1.994
LP2(O1)	1.893
σ(C-O2)	1.948
Donor Orbital	Acceptor Orbital	E(2), kcal/mol	E(i) – E(j), a. u.	Fij, a. u.
σ(C-O2)	σ* (C-O1)	10.70	1.27	0.113
σ (C-N2)	σ* (C-O1)	95.84	0.71	0.241
π (C-N2)	σ* (C-O1)	32.84	1.02	0.173
π (C-N2)	π* (C-N2)	99.36	1.21	0.320
σ (C-O1)	σ* (C-N2)	57.92	0.84	0.204
LP(N1)	σ* (C-O1)	18.79	0.61	0.096
LP2(O1)	σ* (O2 -H)	41.80	0.74	0.157
σ* (C-O1)	σ* (C-N2)	376.60	0.19	0.445
σ* (C-O1)	π* (C-N2)	170.99	0.08	0.209

^aO₁ belongs to H₂O; O₂ is the carbonyl oxygen atom

Conclusions

The mechanism of uncatalyzed decomposition of urea in aqueous solution has been examined using a variety of computational techniques, including QM/MM/FEP calculations in explicit TIP4P water. The preferred reaction route, ammonia elimination (Figure 2), is initiated via hydrogen transfer between the two amino groups mediated by one water molecule. The forming zwitterionic intermediate, H₃NCONH, receives substantial stabilization via extended hydrogen-bonding to the solvent, and its subsequent decomposition is found here to be rate-determining. The explicit representation of the solvent appears to be essential for modeling the mechanism, as calculations in the gas phase and with the use of continuum hydration models yield overly simplified reaction profiles. The activation barrier for ammonia elimination from the QM/MM/FEP calculations, 36.6 kcal/mol, is somewhat higher than the reported experimental values of 28.4–32.4 kcal/mol. However, it is lower than ΔG^‡ for hydrolysis by the alternative addition-elimination mechanism (39.9 kcal/mol). The resultant rate ratio of ca. 150 favoring elimination is similar to recent experimental estimates.²¹ Furthermore, an NBO analysis of the resonance stabilization in urea and its evolution during decomposition was carried out. It showed that large resonance-disruption is required to reach the transition state of the rate-determining step for hydrolysis, while in the transition state corresponding to the first step of ammonia elimination, the original resonance is preserved.

On the technical side, the present results emphasize that computational study of hydrolysis reactions is challenging. Multiple possible mechanisms can be envisaged with different sequences of hydrogen transfers and possibilities of water participation. There are also the usual issues with the level of the QM calculations and details of the liquid-state simulations including extent of sampling and representation of intermolecular interactions. Thus, it is not expected that the present study represents the last word on urea decomposition in water. However, it has further demonstrated the viability of the present QM/MM/FEP approach that features PDDG/PM3 as the QM method,^32,33 and it points to need for further examination of the elimination mechanism including the existence of the H₃NCONH zwitterion as an intermediate and its decomposition being the rate-determining step.