A Circuit-Level Model of Hippocampal Place Field Dynamics Modulated by Entorhinal Grid and Suppression-Generating Cells

Abstract

Hippocampal “place cells” and the precession of their extracellularly recorded spiking during traversal of a “place field” are well-established phenomena. More recent experiments describe associated entorhinal “grid cell” firing, but to date only conceptual models have been offered to explain the potential interactions among entorhinal cortex (EC) and hippocampus. To better understand not only spatial navigation, but mechanisms of episodic and semantic memory consolidation and reconsolidation, more detailed physiological models are needed to guide confirmatory experiments. Here, we report the results of a putative entorhinal-hippocampal circuit level model that incorporates recurrent asynchronous-irregular non-linear (RAIN) dynamics, in the context of recent in vivo findings showing specific intracellular–extracellular precession disparities and place field destabilization by entorhinal lesioning. In particular, during computer-simulated rodent maze navigation, our model demonstrate asymmetric ramp-like depolarization, increased theta power, and frequency (that can explain the phase precession disparity), and a role for STDP and K_AHP channels. Additionally, we propose distinct roles for two entorhinal cell populations projecting to hippocampus. Grid cell populations transiently trigger place field activity, while tonic “suppression-generating cell” populations minimize aberrant place cell activation, and limit the number of active place cells during traversal of a given field. Applied to place-cell RAIN networks, this tonic suppression explains an otherwise seemingly discordant association with overall increased firing. The findings of this circuit level model suggest in vivo and in vitro experiments that could refute or support the proposed mechanisms of place cell dynamics and modulating influences of EC.

Introduction

Understanding the physiology of mammalian memory requires a deeper understanding of circuit-specific interactions of medial temporal neocortex and hippocampus. A basic behavior shared by all mammals is the task of navigating in a novel environment (Fleischer et al., 2007), which requires reliable short-term landmark memory. During evolution, episodic and semantic memory in primates may have co-opted this hippocampal navigational system for generic short-term memory as a way-station to manipulation and long-term consolidation (and reconsolidation) in the neocortex (Buzsaki, 2005; Samsonovich and Ascoli, 2005), and possibly even human creativity (Balter, 2010) and imagination (Hassabis et al., 2007).

The most commonly studied relationship of navigational behavior and electrophysiology relate to the phenomena of hippocampal “place cells” (O'Keefe and Dostrovski, 1971), and phase precession of extracellularly recorded action potential units with respect to theta (6–10 Hz) inhibition (O'Keefe and Recce, 1993; Kamondi et al., 1998). During rodent navigation, hippocampal place cells encode spatial information using rate and temporal codes (O'Keefe and Burgess, 2005).

Recent awake-behaving measurements correlated extracellular with intracellular CA1neuronal physiology during navigation (Harvey et al., 2009). This confirmed extracellularly measured theta phase precession, but showed that precession does not occur with respect to intracellular theta. Rather, higher frequency of intracellular theta toward the center of place fields explained this disparity. These authors also observed asymmetric subthreshold ramp-like depolarization, but could not explain this behavior using their proposed model.

Recently, entorhinal “grid cells” were reported as part of a generalized path-integration-based map of the spatial environment (Hafting et al., 2005). However, the specific mechanism whereby entorhinal grid cells modulate hippocampal place cells remains unclear (Van Strien et al., 2009). Insight into this relationship was provided by subsequent lesioning results of Van Cauter et al. (2008) and Brun et al. (2008) demonstrating that entorhinal cell populations are responsible for stabilizing place fields in several ways via layer-specific direct projections to hippocampal CA regions.

Several classes of theoretical models have been offered to explain grid cell effects. McNaughton et al. (2006) proposed a topographically arranged network that serves as a tutor to train medial entorhinal cortex (EC) cell modules. Another local-network model, Gaussier et al. (2007) proposed that stabilization of hippocampal place cells is due to the combination of modulo projections from EC grid cells and EC visual place cells. Another class of models is based upon the hypothesis that path integration occurs at the single cell level and is related to phase precession (Moser et al., 2008). In particular, Tsodyks et al. (1996) proposed a neural network model based on integrate-and-fire neurons that accounts for phase precession.

Despite this series of discoveries and other computational models, the interactions between place cells and grid cells, their individual and interactive mechanisms, their significance for memory storage, and their dynamics with representations in other cortical regions remain to be determined (Moser et al., 2008).

We present here the first comprehensive, spike timing, circuit-specific synaptic model of the hippocampal formation-neocortical system that may explain the role of grid cells in stabilizing rather than establishing place cell activity. Our model suggests mechanisms of both place field formation and stabilization during computer-simulated rodent maze navigation, demonstrating subthreshold dynamics consistent with the recent in vivo recordings reported by Harvey et al. Our model utilizes recent theoretical microcircuitry dynamics, called “Recurrent Asynchronous-Irregular Non-linear” (RAIN) networks, which are self-sustaining once activated, and silenced under certain perturbations (Vogels and Abbott, 2005).

Our RAIN-Entorhinal-Hippocampal model has four components: (1) spontaneously activating and de-activating RAIN networks corresponding to place cell activity; (2) interacting RAIN networks that incorporate K_AHPchannels which creates irregular, intracellular, and field potential theta inhibitory oscillation; (3) tonic suppression from the EC to the hippocampus stabilizing place field formation; and (4) anti-phase of intracellular and extracellular theta responsible for phase precession. We established and achieved performance criteria for our model, based on the reported awake-behaving intracellular recordings of Harvey et al. (2009), and the entorhinal cortical lesions of Van Cauter et al. (2008). Our circuit-specific mechanistic model is framed so that predictions can be biologically represented and tested experimentally.

Materials and Methods

Navigational paradigm

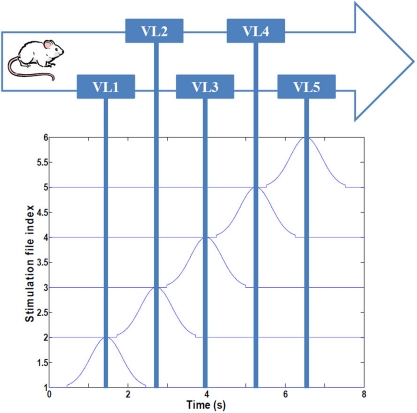
To replicate the virtual linear maze of Harvey et al. (2009), we developed a computational system representing a navigating rodent (Figure 1). The animal is assumed to have been trained to run with minimal hesitation along a 180 cm linear track, passing en route five visual landmarks demarcating an environment we refer to as VL1 to VL5. VL characterizes a distribution of spiking signals derived from the ventral visual stream through temporal “what” pathway, involved with object identification, which here represents potential place field activity (45 cm long), modeled as a 2 s Gaussian distribution of spike probability along an assumed occipital–parietal–temporal axonal pathway terminating in CA regions of the hippocampus. Consistent with the experimental findings (Harvey et al., 2009), VL overlap is 37%, the total duration of the run is 8 s, and the average speed of the animal is 22.5 cm/s. Three consecutive passes through the maze were analyzed for each experimental condition (an additional fourth pass was simulated, but no changes in dynamics were observed beyond three passes).

Figure 1.

Simulated navigational environment. The virtual linear track (180 cm) is divided into five visual regions with 37% overlap, consistent with Harvey et al. (2009). See text for details.

Computational brain model implementation

The hippocampal model included a total of 37,500 leaky integrate-and-fire neurons with conductance-based synapses with a sampling frequency of 1,000/s. All simulations were performed using Neo Cortical Simulator, also known as NCS (Courtenay Wilson et al., 2001; Brette et al., 2007; Drewes et al., 2009) on a shared-memory 16-processor Sun Fire X4600. Each of five place-field subnetworks included 3,200 neurons, comprised of 2,600 pyramidal and 600 single-compartment interneurons. Pyramidal cells were represented as quasi-bicompartmental (Izhikevich et al., 2004) neurons by the inclusion of a population of single-compartment apical tuft cells that connect to the pyramidal somatic compartment. It allowed us mix incoming VL excitatory activity with anti-phase theta inhibitory activity in the distal tuft independent of somatic currents. Excitatory synapses among pyramidal cells (CA RAIN networks) underwent STDP:

$$\Delta W^{\pm }=A^{\pm }{\text{e}}^{\left(-\frac{\Delta t}{{\tau }^{\pm }}\right)}$$

with positive and negative fractional changes in synaptic strength (ΔW) of 0.003, with positive window (+A) of 50 ms and negative window (−A) of 90 ms, and with positive decay constant (+τ) of 15 ms and negative decay constant (−τ) of 30 ms (Dan and Poo, 2004).

Each integrate-and-fire neuron is characterized by a membrane time constant of 20 ms, a membrane resistance of 100 MΩ, and a resting membrane potential of −60 mV. Whenever the membrane potential crosses the spiking threshold of −50 mV, an action potential is generated and the membrane potential is reset to the resting potential, where it remains clamped for a 5 ms refractory period. Membrane voltages are updated at each time step as follows:

$$C_{\text{N}}\frac{dV}{dt}=I_{\text{AHP}}+I_{\text{syn}}+I_{\text{leak}}+I_{\text{ext}}$$

where the charge delivered after each time step is updated as:

$$I_{\text{AHP}}=g_{\text{AHP}}S{m}^{\text{P}}\left(E_{\text{AHP}}-V\right)$$

$$I_{\text{syn}}=g_{\text{syn}}PSG\left(t\right)\left(E_{\text{syn}}-V\right)$$

$$I_{\text{leak}}=g_{\text{leak}}\left(E_{\text{rest}}-V\right)$$

I_extis injected from external input at times appropriate for igniting the RAIN networks, and activating the GC and VL pathways (Figure 1). I_syn include excitatory and inhibitory afferents described in Section “Hippocampal Place Field and Entorhinal Cell Representation”. Reversal potentials are E_AHP = −80 mV, E_syn = 0 mV for excitatory and −80 mV for inhibitory synapses, and E_rest = −60 mV (resting membrane). Synaptic conductances (g) are modeled as:

$${\tau }_s\frac{dg}{dt}=-g$$

g←g+w_i upon spike arriving at synapse i

with post-synaptic conductance time constants of 5 ms (excitatory) and 10 ms (inhibitory) (Brette et al., 2007). The K_AHP m particle is modeled as:

$$\frac{dm}{dt}=\frac{m_{\infty }-m}{{\tau }_{\text{m}}}$$

$$\tau m=\frac{\in }{f\left(Ca\right)+b}$$

$$m_{\infty }=\frac{f\left(Ca\right)}{f\left(Ca\right)+b}$$

$$f\left(Ca\right)=k{\left[Ca\right]}_i^{\alpha }$$

$${\left[Ca\right]}_i(t+1)={[Ca]}_i\left(t\right)\left(1-\frac{dt}{{\tau }_{Ca}}\right)$$

where the scale factor, k, is 0.000125, the exponential factor, α, is 2, the half-min, b, is 2.5, the tau scale factor, ε, is 0.01, and unitary channel strength, is 0.00044.

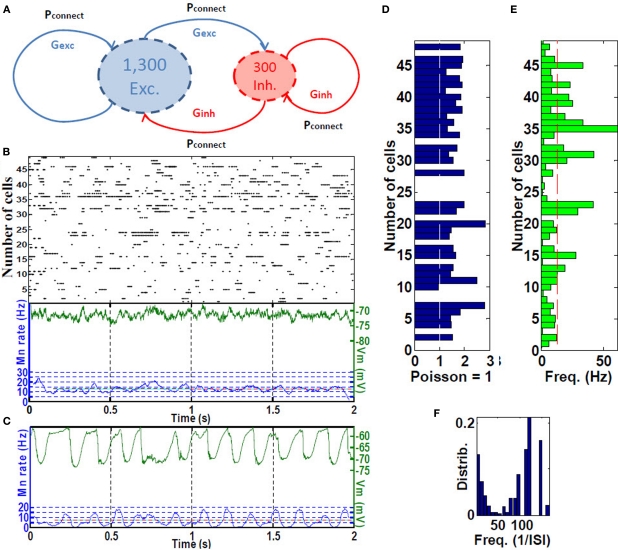
We hypothesized that grid cell activation at place-field boundaries followed by visual-parietal input should trigger self-sustained, asynchronous background activity limited to the place field. This type of activity was achieved using the baseline parameters including inhibition of the inhibition, sparse connectivity (3% among all cells) among approximately 4:1 ratio of excitatory to inhibitory neurons with 10-fold greater inhibitory than excitatory conductance (Van Vreeswijk and Sompolinsky, 1998; Brunel, 2000; Kumar et al., 2005; Vogels and Abbott, 2005; Gewaltig, 2009). Self-sustained firing activity of CA place-field cells is achieved by a brief (300 ms) irregular input. The resultant firing pattern of any given cell is irregular, with periods of higher firing rates separated by generally longer periods of low inactivity. Because the cells fire asynchronously with respect to one another, we refer to this as RAIN activity (Figures 2A–F).

Figure 2.

Place cell RAIN activity. (A) A RAIN (recurrent asynchronous irregular non-linear) network using 1,300 excitatory for 300 inhibitory cells with 3% connectivity and synaptic conductances G_exc and G_inh. (B) Sample of RAIN activity. Membrane potential (green), and mean rate (blue). (C) Mean membrane potential and firing rates showing biological-like theta activity obtained when two RAIN networks interact. (D) Supra-Poissonian coefficient of variation (typically 30–50% greater than a Poisson spiking process. (E) Wide range of RAIN firing rates of 2–60 Hz with mean rate of 14.8 Hz. (F) Bimodal distribution of firing. (n = 50 cells).

We used three variations of RAIN networks. To represent the five CA place-fields, 3,200-cell RAIN subnetworks were used that included K_AHP channels in the pyramidal somas, with synaptic inputs as described in Section “Hippocampal Place Field and Entorhinal Cell Representation”. To generate theta activity, we used a 1,600-cell RAIN network weakly (0.23%, one E to E group) connected to a 1,600-cell RAIN network whose excitatory cells contain K_AHPchannel activity, the latter oscillates at 6–10 Hz oscillation with variability that appear biologically plausible (Figure 2C). We used these oscillating networks to represent synchronized basket cells (BC) activity, with connections to pyramidal and OLM cells as described in Section “Hippocampal Place Field and Entorhinal Cell Representation”.

Analytic and statistical methods

We established specific performance criteria with respect to the published awake-behaving intracellular recordings of Harvey et al. (H), and the entorhinal cortical lesions of Van Cauter et al. (V):

• H1:Intracellular theta oscillations increase in amplitude toward the center of the place field.
• H2:Asymmetric ramp-like depolarization of the DC-filtered baseline membrane potential.
• H3:Spike precession relative to extracellular LFP theta associated with increased frequency of intracellular theta.
• V1:EC cells regulate the location of place fields.
• V2:EC lesions reduce place cell discharge firing rate by about a forth and approximately double the number of active place cells responding in a given place field.

Frequency of intracellular theta

We filtered inhibitory LFP and somatic Vm using Matlab fir1 notch-filtering from 6 to 10 Hz (Figure 7A). Extracellular LFP theta was measured 2 s before entering, and during each place field. To determine whether our findings were consistent with the rising intracellular theta frequency reported by Harvey et al. (2009), we fit the sequence of filtered intracellular inter-theta peak intervals using locally weighted least squares regression (LOWESS) for display purposes, and statistically compared the mean frequency of theta oscillations during the central third with the first and last thirds of each field (Figures 5A–C).

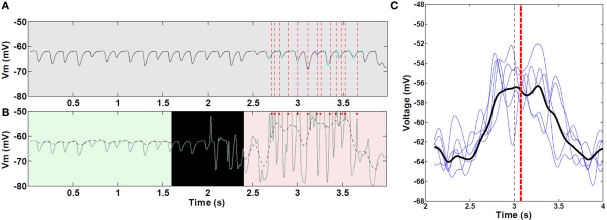
Figure 7.

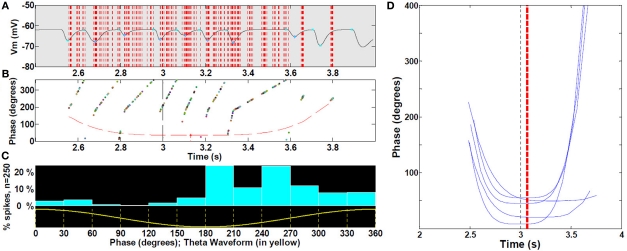
Asymmetric ramp-like membrane potential depolarization inside place fields. (A) LFP as measured from within the soma of a CA pyramidal cell, outside (0–2 s) and within a place field (2–4 s); spike unit timing is indicated by dotted red lines. Cyan and magenta markers indicate auto-detection of 0 and 180° theta limits. (B) Corresponding intracellular Vm (green line), and superimposed 1–2 Hz filtering (dashed black line). Red dots indicate spike timing (truncated, n = 1 cell as an example). (C) Representative sample of mean 1–2 Hz filtered ramps from third place field; statistics were performed on all 30 control (unlesioned) runs (n = 472 cells with increasing mean). Black line, mean of all curves; black vertical dashed line, true center of place field; red vertical dashed line, mean timing of the peak of individual ramps. Asymmetric ramp depolarization is attributable to the propagation delay, or “momentum” of RAIN networks; perturbation of a RAIN network affects all other cells with delays ranging from 50 to 100 ms, because both excitatory and inhibitory cells are sparsely connected and tonically inhibited, resulting in widely spaced irregular bursting. In this case, the CA RAIN networks experience an average delay of about 70 ms.

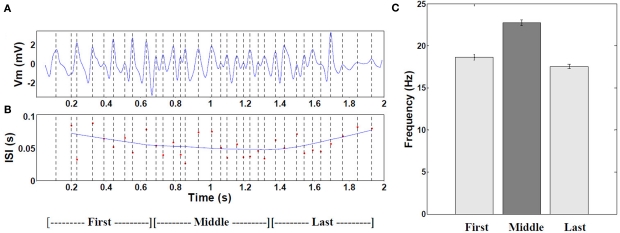
Figure 5.

Frequency of intracellular theta. (A) Example of 6–10 Hz filtered mean theta within a typical place field. (B) Corresponding moving window-average of the theta oscillation period. (n = 19 cells with increasing mean). (C) Comparison of the mean frequency during the first, middle, and last thirds of all fields (P < 0.001 by ANOVA, middle versus combined first and last thirds, n = 472 cells with increasing mean). Error bars are ±1 S.E.M. The increased frequency results from interference of signal arriving from the apical dendrites (mixture of visual pathway and local OLM inhibitory theta) and the local BC theta effect (180° out of phase with OLM, as experimental shown by Kamondi et al. (1998).

Spectral analysis of intracellular membrane potential

We analyzed theta power spectra for epochs inside and out of the place field using multi-taper spectral analysis methods (function mtspecgramc from the Chronux toolbox, http://chronux.org, Figure 6A). We also calculated the ratio of power during epochs inside to outside the place field for bands from 6 to 10 Hz (Figure 6B).

Figure 6.

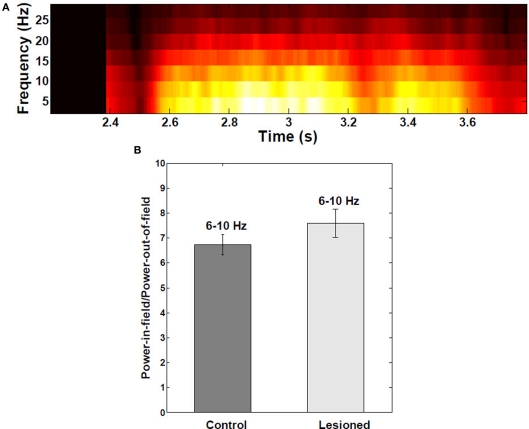
Spectral analysis of intracellular membrane potential recordings. (A) Power spectral analysis as a function of the mouse's position on the linear track (n = 30 fields). Theta-band (6–10 Hz) power in the membrane potential trace was greater and redistributed to upper theta range toward middle of place fields, due interference of local inhibitory theta with visually-driven apical dendritic input. (B) Ratio of theta power inside:outside the place field to power did not change significantly when EC was lesioned (n = 390 cells from both control and lesioned groups). Error bars are ±1 S.E.M.

Membrane potential depolarization inside place fields

We obtained low frequency Vm during the place field tracings using notch-filtering from 1 to 2 Hz (Figure 7B). We defined the baseline membrane potential as the low frequency mean just prior to entering the place field, and subtracted this from the in-field membrane potential values to derive the ramp ΔV. From this, we computed the magnitude and, to estimate asymmetry, the timing of the peak ramp ΔV with respect to its location in the place field (Figure 7C).

Spike precession with respect to LFP

To analyze phase precession, we computed spike timing with respect to LFP theta phase within the place field (Figure 8A). All cells with increasing mean ramp ΔV in the place field were included. For the phase versus position distribution, we first computed its outer hull; to that curve we fit a non-linear parabolic curve to obtain parameters estimating the phase and timing of the phase of greatest precession (Figure 8B). From this, we computed the magnitude and, to estimate asymmetry, the timing of the trough (maximal precession) with respect to theta (Figure 8D).

Figure 8.

Spike precession with respect to LFP during place fields. (A) Magnification of first spike timing of all 19 cells (sample of cells with increasing mean) from a single run superimposed on extracellular theta within the third place field (B) For each spike in (A), phase with respect to LFP, with outer hull fit. (C) Location of spikes with respect to theta waveform. (See text, n = 30 fields). (D) Representative sample for clarity (25%) of outer hull fit of precession during third place fields; statistics were performed on all 30 runs (472 control cells, with increasing mean). Black dashed line, true center of place field; red dashed line, mean timing of the troughs (maximal precession). Because spikes occur reliably at or near the peak of intracellular oscillation (i.e., there is no intracellular precession per se), and the intracellular oscillation frequency increases near the middle of the field, spike timing will appear to precess with respect to extracellularly measured theta LFP.

Entorhinal cortex lesioning

To analyze the effect of putative EC suppression, we compared the population size and firing rate of active place cells in both control and lesioned groups (Figure 9). Place field stabilization by EC was explored by comparing place field activation during full 8 s runs in the control versus lesioned groups (Figure 10).

Figure 9.

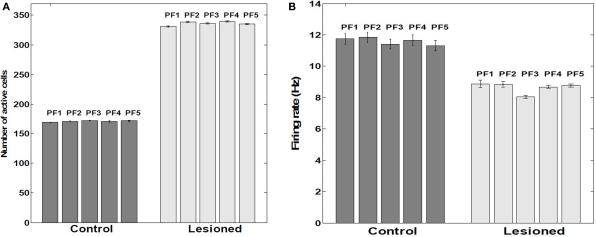
Number of active cells and their firing rates within place fields. (A) Average number of active cells within five Place Fields (n = 390 cells as a sample). (B) Average firing rates within five place fields. Control versus lesioned groups (n = 390 cells as a sample). Tonic extrinsic inhibition (as postulated to arise from EC) into CA principle cells was manually adjusted to suppress about half the population excitatory cells from firing; rather than a net decrease in firing rate among the remaining, active cells, an increase of about 24% was observed, consistent with EC-lesioning findings of Van Cauter et al. (2008). The paradoxical response is attributable within RAIN networks to an auto-regulatory increase of inhibition of inhibition (i.e., less net inhibition).

Figure 10.

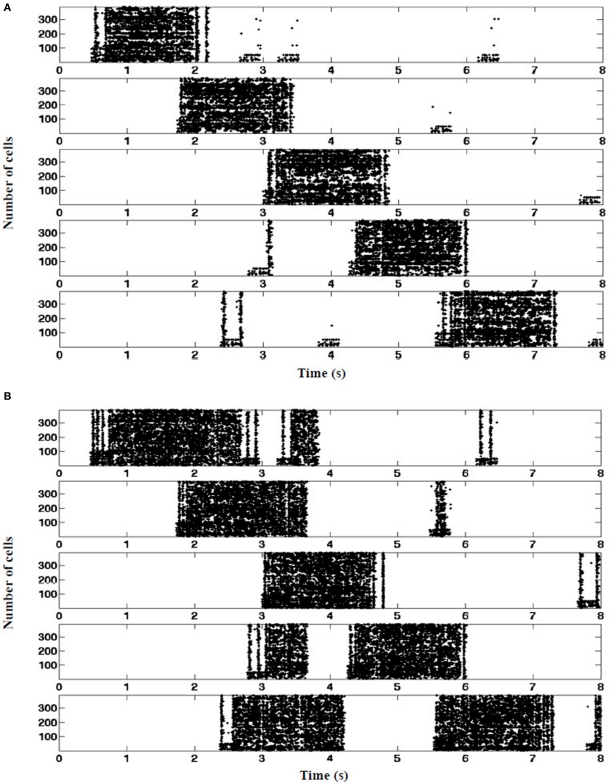
Place fields stabilization. (A) Control: entorhinal cortex grid cells contribute tonic suppression during all five place fields. Tonic EC-derived inhibition mediated by PPA interneurons (EC SG) is sufficient to suppress RAIN CA networks from triggering in the absence of concurrent visual pathway stimulation. (B) EC-lesioned. In the absence of tonic suppression, random surges arising within the hippocampus can spuriously ignite the CA networks when mouse is between place fields, consistent with in vivo findings of Van Cauter et al. (2008).(one typical 8 s run shown, n = 390 cells as a sample).

Statistics

To assess reproducibility, we ran the entire simulation under ten different pseudo-random seeds. Because firing pattern means and variances did not differ statistically by 1-way ANOVA comparisons, in the subsequent analyses we combined the passes through the track, and then compared the results of 30 runs of the EC-lesioned group with 30 runs of the control group. All runs included K_AHPchannels in CA pyramidal cell somas. Group means were compared using appropriate paired or unpaired student t-test or one-way ANOVA, and medians compared by the SIGNRANK test.

Results

Model description

Hippocampal place field and entorhinal cell representation

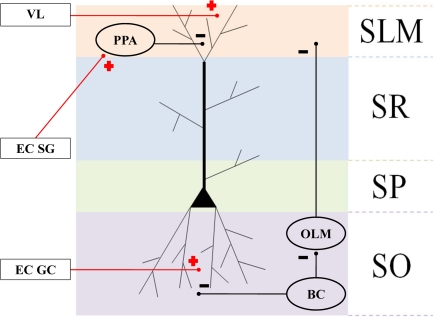
Integrate and fire neuronal simulations are increasingly being used to represent interacting cortical and subcortical interactions (Fox et al., 2009). Here, we represented CA pyramidal neurons as bicompartmental cells, with a soma in the stratum pyramidale (SP) and apical dendritic tuft in the stratum lacunosum moleculare (SLM), as shown in Figure 3. Pyramidal cells are arranged into subnetworks (see Computational Brain Model Implementation) receiving inputs from (1) sensory parietal-temporal axonal pathways responding to VL, (2) EC cell populations, (3) BC in the stratum oriens (SO), (4) oriens-lacunosum moleculare cells (OLM) interneurons (Klausberger, 2009), and (5) perforant pathway associated (PPA) interneurons (Klausberger, 2009). We assume that visual neocortical activity, along with entorhinal cell activity pass through the perforant pathway to activate the distal tufts of hippocampal CA networks. VL may or may not synapse in the EC specifically, but fibers could pass through EC or parahippocampal regions en passant to hippocampus. We also assume that the GC network was already formed during the development of the mouse, and is modeled as a group of simple single cell leaky integrate and fire neurons. We program the model to inject short sequence of square-wave pulses (1 ms width, 3 nA) just as the mouse crosses the boundary of the grid between place fields (because this is a linear maze, the “grid” tiling becomes simple linear spacing, or repeating pattern at the boundaries).We modeled five such discrete networks serving as the potential basis for corresponding place-field representation. We assume that BC are activated by global CA activity and give rise to theta (6–10 Hz) phasic field activity (Andersen et al., 2006), which in turn is broadcast as inhibitory input to the proximal dendritic branches of the pyramidal cells. BC also inhibit OLM interneurons, given rise to an anti-phase inhibitory theta activity that projects to dendritic tufts in SLM (Kamondi et al., 1998). To simulate the putative effects of EC-lesioning described by Van Cauter et al. (2008), we included two populations of EC cells: (1) “suppression-generating” (EC SG) cells connecting to PPA interneurons, which in turn inhibit the pyramidal apical tufts, resulting in fewer cells responding in place fields, and (2) grid cells (EC GC) connecting to the basilar dendrites, responsible for triggering activity at the boundaries of place fields (Hafting et al., 2005).

Figure 3.

Connectivity of the hippocampal structures and surrounding regions. Anatomical layers of a CA1 pyramidal neuron: stratum lacunosum moleculare (SLM), stratum radiatum (SR), apical dendrites stratum pyramidale (SP), and stratum oriens (SO). Oval areas represent interneurons: basket cells (BC), oriens-lacunosum moleculare cells (OLM), and perforant pathway associated (PPA). Plus signs: excitatory connections. Negative signs: inhibitory connections.

Hippocampal place field and entorhinal cell modeling

The description of neuronal network models should communicate enough information for readers to comprehend and re-implement a model, and to compare different models (Nordlie et al., 2009). Table 1 gives an outline of the model, which validates its implementation (see Computational Brain Model Implementation).

Table 1.

Tabular description of model. The model is summarized in panel (A) and detailed in panels (B–E).

A. MODEL SUMMARY
Populations	Seven: CA pyramidal cells, axonal pathway (VL), EC cells (2), basket cells, OLM interneurons, PPA interneurons
Neuron model	Leaky integrate-and-fire, fixed threshold, refractory time
Plasticity	STDP
Channel model	]annels
Synapse model	Conductance-based
Measurements	Membrane potential

Name	Elements	Size
B. POPULATIONS
CA	5 RAIN networks	3,200 cells
VL	5 E cell groups	200 cells
EC SG	Linear positive current	N/A
EC GC	Current file based	N/A
BC (theta)	RAIN network	1,600 cells
OLM	I cell group	300 cells
PPA	Linear negative current	N/A

C. NEURON AND SYNAPSE MODEL
Type	Leaky integrate-and-fire neurons, conductance-based synapses
Dynamics/spiking	See Section “Computational Brain Model Implementation” for equations
D. CHANNEL AND PLASTICITY MODEL
KAHP and STDP	See Section “Computational Brain Model Implementation” for equations
E. MEASUREMENTS
Membrane potential V of all neurons

Model analysis

Analytical and numerical experiments

The first part of model analysis gives a description of analytical and numerical data used in the model, as shown in Table 2.

Table 2.

Tabular analysis of model. The description of the model connectivity is shown in panel (A) and the model input is given in panel (B).

Type	Probability (%)	Conductance strength (mS)
A. CONNECTIVITY
RAIN–BC	3	0.004
BC–CA	3	0.003
BC–OLM	3	0.2
OLM–VL	3	0.01
VL–CA	5	0.006

Type	Description
B. INPUT
Visual cortex	2 s Gaussian distribution (5 of them)
Entorhinal cortex (SG)/PPA	Linear negative current suppressing CA networks (50%) with amplitude of −4 mA and constant duration
Entorhinal cortex (GC)	File based current exciting CA networks (100%) with amplitude of 3 mA and duration of 300 ms

The second part of model analysis describes the results obtained. These results are designed to test hypotheses V1, V2, and V3 (see Hippocampal Formation Dynamics), and hypotheses H1 and H2 (see Entorhinal Cortex Lesioning).

Hippocampal formation dynamics

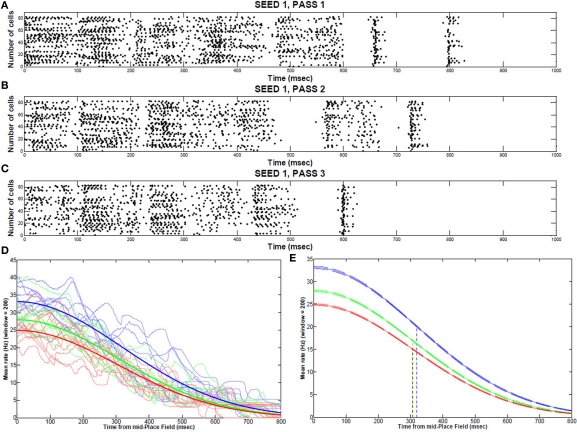
During the first two passes, place field activity spread over most of the 2 s traversal period, but after the virtual mouse ran an additional repetition through the maze, place cell localized to a narrower field, with a mean rate decrease from 33.1% (pass 1) to 27.9% (pass 2) to 24.9% (pass 3) (Figures 4A–C). This narrowing corresponded to a mean decrease in synaptic strength of 1.6% over the course of three passes through the track. The peak rates (maximum, at the middle of the place field) are statistically different from one pass to the next (P < 0.001; Figures 4D,E). However, the decay rates (variances of the curves) are not statistically different. Removing K_AHPchannels affected these results by decreasing theta resonance.

Figure 4.

Place field activity during multiple runs through the track. Typical place field firing (from the middle to the end, 1 s) during the first traversal (A), second traversal (B), and third traversal (C) through the maze (sample of 100 cells). (D) Individual repetitions of a place field for 10 consecutive runs (seeds) showing each pass through the maze (1: blue; 2:green; 3: red) (E) Gaussian fit from the middle to the end of a place field (99% CI bands) for the first pass (blue), second pass (green), and third pass (red) though the maze.

The frequency of intracellular theta gradually increased toward the center of the field (4.75 Hz, P < 0.001, n = 30 fields) and fell again toward the end of the field, as shown in Figure 5.

Theta-band power of the membrane potential was significantly higher within place fields than outside (Figure 6A), with average ratio of power in-field to power out-of-field of 6.7 (P < 0.001; Figure 6B). There were no significant differences between control and EC-lesioned groups (P > 0.05).

As the virtual mouse approached a visual landmark, the average membrane potential increased in a ramp-like manner and remained increased beyond the center of place field (Figure 7C). The ramp of depolarization often began before the start of action potential firing in the place field. In some cases, the ramp reached a depolarization as large as 13.5 mV (average peak depolarization, 8.2 ± 2.6 mV). On complete runs through the place field, ramps of depolarization were asymmetric, with timing of the peak depolarization shifted toward the end of the field. The average right-shift of the peak was 0.07 s (P < 0.05), and the average right skewness was 0.5 (P < 0.001). There were no significant differences among the five place fields (ANOVA P > 0.05) for these measurements. Removing K_AHPchannels resulted in statistically symmetric ramps of depolarization (P > 0.05).

Phase precession with respect to LFP theta spanned the entire range between 0 and 360° (Figure 8A). Figures 8B,C show a typical distribution of spike timing with respect to theta phase while traversing a place field. A parabolic outer hull fit had significant (P < 0.001) curvature and maximal precession shifted asymmetrically toward the right half of the field (0.06 s), as shown in Figure 8D (P < 0.001). There were no significant differences among the five place fields (ANOVA P > 0.05) for these measurements.

Entorhinal cortex lesioning

Lesioning the putative suppressive input from EC resulted in approximate doubling (P < 0.001) of the proportion of cells firing within a place field (Figure 9A). Contrary to this increased population response, the actual mean firing rate decreased by 24.3% (P < 0.001) (Figure 9B). Removing K_AHPchannels did not affect these results (P > 0.05).

The presence of EC suppression stabilized the location of every place field throughout the run. As shown in Figure 10A, each place field fired at its corresponding visual landmark along the track when the EC was intact. On the other hand, when EC was lesioned, place field location varied and often triggers at anomalous locations (Figure 10B).

Discussion

We report here two unique circuit-level network features that can explain intracellular and extracellular CA place field dynamics observed during in vivo spatial navigation: (1) self-sustained RAIN networks underlying place cell responsiveness, and, (2) EC neuron groups providing both transient excitatory ignition (EC GC) and tonic suppression (EC SG). In particular, RAIN networks incorporating K_AHPchannel-like dynamics provide a mechanism for the in vivo asymmetry of intracellular place field ramping not explained by the models of Harvey et al. (2009) and Gasparini and Magee (2006). Additionally, these dynamics explain the apparent population-rate discordance of the EC-lesioning results of Van Cauter et al. (2008).

Recurrent asynchronous-irregular non-linear networks are easily ignited by transient (50–300 ms), sparse (<100 spikes) external stimulation, self-sustain non-Poissonian bimodal firing similar to that observed in most in vivo mammalian recordings (Mormann et al., 2008), yet readily shut down with unopposed theta range inhibitory input. This bimodally distributed firing requires conduction-based synapses (Vogels and Abbott, 2005). Interaction among RAIN networks spontaneously gives rise to biological appearing, variable background inhibitory theta activity. Several studies have shown that networks of sparsely connected current-based synaptic spiking model neurons can produce highly irregular, chaotic activity without any external source of noise (Van Vreeswijk and Sompolinsky, 1998; Brunel, 2000). Conductance-based synaptic models exhibiting asynchronous-irregular firing patterns have been proposed as the basis for prefrontal working memory (Compte et al., 2000), but to our knowledge this is the first such application to the hippocampal formation.

Simulated hippocampal place-cell activity was consistent with that reported by Harvey et al. (2009). Our model showed increased theta power (H1, as defined in Section “Analytic and Statistical Methods”.) toward the middle of a place field. This results from a net increase in theta-modulated signal arriving from apical dendrites, which overrides the relatively constant anti-phase interference of the local BC theta inhibition onto the principal cells (Kamondi et al., 1998). Asymmetric ramp-like depolarization (H2) during place field traversals is attributable to the propagation delay, or “momentum” of RAIN networks; perturbation of a RAIN network affects all other cells with delays ranging from 50 to 100 ms, because both excitatory and inhibitory cells are sparsely connected and tonically inhibited, resulting in widely spaced irregular bursting. In this case, the CA RAIN networks experience an average delay of about 70 ms. Of note, the model proposed by Harvey et al. could not explain this asymmetry. Our model also confirmed an increased frequency of intracellular theta oscillations toward the middle of place fields (H3), which explains phase precession of spikes with respect to extracellular LFP theta activity. Spikes occurred reliably at or near the peak of intracellular oscillation, but the intracellular oscillation frequency increased near the middle of the field, which made spike timing appear to precess with respect to extracellularly measured theta LFP. The increased frequency results from interference of signal arriving from the apical dendrites (mixture of visual pathway and local OLM inhibitory theta) and the local BC theta effect [180° out of phase with OLM (Gasparini and Magee, 2006), as experimental shown by Kamondi et al. (1998)].

Our incorporation of STDP in the excitatory connections within the place cell networks and K_AHP dynamics in the RAIN theta networks resulted in stabilization of place field response generally by the third pass through the track, consistent with such delays reported by Wilson and McNaughton (1993) and Frank et al. (2004).

To test our hypotheses about the mechanism of EC regulation of CA place field behavior, we simulated the lesioning experiments of Van Cauter et al. (2008). Our results support dual roles for entorhinal cell populations projecting to CA regions: triggering place-specific pyramidal cell firing, and, mediated by local CA interneurons, suppressing sporadic place cell activation of established place fields (V1). It is the self-regulating characteristic of RAIN networks that account for the seemingly discordant EC-lesioning results, where increased number of active place cells is associated with reduced, rather than increased overall place cell firing rates (V2). If CA networks did not have the inhibition of the inhibition feature of RAIN activity, tonic inhibition of the principle cells would lead to a decrease in firing rate rather than an increase, but also to the destabilization of place field activity (Van Cauter et al., 2008).

We speculate that transient activation of neural architectures consistent with RAIN-like networks may subserve hippocampal CA place field dynamics. This insight would be important to better understand not only mammalian navigation, but more complex episodic and semantic short-term memory, and mechanisms of long-term memory consolidation and reconsolidation. Our results suggest further biological experiments to test our proposed mechanistic explanation. First, stimulation of subsets of EC perforant path axons should result in enhanced tonic inhibition of CA pyramidal cells. Then, knock-out or knock-in experiments (potentially with rhodopsin optical modulation or monitoring) will test the role of specific CA interneurons. Finally, pharmacologic blockade or agonists of K_AHP channels (Stocker, 2004) should modulate theta field activity of ex vivo hippocampal preparation (Goutagny et al., 2009).

Dedication

We would like to dedicate this article to Dr. Phil Goodman, who suddenly passed away, recently. He was a great mentor, friend, role model, and inspiration to all of us.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.