Effects of model-based physiological noise correction on default mode network anti-correlations and correlations

Abstract

Previous studies have reported that the spontaneous, resting-state time course of the default-mode network is negatively correlated with that of the “task-positive network”, a collection of regions commonly recruited in demanding cognitive tasks. However, all studies of negative correlations between the default-mode and task-positive networks have employed some form of normalization or regression of the whole-brain average signal (“global signal”); these processing steps alter the time series of voxels in an uninterpretable manner as well as introduce spurious negative correlations. Thus, the extent of negative correlations with the default mode network without global signal removal has not been well characterized, and it is has recently been hypothesized that the apparent negative correlations in many of the task-positive regions could be artifactually induced by global signal pre-processing. The present study aimed to examine negative and positive correlations with the default-mode network when model-based corrections for respiratory and cardiac noise are applied in lieu of global signal removal. Physiological noise correction consisted of (1) removal of time-locked cardiac and respiratory artifacts using RETROICOR (Glover et al., 2000), and (2) removal of low-frequency respiratory and heart rate variations by convolving these waveforms with pre-determined transfer functions (Birn et al., 2008; Chang et al., 2009) and projecting the resulting two signals out of the data. It is demonstrated that negative correlations between the default-mode network and regions of the task-positive network are present in the majority of individual subjects both with and without physiological noise correction. Physiological noise correction increased the spatial extent and magnitude of negative correlations, yielding negative correlations within task-positive regions at the group level (p<0.05, uncorrected; no regions at the group level were significant at FDR=0.05). Furthermore, physiological noise correction caused region-specific decreases in positive correlations within the default-mode network, reducing apparent false positives. It was observed that the low-frequency respiratory volume and cardiac rate regressors used within the physiological noise correction algorithm displayed significant (but not total) shared variance with the global signal, and constitute a model-based alternative to correcting for non-neural global noise.

Introduction

Functional magnetic resonance imaging (fMRI) studies of the brain have revealed temporal synchrony between the blood oxygen level dependent (BOLD) signals of anatomically distinct regions during the absence of an explicit task, i.e. in the resting state (for reviews, see (Buckner and Vincent, 2007; Fox and Raichle, 2007)). Several such sets of temporally correlated regions, known as resting-state networks, can be identified consistently across human subjects (Beckmann et al., 2005; Damoiseaux et al., 2006; De Luca et al., 2006) and are presumed to reflect a basic functional organization of the brain.

A particular resting-state network, known as the default-mode network (DMN), has received much recent attention (see (Buckner et al., 2008) for a review). The DMN comprises brain regions that, in addition to having coherent fluctuations in the absence of a task, are commonly deactivated (exhibit sub-baseline signal deflections) in response to a broad range of cognitive and attentional tasks (Mazoyer et al., 2001; Raichle et al., 2001; Shulman et al., 1997) and may underlie self-referential processing (Gusnard et al., 2001) (see (Buckner et al., 2008) for a review). Core regions of the DMN include the precuneus/posterior cingulate cortex (PCC), medial prefrontal cortex, ventral anterior cingulate, lateral parietal cortex, inferior temporal cortex, and parahippocampal cortex.

It has been reported that the spontaneous, resting-state time course of the DMN is negatively correlated (“anti-correlated”) with that of the task-positive network (TPN), a set of regions that are (positively) activated in response to cognitive and attentional tasks (Fox et al., 2005; Fransson, 2005). The TPN includes dorsolateral prefrontal cortex (DLPFC), supramarginal gyrus and posterior parietal cortex, insula, premotor cortex, and supplementary motor area (SMA). The finding of negative correlations between the two networks has been hypothesized to reflect a competitive relationship between internally- and externally-oriented processes, or between mind wandering and focused attention, and mirrors the opposing signal changes displayed by the two networks during controlled tasks (Fox et al., 2005; Fransson, 2005; Greicius et al., 2003). Subsequent studies have asserted that the strength of the negative correlations between the DMN and TPN mediates behavioral variability (Clare Kelly et al., 2008) and may distinguish Alzheimer's patients from healthy controls (Wang et al., 2007).

However, studies reporting significant negative correlations between the DMN and the TPN in resting state have removed a whole-brain average time series from the data, either by proportional scaling (time-point-wise division), regressing it out as a pre-processing step, or including it as a nuisance covariate when assessing functional connectivity using the general linear model (Clare Kelly et al., 2008; Fair et al., 2008; Fox et al., 2005; Fransson, 2005, 2006; Greicius et al., 2003; Tian et al., 2007; Uddin et al., 2009; Wang et al., 2007). Removing a global signal is intended to remove undesired non-neural fluctuations that affect large numbers of voxels. Unfortunately, since the global signal is derived from the data itself and is an unknown mixture of neural and non-neural fluctuations, these steps alter inter-regional correlations and complicate their interpretation. Furthermore, if the global signal has been regressed out of each voxel's time series, the resulting correlation coefficients between a seed voxel and all other voxels in the brain will have a mean value that is less than or equal to zero, necessarily introducing spurious negative correlations (Fox et al., 2008; Murphy et al., 2009). Consequently, it has been hypothesized that global signal removal may be the cause of the observed negative correlations between the DMN and TPN (Murphy et al., 2009). Studies by (Golland et al., 2007; Murphy et al., 2009) did not employ global signal removal and failed to observe negative correlations at any statistical threshold, but Fransson (Fransson, 2005) noted that when reanalyzing data without performing global signal regression, negative correlations in some TPN regions were present when the statistical threshold was lowered from p<0.01 to p<0.07 (corrected), and Uddin et al. (2009) showed that bilateral clusters in the insula were negatively correlated with the PCC when data were reanalyzed without global signal regression. The question of whether negative correlation between the two networks is a real phenomenon, or simply an artifact of global signal removal, is currently under debate (Buckner et al., 2008).

The present study aimed to determine the spatial extent and magnitude of negative and positive correlations with the DMN when model-based physiological noise corrections, instead of global signal removal, are applied. Respiration and cardiac processes are known to modulate the BOLD signal (Biswal et al., 1993; Dagli et al., 1999; Jezzard et al., 1993; Shmueli et al., 2007; Weisskoff et al., 1993; Wise et al., 2004), and their effects can be reduced by monitoring respiratory and cardiac cycles throughout the scan and filtering them out of the fMRI data using a priori models (Birn et al., 2006; Birn et al., 2008; Chang et al., 2009; de Munck et al., 2008; Glover et al., 2000). In this way, known sources of noise that affect functional connectivity can be reduced in an unbiased manner. A previous study, employing the same physiological noise corrections applied here, demonstrated increased spatial specificity of positive correlations within the DMN after correction (Chang et al., 2009). It was thus hypothesized that such corrections might increase the sensitivity of detecting regions that are negatively correlated with the DMN as well.

It is important to note, however, that the determination of sensitivity and specificity in functional connectivity analysis is not straightforward. In ROI-based functional connectivity analysis, where the time series of both the reference (seed ROI) and each voxel in the brain are considered to contain both a neuronal component and a noise component, the null hypothesis (H₀) is that there is no correlation between the respective neuronal components of the seed ROI and a given voxel. Accordingly, a Type I error (false positive) occurs when there is an absence of neuronal correlation, and yet the noise components correlate strongly enough so that the overall correlation coefficient exceeds a threshold; a Type II error (false negative) occurs when the neuronal components of the seed ROI and a given voxel are correlated, but the correlation is not detected because of noise in the seed ROI and/or the queried voxel. In contrast with a standard analysis of task activation, wherein the reference time series is the expected noise-less neuronal time course (often modeled by a binary stimulus waveform convolved with a hemodynamic response function), the reference time series in functional connectivity is derived from a region of the brain itself, and it is not known which part of the signal is due to neural activity and which is due to noise. Nevertheless, physiological noise correction – by reducing the noise component of BOLD signal time series – aims to improve the estimation of neuronally-driven correlations between regions of the brain. Here, after correction, it was hypothesized that: (1) positive correlations with the DMN seed time series will diminish, as correlations will be reduced in voxels that had been falsely coupled due to the common influence of respiratory and cardiac noise, and that (2) negative correlations with the DMN seed time series, if they exist, will increase due to the reduction of respiratory and cardiac noise that can obscure these dynamics.

Methods

Subjects

Participants included 15 healthy adults (7 female, aged 29 ± 11.5 years). All subjects provided written, informed consent, and all protocols were approved by the Stanford Institutional Review Board.

Imaging parameters

Magnetic resonance imaging was performed at 3.0 T using a GE whole-body scanner (GE Healthcare Systems, Milwaukee, WI). Seven of the 15 subjects were scanned on a GE Signa HDX (rev. 12M5) using a custom quadrature birdcage head coil, while the remaining 8 subjects were scanned on a GE Signa 750 (rev. 20) using an 8-channel head coil. Head movement was minimized with a bite bar. Thirty oblique axial slices were obtained parallel to the AC-PC with 4-mm slice thickness, 1-mm skip. T2-weighted fast spin echo structural images (TR = 3000 ms, TE = 68 ms, ETL = 12, FOV = 22 cm, matrix 192 × 256) were acquired for anatomical reference. A T2*-sensitive gradient echo spiral-in/out pulse sequence (Glover and Lai, 1998; Glover and Law, 2001) was used for functional imaging (TR = 2000 ms, TE = 30 ms, flip angle = 77°, matrix 64 × 64, FOV = 22 cm, same slice prescription as the anatomic images). A high-order shimming procedure was used to reduce B0 heterogeneity prior to the functional scans (Kim et al., 2002). Importantly, a frequency navigation correction was employed during reconstruction of each image to eliminate blurring from breathing-induced changes in magnetic field; no bulk mis-registration occurs from off-resonance in spiral imaging (Pfeuffer et al., 2002).

Resting state scan

All subjects underwent a resting state scan, for which they were instructed only to keep their eyes closed and remain awake. For 7 of the subjects, the duration of the scan was 8 min; for the remaining 8 subjects, the duration was 16 min, but only the first 8 min of data were used for the present analysis.

Working memory task

Seven of the 15 subjects (all scanned on the Signa HDX) performed an event-related Sternberg working memory (WM) task (Sternberg, 1969), consisting of 3 back-to-back 5 s trials (0.5 s encoding, 3 s maintenance, 1.5 s probe) followed by 45 s of fixation, repeated 10 times (total duration = 10 min). Encoding stimuli consisted of 4 randomly-selected uppercase letters in a cross-like configuration around the center of the screen, and the probe stimulus was a single lowercase letter presented at the center of the screen. This task was used only in choosing a seed coordinate for the resting-state functional connectivity analysis and for identifying regions of interest (ROIs) associated with task-induced deactivation (described below).

Physiological monitoring

Cardiac and respiratory processes were monitored using the scanner's built-in photoplethysmograph placed on a finger of the left hand and a pneumatic belt strapped around the upper abdomen, respectively. Cardiac and respiratory data were both sampled at 40 Hz on the Signa HDX, and at 100 Hz and 25 Hz, respectively, on the Signa 750. A file containing cardiac trigger times and respiratory waveforms was generated for each scan by the scanner's software. Values in the respiratory waveform were converted to a percentage of the full scale (difference between the maximum and minimum belt positions measured over the scan). Only the fractional variations in the waveform, rather than the absolute amplitude values, were of importance in the current study.

fMRI data pre-processing

Functional images were pre-processed using custom C and Matlab routines. Pre-processing included slice-timing correction using sinc interpolation, spatial smoothing with a 3D Gaussian kernel (FWHM=5 mm), and removal of linear and quadratic temporal trends. No additional temporal band-pass filtering was performed. The first 6 time frames were discarded to allow the MR signal to equilibrate. Spatial normalization to a standard template was not performed; computations were done in the original subject-space and voxel dimensions (3.4375 mm × 3.4375 mm × 4 mm).

Motion analysis

Motion parameters were calculated using methods described in (Friston et al., 1996). Image coregistration was not performed because of possible interpolation errors and unintended smoothing across voxels. Therefore, even though a bite bar was used, it was important to verify that motion was minimal. The maximum peak-to-peak excursion and root mean square (RMS) fluctuation for the 3 translational and 3 rotational motion parameter time series were calculated for the segment of resting state data used in the analysis. Rotations were converted to worst-case translations by multiplying by 65 mm, an average head radius (Thomason and Glover, 2008). Summary statistics are reported as the maximum of these values over the 6 axes of motion.

Physiological noise correction

Physiological noise correction consisted of (1) removal of time-locked cardiac and respiratory artifacts using RETROICOR (Glover et al., 2000), and (2) removal of low-frequency respiratory and heart rate effects using methods described in (Chang et al., 2009), which will be referred to as RVHRCOR. Briefly, RVHRCOR utilizes the following steps: First, a “respiratory variations” (RV) time series is computed as the root-mean-square amplitude of the respiration waveform across a 6 s sliding window, and is then convolved with an impulse response known as the “respiration response function” (Birn et al., 2008). Secondly, a heart rate (HR) time series is computed as the inverse of the average beat-to-beat interval in a 6 s sliding window, and convolved with the “cardiac response function” (Chang et al., 2009). The convolved RV and HR waveforms (RVx and HRx, respectively) are then simultaneously projected out of every voxel's time series using multiple regression (see Appendix A for further details). It was determined that reversing the order in which RETROICOR and RVHRCOR were applied made little difference. Unless otherwise specified, “physiological noise correction” will henceforth refer to the application of the 2 corrections described here.

WM (de)activation analysis

WM data were corrected for physiological noise. A binary (“boxcar”) WM task design waveform was convolved with a standard hemodynamic response function (Glover, 1999), and linear regression was applied to produce a negative (deactivation) contrast map for this covariate. The resulting individual-subject contrast maps were normalized to the SPM5 EPI template and entered into a group-level random-effects analysis using SPM5 (http://www.fil.ion.ucl.ac.uk/spm). Although only a subset of subjects performed the WM task, this task was used only to localize a seed ROI for functional connectivity and to define regions exhibiting task-induced deactivation for post-hoc ROI analysis of functional connectivity maps (described below).

Resting-state functional connectivity analysis

The DMN and its anti-correlated network were quantified using a standard ROI-based functional connectivity analysis (Biswal et al., 1995). An 8mm-radius sphere centered at (-4,-58,30) mm (Talairach coordinate = (-4,-55,30)) in the precuneus/PCC was chosen as the seed ROI. This center coordinate was a local maximum in the group-level WM deactivation map derived as above, and the resulting spherical ROI was observed to overlap with those of several previously-published studies (Fox et al., 2005; Fransson, 2005; Greicius et al., 2003). The ROI was defined in MNI space using MarsBar (http://marsbar.sourceforge.net) and reverse-normalized to each subject's mean functional image using SPM5. For each subject, the mean time series across all voxels in the ROI was extracted, and the Pearson correlation coefficient (r) was computed with the time series of every voxel in the brain. Positive and negative correlation maps were thresholded at |r|>0.15 (T>2.34, corresponding to p<0.01 uncorrected for N=240 time points).

The process of extracting the mean precuneus/PCC ROI time series and correlating it against all brain voxels was performed both before and after physiological noise correction was applied to the data. For comparison, these steps were also performed after a global signal removal (and no physiological noise correction) was applied to the data. Global signal removal was carried out by extracting the whole-brain average time series and projecting it out of every voxel's time series using linear regression. In other words, if y is the (mean-centered) time series of a voxel and g is the whole-brain average time series, then the voxel time series after global signal removal (y_glob) would be y_glob = y − g(g^Tg)⁻¹ g^Ty.

An additional comparison was performed, in which only the time series of white matter and cerebrospinal fluid (CSF) ROIs were regressed out of the data prior to correlation analysis. The assumption underlying this method is that white matter and CSF time series may carry physiological fluctuations that are similar to those affecting gray matter, while containing little contribution from neural activity (Behzadi et al., 2007; Fox et al., 2005). But, as previous studies of resting-state networks have removed white matter and CSF signals only in conjunction with removing the global average brain signal (e.g. Fox et al., 2005; Fair et al., 2008; Clare Kelly et al., 2008), the effects of regressing out white matter and CSF signals alone are unknown. This method is of particular interest because it can be applied without separately monitoring physiological responses, and – although derived from the fMRI data itself – does not pose the same problems as global signal removal since the white matter and CSF ROIs should not overlap with resting-state networks. In the present study, white matter and CSF (right lateral ventricle) ROIs were first defined as 6mm-diameter spheres in MNI space, where the choice of center coordinates for each ((26,-12,35) and (19, -33, 18), respectively) was guided by the SPM5 a priori masks. These spherical ROIs were then reverse-normalized to each subject's native space, and intersected with subject-specific white matter and CSF partial volume images (thresholded at a partial volume fraction >90%) to minimize overlap with gray matter. Subject-specific partial volume images were obtained by segmenting the T2-weighted anatomical image using the FAST software implemented in FSL(Smith et al., 2004; Zhang et al., 2001). Time series were extracted and projected out of the data via linear regression.

To examine negative and positive correlations with the DMN at the group level, individual subjects' correlation maps were normalized into a common space (the SPM EPI template). To perform group-level statistical analyses, individual subjects' correlation maps were first converted into linear regression weights (β = r · σ_y/σ_x, where σ_y is the standard deviation of the voxel time series and σ_x is the standard deviation of the seed ROI time series), and were subsequently normalized to the SPM5 EPI template, spatially resampled at a voxel size of 2 mm isotropic, and entered into a group-level random-effects analysis using SPM5. A nuisance factor of “scanner” was included since subjects had been scanned on 1 of 2 different scanners; it was furthermore verified that separate analyses of the 2 within-scanner groups of subjects yielded results consistent with the analysis of the entire group. Group-level statistical maps appear superimposed on the ch2 template brain from the MRIcro software (http://www.mricro.com), and anatomical regions/Brodmann areas were determined using MRIcro built-in atlases. All maps (individual and group-level) are shown in radiological convention.

An ROI analysis was used to quantify region-specific changes in DMN connectivity. ROIs were defined by taking the intersection of (1) the group-level random-effects map of positive correlation with the precuneus/PCC ROI (p<0.001) when no corrections were applied to the data, and (2) the working memory deactivation contrast (p<0.05). Six separate ROIs were defined by intersecting the resulting map with six anatomically-defined (AAL) ROIs (anterior cingulate cortex, bilateral angular gyri, dorso-medial prefrontal cortex (DMPFC), and bilateral parahippocampal gyri (PHG)) using the MarsBar software.

Results

Motion

Across subjects, the peak and RMS excursion in head motion were 0.67±0.42 mm and 0.10±0.07mm, respectively (mean ± SD).

Comparison of physiological noise regressors, white/CSF signals, and the global signal

Correlation coefficients between the global signal and both respiratory and cardiac RVHRCOR regressors are shown in Table 1. Correlations with the global signal ranged from -0.10 to 0.69 for RVx, and from -0.15 to 0.49 for HRx. The white matter and CSF ROIs also demonstrated significant correlations with the global signal (Table 1), ranging from -0.02 to 0.57 for white matter and -0.36 to 0.46 for CSF. Further analysis revealed that both white matter and CSF signals tended to correlate more strongly with HRx than RVx: across subjects, white matter was correlated with HRx at r = 0.24±0.17, and with RVx at r = 0.00±0.16; CSF was correlated with HRx at r = 0.17±0.21, and with RVx at 0.01±0.15 (mean ± SD).

Table 1. Correlations between the global signal and RVHRCOR physiological regressors, white matter ROI signal, and CSF ROI signal.

Correlation coefficients between the global (whole-brain average) signal and the RVHRCOR regressors, white matter ROI signal, and CSF ROI signal for each subject's 8-min resting state scan. ‘RVx’ refers to the RV signal convolved with the respiration response function, and ‘HRx’ refers to the HR signal convolved with the cardiac response function.

subject	RVx v. global (r)	HRx v. global (r)	White v. global (r)	CSF v. global (r)
1	0.25 **	0.43 **	0.45 **	-0.08
2	0.46 **	0.44 **	0.39 **	0.37 **
3	0.48 **	0.35 **	0.50 **	0.33 **
4	0.34 **	0.49 **	0.25 **	0.46 **
5	0.44 **	0.24 **	-0.02	-0.05
6	-0.10	0.44 **	0.34 **	0.23 **
7	0.11	0.31 **	0.57 **	0.27 **
8	0.45 **	0.15 *	0.04	0.05
9	0.57 **	-0.03	0.19 *	0.11
10	0.69 **	-0.15	0.35 **	0.30 **
11	0.10	-0.06	-0.02	0.03
12	0.52 **	0.31 **	0.04	-0.36 **
13	0.17 *	0.21 **	0.44 **	-0.08
14	0.08	0.09	0.07	-0.15
15	-0.03	0.18 *	0.08	-0.15

^**p<0.001 (r>0.20);

^*p<0.01 (r>0.15)

Negative correlations with the DMN

Negative correlations (r<-0.15) with the precuneus/PCC seed region are shown for 3 different subjects in Fig. 1 (blue color scale). The spatial extent of negatively-correlated voxels before correction and after physiological noise correction, white/CSF signal removal, and global signal removal are quantified for all subjects in Fig. 2A.

Figure 1.

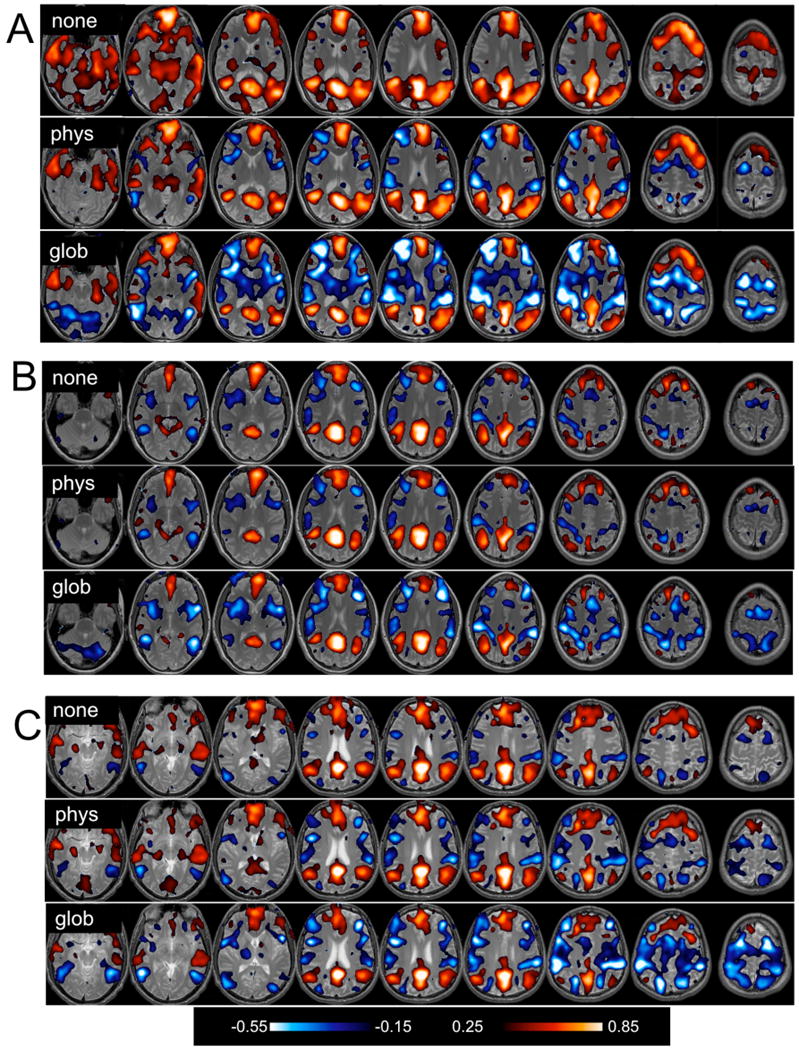
Positive (red) and negative (blue) correlations with the precuneus/PCC ROI, thresholded at |r|>0.15. Maps for 3 different subjects (A, B, and C) depict correlation coefficients before correction (“none”), after physiological noise correction (“phys”), and after global signal removal (“glob”).

Figure 2.

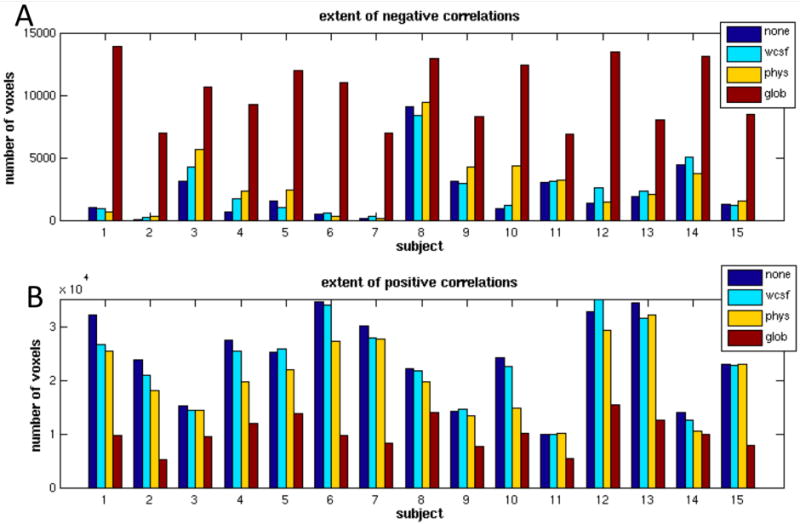
Spatial extent of (A) negative (r<-0.15) and (B) positive (r>0.15) correlations for each subject before correction (blue), after white/CSF signal removal (cyan), after physiological noise correction (yellow), and after global signal removal (red).

Negative correlations were present within individual subjects even without physiological or global signal removal, and Fig. 1 indicates that they were primarily localized to regions of the TPN. In 11 out of 15 subjects (including the subjects in A and C of Fig. 1), physiological noise correction increased the extent of negative correlations, though to a much lesser degree than global signal removal. Across subjects, the percent change in the number of negatively correlated (r<-0.15) voxels was 28.5% ± 9.24% after physiological noise correction, and 382% ± 106% after global signal removal (mean ± SE). White/CSF signal removal also slightly increased the extent of negative correlations, though to a lesser degree than physiological noise correction (6.9% ± 4.0%),.

To visualize the anatomical locations of negative correlations across subjects, a map was constructed that depicts – for each voxel – the number of subjects for which that voxel was negatively correlated at r<-0.15. Separate maps were constructed for each condition (no correction, physiological noise correction, white/CSF signal removal, and global signal removal); see Fig. 3. Figure 3 shows that physiological noise correction not only increased the extent of negative correlations, but tended to increase them in brain areas that were common across subjects. Anatomical regions in which at least 4 subjects exhibited suprathreshold negative correlations before and after physiological noise correction are presented in Table 2. Global signal removal greatly increased the negative correlations over more widespread regions of the brain, as well as inter-subject variability (Figs. 1-3); however, it is apparent that regions with the greatest consistency across subjects after global signal removal were aligned with those having the greatest consistency after physiological noise correction.

Figure 3.

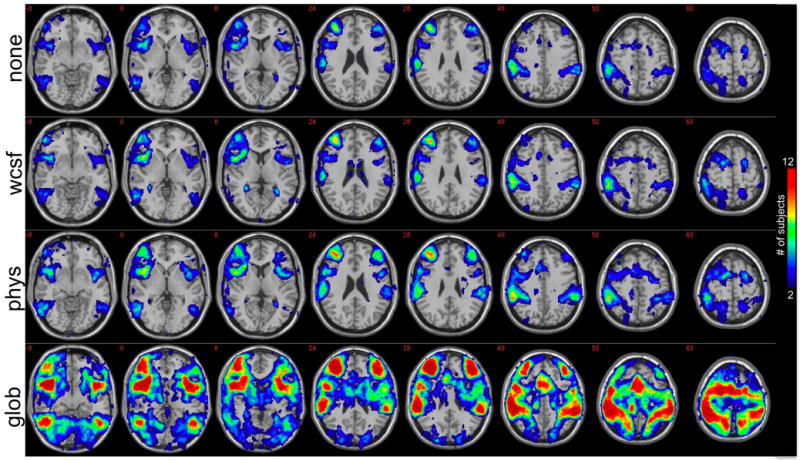
Anatomical locations where individual subjects had negative correlations with the precuneus/PCC ROI. The value at each pixel depicts the number of subjects that had a negative correlation (r<-0.15) at that pixel before any corrections were performed on the data (1st row; “none”), after white/CSF signal removal (2nd row; “wcsf”), after physiological noise correction (3rd row; “phys”), and after global signal removal (4th row; “glob”). Maps have been thresholded to show only voxels for which 2 or more subjects showed a negative correlation at r<-0.15.

Table 2. Negative correlations with precuneus/PCC in individual subjects before and after physiological noise correction.

Anatomical regions in which 4 or more subjects had negative correlations with the precuneus/PCC ROI (r<-0.15) before any corrections were applied to the data. After physiological noise correction, there were additional regions (beyond those present before correction) for which ≥4 subjects had negative correlations; these are indicated in boldface. BA, Brodmann area; operc, opercularis; tri, triangularis; SMA, supplementary motor area

Region	BA
L/R middle temporal	37
L/R insula	48
L/R inferior frontal (operc)	6/44
L/R middle frontal, inferior frontal (tri)	9/45/46/47
L/R superior frontal	6
R SMA	6
R mid cingulate	32
L/R precentral	6
R postcentral	2/3
L/R supramarginal, inferior parietal	40

Results of a group-level random-effects analysis of negative correlations with the precuneus/PCC are shown in Fig. 4, and clusters attaining a threshold of p<0.05 (uncorrected) are reported in Table 3. Before physiological noise correction, small clusters were present in bilateral inferior parietal cortices (supramarginal gyri; BA 40) and right DLPFC (BA 46). After physiological noise correction, cluster sizes increased and included the bilateral inferior parietal cortices (BA 40), bilateral insula/frontal operculum, and right DLPFC (BA 45/46). No regions, either before or after physiological noise correction, were significant at a corrected threshold of FDR=0.05. For comparison, results after global signal removal and white/CSF signal removal are also presented in Fig. 4. After global signal removal, negatively-correlated regions included bilateral superior and inferior parietal cortices (BA 7/40), bilateral middle/inferior temporal cortices (BA 37), bilateral DLPFC and ventrolateral preforntal cortex (BA 9/45/46/47), mid cingulate/SMA (BA 24/32), and premotor cortex (BA 6). White/CSF signal removal increased the cluster sizes of regions in the uncorrected (“none”) map, and introduced an additional cluster in the right insula, but the increases were smaller than those obtained with physiological correction.

Figure 4.

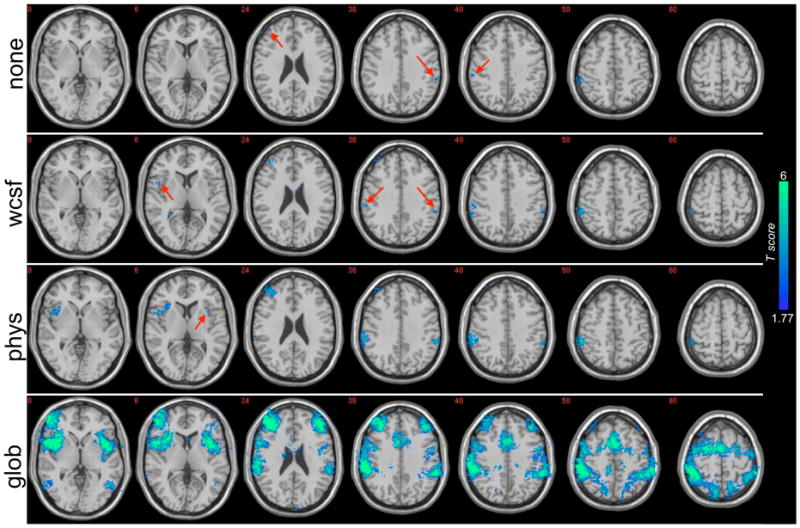
Regions having negative correlation (p<0.05 uncorrected) with the precuneus/PCC in a group-level (N=15), random-effects analysis. Results are shown before corrections were applied (“none”), after white/CSF signal removal (“wcsf”), after physiological noise correction (“phys”), and after global signal removal (“glob”). Locations of small clusters are indicated with red arrows. Intensity values represent T-statistics.

Table 3. Group-level negative correlations with the precuneus/PCC before and after physiological noise correction.

Region (BA), peak coordinates, cluster extent (# voxels), and peak Z-scores are reported for all foci exceeding p<0.05 (uncorrected) and having a minimum cluster extent of 10 voxels. Coordinates are reported in MNI space (mm). BA, Brodmann area; inf, inferior; mid, middle; operc, operculum.

Region	BA	x	y	z	Peak Z	Cluster size
Before Physio Correction
R inf parietal	40	58	-36	48	2.42	185
R supramarginal	40	62	-28	34	1.71
L inf parietal	40	-56	-38	38	2.37	32
R mid frontal	46	46	50	28	1.81	19
After Physio Correction
R inf parietal	40	58	-36	50	3.64	885
R supramarginal	40	64	-30	34	3
R supramarginal	40	64	-32	42	2.88
L supramarginal	40	-58	-38	36	3.38	155
L inf parietal		-50	-40	38	2.06
R mid frontal	45/46	44	48	22	2.99	560
R inf frontal operc	48	54	10	6	2.85	327
R insula	48	46	12	0	2.69
R insula	48	34	22	8	2.34
L insula	48	-34	14	6	2.02	17

After physiological noise correction, an increase in the (negative) value of the correlation coefficient between the seed ROI and a given voxel would arise from a reduction in the noise variance of the voxel and/or the seed time series, as well as from an increase in the covariance between a voxel and the seed. To further understand the sources of increased negative correlation, the percent increase in the magnitude of the numerator (covariance between the voxel and seed time series) and percent decrease in the denominator (product of the voxel and seed temporal standard deviations) of the correlation coefficient were separately examined, across all voxels demonstrating increased negative correlation after noise correction. From a linearization analysis, it can be seen that for small changes, the fractional change in a correlation coefficient can be approximated by the sum of the fractional changes of its numerator and denominator (Appendix B). It was observed that in 9 out of the 15 subjects, the percent increase in the numerator exceeded the percent decrease in denominator within the majority of voxels queried, while the reverse was true for the remaining 6 subjects. Hence, it appears that both the increased covariance, as well as decreased noise variance, contributed to the increased negative correlations obtained after physiological noise correction.

Positive correlations within the DMN

Positive correlations with the precuneus/PCC are shown for 3 different subjects in Fig. 1 (red color scale). Results of the group-level random-effects analysis of positive correlations are shown in Fig. 5, and the extent of positively-correlated voxels is quantified in Fig. 2B. The spatial extent of significant positive correlations is diminished after physiological noise correction is applied, and even further diminished after global signal removal. White/CSF signal removal also introduced slight decreases in the extent of positive correlations. Across subjects, the percent change in the number of positively correlated (r>0.15) voxels was -8.5% ± 1.1% after white/CSF signal removal, -19.1% ± 0.53% after physiological noise correction, -64.0% ± 1.0% after global signal removal (mean ± SE).

Figure 5.

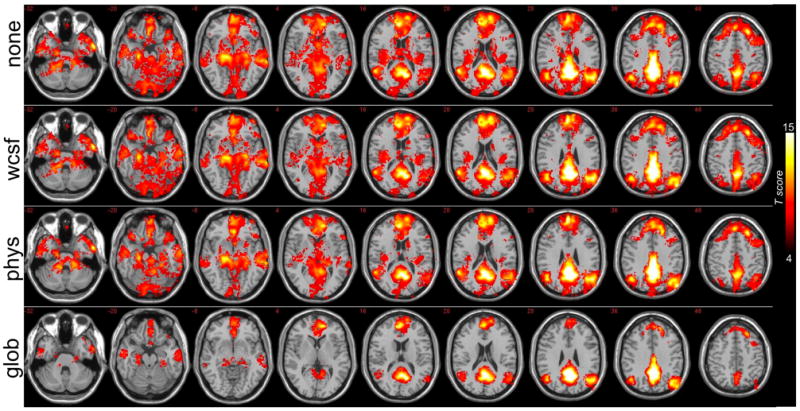
Group analysis (N=15) of regions having significant positive correlations with the precuneus/PCC before correction (“none”), after white/CSF signal removal (“wcsf”), after physiological noise correction (“phys”), and after global signal removal (“glob”). Intensity values represent T-statistics.

Figure 6 shows the mean T-scores from 6 default-mode ROIs, computed by averaging over voxels in the group-level T-maps for each of the 4 conditions (Fig. 5). The magnitude of positive correlations decreased after physiological noise correction, but decreased even more after global signal removal. Voxel-wise reductions in T-score due to physiological noise correction, however, were significant only in the PHG, while reductions due to global signal removal were significant in all 6 ROIs (p<0.01, paired t-test).

Figure 6.

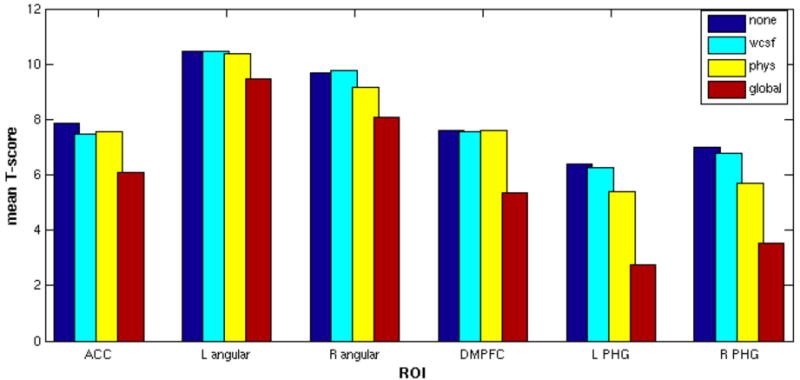
ROI analysis of DMN group-level statistics. For each of the 4 statistical maps of the DMN (shown in Figure 5), average T-scores were computed across voxels within 6 core regions of the DMN. ACC, anterior cingulate cortex; DMPFC, dorso-medial prefrontal cortex; PHG, parahippocampal gyrus.

Magnitude reductions varied across regions; for example, the left angular gyrus and DMPFC experienced only minor reductions due to physiological noise correction (ΔT̄ = 0.1 and 0.02, respectively), whereas decrements in the PHG were more pronounced (ΔT̄ =1.0 for the left hemisphere, and 1.3 for the right). Global signal reduction also had differential effects across ROIs, with average T-score decrements of 1.0 in the left angular gyrus and 3.7 in the left PHG.

Discussion

In the present study, negative correlations between the DMN and multiple key regions of the TPN were observed in the resting state, despite the fact that no global signal removal or scaling steps were performed in pre-processing. While regions of negative correlation were observed in some individual subjects prior to any noise correction, the use of model-based corrections for respiratory and cardiac noise substantially increased their magnitude and extent. The present study indicates that DMN and TPN regions may exhibit, on average, opposing (or nearly 180° out of phase) fluctuations in the absence of external stimuli.

Physiological noise correction enhanced the spatial extent and inter-subject consistency of negative BOLD signal correlations with the DMN. This suggests that cardiac and respiratory processes can obscure the underlying dynamics between brain regions, and illustrates the efficacy of procedures applied herein to remove such noise. The significant correspondence between the global average brain signal and both the RVx and HRx regressors (Table 1) indicates that much of the common signal expressed by voxels is due to these physiological processes, and argues that their removal should become a standard part of fMRI analyses.

The overlap with the global signal was not complete, however, indicating that the global signal contains sources that are not modeled by RETROICOR and RVHRCOR. Some of these sources could be of neural origin, such as regions involved in resting state networks that exhibit coherent neuronal fluctuations over widespread regions of the brain. In addition, noise signals from voxels with high temporal standard deviation due to motion or pulsation, such as the eye regions, edges of the brain, and CSF, are also weighted strongly in the global signal. Lastly, unmodeled physiological noise, such as autoregulatory processes and nonlinear interactions between respiratory and cardiac effects, may also contribute to noise in the brain and possibly the global signal.

After correction for physiological noise, negative correlations at the group level were observed in the DLPFC and bilaterally in the supramarginal gyri and insula/frontal operculum, areas that are commonly recruited in tasks involving attentional control and working memory (Corbetta and Shulman, 2002; Dosenbach et al., 2006). The fronto-insular region has also been implicated in emotional arousal (Critchley et al., 2002) and interoceptive awareness (Critchley et al., 2004). Additional regions of negative correlation, observed in at least 4 out of 15 individual subjects, included bilateral middle temporal cortices, premotor cortex, SMA, and a greater amount of prefrontal cortex (extending into BA 9 and BA 47)). The existence of negative correlations between these task-positive regions and the DMN may support existing theories that resting-state brain signals, on the level of large-scale networks, reflect shifts in state between an introspective, self-reflective mode and an outwardly-oriented, attentive mode (Buckner et al., 2008; Fox et al., 2005; Fransson, 2005).

Regions having negative correlation after physiological noise correction overlapped substantially with those having the greatest negative correlation magnitudes after global signal removal, both here and in previous studies that applied global signal removal (e.g. (Fox et al., 2005; Fransson, 2005)). Although a number of negatively-correlated voxels produced by global signal removal are artificial (Fox et al., 2008; Murphy et al., 2009), it is possible that regions that emerge consistently across subjects (e.g. the brightest regions in Fig. 3, bottom row) are indeed real, especially when they are significant after only physiological noise correction. Global signal removal may thus be useful for identifying candidate regions that are anti-correlated with the DMN; however, one must be careful about interpreting the precise magnitudes of these negative correlation coefficients, since (1) global signal regression is known to skew the distribution of correlation coefficients in ROI-based functional connectivity toward zero-mean (Murphy et al., 2009), and (2) the global signal, while containing some respiratory and cardiac components (Table 3), is not based in hypothesis and – since it is derived from the data itself – may contain important neural signals in addition to noise (see (Murphy et al., 2009) for a thorough discussion of the impact of global signal removal on fMRI time series).

One recent study (Murphy et al., 2009) also performed physiological noise corrections, but negative correlations with the DMN in task-positive regions could not be found at any threshold. One potential reason for this disparity is the difference in physiological correction algorithms: although RETROICOR was applied, just as in the present study, correction for low-frequency heart rate effects was not performed and correction for respiratory variations was accomplished by computing a respiratory volume per time (RVT) signal (defined as the breath-to-breath volume divided by breath-to-breath time interval) and regressing it out of the fMRI data at time shifts ranging from -10 to 40 s. In contrast, the present study convolved the respiratory variation time series with an impulse response (respiration response function (Birn et al., 2008))) before regressing it out of the fMRI time series, and used a sliding-window measure of breathing volume (RV) rather than a breath-to-breath measure. While RV and RVT tend to be correlated during normal breathing (Chang et al., 2009), the convolution step is likely to introduce differences since the respiration response function employed here does not resemble a delta function.

However, given that the present study found negative correlations with the DMN within single subjects even before corrections were applied (e.g. Fig. 1), it is possible that other factors, such as image acquisition methods, were critical for obtaining the present results. While studies failing to observe negative correlations have used conventional echo-planar sequences (Golland et al., 2007; Murphy et al., 2009), the current study used a spiral-in/out sequence that has been shown to improve the signal-to-noise ratio (SNR) in uniform brain regions as well as to reduce susceptibility dropout in frontal and parietal regions (Glover and Law, 2001). In addition, a navigator correction was performed to correct for breathing-induced modulation of the magnetic field (Pfeuffer et al., 2002). The additional SNR provided by these techniques may have enabled the observation of anti-correlations with the DMN in the absence of any noise correction.

Most previous ROI-based functional connectivity studies have applied low-pass temporal filtering as a pre-processing step to increase the contrast-to-noise ratio (e.g. (Fox et al., 2005; Fransson, 2005; Murphy et al., 2009)), since prior work has indicated that resting-state correlations are based primarily in the low-frequency (<0.1 Hz) spectrum (Cordes et al., 2001). While no temporal filtering was originally performed in the present study, the use of the full frequency bandwidth may account for some of the observed differences with previous work – particularly, the presence of negative correlations. To understand the impact of low-pass filtering, data were re-analyzed after applying a low-pass filter (<0.1 Hz) prior to calculating positive and negative correlations with the PCC. Results after low-pass filtering were similar to those of the unfiltered data; in fact, low-pass filtering served to slightly increase the extent and magnitude of negative correlations in both the uncorrected and physiologically-corrected data (Fig. 7a), and decrease the extent and magnitude of positive correlations (Fig. 7b). Thus, low-pass filtering is not believed to be a source of difference with previous studies, and appears to exert an influence in the same direction as physiological noise correction.

Figure 7.

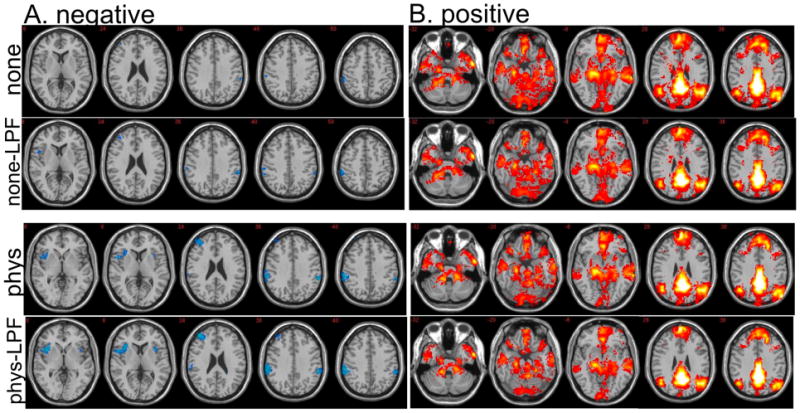
Effect of temporal low-pass filtering on a group-level, random-effects analysis of (A) negative and (B) positive correlations with the PCC. Maps are thresholded identically to Figs. 4 and 5: negative correlations are shown at 1.77<T<6, and positive correlations are shown at 4<T<15. Slices shown are a subset of those in Figs. 4 and 5. (“none” = uncorrected data; “none-LPF” = uncorrected data after low-pass filtering; “phys” = physiological noise-corrected data; “phys-LPF” = physiological noise-corrected data after low-pass filtering.)

While physiological noise correction increased the extent of regions negatively correlated with the precuneus/PCC, the extent of positive correlations was reduced. This is consistent with previous accounts (Birn et al., 2006; Chang et al., 2009), and with observations that physiological noise exerts a nearly global influence on the BOLD signal that can artificially couple widespread regions of the brain (Birn et al., 2006; Birn et al., 2008; Chang et al., 2009; de Munck et al., 2008; Glover et al., 2000; Shmueli et al., 2007; Wise et al., 2004). While the overall extent was reduced, Fig. 6 indicates that mean T-scores in all queried ROIs except the PHG were not significantly reduced by physiological noise correction. On the other hand, global signal removal significantly diminished DMN correlations within these areas, which further cautions against its use.

Regression of white matter and CSF ROIs also elicited increases in negative correlations with the PCC (Figs. 3 and 4), as well as reductions in positive correlations (Fig. 5), though to a lesser extent on average than physiological noise correction. Differences between the two correction methods might arise because white matter and CSF signals may not adequately capture respiratory-related signals, since previous work has shown that respiration-induced modulation of arterial CO₂ primarily affects gray matter (Birn et al., 2006; Birn et al., 2008; Chang et al., 2009; Glover et al., 2000), and the present study also observed a lack of correlation between the white/CSF signals and the respiratory variations regressor (RVx; data not shown). In addition, it is possible that varying the size and location of white/CSF ROIs can alter the outcome of the correction; future work will be necessary to resolve this question.

By contrasting Figs. 4 and 5, it is evident that negative correlations with the PCC were weaker and less consistent across subjects than positive correlations. One possible explanation is that residual physiological noise, as well as other unmodeled, common noise sources, skews correlation coefficients in the positive direction. Another possibility is that the anti-correlated behavior between the DMN and TPN networks is a transient, rather than persistent, phenomenon that is dependent upon particular states of cognition and/or arousal. Figure 8 depicts, for one subject, time series averaged across regions positively (red) and negatively (blue) correlated with the PCC ROI at |r|>0.15. These traces indicate that phase differences between the networks may vary over time. Further work will be necessary to illuminate and understand the dynamic behavior of these networks.

Figure 8.

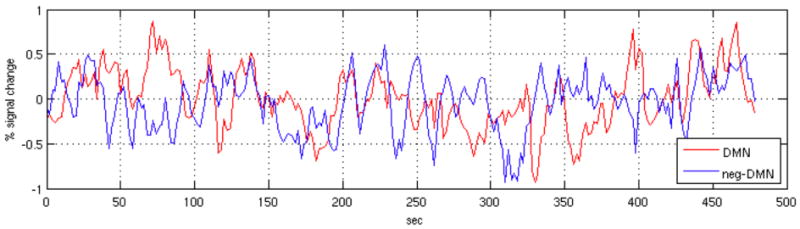
Mean time series of voxels positively (r>0.15; red line) and negatively (r<-0.15; blue line) correlated with the precuneus/PCC ROI, for one subject.

Conclusions

The current findings indicate that negative correlations between DMN and task-positive regions can be observed in the absence of global signal removal. A group-level random effects analysis revealed clusters at an uncorrected (p<0.05) threshold (though none were significant at FDR=0.05). Physiological noise correction, based on respiratory and cardiac monitoring in conjunction with a priori models, both increased the extent of negative correlations and decreased the extent of positive correlations. Regression of white matter and CSF ROI signals also increased and decreased the extent of negative and positive correlations, respectively, though to a lesser degree than physiological noise correction. Results suggest that modeling physiological noise will be crucial for accurately quantifying dynamic relationships within and across brain networks.

Appendix A: RVHRCOR

Let x_r and x_h denote the respiratory variations and heart rate time series, respectively, and h_r and h_h denote the respiration response function (Birn et al., 2008) and cardiac response function (Chang et al., 2009), respectively:

$$h_r(t)=0.6t^{2.1}{e}^{-t/1.6}-0.0023t^{3.54}{e}^{-t/4.25},$$

$$h_h(t)=0.6t^{2.7}{e}^{-t/1.6}-16\frac{1}{\sqrt{2\pi (9)}}\text{exp}(-\frac{1}{2}\frac{{(t-12)}^2}{9}).$$

Let z_r ≡ x_r ⊗ h_r and z_h ≡ x_h ⊗ h_h, where “⊗” indicates convolution. The convolved signals, z_r and z_h (referred to as RVx and HRx in the text), represent the modeled BOLD signal response to low-frequency respiratory and cardiac processes. In the model proposed in (Chang et al., 2009), these 2 sources of physiological noise contribute additively to the time series of a voxel (y):

$$y={\beta }_r{z}_r+{\beta }_h{z}_h+\varepsilon$$

where ε contains the desired (neural) component of the time series as well as unmodeled noise, and is assumed to be small compared to the physiological noise components. The coefficients β_r and β_h can be estimated using least squares:

$$\left[\begin{array}{c}{\widehat{\beta }}_r\\ {\widehat{\beta }}_h\end{array}\right]={({\mathit{\text{Z}}}^{\mathit{\text{T}}}\mathit{\text{Z}})}^{-1}{\mathit{\text{Z}}}^{T}y$$

where Z = [z_r, z_h], and the corrected voxel time series is taken to be the residual:

$$y_{\mathit{\text{phys}}}=y-{\widehat{\beta }}_r{z}_r-{\widehat{\beta }}_h{z}_h.$$

Appendix B

Let $r=\frac{n}{d}$, where n = σ_xy, d = σ_xσ_y, and r is the correlation coefficient between the time series of a seed region (x) and a voxel (y). Let Δn denote the increase in the numerator, and let Δd denote the decrease in the denominator. Then $\Delta r=\frac{\partial r}{\partial n}\Delta n+\frac{\partial r}{\partial d}(-\Delta d)=\frac{1}{d}\Delta n+r\frac{\Delta d}{d}=r(\frac{\Delta n}{n}+\frac{\Delta d}{d})$, and therefore $\frac{\Delta r}{r}=\frac{\Delta n}{n}+\frac{\Delta d}{d}$.