Abstract
Quantum noise as well as anatomic and uptake variability in patient populations limits observer performance on a defect detection task in myocardial perfusion SPECT (MPS). The goal of this study was to investigate the relative importance of these two effects by varying acquisition time, which determines the count level, and assessing the change in performance on a myocardial perfusion (MP) defect detection task using both mathematical and human observers. We generated 10 sets of projections of a simulated patient population with count levels ranging from 1/128 to around 15 times a typical clinical count level to simulate different levels of quantum noise. For the simulated population we modeled variations in patient, heart and defect size, heart orientation and shape, defect location, organ uptake ratio, etc. The projection data were reconstructed using the OS-EM algorithm with no compensation or with attenuation, detector response and scatter compensation (ADS). The images were then post-filtered and reoriented to generate short axis slices. A channelized Hotelling observer (CHO) was applied to the short-axis images, and the area under the receiver operating characteristics (ROC) curve (AUC) was computed. For each noise level and reconstruction method, we optimized the number of iterations and cutoff frequencies of the Butterworth filter to maximize the AUC. Using the images obtained with the optimal iteration and cutoff frequency and ADS compensation, we performed human observer studies for 4 count levels to validate the CHO results. Both CHO and human observer studies demonstrated that observer performance was dependent on the relative magnitude of the quantum noise and the patient variation. When the count level was high, the patient variation dominated, and the AUC increased very slowly with changes in the count level for the same level of anatomic variability. When the count level was low, however, quantum noise dominated, and changes in count level resulted in large changes in the AUC. This behavior agreed with a theoretical expression for the AUC as a function of quantum and anatomical noise levels. The results of this study demonstrates the importance of the tradeoff between anatomical and quantum noise in determining observer performance. For myocardial perfusion imaging, it indicates that, at current clinical count levels, there is some room to reduce acquisition time or injected activity without substantially degrading performance on myocardial perfusion defect detection.
INTRODUCTION
In nuclear medicine imaging it is essential to find a balance between diagnostic quality of the images, which can, in principle, be improved by longer acquisition times, with the need to reduce acquisition time or injected activity. It is therefore important to study the tradeoff between image quality and count level (which is proportional to the product of injected activity and acquisition time for a given patient and imaging system). A major goal of this paper was to investigate these tradeoffs in the context of myocardial perfusion SPECT (MPS). In the process, we provide some theoretical and experimental results that shed light on the important issues that determine the tradeoff for other applications.
Human and mathematical observer studies and ROC analysis are powerful tools for optimizing and evaluating image quality for a variety of applications (Barrett et al., 1993; Barrett et al., 1992; Metz, 1978, 1986; Barrett, 2003). Human and mathematical observer performance is affected by both quantum noise and object variability (Barrett, 1990). In nuclear medicine imaging, quantum noise results from the random nature of radioactive decay and absorption, resulting in Poisson noise in acquired projection data. As a result, the noise level in nuclear medicine images is a function of the count level of the projection data. Variations in anatomy and uptake across a patient population, referred to herein as object variability, are also a stochastic phenomenon. The level of anatomical noise resulting from this variability is a constant for a given patient population.
It is well known that quantum noise has a significant impact on the reconstructed image quality in SPECT. Several previous studies have characterized the quantum noise propagation for different reconstruction algorithm (Barrett et al., 1994; Soares et al., 2000; Soares et al., 2005; Wilson et al., 1994). Barrett et al. (Barrett et al., 1994) derived a theoretical formulation to characterize the ensemble statistical properties for the maximum likelihood-expectation maximization (ML-EM) algorithm as a function of iteration; this formulation was then validated by Wilson et al (Wilson et al., 1994). Soares et al. (Soares et al., 2000; Soares et al., 2005) extended the formulation to rescaled block-iterative (RBI) image reconstruction methods, a class to which the ordered subset-expectation maximization (OS-EM) belongs.
The effects of object variability have been less well studied. Barrett gives a general formalism for including the effects of object variability and quantum noise in the covariance matrix (Barrett, 1990). In this formalism, the total covariance is the sum of object covariance matrix and quantum noise covariance matrix. We have previously demonstrated the importance of including object variability in CHO studies in order to realistically model the clinical task in MPS imaging (He et al., 2004).
In this paper, we investigated the effects of quantum noise and object variability noise on MPS images. First, we derived an expression for observer performance that explicitly gives an expression for the signal-to-noise ratio (SNR) for a Hotelling Observer that includes the effects of both anatomical and quantum noise. We then empirically investigated the effect of count level on performance on a MPS defect detection task for both a previously validated Channelized Hotelling observer (CHO) and human observers. Using a previously developed phantom population (He et al., 2004), we generated a projection population for 10 noise levels. These projection data populations were then reconstructed with the OS-EM algorithm including no compensation or compensation for attenuation, the collimator-detector response, and scatter (ADS). We applied standard post processing methods to the reconstructed images, including low-pass filtering, reorientation to short axis, cropping and windowing to a 256-level gray scale. CHOs were then applied to the short axis image ensemble for each noise level and AUC values for CHOs were estimated. We then validated the ability of the CHO to predict human observer performance by performing a human observer study using images from four of the noise levels.
THEORY
In the following we seek to derive an expression for the change in defect task detection performance as a function of changes in the count level. We start by writing that the reconstructed image is the sum of the mean reconstructed image plus the noise. That is,
| (1) |
where f̂, â and Ê are the estimate, mean estimate over noise realizations of the object, and noise contribution to the object estimate after k iterations, respectively.
We first consider averaging over noise realizations. This gives:
| (2) |
where f is the object that was imaged, and the expectation of the noise is zero, .i.e.,
| (3) |
We define ā as the average of f̂ over an ensemble of objects:
| (4) |
where the subscript f indicates averaging over all the objects in the ensemble. The ensemble covariance matrix, Kf̂, can then be expressed as:
| (5) |
where the subscript n denotes the average over noise realizations for a particular object and the subscript f denotes averaging over all objects in the ensemble. The terms in Eqn. (5) labeled by the asterisks can be simplified to give:
| (6) |
| (7) |
| (8) |
and
| (9) |
So, we have that the ensemble covariance matrix in (5) is given by:
| (10) |
where < Ka >f characterizes the object variability that includes the effects of anatomical, uptake ratio and count level variability from patient to patient. However, note that < Ka >f is not an estimate of the object covariance matrix, but rather the object variability of the mean reconstructed images. Further, < KE|f >f is the contribution of quantum noise to the ensemble covariance matrix of the reconstructed images.
In a binary classification task where the two classes have the same covariance matrices, the SNR of the Hotelling observer test statistics, SNR, can be expressed as:
| (11) |
where Δf̄ is the difference in the ensemble mean difference of the two classes. i.e.
| (12) |
Substituting (10) and (12) into (11) we have
| (13) |
In Eqn (13), is the square of SNR of the reconstructed images.
To perform a CHO study, the reconstructed images are often filtered and reoriented and then channelized. All these operations can be treated as linear operations, and we thus combine them in a single linear operator, O to represents the overall effect of the post-processing and channelizing process. Application of O results in feature vectors, each element of which results from application of a linear operation to the image. Let ν⇀ = Of⇀, where ν⇀ is the feature vector. As a result, from the central limit theorem, each element in the feature vector is approximately Gaussian distributed. Eqn. (13) thus becomes
| (14) |
where Δν̄ = OΔf̄, Kν̂ = OKf̂Ot, âν = Oâ, Kaν = OKaν Ot, and KEν|f = OKE|fOt. When the feature vectors follow a multi-variate Gaussian distribution, the area under the receiver operating characteristics (ROC) curve (AUC) for the channelized Hotelling observer is related to the Hotelling SNR by (Barrett, 2003):
| (15) |
where erf() represents the error function. So, studying the properties of SNRs for different count levels provides information about the AUC.
Another measure of the separability of the two classes is the Hotelling trace, given by
| (16) |
where S2 is the intraclass scatter matrix, and S1 is the interclass scatter matrix. S2 and S1 are written as sums of class contributions weighted by class prevalence. The relationship between the Hotelling trace, J, and SNR is given in (Barrett, 2003) by the expression
| (17) |
For a certain count level (or noise level), the test statistic’s SNRν can be estimated. Suppose we now change the noise level by scaling activity by n. Then we have f′ = nf, and ν′ = nν. Note that, since the origin of the noise is Poisson in nature, the noise term in (1) is not linearly scaled. We use E′ to represent the noise term after changing the noise level. Further, since each of the objects in the ensemble is scaled by n, we have that both the noise and object portions of the covariance will be scaled by n2. Thus, the SNRν for the new count level, , is given by:
| (18) |
From Eqn. (18) we can see that, for the same ensemble, the change in the SNR is completely determined by the quantum noise. In other words, change of noise level does not affect the anatomical covariance term. Thus, the SNR (or AUC) is determined by the relative magnitude of the quantum noise variability with respect to the object variability.
Again, note that < Ka >f is not an estimate of the object covariance matrix, but rather the object variability of the mean reconstructed images, and Δν̄ is the mean difference of the estimate ν. This means that, when performing an observer study, we must calculate the statistics of the ensemble of object estimates, f̂, and not the ensemble of objects. This makes sense, since it is the object estimates (i.e., the reconstructed images) that are used in the diagnosis as opposed to the objects.
From Eqn. (18), we see that when the count level is high (the noise level is low), object variability dominates, and the AUC will be relatively constant as the count level increases. However, when the count level is low, quantum noise dominates, and changes in count level will result in large changes in the AUC value. Thus, based on this, we predict a rapid increase in the AUC value for low count situations, with a saturation of the AUC for high count situations when defect detectability performance is limited by object variability.
Note that any reconstruction of objects with quantum noise and object variability will have this behavior with exposure time, i.e. AUC saturation at high exposure time and steep rise in AUC at low exposure time. The above derivation illustrates this very general behavior for the case of post-processed OS-EM.
METHODS
In order to realistically model object variability, we used a previously developed NCAT phantom ensemble and corresponding set of Monte Carlo simulated projection data. An overview of the simulation methods is provided below. For details on the phantom population parameters, and simulation methods, please refer to (He et al., 2004).
Phantom population and projection data
The object variability modeled includes anatomical, organ uptake ratio, and count level variabilities based on measurements from clinical patient data (He et al., 2004). The phantom population was developed using the 3D NCAT phantom (He et al., 2004). We varied anatomical parameters by randomly sampling them from distributions obtained from the Emory PET Torso Model Database (He et al., 2004). The parameters varied included: torso size, shape, heart size, shape, orientation, translation, defect size, location and lung volume, etc. Twenty-four phantoms were created, representing 12 male and 12 female anatomies. We simulated defects in 6 locations, and, for each phantom, the sizes were randomly sampled ±25% (with a uniform distribution) around the mean angular and axial defect extent.
We used the SimSET Monte Carlo code (2004) to separately simulate low noise Tc-99m projection data for the heart, liver, lung, kidney + spleen, and the body (including other organs). Table 1 shows the simulation parameters. These individual sets of projection data were scaled and summed to model various combinations of organ activity ratios and overall count levels. The values used were based on distributions of the organ uptakes and count levels obtained from 34 clinical myocardial perfusion studies. Using this method, we generated a total of 1,728 sets of low noise phantom projections.
Table 1.
Simulation Parameters
| Pixel size (cm) |
Energy Resolution |
Energy Window |
No. of Views |
|---|---|---|---|
| 0.60 | 10% | 140kev±10% | 64 |
| Radius of Rotation (cm) |
Hole Radius (cm) |
Collimator Type |
Collimator Length (cm) |
| 25 | 0.09975 | Parallel | 4.1 |
In order to simulate different noise levels, we scaled the low noise projection to a nominal count level, then simulated Poisson noise using a Poisson distributed pseudorandom number generator. We generated 9 sets of noisy projections with nominal relative count levels (counts divided by average clinical counts) of: 1/128, 1/32, 1/16, 1/8, 1/2, 1.0, 2.0, 8.0 and 256. The low-noise projection data (without the addition of Poisson noise) were also used, providing data for a total of 10 noise levels.
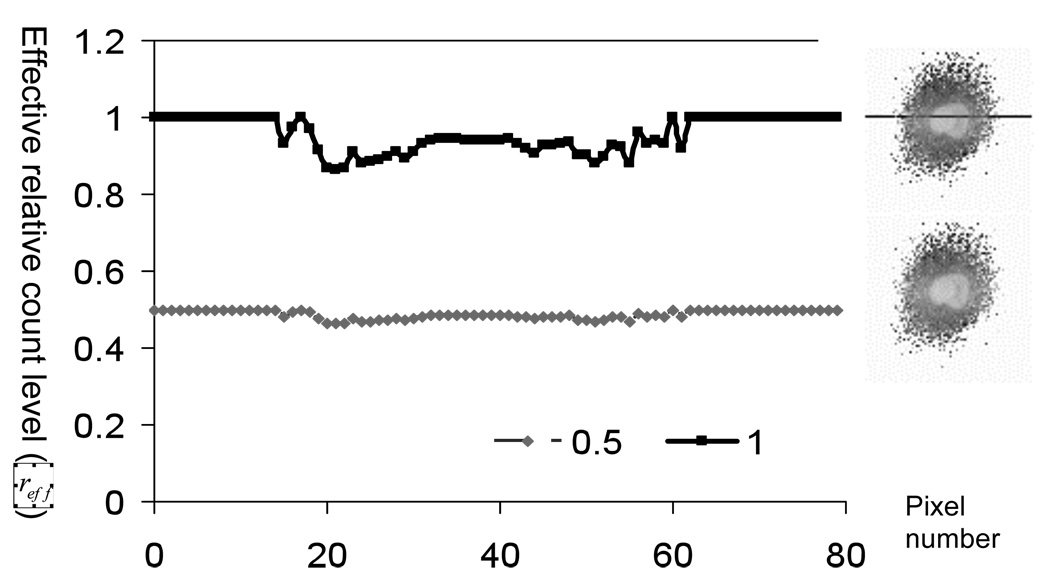
For Monte Carlo simulations, even with variance reduction, the noise goes as . It thus takes large increases in the number of photons to make any significant impact on the noise level. In our study, since we are modeling so many phantoms, the simulation time was already long. While it would be better to have simulated more photons so that residual noise in the projection data was small compared to the noise at any desired nominal count level, it was not very practical to do this. We thus investigated the effect of noise in the Monte Carlo simulated images. As described in the Appendix, the noise in the low-noise projection data due to the Monte Carlo simulation makes the noise in the projection datasets obtained after adding Poisson noise have a higher variance than appropriate for the given count levels. In order to take this into account, we derived an expression for the relative Poisson effective count level. The relative count level is the count level divided by that of the standard clinical count level. The Poisson effective count level is the Poisson count level having the same standard deviation to mean ratio as that observed for the nominal count level. To estimate the variance in the low-noise projection data, we took advantage of SimSET’s ability to generate variance images. We computed the effective count level in each pixel of the projection of the heart using the projection data for the heart alone; images and profiles for nominal relative count levels of 0.5 and 1.0 are shown in Figure 1.
Figure 1.
Images and profiles (at the position indicated) showing the effective relative count level in projections of the heart for nominal count levels of 0.5 and 1.0 times the clinical count level.
We then averaged the variance and pixel value over the projection region containing the heart. These values of the mean and variance were used to calculate the relative Poisson effective count level for four nominal count levels, including the low noise projection data; values for these are shown in Table 1. Note that for the lowest count levels, the relative Poisson effective count level is very close to the assumed level. However, for the low-noise case, the equivalent relative count level was ~14.8 even though no additional Poisson noise was added.
Table 2 shows the relative Poisson effective count level images of the heart projection. It can be seen that the effective count level was lower than the nominal count level, as would be expected since the simulation noise adds addition variance to that added by the random number generator. When the nominal count level was relatively high, i.e., the noise level was low, the noise contributed by the SimSET simulation was more prominent. Thus, the 0.5 relative count level corresponded to a relative effective count level of 0.48, as shown in Table 2, and the low-noise (no added noise) count level corresponded to a relative effective count level of 14.8.
Table 2.
Average relative count levels corresponding to the each nominal count level
| Nominal relative count level |
0.5 | 1 | 2 | 8 | no added noise |
|---|---|---|---|---|---|
| Poisson effective relative count level |
0.48 | 0.92 | 1.68 | 4.88 | 14.8 |
Reconstruction and post-reconstruction processing
Images were reconstructed using a previously described iterative reconstruction-based compensation method that uses the ordered subsets-expectation maximization (OS-EM) iterative reconstruction algorithm. Reconstructions were performed that included with both no (N) compensation or with attenuation, detector response and scatter (ADS) compensation (Frey et al., 2002; Kadrmas et al., 1998a; Kadrmas et al., 1996, 1997, 1998b). Four angles per subset were used. Based on the results of previous studies to find the optimal number of iterations for an MPS defect detection task, we investigated up to 10 iterations with no compensation and 25 reconstruction with ADS compensation. After reconstruction, the images were post-processed using low pass Butterworth filtering with various cutoff frequencies, reoriented to short axis views, windowed to a range of 0–255, and truncated to integers.
Application of Channelized Hotelling Observer (CHO)
For each noise level and reconstruction method, we optimized the number of iterations and cutoff frequencies of the Butterworth filter using CHO methodology. The methodology used was similar to that in previous studies (Frey et al., 2002; He et al., 2004; He et al., 2006). Four octave-wide rotationally symmetric frequency channels were used, as described in (Frey et al., 2002; He et al., 2004; He et al., 2006). For each short axis image of a given compensation method, iteration and post-reconstruction filter, we obtained a 4-element feature vector by taking the dot product of the image with the spatial domain template for each channel. This CHO was previously validated to predict human observer performance in a similar myocardial perfusion defect detection task (Sankaran et al., 2002). In this study, a CHO was trained separately using half the feature vectors for each combination of noise level, reconstruction method, iteration, and post-reconstruction filter. In the training process, we thus used 432 pairs of defect present/absent images to compute the mean and covariance of the feature vectors. Each CHO was tested with the remaining half of the feature vectors. The resulting rating values for each method, iteration and filter combination were then analyzed to determine the area under the ROC curve (AUC) using the LABROC4 and PROPROC (Metz, 1993; Pesce and Metz, 2007) programs. The area under the receiver operating characteristics curve (AUC) for each set of parameters was estimated, and optimum values were those that gave the maximum AUC.
Human observer study
We designed a human observer study to further investigate and validate the count level and image quality relationship observed in the CHO study. Due to time required by humans to perform the study, it was not practically possible to perform the study for every count level and both ADS and no compensation. Instead, we used data from the following nominal relative count levels:. 0.125, 0.5, 8.0 and no added noise and investigated only images reconstructed with ADS compensation. We recruited three medical imaging physics graduate student observers to participate in the study. Each of the observers completed the study over four days. In the first day, before the study, there is a long training session with 10 pairs of images for each noise level. In each day, four consecutive subsets of data were read, one for each noise level. The order of the count level subsets was randomized for each observer and each day. Each subset consisted of a training session (10 pairs of images) preceding the actual data collection session (30 pairs of images). A total of 320 images were rated by each observer each day, which took around one and half hours for each observer. The rating procedure was the same used in (Sankaran et al., 2002). In this procedure, the observers rated their confidence that a defect was present or absent at a particular position in the image on a near-continuous rating scale. Four ROC curves were obtained for each observer, with each characterizing the observer performance for one noise level. For each curve, 40 pairs of ADS compensated images were used for training and 120 pairs for testing.
RESULTS
CHO Performance
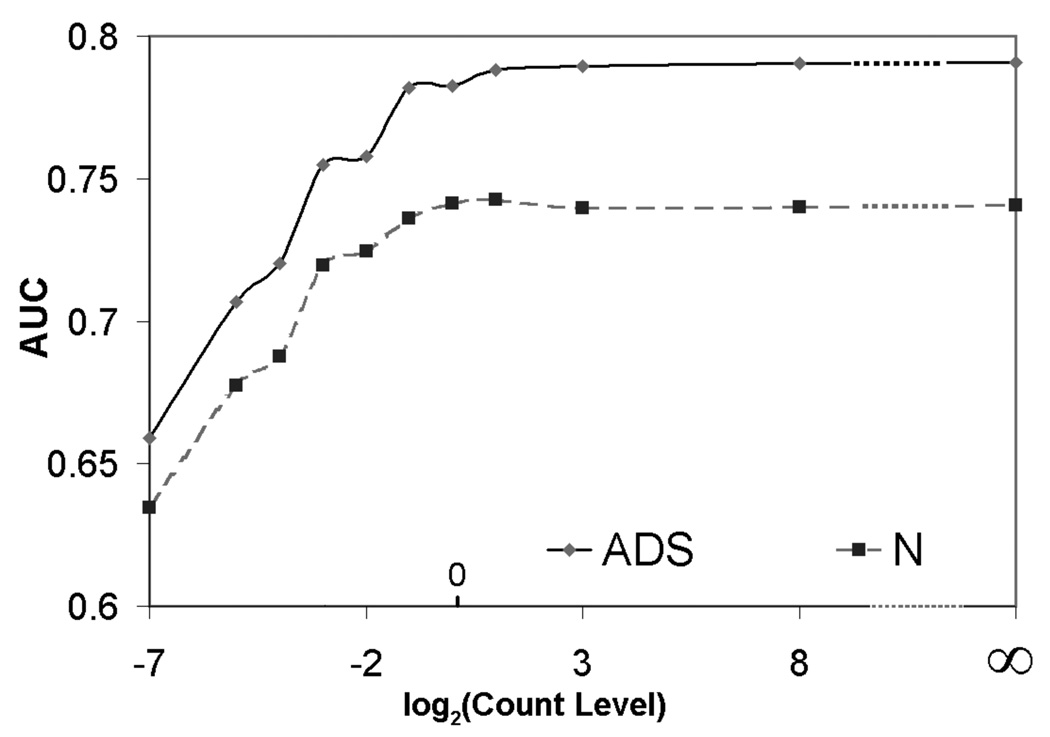
Figure 2 shows a plot of the AUC for the CHO as a function of the base 2 logarithm of the nominal relative count level. The AUC values for each nominal count level are the maximum over iteration numbers and post-processing cut-off frequencies for a given count level and reconstruction method. Note that, as predicted in the theoretical work, observer performance first increased as a function of count level and then saturated. This was true for both no (N) and ADS compensation. Also note that the shoulder of the curve, i.e. the transition from increasing performance to saturation, occured at approximately the clinical count level. This indicates that increasing clinical count levels, e.g., by using larger injected doses, longer acquisition times, or the use of more sensitive collimators, is not likely to significantly improve average performance for the population. Further improvements in task performance require reduction of the object variability component of the ensemble covariance.
Figure 2.
Optimal AUC value at different noise levels for Hotelling observer.
Finally, these data show that ADS compensation substantially improved performance compared to no compensation. They also demonstrate that it is possible to trade this performance improvement for reduced acquisition time or reduced injected activity. In fact, based on this data, a reduction of these by two or four fold could be achieved without reducing observer performance below the level obtained in current clinical practice using no compensation.
Human Observer Performance
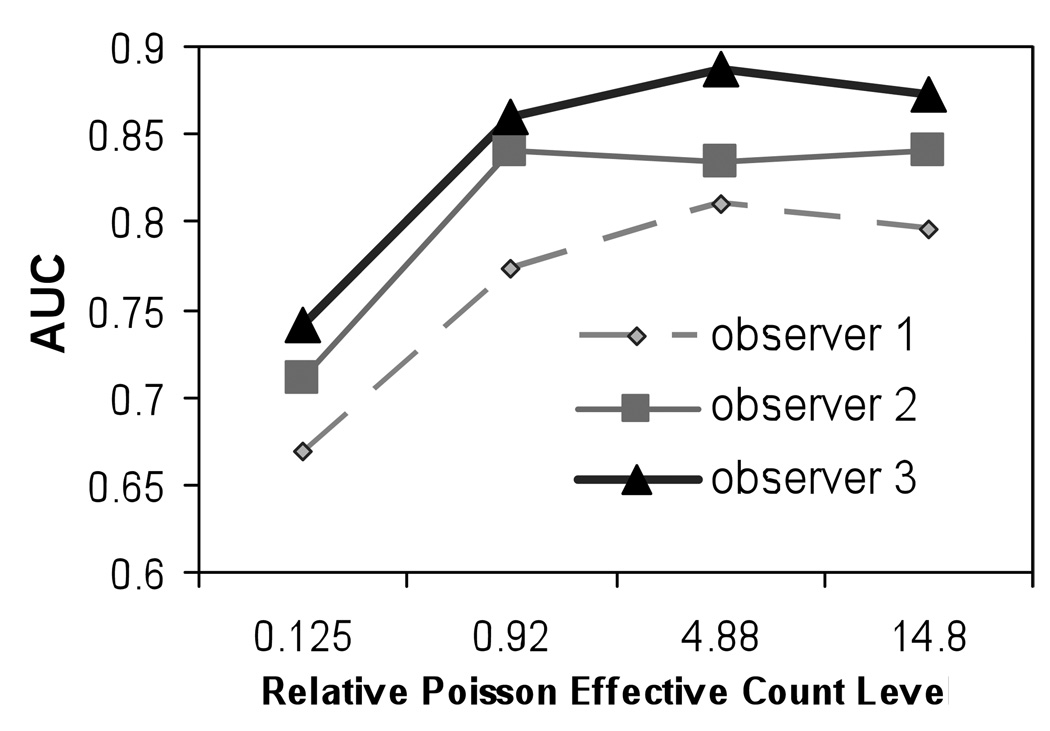
Figure 3 shows the AUC values for three human observers for different effective count levels using images corrected with ADS method. It can be seen that, although the absolute AUC value at each count level varied from observer to observer, the trend of the observer performance was similar among the observers: at lower effective relative count levels, AUC increased with increasing effective relative count level, and then saturated. This behavior is consistent with that predicted theoretically and observed in the CHO studies.
Figure 3.
Optimal AUC value at different noise levels for human observer using images reconstructed with ADS compensation.
DISCUSSION
This study relied heavily on the use of simulation. In order to make the results as clinically relevant as possible, we have endeavored to make the simulation as realistic as reasonably possible. To this end, we used an anatomically realistic phantom, and organ activities and count levels based on patient studies. We also validated the results for the CHO using a human observer study. Despite this, there are several limitations of the study. First, the defects simulated shapes that were not based on expected patterns of myocardial blood flow. In addition, the simulation did not model respiratory, cardiac, or voluntary motions. It is reasonable to ask how each of these factors affects the clinical applicability of these results.
In terms of the defect shape, we would expect the impact to be small due to the resolution of the images compared to the size of the defects. Cardiac motion would tend to blur the defect and myocardium. However, previous studies have generally shown this to be a small effect for MPS SPECT. Breathing motion tends to blur images if acquisition times per view are long compared to the respiratory period length. However, as acquisition times are decreased, respiratory motion might introduce artifacts in the images due to differences in the respiratory blurring for each of the projection views. This might tend to degrade performance for shorter acquisition times. On the other hand, shorter acquisition times would tend to reduce the incidence of voluntary motion. This would then give shorter acquisition times an added improvement in image quality if the voluntary motion were not compensated for.
Despite the fact that this study involved simulations which did not model motions there are several reasons that the results are still clinically relevant. First, there have been several recent studies demonstrating the ability of advanced reconstruction methods to give equivalent image quality with half the acquisition time (Ali et al., 2009; DePuey et al., 2008). The results of this study support the observations in those studies. In addition, they provide a theoretical justification both for those results and a for investigation of the effects of dose or acquisition time reduction in general. Second, the AUC values for the human observers in this study were in the same range as those reported in evaluations of similar reconstruction methods using clinical studies. For example, Narayanan et al obtained AUC values of 0.8 for filtered backprojection and 0.89 for OS-EM with attenuation, scatter, and CDR compensation (Narayanan et al., 2003). That study involved was patient data read by expert observers. The task performance reported was very similar range to that obtained in our human observer studies (average of 0.82 for all observers). This data indicates that the presence of motion is not such a big effect that it completely dominates defect detection performance. Finally, it is possible to consider how motion would likely have affected the results of this study. Motion would change defect task performance in two ways: by reducing the mean defect contrast due to blurring, and by increasing background variability through the introduction of artifacts that differ with each patient. The former will result in generally degraded perfusion defect detection performance. However, this generally degraded performance would not have changed the shape of the tradeoff curve between image quality and count level. Increased background variability, on the other hand, would change the shape of the tradeoff curve. For example, increased background variability would tend to degrade performance in the region where performance is limited by background variability. It would also tend to shift the point where quantum noise becomes a limiting factor to decreased count levels.
Finally, the results of these studies are not important solely because they help justify the use of reduced acquisition time. Instead, they provide a framework for thinking about ways to improve image quality or reduce acquisition time or dose. For example, these data suggest that increasing system sensitivity alone would not tend to improve performance on myocardial defect detection. Instead, methods which reduce background variability are needed. Several of these have already been developed, such as attenuation compensation, which reduces background variability caused by attenuation artifacts. Background variability could also be reduced by increasing system resolution, as this reduces partial volume effects from surrounding organs (which vary by patient) on the organ of interest. Thus improved system sensitivity could at least partially be traded for improved resolution in order to improve myocardial perfusion defect detection perormance.
CONCLUSION
In this study, we used theoretical derivations and mathematical and human observer experiments with simulated data to demonstrate the importance of anatomical and quantum noise on a defect detection task. In the experiments, we used a population of phantoms and corresponding low-noise projections that realistically modeled patient variability. From these low-noise projections we generated noisy projections with 10 different noise levels. The projections were reconstructed with OS-EM combined with no compensation or compensation for attenuation, collimator-detector response, and scatter (ADS). We determined the area under the ROC curve (AUC) value for channelized Hotelling observers applied to these images. In addition, we measured the human observer performance for 4 different noise levels for ADS compensation. We found that increased count levels offer improved performance only up to some critical count level. After this level, performance saturates with increasing count level. In other words, when the quantum noise level is low, the AUC value did not increase with increases in the count level; when the quantum noise level is high, the AUC value increased as a function of count level. For the myocardial perfusion defect detection task studied, the critical count level is approximately equal to the current clinical count level. We also found that ADS compensation provided improved detection compared to no compensation at all count levels, and that this improvement could, if desired, be traded for a factor of 2–4 reduction in acquisition time or injected activity. It should be noted that this study did not model the effects of cardiac, respiratory, or involuntary motion. These effects could change the tradeoff between count level and image quality by increasing the level of anatomical noise for a given level of quantum noise. In addition, motion could have different effects on acquisition times of different durations. Thus, a further investigation of the effects of motion on acquisition time is essential before adopting the observations of this work clinically. Nevertheless, this study does demonstrate the potential for reducing acquisition time or patient dose through the use of improved reconstruction methods.
Acknowledgments
Supported in part by:
R01-EB000288
R01-HL068575
Appendix 1
Relative Poisson effective count level of Monte Carlo simulated projection data with added Poisson noise
In order to take into account the contribution from the noise in the low-noise projection to the final projection data, we calculated the relative effective count level of the four sets of projection data used in human observer study. We define the relative count level to be the counts in a set of projection data with Poisson distributed noise divided by the counts in a set of clinical projection data. The simulated projection data are not strictly Poisson distributed due to the residual noise in the Monte Carlo simulation. As a result, we define the Poisson effective count level as the number of counts in the projection data having the same coefficient of variation (COV), equal to the mean divided by standard deviation, as is found in the projection data after the addition of Poisson noise. Combining these concepts, we define the relative Poisson effective count level (or relative effective count level) as the Poisson effective count level divided by the clinical count level.
Let the variance and mean of the pixel value in the simulated (low-noise) projection data be denoted by , and µs, respectively. Let s be equal to the scaling factor needed to scale this simulated projection data so that it has a clinically realistic count level, r be the nominal (or intended) relative count level, and reff be the effective relative count level, which includes the effects of the noise in the simulated projections, corresponding to the nominal relative count level.
To derive an expression for reff,, we first note that the variance in the projection data after adding simulated noise will be equal to the sum of the variance contributions from the low-noise projection and the Poisson random number generator (RNG). The variance contribution due to noise in the low-noise projections is equal the variance before scaling, , times the square of the scale factor required to get the desired count level, r2s2; the variance due to the RNG is equal to the nominal count level, rsµs. The total variance is thus
| (A1) |
and the corresponding standard deviation is
| (A 2) |
Let λ be the Poisson effective count level. The variance for this count level is also equal to λ. We now equate the COV for this effective count level with the COV for the simulated projection data after the addition of Poisson noise. Thus we have that
| (A 3) |
Thus the Poisson effective count level is,
| (A 4) |
the relative Poisson effective count level is
| (A2) |
Note that this has the expected behavior: when the variance in the low-noise projection data, σs, becomes small relative to the clinical count level, the relative effective count level approaches the count level; for other cases, the relative effective count level will be smaller than the nominal relative count level.
REFERENCES
- SIMSET Overview. University of Washington; 2004. SimSET version 2.6. http://depts.washington.edu/~simset/html/simset_home.html. [Google Scholar]
- Ali I, Ruddy TD, Almgrahi A, Anstett FG, Wells RG. Half-time SPECT myocardial perfusion imaging with attenuation correction. J Nucl Med. 2009;50:554–562. doi: 10.2967/jnumed.108.058362. [DOI] [PubMed] [Google Scholar]
- Barrett HH. Objective Assessment of Image Quality - Effects of Quantum Noise and Object Variability. Journal of the Optical Society of America a-Optics Image Science and Vision. 1990;7:1266–1278. doi: 10.1364/josaa.7.001266. [DOI] [PubMed] [Google Scholar]
- Barrett HH. Foundations of Image Science. 2003 the. [Google Scholar]
- Barrett HH, Gooley T, Girodias K, Rolland J, White T, Yao J. Linear Discriminants and Image Quality. Image and Vision Computing. 1992;10:451–460. [Google Scholar]
- Barrett HH, Wilson DW, Tsui BMW. Noise Properties of the Em Algorithm .1. Theory. Phys Med Biol. 1994;39:833–846. doi: 10.1088/0031-9155/39/5/004. [DOI] [PubMed] [Google Scholar]
- Barrett HH, Yao J, Rolland JP, Myers KJ. Model Observers for Assessment of Image Quality. Proceedings of the National Academy of Sciences of the United States of America. 1993;90:9758–9765. doi: 10.1073/pnas.90.21.9758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePuey EG, Gadiraju R, Clark J, Thompson L, Anstett F, Shwartz SC. Ordered subset expectation maximization and wide beam reconstruction "half-time" gated myocardial perfusion SPECT functional imaging: a comparison to "full-time" filtered backprojection. J Nucl Cardiol. 2008;15:547–563. doi: 10.1016/j.nuclcard.2008.02.035. [DOI] [PubMed] [Google Scholar]
- Frey EC, Gilland KL, Tsui BM. Application of task-based measures of image quality to optimization and evaluation of three-dimensional reconstruction-based compensation methods in myocardial perfusion SPECT. IEEE Trans Med Imaging. 2002;21:1040–1050. doi: 10.1109/TMI.2002.804437. [DOI] [PubMed] [Google Scholar]
- He X, Frey EC, Links JM, Gilland KL, Segars WP, Tsui BMW. A mathematical observer study for the evaluation and optimization of compensation methods for myocardial SPECT using a phantom population that realistically models patient variability. Ieee T Nucl Sci. 2004;51:218–224. [Google Scholar]
- He X, Links JM, Gilland KL, Tsui BMW, Frey EC. Comparison of 180 degrees and 360 degrees acquisition for myocardial perfusion SPECT with compensation for attenuation, detector response, and scatter: Monte Carlo and mathematical observer results. J Nucl Cardiol. 2006;13:345–353. doi: 10.1016/j.nuclcard.2006.03.008. [DOI] [PubMed] [Google Scholar]
- Kadrmas DJ, Frey EC, Karimi SS, Tsui BMW. Fast implementations of reconstruction-based scatter compensation in fully 3D SPECT image reconstruction. Phys Med Biol. 1998a;43:857–873. doi: 10.1088/0031-9155/43/4/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadrmas DJ, Frey EC, Tsui BMW. An SVD investigation of modeling scatter in multiple energy windows for improved SPECT images. Ieee T Nucl Sci. 1996;43:2275–2284. doi: 10.1109/23.531892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadrmas DJ, Frey EC, Tsui BMW. Analysis of the reconstructibility and noise properties of scattered photons in Tc-99m SPECT. Phys Med Biol. 1997;42:2493–2516. doi: 10.1088/0031-9155/42/12/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadrmas DJ, Frey EC, Tsui BMW. Application of reconstruction-based scatter compensation to thallium-201 SPECT: Implementations for reduced reconstructed image noise. Ieee T Med Imaging. 1998b;17:325–333. doi: 10.1109/42.712122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metz CE. Basic Principles of Roc Analysis. Seminars in Nuclear Medicine. 1978;8:283–298. doi: 10.1016/s0001-2998(78)80014-2. [DOI] [PubMed] [Google Scholar]
- Metz CE. Roc Methodology in Radiologic Imaging. Investigative Radiology. 1986;21:720–733. doi: 10.1097/00004424-198609000-00009. [DOI] [PubMed] [Google Scholar]
- Metz CE. 1993 LABROC4. [Google Scholar]
- Narayanan MV, King MA, Pretorius PH, Dahlberg ST, Spencer F, Simon E, Ewald E, Healy E, MacNaught K, Leppo JA. Human-observer receiver-operating-characteristic evaluation of attenuation, scatter, and resolution compensation strategies for (99m)Tc myocardial perfusion imaging. J Nucl Med. 2003;44:1725–1734. [PubMed] [Google Scholar]
- Pesce LL, Metz CE. Reliable and computationally efficient maximum-likelihood estimation of "proper" binormal ROC curves. Acad Radiol. 2007;14:814–829. doi: 10.1016/j.acra.2007.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankaran S, Frey EC, Gilland KL, Tsui BMW. Optimum compensation method and filter cutoff frequency in myocardial SPECT: A human observer study. J Nucl Med. 2002;43:432–438. [PubMed] [Google Scholar]
- Soares EJ, Byrne CL, Glick SJ. Noise characterization of block-iterative reconstruction algorithms: I. Theory. Ieee T Med Imaging. 2000;19:261–270. doi: 10.1109/42.848178. [DOI] [PubMed] [Google Scholar]
- Soares EJ, Glick SJ, Hoppin JW. Noise characterization of block-iterative reconstruction algorithms: II. Monte Carlo simulations. Ieee T Med Imaging. 2005;24:112–121. doi: 10.1109/tmi.2004.836876. [DOI] [PubMed] [Google Scholar]
- Wilson DW, Tsui BMW, Barrett HH. Noise Properties of the Em Algorithm .2. Monte-Carlo Simulations. Phys Med Biol. 1994;39:847–871. doi: 10.1088/0031-9155/39/5/005. [DOI] [PubMed] [Google Scholar]