Abstract
Computational studies are performed to analyze the physical properties of hydrogen bonds donated by Tyr16 and Asp103 to a series of substituted phenolate inhibitors bound in the active site of ketosteroid isomerase (KSI). As the solution pKa of the phenolate increases, these hydrogen bond distances decrease, the associated NMR chemical shifts increase, and the fraction of protonated inhibitor increases, in agreement with prior experiments. The quantum mechanical/molecular mechanical calculations provide insight into the electronic inductive effects along the hydrogen-bonding network that includes Tyr16, Tyr57, and Tyr32, as well as insight into hydrogen bond coupling in the active site. The calculations predict that the most-downfield NMR chemical shift observed experimentally corresponds to the Tyr16-phenolate hydrogen bond and that Tyr16 is the proton donor when a bound naphtholate inhibitor is observed to be protonated in electronic absorption experiments. According to these calculations, the electronic inductive effects along the hydrogen-bonding network of tyrosines cause the Tyr16 hydroxyl to be more acidic than the Asp103 carboxylic acid moiety, which is immersed in a relatively nonpolar environment. When one of the distal tyrosine residues in the network is mutated to phenylalanine, thereby diminishing this inductive effect, the Tyr16-phenolate hydrogen bond lengthens, and the Asp103-phenolate hydrogen bond shortens, as observed in NMR experiments. Furthermore, the calculations suggest that the differences in the experimental NMR data and electronic absorption spectra for pKSI and tKSI, two homologous bacterial forms of the enzyme, are due predominantly to the third tyrosine that is present in the hydrogen-bonding network of pKSI but not tKSI. These studies also provide experimentally testable predictions about the impact of mutating the distal tyrosine residues in this hydrogen-bonding network on the NMR chemical shifts and electronic absorption spectra.
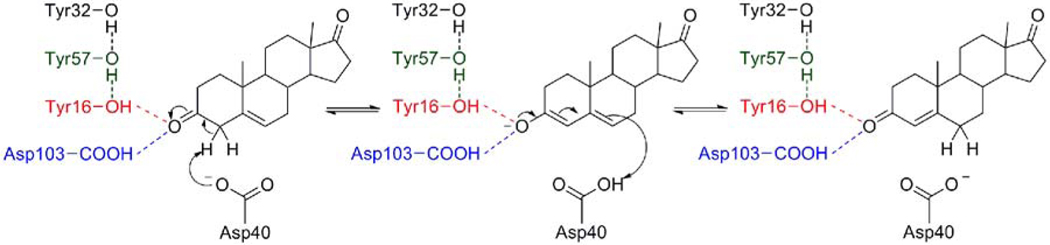
Δ5-3-Ketosteroid isomerase (KSI) has served as a model system for probing the structural and functional roles of hydrogen bonding in enzyme active sites. Two homologous bacterial forms of this enzyme, from Commamonas testosteroni (tKSI) and Pseudomonas putida (pKSI), have been studied extensively with both experimental and theoretical methods. (In this paper, the residues are numbered according to pKSI.) In both species, the steroid isomerization reaction proceeds by a two-step general acid-base mechanism (1, 2). As depicted in Figure 1, Asp40 abstracts a proton from the steroid C4 position to form a dienolate intermediate, followed by proton transfer from Asp40 to the C6 position. The negative charge accumulated on the steroid oxygen in the dienolate intermediate is stabilized by two direct hydrogen bonds with Tyr16 and protonated Asp103. In both pKSI and tKSI, Tyr16 is hydrogen-bonded to Tyr57. In pKSI, Tyr57 is also hydrogen bonded to Tyr32, but the analogous residue is a phenylalanine rather than a tyrosine in tKSI.
Figure 1.
Mechanism of the isomerization of the substrate, 5-androstene-3,17-dione, by Δ5-3-ketosteroid isomerase. The pKSI active site hydrogen-bonding network is shown with the Tyr16-substrate hydrogen bond in red, the Asp103-substrate hydrogen bond in blue, and the Tyr57-Tyr16 hydrogen bond in green.
Experimental NMR and electronic absorption data for phenolate (3, 4) and naphtholate (5, 6) inhibitors bound to KSI have probed the structural properties of the active site hydrogen bonds. In these experiments, the steroid in Figure 1 was replaced by a phenolate or naphtholate inhibitor serving as an analog of the dienolate intermediate. Substitutions of electron-withdrawing groups on the phenolates or naphtholates altered the solution pKa of the inhibitor from 5.4–10.0, enabling systematic studies of the effects of increasing negative charge localization on the inhibitor oxygen. The substitutions led to significant changes in the NMR chemical shifts observed for active site hydrogen bonds and the fraction of inhibitor bound as the neutral phenol or naphthol as determined from the absorption spectra.
Recently the proton NMR chemical shifts were measured for a series of substituted phenolates bound to the D40N mutant of tKSI (4). Two downfield peaks with chemical shifts ≥14 ppm appeared upon phenolate binding and moved progressively downfield by 0.76 and 0.50 ppm per unit increase in the phenolate pKa. These two peaks were assigned to the hydrogen-bonded protons of Tyr16 and Asp103, but these experiments could not distinguish which peak arose from which residue. These NMR data, in combination with prior correlations of hydrogen bond distances and NMR chemical shifts derived from small molecule studies (7–9), suggested that the O–O distances of the Tyr16 and Asp103 hydrogen bonds donated to the bound phenolate shorten with increasing phenolate pKa by ~0.02 Å/pKa unit.
Furthermore, the electronic absorption spectra were measured for a series of substituted naphtholates bound to the D40N mutant of both tKSI and pKSI (6). The absorption spectra were fit to a linear combination of the protonated and deprotonated naphthol solution spectra to estimate the fractions of protonated and ionized forms of the ligand bound to KSI. According to these fits, the fraction of protonated inhibitor in pKSI D40N decreased from 0.71 to 0.08 as the pKa decreased from 10.1 to 8.4. For tKSI D40N, the inhibitor exhibited more anionic character, with an observed fraction of protonated inhibitor of only 0.30 for tKSI versus 0.71 for pKSI at a ligand pKa of 10.1. These data were used to estimate an apparent proton affinity of the oxyanion hole of 9.8 for pKSI D40N and 10.5 for tKSI D40N (10).
In addition, the hydrogen-bonding network was investigated by mutating a distal tyrosine residue in the hydrogen-bonding network to phenylalanine (11–14). NMR spectra for 3,4-dinitrophenolate bound to tKSI D40N suggested that mutation of Tyr57 to Phe leads to a lengthening of the Tyr16–phenolate hydrogen bond and a shortening of the contiguous Asp103–phenolate hydrogen bond (14). This result provides evidence for coupling between these two hydrogen bonds, in agreement with deuterium substitution studies of the unmodified KSI oxyanion hole that detected the propagation of structural perturbations through this hydrogen-bonding network (14).
The reaction catalyzed by KSI has been studied theoretically with both electronic structure methods (15–18) and molecular dynamics simulations (18–25). Warshel and coworkers have examined the binding energies of the phenolate transition state analogues, as well as the binding energies of equilinen and the dienolate intermediate for the catalytic isomerization reaction (22, 23). In the present paper, we do not calculate binding energies or catalytic rate constants, as done in these previous studies, but rather focus mainly on structural aspects of the hydrogen-bonding interactions in the active site.
The objective of this paper is to elucidate the physical properties of hydrogen-bonding interactions in the KSI active site for a series of substituted phenolate inhibitors. We use quantum mechanical/molecular mechanical (QM/MM) calculations to analyze the changes in hydrogen-bonding distances between the phenolate and the protein, as well as the degree of phenolate protonation, along this series. To directly compare our pKSI D40N calculations with experiment, and since the prior NMR studies of bound phenolates were performed only with tKSI (4), we have acquired proton NMR spectra for phenolates bound to pKSI D40N. To relate the results of the QM/MM calculations on phenolates to the steroid isomerization reaction catalyzed by KSI, we compare the hydrogen-bonding interactions of these inhibitors to the hydrogen-bonding interactions of a steroid substrate along the isomerization reaction pathway. In addition, we examine how mutations of distal tyrosines in the hydrogen-bonding network impact the structures of active site hydrogen bonds donated to the bound phenolate. These calculations provide insight into the electronic inductive effects along the hydrogen-bonding network and the physical coupling between the hydrogen bonds formed with the inhibitor. Moreover, these results suggest that the observed differences in hydrogen bond and ligand ionization properties within the active sites of tKSI versus pKSI can be explained on the basis of the extra tyrosine in the hydrogen-bonding network of pKSI.
METHODS
Our calculations are based on the 1.25 Å resolution crystal structure of the D40N mutant of pKSI complexed with phenolate (PDB: 2PZV) (4). The first monomeric unit, its corresponding phenolate, and all crystallographic water molecules within 5 Å of the monomer were extracted from the crystal structure. The heavy atoms of the N-terminal and C-terminal residues, as well as an unresolved loop region (residues 62 – 64), were reconstructed from the amino acid sequence using the JACKAL protein modeling package (26, 27). Protonation states were determined using H++ (28), which correctly identified Asp103 as protonated, and protons were added using the Maestro modeling program (29). The hydrogen bond orientations of Tyr16, Tyr32, and Tyr57 were chosen to agree with the hydrogen-bonding network that can be inferred from the short O–O distances observed in the crystal structure, assuming the phenolate ligand to be deprotonated.
We included explicit solvent in our QM/MM geometry optimizations to provide a more accurate description of the solvated protein system. To obtain a physically meaningful configuration of the explicit solvent, the protein monomer was solvated by 6185 TIP3P water molecules (30, 31) in an orthorhombic box, with five sodium ions added to maintain charge neutrality. Initially, the positions of the added water molecules and ions were optimized by minimizing the energy of the system using the OPLS2005 force field (32). This minimization was followed by 500 ps of molecular dynamics (MD) equilibration of the solvent and ions with the protein and ligand fixed. This equilibration was performed for a canonical ensemble (i.e., constant NVT) at 300 K using the Berendsen thermostat (33), a time step of 1 fs, a 12 Å non-bonded cutoff, and Smooth Particle Mesh Ewald (34) for long-range electrostatics. The hydrogen atoms bonded to heavy atoms were constrained to their equilibrium distances with the SHAKE algorithm (35). All of the classical MD calculations were performed using the Desmond MD program (36, 37), while the QM/MM calculations described below were performed using the Qsite program (38).
We built the series of substituted phenolates studied experimentally in Ref. (4) by substituting the appropriate positions of the bound phenolate in the crystal structure, including both possible configurations of the asymmetrical phenolates. (The pKa values of the phenols used in this study are given in Table S1 of Supporting Information.) The geometry of each substituted phenolate was optimized by energy minimization at the QM/MM level with all other atoms fixed, followed by geometry optimization of a residue-based 10 Å sphere centered at the phenolate oxygen. Each geometry optimization was started from the crystal structure geometry immersed in the same equilibrated solvent configuration. The QM region was treated at the density functional theory (DFT) B3LYP/6-31G** level of theory with an ultrafine grid, a level shift of 1 au for virtual orbitals, and a 20 Å residue-based non-bonded cutoff. The OPLS2005 force field was used for the MM region. The substituted phenolate, the side chain of Asp40Asn, and the full residues Tyr16 and Asp103 were included in the QM region in all QM/MM calculations, using the frozen orbital methodology employed in QSite for the QM-MM boundaries. Two additional sets of geometry optimizations were performed using the same procedure with either Tyr57 or both Tyr57 and Tyr32 added to the QM region.
Following these geometry optimizations, we calculated the NMR shielding tensors of the hydrogen-bonded protons from a single point QM/MM calculation at the Hartree-Fock (HF) and DFT B3LYP levels of theory using the cc-pVTZ basis set (39) and gauge-including atomic orbitals (GIAOs) (40–42). The amino acid residues in the QM region were truncated with hydrogen caps between Cα and Cβ. The local hydrogen-bonding geometry is expected to dominate the chemical shifts of the hydrogen-bonded protons (43). Chemical shifts were calculated as the difference between the shielding of tetramethylsilane (TMS) calculated at the same level of theory in the gas phase and the shielding of the nucleus under investigation. Note that the shielding of TMS calculated in explicit water differed from that calculated in the gas phase by <0.5 ppm.
To further investigate the nature of the oxyanion hole hydrogen bonds, we calculated the proton potential energy curves corresponding to each hydrogen bond for phenolate and 3,4,5-trifluorophenolate. For this purpose, each hydrogen-bonded proton was moved on a grid along its O–O axis in increments of 0.05 Å, with all other atoms fixed at the minimum energy geometry. In these calculations, the scanned hydrogen bond was assumed to be linear, although the minimum energy angles were ~173° and ~163° for the Tyr16-phenolate and Asp103-phenolate hydrogen bonds, respectively. The QM/MM energy was calculated for each proton position at the DFT B3LYP/6-31G** level using frozen orbitals at the QM-MM boundaries. An interpolation scheme was used to obtain a one-dimensional potential energy curve for each hydrogen bond. One-dimensional proton vibrational wave functions were generated for each potential energy curve using the Fourier Grid Hamiltonian method (44, 45).
We examined the impact of the active site hydrogen-bonding network on the oxyanion hole hydrogen bonds by mutating the distal tyrosine residues in the network. Starting from the crystal structure of the pKSI D40N monomer with the equilibrated solvent configuration described above, we mutated tyrosine to phenylalanine to model the Y32F and Y32F/Y57F mutations. These mutants were chosen because they are not expected to cause major structural rearrangements in the active site (12). For each mutant, first the geometry of only the mutated residue was optimized by QM/MM energy minimization, then the geometry of only the QM region was optimized, and finally the geometry of a 10 Å sphere centered at the phenolate oxygen was optimized. The resulting configuration was used as a starting structure for phenolate substitution, and the QM/MM geometry optimization procedure performed above for substituted phenolates in pKSI D40N was repeated for these mutants. We also calculated the proton potentials and associated proton vibrational wave functions for these hydrogen bonds. In these calculations, the full residues 32 and 57, as well as the substituted phenolate, the side chain of Asp40Asn, and the full residues Tyr16 and Asp103, were included in the QM region. We also studied the impact of mutating the most distal tyrosine in the hydrogen-bonding network (i.e., Tyr32 in D40N, Tyr57 in Y32F/D40N, and Tyr16 in Y32F/D40N/Y57F) to the unnatural amino acids 2,6-difluorotyrosine and 2,3,5,6-tetrafluorotyrosine. We followed the same procedure for these mutants as for the phenylalanine mutants, although these calculations were performed for only the unsubstituted phenolate.
In addition, we compared the hydrogen-bonding structures of the phenolate ligands bound to KSI to those of the bound steroid substrate, dienolate intermediate, and product. For this purpose, we used a similar QM/MM geometry optimization procedure to model the reactant, intermediate, and product states of the KSI steroid isomerization reaction. These calculations were based on the 2.50 Å resolution crystal structure of pKSI D40N bound to the substrate analog androstene-3β-ol-17-one (PDB: 1E3R) (46). The first monomer and its ligand were solvated by explicit water and sodium ions using the same equilibration procedure for the water molecules and ions as described above. The amide nitrogen of D40N was converted to oxygen to model wild-type pKSI, and states corresponding to the reactant, intermediate, and product were constructed using the Maestro modeling program (29). For each state, the geometry of the steroid was optimized by energy minimization at the MM level, followed by geometry optimization at the QM/MM level with the protein, solvent, and ions fixed. This optimization of the steroid was followed by geometry optimization at the QM/MM level of a residue-based 10 Å sphere centered at the steroid oxygen. The substrate, the side chain of Asp40, and the full residues of Tyr16 and Asp103 were included in the QM region in these calculations. Additional calculations were performed with Tyr57 or with both Tyr32 and Tyr57 included in the QM region.
1H NMR spectra for phenolates bound to pKSI D40N were acquired at the Stanford Magnetic Resonance Laboratory on an 800 MHz Varian UNITYINOVA spectrometer using previously reported methods (4). NMR samples consisted of 0.5 mM pKSI D40N and 0.5 – 5.0 mM substituted phenol in 40 mM potassium phosphate buffer (pH 7.2), 1 mM EDTA, 2 mM DTT, and 10% (v/v) DMSO-d6. One-dimensional proton spectra were acquired at −3.0 ± 0.5 °C using the 1331 binomial pulse sequence (47) to suppress the water signal, with a spectral width of 30 ppm (carrier frequency set on the water resonance) and an excitation maximum of 14–18 ppm. Data were collected for 512-5120 scans and processed using a 10 Hz line broadening and baseline correction applied over the peaks of interest. Chemical shifts were referenced internally to the water resonance (5.1 at −3.0 °C) and externally to a sample of sodium 3-trimethylsilylpropionate-2,2,3,3-d4 (0 ppm) under the same buffer conditions.
RESULTS AND DISCUSSION
Hydrogen Bonding of Phenolates in KSI Active Site
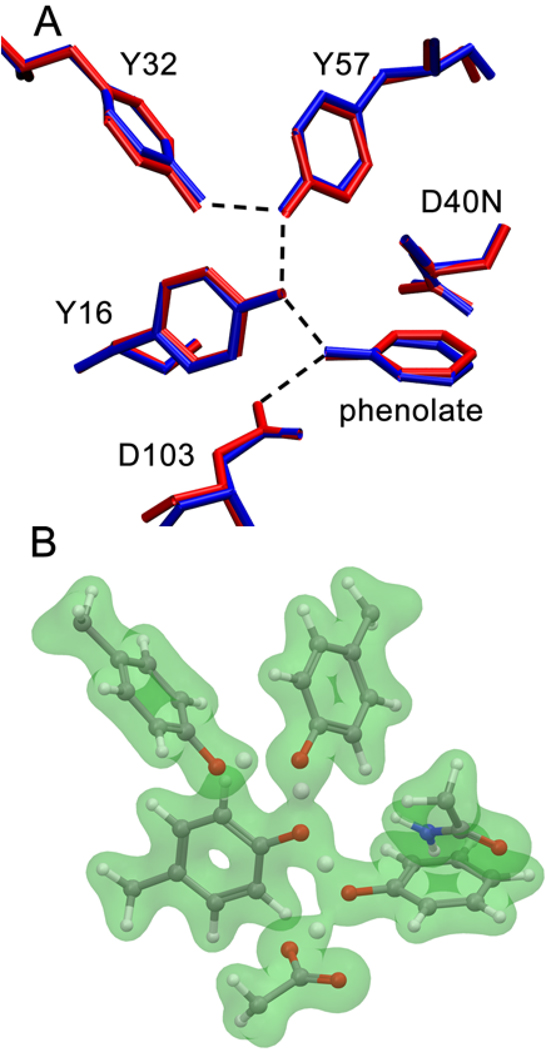
To analyze the effects of phenolate charge delocalization on the structures of the oxyanion hole hydrogen bonds, we performed QM/MM geometry optimizations for a series of pKSI-bound phenolates bearing electron-withdrawing substituents. These calculations were carried out using three different QM regions that excluded both Tyr57 and Tyr32, included Tyr57 but not Tyr32, or included both Tyr57 and Tyr32 in the QM region. Since the QM/MM methodology accounts for the electronic inductive effects of only residues within the QM region, these three QM regions allowed us to examine the impact of excluding the electronic inductive effects of specified residues in the hydrogen-bonding network. Figure 2 provides a comparison between the X-ray crystal structure (PDB: 2PZV) and the QM/MM optimized geometry obtained with the largest QM region, as well as a depiction of the calculated electron density for the active sites residues and bound phenolate. The root-mean-square deviation (RMSD) between the crystal structure and the QM/MM optimized geometry for the active site residues and the phenolate shown in Figure 2 was 0.26 Å, indicating only minor structural rearrangements upon geometry optimization.
Figure 2.
(A) Comparison of the X-ray crystal structure (PDB: 2PZV) (blue) and the QM/MM optimized geometry (red) for phenolate bound to pKSI D40N. The hydrogen-bonding interactions are indicated by dashed lines. The RMSD between these structures for the active site residues and the phenolate is 0.26 Å. (B) Depiction of the calculated electron density (green) with an isovalue of 0.05 electrons per cubic Bohr for QM residues and phenolate in the active site. In these QM/MM calculations, the QM region included Tyr16, Asp103, Asp40Asn, Tyr32, Tyr57, and the phenolate.
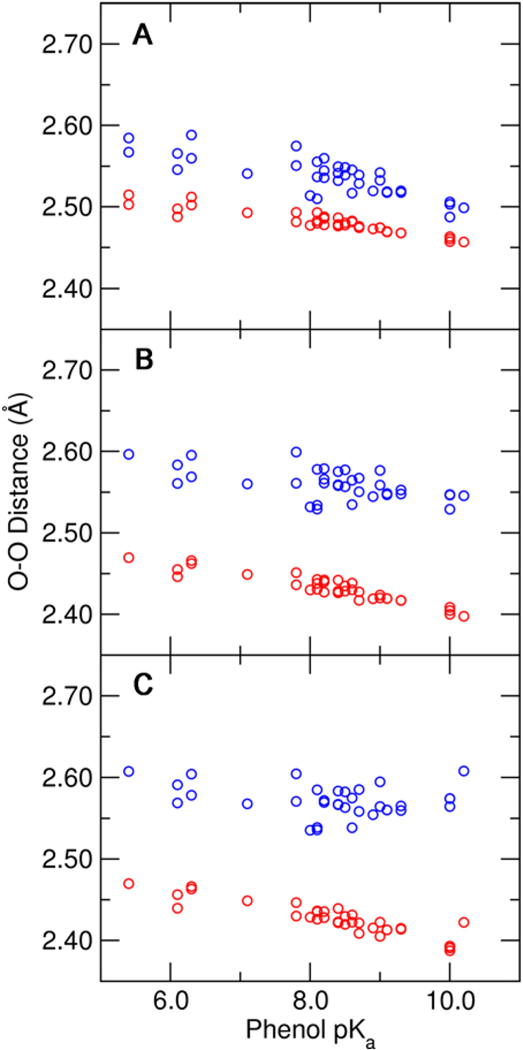
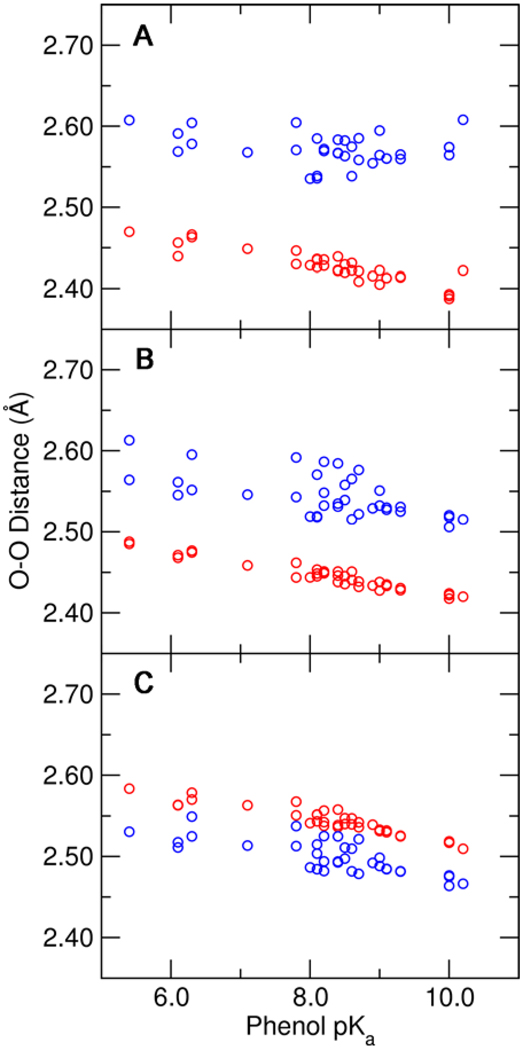
The calculated O–O distances for the hydrogen bonds donated by Tyr16 and Asp103 to the substituted phenolate are depicted in Figure 3 for the three QM regions investigated. These hydrogen bond distances shorten as the solution pKa of the phenolate increases, as indicated by NMR experiments. Moreover, the Tyr16-phenolate hydrogen bond is shorter than the Asp103-phenolate hydrogen bond by ~0.1 Å, in agreement with the X-ray structure (4). Successive addition of Tyr57 and Tyr32 to the QM region causes the Tyr16-phenolate hydrogen bond distance to decrease and slightly enhances the pKa dependence of the hydrogen bond distance. Conversely, the Asp103-phenolate hydrogen bond distance increases slightly, and the pKa dependence of the hydrogen bond distance is somewhat reduced when these tyrosine residues are represented quantum mechanically. The impact of including additional tyrosines in the QM region on the calculated hydrogen bond distances is consistent with an electronic inductive effect along the hydrogen-bonding network.
Figure 3.
Hydrogen bond O–O distances for the Tyr16-phenolate hydrogen bond (red) and the Asp103-phenolate hydrogen bond (blue) as functions of the solution pKa of the substituted phenolate. These distances were determined from QM/MM calculations of the phenolate bound to pKSI D40N with three different QM regions: (A) Tyr57 and Tyr32 MM, (B) Tyr57 QM and Tyr32 MM, and (C) Tyr57 and Tyr32 QM. All calculations included Tyr16, Asp103, Asp40Asn, and the phenolate in the QM region.
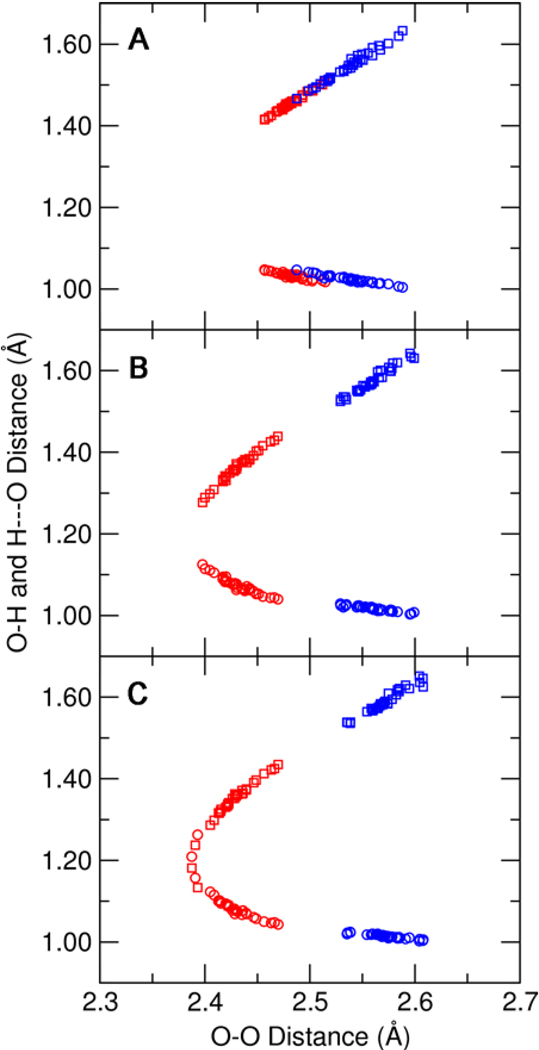
The calculated O–H distances of each hydrogen bond exhibit trends consistent with those observed for the O–O distances. Figure 4 illustrates that the shortening of the O–O distance is accompanied by migration of the bridging proton toward the acceptor oxygen. In the absence of inductive effects from the hydrogen-bonding network, both hydrogen-bonded protons remain localized on the amino acid over the full pKa range investigated. The inclusion of inductive effects arising from the quantum mechanical treatment of Tyr57 and Tyr32, however, causes the optimized position of the Tyr16 hydrogen-bonded proton to approach the O–O midpoint at high pKa values.
Figure 4.
Donor O–H distances (circles) and H---O-phenolate distances (squares) for the Tyr16-phenolate (red) and Asp103-phenolate (blue) hydrogen bonds as functions of the O–O distance of each hydrogen bond. These distances were determined from QM/MM calculations of the phenolate bound to pKSI D40N with three different QM regions: (A) Tyr57 and Tyr32 MM, (B) Tyr57 QM and Tyr32 MM, and (C) Tyr57 and Tyr32 QM. All calculations included Tyr16, Asp103, Asp40Asn, and the phenolate in the QM region.
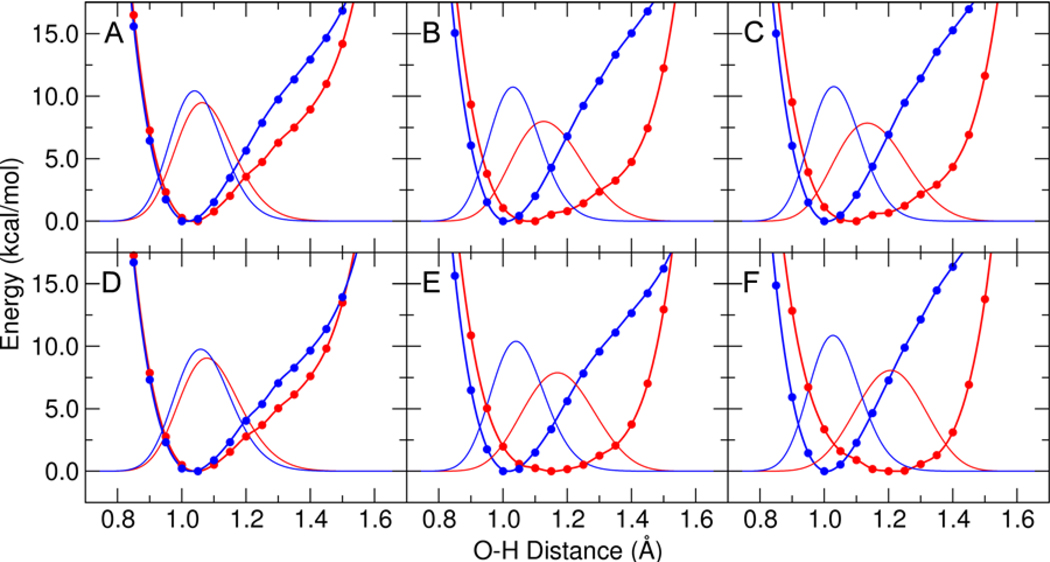
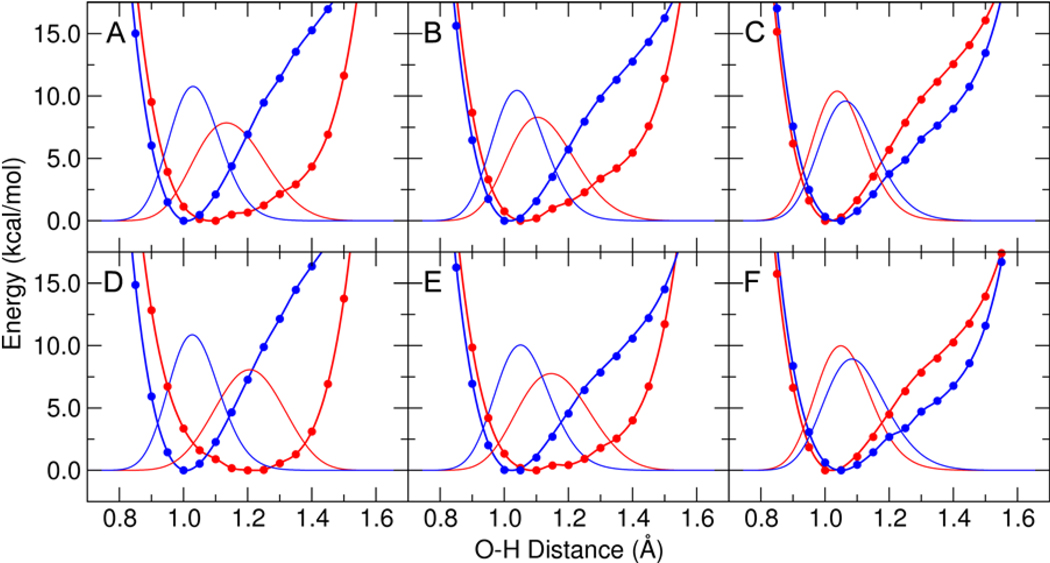
To further explore the effects of phenolate substitution on the nature of the two hydrogen bonds, we calculated the proton potential energy curves for each hydrogen bond, both with and without the inductive effects of the distal tyrosines. Figure 5 depicts the proton potential energy curves and corresponding proton vibrational wavefunctions for phenolate, which has a solution pKa of 10.0, and 3,4,5-trifluorophenolate, which has a solution pKa of 8.2. In the absence of inductive effects, the proton potential energy curves corresponding to both hydrogen bonds are asymmetric with the minimum closer to the amino acid oxygen. When the inductive effects of Tyr57 are included, however, the proton potential energy curve corresponding to the Tyr16-phenolate hydrogen bond becomes a broader single well, which is somewhat asymmetric in the case of 3,4,5-trifluorophenolate and nearly symmetric in the case of phenolate. The addition of the inductive effects of Tyr32 extends this trend, resulting in the minimum of the broader single well being slightly closer to the phenolate for the Tyr16-phenolate hydrogen bond. As discussed below, however, DFT does not provide quantitatively accurate intermolecular distances or barriers, but rather is capable of predicting only qualitative trends. Due to the limitations of DFT, the proton potential energy curves may not be quantitatively accurate. Thus, we interpret these results to implicate only a qualitative movement of the proton toward the hydrogen bond acceptor as the phenolate pKa increases.
Figure 5.
Proton potential energy curves and corresponding proton vibrational wavefunctions for 3,4,5-trifluorophenolate in (A), (B), and (C) and for phenolate in (D), (E), and (F). The proton potentials were determined from QM/MM calculations of the phenolate bound to pKSI D40N with Tyr32 and Tyr57 in the MM region for (A) and (D), with Tyr57 in the QM region for (B) and (E), and with both Tyr32 and Tyr57 in the QM region for (C) and (F). All calculations included Tyr16, Asp103, Asp40Asn, and the phenolate in the QM region. The single point QM/MM energies are depicted with points, the fits are depicted with thick lines, and the proton vibrational wavefunctions are depicted with thin lines. Results are shown in red for the Tyr16-phenolate hydrogen bond and in blue for the Asp103-phenolate hydrogen bond.
These calculations are qualitatively consistent with the observed trends of absorption spectra measured for a series of naphthols bound to KSI (6) and provide an explanation for the experimentally measured differences between pKSI and tKSI. The fraction of protonated form of the naphthol bound to KSI, as determined experimentally by fitting the absorption spectra to a linear combination of protonated and deprotonated naphthol spectra, differed for pKSI and tKSI. Specifically, a substantially smaller fraction of protonated naphtholate (i.e., neutral naphthol) was observed in the tKSI active site than in the pKSI active site. Although our calculations are performed on a single configuration that does not exhibit proton transfer, the trends in the hydrogen-bonding distances and proton potential energy curves provide an indication of relative proton transfer character. These calculations suggest that Tyr16 is the most likely proton donor to the naphtholate when this ligand is observed experimentally to bind as a neutral naphthol at high pKa (6). These calculations also suggest that the differences in the experimentally measured fraction of protonated form of bound inhibitor for pKSI and tKSI may arise from the presence of Tyr32 in the hydrogen-bonding network of pKSI but not in tKSI. Additional experiments on tKSI with the F32Y mutation and pKSI with the Y32F mutation could be performed to test this hypothesis.
NMR Chemical Shifts Shifts of Hydrogen Bonded Protons in the KSI Oxyanion Hole
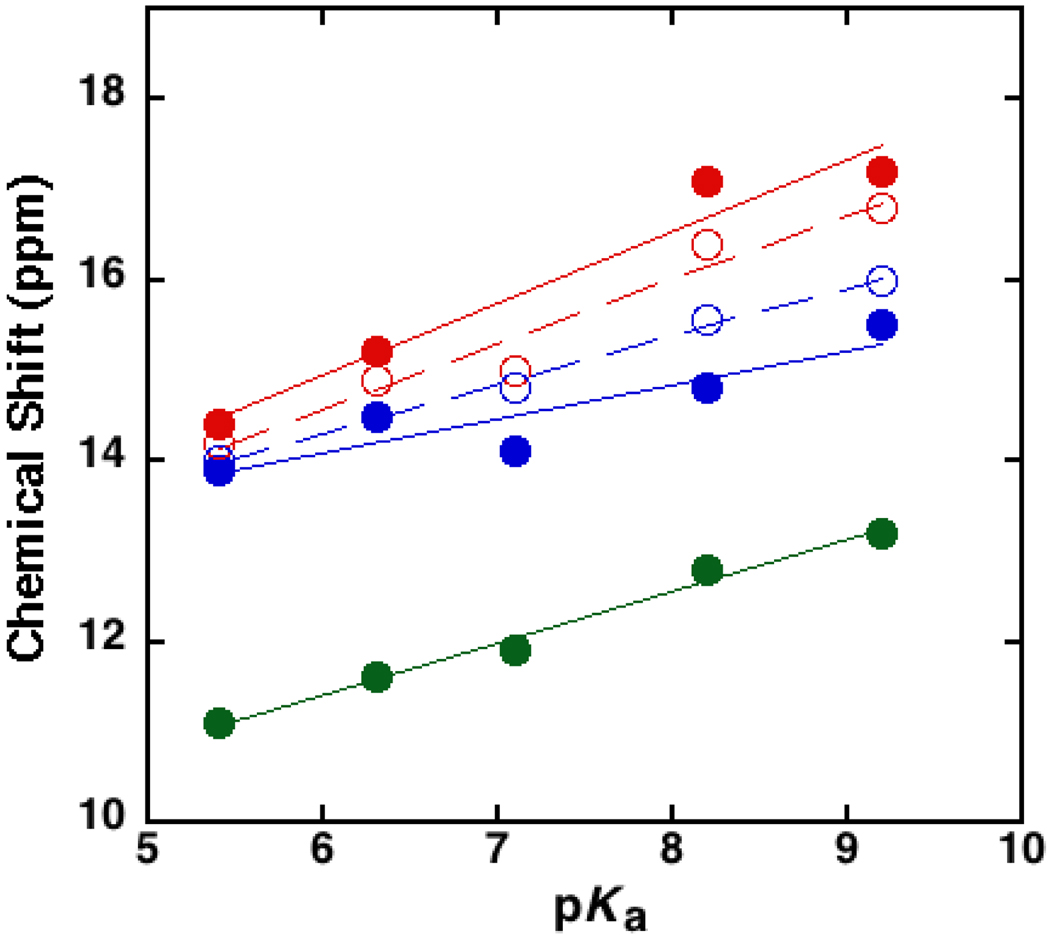
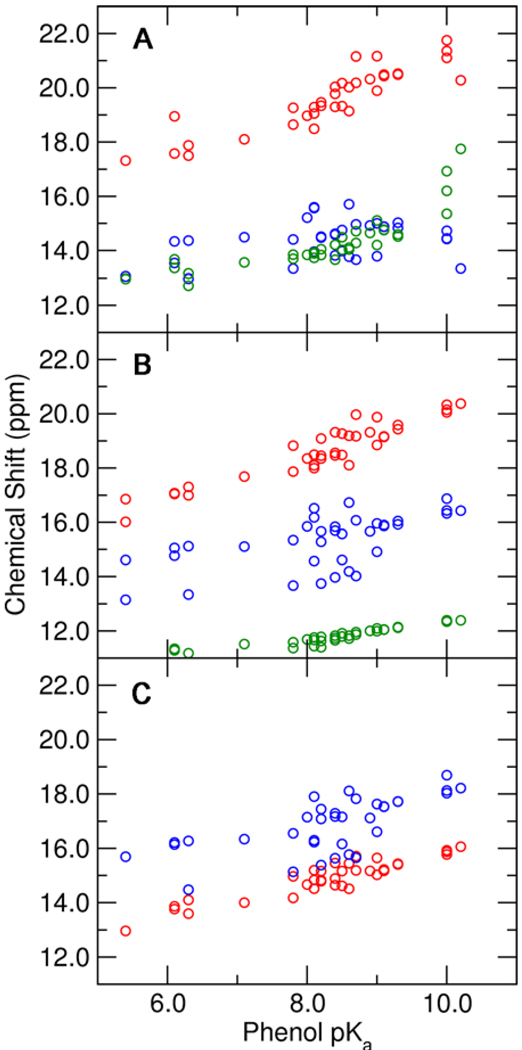
The downfield NMR chemical shifts observed for the series of substituted phenolates bound to tKSI D40N were previously published (4). In order to directly compare our theoretical calculations for pKSI D40N-bound phenolates to experimental data measured on the same enzyme, we acquired 1H NMR spectra for substituted phenolates bound to pKSI D40N. As shown in Figure S1, these spectra are generally similar to the previously published data for tKSI D40N: phenolate binding to both enzymes results in the appearance of downfield peaks >14 ppm that move progressively downfield with increasing phenolate pKa. Nevertheless, there are notable differences between the two enzymes: (1) the pKSI D40N peaks are generally broader than those observed for tKSI, (2) only one peak is observed for pKSI D40N upon 4-nitrophenolate binding, whereas two are observed for tKSI, and (3) for pKSI a third downfield peak appears at ~11 ppm and moves downfield to 14 ppm with increasing phenolate pKa. When the observed downfield peaks for pKSI D40N are plotted as a function of phenolate pKa and compared to the corresponding data for tKSI D40N (Figure 6), we note that the chemical shift of the most downfield peak is greater for pKSI, while the chemical shift of the second most downfield peak is greater for tKSI. While the slope representing the pKa dependence for the most downfield peak is nearly identical for both enzymes, the slope of the second most downfield peak is slightly reduced in pKSI compared to tKSI.
Figure 6.
Experimental chemical shifts of downfield 1H NMR peaks observed upon phenolate binding to pKSI D40N (closed circles) and tKSI D40N (open circles) as functions of the solution pKa of the substituted phenolate. The phenolates (pKa) shown are: 3,4-dinitrophenol (5.4), 3-trifluoromethyl-4-nitrophenol (6.3), 4-nitrophenol (7.1), 3-fluoro-5-trifluoromethylphenol (8.2), 3-iodophenol (9.2). Linear fits to the data are shown with solid (pKSI D40N) and dashed (tKSI D40N) lines. Data for tKSI were previously published in Ref. (4). Spectra for pKSI D40N are shown in Fig. S1.
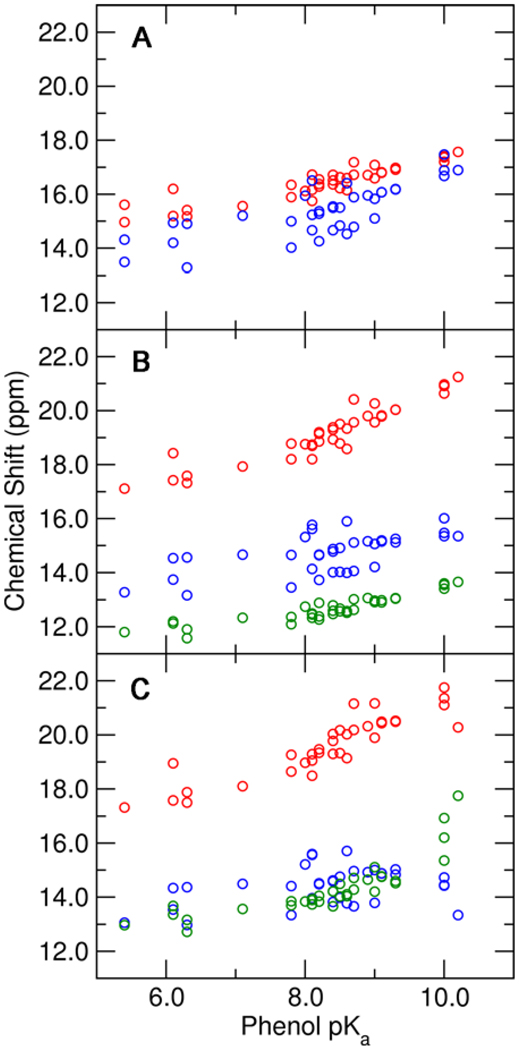
The previous NMR study of phenolates bound to tKSI D40N was able to assign the observed downfield peaks to the hydrogen-bonded protons of Tyr16 and Asp103 but could not further distinguish which proton corresponds to each peak (4). A more detailed discussion of these NMR assignments is provided in Supporting Information. To assist with the assignments of these NMR chemical shifts and provide insight into the differences between pKSI and tKSI, we calculated the NMR chemical shifts for the substituted phenolates bound to pKSI D40N. Figure 7 depicts the calculated chemical shifts for the protons in the Tyr16-phenolate and Asp103-phenolate hydrogen bonds, as well as the proton in the Tyr16-Tyr57 hydrogen bond when Tyr57 is included in the QM region. This figure illustrates that the chemical shifts increase as the solution pKa of the phenolate increases, in agreement with the experimental data and as expected based on the calculated shortening of the O–O distances and elongation of the donor O–H bond with increasing phenolate pKa (Figures 3 and 4). Proton migration away from the donor oxygen is expected to decrease local electron density, deshielding the proton and increasing its isotropic chemical shift.
Figure 7.
Calculated NMR chemical shifts for the protons in the Tyr16-phenolate hydrogen bond (red), the Asp103-phenolate hydrogen bond (blue), and the Tyr16-Tyr57 hydrogen bond (green) as functions of the solution pKa of the substituted phenolate. These chemical shifts were determined from QM/MM calculations of the phenolate bound to pKSI D40N with three different QM regions: (A) Tyr57 and Tyr32 MM, (B) Tyr57 QM and Tyr32 MM, and (C) Tyr57 and Tyr32 QM. All calculations included Tyr16, Asp103, Asp40Asn, and the phenolate in the QM region.
According to our calculations, the most downfield chemical shift corresponds to the Tyr16 hydroxyl proton. Since available NMR data cannot distinguish which downfield peak arises from Tyr16 versus Asp103 (as discussed above and in Supporting Information), future experiments will be required to test this prediction. We note that this assignment is consistent with the shorter O–O distance refined for the Tyr16 hydrogen bond (relative to the Asp103 hydrogen bond) in all four independently-refined monomers in the asymmetric unit of the 1.25 Å pKSI•phenolate X-ray structure (4) and the expectation that a shorter hydrogen bond will lead to a more downfield chemical shift (7).
When the inductive effects of the hydrogen-bonding network are included by adding Tyr57 and Tyr32 to the QM region, the chemical shift and its dependence on phenolate pKa increase for Tyr16 but decrease for Asp103. These results suggest that the experimentally observed differences between the magnitude and pKa dependence of the NMR chemical shifts for phenolates bound to pKSI D40N and tKSI D40N may arise from the additional hydrogen bond donated by Tyr32 in the hydrogen-bonding network of pKSI. This issue will be discussed further in the context of mutants below. In addition, these calculations predict that a third pKa-dependent downfield peak >10 ppm corresponding to the Tyr16-Tyr57 hydrogen bond should be detectable for tKSI but at a higher pKa than for pKSI. Inspection of the previously published tKSI spectra (4) reveals that such a peak does indeed become detectable at a phenolate pKa value of ~9, consistent with this prediction.
The calculated NMR chemical shifts agree qualitatively but not quantitatively with the experimental data. The calculated chemical shifts of the Tyr16 and Asp103 hydroxyl protons are overestimated and underestimated, respectively, relative to the experimental values. The quantitative errors may be explained in part by the known systematic underestimation of hydrogen-bonding distances with DFT (48, 49). Underestimation of the hydrogen bond O–O distance would be expected to increase the donor O–H distance in the hydrogen bond, thereby increasing the calculated chemical shift of the proton. Due to the physical coupling between the Tyr16 and Asp103 hydrogen bonds to the phenolate described above, underestimation of the Tyr16-phenolate hydrogen bond distance may result in overestimation of the Asp103-phenolate hydrogen bond distance, which is consistent with the observed quantitative discrepancies between the calculated and experimentally determined NMR data. Nevertheless, DFT is able to reproduce the trends in the hydrogen-bonding distances and chemical shifts for the series of substituted phenolates.
In addition to the limitations of DFT, additional errors are introduced by the lack of conformational sampling in the calculations (i.e., the investigation of only a single optimized geometry). Since the same equilibrated solvent configuration and initial protein structure were used for all calculations, the trends for the series of substituted phenolates are expected to be reasonable. As an additional test, we performed some of these calculations for a different equilibrated solvent configuration and found that the results were qualitatively similar, as shown in Figure S2.
Hydrogen Bonding in KSI Mutants
To further explore the effects of Tyr32 and Tyr57 on the oxyanion hole hydrogen bonds and their NMR chemical shifts, we performed additional calculations on the Y32F/D40N and Y32F/D40N/Y57F pKSI mutants. The calculated O–O hydrogen bond distances and NMR chemical shifts of pKSI D40N and these mutants are depicted in Figures 8 and 9, respectively. (In all of these calculations, both residues 32 and 57 are included in the QM region.) As tyrosine residues are removed from the hydrogen-bonding network by mutation to phenylalanine, the Tyr16-phenolate hydrogen bond lengthens, while the Asp103-phenolate hydrogen bond shortens relative to pKSI D40N. This shortening of the Asp103 hydrogen bond in response to lengthening of the Tyr16 hydrogen bond indicates a coupling between these two hydrogen bonds, in agreement with experimental identification of coupling between these residues by NMR (14). In the Y32F/D40N/Y57F mutant, our calculations suggest that the Asp103-phenolate hydrogen bond is shorter than the Tyr16-phenolate hydrogen bond, resulting in a reversal of the chemical shift assignments for this mutant. This analysis is further supported by calculations of the proton potentials and corresponding proton vibrational wavefunctions for these mutants, as depicted in Figure 10.
Figure 8.
Hydrogen bond O–O distances for the Tyr16-phenolate hydrogen bond (red) and the Asp103-phenolate hydrogen bond (blue) as functions of the solution pKa of the substituted phenolate. These distances were determined from QM/MM calculations of the phenolate bound to pKSI D40N with (A) the unmodified hydrogen-bonding network, (B) the Y32F mutation, and (C) the Y32F/Y57F mutations. All calculations included Tyr16, Asp103, Asp40Asn, residue 32, residue 57, and the phenolate in the QM region.
Figure 9.
Calculated NMR chemical shifts for the protons in the Tyr16-phenolate hydrogen bond (red), the Asp103-phenolate hydrogen bond (blue), and the Tyr16-Tyr57 hydrogen bond (green) as functions of the solution pKa of the substituted phenolate. These chemical shifts were determined from QM/MM calculations of the phenolate bound to pKSI D40N with (A) the unmodified hydrogen-bonding network, (B) the Y32F mutation, and (C) the Y32F/Y57F mutations. All calculations included Tyr16, Asp103, Asp40Asn, residue 32, residue 57, and the phenolate in the QM region.
Figure 10.
Proton potential energy curves and corresponding proton vibrational wavefunctions for 3,4,5-trifluorophenolate in (A), (B), and (C) and for phenolate in (D), (E), and (F). The proton potentials were determined from QM/MM calculations of the phenolate bound to pKSI D40N in (A) and (D), with the additional Y32F mutation in (B) and (E), and with the additional Y32F/Y57F mutation in (C) and (F). The single point QM/MM energies are depicted with points, the fits are depicted with thick lines, and the proton vibrational wavefunctions are depicted with thin lines. Results are shown in red for the Tyr16-phenolate hydrogen bond and in blue for the Asp103-phenolate hydrogen bond. All calculations included Tyr16, Asp103, Asp40Asn, residue 32, residue 57, and the phenolate in the QM region.
These calculations indicate that the hydrogen-bonding network comprised of Tyr57 and Tyr32 impacts the relative lengths of the two active site hydrogen bonds in pKSI. These calculations also suggest that the Tyr16 hydroxyl is more acidic than the Asp103 carboxylic acid moiety because of the electron-withdrawing inductive effects of the hydrogen-bonding network, in contrast to the predominantly nonpolar environment surrounding Asp103. In the absence of these tyrosine residues, Asp103 is observed computationally to form a shorter hydrogen bond and donate its proton more readily than Tyr16, consistent with the relative solution pKa values of these amino acids. Future experiments will be required to test our prediction that Tyr16 is more acidic than Asp103 in pKSI D40N.
These calculations are consistent with experimental data on a related mutant. Experimental NMR spectra for 3,4-dinitrophenolate bound to tKSI D40N/Y57F indicated a lengthening of the Tyr16-phenolate hydrogen bond and a shortening of the Asp103-phenolate hydrogen bond (14). These data implicate an inductive effect from the hydrogen-bonding network, as well as hydrogen bond coupling. Specifically, when the inductive effects of the hydrogen-bonding network are diminished by mutating Tyr57 to Phe, the Tyr16-phenolate hydrogen bond lengthens and the Asp103-phenolate hydrogen bond shortens.
To further test the hypothesis of an inductive effect through the hydrogen-bonding network in KSI, we mutated the most distal tyrosine in the network to 2,6-difluorotyrosine and 2,3,5,6-tetrafluorotyrosine for both wild-type and mutant pKSI. As expected, the optimized geometries of the protons in the hydrogen-bonding network of tyrosines are shifted toward the phenolate in all cases. These calculations lead to the prediction that the degree of protonated ligand identified in the electronic absorption spectra (6) should be greater for these fluorotyrosine mutants than for their natural counterparts. Furthermore, the hydroxyl proton in the Asp103-phenolate hydrogen bond was observed to further localize on the aspartic acid, leading to the prediction of a reduction of the NMR chemical shift observed for this proton.
Comparison to Steroid Isomerization Reaction
To determine the relation between the changes in hydrogen bonding occurring along the series of substituted phenolates and those occurring along the KSI reaction coordinate, we performed QM/MM geometry optimizations for the reactant, intermediate, and product states of the natural substrate in pKSI. In the intermediate state, relatively short hydrogen bonds are formed between both Tyr16 and Asp103 and the dienolate oxyanion, with Tyr16 forming the shorter hydrogen bond. These hydrogen bonds are ~0.1 Å shorter for the dienolate intermediate than for the reactant and product. These results are qualitatively consistent with X-ray crystal structures indicating that the oxyanion hole hydrogen bonds are ~0.2 Å shorter with bound intermediate analogs than with product analogs (15).
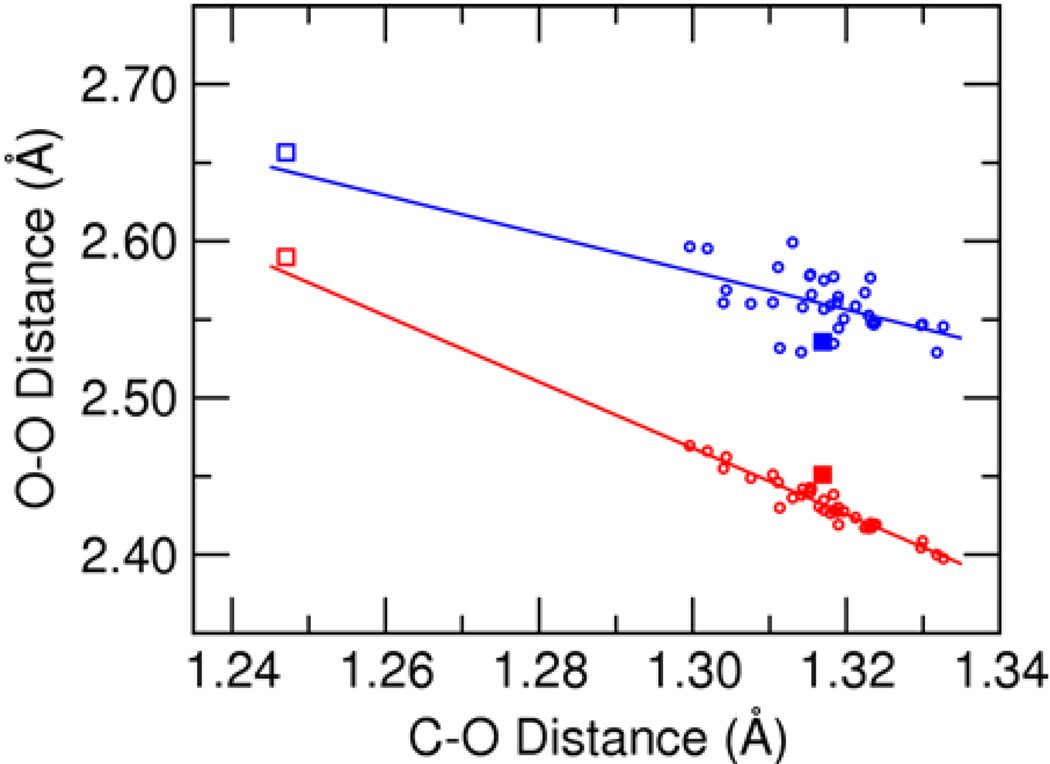
To assess possible differences between the physical properties of hydrogen bonds formed to the phenolates and to the bound steroid substrate and reaction intermediate, we plotted the hydrogen bond O–O distances as a function of ligand C–O distance for each species, as depicted in Figure 11. The open circles in this figure correspond to the series of substituted phenolates, and the open and filled square symbols correspond to the reactant and dienolate intermediate, respectively, for the steroid isomerization. Calculated distances for substituted phenolates span a range around the dienolate intermediate but do not extend to the reactant state. Nevertheless, extrapolation of linear fits of the phenolate data suggests that the distances for the bound substrate and intermediate fall on the same correlation line as those for the phenolates. On the basis of this analysis, we conclude that hydrogen bonds formed to phenolates and steroids bound within the KSI active site exhibit similar physical properties.
Figure 11.
Correlation between the ligand C–O distances and the hydrogen bond O–O distances for the Tyr16-ligand hydrogen bond (red) and the Asp103-ligand hydrogen bond (blue) determined from QM/MM calculations of the ligand bound to pKSI D40N. The open circles correspond to the series of substituted phenolates. The open and filled squares correspond to the steroid substrate (i.e., the reactant) and the dienolate intermediate, respectively. All calculations included Tyr16, Asp103, residue 40, Tyr57, and the bound ligand in the QM region. The lines represent linear fits to the phenolate data.
CONCLUSIONS
The QM/MM calculations presented in this paper provide insight into the electronic inductive effects and hydrogen bond coupling in the active site of KSI. As a result of inductive effects arising from substitutions on bound phenolate inhibitors, the hydrogen bond distances decrease, the NMR chemical shifts increase, and the fraction of protonated inhibitor increases as the solution pKa of the phenolate increases, in agreement with prior experimental data. The calculations predict that the most-downfield NMR chemical shift observed experimentally corresponds to the Tyr16-phenolate hydrogen bond and that Tyr16 is the proton donor when the naphtholate is observed to be protonated in the electronic absorption experiments. These results also provide support for an electronic inductive effect along the hydrogen-bonding network formed by Tyr16, Tyr57, and Tyr32. As a result of this inductive effect observed in our calculations, the Tyr16 hydroxyl is predicted to be more acidic than the Asp103 carboxylic acid moiety, which is immersed in a relatively nonpolar environment. When one of the more distal tyrosine residues in the network is mutated to phenylalanine, thereby diminishing this inductive effect, the Tyr16-phenolate hydrogen bond lengthens, and the Asp103-phenolate hydrogen bond shortens, as observed in NMR experiments.
These studies also provide experimentally testable predictions. The calculations predict that mutation of both distal tyrosine residues in the pKSI network to phenylalanine will lead to a decreased chemical shift for the Tyr16-phenolate hydrogen bond and an increased chemical shift for the Asp103-phenolate hydrogen bond, potentially leading to a reversal of the chemical shift assignments, as well as a smaller fraction of protonated ligand. The calculations also predict that fluorination of the distal tyrosines in this network will enhance this inductive effect, leading to a shortening of the Tyr16-phenolate hydrogen bond and a lengthening of the Asp103-phenolate hydrogen bond. These effects of fluorination should be experimentally observable through a larger fraction of protonated ligand, identifiable by the electronic absorption spectra. Furthermore, these studies suggest that the differences in the experimental NMR data and electronic absorption spectra for pKSI and tKSI are due predominantly to the third tyrosine that is present in the hydrogen-bonding network of pKSI but not tKSI. This hypothesis can be tested experimentally by mutation of this third tyrosine to phenylalanine in pKSI or the reverse mutation in tKSI.
Supplementary Material
Funding Acknowledgment
This work was funded by NIH Grant No. GM56207 (SHS) and NSF Grant MCB-0641393 (DH). PAS was supported in part by HHMI and G. Lieberman Predoctoral Fellowships. This work was supported in part through instrumentation funded by the National Science Foundation through grant OCI-0821527. NMR spectra were acquired at the Stanford Magnetic Resonance Laboratory which is funded, in part, by the Stanford University School of Medicine.
Abbreviations
- KSI
Δ5-3-ketosteroid isomerase
- pKSI
ketosteroid isomerase from Pseudomonas putida
- tKSI
ketosteroid isomerase from Commamonas testosteroni
- QM/MM
quantum mechanical/molecular mechanical
- MD
molecular dynamics
- DFT
density functional theory
- GIAO
gauge-including atomic orbitals
Footnotes
SUPPORTING INFORMATION AVAILABLE
Downfield region of 1H NMR spectra for substituted phenolates bound to pKSI D40N; comparison of QM/MM results obtained for two different solvent configurations; discussion of previous NMR assignments with supporting NMR data; complete list of phenols and their solution pKa values. This material is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Pollack RM. Enzymatic mechanisms for catalysis of enolization: ketosteroid isomerase. Bioorg. Chem. 2004;32:341–353. doi: 10.1016/j.bioorg.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 2.Hawkinson DC, Eames TCM, Pollack RM. Energetics of 3-oxo-Δ5-steroid isomerase: Source of the catalytic power of the enzyme. Biochemistry. 1991;30:10849–10858. doi: 10.1021/bi00109a007. [DOI] [PubMed] [Google Scholar]
- 3.Petrounia IP, Pollack RM. Substituent effects on the binding of phenols to the D38N mutant of 3-oxo-Δ5-steroid isomerase: A probe for the nature of hydrogen bonding to the intermediate. Biochemistry. 1998;37:700–705. doi: 10.1021/bi972262s. [DOI] [PubMed] [Google Scholar]
- 4.Kraut DA, Sigala PA, Pybus B, Liu CW, Ringe D, Petsko GA, Herschlag D. Testing electrostatic complementarity in enzymatic catalysis: Hydrogen bonding in the ketosteroid isomerase oxyanion hole. PLoS Biology. 2006;4:501–519. doi: 10.1371/journal.pbio.0040099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Petrounia IP, Blotny G, Pollack RM. Binding of 2-naphthols to D38E mutants of 3-oxo-Δ5-steroid isomerase: Variation of ligand ionization state with the nature of the electrophilic component. Biochemistry. 2000;39:110–116. doi: 10.1021/bi9917838. [DOI] [PubMed] [Google Scholar]
- 6.Childs W, Boxer SG. Proton affinity of the oxyanion hole in the active site of ketosteroid isomerase. Biochemistry. 2010;49:2725–2731. doi: 10.1021/bi100074s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jeffrey J, Yeon Y. The correlation between hydrogen-bond lengths and proton chemical shifts in crystals. Acta Crystallography B. 1986;42:410–413. [Google Scholar]
- 8.Zhao Q, Abeygunawardana C, Gittis AG, Mildvan AS. Hydrogen bonding at the active site of Δ5-3-ketosteroid isomerase. Biochemistry. 1997;36:14616–14626. doi: 10.1021/bi971549m. [DOI] [PubMed] [Google Scholar]
- 9.Harris TK, Mildvan AS. High-precision measurement of hydrogen bond lengths in proteins by nuclear magnetic resonance methods. Proteins: Struct., Funct., Genet. 1999;35:275–282. doi: 10.1002/(sici)1097-0134(19990515)35:3<275::aid-prot1>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 10.Zeng B, Pollack RM. Microscopic rate constants for the acetate ion catalyzed isomerization of 5-androstene-3,17-dione to 4-androstene-3,17-dione: A model for steroid isomerase. J. Am. Chem. Soc. 1991;113:3838–3842. [Google Scholar]
- 11.Kim D-H, Jang DS, Nam GH, Choi G, Kim J-S, Ha N-C, Kim M-S, Oh B-H, Choi KY. Contribution of the hydrogen-bond network involving a tyrosine triad in the active site to the structure and function of a highly proficient ketosteroid isomerase from Pseudomonas putida Biotype B. Biochemistry. 2000;39:4581–4589. doi: 10.1021/bi992119u. [DOI] [PubMed] [Google Scholar]
- 12.Choi G, Ha N-C, Kim M-S, Hong B-H, Oh B-H, Choi KY. Pseudoreversion of the catalytic activity of Y14F by the additional substitution(s) of tyrosine with phenylalanine in the hydrogen bond network of Delta-5-3-ketosteroid isomerase from Pseudomonas putida biotype B. Biochemistry. 2001;40:6828–6835. doi: 10.1021/bi002767+. [DOI] [PubMed] [Google Scholar]
- 13.Jang DS, Cha HJ, Cha S-S, Hong BH, Ha N-C, Lee JY, Oh B-H, Lee H-S, Choi KY. Structural double-mutant cycle analysis of a hydrogen bond network in ketosteroid isomerase from Pseudomonas putida biotype B. Biochem. J. 2004;382:967–973. doi: 10.1042/BJ20031871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sigala PA, Caaveiro JMM, Ringe D, Petsko GA, Herschlag D. Hydrogen bond coupling in the ketosteroid isomerase active site. Biochemistry. 2009;48:6932–6939. doi: 10.1021/bi900713j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Oh KS, Cha S-S, Kim D-H, Cho H-S, Ha N-C, Choi G, Lee JY, Tarakeshwar P, Son HS, Choi KY, Oh B-H, Kim KS. Role of catalytic residues in enzymatic mechanisms of homologous ketosteroid isomerases. Biochemistry. 2000;39:13891–13896. doi: 10.1021/bi001629h. [DOI] [PubMed] [Google Scholar]
- 16.Kim KS, Oh KS, Lee JY. Catalytic role of enzymes: Short strong H-bond-induced partial proton shuttles and charge redistributions. Proc. Natl. Acad. Sci. U.S.A. 2000;97:6373–6378. doi: 10.1073/pnas.97.12.6373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pan Y, McAllister MA. Theoretical investigation of the role of hydrogen bonding during ketosteroid isomerase catalysis. J. Mol. Struct. (THEOCHEM) 2000;504:29–33. [Google Scholar]
- 18.Park H, Merz KM., Jr Molecular dynamics and quantum chemical studies on the catalytic mechanism of Δ5-3-ketosteroid isomerase: The catalytic diad versus the cooperative hydrogen bond mechanism. J. Am. Chem. Soc. 2003;125:901–911. doi: 10.1021/ja0208097. [DOI] [PubMed] [Google Scholar]
- 19.Feierberg I, Aqvist J. The catalytic power of ketosteroid isomerase investigated by computer simulation. Biochemistry. 2002;41:15728–15735. doi: 10.1021/bi026873i. [DOI] [PubMed] [Google Scholar]
- 20.Feierberg I, Aqvist J. Computational modeling of enzymatic ketoenol isomerization reactions. Theor. Chem. Acc. 2002;108:71–84. [Google Scholar]
- 21.Mazumder D, Kahn K, Bruice TC. Computational study of ketosteroid isomerase: Insights from molecular dynamics simulation of enzyme bound substrate and intermediate. J. Am. Chem. Soc. 2003;125:7553–7561. doi: 10.1021/ja030138s. [DOI] [PubMed] [Google Scholar]
- 22.Warshel A, Sharma PK, Chu ZT, Aqvist J. Electrostatic contributions to binding of transition state analogues can be very different from the corresponding contributions to catalysis: Phenolates binding to the oxyanion hole of ketosteroid isomerase. Biochemistry. 2007;46:1466–1476. doi: 10.1021/bi061752u. [DOI] [PubMed] [Google Scholar]
- 23.Kamerlin SCL, Sharma PK, Chu ZT, Warshel A. Ketosteroid isomerase provides further support for the idea that enzymes work by electrostatic preorganization. Proc. Natl. Acad. Sci. U.S.A. 2010;107:4075–4080. doi: 10.1073/pnas.0914579107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chakravorty DK, Soudackov AV, Hammes-Schiffer S. Hybrid quantum/classical molecular dynamics simulations of the proton transfer reactions catalyzed by ketosteroid isomerase: Analysis of hydrogen bonding, conformational motions, and electrostatics. Biochemistry. 2009;48:10608–10619. doi: 10.1021/bi901353v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chakravorty DK, Hammes-Schiffer S. Impact of mutation on proton transfer reactions in ketosteroid isomerase: Insights from molecular dynamics simulations. J. Am. Chem. Soc. 2010;132:7549–7555. doi: 10.1021/ja102714u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xiang Z, Honig B. Extending the accuracy limits of prediction for side-chain conformations. J. Mol. Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
- 27.Xiang JZ, Honig B. JACKAL: A Protein Structure Modeling Package. New York: Columbia University & Howard Hughes Medical Institute; 2002. [Google Scholar]
- 28.Gordon JC, Myers JB, Folta T, Shoja V, Heath LS, Onufriev A. H++: a server for estimating pKas and adding missing hydrogens to macromolecules. Nucleic Acids Res. 2005;33:W368–W371. doi: 10.1093/nar/gki464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Maestro, 9.0 ed. New York: Schrodinger, LLC; 2009. [Google Scholar]
- 30.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. Journal of Chemical Physics. 1983;79:926–935. [Google Scholar]
- 31.Mahoney MW, Jorgensen WL. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. Journal of Chemical Physics. 2000;112:8910–8922. [Google Scholar]
- 32.Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 33.Berendsen HJC, Postma JPM, Van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 34.Darden T, York D, Pedersen L. Particle mesh Ewald - an N.Log(N) method for Ewald sums in large systems. Journal of Chemical Physics. 1993;98:10089–10092. [Google Scholar]
- 35.Ryckaert JP, Ciccotti G, Berendsen HJC. J. Comput. Phys. 1977;23:327. [Google Scholar]
- 36.Desmond Molecular Dynamics System, 2.2 ed. New York: D.E. Shaw Research; 2008. [Google Scholar]
- 37.Bowers KJ, Chow E, Xu H, Dror RO, Eastwood MP, Gregersen BA, Klepeis JL, Kolossvary IK, Moraes MA, Sacerdoti FD, Salmon JK, Shan Y, Shaw DE. Scalable algorithms for molecular dynamics simulations on commodity clusters. Proceedings of the ACM/IEEE Conference on Supercomputing (SC06); Tampa, Florida: 2006. [Google Scholar]
- 38.QSite, 5.5 ed. New York: Schrodinger, LLC; 2009. [Google Scholar]
- 39.Dunning TH., Jr Gaussian basis sets for use in correlated molecular calculations: 1. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989;90:1007–1023. [Google Scholar]
- 40.Cheeseman JR, Trucks GW, Keith TA, Frisch MJ. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 1996;104:5497–5509. [Google Scholar]
- 41.Helgaker T, Jaszunski M, Ruud K. Ab initio methods for the calculation of NMR shielding and indirect spin-spin coupling constants. Chem. Rev. 1999;99:293–352. doi: 10.1021/cr960017t. [DOI] [PubMed] [Google Scholar]
- 42.Cao Y, Beachy MD, Braden DA, Morrill L, Ringnalda MN, Friesner RA. Nuclear-magnetic-resonance shielding constants calculated by pseudospectral methods. J. Chem. Phys. 2005;122:224116. doi: 10.1063/1.1924598. [DOI] [PubMed] [Google Scholar]
- 43.Rohlfing CM, Allen LC, Ditchfield R. Proton chemical shift tensors in hydrogen-bonded dimers of RCOOH and ROH. J. Chem. Phys. 1983;79:4958–4966. [Google Scholar]
- 44.Marston CC, Balint-Kurti GG. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions. J. Chem. Phys. 1989;91:3571–3576. [Google Scholar]
- 45.Webb SP, Hammes-Schiffer S. Fourier grid Hamiltonian multiconfigurational self-consistent-field: A method to calculate multidimensional hydrogen vibrational wavefunctions. J. Chem. Phys. 2000;113:5214–5227. [Google Scholar]
- 46.Ha N-C, Kim M-S, Lee W, Choi KY, Oh B-H. Detection of large pKa perturbations of an inhibitor and a catalytic group at an enzyme active site, a mechanistic basis for catalytic power of many enzymes. J. Biol. Chem. 2000;275:41100–41106. doi: 10.1074/jbc.M007561200. [DOI] [PubMed] [Google Scholar]
- 47.Turner DL. Binomial solvent suppression. J. Magn. Reson. 1983;54:146–148. [Google Scholar]
- 48.Ruiz E, Salahub DR, Vela A. Defining the domain of density functionals: Charge transfer complexes. J. Am. Chem. Soc. 1995;117:1141–1142. [Google Scholar]
- 49.Zhao Y, Truhlar DG. Benchmark databases for nonbonded interactions and their use to test density functional theory. J. Chem. Theory Comput. 2005;1:415–432. doi: 10.1021/ct049851d. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.