In silico investigation of intracranial blast mitigation with relevance to military traumatic brain injury

Abstract

Blast-induced traumatic brain injury is the most prevalent military injury in Iraq and Afghanistan, yet little is known about the mechanical effects of blasts on the human head, and still less is known about how personal protective equipment affects the brain’s response to blasts. In this study we investigated the effect of the Advanced Combat Helmet (ACH) and a conceptual face shield on the propagation of stress waves within the brain tissue following blast events. We used a sophisticated computational framework for simulating coupled fluid–solid dynamic interactions and a three-dimensional biofidelic finite element model of the human head and intracranial contents combined with a detailed model of the ACH and a conceptual face shield. Simulations were conducted in which the unhelmeted head, head with helmet, and head with helmet and face shield were exposed to a frontal blast wave with incident overpressure of 10 atm. Direct transmission of stress waves into the intracranial cavity was observed in the unprotected head and head with helmet simulations. Compared to the unhelmeted head, the head with helmet experienced slight mitigation of intracranial stresses. This suggests that the existing ACH does not significantly contribute to mitigating blast effects, but does not worsen them either. By contrast, the helmet and face shield combination impeded direct transmission of stress waves to the face, resulting in a delay in the transmission of stresses to the intracranial cavity and lower intracranial stresses. This suggests a possible strategy for mitigating blast waves often associated with military concussion.

The military context and societal consequences of blast-induced traumatic brain injuries (TBIs) in the recent conflicts in Iraq and Afghanistan have been well documented (1–6). The US Department of Defense has estimated that ∼130,000 servicemembers deployed in Iraq and Afghanistan have sustained a TBI while deployed, with ∼5% of servicemembers suffering residual symptoms (7). A recent study also found that 22.8% of soldiers in an Army Brigade Combat Team returning from Iraq had clinician-confirmed TBI (6). Among those who have been medically evacuated from theater, the proportion who have suffered a TBI is even higher (1).

Although falls, motor vehicle crashes, and sports collisions are the leading causes of TBI in the civilian population (8), blast events are now the primary cause of TBI for active duty military personnel in war zones (2). Of all the returnees who screened positive at the Walter Reed Army Medical Center, for example, 68% had been injured by a blast (9). Because of the asymmetrical nature of the Iraq and Afghanistan conflicts, servicemembers have been exposed to improvised explosive devices (IEDs) with associated blast events with increasing frequency. As a result, approximately 60% of total combat casualties (10) and 67% of Army war zone evacuations (1) have been attributed to explosive blasts. One study found that 88% of US military personnel treated by a medical unit in Iraq had been injured by IEDs or mortar ordnance, with 47% of the injuries involving the head (11).

Blast-induced TBI may also have become more prominent because advances in personal protective equipment (PPE), military medicine, and military evacuation procedures allow US servicemembers to survive blasts that previously would have been fatal due to penetrating injuries or primary blast injury to gas-filled organs such as the lungs or gastrointestinal system. As a result, the survival rates in the current conflicts are dramatically higher than in previous conflicts (10, 12, 13). However, although current PPE may allow soldiers to survive more violent blast explosions, it is not clear how it contributes to preventing blast-related TBI. Specifically, the Advanced Combat Helmet (ACH) has been extensively tested for blunt impact mitigation and ballistic penetration resistance, but its influence on the effects of blast waves on the brain is largely unknown.

Despite the importance of understanding and mitigating blast-induced TBI, little is known about injury mechanisms, injury thresholds, or the effect of PPE. A number of computational studies of impact-related TBI have established injury tolerance criteria and have linked head injuries in real-world sports and motor vehicular accidents to relevant mechanical fields (e.g., refs. 14–16). For example, Zhang reconstructed collisions from National Football League games and determined that shear stress response in the brain stem was a strong predictor for impact-related mild TBI (15). By contrast, although significant progress has been made in recent efforts to improve the understanding of blast-induced TBI via animal (e.g., ref. 10) and computational (e.g., refs. 17 and 18) studies, the specific pathways and mechanisms of injury, as well as blast-induced traumatic brain injury criteria defining adequate injury metrics and thresholds, remain undetermined. Further, few studies exist analyzing the impact of protection equipment such as the ACH on blast-induced TBI. One recent simulation study suggests a wave-focusing effect in the space between the helmet shell and the head, leading to higher overpressures than in the unhelmeted head (19). However, the model used lacked a realistic description of the head and helmet geometries and did not consider the helmet pads.

Biofidelic computer models provide an invaluable tool for characterizing the physics of the problem by providing spatial and temporally resolved descriptions of relevant mechanical fields such as stress, strain, and acceleration. This enables us to establish a connection between the external blast event and the mechanical tissue response. The resulting characterization of the local loading environment history can then be used to inform the biological response, from which the specific tissue and cell-level injury mechanisms can be further elucidated.

Current efforts to extend the scope and biofidelity of computer models include the incorporation of advanced tissue constitutive models informed with mechanical properties obtained from in vivo (20) and in vitro dynamic testing of mammalian brain tissue (21) and model validation against lab-scale and field blast tests on animal and physical surrogate models (22).

In this work, we utilize and extend the Defense and Veterans Brain Injury Center (DVBIC)/Massachusetts Institute of Technology (MIT) Full Head Model (17) to investigate strategies to mitigate the intensity of stress waves within the brain tissue resulting from direct exposure to blast waves. Simulations of blast waves interacting with the unprotected head and with two different types of protection are compared to quantify the characteristics of the stress waves transmitted to the brain tissue in each case. The results provide insights on the blast mitigation characteristics of the existing helmet, as well as suggest a possible strategy to further mitigate blast effects on the brain.

Results

Simulations of a blast wave interacting with the unhelmeted head, head with helmet, and head with helmet and face shield were conducted using the computational framework described below. The incident free-field overpressure was selected to be above the threshold for unarmored blast lung injury given by the Bowen curves, which estimate the tolerance to a single blast at sea level for a 70-kg human oriented perpendicular to the blast (23). Specifically, the blast conditions used correspond to a free air explosion of 3.16 g TNT at 0.12 m standoff distance, producing an incident overpressure of 10 atm. The simulations were run to a final time of 0.76 ms to evaluate the early-time response of the head when the severity of the events inside the cranium is largest and the opportunities for mitigation using protective devices are greatest.

The simulations furnish a full-field description of the mechanical fields involved in the dynamics of the problem, including vector fields such as particle velocity and acceleration and tensor fields such as stress and strain. In this study, we focus on analyzing stress wave propagation, which is the main dynamic effect loading the brain tissue during a blast event. We consider two key metrics of stress intensity: the pressure (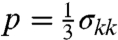), which is associated with hydrostatic or volumetric tissue deformation, and the von Mises or equivalent stress (), which is associated with isochoric distortions in the tissue. Here σ_ij are the components of the Cauchy stress tensor, and 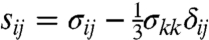are the components of the deviatoric stress tensor (24).

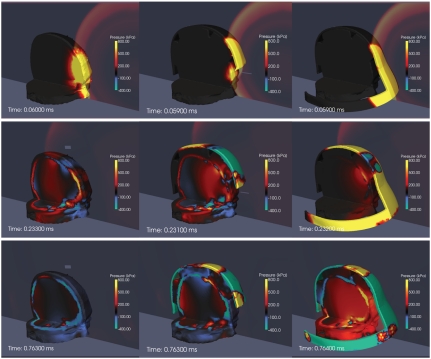
Fig. 1 shows snapshots of the pressure fields in the fluid and solid structures illustrating the progression of the interaction of the blast wave with the head and protective structures in the three simulations. Partial sagittal and axial cuts of the head are used to uncover the pressure fields within.

Fig. 1.

Pressure contours in the head (Left), helmet (Center), and face shield simulations (Right). Starting at the top, the rows correspond to time snapshots at 0.06, 0.23, and 0.76 ms. The scale is from -400 to 800 kPa.

The series of figures in the left column of Fig. 1 correspond to the unhelmeted head simulation. At t = 0.06 ms, it can be clearly seen that the blast wave impinging directly on the face transmits a strong pressure wave to the brain tissue, primarily through the soft tissues. At t = 0.233 ms, the negative phase of the incident wave can be observed as a blue underpressure region interacting with the front of the face and the top of the skull. This leads to negative pressures in the adjacent areas of the cerebrospinal fluid (CSF), indicating the possibility of fluid cavitation. At this point, the pressure wave has traveled faster in the skull than in all the other brain tissues due to its higher relative stiffness. Inside the brain, strong pressure gradients can be observed at the interface between the CSF and the cerebrum. The simulation proceeds with fluctuations in the pressure field of decreasing intensity, with occasional spikes at specific tissue interfaces resulting from the interaction of waves reflecting from the skull and into the cranial cavity. There are also locations where the pressure becomes negative and in some cases attains values exceeding those produced by the negative phase of the incident blast wave. This suggests the possibility that cavitation may be associated with endogenous wave reflection or rarefaction rather than with the negative phase of the incident blast wave. By t = 0.76 ms, the stresses in the intracranial cavity have largely dissipated, with the largest remaining stresses located in the skull.

In the helmet simulation (center column of Fig. 1), it can be seen that the presence of the helmet slightly delays the arrival of the blast wave but does not impede direct transmission of stress waves into the intracranial cavity because it does not protect the face. The snapshot at t = 0.231 ms shows that the negative phase of the blast wave still causes underpressure behind the eyes, but the presence of the helmet avoids the underpressure in the CSF observed in the unhelmeted head simulation. By contrast, slightly higher pressures are transmitted to the skull via the foam padding elements, which act as load concentration points for the impulse transferred from the blast wave to the surface of the helmet. Because it does not cover the face, the helmet does not significantly contribute to mitigating the stress waves transmitted to the brain tissue. Although it does protect the top part of the head from direct exposure to the blast, the advantage is minimal because this is not a major pathway of load transmission into the intracranial cavity. Conversely, these results show that the existing ACH does not enhance blast effects on brain tissue as has been suggested recently with more simplistic models (19).

The column on the right of Fig. 1 shows snapshots of the simulation including face protection. It can be seen that the immediate effect of the face shield is to impede direct transmission of stress waves to the face, both for the positive and negative phases, t = 0.059, 0.232 ms. Initially, the main load transmission pathway to the head is via the foam padding, t = 0.232 ms. This causes a delay in the transmission of stress waves into the head. The magnitude of the transmitted stress is also limited by the crushing stress of the foam, which can be made significantly lower than the reflected blast overpressure, thus affording a passive (soft catch) mitigation mechanism, as discussed recently in ref. 25. By contrast, the total impulse transmitted via the foam padding increases by the extra amount transmitted to the face shield surface. The late increase of the pressure on and inside the head can be attributed to the external shock wave wrapping around the back of the face shield surface and into the interstitial volume between the head and the shield. This points to the need to improve this particular conceptual design.

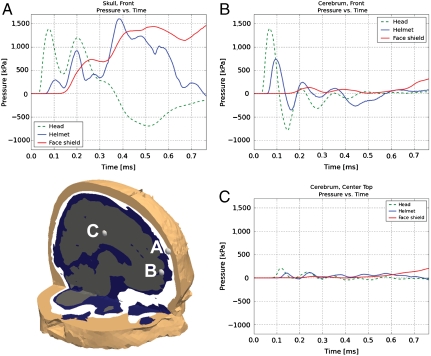
To develop a more quantitative understanding of the simulation results, pressure histories at three points within the skull and cerebrum were extracted and compared for all three simulations, Fig. 2. It can be observed that the helmet alone only slightly delays and reduces the magnitude of pressure peaks, whereas the mitigating effect of the helmet–face shield combination is much more pronounced. For example, although point B in the front of the cerebrum experiences an initial pressure peak of 1,392 kPa at 0.067 ms in the head simulation, in the helmet simulation the peak is delayed by 0.03 ms and reduced to 734 kPa. In the face shield simulation, the same peak is delayed by an additional 0.141 ms and the magnitude is reduced to 132 kPa, a tenth of the magnitude in the head simulation. Although the specific impulse (area underneath the pressure vs. time curve) in the skull (point A) is greater in the helmet and face shield simulations than in the unprotected case, as expected from the additional impulse transmission surface, the delay and reduction in magnitude of the early blast response is significant. Fig. 2 also suggests that the highest pressures occur in the skull (point A), which, due to its stiffness, provides some natural protection to the brain tissue. Inside the brain, the maximum stresses are observed in the anterior region, where the transmitted stress waves initially enter the head for the front blast case analyzed.

Fig. 2.

Pressure profiles from points in the cerebrum and skull for the head, helmet, and face shield simulations. The scale is from -1,200 to 1,700 kPa.

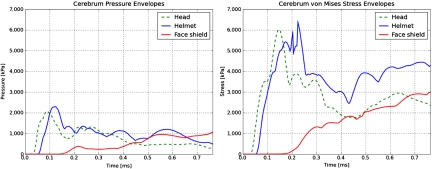
Fig. 3 shows pressure and von Mises stress envelopes (plots of the highest value at each time step) in the cerebrum for the three simulations. These figures further confirm that the helmet slightly delays and does not significantly increase or mitigate stresses transmitted to the brain tissue, whereas a face-protecting device does.

Fig. 3.

Pressure and von Mises stress envelopes for the cerebrum. The scale is from 0 to 7000 kPa.

Discussion

A simulation-based investigation of possible strategies to mitigate the effects of blasts on the human head was conducted. A first simulation was run using an advanced model of the human head without protection exposed to a frontal blast wave of intensity comparable to threshold values of blast lung injury (23, 26). The results suggest that the main wave transmission pathways are the soft tissues in direct contact with the incident blast wave. This simulation also showed that cavitation, if possible, is more likely to be associated with endogenous wave reflections than with the negative phase of the incident blast wave. Tissue cavitation has been proposed as a potential physical mechanism conducive to brain injury (27–29). The second simulation was intended to evaluate the blast protection properties provided by the ACH. The results suggest that the ACH provides no significant mitigation of blast effects on brain tissue. However, no significant deleterious wave-focusing effects were observed either. A third simulation included a conceptual face shield rigidly attached to the helmet shell. It was found that the presence of this device contributed significantly to reducing the magnitude of the stresses propagated inside the brain. However, the particular preliminary design of the face shield adopted needs significant optimization.

The study was limited to a single set of material and blast characteristics (frontal incidence, fixed explosive mass, type, and standoff), which was sufficient to establish theoretical evidence that covering the exposed head surfaces will likely contribute to mitigating blast-induced mild TBI. The conclusions are based on the trends and differences observed among the three simulations, which clearly show the effect of protection equipment. The computational framework has been validated in nonbiological systems, e.g. (25, 30). Current experimental validation efforts involve shock-tube tests on in vivo instrumented porcine specimens, in vitro laboratory-scale blast tests, as well as free-field blast tests. The validation process involves a comparison of the simulation results with the recorded experimental data consisting of pressure histories at sensor locations outside and inside the head for different blast standoff distances. Extensions to the model will include the neck and torso, which have been suggested as a possible indirect pathway for blast-induced brain injury (31). Optimization of the face shield to achieve specific mitigation targets will be explored via parametric studies considering more general blast conditions (incidence angle and intensity), face shield geometries, and material properties. Improvements may include increasing the stiffness and extending the face shield in the posterior lower region of the head to reduce wave diffraction around the tip.

Materials and Methods

Computational Framework for Simulating Blast–Head–Helmet Interactions.

The simulations were conducted using an extension of the Virtual Test Facility (VTF) (30, 32) to simulate blast wave-structure interactions. The VTF is a suite of integrated computational fluid and solid mechanics solvers for the fully coupled analysis of the response of solids to blast and detonation-wave loading on massively parallel computing platforms. Constitutive models to describe the response of various tissues and biological structures have been added to the solid mechanics solver. In addition, the capability to simulate blast waves in air of arbitrary intensity has been integrated in the code to initialize the simulations. The characteristics of the blast wave are specified by the type, mass, and spatial location of the explosive.

The DVBIC/MIT Full Head Model and Extensions Including Protective Equipment.

The three-dimensional computational model of the human head developed by DVBIC and MIT (17) was adapted to this study’s requirements and used in the simulations. It consists of a biofidelic representation of the human head including the following 11 distinct structures: skin and fat, muscle, skull, air sinus, eyes, CSF, gray matter, white matter, ventricles, venous sinus, and glia. The model was obtained by reconstruction from high-resolution T1 MR images and bone-windowed computed tomography images of a human head via registration, segmentation, and posterior computational mesh generation. For the purpose of the current study, the 11 structures were consolidated into 4: cerebrum, skull, CSF, and soft tissue.

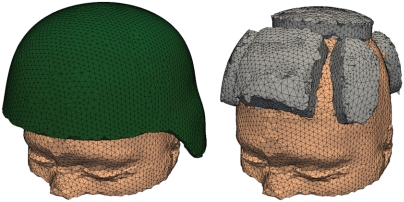
A computer-aided design model of the actual ACH shell and pad geometries provided by Natick Soldier Research Development and Engineering Center was combined with the head model into a single computational model of the head/helmet system. A simple face shield geometry was then created such that the top edge of the face shield was coincident with the front edge of the helmet. The geometry of the face shield was designed to smoothly project from the surface of the helmet shell.

The main characteristics of the head, helmet, and face shield computational models are illustrated in Figs. 4 (cerebrum and CSF), 5 (head surface, ACH, and foam pads), and 6 (face shield and interior view of fully assembled model).

Fig. 4.

Computational mesh of the consolidated cerebrum and CSF structures.

Fig. 5.

Head model with ACH shell and padding.

Fig. 6.

Head model with ACH and conceptual face shield: (A) geometry of the face shield and (B) combined sagittal and axial cut showing a detail of the full mesh.

All finite element meshes were generated using the Octree algorithm in Ansys. Bad quality tetrahedra, which were commonly obtained, were eliminated using the HealMesh* mesh optimization library. The resulting mesh of the complete head model with helmet and face shield consists of 443,452 tetrahedra with quadratic interpolation (10 nodes). In the simulations, 30 processors were used for the solid solver and 10 for the fluid solver. The fluid grid used two levels of subdivision with an equivalent resolution of 1,200 × 1,000 × 580 grid points.

Material Models and Properties.

The constitutive models adopted in the simulations were selected to accurately describe the propagation of stress waves inside the head and protective structures transmitted from the air blast wave. To this end, suitable equations of state describing the volumetric (pressure) response were adopted for each tissue or material type. In addition, the deviatoric recoverable response was described using a nonlinear elastic model. Finally, dissipative effects in the brain tissue were considered through a linear viscosity model. The advantage of this simplified constitutive modeling approach is that it requires few physical material or tissue parameters, which can be quantified with some certainty.

For the skull, we adopted the Hugoniot equation of state (33), which is widely used to describe the shock response of many solid materials:

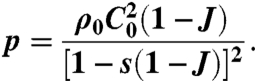[1]

In this expression, p is the pressure, J is the local volume change given by the determinant of the deformation gradient tensor, and C₀ and s are material parameters. For the remaining head structures, we adopted the Tait equation of state, which is commonly used to model fluids subject to large pressure variations (34):

[2]

In this expression, B = K/(Γ₀ + 1) and Γ₀ are material parameters. The Tait equation provides a reasonable representation of the volumetric response of soft tissues embedded in a fluid medium.

The deviatoric elastic response σ^e,dev was computed using the neo-Hookean model extended to the compressible range, in which the strain energy density is given by

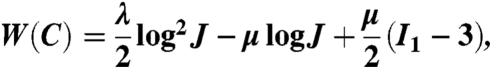[3]

where μ and λ are Lamé constants and I₁ is the first invariant of the right Cauchy–Green deformation tensor.

To complete the constitutive description of each different tissue or material structure, a linear viscosity model was added to both the deviatoric and the volumetric response, furnishing a final expression for the Cauchy stress components:

[4]

where d_ij are the components of the rate of deformation tensor and μ_v, κ, are, respectively, the deviatoric and volumetric viscosity parameters.

The model parameters used for the head components were obtained from literature data (17), Tables 1 and 2.

Table 1.

Material properties for skull

Material	Density, kg/m3	K, Pa	G, Pa	κ, Pa·s	μ, Pa·s	C0, m/s	s
Skull	1,412	3.86 × 109	2.665 × 109	0.0	0.0	1,850.0	0.94

Table 2.

Material properties for CSF, cerebrum, and skin/fat

Material	Density, kg/m3	K, Pa	G, Pa	κ, Pa·s	μ, Pa·s	Γ0
CSF	1,040	2.19 × 109	4.38 × 102	1.0 × 103	0.0	6.15
Cerebrum	1,040	2.19 × 109	2.253 × 104	1.0 × 103	0.0	6.15
Skin/fat	1,100	3.479 × 107	5.88 × 106	1.59 × 101	0.0	6.15

Given the intensity of the blast waves under consideration, the response of the engineering materials used in the protective structures was expected to stay well in the elastic regime. Consequently, the use of a simple neo-Hookean elastic model for these materials was justified for this application. Standard properties for the Kevlar shell and foam were respectively used for the helmet/face shield and padding, Table 3.

Table 3.

Material properties for helmet, face shield, and padding used in simulations

Material	Density, kg/m3	E, Pa	ν
Helmet/face shield	1,440	1.24 × 109	0.36
Padding	136	8 × 106	0.2