Measurement of adherent cell mass and growth

Abstract

The characterization of physical properties of cells such as their mass and stiffness has been of great interest and can have profound implications in cell biology, tissue engineering, cancer, and disease research. For example, the direct dependence of cell growth rate on cell mass for individual adherent human cells can elucidate the mechanisms underlying cell cycle progression. Here we develop an array of micro-electro-mechanical systems (MEMS) resonant mass sensors that can be used to directly measure the biophysical properties, mass, and growth rate of single adherent cells. Unlike conventional cantilever mass sensors, our sensors retain a uniform mass sensitivity over the cell attachment surface. By measuring the frequency shift of the mass sensors with growing (soft) cells and fixed (stiff) cells, and through analytical modeling, we derive the Young’s modulus of the unfixed cell and unravel the dependence of the cell mass measurement on cell stiffness. Finally, we grew individual cells on the mass sensors and measured their mass for 50+ hours. Our results demonstrate that adherent human colon epithelial cells have increased growth rates with a larger cell mass, and the average growth rate increases linearly with the cell mass, at 3.25%/hr. Our sensitive mass sensors with a position-independent mass sensitivity can be coupled with microscopy for simultaneous monitoring of cell growth and status, and provide an ideal method to study cell growth, cell cycle progression, differentiation, and apoptosis.

Cells undergo multiplication and differentiation within multicellular organisms. Understanding how these events are orchestrated by individual cells and cell populations has been of great interest for nearly 50 years. Direct measurements of changes in mammalian cell mass versus growth rate have been among this quest (1–5). Such measurements have the potential of elucidating the intrinsic mechanism for coordination between cell cycle and cell growth (6–8) and determining whether the growth rate is proportional to the cell size (1, 9–11) or the growth rate is constant over cell size and cell cycle (4, 12–15). The linear growth model is based on the assumption that the rate of biosynthesis is limited by the “gene dosage” or the amount of DNA that can initiate the transcription process (3). On the other hand, the exponential growth model is based on the assumption that the increase of cell mass depends on the amount of ribosomal machinery and cytoplasm (3). Therefore, as a cell grows larger (or heavier), it has a greater capacity to produce more mass and increase the growth rate. Theoretically, the linear growth can maintain cell-size homeostasis without a size-dependent mechanism (12), whereas the exponential growth requires a size-dependent mechanism for size homeostasis (11).

Recently, great strides have been made toward this goal by interferometric measurements of dry cell mass (16), population measurements of buoyant mass (analogous to dry cell mass) of suspended cells (17–19), and volume measurements of gently synchronized subpopulations of suspended mammalian cells (11). However, the long-term dependence of growth rate versus cell mass for individual adherent mammalian cells is unknown. To measure cell mass with resonating sensors, the biomechanical properties of the cell must be considered. It has also been established now that the stiffness of the cell is a very important parameter affecting cellular differentiation (20), cancer metastasis (21), and cell spreading (22). Hence, measurement techniques that provide further perspective into the mechanics of cells would be very useful, particularly for examining the dependence of stiffness on the mass measurements.

In an earlier work (23), we used resonant cantilever sensors for the mass measurement of HeLa cells. Due to nonuniform mass sensitivity of the cantilever sensors and absence of active actuation, the mass resolution was not sufficient for detailed analysis of cell growth. In this study, we characterized the biophysical properties and growth of adherent human colorectal carcinoma cells (HT29) using a unique array of silicon resonant mass sensors. Unlike cantilever based sensors (17–19, 23, 24), our unique pedestal design retains uniform mass sensitivity irrespective of cell position on the sensor and also allows simultaneous imaging of the cells. Through measurements of fixed and unfixed cells, and biophysical modeling, we also estimated whole cell mass and demonstrate that other physical parameters of the cell (i.e., Young’s modulus) can be extracted and have implications on understanding cell growth. Most importantly, we find that for HT29 cells, the growth rate increases with cell mass. Because the majority of research in cell biology is on cells attached to a surface, our sensors and approach can be utilized in studies on epithelial and parenchymal cells, which are critical for applications in cancer and tissue regeneration.

Pedestal Mass Sensor Design and Fabrication

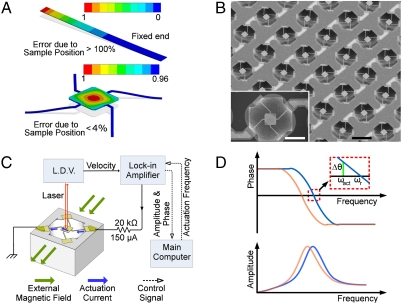
The mass of a target sample attached to a resonant mass sensor can be determined by measuring changes in the resonant frequency of the sensor. The resonant frequency of the sensors, ω_o, is inversely proportional to the square root of its total mass (ω_o ∼ (1/m)^0.5). Hence, by measuring the resonant frequency, the mass of the sensor and the target sample can be measured through time. Cantilever structures have been widely used as a resonant mass sensor. However, conventional cantilever sensors (Fig. 1A) exhibit severe nonuniform mass sensitivity, i.e., the location of the cell relative to the free end determines the mass sensitivity or the ratio of the resonant frequency shift to the actual mass (24). Thus, cell migration can be falsely reported as a change in mass because of the nonuniform mass sensitivity of a cantilever. In this work, a unique sensor structure for uniform mass sensitivity was developed for accurate measurement of the cell mass. Because the mass sensitivity is linearly proportional to the square of the vibration amplitude of the sensor structure (25), a four beam-spring sensor structure (Fig. 1A) was designed to minimize the variation of the vibration amplitude across the vibrating platform.

Fig. 1.

Sensor schematic and experimental set up. (A) The first mode of resonance is shown with the mass sensitivity (color bar) normalized to its maximum value. Modal analysis of cantilevers in liquid via finite element simulations show that they have a spatially nonuniform mass sensitivity or error due to cell positioning of greater than 100% from the free end of the cantilever to the middle of the cantilever (top image), whereas resonating platform designs demonstrate spatial nonuniformity of mass sensitivity or error due to cell position to be less than 4% from the center to the edge of the platform (bottom image). (B) SEM image showing a sensor array; an individual sensor is shown in the inset. (C) Schematic diagram summarizing the automated frequency measurements setup. (D) Frequency response of the sensor with (orange) and without (blue) cell.

Through MEMS fabrication processes (SI Text, Fig. S1), we have fabricated a 9 × 9 array of 81 resonant mass sensors that achieves spatially uniform mass sensitivity (Fig. 1B). Each sensor within the array consists of a square pedestal (60 × 60 μm²) suspended by four beam springs (l = 80 μm, w = 4 μm) over an approximately 50 μm deep pit. Due to its unique structure, the sensor exhibits a maximum 4% difference of mass sensitivity on any position on the pedestal (25). The sensor operates in a first resonance mode, where the platform vibrates vertically at approximately 160 kHz in air and approximately 60 kHz in liquid. Our sensor shows mass sensitivity of 3 Hz/pg in air and 221 Hz/ng in liquid. The sensor was actuated by a Lorentz force generated by passing an actuation current through the sensor in a static magnetic field (Fig. 1C). Throughout the experiment, an undamped resonant frequency (where the velocity of the sensor is in sync with the external sinusoidal excitation) was measured and used for cell mass determination. Both the slope and the average value of the phase (Δθ) were measured at the actuation frequency (ω_act) close to the resonant frequency (ω_r); the frequency at which the phase becomes zero was estimated for the resonant frequency (Fig. 1D). The average phase was calculated from a large number of repeated measurement (n = 250) to suppress any noise component, thus, the resonant frequency can be determined within ± 0.94 Hz (95% CI), yielding a mass resolution of 8.5 pg (95% CI) in liquid (Fig. S2 A–C).

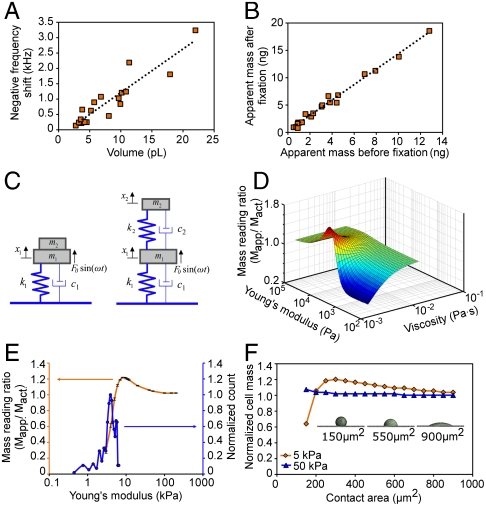
To culture the adherent cells on the sensor for a direct mass measurement, a PDMS micro-incubation well (100 μL) was attached to the chip—the well was hermetically and reversibly sealed—with a cover slip for extended measurement at 37 °C (Fig. S2D). The frequency decrease due to the mass of HT29 cells, measured after the cells were cultured for 50–60 h, shows a linear relationship to the cell volume, estimated by image analysis from confocal and dark field microscopy images (Fig. S3); the data accounts for single cells and up to clusters of four or five cells (Fig. 2A). Light microscopy of cells on the pedestals provides a real-time perspective of cell state that is coordinated with the cell mass measurements for comparing cell behavior with cell mass (Movies S1–S5). This permits greater insight into cell migration and division in relation to the mass.

Fig. 2.

Measurement of frequency shift of adherent cells on pedestal sensors for extracting material properties of the cells. (A) The resonant frequency shift (decrease) is directly related to cell volume of attached cells, confirming the general trend that an increase in cell volume (and mass) decreases the resonant frequency. (B) The apparent mass of HT29 cells after fixation is 1.4 times greater than before fixation. (C) Schematics of dynamical models demonstrating the conventional “mass-spring-damper system” (left), and the improved mass-spring-damper system used to obtain the Young’s modulus, and cell mass from experimental data. (D) A three-dimensional plot summarizing how cell stiffness (Young’s modulus) and viscosity influence mass measurement (mass reading ratio is apparent mass divided by actual mass). The estimated Young’s modulus and viscosity from the 2-DOF model is 4.09 ± 1.22 kPa and 4 ± 2 mPa·s. (E) Calculated dependence of the mass reading ratio on the stiffness of the cell is shown in orange curve (see Materials and Methods) and a normalized histogram of the Young’s modulus is shown in blue curve (see Materials and Methods). (F) The effect of the cell geometry to the mass measurement of a cell with a constant volume. In vitro, an HT29 cell is observed to have the contact area of 200 ∼ 300 μm² (Fig. S3B).

Interplay Between Cell Stiffness and Cell Mass Measurements

First, we measured the mass of fixed cells and compared the results with the mass of the same cells before fixation (Fig. 2B). We found that the measured apparent mass is 1.4 times greater for paraformaldehyde (PFA)-fixed cells than for the corresponding live cell, which demonstrates that indeed the measured apparent mass is a function of the stiffness of target cells. It is well-known that fixation of tissue samples increases their stiffness as compared to fresh, unfixed tissues (26, 27), and causes a minor (∼3%) shrinkage in volume (28). Hence, we assumed that the fixation process does not introduce any additional confounds in the measurement and subsequent analysis. The reduced mass readings of visco-elastic materials on quartz crystal microbalance sensors have been reported (29), and the vibration amplitude of cells on a vibrating substrate has also been shown to increase with increasing cell stiffness (30). In prior studies, the cell has been modeled as a point mass, and it has been assumed that the attached cell vibrates at the same amplitude and is completely in phase with the resonating sensor. The conventional model is shown in Fig. 2C Left, where the sensor vibrating in liquid is modeled as a mass-spring-damper system. Clearly the mass of the adherent cell (live or fixed) is distributed throughout the cell body. Due to the finite elasticity of the cell, the cell body may not vibrate in phase and at the same amplitude with the vibrating sensor as a rigid body (Movie S6, S7). Therefore the measured apparent mass, which was derived from the resonant frequency shift, should be a function of the cell stiffness.

To obtain the actual cell mass and derive the mechanical properties of the cell beyond the conventional model, we introduce a dynamical model of a mass-spring-damper system as an idealized cell and modeled the sensor and the cell body as a two-degree-of-freedom (2-DOF) system as shown in Fig. 2C Right. To elucidate the effect of the elasticity of the cell on the apparent mass, the ratio of the apparent mass to the actual mass was calculated with a wide range of Young’s modulus and viscosity of cells (Fig. 2D). This simple model demonstrates that the apparent mass using resonant sensors can be a function of the stiffness and viscous damping of the cell body. The equations of motion of this damped 2-DOF system can be solved through mathematical modeling of multiple nonlinear equations. Assuming that the actual cell mass does not change during fixation, the 2-DOF model can be used to estimate the Young’s modulus, viscosity, and the actual mass of the living cell using the experimentally measured values of cell mass before and after fixation (SI Text, Fig. S4). By using this approach, the Young’s modulus of the living cell was found to be 4.09 ± 1.2 kPa (Fig. 2E, blue curve). With the extracted Young’s modulus, the apparent mass of living cell is expected to be 64.3% of the actual cell mass, based on the mass reading ratio (Fig. 2E, orange curve), which was independently obtained using a 3D finite element analysis by simulating the resonant frequency shift of a sensor with a cell on it (SI Text, Fig. S5). This prediction matches well with the actual mass derived from the 2-DOF model, which gives the apparent mass of the living cell to be 75% of the actual cell mass (Fig. S4D). Thus, all measured mass values in the remainder of this work were corrected by 1.4 (∼1/0.7) to account for the finite stiffness of the cell, which is assumed not to change through the cell growth.

We also explored the dependence of the apparent mass measurement on the cell geometry with 3D finite element analysis (SI Text, Fig. S5). With a constant cell volume, the apparent mass of a single cell was calculated, as a function of an increasing contact area of the cell and a decreasing cell height and vice versa, as shown in Fig. 2F. The soft cells (orange) show a higher dependence to the geometry than the stiff cells (blue). As the contact area decreases below approximately 200 μm², the apparent cell mass of the soft cell decreases rapidly. This can be explained by the reduced vibration amplitude and shifted vibration phase of the cell body due to a low stiffness, reducing the coupling of the cell’s inertial loading with the sensor.

Mass Measurements Versus Time for Adherent Cells

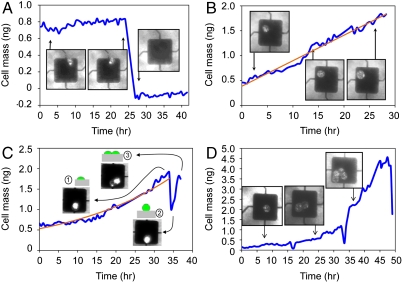
From direct, long-term measurements of HT29 cells, the growth rate of a single cell or multiple cells could be characterized. We observed a loss of mass (-0.85 ng) when a dead cell was removed during the media change after 25 h in culture (Fig. 3A); the empty sensor data demonstrates the background noise less than 0.1 ng for over 10 hrs. When single cells grow on the mass sensors, the mass increases from cell growth and proliferation can be repeatedly measured to generate long-term growth profiles of individual cells and daughter cells (Figs. 3 B–D and 4A). Individual attached cell data demonstrate an increasing mass versus time where the results could be fitted by linear (Fig. 3B) or exponential curve fits (Fig. 3C). Interestingly, it was also found that individual cell division events can be detected by a sharp decrease in apparent cell mass (Fig. 3C). During mitosis, a cell partially detaches from the platform and decreases its contact area. Because the estimated Young’s modulus is around 4 kPa, this temporary geometry change leads to reduction of the cell’s inertial loading and decrease of the apparent mass, as predicted by finite element modeling in Fig. 2F. It is also important to note, as shown from simulation results (Fig. 2F) and experiments (Fig. 3), that the increase in apparent mass during the cell growth is not a geometry-related effect or due to the increase in contact area but rather represents a true increase in cell mass. Fig. 3D also shows the growth of a single cell and the mass of dividing daughter cells that are inherently synchronized; division events show characteristic mass decreases at 16.5 h intervals with the respective number of cells for each of the three growth periods being 1, 2, and 4 cells (Movie S5).

Fig. 3.

Mass measurement of adherent cells versus time. (A) A mass decrease is observed when dead cells or debris are removed during media changes, an internal measurement control. (B) The mass increase of a single adherent cell (blue line) with a linear curve fitting (orange line, y = 0.0513x + 0.3848). (C) Prior to cell division, an individual cell growth data (blue line) conforms to an exponential curve fitting (orange line, y = 0.5303e^0.0353x). Cell division events are marked by sharp mass decreases (inset 1–3), as confirmed by numerical modeling. (D) Mass changes versus time of an inherently synchronized cell growing and dividing into two and four cells; three divisions distinguish the growth profiles.

Fig. 4.

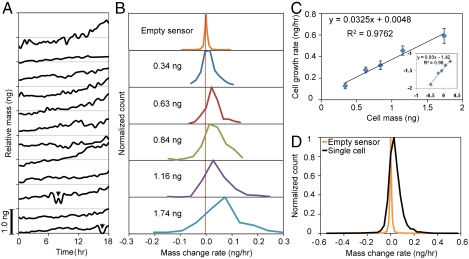
Analysis of cell growth rate versus cell mass. (A) Relative mass increases from 12 different individual cells. For single cell growth analysis, the data was analyzed prior to mitotic events (two divisions are shown, arrowheads). (B) Five histograms account for all cell mass accumulation data of cells. Top plot shows the background noise of an empty sensor while the bottom four plots show an increasing distribution of mass; data bins are nonoverlapping and show average cell mass per bin. (C) Average cells acquire an additional 3.25% of its whole cell mass every hour. The log–log relation in the inset shows a power law of < 1, which is consistent with scaling rules of energy consumption versus size of an organism (31). (D) Background sensor (orange curve) and cell data (black curve) are from a single cell.

To understand the growth characteristics of the attached epithelial cell population, we analyzed the mass data from characteristically different single cell profiles. Fig. 4A shows representative individual cell mass profiles and further displays the range in single cell growth characteristics shown in Fig. 3. Fig. 4B shows the mass and growth rate data (Fig. S6) divided into five groups according to their mass (SI Text). Negative mass change rates, suggesting decrease of mass readings within short time periods, could arise from oscillations in the cell mass or could be explained by changes in cell stiffness, viscosity, or the density. It is likely that it is no single effect but rather a combined effect of more than one; the biological source could be changes in the cytoskeleton, mass accumulation or redistribution, or changes in cell contact adhesion. Small fluctuations of these properties are naturally expected and can be detected by our sensors. In spite of these fluctuations, we find that over longer periods there is an overall increase in measured cell mass (Fig. 3), as also confirmed by optical microscopy (Movies S1–S5). The distribution of mass changes depicts an increased rate of mass accumulation for heavier cells and that the cell growth rate is linearly increasing with the cell mass (Fig. 4C). From the analysis of growth rates of single cells, we find that the HT29 cells grow on average 3.25% of mass every hour, which leads to about 22( = log 2/ log 1.032) hours of mass doubling time. We extended our analysis beyond single adherent cells per pedestal to include those pedestals that captured multiple cells (Fig. S7). From the 50+ hours of cell growth, the mean population growth rate is 3.98% per hour.

Discussion and Conclusions

The replication of intracellular materials and/or organelles is a highly regulated process during cell growth. As a direct result, this biomass accumulation increases the physical cell size, which corresponds to changes in the volume and mass of the cell. While the aggregate data from population studies supports linear or exponential growth regimes, it can depend on the status of the cell, and the cell type, under investigation. Nevertheless, it is reasonable to expect that growth variations exist between individual cells within the same population and between differentiation states. We recognize that the human cells used here are cancer-derived, yet our system of measurement is able to preserve the growth characteristics of individuals, simultaneously acquired through long-term mass measurement and light microscopy.

With insight into the growth and mass accumulation of single cells through time, we gain greater perspectives into how cells grow individually and as a population. Though the average population growth rate of the adherent epithelial cells is size-dependent and increases as the cell mass increases, cell-to-cell growth characteristics can be strikingly different. In the larger context, it is proposed that linear growth versus time can lead to size homeostasis (12), whereas the exponential growth versus time requires a certain cell-size related checkpoint to maintain cell size homeostasis (11, 19). While the precise mechanisms of size homeostasis remain elusive, it is likely that size is differentially regulated by many factors, including: cell contact (adherent vs. suspended cells), diffusive and surface bound signaling cues, genetic and epigenetic programs operating in the range of cells (quiescent or dividing) in the various tissues. With our system, we show that the growth rate of the adherent cells increases with the cell mass. Interestingly, as shown in the inset in Fig. 4C, the cell growth rate scales as a power law of < 1 versus the mass of the cell. Even though in the larger context, this analysis is for a narrow range of size or cell mass, our finding is consistent with the earlier reports (31) that the scaling rules of energy consumption (here analogous to cell growth) versus size (here analogous to cell mass) of all biological organisms follows a power law of < 1.

By using a simple dynamical model, we have also been able to account for the effects of stiffness and damping of the cell on the measurement of cell mass. Our results on live and fixed cells indeed indicate that the apparent cell mass measured by us (and by others) could depend on the stiffness of the cell. Such a model can also be used to explain the previously observed “missing mass effect” (29). It should, however, be noted that the dynamical model used in our analysis is a simplified one, and while it can elegantly capture the essential mechanisms, it should only be expected to yield a trend rather than accurate quantitative results. Considering the elasticity and viscosity of the cell using a dynamical model represents a crucial improvement over existing methods that treat the cell as a point mass perfectly attached to the sensor.

In conclusion, our MEMS sensors expand our understanding on the adherent cell’s growth profile in a least-invasive way. Moreover, the ability to optically monitor the cell while being able to measure their mass can open up a wide set of analysis; for example, fluorescent biomarkers, such as cycle reporters (S-phase marker or FUCCI) or other reporters, can be used to correlate the growth profile or the differentiation pathway with the cell cycle more precisely. With enhanced throughput with smart cell placement and additional capabilities with fluorescent imaging, we believe that our measurement system can make a significant contribution to understanding various cellular processes, such as cell growth, apoptosis, cell differentiation, and cell proliferation.

Materials and Methods

Sensor Fabrication.

Silicon-on-Insulator (SOI) wafers with a 2 μm device layer and a 0.3 μm buried oxide layer (BOX) were used as the starting material. A 25 nm silicon dioxide layer was grown by a thermal oxidation, to electrically insulate the device layer from the subsequent metal layers. The first lithographic process to define the first metal layer for electrode and sensor platform used S-1508 (AZ Electronic Materials) and LOR-3A (Microchem) for subsequent liftoff process. Then chrome (10 nm) and gold (50 nm) layers were deposited by e-beam evaporator and patterned by a liftoff process. The second lithographic process with AZ-9260 (AZ Electronic Materials) defined the etch mask for following silicon etching. The first metal layer and the photoresist layer from the second lithography were used to define the areas of sensor structure. Then, the exposed device layer was etched completely by ICP RIE to form the springs and the platform. A third photolithographic step with LOR-20B (Microchem) and AZ-9260 was used for the second liftoff process, followed by the deposition of a 100-nm chrome layer and a 900-nm gold layer for wire-bonding pads. A release window was defined by the fourth lithograph process (AZ-9260) and the exposed BOX was etched by RIE, leaving the silicon substrate exposed. Through the release window, the exposed Si substrate was etched by xenon difluoride (XeF₂) to release the sensor structure to form a “pit” beneath the platform and springs. After XeF₂ etching, the photoresist and the BOX were removed by buffered hydrofluoric acid (BHF) etching and solvent cleaning. A 100 nm thick silicon dioxide layer was deposited with plasma enhanced chemical vapor deposition (PECVD) for insulation. The PECVD oxide on the bonding pads was selectively etched for wire-bonding with BHF. Finally, each die was attached to a printed circuit board and wire-bonded.

Experimental Setup.

The sensor was placed in the spatially uniform magnetic field generated by the permanent magnet and guided by a magnetic core (Fig. S2E). The sensor was electromagnetically actuated with a reference signal from a lock-in amplifier (Model 7280, Signal recovery). The reference signal (max amplitude: 1V_rms) was connected to each row of the sensor array through a data acquisition switch unit (34970A, Agilent) for signal routing, and then a 20 kΩ resistor to limit the actuation current, down to 150 μA. The velocity of the sensor was measured by the laser Doppler vibrometer (MSV-300, Polytec). The LDV measurement requires two laser beams on the device, one on the moving platform as a signal beam and the other on the stationary substrate as a reference beam. The location of the two laser beam spots with a 4 μm diameter was carefully selected for each sensor to prevent cells from being directly exposed to the laser. The measured velocity was analyzed with the lock-in amplifier to produce the magnitude and the phase with respect to the reference signal. The device and magnetic setup were enclosed in a temperature-controlled chamber to provide constant physiological condition for cell culture. The whole setup was mounted on a microscope with a motorized stage for the automated measurement and imaging.

Cell Culture and Fixation Protocol.

Human colon adenocarcinoma cell (HT29) was cultured in McCoy’s (Sigma Aldrich) with 10% fetal bovine serum. For culture experiments, HT29 cells were grown in 37 °C with L-15 (Sigma Aldrich) media with 30% serum concentration. The sensor was sterilized and then functionalized with collagen type I solution (100 μg/mL) for 30 min at 37 °C. Then the cell suspension (total 9,000 cells per chip) was introduced in the PDMS chamber, and the chamber was closed for the measurement. For cell fixation measurements the cell mass was measured before and after fixation with 4% paraformaldehyde for 30 min. Representative images of fixed cells on sensors are available (Fig. S8). All measurements of live and fixed cells were performed in the same culture media to ensure that observed frequency shifts are attributed to changes in the cell status rather than changes between fluid compositions.

Measurement Protocol.

For each sensor, three different resonant frequencies were measured. The resonant frequency in air was measured to extract the spring constant of each individual sensor and to compensate for minute sensor-to-sensor differences that may exist from chip fabrication. After sterilizing and functionalizing, the resonant frequency (reference frequency for cell measurements) of each sensor in L-15 growth media was measured. Then the cells were cultured on the sensor array and the resonant frequencies and optical images of each selected sensor were collected every 30 to 40 min for over 60 h. With the spring constant and the reference frequency, the measured frequencies were converted to the mass of individual sensors, with and without cells. The resonant frequency of the sensor in L-15 media showed a negative drift, which is independent of the cell growth. The resonant frequency shifts of nearby sensors without cells were measured to compensate for the frequency drift of the sensors with cells. The growth rate of a cell was obtained by a linear-regression based on the five time points of the measured cell mass. Each data point, consisting of mass and growth rate, was sorted and divided into five populations with respect to its cell mass.

Modeling of the Cell and the Sensor System.

Based on the frequency response of the sensor, the effective sensor mass, m₁ is 110 ng, the spring constant, k₁ is 19.4 N/m and the damping coefficient, c₁ is 9.5 ∗ 10^-6 kg/s. The cell deposited on the sensor is simplified as a spring-mass-damper system, as seen in Fig. 2C, Right. The system can be described with following equation, where x₁ and x₂ are the displacement of the sensor and the cell, respectively.

[1]

The undamped resonant frequency, ω₀, is a function of the cell mass m₂, cell stiffness k₂, and cell damping coefficient c₂, where k₂ and c₂ could be ultimately related to Young’s modulus E and viscosity μ of the cell with assumed cylindrical cell shape and optically measured cell area. With a given cell mass, the resonant frequency or the apparent mass can be calculated, as shown in Fig. 2D.

Extraction of Mechanical Property.

With a resonance condition, where the phase of the sensor velocity is zero, Eq. 1 leads to an equation with three unknowns, m₁, E, and μ, for each measured ω₀. To extract the mechanical property of the cell, we assume that the cell mass stays the same before and after fixation for each individual cell. We also assume that, for all 18 cells, there are only two distinct Young’s modulus values of the cells, the value before fixation and that after fixation. The same assumption is made for viscosities. Measured data for randomly selected four cells in the Fig. 2B are substituted into Eq. 1 with a resonance condition. This would generate eight equations for each unfixed case, fixed case, for eight unknowns, eight cell masses for each cell, and for eight Young’s moduli and viscosities before and after fixation. With eight unknowns in eight equations, the nonlinear algebraic equations can be solved numerically. A large number of randomly selected groups of four cells is used for the calculation, to generate the histogram of the Young’s modulus (Fig. 2E, blue profile), and the histogram of the viscosity (Fig. S4).

Finite Element Analysis.

Finite element analysis was performed (ANSYS 12, ANSYS Inc.), to investigate the effect of cells’ finite stiffness and cell geometry on the apparent mass measurement. The adherent cell on the resonant platform was modeled as an elastic hemisphere attached to the resonant platform (Fig. S5A), and the growth media was assumed as Newtonian fluid. The Young’s modulus of the live cell was chosen as 5 kPa based on the experimental data and the results from the mass-spring damper model, and the structural damping coefficient was chosen as 0.45. The resonant frequency of the sensor structure with and without a cell was simulated. The apparent mass was calculated from the spring constant and the resonant frequency shift of the sensor. To compute the effect of Young’s modulus on the mass reading ratio, the Young’s modulus of the cell was changed while the geometry and volume were conserved (Fig. 2E, orange profile). Error bars were standard deviations from the six different cell geometries based on morphologies of real cells from experiments. In order to investigate the effect of the cell geometry on the mass measurement, we changed the cell height and the contact area between the cell and the platform, while conserving the cell volume (Fig. 2F). The apparent mass of the cell was normalized with respect to the actual mass, calculated by the cell volume and the density.