Abstract
Intracellular protein concentration gradients are generally thought to be unsustainable at steady-state due to diffusion. Here we show how protein concentration gradients can theoretically be sustained indefinitely through a relatively simple mechanism that couples diffusion to a spatially segregated kinase-phosphatase system. Although it is appreciated that such systems can theoretically give rise to phosphostate gradients, it has been assumed that they do not give rise to gradients in the total protein concentration. Here we show that this assumption does not hold if the two forms of protein have different diffusion coefficients. If, for example, the phosphorylated state binds selectively to a second larger protein or protein complex then a steady state gradient in total protein concentration will be created. We illustrate the principle with an analytical solution to the diffusion-reaction problem and by stochastic individual-based simulations using the Smoldyn program. We argue that protein gradients created in this way need to be considered in experiments using fluorescent probes and could in principle encode spatial information in the cytoplasm.
Keywords: intracellular organization, diffusion, phophorylation states, mathematical analysis, Brownian dynamics simulation, bacterial chemotaxis
Introduction
During embryonic development, spatial gradients of extracellular protein ligands serve to locally instruct cell behavior. In principle, it seems that intracellular protein gradients could play a similar role in instructing the morphogenesis of the cell cytoplasm and associated organelles. However, it is often assumed that intracellular protein concentration gradients could only be generated transiently, and could not be maintained indefinitely in the cytoplasm. For example, given a typical protein diffusion coefficient in the cytoplasm of ~10 μm2/s, and a cell length of ~10 μm, a protein would diffuse to all parts of the cell within a few seconds. Certainly, the apparent diffusion coefficients could be much lower due to reversible, weak binding to relatively immobile binding sites, so that the diffusion coefficient could appear to be much lower than that of free diffusion in the cytoplasm. However, even with an apparent diffusion coefficient of 0.1 μm2/s, the time scale of diffusion across a 10 μm cell would still be on the order of a few minutes. Of course protein synthesis in one intracellular location and degradation in another will lead to gradients. However, since the lifetime of a protein (hours to days) is typically much longer than the time to diffuse across a somatic cell (typically seconds to minutes) these gradients are expect to be extremely weak or transient14. So it has seemed reasonable to assume that protein concentration gradients are in most cases unsustainable in the cytoplasm.
However, recent studies have shown that the phosphorylated form of a protein can exhibit a spatial gradient that is temporally stable. For example, the microtubule-associated protein Op18/stathmin, which is overexpressed in certain types of cancers4, is observed via fluorescence microscopy to exhibit a gradient in phosphostate in both interphase and mitotic cells19. In mitotic cells, Op18/stathmin is most highly phosphorylated in the vicinity of the chromatin near the spindle equator, while in interphase cells it is most highly phosphorylated in the leading edge. The origin of the gradient is not clear, but it is suspected to arise from a spatially segregated antagonistic kinase-phosphatase system, as suggested by the earlier theoretical analyses of Swillens et al.25 and Brown and Kholodenko3.
In their mathematical model, Brown and Kholodenko assumed that a plasma membrane-bound kinase generates the phosphorylated form of the substrate, which then diffuses into the cytoplasm where it is subsequently dephosphorylated by the antagonistic phosphatase. The dephosphorylated form of the substrate then diffuses until it reaches the plasma membrane, where the kinase can act yet again, and the cycle repeats. Because of the spatial segregation of the kinase and phosphatase, there will exist at steady-state a spatial gradient in phosphostate, with the phosphorylated form being concentrated near the kinase, and the dephosphorylated form being concentrated away from the kinase. Brown and Kholodenko used experimentally measured values for diffusion coefficients and phosphatase rates to show that there should theoretically exist spatial concentration gradients of phosphostate concentration that diminish over micrometer distances.
In addition to spatially segregated antagonistic kinase-phosphatase systems, it has been hypothesized that spatially segregated antagonistic guanosine nucleotide exchange factor (GEF) - GTPase activating protein (GAP) systems can act to generate the GTP and GDP forms of their G protein substrate, respectively. These systems would then have gradients in the GTP and GDP forms of the G protein that are temporally stable, with the GTP form prevailing in the vicinity of the GEF, and the GDP form prevailing in the vicinity of the GAP. Using novel fluorescence-based methods, a number of studies have recently demonstrated the existence of such GEF-GAP-generated gradients in cell extracts and in living cells5, 11, 12, 18. These phosphostate gradients are believed to play an important role in the spatial regulation of the cytoskeletal dynamics during cell division, adhesion, and migration.
In previous theoretical analyses of phosphostate gradients, it has usually been assumed that the concentrations of the two forms of the substrate sum to a constant total protein concentration throughout the cell3, 8, 9, 17, 23, 28. Here we show that this is only the case when the diffusion coefficients of the two forms are equal to each other. More generally, if the diffusion coefficients are different, mathematical modeling demonstrates that gradients in total protein concentration emerge naturally. We discuss the possible origins and consequences of this situation. Our results show that total protein gradients should naturally arise and be sustained indefinitely in the cytoplasm, provided that the protein is acted upon by a spatially-segregated antagonistic enzyme system, and provided that the two phosphostates of the protein have different diffusion coefficients, for example if one binds selectively to another macromolecule in the cytoplasm.
Results
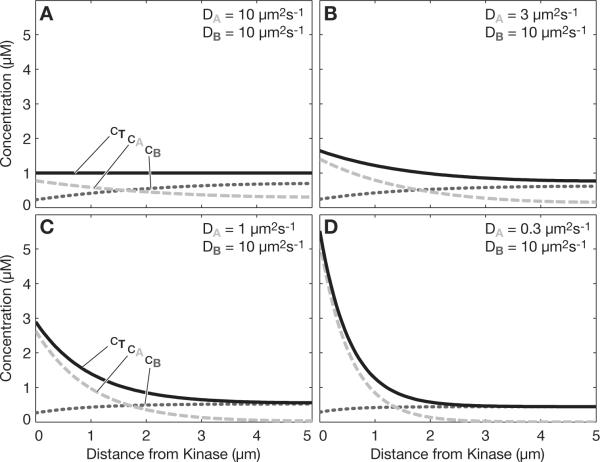
To understand how protein concentration gradients might stably exist in the cytoplasm, we first consider the case where the diffusion coefficient of the phosphorylated form (A) is equal to the diffusion coefficient of the dephosphorylated form (B). Under these conditions, as previously shown by Brown and Kholodenko (1999), a gradient in phosphostate will exist at steady-state (Fig. 1a). Here we assume that the kinase is confined to the left boundary (i.e. at x=0), that the phosphatase is uniformly distributed throughout the cytoplasm (i.e. over the domain 0<x<L), and that there is symmetry (i.e. no flux) at the right boundary (i.e. at x=L). For simplicity and illustration, we have chosen a one-dimensional Cartesian coordinate system, but the same principles apply in any arbitrary coordinate system such as spherical or cylindrical. Also, we use the terms “kinase” and “phosphatase”, but could just as easily use the terms “GEF” and “GAP” for G-protein activation. Our results could also apply to any of the other multiple kinds of protein posttranslational modification known to occur, such as methylation, glycosylation and sumoylation.
Fig. 1.
Total protein gradient. (a) When the diffusion coefficients of the phosphorylated form and the dephosphorylated form are equal (DA=DB), then a kinase at the left boundary and a phosphatase uniformly distributed in the cytoplasm will establish a phosphostate gradient (dashed light gray = phosphorylated, dotted dark gray = dephosphorylated), as previously noted, but no gradient in the total protein concentration (black). (b) When the diffusion coefficients of the two forms differ (DA≠DB), then there will be a gradient in not only the phosphostate, but also the total protein concentration. (c) and (d) Further disparity in the diffusion coefficients further increases the total protein concentration gradient. Kinase rate constant kk=10 μm/s, phosphatase rate constant kp=1 s−1, overall protein concentration 1 μM in all panels.
What is also evident in Fig. 1a is that when the diffusion coefficients of A and B are equal, then the overall concentration of the protein — the sum of both its forms A and B — is constant. However, the situation changes when the diffusion coefficients of A and B are not equal, as may be the case when phosphorylation promotes (or inhibits) association with a large cytoplasmic complex. For example, if we lower the diffusion coefficient of A by a factor of ~3, from 10 μm2/s to 3 μm2/s, then we see that, in addition to the phosphostate gradient that is still present, a gradient in the total concentration of the protein now exists (black line in Fig. 1b). The steepness of the total protein concentration gradient increases with the disparity of the diffusion coefficients (Figs. 1c and 1d). This analysis establishes a simple mechanism by which a cytoplasmic protein could maintain a total protein concentration gradient indefinitely by coupling to a kinase-phosphatase reaction scheme.
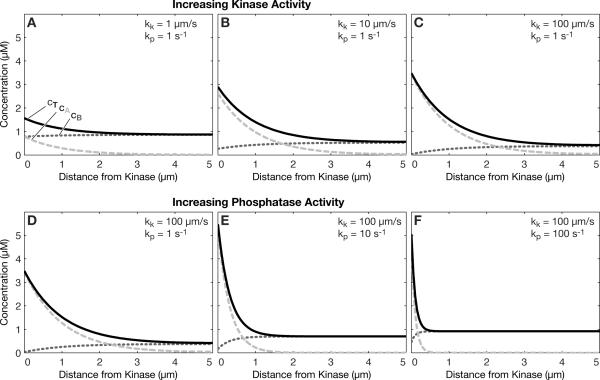
Of course, the other parameters in the model could also affect the total protein concentration gradient. For example, the rate of the kinase reaction at the left boundary could be increased to further increase the total protein concentration gradient, as shown in Fig. 2a–c. As the rate of the kinase reaction increases, it will asymptotically reach the diffusion-limited rate, at which point further increases will no longer have an effect. Note that the rate of decay of the gradient is independent of the kinase reaction rate. For a given kinase rate constant, increasing the phosphatase reaction rate constant will further steepen the total protein concentration, as shown in Fig. 2d–f. An interesting aspect here is that increasing the phosphatase rate slightly increases the absolute concentration at the left boundary. The reason for this is that increasing the phosphatase rate makes the gradient of the dephospho-form steeper, and thus the production rate of the phospho-form at the boundary is higher.
Fig. 2.
Effect of kinase and phosphatase rate constants on the total protein concentration gradient. (a–c) The total protein concentration gradient increases with increasing kinase rate constant, kk. (d–f) The total protein concentration gradient also increases, and decays over a shorter distance with increasing phosphatase rate constant, kp. Diffusion coefficients DA=1 μm2s−1, DB=10 μm2s−1, overall protein concentration 1 μM in all panels.
The phosphatase rate has a direct effect on the decay of the gradient, as the gradient length is directly dependent on the phosphatase rate constant according to
| (1) |
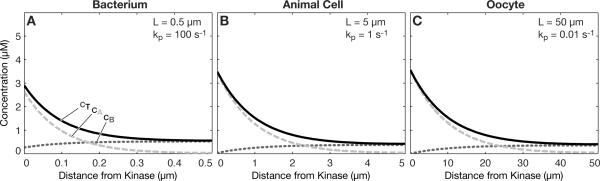
as shown previously17. If kp is sufficiently large, then the gradient will decay rapidly. This means that a gradient in total protein concentration can appear within even a cell as small as a bacterium as shown in Fig. 3a, provided the phosphatase reaction rate constant is sufficiently large. In this case, kp is set to 100 s−1, which is within the observed range for phosphatases, albeit at the high end, as summarized previously by Brown and Kholodenko3. By reducing the phosphatase rate constant appropriately, the gradient can be scaled to any particular cell type, including animal cells (Fig. 3b) and oocytes or embryos (Fig. 3c). The key dimensionless parameter is the Thiele modulus17, which is given by
| (2) |
If Φ>1, then gradients will be substantial; for Φ<1 gradients will be small. These results show that the total protein concentration gradient could potentially play a role in all cell types, ranging from bacteria to oocytes and embryos.
Fig. 3.
Total protein gradients could act across a range of cell sizes. (a) At a very high phosphatase rate (kp=100 s−1), the gradient is predicted to be appreciable in cells as small as a bacterium. (b) Animal cells and (c) oocytes/embryos can experience total protein gradients, simply by reducing the phosphatase rate constant, kp, according to the cell dimension. Diffusion coefficients DA=1 μm2s−1, DB=10 μm2s−1, kinase rate constant kk=100 μm/s, overall protein concentration 1 μM in all panels.
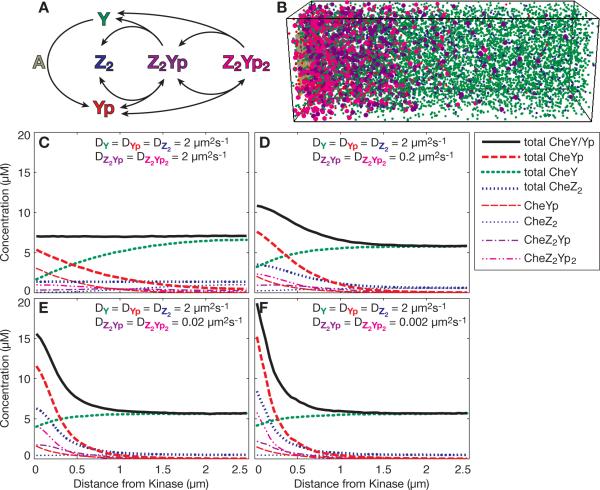
Finally, we wished to explore the possibility of total protein gradients occurring in a specific cell. To do so, we considered the chemotaxis signaling pathway in Escherichia coli, where the signaling protein CheY is phosphorylated at the anterior end of the cell by the histidine kinase CheA, and then diffuses to distal regions to control flagellar rotation. To retain responsiveness, dephosphorylation of phosphorylated CheY (CheYp) is aided by the protein CheZ22. CheZ is a stable dimer, which binds up to two CheYp monomers with high specificity2, 29. To analyze protein gradients, we simulated the relevant portions of the chemotaxis pathway, i.e. the phosphorylation of CheY by CheA and the stepwise binding and subsequent dephosphorylation of CheYp by CheZ, using the Smoldyn model of chemotaxis, which models each individual molecule and its reactions stochastically with high spatial resolution15, 16 (Fig. 4a). Published rate constants were used when available (Table 1). For simplicity and clarity, we chose to distribute both CheY/CheYp and CheZ2 in the cytoplasm and made them freely diffusible. As expected and shown before16, the unequal distribution of CheA kinase at the cell pole and CheZ phosphatase in the cytoplasm leads to a gradient of CheYp with all diffusion coefficients (Fig. 4b–e, dashed red lines). If the complexes of CheYp and CheZ are assigned a lower diffusion coefficient than the unbound molecules (Fig. 4c–e), there is also a gradient of the total of all CheY species and CheY-containing complexes (thick black line), consistent with the arguments given above. Interestingly, even the total of CheZ-molecules and complexes forms an anterior-posterior gradient (thick blue line, short dashes). This is because the complex-forming CheYp molecules are predominantly near the pole. These results for the specific case of bacterial chemotaxis show that a total protein concentration gradient is expected to form even where the cell size is small compared to animal cells.7, 21, 24
Fig. 4.
Total protein gradients in the bacterial chemotaxis signaling pathway. (a) Schematic of the relevant reactions modeled. CheY (Y) is phosphorylated by the kinase CheA (A). Up to two CheY-phosphates (Yp) can bind sequentially and reversibly to the dimeric phosphatase CheZ (Z2). Upon hydrolysis, unphosphorylated CheY is released. The phosphorylation reaction at CheA consists of several reactions. For details and all rate constants, see Table 1. (b) Snapshot of a Smoldyn simulation at steady state; diffusion coefficients as in (d). On the left is a fixed array of CheA kinases, all other molecules are diffusing freely. Colors as in (a). Monomers and dimers are shown as small spheres, all larger complexes as large spheres. (c–f) Results of stochastic simulations with Smoldyn. Means of 1000 timepoints.
Table 1.
Bacterial chemotaxis reactions
| Reaction | Rate (forward) | Rate (reverse) | Description |
|---|---|---|---|
| A2 <-> A2* | Immediate equilibration | (13.2% active) | CheA activation |
| A2p <-> A2*p | Immediate equilibration | (13.2% active) | CheAp activation |
| A2* -> A2*p | 34 s−1 | - | CheA autophosphorylation7,21 |
| Y + A2p -> Yp + A2 | 1 × 108 M−1s−1 | - | Phosphotransfer24 |
| Y + A2*p -> Yp + A2* | 1 × 108 M−1s−1 | - | Phosphotransfer24 |
| Yp + Z2 <=> Z2Yp | 2 × 107 M−1s−1 | 0.5 s−1 | Complex formation |
| Yp + Z2Yp <=> Z2Yp2 | 1 × 107 M−1s−1 | 0.5 s−1 | Complex formation |
| Z2Yp -> Y + Z2 | 5 s−1 | - | CheYp hydrolysis |
| Z2Yp2 -> Y + Z2Yp | 5 s−1 | - | CheYp hydrolysis |
Reactions labeled with `immediate equilibration' are the system's input: Every 10 ms throughout the simulation, the ratio of the two indicated molecular species was adjusted stochastically. The following abbreviations are used: Y, CheY; Yp, CheYp, phosphorylated CheY; A2, CheA dimer, inactive; A2*, CheA dimer, active; A2p, phospho-CheA dimer, inactive; A2*p, phospho-CheA dimer, active; Z2 CheZ dimer; Z2Yp, complex of CheZ and CheYp; Z2Yp2, complex of CheZ and two CheYp.
Discussion
Our theoretical analysis shows that protein concentration gradients could exist indefinitely in the cytoplasm. The gradients in the model are driven by spatially segregated, antagonistic kinase-phophatase (or GEF-GAP) reactions, and furthermore require that the two phosphostates of the protein have differing diffusion coefficients. In this way, energy consumption in the form of ATP (or GTP) hydrolysis could be used to drive a standing concentration gradient of a protein diffusing in the cytoplasm.
What could be the origin of differing diffusion coefficients?
Since for constant density, the mass of the diffusing species m~V~R3, then D~m−1/3. Since the presence of a phosphoryl group on a protein has a negligible effect on the mass of the protein, the presence of the phosphoryl group more likely alters the affinity of binding to other proteins and protein complexes, which may be large enough to slow diffusion. For example, if the resulting complex has 100 similarly sized proteins, then the diffusion coefficient will decrease about 5-fold. For complexes that are approaching ~100 nm in size, the diffusion in the cytoplasm is expected to decrease even more dramatically due to the pore structure created by the cytoskeleton10. Alternatively, proteins may bind to vesicles or lipid droplets (~μm diameter), which may serve as major storage reservoirs of cytoplasmic proteins6. In this case the transport will be slowed substantially, and will be limited by motor-based mechanisms. Finally, it may be that in one phosphostate the protein binds weakly to a large or immobile object, such as the cytoskeleton, and the other phosphostate does not bind at all, again leading to differing diffusion coefficients. For example, if the concentration of weak, immobile binding sites was 10 μM, and the Kd of binding for the phosphoprotein to the site was 1 μM, then the diffusion coefficient would be reduced by a factor of ~1020. In general, there are multiple potential mechanisms that would give rise to diffusion coefficients that are different for each of the two phosphostates of the protein.
The best example of a phosphostate gradient in living cells is perhaps that of the Ran-GTP gradient, where the G protein Ran is activated (i.e. in the GTP state) by its GEF (i.e. RCC1), and deactivated by its GAP (i.e. RanGAP). In mitosis there is a steep gradient of Ran-GTP in the vicinity of chromatin, which has RCC1 bound to it11. Interestingly, Ran-GTP has a relatively high affinity for importin-β, which has a much higher molecular weight than Ran-GTP itself, so that when the complex forms it is estimated that the diffusion coefficient decreases by almost two-fold (see Table S1 in5). In contrast Ran-GDP has a low affinity for importin-β, and so would not experience a decrease in diffusion coefficient. In this case, we predict that there will be a gradient in Ran concentration, with Ran being highest near the chromatin, and the concentration decaying with increasing distance away from the chromatin.
Consistent with our results on bacterial chemotaxis, there is experimental evidence for total gradients of both CheY and CheZ: Careful analysis of FRET data in single E. coli cells with delocalized CheZF98S indicate not only the presence, but also the redistribution of such gradients27. Intriguingly, the direction of this change is as we would predict: Addition of the chemoattractant serine, which indirectly reduces the level of CheA activity and therefore of CheY phosphorylation22, leads to a decrease of the total gradients of CheY-YFP and CheZF98S-CFP. This effect is clear with delocalized (all cytoplasmic) CheZF98S-CFP, but not as strong with the (otherwise) wildtype fusion protein, which is mostly localized to the cell pole. In fully wildtype cells, the gradients could be further enhanced by polar oligomerization of CheZ and CheYp15. This has the potential to significantly enhance signaling properties such as speed, range and robustness. The additional total gradients described here would add to these effects.
Finally, it is worth considering how cell size and shape might affect the protein concentration gradients predicted by our model. Recent theoretical analysis shows that for a plasma membrane-bound activator (e.g. kinase or GEF) and cytoplasmic deactivator (e.g. phosphatase or GAP, respectively), the thinner and smaller a cell is the more highly activated the substrate will be, even with all molar concentrations of activator, deactivator, and substrate being held constant17. The reason is that it is difficult for the activated substrate to diffuse very far without first being deactivated. So, large and thick cells are predicted to be relatively less activated than small and thin cells. Similarly, thin regions of the cell (e.g. lamellipodia and filopodia) are predicted to be more activated than thick regions of the cell. If the two forms of the substrate have different diffusion coefficients, then it is predicted that total gradients will be altered simply by alterations in cell size and shape. In particular, large and thick cells will be able to sustain total protein gradients more readily than small and thin ones. Adding more realistic boundary conditions, as discussed by Haugh9, will serve to further amplify this effect. At any rate, the key requirement for our analysis is only that the fluxes at the boundary be equal and opposite, and the simple first-order assumption serves this purpose.
Mathematical model
We considered the steady-state behavior of a phosphoprotein that interconverts between the phosphorylated form (A) and the dephosphorylated form (B) through the action of an antagonistic kinase and phosphatase pair. Note that the model applies equally to other antagonistic enzyme pairs that switch a substrate between two states. For example, the model applies equally to G proteins that are activated to their GTP-bound form via guanosine nucleotide exchange factors (GEFs) and deactivated to their GDP-bound form via GTPase activating proteins (GAPs). For concreteness, we will use the kinase-phosphatase terminology throughout this article.
Consider the simple case where the kinase is located at the left boundary of a rectangular cell at x=0, the phosphatase is distributed uniformly throughout the cytoplasm over 0<x<L, and there is no flux of the substrate through the right boundary of the cell at x=L. At steady-state, the reaction-diffusion of A over the domain 0<x<L is governed by
| (3) |
and for B similarly
| (4) |
where DA and DB are the diffusion coefficients of A and B, respectively, cA and cB are the molar concentrations of A and B, respectively, and kp is the first-order phosphatase rate constant. Note that the assumption of first-order kinetics is valid in the case where cA<<KM (where KM is the Michaelis-Menten binding constant; units: μM), which is often the case for phosphatases3, 17. Alternatively, if cA>>KM, then the kinetics are zeroth-order, and if cA≈KM, then the kinetics are of an intermediate, fractional order. For illustration, we chose first-order kinetics, which is consistent with many cases and allows an analytical solution to Eqs. 3 and 4.
The boundary conditions for A are: 1) at the left boundary at ×=0, the departure rate of A by diffusion equals the rate of production of A via the kinase reaction, and 2) at the right boundary at ×=L is an impenetrable wall (i.e. no flux). Mathematically these are given by
| (5) |
and
| (6) |
where kk is the first-order rate constant for the heterogeneous kinase reaction at the left boundary at ×=0. The units for kk are μm/s, and kk is given by kk=kk'L where kk' is the homogeneous, first-order reaction rate constant (units s−1) for the same number of kinases if they were free in the bulk cytoplasm. Similarly, the boundary conditions for B are given by
| (7) |
and
| (8) |
We assume that the substrate is itself neither synthesized nor degraded, so that the total number of substrate molecules, NT, is conserved, which for constant volume can be written as
| (9) |
where Ax is the cross-sectional area of the cell, which we assume constant, so that the volume of the cell is Vcell=AxL. At any point in the system, the total protein concentration, cT, is given by
| (10) |
The concentration of A then varies spatially at steady-state, and is given by
| (11) |
and the concentration of B is given by
| (12) |
where
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
Note that if DA=DB, then cA and cB sum to a constant value of cT=<cT> everywhere in the cell. Alternatively, if DA≠DB, then cA and cB do not sum to a constant value of cT everywhere in the cell. In this case there will be a total protein concentration gradient, and cT will be a function of position, x, in the cell. This can also be understood by adding Eqs. 3 and 4 together to yield
| (32) |
which when integrated and combined with Eqns. 6 and 7 yields
| (33) |
Therefore, the concentration gradients are only equal and opposite when DA=DB, but in general the individual concentration gradients are opposite in sign and scaled to each other by the ratio of the diffusion coefficients
| (34) |
For DA≠DB, the gradients will not be equal and opposite, and so there will be a nonzero total protein concentration gradient. The use of a continuum model can apply even to noisy situations due to low copy number, since these systems can theoretically suppress the noise by temporal averaging26.
Computational Model
For the chemotaxis simulations, the Smoldyn algorithm1 was used to create a model of an Escherichia coli cell, as in15, 16. Smoldyn source code, executable program, manuals and detailed documentation are downloadable from http://www.smoldyn.org (Steven Andrews) and http://www.pdn.cam.ac.uk/groups/comp-cell/Smoldyn.html (Dennis Bray's group). In a rectangular box of 2.5 × 0.88 × 0.88 μm3, 1260 dimers of the CheA kinase were placed in a grid, 15 nm from each other, and 20 nm from the anterior cell pole. 8200 CheY monomers and 1600 CheZ dimers were distributed randomly in the cell volume (numbers from13). CheA molecules were immobile; diffusion coefficients for CheY, CheZ and their complexes were as specified in Figure 4. At each 0.1 ms timestep, each mobile molecule was moved by a small distance in a random direction. It would react when finding itself in close proximity to a reaction partner or, for unimolecular reactions, at a certain probability (see Table 1). After a simulation time of 9 s, when molecular species numbers had reached a steady state, the exact position of each mobile molecule was recorded every 10 ms for 10 s. These data were used to create histograms of 50 nm slices in the longitudinal direction.
Acknowledgements
The authors acknowledge funding from National Science Foundation Career Award (BES 9984955), NIH-National Institute of General Medical Sciences (GM71522), McKnight Land-Grant Professorship to DJO, Royal Society University Research Fellowship to KL, and from NIH-NIGMS (GM64713) to Dennis Bray. We thank Dennis Bray for helpful discussions, and him and Matthew D. Levin for insightful comments on the manuscript.
Abbreviations
- A
CheA
- Y
CheY
- Yp
CheYp, phosphorylated CheY
- Z2
CheZ dimer
References
- 1.Andrews SS, Bray D. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Phys Biol. 2004;1:137–51. doi: 10.1088/1478-3967/1/3/001. [DOI] [PubMed] [Google Scholar]
- 2.Blat Y, Eisenbach M. Phosphorylation-dependent binding of the chemotaxis signal molecule CheY to its phosphatase, CheZ. Biochemistry. 1994;33(4):902–6. doi: 10.1021/bi00170a008. [DOI] [PubMed] [Google Scholar]
- 3.Brown GC, Kholodenko BN. Spatial gradients of cellular phospho-proteins. FEBS Lett. 1999;457(3):452–4. doi: 10.1016/s0014-5793(99)01058-3. [DOI] [PubMed] [Google Scholar]
- 4.Cassimeris L. The oncoprotein 18/stathmin family of microtubule destabilizers. Curr Opin Cell Biol. 2002;14(1):18–24. doi: 10.1016/s0955-0674(01)00289-7. [DOI] [PubMed] [Google Scholar]
- 5.Caudron M, Bunt G, Bastiaens P, Karsenti E. Spatial coordination of spindle assembly by chromosome-mediated signaling gradients. Science. 2005;309(5739):1373–6. doi: 10.1126/science.1115964. [DOI] [PubMed] [Google Scholar]
- 6.Cermelli S, Guo Y, Gross SP, Welte MA. The lipid-droplet proteome reveals that droplets are a protein-storage depot. Curr Biol. 2006;16(18):1783–95. doi: 10.1016/j.cub.2006.07.062. [DOI] [PubMed] [Google Scholar]
- 7.Francis NR, Levit MN, Shaikh TR, Melanson LA, Stock JB, DeRosier DJ. Subunit organization in a soluble complex of tar, CheW, and CheA by electron microscopy. J Biol Chem. 2002;277(39):36755–9. doi: 10.1074/jbc.M204324200. [DOI] [PubMed] [Google Scholar]
- 8.Gardner MK, Pearson CG, Sprague BL, et al. Tension-dependent regulation of microtubule dynamics at kinetochores can explain metaphase congression in yeast. Mol Biol Cell. 2005;16(8):3764–75. doi: 10.1091/mbc.E05-04-0275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Haugh JM. Membrane-binding/modification model of signaling protein activation and analysis of its control by cell morphology. Biophys J. 2007;92(11):L93–5. doi: 10.1529/biophysj.107.105213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jacobson K, Wojcieszyn J. The translational mobility of substances within the cytoplasmic matrix. Proc Natl Acad Sci U S A. 1984;81(21):6747–51. doi: 10.1073/pnas.81.21.6747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kalab P, Pralle A, Isacoff EY, Heald R, Weis K. Analysis of a RanGTP-regulated gradient in mitotic somatic cells. Nature. 2006;440(7084):697–701. doi: 10.1038/nature04589. [DOI] [PubMed] [Google Scholar]
- 12.Kalab P, Weis K, Heald R. Visualization of a Ran-GTP gradient in interphase and mitotic Xenopus egg extracts. Science. 2002;295(5564):2452–6. doi: 10.1126/science.1068798. [DOI] [PubMed] [Google Scholar]
- 13.Li M, Hazelbauer GL. Cellular stoichiometry of the components of the chemotaxis signaling complex. J Bacteriol. 2004;186(12):3687–94. doi: 10.1128/JB.186.12.3687-3694.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin AC, Holt CE. Local translation and directional steering in axons. Embo J. 2007;26(16):3729–36. doi: 10.1038/sj.emboj.7601808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lipkow K. Changing cellular location of CheZ predicted by molecular simulations. PLoS Comput Biol. 2006;2(4):e39. doi: 10.1371/journal.pcbi.0020039. DOI: 10.1371/journal.pcbi.0020039.eor. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lipkow K, Andrews SS, Bray D. Simulated diffusion of phosphorylated CheY through the cytoplasm of Escherichia coli. J Bacteriol. 2005;187(1):45–53. doi: 10.1128/JB.187.1.45-53.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Meyers J, Craig J, Odde DJ. Potential for control of signaling pathways via cell size and shape. Curr Biol. 2006;16(17):1685–93. doi: 10.1016/j.cub.2006.07.056. [DOI] [PubMed] [Google Scholar]
- 18.Nalbant P, Hodgson L, Kraynov V, Toutchkine A, Hahn KM. Activation of endogenous Cdc42 visualized in living cells. Science. 2004;305:1615–9. doi: 10.1126/science.1100367. 5690 [DOI] [PubMed] [Google Scholar]
- 19.Niethammer P, Bastiaens P, Karsenti E. Stathmin-tubulin interaction gradients in motile and mitotic cells. Science. 2004;303(5665):1862–6. doi: 10.1126/science.1094108. [DOI] [PubMed] [Google Scholar]
- 20.Odde D. Diffusion inside microtubules. Eur Biophys J. 1998;27(5):514–20. doi: 10.1007/s002490050161. [DOI] [PubMed] [Google Scholar]
- 21.Shrout AL, Montefusco DJ, Weis RM. Template-directed assembly of receptor signaling complexes. Biochemistry. 2003;42(46):13379–85. doi: 10.1021/bi0352769. [DOI] [PubMed] [Google Scholar]
- 22.Sourjik V. Receptor clustering and signal processing in E. coli chemotaxis. Trends Microbiol. 2004;12(12):569–76. doi: 10.1016/j.tim.2004.10.003. [DOI] [PubMed] [Google Scholar]
- 23.Sprague BL, Pearson CG, Maddox PS, Bloom KS, Salmon ED, Odde DJ. Mechanisms of microtubule-based kinetochore positioning in the yeast metaphase spindle. Biophys J. 2003;84(6):3529–46. doi: 10.1016/S0006-3495(03)75087-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stewart RC, Jahreis K, Parkinson JS. Rapid phosphotransfer to CheY from a CheA protein lacking the CheY-binding domain. Biochemistry. 2000;39(43):13157–65. doi: 10.1021/bi001100k. [DOI] [PubMed] [Google Scholar]
- 25.Swillens S, Paiva M, Dumont JE. Consequences of the intracellular distribution of cyclic 3',5'-nucleotides phosphodiesterases. FEBS Lett. 1974;49(1):92–5. doi: 10.1016/0014-5793(74)80639-3. [DOI] [PubMed] [Google Scholar]
- 26.Tostevin F, ten Wolde PR, Howard M. Fundamental limits to position determination by concentration gradients. PLoS Comput Biol. 2007;3(4):e78. doi: 10.1371/journal.pcbi.0030078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vaknin A, Berg HC. Single-cell FRET imaging of phosphatase activity in the Escherichia coli chemotaxis system. Proc Natl Acad Sci U S A. 2004;101(49):17072–7. doi: 10.1073/pnas.0407812101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wollman R, Cytrynbaum EN, Jones JT, Meyer T, Scholey JM, Mogilner A. Efficient chromosome capture requires a bias in the `search-and-capture' process during mitotic-spindle assembly. Curr Biol. 2005;15(9):828–32. doi: 10.1016/j.cub.2005.03.019. [DOI] [PubMed] [Google Scholar]
- 29.Zhao R, Collins EJ, Bourret RB, Silversmith RE. Structure and catalytic mechanism of the E. coli chemotaxis phosphatase CheZ. Nat Struct Biol. 2002;9(8):570–5. doi: 10.1038/nsb816. [DOI] [PubMed] [Google Scholar]