A displaced-solvent functional analysis of model hydrophobic enclosures

Abstract

Calculation of protein-ligand binding affinities continues to be a hotbed of research. Although many techniques for computing protein-ligand binding affinities have been introduced--ranging from computationally very expensive approaches, such as free energy perturbation (FEP) theory; to more approximate techniques, such as empirically derived scoring functions, which, although computationally efficient, lack a clear theoretical basis--there remains pressing need for more robust approaches. A recently introduced technique, the displaced-solvent functional (DSF) method, was developed to bridge the gap between the high accuracy of FEP and the computational efficiency of empirically derived scoring functions. In order to develop a set of reference data to test the DSF theory for calculating absolute protein-ligand binding affinities, we have pursued FEP theory calculations of the binding free energies of a methane ligand with 13 different model hydrophobic enclosures of varying hydrophobicity. The binding free energies of the methane ligand with the various hydrophobic enclosures were then recomputed by DSF theory and compared with the FEP reference data. We find that the DSF theory, which relies on no empirically tuned parameters, shows excellent quantitative agreement with the FEP. We also explored the ability of buried solvent accessible surface area and buried molecular surface area models to describe the relevant physics, and find the buried molecular surface area model to offer superior performance over this dataset.

I. Introduction

Calculation of relative and absolute protein-ligand binding affinities continues to be an active hotbed of research in the field of computational biophysics.^1–4 Although many techniques for computing protein-ligand binding affinities have been introduced--ranging from computationally very expensive ab initio approaches, such as free energy perturbation (FEP) theory; to more approximate techniques, such as empirically derived scoring functions, which, although computationally efficient, lack a clear theoretical basis--there remains a pressing need for more robust approaches. A recently introduced technique, the displaced-solvent functional (DSF) method⁵ was developed to bridge the gap between the high accuracy of FEP and the computational efficiency of empirically derived scoring functions. This technique proceeds by first using explicitly solvated molecular dynamics simulations of a protein conformation which is complementary to a given ligand series (or, in some cases, a protein-ligand complex which can be used to build the remaining members of the series) to map out the approximate thermodynamic properties of water molecules solvating various regions of the protein active site; second, constructing a DSF to compactly represent this information; and third, computing the relative binding affinities of congeneric ligands for the given receptor by correlating the relative binding affinities of the congeneric ligands with the excess chemical potential of the solvent that is evacuated from the active site by the binding of the ligand.

This method has shown great promise in a number of pharmaceutically relevant applications such as accurately describing the relative binding thermodynamics of proteases, kinases, PDZ domain, and GPCR inhibitors; elucidating the role of hydration in kinase binding specificity; and offering novel qualitative insights into PCSK9-peptide binding kinetics.^5–12 However, despite the wide range successful applications of the technique to describe and explain experimental binding data, the physical-chemical basis of the DSF method has not yet been fully clarified in print. This work derives the DSF approach from first principles and clarifies the physical-chemical basis of the technique. Further, this derivation elucidates the key approximations of the method, which facilitates an understanding of when the technique is expected to succeed and fail. In order to develop a set of reference data to test the DSF theory for calculating absolute protein-ligand binding affinities, we have pursued FEP theory calculations of the binding free energies of a methane ligand with 13 different types of model hydrophobic enclosures of varying hydrophobicity. The binding free energies of the methane ligand with the various hydrophobic enclosures were then recomputed by the DSF theory presented herein and the results of the calculations were compared with the FEP reference data. We find that the DSF theory predictions, which rely on no empirically tuned parameters, show excellent quantitative agreement with the FEP results (root-mean-square error of 0.40 kcal/mol and an R² value of 0.95). Thus, DSF theory may offer, for systems that satisfy the necessary approximations, a method of calculating absolute binding affinities with FEP-like accuracy at only a small fraction of the computational expense. A further point is that the DSF approach can be unambiguously converged with current hardware capabilities, whereas convergence becomes quite challenging for FEP and related methods when applied to complex problems like protein-ligand binding (as opposed to the model systems studied in this paper).

II. Methods

A. Derivation of the displaced solvent functional approach to computing protein ligand binding free energies

It is well known¹ that the binding free energy of a small molecule for its cognate protein receptor can be computed as

$$\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{o}}=-\text{RT}ln\left[\frac{{\text{C}}_{\text{o}}}{8{\pi }^2}\frac{\int {\text{e}}^{-\left[\left(\text{U}({\overrightarrow{\text{r}}}_{\text{PL}})+\text{W}({\overrightarrow{\text{r}}}_{\text{PL}})\right)/\text{RT}\right]}{\text{d}\overrightarrow{\text{r}}}_{\text{PL}}}{\left(\int {\text{e}}^{-\left[\left(\text{U}({\overrightarrow{\text{r}}}_{\text{P}})+\text{W}({\overrightarrow{\text{r}}}_{\text{P}})\right)/\text{RT}\right]}{\text{d}\overrightarrow{\text{r}}}_{\text{P}}\int {\text{e}}^{-\left[\left(\text{U}({\overrightarrow{\text{r}}}_{\text{L}})+\text{W}({\overrightarrow{\text{r}}}_{\text{L}})\right)/\text{RT}\right]}{\text{d}\overrightarrow{\text{r}}}_{\text{L}}\right)}\right]$$ (1)

where the subscript P represents the protein in the unbound state, the subscript L represents the ligand in the unbound state, the subscript PL represents the protein and ligand in their bound state, R is the gas constant, C_o is the standard concentration, U is the interaction energy term, and W represents the solvation free energy terms. From this expression one can readily derive

$$\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{o}}={\langle {\text{U}}_{\text{PL}}\rangle }_{\text{PL}}-{\langle {\text{U}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{U}}_{\text{L}}\rangle }_{\text{L}}+{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{PL}}-{\langle {\text{W}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{W}}_{\text{L}}\rangle }_{\text{L}}-\text{T}\mathrm{\Delta }{\text{S}}_{\text{config}}^{\text{o}}$$ (2)

where the brackets (<>) imply Boltzmann weighted averages over the specified ensemble, the changes of the configurational entropies of the protein and the ligand after binding have been grouped in a single term (−TΔS_config), and the terms related to the change in the interaction energies (U) and solvation free energies (W) of the protein and the ligand are enumerated explicitly. We note here that the −TΔS^o_config term may be made arbitrarily small in equation 2 by first computing the free energy of restraining internal and relative degrees of freedom of the protein and the ligand to some appropriately chosen reference state by FEP, thermodynamics integration, or any other suitable ab initio approach, and then computing the binding free energy of the protein and ligand after these restraints have been removed.^13,14

Equation 2, although complete, has poor convergence properties since it is a series of very large terms that sum to a very small number. Thus, each individual term must be computed to very high accuracy and precision. This may in practice be more difficult than sampling Equation 1 directly, for example by FEP. However, we have made a series of observations in our recent work^5,6 that suggest a path to improve the convergence of this expression.

The first observation is that the protein-ligand interaction energy (U_PL) can be expanded into an intra-protein term, a protein-ligand interaction term, and an intra-ligand term:

$${\langle {\text{U}}_{\text{PL}}\rangle }_{\text{PL}}={\langle {\text{U}}_{\text{P}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{L}}\rangle }_{\text{PL}}$$ (3)

where the first term (U_P) is the intra-protein interaction energy, the second term (U_P-L) is the protein-ligand interaction energy, and the third term (U_L) is the intra-ligand interaction energy. Therefore,

$$\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{o}}={\langle {\text{U}}_{\text{P}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{L}}\rangle }_{\text{PL}}-{\langle {\text{U}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{U}}_{\text{L}}\rangle }_{\text{L}}+{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{PL}}-{\langle {\text{W}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{W}}_{\text{L}}\rangle }_{\text{L}}-\text{T}\mathrm{\Delta }{\text{S}}_{\text{config}}^{\text{o}}.$$ (4)

We will assume in this work that the loss of conformational entropy of the protein and ligand is compensated by the ligand and the strain energy incurred by the protein and ligand upon binding. For example a ligand with freely rotatable bonds binding to a protein will generally induce little protein strain energy, but will lose a great deal of conformational entropy upon binding. Conversely, a highly rigid ligand, which will avoid such entropic penalties, will likely require substantial “induced fit” of the protein, which will in turn increase the strain energy of the protein upon binding. Posed formally, this argument suggests

$$0\approx {\langle {\text{U}}_{\text{P}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{L}}\rangle }_{\text{PL}}-{\langle {\text{U}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{U}}_{\text{L}}\rangle }_{\text{L}}-\text{T}\mathrm{\Delta }{\text{S}}_{\text{config}}^{\text{o}}$$ (5)

In turn, equation 4 may be rewritten as

$$\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{o}}\approx {\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}+{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{PL}}-{\langle {\text{W}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{W}}_{\text{L}}\rangle }_{\text{L}}+{\delta }_{\text{strn}}[{\langle {\text{U}}_{\text{P}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{L}}\rangle }_{\text{PL}}-{\langle {\text{U}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{U}}_{\text{L}}\rangle }_{\text{L}}-\text{T}\mathrm{\Delta }{\text{S}}_{\text{config}}^{\text{o}}]$$ (6)

where switching function δ_strn allows equation 6 to be exact for δ_strn =1, and approximately correct for δ_strn =0. Equation 6 may be recognized as equivalent to the MM-GBSA method, where the protein and ligand strain energies and the change in the configurational entropy are neglected when δ_strn =0, although various formulations have emerged in the literature.^15–17 Note, the δ_strn =0 approximation will be exactly satisfied by the model enclosure studied herein, but is expected to apply generally to any series of congeneric ligands binding to a given protein receptor. The reason we expect the δ_strn =0 approximation to be a reasonable approach to treating a series of congeneric ligands is that small modification of the ligand scaffold can be loosely understood to either make the scaffold slightly more or slightly less rigid, thereby changing the associated entropic cost of the protein binding the ligand. Those modification that make the ligand more rigid will lead to a less unfavorable binding entropy, but will also likely increase the protein strain energy, since the protein must now deform to accommodate a more rigid object. Conversely, small modifications which increase the flexibility of the ligand will reduce the protein strain energy, since less deformation of the protein active site will be required upon binding the ligand, but will increase the entropic penalty of the binding process. It is this hypothesized general compensation of the strain energy with the loss of conformational entropy that should lead to the general applicability of the δ_strn =0 approximate form of Equation 6 to congeneric series.

The next series of approximations requires us to restrict our investigations to complementary ligands--ie, ligands that form hydrogen bonds with the protein receptor where appropriate, hydrophobic contacts otherwise, and sterically “fit” within the accessible volume of the active site of the receptor. Such ligands will form interactions with the surrounding protein similar to the interactions the ligand made with the bulk solvent--i,e hydrogen bonds where appropriate and van der Waals contacts otherwise, be they with the protein active site or with the solvating water. With this in mind, we may rewrite the solvation free energy terms as

$${\langle {\text{W}}_{\text{PL}}\rangle }_{\text{PL}}-{\langle {\text{W}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{W}}_{\text{L}}\rangle }_{\text{L}}=\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}=\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{cav}}+\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}$$ (7)

where Δ〈W_PL〉_P,L;PL is the difference in the solvation free energy of the free ligand and protein versus the complex, $\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{cav}}$ is the free energy of growing the repulsive core of the ligand in the bulk versus within the protein active site, and $\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}$ is the difference in the free energy of charging the ligand-solvent dispersion and electrostatic interactions in the bulk versus within the protein active site. Such a separation of the charging and cavitation terms is common in FEP studies of protein-ligand binding.^18,19

With the introduction of this notation, we find

$$\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{o}}\approx {\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}+\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}+\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{cav}}+{\delta }_{\text{strn}}[{\langle {\text{U}}_{\text{P}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{L}}\rangle }_{\text{PL}}-{\langle {\text{U}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{U}}_{\text{L}}\rangle }_{\text{L}}-\text{T}\mathrm{\Delta }{\text{S}}_{\text{config}}^{\text{o}}]$$ (8)

We now introduce a rather aggressive approximation

$${\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}\approx -\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}+{\delta }_{\text{sie}}\lfloor {\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}+\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}\rfloor$$ (9)

where an exact result is obtained for δ_sie =1, but an approximate result is generated for δ_sie =0. The rationale for this approximation can be explained as followed: $\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}$ is the free energy difference in turning on the attractive and electronic interaction between the ligand and the solvent in bulk water versus in the active site of protein (see Figure 1), which is the interaction between the ligand and the solvent that would be excluded by the protein (depicted by dashed line in figure 1); <U_P-L>_PL is the interaction energy between the ligand and the protein in the complex (right). For complementary ligands binding to the protein receptor, the two terms would be expected to be similar in magnitude: (1) for polar ligands that make strong interactions with the protein receptor such as a salt bridge, the interaction of the ligands with water would also be strong; (2) for apolar ligands that make weak dispersion interactions with the protein, the interactions between the ligands and water would also be weak. The reader may wish to note the approximation described in equation 9 is “aggressive” in the sense that it would be expected to be generally false for an arbitrary ligand binding to an arbitrary receptor. Thus, by employing the approximation described by equation 9, we would only expect the following treatment to well describe ligands that satisfy the underlying assumptions, ie that the ligand form hydrogen bonds where appropriate and hydrophobic contacts otherwise. However, with the above caveat notes, we may approximate the binding free energy as

Figure 1.

Cartoon depicting the relationship between $\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}$ and <U_P-L>_PL. $\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}$ is the free energy difference in turning on the attractive and electronic interaction between the ligand and the solvent in the bulk water (left) versus in the active site of protein (right), which is the interaction between the ligand and the solvent that would be excluded by the protein (depicted by dashed line on the left). <U_P-L>_PL is the interaction energy between the ligand and the protein in the complex (right). For complementary ligands binding to the protein receptor, the two terms would be expected to be of similar magnitude.

$$\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{o}}\approx \mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{cav}}+{\delta }_{\text{sie}}\lfloor {\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}+\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}\rfloor +{\delta }_{\text{strn}}[{\langle {\text{U}}_{\text{P}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{L}}\rangle }_{\text{PL}}-{\langle {\text{U}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{U}}_{\text{L}}\rangle }_{\text{L}}-\text{T}\mathrm{\Delta }{\text{S}}_{\text{config}}^{\text{o}}]$$ (10)

where our identified approximate equivalence between the relative protein-ligand direct interaction energy and the solvation-charging free energies has been explicitly noted in the grouping of the terms. Equation 10 suggests that the binding free energy may be approximated by computing the relative free energies of forming a cavity isosteric to the ligand in the protein active site, versus forming the same cavity in the bulk fluid.

Our remaining task is to develop a computationally efficient procedure to approximate the $\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{cav}}$ term. This term corresponds to the difference in the free energy of growing the repulsive ligand cavity within the protein active site versus growing the ligand cavity in the bulk, or equivalently dragging the ligand cavity from the bulk through the volume of the system into the active site of the protein. The $\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{cav}}$ term may be exactly expanded as

$$\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{cav}}=\left({\text{G}}_{\text{IST}}^{{\text{PL}}_{\text{cav}}}-{\text{G}}_{\text{IST}}^{\text{P}}\right)-\left({\text{G}}_{\text{IST}}^{{\text{L}}_{\text{cav}}}-{\text{G}}_{\text{IST}}^{{\text{H}}_{\text{2}}{\text{O}}_{(1)}}\right)=\mathrm{\Delta }{\text{G}}_{\text{IST}}^{{\text{P},\text{PL}}_{\text{cav}}}-\mathrm{\Delta }{\text{G}}_{\text{IST}}^{{\text{H}}_{\text{2}}{\text{O}}_{(1)},{\text{L}}_{\text{cav}}}=\mathrm{\Delta }{\mathrm{\Delta }}_{\text{IST}}^{{\text{L}}_{\text{cav}}}$$ (11)

where ${\text{G}}_{\text{IST}}^{\text{X}}$ is the inhomogenous solvation theory²⁰ (IST) integral over the system designated by superscript X, ie

$$\begin{array}{l}{\text{G}}_{\text{IST}}^{\text{X}}={\text{E}}_{\text{IST}}^{\text{X}}-{\text{TS}}_{\text{IST}}^{\text{X}}\\ {\text{E}}_{\text{IST}}^{\text{X}}={({\text{E}}^{\text{K}}+{\text{E}}^{\text{sw}}+{\text{E}}^{\text{ww}})}^{\text{X}}+\frac{3}{2}{\text{N}}_{\text{w}}\text{kT}+\rho \int {\text{g}}_{\text{sw}}^{\text{X}}(\overrightarrow{\text{r}}){\text{u}}_{\text{sw}}^{\text{X}}(\overrightarrow{\text{r}})\text{d}\overrightarrow{\text{r}}+\frac{{\rho }^2}{2}\int {\text{g}}_{\text{ww}}^{\text{X}}({\overrightarrow{\text{r}}}_1,{\overrightarrow{\text{r}}}_2){\text{u}}_{\text{ww}}^{\text{X}}({\overrightarrow{\text{r}}}_1,{\overrightarrow{\text{r}}}_2){\text{d}\overrightarrow{\text{r}}}_1{\text{d}\overrightarrow{\text{r}}}_2\\ {\text{S}}_{\text{IST}}^{\text{X}}={({\text{S}}^{\text{id}}+{\text{S}}^{(1)}+{\text{S}}^{(2)}\dots )}^{\text{X}}=\left[\frac{5}{2}{\text{N}}_{\text{w}}\text{k}-{\text{kN}}_{\text{w}}ln(\rho {\mathrm{\Lambda }}^3)\right]-\text{k}\rho \int {\text{g}}_{\text{sw}}^{\text{X}}(\overrightarrow{\text{r}})ln{\text{g}}_{\text{sw}}^{\text{X}}(\overrightarrow{\text{r}})\text{d}\overrightarrow{\text{r}}-\frac{1}{2}\text{k}{\rho }^2\int {\text{g}}_{\text{sww}}^{\text{X}}({\overrightarrow{\text{r}}}_1,{\overrightarrow{\text{r}}}_2)\left[ln\delta {\text{g}}_{\text{sww}}^{\text{X}}({\overrightarrow{\text{r}}}_1,{\overrightarrow{\text{r}}}_2)-\delta {\text{g}}_{\text{sww}}^{\text{X}}({\overrightarrow{\text{r}}}_1,{\overrightarrow{\text{r}}}_2)+1\right]{\text{d}\overrightarrow{\text{r}}}_1{\text{d}\overrightarrow{\text{r}}}_2\dots \\ \delta {\text{g}}_{\text{sww}}^{\text{X}}({\overrightarrow{\text{r}}}_1,{\overrightarrow{\text{r}}}_2)=\frac{{\text{g}}_{\text{sww}}^{\text{X}}({\overrightarrow{\text{r}}}_1,{\overrightarrow{\text{r}}}_2)}{{\text{g}}_{\text{sw}}^{\text{X}}({\overrightarrow{\text{r}}}_1){\text{g}}_{\text{sw}}^{\text{X}}({\overrightarrow{\text{r}}}_2)}\end{array}$$ (12)

where g_sw, g_ww, and g_sww are the solute-water, water-water, and solute-water-water correlation functions; u_sw and u_ww are the solute-water and water-water interaction energy terms; r⃗ is the solvent degrees of freedom of system X; ρ is the density of the bulk fluid, and k is the Boltzmann constant.

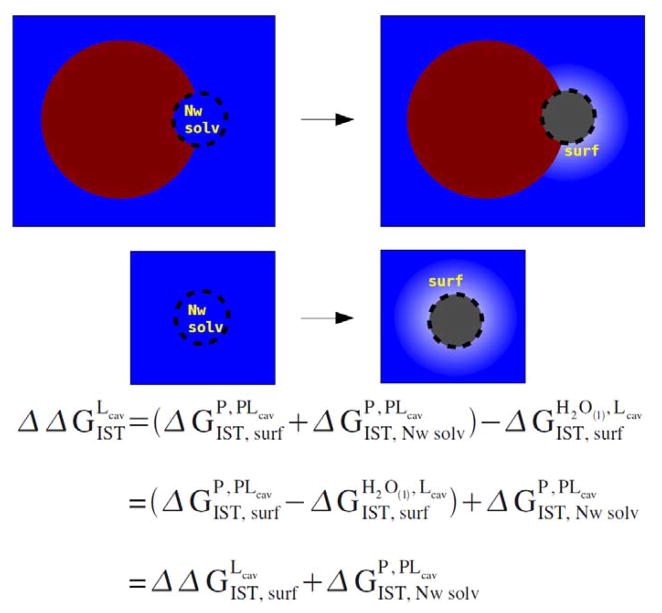
Another simplification can be made by noting that the IST integrals appearing in equation (12) can be decomposed into two contributions: the contribution coming from the integral over the space of ligand cavity and the contribution coming from the integral over the rest of the space. So the ΔGIST integrals appearing in equation 11 (be they in the bulk fluid or the protein active site) can also be decomposed into the corresponding two contributions: (1) the solvation free energies of ~Nw the water molecules that were formerly solvating the protein active site and are evacuated into solution by the growth of the ligand cavity (ΔG_{IST,Nw solv}) (which comes from the integral over the ligand cavity part) (2) the contribution from the solvent located at the L cavity surface (ΔG_IST,surf) (which comes from the integral over the rest of the space) This decomposition of the total IST integrals into ΔG_IST,surf and ΔG_{IST,Nw solv} terms may be clarified by inspecting the graphical depiction of the decomposition to be found in figure 2. It is also worth noting that in this notation $\mathrm{\Delta }{\text{G}}_{\text{IST}}^{{\text{H}}_2{\text{O}}_{(1)},{\text{L}}_{\text{cav}}}=\mathrm{\Delta }{\text{G}}_{\text{IST},\text{surf}}^{{\text{H}}_2{\text{O}}_{(1)},{\text{L}}_{\text{cav}}}$ exactly, since the water is evacuated from a bulk environment to a bulk environment by the growth of the ligand cavity (ie, $\mathrm{\Delta }{\text{G}}_{\text{IST},\text{Nwsolv}}^{{\text{H}}_2{\text{O}}_{(1)},{\text{L}}_{\text{cav}}}=0$ strictly). Therefore,

Figure 2.

Cartoon depicting the spatial decomposition of the IST integral equations introduced in equations 11 to 13. The net “surf” term is the difference in the free energetic cost of the fluid reorganizing its configuration around the surface of the ligand cavity when the cavity is bound to the protein versus free in solution, and the net “N_w solv” term corresponds to the difference in the local IST integral free energy of the N_w water occupying the active site of the protein versus the IST integral free energy of the same N_w water molecules in the bulk fluid.

$$\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{IST}}^{{\text{L}}_{\text{cav}}}=\left(\mathrm{\Delta }{\text{G}}_{\text{IST},\text{surf}}^{\text{P},{\text{PL}}_{\text{cav}}}+\mathrm{\Delta }{\text{G}}_{\text{IST},\text{Nwsolv}}^{\text{P},{\text{PL}}_{\text{cav}}}\right)-\mathrm{\Delta }{\text{G}}_{\text{IST},\text{surf}}^{{\text{H}}_2{\text{O}}_{\text{(1)}}{,\text{L}}_{\text{cav}}}=\left(\mathrm{\Delta }{\text{G}}_{\text{IST},\text{surf}}^{\text{P},{\text{PL}}_{\text{cav}}}-\mathrm{\Delta }{\text{G}}_{\text{IST},\text{surf}}^{{\text{H}}_2{\text{O}}_{\text{(1)}}{,\text{L}}_{\text{cav}}}\right)+\mathrm{\Delta }{\text{G}}_{\text{IST},\text{Nwsolv}}^{\text{P},{\text{PL}}_{\text{cav}}}=\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{IST},\text{surf}}^{{\text{L}}_{\text{cav}}}+\mathrm{\Delta }{\text{G}}_{\text{IST},\text{Nwsolv}}^{\text{P},{\text{PL}}_{\text{cav}}}$$ (13)

where the “surf” term is the difference in the free energetic cost of the fluid reorganizing its configuration around the surface of the ligand cavity when the cavity is bound to the protein versus free in solution, and the “N_w solv” term corresponds to the difference in the local IST integral free energy of the N_w water occupying the active site of the protein versus the IST integral free energy of the same N_w water molecules in the bulk fluid. Our final approximation is to assume that for small ligands that are expected to displace only one or a few water molecules deep within the protein active site, the “N_w solv” term should dominate this expression. Therefore, our final approximation to the binding free energy of the complex is

$$\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{o}}\approx \mathrm{\Delta }{\text{G}}_{\text{IST},\text{Nwsolv}}^{\text{P},{\text{PL}}_{\text{cav}}}+{\delta }_{\text{surf}}\mathrm{\Delta }\mathrm{\Delta }{\text{G}}_{\text{IST},\text{surf}}^{{\text{L}}_{\text{cav}}}+{\delta }_{\text{sie}}\lfloor {\langle {\text{U}}_{\text{P}-\text{L}}\rangle }_{\text{PL}}+\mathrm{\Delta }{\langle {\text{W}}_{\text{PL}}\rangle }_{\text{P},\text{L};\text{PL}}^{\text{chrg}}\rfloor +{\delta }_{\text{strn}}[{\langle {\text{U}}_{\text{P}}\rangle }_{\text{PL}}+{\langle {\text{U}}_{\text{L}}\rangle }_{\text{PL}}-{\langle {\text{U}}_{\text{P}}\rangle }_{\text{P}}-{\langle {\text{U}}_{\text{L}}\rangle }_{\text{L}}-\text{T}\mathrm{\Delta }{\text{S}}_{\text{config}}^{\text{o}}]$$ (14)

where difference in the IST “surf” integrals are approximated as negligible when δ_surf is set to zero. Thus, our remaining task is to develop a numerical estimate the “N_w solv” term.

Interestingly, a possible candidate estimator of $\mathrm{\Delta }{G}_{\text{IST},\text{Nwsolv}}^{\text{P},{\text{PL}}_{\text{cav}}}$ was previously introduced in reference ⁵, although its connection to the more rigorous expressions for computing protein-ligand binding affinities was not fully understood at the time of its introduction. In the so called, displaced-solvent functional (DSF) approach, the local values of the IST integrals are computed for regions of high solvent occupancy in the active site, denoted by hydration sites. Note, that the volume of each hydration site is chosen such that the number of hydration sites will correspond to the N_w water molecules that are evacuated from the protein active site to the bulk fluid upon the binding of the ligand. This estimator itself was based on the following assumptions: (1) if atoms of a ligand overlapped with a hydration site, they displace the water from that site; and (2) the less energetically or entropically favorable the expelled solvent, the more favorable its contributions to the binding free energy. Thus, the relative binding free energy of the ligand is approximated as

$$\begin{array}{l}\mathrm{\Delta }{\text{G}}_{\text{IST},\text{Nwsolv}}^{\text{P},{\text{PL}}_{\text{cav}}}\approx \mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{DSF}}=\sum _{\text{lig},\text{hs}}({\text{E}}_{\text{bulk}}-{\text{E}}_{\text{hs}})\left(1-\frac{\mid {\overrightarrow{\text{r}}}_{\text{lig}}-{\overrightarrow{\text{r}}}_{\text{hs}}\mid }{{\text{R}}_{\text{co}}}\right)\mathrm{\Theta }({\text{R}}_{\text{co}}-\mid {\overrightarrow{\text{r}}}_{\text{lig}}-{\overrightarrow{\text{r}}}_{\text{hs}}\mid )-\text{T}\sum _{\text{lig},\text{hs}}{\text{S}}_{\text{hs}}^{\text{e}}\left(1-\frac{\mid {\overrightarrow{\text{r}}}_{\text{lig}}-{\overrightarrow{\text{r}}}_{\text{hs}}\mid }{{\text{R}}_{\text{co}}}\right)\mathrm{\Theta }({\text{R}}_{\text{co}}-\mid {\overrightarrow{\text{r}}}_{\text{lig}}-{\overrightarrow{\text{r}}}_{\text{hs}}\mid )\\ =\sum _{\text{lig},\text{hs}}\mathrm{\Delta }{\text{G}}_{\text{hs}}\left(1-\frac{\mid {\overrightarrow{\text{r}}}_{\text{lig}}-{\overrightarrow{\text{r}}}_{\text{hs}}\mid }{{\text{R}}_{\text{co}}}\right)\mathrm{\Theta }({\text{R}}_{\text{co}}-\mid {\overrightarrow{\text{r}}}_{\text{lig}}-{\overrightarrow{\text{r}}}_{\text{hs}}\mid )\end{array}$$ (15)

where $\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{DSF}}$ is the predicted binding free energy of the ligand, R_co is the distance cutoff for a ligand atom beginning to displace a hydration site, E_hs is the system-interaction energy of water in a given hydration site, S^e_hs was the excess entropy of water in a given hydration site, ΔG_hs is the computed free energy of transferring the solvent in a given hydration site from the active site to the bulk fluid, and Θ is the Heaviside step function. We also capped the contribution from each hydration site, such that it would never contribute more than ΔG_hs to $\mathrm{\Delta }{\text{G}}_{\text{bind}}^{\text{DSF}}$ no matter how many ligand atoms were in close proximity to it. The value R_co might be considered a free parameter. However, an approximate value was adopted by noting that the radius of a carbon atom and a water oxygen atom are both approximately 1.4 Å, thus suggesting contact distances between a water oxygen atom and a ligand carbon atom less than 0.8*(1.4 Å+1.4 Å)=2.24 Å are statistically improbable due to the stiffness of the Van der Waals potential. From the preceding approximate theory we infer that this approach should yield quantitatively accurate predictions of protein-ligand binding free energies versus the FEP reference data when the ligand is complementary to the protein active site and the reorganization entropies and energies of the protein and the ligand are small compared to the other terms contributing to binding.

Here however, the preceding theory also suggests an alternative but related approach to adapting the DSF method to compute the binding free energy of a united atom methane molecule to a model hydrophobic enclosure. Here since the united atom methane molecule is itself simply a sphere that will occupy a known position in the binding site, we may simply collect statistics from the water molecules observed to occupy the volume that will be later occupied by the binding methane. Thus, clustering is unnecessary. From this data the energetic and entropic properties of the solvating water can be readily obtained via an application of inhomogeneous solvation theory. Lastly, it would in principle be possible to approximate the binding free energy of the of the methane molecule via the one evacuated-site-one-evacuated-water approximation introduced in reference ⁵. However, we may also identify an approximate scaling that makes use of the known volume of the methane particle. In particular, if the methane particle is assumed to have a van der Waals radius of 1.865 Å, then the expectation value of the number of water molecules expected to exist within that volume is

$${\text{N}}_{\text{eff}}={\rho }_{\text{bulk}}\left(\frac{4}{3}\pi {\text{R}}_{\text{methane}}^3\right)\approx 0.85$$ (16)

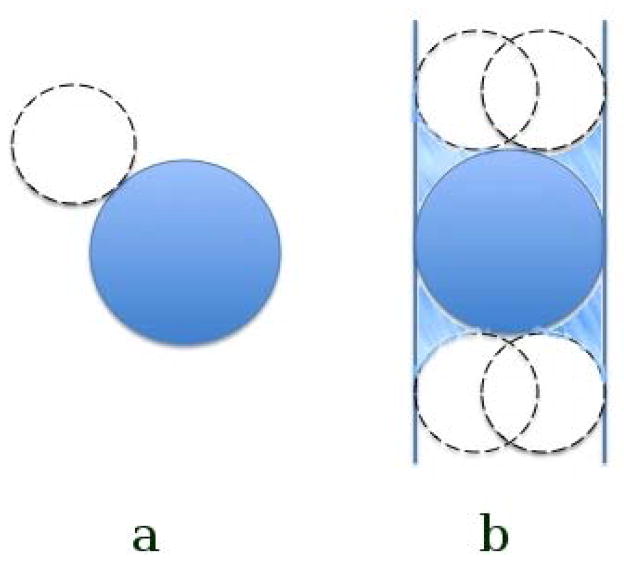
where N_eff is the effective number of water molecules expected be displaced by the bound methane assuming the entire system remains at bulk density, ρ_bulk is the density of liquid water, and R_methane is the Van der Waals radius of the methane particle. Clearly, the number density of water in the active site depends on the environment of the specific enclosure, and in general would be different from bulk. However, the effective volume that is displaced by the binding methane is also different for different enclosures. Taking the situation of methane between two hydrophobic plates for example, considering the solvent-excluded volume consisting of the inward-facing surface of the probe ball with radius 1.4A (size of water), in the bulk water the volume displaced by methane is just the van der Waals volume of methane, but the four corners are also excluded by the methane in between the two plates (see figure 3). It is well known that the number density of water in the hydrophobicly enclosed region is smaller than bulk water because of dewetting. Thus the more enclosed the enclosures are, the smaller the number density of water in the active site, and the larger the effective volume displaced by the methane. These two competing factors make the approximation introduced in equation 16 to be appropriate for all the enclosures. In principle, the exact number of excluded water molecules could be identified by the difference in the average number of water molecules surrounding the enclosure in the presence and absence of the bound methane, but this might require excellent statistics to converge.

Figure 3.

The effective volume displaced by a methane in the bulk(a) and in between two hydrophobic plates(b). The blue particle denotes a methane, and a dashed circle denotes a probe solvent molecular. The volume displaced by a methane in the bulk is just the van der Waals volume of the methane, but in between the two plates, the four corners are also displaced by the methane due to the finite volume of the probe ball.

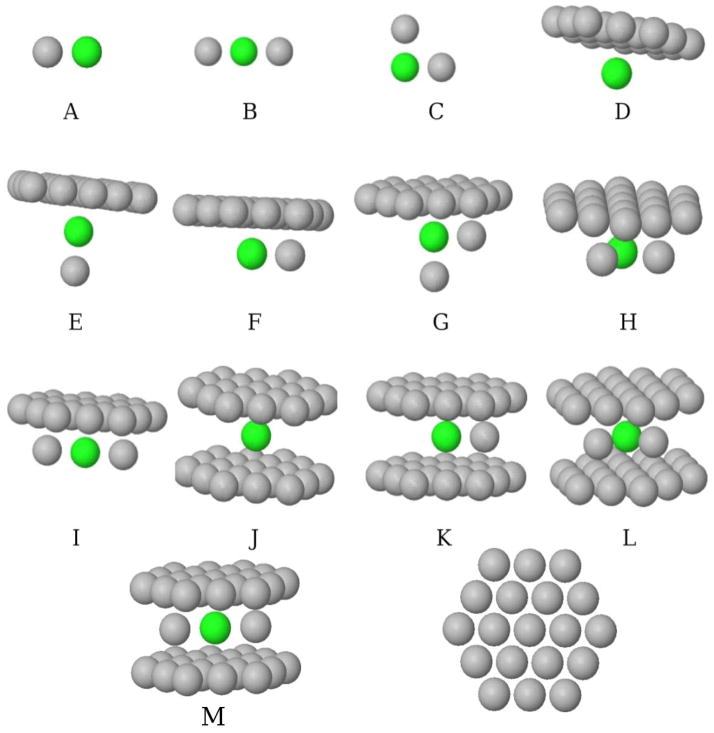
To numerically test the validity of the preceding theory, we have constructed a series of model hydrophobic enclosures, as depicted in figure 4, and computed the binding free energy of a methane ligand for these hydrophobic enclosures both with FEP theory and the proposed DSF theory. The binding free energies of methane for the described enclosures, as computed by FEP, lie over a 5 kcal/mol range, which would correspond to ~4 orders of magnitude of binding affinity. Thus, the ability to accurately predict such free energy differences would be expected to have great utility in a drug-design setting.

Figure 4.

The 13 model hydrophobic enclosures are here depicted in gray. The location of the methane molecule when bound to the respective hydrophobic enclosures is here depicted in green. The geometry of the plate is depicted at the right bottom of this figure. The distance between the neighboring particles in the plate is 3.2 Å, and the distance between the two plates 7.46 Å. All the others particles are at contact distance with linear (B, I and M) and triangle (C, G, H and L) geometries.

A final important point, not relevant to the present model systems but relevant when considering realistic problems such as protein-ligand binding, is the necessity in such real problems for integrating over the solute coordinates. For example, fluctuations of the protein-ligand complex at room temperature can be significant, and in principle this affects the water structure in the active site. In our DSF approach to date, we have employed a single ‘representative” structure for the protein structure (by harmonically restraining the coordinates to a target structure during the DSF molecular dynamics simulation) rather than allowing the solute phase space to be fully explored. For the model hydrophobic enclosures, there is no issue with averaging over solute configurations because the model enclosures are specified as rigid from the beginning.

In the context of our DSF methodology, the interesting question is how good an approximation the harmonically restrained simulation is to the fully fluctuating solute when estimating the free energy changes resulting from solvent displacement by the ligand. A heuristic argument that the approximation is reasonable if it is assumed that, for relatively modest fluctuations of the complex (as opposed to major conformational changes), the solvation in the active site “follows” the solute atoms – in essence an adiabatic approximation in which the solvation structure readjusts quickly to typical excursions of solute atoms from the central configuration. If this is in fact the case, then the free energy of displacement of a given water molecule at all accessible solute configurations can be approximated by the displacement free energy at the central configuration. This is not a rigorous or controlled approximation, but it appears to work reasonably well based on a range of examples that we have investigated to date. We do not consider this point further in the present paper, as our focus is on a series of rigid solutes; however, in future work, explicit investigation of this hypothesis, based on computing DSFs for different solute configurations and comparing them, will be pursued.

B. Simulation details

DSF analysis

To generate the data required to apply the DSF method of computing protein-ligand binding free energies to the model hydrophobic enclosures, each of the thirteen hydrophobic enclosures depicted in figure 4 were subjected to explicitly solvated molecular dynamics with the Desmond molecular dynamics program.²¹ The Maestro²² System Builder utility was used to insert each enclosure into a cubic water box with a 10 Å buffer. The SPC²³ water model was used to describe the solvent, and the united atom methane molecules that formed the “atoms” of the enclosures were uniformly represented with σ=3.73 Å and ε=0.294 kcal/mol Lennard Jones parameters. The atoms of the enclosures were constrained to their initial positions throughout their dynamics, and only the solvent degrees of freedom were sampled. The energy of the system was minimized, and then equilibrated to 298 K and 1 atm with Nose-Hoover^24,25 temperature and Martyna-Tobias-Klein pressure²⁶ controls over 500 ps of molecular dynamics. A cutoff distance of 9 Å was used to model the Lennard Jones interactions, and the particle-mesh Ewald²⁷ method was used to model the electrostatic interactions. Following the equilibration, a 20 ns production molecular dynamics simulation was used to obtain statistics of the water solvating the enclosures, and configurations of the system were collected every 1.002 ps.

Following the previously developed approach^5,6, the position the ligand would occupy in the enclosures was used to define the active site volume. Here, a 1 Å cutoff distance from the center of where the ligand center would be was used to define the solvent volume of interest. A water molecule was identified to be in the active site when its oxygen lay within the sphere, and otherwise not. For each solvent molecule identified in this volume, we computed the system-interaction energy of the solvent molecule (ie the interaction energy of the solvent molecule with the rest of the system), and recorded its orientation and position. From this data, we computed the average system-interaction energy of solvent occupying this volume, and the excess entropy of this solvent from an expansion of the entropy in terms of translational and orientational correlation functions.

The calculation of excess entropies of water in the hydration sites was processed in a two-step manner: (1) introduce an intermediate reference state with the same average number density as the hydration site we are studying but a flat translational and orientational distribution, and calculate the excess entropy of the hydrogen site water with respect to this intermediate reference state due to the local ordering of water in the hydration site (2) determine the entropy difference between the intermediate reference state and the bulk water that is due to the difference of number density. The entropy difference between water in the hydration site and the intermediate state was calculated through the integral introduced in equation 12, with g_sw (r) defined with respect to the intermediate reference state number density. In order to integrate this entropy expansion, we adopted a k-th nearest neighbors approach as introduced in reference ²⁸.

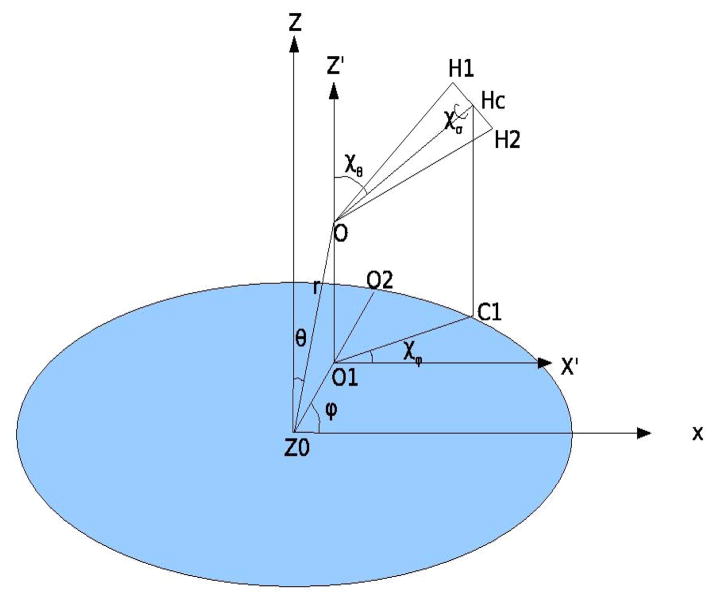
To characterize the orientation of waters in the hydration site, we built the coordinate system such that the center of the hydration site was taken to be the origin, the z axis was perpendicular to the plate (take enclosure F, for example), and a second methane not lying on the z axis was arbitrarily chosen to define the direction of the x axis. The orientation of water in the hydration site was defined by six variables, [r, θ, ϕ,χ_θ,χ_ϕ,χ_σ], where [r, θ, ϕ] are the typical spherical coordinates which define the position of the oxygen atom, and [χ_θ, χ_ϕ, χ_σ] are the three angles which define the orientation of the water around its oxygen (see figure 5). To clarify, [χ_θ,χ_ϕ] are similar to the typical spherical coordinate angles [θ, ϕ] which define the orientation of the dipole vector of water, and χ_σ defines the rotation of hydrogen around the dipole vector. For enclosures with rotational symmetry about the z axis, the distribution along ϕ angle is flat by symmetry, so we only need five angles to define the orientation of water. The calculation of the entropy difference is performed through the following equation:

$${\text{S}}_1=-\text{k}\frac{1}{\text{V}\mathrm{\Omega }}\int \text{J}(\text{r},\theta ,\varphi ,{\chi }_{\theta },{\chi }_{\varphi },{\chi }_{\sigma })\text{g}(r,\theta ,\varphi ,{\chi }_{\theta },{\chi }_{\varphi },{\chi }_{\sigma })\text{lng}(r,\theta ,\varphi ,{\chi }_{\theta },{\chi }_{\varphi },{\chi }_{\sigma })\text{drd}\theta \text{d}\varphi \text{d}{\chi }_{\theta }\text{d}{\chi }_{\varphi }\text{d}{\chi }_{\sigma }$$ (17)

where g(r, θ, ϕ,χ_θ, χ_ϕ, χ_σ) is the solute water pair correlation function (PCF), and J(r, θ, ϕ, χ_θ, χ_ϕ, χ_σ) is the Jacobian associated with these variables. Here g(r, θ, ϕ, χ_θ,χ_ϕ, χ_σ) has the property that

Figure 5.

The coordinate system to characterize the position and orientation of water inside the hydration site. The z axis is perpendicular to the model hydrophobic plate, and the x axis is such defined that the other methane lie on the x axis. [r, θ, ϕ] are the typical spherical coordinates which define the position of the oxygen atom, and [χ_θ, χ_ϕ, χ_σ] are three angles which define the orientation of the water around its oxygen.

$$\frac{1}{\text{V}\mathrm{\Omega }}\int \text{J}(\text{r},\theta ,\varphi ,{\chi }_{\theta },{\chi }_{\varphi },{\chi }_{\sigma })\text{g}(\text{r},\theta ,\varphi ,{\chi }_{\theta },{\chi }_{\varphi },{\chi }_{\sigma })\text{drd}\theta \text{d}\varphi \text{d}{\chi }_{\theta }\text{d}{\chi }_{\varphi }\text{d}{\chi }_{\sigma }=1$$ (18)

where V is the volume of the sphere and Ω is the total angular volume over angular variables [χ_θ,χ_ϕ, χ_σ], ie

$$\mathrm{\Omega }=\int \text{J}({\chi }_{\theta },{\chi }_{\varphi },{\chi }_{\sigma })\text{g}({\chi }_{\theta },{\chi }_{\varphi },{\chi }_{\sigma })\text{d}{\chi }_{\theta }\text{d}{\chi }_{\varphi }\text{d}{\chi }_{\sigma }$$ (19)

In line with reference ²⁸ we approximate the total pair correlation function (PCF) through generalized Kirkwood superposition approximation²⁹ (GKSA), which allowed the entropy to be approximated by the summation and subtraction of one- and two-dimensional entropies, and calculated the one- and twodimensional entropies through NN method.

The entropy difference between the reference state and bulk water can be simply calculated by recognizing the entropy expression for homogeneous ideal-gas:

$${\text{S}}_{\text{id}}=\frac{3}{2}-\text{k}ln(\rho {\mathrm{\Lambda }}^3)$$ (20)

where Λ is the thermal wavelength. So the excess entropy of the second step is simply:

$${\text{S}}_2=-\text{k}ln\left(\frac{{\rho }_{\text{ref}}}{{\rho }_{\text{bulk}}}\right)$$ (21)

where ρ_ref, ρ_bulk are the number density of the reference state and bulk water respectively.

The total excess entropy is the sum of S₁ and S₂ as defined by equation 17 and 21.

FEP analysis

The dynamics simulation used to perform the FEP analysis of the binding free energy of the methane ligand to the model hydrophobic enclosures were run under identical simulation protocols as the DSF analysis. The ligand was “turned on” inside the model enclosures over 9 lambda windows with λ=[0,0.125,0.25,0.375,0.50,0.625,0.75,0.875,1], where λ is the coupling parameter to turn on/off the interaction between the methane and the rest of the system with initial state and final state correspond to λ=0 and λ=1 respectively. At different λ windows, we performed molecular dynamics simulations, and calculated the energy difference between neighboring λ values for each configuration saved. In these simulations, the soft-core interactions were used for the Lenard-Jones potential. Bennett acceptance ratio method were then used to calculate the free energy difference between neighboring states. The sum of the free energy differences between neighboring states gave the solvation free energy of methane in question. The same procedure was followed to calculate the solvation free energy of methane in bulk water. The difference between the two solvation free energy gave the binding free energy to bring a methane from infinitely far to inside the hydrophobic enclosure. (We can also interpret the binding free energy as the potential of mean force between the methane and the enclosure.)

Buried surface area analysis

The solvent accessible surface area (SASA) and molecular surface area (MSA, or Connolly surface) of each enclosure with and without the bound methane was computed with the Connolly molecular surface package²³⁰, as was the SASA and MSA of the methane particle by itself. From this data the buried solvent accessible surface area upon methane-enclosure complexation was determined. The Lennard Jones interaction energy of the methane particle with the model enclosure was similarly computed. The buried surface area times the surface tension would give the solvent induced interaction energy, and together with the direct Lennard-Jones interaction energy, the total binding energy of methane with different enclosures can be calculated, as routinely estimated in various empirical methods to estimate the contribution of the nonpolar term to the binding energy.

Results

The binding free energies of methane for the model hydrophobic enclosures, as measured by FEP, are reported in table 1. It is found that the range of binding free energies of the methane ligand for the model enclosures is nearly 5 kcal/mol. Also reported in table 1 are the system-interaction energies and excess entropies of the water displaced by the methane ligand, the buried surface area upon complexation, (both SASA and MSA), the change of the Lennard Jones interaction energy between the methane particle and the enclosure upon complexation, the DSF prediction of the binding free energy of the complex, and the scaled DSF prediction that makes use of the scaling coefficient deduced from first principles in section II. The R² value, mean-absolute-error (MAE) and the root-mean-square-error (RMSE) between the various predictions with the FEP-reference date are also listed in the last few rows of the table. Note here that the surface tension coefficients for the buried surface area/molecular mechanics predictions (Both SASA and MSA) were explicitly tuned to minimize the MAE of the predictions. Such explicit tuning yields significantly better results than could reasonably be expected to be obtained if such methods were employed with fixed coefficients across realistically variable data sets.

Table 1.

The binding thermodynamics of methane for the various model hydrophobic enclosures as computed from DSF theory and FEP theory. E_hs was the hydration site system interaction energy, S^e_hs was the hydration site solute-water correlation entropy, ΔSASA was the buried solvent accessible surface area using a 1.4 Å radius probe, ΔE_LJ was the Lennard Jones interaction energy of the bound methane with the rest of the enclosure, DSF-ΔG_bind was the predicted binding free energy of the methane molecule for the model enclosure as computed from DSF theory, N_eff was scaling coefficient derived by determining the expectation value of the number of water molecules occupying a volume in the bulk fluid equal to the volume of the methane probe molecule, and FEP-ΔG_bind was the predicted binding free energy of the methane molecule for the model enclosure as computed from FEP theory. Note that the standard deviation of the E_hs values reported below were found to be uniformly less than 0.4 kcal/mol (as obtained from block averaging), and the standard errors of the FEP-ΔGbind values were uniformly less than 0.02 kcal/mol.

Model Enclosure*	Ehs (kcal/mol)	Sehs (cal/mol* K)	Δ SASA (Å2)	ΔMSA(Å2)	ΔELJ (kcal/mol)	DSF-ΔGbind (kcal/mol)	Neff* DSF-ΔGbind (kcal/mol)	FEP-ΔGbind (kcal/mol)
bulk	−19.8	0	0	0	0	0	0	0
A	−19.6	−1.2	−59.45	−3.84	0	−0.5	−0.46	−0.61
B	−18.9	−2.0	−118.9	−7.67	0	−1.5	−1.28	−1.15
C	−19.2	−1.8	−98.21	−10.49	0	−1.1	−0.97	−1.41
D	−18.7	−1.2	−91.32	−13.51	−1.41	−1.5	−1.26	−1.66
E	−17.7	−2.3	−151.15	−17.35	−1.41	−2.8	−2.39	−2.17
F	−17.3	−1.5	−117.52	−24.06	−1.41	−2.9	−2.5	−2.63
G	−16.0	−3.0	−156.39	−30.7	−1.41	−4.7	−4	−3.41
H	−15.6	−1.2	−132.41	−37.35	−1.41	−4.6	−3.92	−3.43
I	−15.6	−1.8	−143.71	−34.6	−1.41	−4.8	−4.05	−3.47
J	−17.8	−2.6	−182.65	−27.02	−2.82	−2.8	−2.41	−2.86
K	−15.5	−2.1	−175.59	−44.27	−2.82	−4.9	−4.17	−4.59
L	−13.0	0.3	−166.61	−64.21	−2.82	−6.8	−5.74	−5.24
M	−13.3	−0.1	−168.52	−61.51	−2.82	−6.6	−5.6	−5.45
R2 versus FEP:	0.94	0.16	0.76(a)	0.92(b)	0.73	0.95	0.95	N/A
MAE versus FEP	0.61	N/A	0.54(a)	0.47(b)	1.41	0.66	0.36	N/A
RMSE versus FEP	0.75	N/A	0.74(a)	0.58(b)	1.63	0.85	0.40	N/A

^*the enclosures are labeled as described in figure 3.

^(a)these values correspond to the correlation between the buried SASA/LJ interaction with optimized surface tension coefficient (γ =0.044 kcal/mol*Ų) and the FEP reference data.

^(b)these values correspond to the correlation between the buried MSA/LJ interaction with optimized surface tension coefficient (γ =0.011 kcal/mol*Ų) and the FEP reference data.

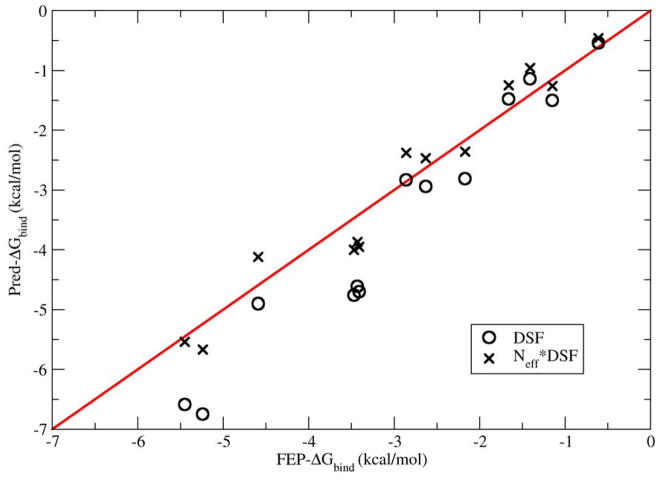
The DSF predictions show very high correlation with the FEP reference data, as indicated by the R² value of 0.95, (which can also be seen in figure 6) where the buried surface area/Lennard Jones interaction predictions show reduced correlations, as indicated by R² values of 0.92 for MSA/MM and 0.76 for SASA/MM respectively. The DSF method also allows for the decomposition of the binding free energy prediction into separate enthalpic and entropic components. Inspection of the data reported in table 1 indicates that the DSF predictions are dominated by the enthalpic contribution to the binding affinity, which by itself manifests a R² value of 0.94 versus the FEP reference data. Detailed analysis of these data indicates that, except for the first three systems, the binding of the methane molecule to these hydrophobic enclosures is mainly an enthalpy driven event, which is consistent with our knowledge about large length scale hydrophobicity.^31–33 Recent calorimetry data obtained for Major Mouse Urinary Protein by Homans et al³⁴, appear to indicate such enthalpy driven hydrophobic binding events are witnessed in vivo, as well.

Figure 6.

The correlation of the of the DSF predictions of the methane-enclosure binding free energies with the FEP reference data.

The inspection of the trajectory indicates the atomistic basis of the enthalpy driven effect is that water molecules that solvate such enclosures are forced to break hydrogen bonds. The effect is most obvious for hydrophobic enclosures L and M, where the solvent suffers a ~7 kcal/mol reduction in system-interaction energy when occupying these enclosures, while almost no reduction in excess entropy versus bulk water. Conversely, the methane dimerization free energy described by methane binding to “enclosure” A is dominated by the entropic contribution, again consistent with entropy driven small length scale hydrophobic effect. This finding is analogous to the well characterized length scale dependence of the hydrophobic effect, while small hydrophobes are found to induce entropic ordering of the solvent, large hydrophobes are found to break water-water hydrogen bonds.^31,33 The enclosures L and M can thus be understood as manifesting extreme large-length scale hydrophobic character from the perspective of the solvating water.

Figure 6 plots the correlation of the DSF binding free energies versus the FEP reference data with and without the derived scaling coefficient deduced from the size of the methane ligand itself. As can be seen from the figure, both sets of predictions track the FEP reference data quite well. However, the scaled predictions have greater quantitative agreement with the FEP, which may be quantified by the mean-absolute error (MAE) and root-mean-square error (RMSE) metrics. Here the scaled predictions are found to have a MAE of 0.36 kcal/mol and a RMSE of 0.40 kcal/mol, while the unscaled predictions have a MAE of 0.66 kcal/mol and a RMSE of 0.84 kcal/mol. Thus, the deduced scaling coefficient appears to increase the quantitative accuracy of the approach, in line with the expectation of the theoretical analysis.

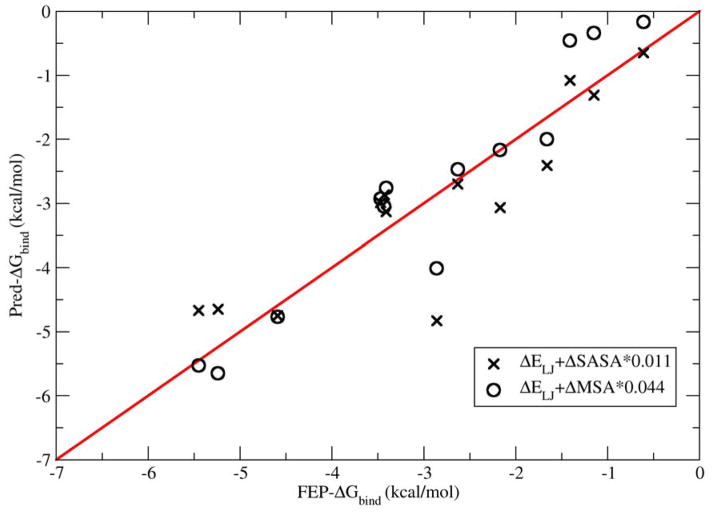
We also investigated to what extent a combined buried surface area/Lennard-Jones interaction energy model might be able to reproduce the binding affinities. Tuning the model to minimize the MAE of the fit, we obtained an optimal surface tension coefficient of γ=0.011 kcal/mol*Ų for SASA and 0.044 kcal/mol*Ų for MSA for these enclosures, which is somewhat smaller than the reported literature values.³⁵ These predictions versus the FEP reference data are reported in figure 7. It is found that MSA/MM performed much better compared with SASA/MM, which is indicated by much higher R² value, and smaller MAE and RMSE values. (Data listed in last 3 rows in table 1.) However, both of them performed less well than the DSF predictions with the scaling coefficient correction, and much worse results would be expected with such an model in general, as noted above, since it would not benefit from explicit fitting to the reference data.

Figure 7.

The correlation of buried surface area/molecular mechanics predictions of the methane-enclosure binding free energies with the FEP reference data. The water SASA surface tension coefficient (0.011 kcal/mol*Ų) and MSA surface tension coefficient (0.044 kcal/mol*Ų) were tuned to minimize the absolute average error of the predictions with respect to the reference data.

The better performance of MSA/MM versus SASA/MM is due to the better characterization of MSA for the topology of enclosures J, K, L, M. SASA/MM predicts enclosure J to be most hydrophobic, which corresponds to a methane molecule binding between two hydrophobic plates, because large swaths of formerly SASA on the faces of the plates are buried by the presence of the methane ligand for enclosure J, while for enclosures K, L, and M several methane molecules already lie between the plates in the absence of the binding ligand and thus some of the surface area that would be buried by the binding methane is already buried by the other particles. However, MSA can better characterize the curvature of these enclosures and predict the right order of binding affinity.

Conclusion

Calculations suggest that the DSF method of computing protein-ligand binding affinities may offer near-FEP accuracy at a substantially reduced computational expense for systems that satisfy the requisite approximations and should offer greater quantitative accuracy than competing implicit solvent methodologies. Further, the clear connection between the DSF method and more rigorous statistical mechanical expressions may offer a rational path to systematically improve the accuracy and rigor of the method by progressive inclusion of those counter-balancing terms currently approximated to exactly cancel. This previously opaque connection to the underlying theory facilitated the derivation of a scaling coefficient that was seen to increase the quality of the predictions of the method versus the FEP reference data. Lastly, the molecular detail afforded by the technique may offer insight into protein-ligand binding processes, such as highlighting the importance of the enthalpy in the binding of methane to such model enclosures, which may have been difficult to discern from only FEP or implicit modeling.