Understanding the factors affecting the activation of alkane by Cp^′Rh(CO)₂ (Cp^′ = Cp or Cp*)

Abstract

Fast time-resolved infrared spectroscopic measurements have allowed precise determination of the rates of activation of alkanes by Cp′Rh(CO) (Cp^′ = η⁵-C₅H₅ or η⁵-C₅Me₅). We have monitored the kinetics of C─H activation in solution at room temperature and determined how the change in rate of oxidative cleavage varies from methane to decane. The lifetime of CpRh(CO)(alkane) shows a nearly linear behavior with respect to the length of the alkane chain, whereas the related Cp*Rh(CO)(alkane) has clear oscillatory behavior upon changing the alkane. Coupled cluster and density functional theory calculations on these complexes, transition states, and intermediates provide the insight into the mechanism and barriers in order to develop a kinetic simulation of the experimental results. The observed behavior is a subtle interplay between the rates of activation and migration. Unexpectedly, the calculations predict that the most rapid process in these Cp′Rh(CO)(alkane) systems is the 1,3-migration along the alkane chain. The linear behavior in the observed lifetime of CpRh(CO)(alkane) results from a mechanism in which the next most rapid process is the activation of primary C─H bonds (─CH₃ groups), while the third key step in this system is 1,2-migration with a slightly slower rate. The oscillatory behavior in the lifetime of Cp*Rh(CO)(alkane) with respect to the alkane’s chain length follows from subtle interplay between more rapid migrations and less rapid primary C─H activation, with respect to CpRh(CO)(alkane), especially when the CH₃ group is near a gauche turn. This interplay results in the activation being controlled by the percentage of alkane conformers.

Alkanes are generally unreactive molecules and the lack of ability to utilize such feedstock has thwarted the widespread use of methane, the main component of natural gas, as a feedstock to produce synthetically useful compounds even though this inexpensive source is widely available (1). The facile activation of methane is considered a “holy grail” for chemists (2). The use of transition metals in order to provide a way to activate carbon─hydrogen (C─H) bonds in hydrocarbons offers the potential to address this problem, and useful processes have been developed including alkane dehydrogenation, arene borylation, and alkane metathesis.

The early reports of alkane activation involved an initial photodissociation of a ligand, from a five-coordinate cyclopentadienyl rhodium(I) or iridium(I) complex to form a coordinatively unsaturated intermediate (3, 4). This reactive species subsequently attacks and oxidatively adds a C─H bond to form the alkyl hydride product. There has been considerable research effort directed toward understanding this key reaction in order to allow the full exploitation of the C─H activation process. The photochemistry of Cp^′Rh(CO)₂ [Cp^′ = (η⁵-C₅R₅), R = H (Cp) or CH₃ (Cp*)] has played an important role in developing our understanding particularly because the infrared ν(C─O) bands are a useful spectroscopic tool for characterizing the reactive intermediates and monitoring the C─H activation reaction (5, 6). Photolysis results in CO loss and coordination of the alkane followed by C─H activation to form the alkyl hydride product. Elegant experiments in liquefied krypton and xenon at cryogenic temperatures demonstrated that, on the microsecond time scale, Cp*Rh(CO)Ng (Ng = Xe or Kr) was the primary photoproduct following photolysis of Cp^∗Rh(CO)₂ in either liquefied krypton or xenon. Irradiation of a mixture of alkane and lKr solution resulted in formation of the noble gas complex CpRh(CO)Kr followed by the formation of the alkane complex Cp*Rh(CO)(RH), which subsequently undergoes C─H bond cleavage to give the final alkyl hydride product. Activation was observed for all alkanes studied except methane (6). In solution at room temperature, CpRh(CO)(alkane) was observed on the picosecond time scale (7) and CpRh(CO)(alkyl)H, and the only information for the rate of C─H activation was given by the slight decay on the picosecond time scale providing an estimate for the formation of the alkyl hydride, k_obs = 4.0 × 10⁸ s^-1 (τ_act = 2.5 ns).

The related chemistry of the Rh(Tp^3,5-Me)(CO)₂ [Tp^3,5-Me = HB(3,5-dimethylpyrazolyl)₃] complex has been studied (8, 9), and photolysis of Rh(Tp^3,5-Me)(CO)₂ led to the ejection of a CO ligand and the formation of a monocarbonyl complex, which was rapidly solvated to form Rh(κ³-Tp^3,5-Me)(CO)(RH). This species then decayed to form the more stable Rh(κ²-Tp^3,5-Me)(CO)(RH) complex, which is able to undergo C─H activation to the final oxidative addition product, Rh(κ³-Tp^3,5-Me)(CO)(R)H. Recent investigations into the photochemistry of the tert-butyl-substituted complex Rh(κ³-Tp^4-tBu-3,5-Me)(CO)₂ provided additional evidence on the mechanism. The important step controlling C─H activation in this system is partial rechelation of the Tp ligand to Rh, which forms a less stable intermediate that leads to a product with a fully coordinated Tp (10).

Although there were earlier studies of C─H activation on bare metals and simple model complexes, the computational studies presented in this paper applied density functional theory (DFT) to the reaction of CpRh(CO) with CH₄ including the initial σ-complex, transition state, and methyl-hydride product (11). This work was followed shortly by complementary ab initio studies, which showed that the computed thermodynamic values for C─H activation were very sensitive to the computational method and somewhat sensitive to the basis set (12–14). Of particular relevance to this paper are the studies by Jones and co-workers on the tris(pyrazolyl)borato rhodium complexes,Rh(Tp^3,5-Me)(CNR)(alkyl)H (R = neopentyl) where the thermodynamic preference for a wide variety of hydrocarbon substrates was investigated (15). In addition to the C─H activation process, the formation of the initial alkane σ-complex and the migration of the metal along the alkane chain prior to activation play important roles in the overall reaction.

The combination of supercritical fluids and time-resolved infrared (TRIR) spectroscopy has allowed the characterization of a series of organometallic noble gas complexes at room temperature (16)—an approach that also allows the interaction of the lighter alkanes to be probed in solution at room temperature. In this paper we show that the combination of high precision fast TRIR measurements monitoring the C─H activation of alkanes by Cp^′Rh(CO)₂ together with coupled cluster and density functional calculations yields previously undescribed insight into the factors controlling carbon-hydrogen bond activation. In particular, we report the monitoring of the activation of alkanes (n = 1–10) and demonstrate that there are significant changes in the rate of primary carbon-hydrogen activation depending solely on the length of the alkane chain.

Results and Discussion

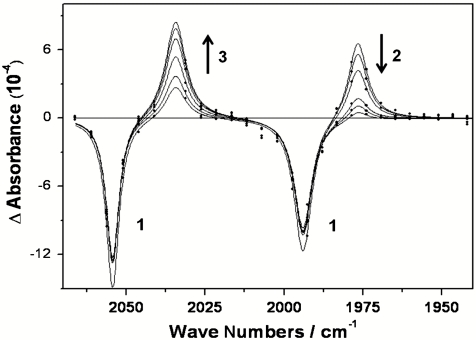
The ns-TRIR spectra obtained following irradiation (267 nm) of CpRh(CO)₂ (1) dissolved in scCH₄ (4,000 psi) in the presence of CO (60 psi) are shown in Fig. 1. It is clear from the transient IR spectrum obtained 1 ns after laser flash that the parent absorptions at 1,995 and 2,056 cm^-1 are bleached and a major new transient band is produced at 1,976 cm^-1. This can be readily assigned to the methane complex CpRh(CO)(CH₄) (2) by comparison with the results obtained from previous TRIR experiments (17). Within 20 ns following laser flash, CpRh(CO)(CH₄) (2) has decayed completely and is replaced by a new band at 2,034 cm^-1, which is assigned to the C─H activated alkyl hydride complex CpRh(CO)(CH₃)H (3).

Fig. 1.

Time-resolved IR spectra obtained following photolysis of CpRh(CO)₂ (1) in scCH₄ showing the depletion of 1 and the formation and subsequent decay of CpRh(CO)(CH₄) (2) to form CpRh(CO)(CH₃)H (3).

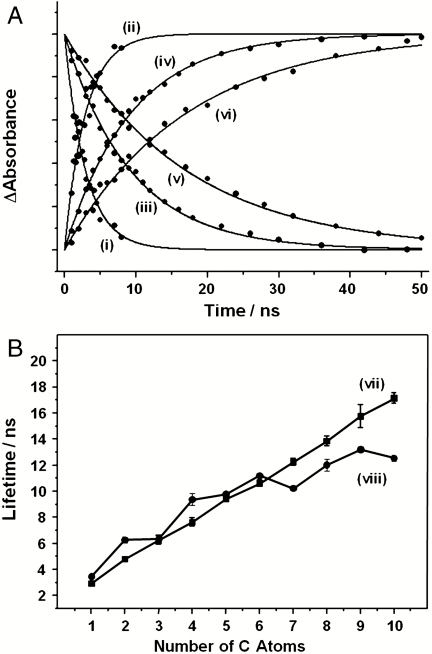
CpRh(CO)(CH₃)H was already visible in the TRIR spectrum obtained 1 ns after laser flash and grows in at the same rate (k_obs = 3.3( ± 0.2) × 10⁸ s^-1) as CpRh(CO)(CH₄) decays (k_obs = 3.3( ± 0.2) × 10⁸ s^-1); see Fig. 2. The lifetime of the C─H activation reaction, 3.0( ± 0.2) ns, is very similar to that reported (7) for the activation of the analogous pentane complex (4.0 × 10⁸ s^-1). This was quite unexpected, and we have repeated the measurement of the activation of CpRh(CO)(pentane) to form CpRh(CO)(pentyl)H and found the lifetime for C─H activation of pentane to be 9.4 (± 0.2) ns; see Fig. 2.

Fig. 2.

(A) Normalized TRIR kinetic traces showing the decay of CpRh(CO)(alkane) and the formation of CpRh(CO)(alkyl)H obtained following irradiation of a solution in either scCH₄ [(i), (ii)], C₅H₁₂ [(iii), (iv)], or C₁₀H₂₂ [(v), (vi)]. (B) A plot of the lifetimes for the C─H activation reaction for the linear alkanes as a function of C the number of carbon atoms for (vii) CpRh(CO)(alkane) and (viii) Cp*Rh(CO)(alkane).

The rate constant we have determined is clearly and significantly different from the rate measured for conversion of CpRh(CO)(CH₄) to CpRh(CO)(CH₃)H. CpRh(CO)(CH₃)H is not stable, and we have also investigated the rate of decay of CpRh(CO)(CH₃)H in scCH₄ in the presence of CO on a much longer time scale. CpRh(CO)(CH₃)H decays to regenerate the CpRh(CO)₂ [k_obs = 3.0( ± 0.3) × 10³ s^-1]. This rate depends linearly on the CO concentration. The rate constant for this reaction in scCH₄ is k_CO = 7.0( ± 0.2) × 10³ dm³ mol^-1 s^-1. The ability to distinguish between the rate of C─H activation in CH₄ and C₅H₁₂ prompted us to investigate the rate of C─H activation for both Rh(Cp′)(CO)(alkane) (Cp^′ = Cp or Cp*); see Fig. 2. The lifetime of CpRh(CO)(alkane) shows a nearly linear behavior with respect to the length of the alkane chain, and the related Cp*Rh(CO)(alkane) has a clear oscillatory behavior upon changing the alkane. However, closer inspection of the CpRh(CO)(alkane) shows that it also has an oscillatory behavior that seems partly out of phase with the rates obtained for the Cp*Rh(CO)(alkane) complexes.

The variation in rate constant can be seen from the results of plotting the residual from either a linear, CpRh(CO)(alkane), or polynomial, Cp*Rh(CO)(alkane), fit to the behavior to the C─H activation rate with alkane chain length from methane to decane (see SI Text). Although there is apparent oscillatory behavior for the variation in the C─H activation rate with chain length for the CpRh(CO)(alkane) system, these changes are within the experimental error of the measurements. However, the change in the C─H activation rate for the Cp*Rh(CO)(alkane) is more marked and is greater than the errors in the rate measurement.

Computational chemistry is a very important technique for understanding the details of transition metal reactions (18) where experimental results often do not have the “resolution” to confirm details of mechanisms. Although the oxidative C─H activation by transition metal complexes has been extensively studied by computational means (19), here, higher level and more detailed calculations of the interactions of alkanes with both CpRh(CO) and Cp*Rh(CO) are made in order to understand the surprising pattern of lifetimes observed experimentally.

[1]

As suggested by previous studies, the C─H activation proceeds in two steps (expression 1), and it has become increasingly clear that alkane complexes, R─H⋯M, in which the alkanes are bound to the metal centers as “σ-complexes,” without their C─H bonds being fully broken, are implicated as intermediates in the overall reaction. For these transient alkane complexes, the Rh coordination center may bind to each of the methylene (─CH₂─) and methyl (─CH₃) sites of longer alkanes (C_nH_2n+2, n≥3) and migrate between these sites.

The short observed lifetimes point to very low barriers for C─H activation in these Rh complexes. At the B3LYP level the CpRh(CO) enthalpic barriers are 5.4, 6.2, and 6.1 kcal mol^-1 for CH₄, C₂H₆, and C₃H₈ (primary CH₃), respectively, whereas at the Perdew–Burke–Ernzerhof (PBE) level, these same barriers are even lower, 1.3, 1.8, and 1.7 kcal mol^-1. Although the differences in the barriers are similar for the two functionals, the obvious absolute discrepancy between these two functionals prompted us to perform additional calculations at the coupled cluster single and double (CCSD) level on the geometries obtained at both B3LYP and PBE levels. The “CCSD/B3LYP barriers” for CpRh(CO) are 4.7, 5.2, and 4.7 kcal mol^-1 for CH₄, C₂H₆, and C₃H₈, respectively, whereas those for the bulky, but electron-rich, Cp*Rh(CO) complex are 4.5, 4.8, and 4.4 kcal mol^-1 for CH₄, C₂H₆, and C₃H₈.

The relative barrier for activating different C─H bonds is also a crucial issue. Consistent with the experimental observation, for longer alkanes (C_nH_2n+2, n≥3), Rh complexes preferentially activate terminal or primary C─H bonds over secondary ones although the primary C-H bonds are substantially stronger than the secondary ones. For example, at CCSD//B3LYP, the C─H CpRh(CO) activation energies for C₃H₈ are 4.7 kcal mol^-1 for CH₃ and 5.0 kcal mol^-1 for -CH₂-, and this selectivity is even larger for the bulker Cp* system, 4.4 kcal mol^-1 for CH₃ and 5.5 kcal mol^-1 for CH₂. A similar trend exists for the activations in longer alkanes and barriers for CH₂ attached to ─C₂H₅ are greater than those attached to ─CH₃ by about 0.8 kcal mol^-1.

Binding to Rh occurs primarily through one C─H bond at any one instant and the rearrangement among geminal H atoms is very easy, but migrations to other CH_x groups have higher barriers. All studies to date have assumed that this migration occurs from one CH_x group to the adjoining one by 1,2-migration. For CpRh(CO)(C₃H₈) at the CCSD//PBE level, the 1,2-migration (the secondary alkane complex → the primary alkane complex for C₃H₈) requires 5.45 kcal mol^-1 of activation energy, whereas the 1,3-migration (migration between the two terminal CH₃ groups for C₃H₈) is easier, needing only 4.25 kcal mol^-1 of activation energy. The migration barriers by Cp*Rh(CO) are much lower than those by CpRh(CO), 4.39 kcal mol^-1 for 1,2-migration and 3.39 kcal mol^-1 for 1,3-migration for C₃H₈. In terms of the overall thermodynamics of binding both Cp- and Cp*Rh(CO) bind primary CH groups more strongly than secondary ones, and the binding energy in CpRh(CO) is greater than that of Cp*Rh(CO). This difference and the difference between this pattern and that predicted previously for W(CO)₅ binding (20) appears to be dominated by steric differences.

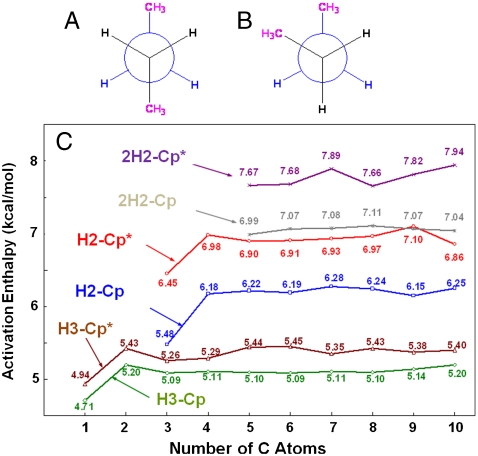
For linear alkanes experimental gauche-trans energy differences were reported ranging from approximately 0.5 to 1.0 kcal mol^-1 (21–23) in the gas phase and are in the range of 0.5–0.6 kcal mol^-1 in the liquid (22). An electron diffraction study of the alkanes butane through heptane revealed that the gas-phase conformations often contain gauche dihedral angles (24), and earlier molecular dynamics studies predicted that gauche population should be enhanced upon transfer from the gas phase to the liquid (25). Hence, for larger alkanes (n > 3) both the gauche and trans conformations are present in the liquid state. Furthermore, in the gauche conformation, 1,4-migrations are also possible. For end-to-end migration in gauche butane, the activation energy for the 1,4-migration is about 0.5 kcal mol^-1 higher than that for the 1,3-migration, but about 1.0 kcal mol^-1 less than that for the 1,2-migration. We also compared the C─H activation barriers for the three terminal hydrogens of both trans and gauche linear butanes (see Fig. 3). Generally, the average enthalphic barriers at CH₃ were slightly larger for the gauche isomers for both Cp and Cp*. However, the free energy barriers were significantly larger for the gauche isomer in the Cp* case.

Fig. 3.

Schematic representation of (A) trans-n-butane and (B) gauche-n-butane. The different terminal C─H bonds have different activation energies because of the different orientation of the alkane chain with respect to CpRh(CO). For CpRh(CO)(alkane) the average difference between A and B is 0.71 kcal mol^-1, whereas for Cp^∗Rh(CO)(alkane) the average difference is 1.93 kcal mol^-1. (C) Calculated C─H activation barriers for the primary (C^∗H₃CH₂CH₂─) C─H bonds activation enthalpies (in kcal mol^-1) vs. number of carbon atoms for the linear alkanes (n = 1 to 10) by CpRh(CO) (H3-Cp; green curve) and by Cp^∗Rh(CO) (H3-Cp*; brown curve) and the secondary C─H activation enthalpies (in kcal mol^-1) vs. number of carbon atoms for the n-alkanes propane through decane by CpRh(CO) (H2-Cp; blue curve for CH₃C^∗H₂CH₂─ and 2H2-Cp; gray curve for CH₃CH₂C^∗H₂─) and by Cp*Rh(CO) (H2-Cp*; red curve for CH₃C^∗H₂CH₂─ and 2H2-Cp*; purple curve for CH₃CH₂C^∗H₂─). All data were calculated at the PBE level and offset upward by 3.43 kcal mol^-1 to obtain the approximate CCSD values. The offset value of 3.43 kcal mol^-1 is the activation enthalpy difference between the PBE calculation and the CCSD//PBE calculation for methane’s C─H activation by CpRh(CO).

Although only shorter hydrocarbons (n ≤ 3) were studied at the CCSD level, we examined long alkane chains at the PBE level. Fig. 3C summarizes the C─H activation enthalpies vs. number of carbon atoms for the all-trans linear alkanes (n = 1 to 10) by CpRh(CO) and Cp*Rh(CO). Generally, the C─H activation enthalpic curves become relatively linear after propane for the ─CH₃ activations and after butane for the ─CH₂─ activations. The relative migration activation enthalpies vs. number of carbons for the linear alkanes (n = 3 to 6) is summarized in SI Text. From the calculated results, we can see that CpRh(CO) C─H activation energies are lower than the Cp*Rh(CO) ones, whereas both migrations (1,2- and 1,3-) are easier in the Cp*Rh(CO) system than in the CpRh(CO) system. The 1,3-migrations are faster than the 1,2-migrations because the two C─H bonds involved are much better aligned to bond well with the metal in the transition state. Secondary C─H activation barriers are much larger than both the primary C─H activation and the two migrations. Hence, C─H activation at ─CH₂─ groups is very unlikely during the reaction with alkanes having ─CH₃ groups. The σ-complexes formed by ─CH₂─ groups following photolysis will migrate to terminal ─CH₃ sites before the C─H activation takes place.

Kinetics Simulations

By using standard transition state theory with a transmission coefficient of 1.0 and the observed lifetime (1/k) of methane in the CpRh(CO) system (∼3 ns), the free energy barrier for the C─H bond activation is calculated as 5.8 kcal mol^-1, which is close to our calculated (CCSD//PBE) free energy value of 6.0 kcal mol^-1. The lifetimes of such fast reactions are very sensitive to ΔG^‡, as an increase in the free energy barrier of 0.1 kcal mol^-1 will bring almost 0.6-ns change in lifetime. Thus, if we want to simulate the observed lifetimes (± 0.2 ns) using the calculated free energy barriers, the error of these calculations must be less than 0.02 kcal mol^-1. Unfortunately, this accuracy is unreachable for molecular systems containing a heavy metal atom with current theoretical and computational methods. Therefore, the calculations can be only a guide to the most important steps and the most important energy changes. The actual simulations of the experimental results will be empirical, but strongly based on computed trends and using the fewest parameters consistent with the computational and experimental results.

1. Summary of Principles Obtained from Calculations.

The basic principles summarized below for the chemical kinetics simulations are based on the computed values displayed in Fig. 3 and SI Text.

• I. For the C-H activations: (i) The activation energy of a C─H bond increases significantly when one of the spectator H atoms on a CH_x group being activated is replaced with a ─CH₃ group. (ii) With longer alkanes, the internal ─CH₂─ groups have higher activation energy than those attached to ─CH₃. (iii) CpRh(CO) activates the C─H bonds of alkanes more easily than Cp*Rh(CO). (iv) Ethane has a higher C─H bond activation barrier than methane. (v) The C─H activation barriers at ─CH₃ in ethane and propane are similar in CpRh(CO) but have somewhat larger differences in Cp*Rh(CO). (vi) Propane and longer alkanes have constant C─H bond activation barriers at their ─CH₃ groups. (vii) Differences in C─H activation barriers between ─CH₃ groups near the gauche turn and those farther away are larger for Cp*Rh(CO) than those for CpRh(CO) because of the crowded structure of Cp* (Fig. 3).

• II. For the migrations between CH_x groups: (i) In the CpRh(CO) system, barriers for 1,2-migrations of alkanes are about constant and similar in magnitude to the C─H activations of ─CH₃. (ii) Barriers for 1,3-migrations of alkanes are smaller than those for 1,2-migrations and decrease with increasing chain length in the CpRh(CO) system. (iii) Both 1,2- and 1,3-migrations have lower barriers in the Cp*Rh(CO) system because of its stronger steric effect. (iv) Generally, the 1,4-migration barriers are larger than 1,3-migration barriers and the differences are smaller for Cp*Rh(CO). Furthermore, because the barriers for ─CH₃ activation near a gauche turn are higher for Cp*Rh(CO), the 1,4-migrations will play a larger role in the activation of Cp*Rh(CO) systems and were included in these simulations.

2. Reaction Kinetics Simulations Based on Above Principles

The qualitative principles from the quantum chemical calculations discussed above form the basis for the following simulations: To determine some of the key factors in the lifetimes of alkanes in their reactions with CpRh(CO) and Cp*Rh(CO), we tested several simulations. First of all, the reactions were simulated without migration between different carbon atom positions to determine the effect of different C─H bond activation barriers at the ─CH₂─ positions. The initial concentrations of Rh─alkane complexes were based on the statistical distribution of the numbers of C─H bonds in each alkane. The C─H activation barriers (free energy) of CH₄ and ─CH₃ were set as 5.8 and 6.1 kcal mol^-1 (close to the DFT calculated results and simulated from experimental lifetimes of methane and ethane). Variable ─CH₂─ activation barriers resulting in the simulated lifetimes of alkanes are shown in the SI Text, where the lifetimes shorten quickly with decreasing the ─CH₂─ activation barriers. The simulations with ─CH₂─ activation barriers of 7.0 and 6.8 kcal mol^-1 bracket the observed lifetimes. However, all of these lifetime trends with different ─CH₂─ activation barriers are smooth and do not have the weak but observable step pattern obtained in experimental measurements. Furthermore, the ─CH₂─ barrier (6.8 kcal mol^-1) that brings the simulated lifetime for C₄H₁₀ into agreement with the experimental lifetime is only 0.7 kcal mol^-1 larger than the ─CH₃ barriers, although the calculations would suggest a difference close to 1.1 kcal mol^-1. Overall lifetimes are predicted to be too long when one applies the average calculated difference between ─CH₂─ and ─CH₃ barriers. Therefore, we need to consider additional aspects in the kinetics simulations, such as the migrations between different CH_x groups bonding to the Rh atom.

The results when different 1,2-migration barriers are introduced into simulations with fixed C─H activation free energy barriers for CH₄, ─CH₃, and ─CH₂─ of 5.8, 6.1, and 7.2 kcal mol^-1, respectively, are also displayed in the SI Text. The smaller 1,2-migration barriers reduce the simulated lifetimes of alkanes in these reactions. With 1,2-migration barriers of 6.2 kcal mol^-1, the simulated lifetimes are very close to the experimental values of alkanes with CpRh(CO). Again, however, the lifetimes are almost linear with the increase of the size of alkanes and do not reproduce the weak observed step pattern. Furthermore, according to the DFT calculations, 1,3-migrations are faster than 1,2-migrations and, thus, must also be introduced in the simulation.

The simulated lifetimes of alkanes with constant barriers for C─H activation of CH₄, ─CH₃, and ─CH₂─ (5.8, 6.1, and 7.2 kcal mol^-1) and 1,2-migration (7.0 kcal mol^-1) but different barriers for 1,3-migrations have also been investigated (SI Text). The plots of reaction lifetimes vs. numbers of C atoms are, of course, linear when 1,3-migrations have the same barriers as the 1,2-migrations. However, when the 1,3-migration barrier is decreased to 6.0 kcal mol^-1, the simulated lifetimes of alkanes begin to display an obvious but weak step pattern that matches extremely well with the experimental lifetimes of alkanes in their reactions with Cp*Rh(CO). The barriers of these 1,3-migrations are actually slightly lower than the C─H bond activation barrier. This is consistent with the quantum chemical calculations. This step pattern arises from alkanes with even carbon numbers, which due to the low barrier 1,3-migrations can move CpRh(CO) to one of the two ─CH₃ ends without ever needing a higher barrier 1,2-migration. However, for alkanes with an odd number of carbon atoms, migrations from some ─CH₂─ groups will require the higher barrier of 1,2-migrations to reach either of the terminal ─CH₃ groups. Therefore, as shown in SI Text, alkanes with an even number of C atoms such as 4 and 6 appear to have slightly shorter lifetimes in general agreement with the experimental results. This step pattern becomes stronger with the decrease of the 1,3-migration barrier.

Although the simulations with the relative reaction barriers of 1,3-migration < ─CH₃ activation < 1,2-migration < ─CH₂ activation exactly reproduce the lifetimes of alkanes reacting with CpRh(CO), no variations of these parameters alone can explain the observed lifetime pattern of alkanes reacting with Cp*Rh(CO). The lifetimes of ethane and butane in the Cp*Rh(CO) system are about 2 ns longer than those in the CpRh(CO) system. The 1,3-migration cannot explain the longer lifetimes of butane and similar lifetime of pentane because the lower 1,3-migration barriers can lead only to a reverse pattern with shorter lifetime of butane and longer lifetime of pentane. Higher 1,3-migration barriers will lead only back to linear behavior. The calculations suggest that for the Cp*Rh(CO) system the C─H activation barriers are higher, whereas the migration barriers are lower than those in the CpRh(CO) system. In addition, because the Cp* structure is sterically more crowded, the Cp* reaction is more sensitive to the conformation of alkanes. For example, near a gauche turn in butane and longer alkanes, the 1,3-migration and C─H activation of ─CH₃ are slower, but a gauche conformation leads to faster 1,4-migrations in pentane and longer alkanes. Furthermore, in the Cp*Rh(CO) system, the 1,2-, 1,3-, and 1,4-migration barriers become lower with increasing chain length.

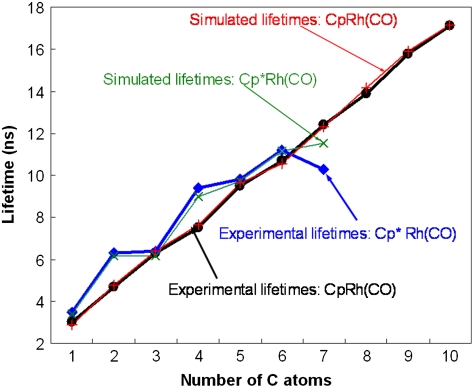
The final simulations for both Cp and Cp* systems are shown in Fig. 4. In particular, Cp*Rh(CO)(butane) is longer-lived because 33% of it is in the gauche conformation, which activates more slowly, whereas Cp*Rh(CO)(pentane) is shorter-lived because faster migrations can move the σ-complexes to the end without the gauche turn. As the chains get longer, there is a higher probability of gauche turns, which shortens the lifetimes (n = 7). Here and in longer alkanes, conformations with multiple gauche turns further complicate the analysis such that simple explanations from static calculations alone cannot be made. When all of these additional effects are introduced into our simulations, a lifetime pattern of alkanes with Cp*Rh(CO) very close to the experimental results is obtained. Heptane has a somewhat larger error as we have simulated it using only three conformations, although in reality it has many more including several with two gauche turns.

Fig. 4.

Final simulated and experimental lifetimes are compared.

Concluding Remarks

Surprisingly, for the CpRh(CO)(alkane) system there is an approximately linear relationship between lifetime and alkane chain length that is unexpected because major differences between primary and secondary alkanes should have a dramatic effect on changing from methane and ethane to heavier alkanes and eventual asymptotic behavior with long chain lengths. Our understanding of the delicate balance in the factors controlling this fundamental reaction came from studying the related Cp*Rh(CO)(alkane) system where an oscillating and asymptotic behavior was observed. Indeed close inspection of the CpRh(CO)(alkane) system revealed a complementary oscillatory behavior albeit barely observable in this unique experimental dataset.

These data have been understood by using theoretical calculations. As we have previously shown, the barrier for oxidative cleavage of the C─H bond by transition metal complexes is sensitive to the functional and somewhat sensitive to the basis set. Because of the sensitivity required to disentangle these experimental results, we have carried out CCSD calculations. The CCSD calculations were combined with the DFT trends to develop kinetic simulations that reproduced the experimentally observed rates of oxidative cleavage and chain migration and led to the elucidation of the mechanism of C─H activation. Our results clearly show that an understanding of the barriers to primary and secondary alkane activation, the rates of 1,2- and 1,3-migrations of the coordination center along the chain, and the importance of the conformation (trans vs. gauche) of the coordinated alkane is required in order to predict the behavior of these fundamental reactions. The observed variation in lifetimes arises from a subtle competition between activation and migration.

Materials and Methods

1. Quantum Calculation Details.

All calculations were performed using the Gaussian 03 suite of ab initio programs for both CCSD and DFT computations. (26) The geometric structures of all species were optimized in the gas phase at the PBE level. For the shorter hydrocarbons (n ≤ 3), the full optimizations were carried out at the B3LYP level, and the single-point calculations with the basis set superposition error (BSSE) corrections were carried out at the CCSD level on the structures obtained at both B3LYP and PBE levels. Stuttgart/Dresden RSC 1997 (SDD) effective core potential and basis set (SDD) was used for the Rh atom, and the cc-pVDZ basis set was applied for all other atoms. Calculating the harmonic vibrational frequencies and noting the number of imaginary frequencies confirmed the nature of all intermediates (no imaginary frequency) and transition state structures (only one imaginary frequency). The latter were also confirmed to connect reactants and products by intrinsic reaction coordinate calculations. The gas-phase free energies, G, were calculated at T = 298.15 K within the harmonic potential approximation at optimized structures. No solvent effects were taken into account as these reactions involve uncharged reactants, transition states, and products in weakly coordinating liquid hydrocarbons.

2. Experimental Details.

CpRh(CO)₂ was prepared in adaptation to a published procedure (27). Cp^∗Rh(CO)₂ was purchased from Strem Chemicals, Inc. The gases argon (99.994%) and methane (grade 4.5) were purchased from Air Products; CO (> 99%), ethane, propane (98%+), and butane (99.5%) were purchased from Aldrich and used as received. The liquid alkanes were heated to reflux over CaH₂ for several hours. The TRIR experiments were performed at the Picosecond Infrared Absorption and Transient Excitation facility at the Rutherford Appleton Laboratory, which also has been described in detail elsewhere (28).