Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans

Abstract

To navigate different environments, an animal must be able to adapt its locomotory gait to its physical surroundings. The nematode Caenorhabditis elegans, between swimming in water and crawling on surfaces, adapts its locomotory gait to surroundings that impose approximately 10,000-fold differences in mechanical resistance. Here we investigate this feat by studying the undulatory movements of C. elegans in Newtonian fluids spanning nearly five orders of magnitude in viscosity. In these fluids, the worm undulatory gait varies continuously with changes in external load: As load increases, both wavelength and frequency of undulation decrease. We also quantify the internal viscoelastic properties of the worm’s body and their role in locomotory dynamics. We incorporate muscle activity, internal load, and external load into a biomechanical model of locomotion and show that (i) muscle power is nearly constant across changes in locomotory gait, and (ii) the onset of gait adaptation occurs as external load becomes comparable to internal load. During the swimming gait, which is evoked by small external loads, muscle power is primarily devoted to bending the worm’s elastic body. During the crawling gait, evoked by large external loads, comparable muscle power is used to drive the external load and the elastic body. Our results suggest that C. elegans locomotory gait continuously adapts to external mechanical load in order to maintain propulsive thrust.

How do neural circuits produce and regulate the rhythmic patterns of muscle activity that drive animal locomotion? The nematode Caenorhabditis elegans—with its well-mapped nervous system (1), relatively simple anatomy (2), and rhythmic undulatory movements (3)—is a promising model for exploring the neural basis of locomotion. To fully understand motor behavior we also need to understand C. elegans locomotory biomechanics: how muscle activity produces movement within the mechanical framework of the worm’s body and its physical environment.

C. elegans moves forward by propagating undulatory waves in a dorsal-ventral plane from head to tail (3). Bending is generated by alternating contraction and relaxation of two dorsal and two ventral muscle groups running along the length of the worm’s body (2). Both the shape and speed of these undulations change in response to the physical environment (3, 4). When moving on moist surfaces such as agarose gels, C. elegans exhibits a crawling gait characterized by undulations with low frequency and short wavelength (5). By contrast, when moving through water, C. elegans exhibits a swimming gait characterized by undulations with higher frequency and longer wavelength (Table 1). The differences in the size and speed of undulations are modest in comparison with the difference in the scales of physical force during swimming and crawling. At the size and speed of C. elegans, forces due to surface tension (surface tension holds the crawling animal to the agar surface) are approximately 10,000-fold larger than forces due to viscosity when swimming in water (6).

Table 1.

Locomotory parameters for swimming and crawling worms

	Wavelength (λ/L)	Frequency (Hz)
Swimming	1.54 ± 0.04	1.76 ± 0.07
Crawling	0.65 ± 0.03	0.30 ± 0.02

Undulatory wavelength and frequency of worms swimming in NGM buffer or crawling on agarose surface. All values given as mean ± SEM. N > 10 for each condition.

By examining nematode locomotion on or within gels of varying stiffness, Wallace (7) and Berri et al. (8) uncovered continuous change in locomotory patterns from gaits that resemble swimming in water to gaits that resemble crawling on surfaces. Gels can impose much larger external forces on a moving animal than viscous fluids, but it is more difficult to quantify all external forces that a gel can impose—a complex blend of elastic, tearing, viscous, and capillary forces. Here, we sought the mechanical determinants of locomotory gait adaptation and so studied nematode locomotion in Newtonian fluids, in which external forces on the worm body are proportional to speed and viscosity. To quantify the worm’s locomotory behavior we applied machine vision algorithms similar to those previously used to describe C. elegans behavior (4, 5, 9–11).

A biomechanical model of worm undulatory dynamics needs to incorporate the mechanical properties of the worm’s body. In recent studies of locomotory dynamics, Sznitman et al. (12, 13) attempted to predict the mechanical properties of the C. elegans body by quantifying the movements of swimming worms. To do this, they measured the shape of locomotory gait of a swimming worm, assumed a particular spatiotemporal pattern for muscle torque, and determined those values of internal viscoelasticity that would fit the undulatory gait of swimming worms (12, 13). However, their predictions of the stiffness of the worm’s body were far lower than direct measurements that were made by probing the worm’s body with piezoelectric cantilevers (14). In this study, we performed direct and independent measurement of the coefficients of internal elasticity and viscosity that are specifically relevant to undulatory locomotion, those that characterize bending the entire worm modeled as a viscoelastic rod. To do this, we quantified the dynamics of relaxation of the worm body after sudden bending deflections in fluids of varying viscosity, as previously done in fluids with the viscosity of water (6).

We incorporate our analyses of internal and external mechanics into a biomechanical model of locomotory gait. The biomechanical model that we use is similar to models that have been applied to the dynamics of flagellated and undulatory microorganisms, which combine slender body theories in elasticity and fluid mechanics (15, 16). In our model, we use linear viscoelasticity to describe the passive component of the worm’s internal biomechanics and traveling waves of muscle torque to describe the active component. To describe the forces of the external fluid on the worm body, we use slender body approximations afforded by low Reynolds number hydrodynamics and small amplitude approximations to obtain the dominant terms of analytical solutions. All of the physical parameters in our model are either well-understood or directly measurable, providing a biomechanical framework for further analysis of the circuits for worm locomotion. Moreover, we present a physiological explanation for the observed load-dependent changes in gait exhibited by C. elegans in different environments.

Results

C. elegans Displays Different Gaits When Swimming and Crawling.

The kinematics of worm undulatory locomotion in the reference frame of the worm body can be represented by the time-varying curvature of the body centerline (Fig. 1). Here, we use a body coordinate, s, to describe position along the centerline from head (s = 0) to tail (s = L), where L is the length of the worm. The time-varying curvature is defined as the partial derivative of the tangent angle to the centerline with respect to the body coordinate:

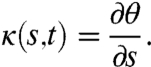[1]

Using this metric of time-varying curvature, we quantified the locomotory gait during swimming and crawling. We recorded dark field video sequences of worms during periods of regular forward movement (Fig. 2, Movies S1 and S2) and used image analysis software to measure the worm’s curvature as a function of space and time (see Methods). From the curvature measurements, we calculated the wavelength and frequency of the undulations (Fig. 2). Consistent with prior reports, worms swimming in buffer with the viscosity of water (η = 1 mPa·s) displayed undulations with long wavelength and high frequency, whereas worms crawling on agar surfaces displayed undulations with short wavelength and low frequency (Table 1).

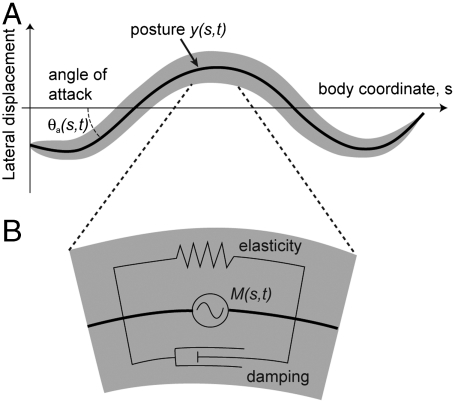
Fig. 1.

The kinematics of an undulating worm. (A) Diagram of a worm moving in a viscous fluid. Body coordinate s describes path length along worm body, starting from the head. Posture y(s,t) describes lateral displacement of worm body centerline. θ_a describes angle of each body component with respect to direction of movement. (B) Worm body is modeled as a rod with elasticity (represented by spring), internal damping (represented by dashpot), and active muscular torque M(s,t).

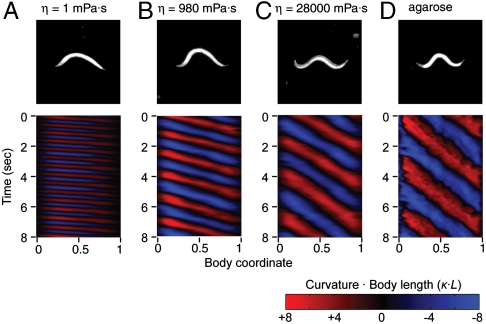
Fig. 2.

Modulation of C. elegans locomotion. Dark field images and time-dependent curvature patterns of adult worms (A) swimming in NGM buffer with viscosity 1 mPas, (B) in dextran solutions with viscosity 980 mPa·s, (C) in dextran solution with viscosity 28,000 mPa·s, (D) crawling on 2% agarose surface. The worm head is to the left in all images. Body curvature as a function of time (in seconds) and normalized body coordinate (varying from 0 at the head to 1 at the tail). Body curvature is represented using the nondimensional product of curvature (the inverse of radius of curvature) and body length.

Next, we quantified the locomotion of worms immersed in solutions containing high molecular weight dextran (MW 2,000,000), which display Newtonian flow characteristics with viscosities ranging from 1 to 28,000 mPa·s (17) that we directly characterized by rheological measurements (see Methods). In our experiments the Reynolds number < 0.05, meaning that inertial forces are negligible in comparison to viscous forces. The advantage of using Newtonian fluids at low Reynolds numbers—as opposed to gels or non-Newtonian fluids such as methylcellulose solutions—is that resistive force theory allows us to estimate the first-order relationship between force, drag, and movement: The external force resisting transverse movement of the worm body is simply proportional to the speed of movement and to the coefficient of viscous drag to transverse movement (18). In describing the external viscous forces encountered by the moving worm, it is useful to describe its undulations in terms of its transverse displacement y(t) in the reference frame of the moving worm (Fig. 1). Thus, the external force per unit length that is transverse to the worm’s body during lateral movement is:

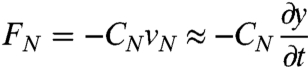[2]

where C_N is the coefficient of viscous drag to transverse movement and ∂y/∂t is the linear approximation for the speed of transverse movement v_N (Fig. 1).

We placed worms in chambers containing Newtonian viscous fluids. Increasing viscosity from 1 to 28,000 mPa·s induced a continuous transition between undulations that resemble swimming in water and crawling on agarose, as measured by the wavelength, frequency, and amplitude of the undulations (Table 1, Fig. 2, and Fig. 3 A–D and Movies S1–S4). At intermediate values of the range of viscosities that we studied, worms exhibited steady undulations that were intermediate in wavelength and frequency to swimming and crawling (Fig. 3B, Movie S3). Recently, Pierce-Shimomura et al. (4) found mutations in C. elegans that caused animals to exhibit abrupt switching between swimming and crawling gaits in water. In our experiments, if locomotory behavior exhibited bistable switching between distinct crawling and swimming gaits, intermediate gaits might be construed from time averages of two distinct gaits. However, we found no evidence for such switching. Abrupt switching between swimming and crawling gaits would be expected to increase the statistical variation in measured wavelength. To the contrary, we did not find the standard deviation of wavelength to be larger for intermediate viscosities, compared with low or high viscosities (Fig. S2). Instead, the normalized standard deviation of wavelength was nearly constant over the range of viscosities studied.

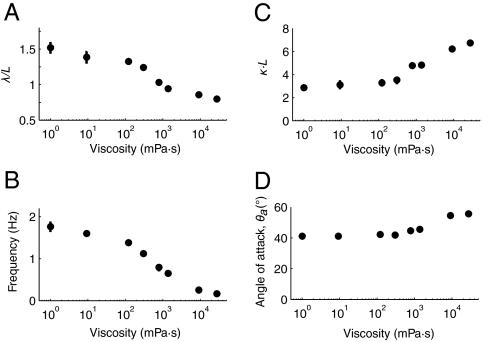
Fig. 3.

Locomotory parameters. (A) Mean wavelength of undulation scaled by worm body length L in different viscous solutions; (B) mean undulatory frequency; (C) mean curvature amplitude of undulation scaled by reciprocal of body length; (D) peak angle of attack, in degrees.

Internal Resistance to Bending.

Next, we quantify the passive internal elastic and viscous forces that resist bending during undulatory locomotion. Following Guo and Mahadevan (19), we consider that the passive body behaves as a viscoelastic rod, described by a bending modulus b and a coefficient of internal viscosity b_v. The passive torque M^p is linear in both curvature κ and its time derivative:

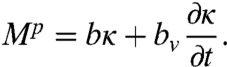[3]

The first term describes the internal elasticity of the worm; the second describes the internal dissipation.

Let N be the internal shear force transverse to the body axis, and M = M^p + M^a the total internal torque, which in general contains an active muscular component M^a. Being at low Reynolds numbers, inertia is negligible and torque must be balanced on any infinitesimal body segment, leading to M_s = N (A_s denotes the partial derivative of A with respect to s). Similarly, transverse force balance leads to N_s = F_N. It follows that M_ss = F_N. Using Eqs. 2 and 3 and the linear approximation κ ≈ y_ss one gets:

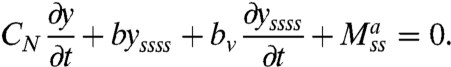[4]

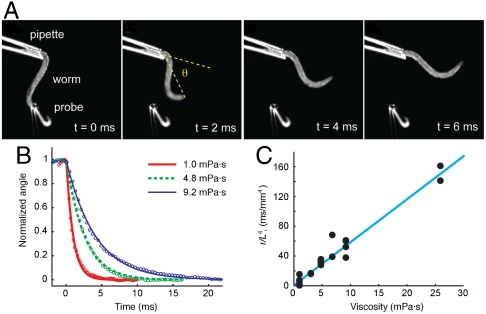
Using Eq. 4 in the absence of active torque (M_a = 0), we estimated the coefficients of internal elasticity and viscosity by measuring the time scale of relaxation of the worm body following deformation in Newtonian fluids of viscosity varied between 1 and 25 mPa·s. To do this, we held a live worm with a glass micropipette immersed in each viscous solution. We used another micropipette with a hooked end to bend the worm to one side and release it (Fig. 4A and Movie S5). Using high-speed video microscopy, we measured the angle between the holding pipette and the vector connecting the end of the pipette and the worm’s head as a function of time (Fig. 4B).

Fig. 4.

Measurements of internal elasticity and viscosity. (A) Images from a video sequence in which worm position decays from deformed posture in NGM medium (viscosity 1 mPa·s). (B) Normalized worm bending angle for three viscosities. Lines show least-squares exponential fit for each viscosity. (C) Decay time scaled with fourth power of length of worm outside pipette, as function of viscosity. Data represents 15 decays from a total of five worms. Line: least-squares linear fit y = Mη + B; fit parameter estimates M = 5.71 ± 0.65, B = 4.82 ± 7.13 in the units of the figure.

We found that worm movement following release had a fast exponential component, owing to passive relaxation of the worm body, and a slow linear component, owing to active movement of the live worm. We quantified the exponential time constant as a function of the viscosity of the surrounding fluid. As expected from linear viscoelastic theory, this exponential time constant was linearly related to external viscosity (see Methods). From the slope of the linear relationship between the time constant and external viscosity (Fig. 4C), we estimated the coefficient of elasticity to be b = 9.5( ± 1.0)·10^-14 Nm². From the y-intercept of this linear relationship, we found that the mechanical load due to internal viscosity is negligible in comparison to internal elasticity. We found the upper limit to the coefficient of internal viscosity: b_v < 5 ∗ 10^-16 Nm² s. We note that the linear dependence between the time constant of exponential relaxation and external viscosity in the range 1 to 25 mPa·s also indicates that the coefficient of elasticity, b, is constant. Our direct measurement of body stiffness is contrary to a prediction by Sznitman et al. (13) that the stiffness of the worm’s body increases linearly with external viscosity in the range 1 to 10 mPa·s. We discuss reasons for this discrepancy below (see Discussion).

Propulsive Thrust Generated by Undulation Depends on Its Angle of Attack.

C. elegans generates propulsive thrust by performing undulations transverse to the direction of net movement. Each body segment of an undulating worm contributes propulsive thrust depending on its angle of attack, θ_a, the angle between the vector of net movement and the tangent vector to the body segment (see Fig. 1). The velocity v of any body segment can be resolved into a longitudinal component, v_L, and a normal component, v_N, so that the force components of each body segment pushing on the fluid can be estimated via resistive force theory: F_L = C_Lv_L and F_N = C_Nv_N, where C_L and C_N are longitudinal and normal resistance coefficients, respectively (18). Total propulsive thrust is determined by integrating the forces over all body segments of the undulating worm. Following ref. 18 we have (see Methods):

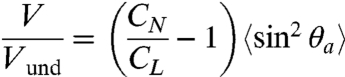[5]

where V is forward swimming speed and V_und is the propagation speed of undulations in the reference frame of the worm body (see Fig. 1).

According to Eq. 5, propulsive thrust decreases rapidly with a drop in θ_a. We quantified θ_a of worms swimming in viscous fluids ranging from 1 to 28,000 mPa·s. Despite changes in undulatory wavelength, frequency, and amplitude, the peak angle of attack remains roughly constant, modestly increasing from 45° to 55° with 28,000-fold increase in viscosity (Fig. 3).

How the Angle of Attack Depends on the Parameters of Undulatory Locomotion.

How might the worm maintain its angle of attack despite dramatic changes in external load? To answer this question, we sought a relationship between the angle of attack and the biomechanical parameters of undulatory movement. The amount of force generated by the muscles of an undulating worm resembles a traveling sinusoidal wave, M^a = M⁰ sin(2πs/λ - ωt), allowing us to use Eq. 4 (neglecting b_v) to estimate the angle of attack as a function of undulatory wavelength and frequency:

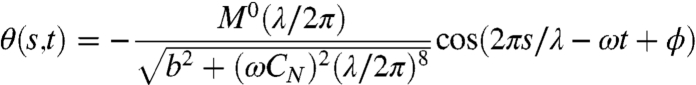[6]

where

[7]

Thus, the angle of attack is explicitly dependent on C_N, which is proportional to external viscosity. How, then, is the angle of attack conserved during a 28,000-fold increase in viscosity? One possibility is that the term in Eq. 6 that involves internal elasticity might be sufficiently larger than the term for viscous drag (b > ωC_N(λ/2π)⁴), such that changes in viscosity have little effect on the angle of attack. Another possibility is that changes in muscle torque, undulatory wavelength, and/or undulatory frequency might compensate for changes in external viscosity. As shown below, the key to evaluating these possibilities lies in accounting for how muscle power is used during locomotion at different viscosities.

Muscle Power Is Used Differently at Low and High Viscosity.

The total muscle power produced per unit length along the worm body is

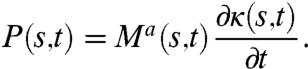[8]

This leads to:

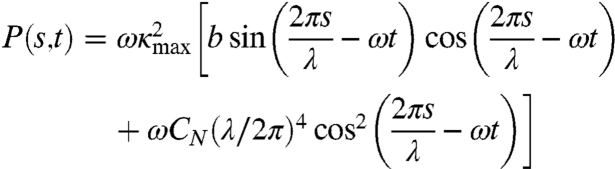[9]

where the maximum curvature of the worm is given by

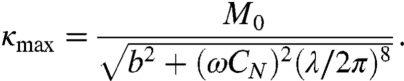[10]

Muscle power consists of two terms. The first is the power used to deform the elastic body of the worm, and the second is the power used to shear the surrounding viscous fluid. During each undulation cycle, the peak power delivered to the elastic body is 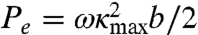and to the viscous fluid is .

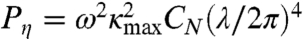The total peak power is given by the maximum of Eq. 8:

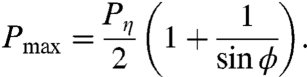[11]

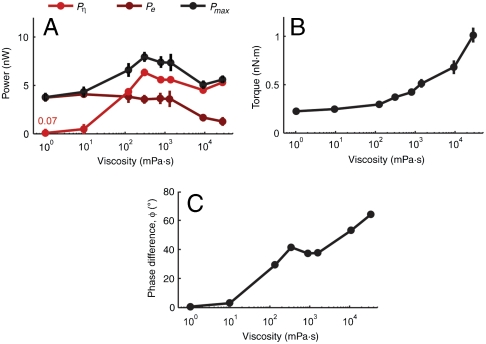
In Fig. 5A, we quantify the relative amounts of muscle power that the worm uses to drive its own elastic body and to drive the surrounding fluid, each as a function of external viscosity. At the lower viscosities that we studied, P_η < P_e, which also defines the regime where b > ωC_N(λ/2π)⁴. In this regime, the angle of attack can be constant despite changes in viscosity, not requiring changes in undulatory wavelength or frequency (Fig. 5A). This observation is consistent with our experimental observation that both undulatory frequency and wavelength exhibit asymptotic behavior in the limit of low viscosities.

Fig. 5.

(A) Estimated external viscous power, peak internal elastic power, and peak total power as a function of viscosity. (B) Maximum torque as a function of viscosity, from Eq. 3. (C) Phase difference between torque and curvature as a function of viscosity, from Eq. 7.

At the higher viscosities that we studied, P_η > P_e. In this regime, significant muscle power is used both to shear the surrounding viscous fluid as well as bend the elastic body. To preserve constant angle of attack as viscosity increases, the worm gradually decreases both frequency and wavelength and gradually increases muscle force.

Finally, our biomechanical model can be used to estimate the phase difference ϕ between the traveling wave of muscle activity and the traveling wave of the curvature itself. In the regime of the swimming gait, peak muscle torque coincides with peak curvature of the worm body (ϕ ≈ 0, Fig. 5C). However, as viscosity increases, a phase difference develops. For the crawling-like gait exhibited at high mechanical load, we predict approximately 60° phase difference between peak muscle activity and peak curvature (Fig. 5C). This variable phase difference between muscle torque and body curvature may be verified by directly imaging the activity of muscle cells (e.g., using calcium imaging) in freely moving animals.

Discussion

The different gaits exhibited by C. elegans represent a continuous adaptability of an underlying locomotory circuit to external mechanical load, as shown by Berri et al. (8). Gradually increasing external mechanical resistance on a swimming worm—which we did by increasing the viscosity of the external Newtonian fluid by nearly five orders of magnitude—induces a continuous transition of locomotory gait, gradually decreasing the wavelength and frequency of undulations until the worm gait resembled that of crawling on agarose surfaces. Our analysis has shown that swimming and crawling are qualitatively different from a mechanical perspective. During swimming, external load is insignificant in comparison to internal elasticity. During crawling, external load and internal elasticity are comparable.

The worm, like other organisms smaller than the capillary length of water, must be able to move through fluids and fluid interfaces that impose external loads spanning several orders of magnitude. Our biomechanical analysis points to the strategic value of the worm’s changes in locomotory gait over this range. Over 28,000-fold changes in viscosity, total muscle power varies by less than a factor of 2, but muscle power that is dissipated in external viscous shear varies by approximately 100-fold. The purpose of gait change in C. elegans is to maintain propulsive thrust, allowing the worm to maintain the angle of attack of its undulation with the constraint of limited muscle power expenditure.

Our analysis has also produced a previously undescribed measurement of the internal elasticity of the worm body, which may be compared with other recent studies of worm biomechanics (12–14). Park et al. (14) used a piezoresistive cantilever to measure the force-displacement relationship of a probe applied to the worm’s surface. They found that stiffness of the worm body is, for the most part, due to the rigidity of its cuticle. Modeling the worm cuticle as a cylindrical shell with radius of approximately 0.018 mm and wall thickness of approximately 0.0004 mm, they used the linear force-displacement relationship of the worm cuticle to estimate its Young’s modulus: E ∼ 380 MPa.

If we assume that the bending stiffness is mostly due to the worm cuticle, and we also model the worm cuticle as a thin-walled cylinder with radius of approximately 0.018 mm and wall thickness of approximately 0.0004 mm, we can use our coefficient of elasticity, b, to estimate the Young’s modulus of the cuticle. Our coefficient of elasticity is the product of the moment of inertia of the cross-section of the cylinder and its Young’s modulus: b = EI (19). The moment of inertia of a thin cylinder with radius r and thickness t is I = πr³t. Thus, we would estimate the Young’s modulus of the cuticle as approximately 13 MPa.

We note that our measurements of the Young’s modulus of the cuticle is approximately 30-fold smaller than that measured by Park et al. (14). However, as pointed out by Park et al. (14), the cuticle is likely to exhibit different amounts of stiffness when stretched in the longitudinal or circumferential directions. Anisotropic elasticity is evidenced by their observations that strong hyperosmotic shocks can greatly reduce nematode length (> 25%) but not radius (< 3%). Our bending measurements, which do not distort the worm circumference, are specifically sensitive to the longitudinal compliance of the cuticle. In contrast, measurements that Park et al. (14) made with a cantilever probe, which distorts the cross-section, would be sensitive to the circumferential compliance of the cuticle. The large anisotropy of the cuticle may have appeared as a resolution to the dilemma of displaying a stiff shell providing protection from the external world while limiting power expenditure during locomotion.

We note that direct measurements of cuticle stiffness made by us and Park et al. (14) are much higher than a prediction of cuticle stiffness made by Sznitman et al. (12, 13). In particular, Sznitman (12, 13) predicted that the Young’s modulus would increase linearly with fluid viscosity from E = 0.6 kPa at η = 1 mPa·s to E = 10 kPa at η = 10 mPa·s. To do this, they assumed a particular spatiotemporal pattern of muscle torque, and they fit the value of internal elasticity that would generate the shape and dynamics of the swimming worm. The reason that the prediction of internal elasticity by Sznitman et al. (12, 13) is much lower than our direct measurements or those of Park et al. (14) is that their prediction is sensitive to their initial assumption of the spatiotemporal pattern of muscle torque. Both we and Sznitman et al. (12, 13) used similar mathematical methods to model internal viscoelasticity and external viscosity, and so the results of Sznitman et al. (12, 13) could be reconciled with higher cuticle stiffness simply by modifying their initial assumption about muscle torque. We also note that better accuracy in modeling the external viscosity in all of these studies would be obtained using more detailed models of external hydrodynamics that incorporate viscous coupling between body segments, as has recently been done in the study of other slender swimming organisms (20, 21).

The neuromuscular mechanisms that underlie load-dependent adaptation of locomotory gait are not yet known. Our biomechanical analysis shows how patterns of muscle activity are transduced into locomotory undulation in different physical surroundings and provides a physiological explanation for changes in locomotory gait. Further work will aim to show how neuromuscular circuits drive the specific patterns of muscle activity that generate the appropriate locomotory gait in different surroundings.

Methods

Worm Strains and Cultivation.

Wild-type worms (N2 Bristol) were cultivated on Escherichia coli OP50 NGM plates at 20 °C according to standard methods. Development was synchronized by hypochlorite bleaching, and all experiments were performed with adult worms 12–18 hrs after the final molt.

Viscous Fluids.

Viscous solutions were composed of 0–45% (w/w) dextran (2,000,000 MW) dissolved in either NGM buffer (for 0–30%) or 10 mM HEPES (pH 6.0) (for 35–45%). The viscoelastic properties of each dextran solution were measured using a AR-G2 rheometer with cone-plate geometry (TA Instruments). For each solution that we used, we measured the viscosity using a shear rate of 1 s^-1 and further verified that viscosity varied by less than a factor of 1.5 over a range of shear rates from 0.1 to 100 s^-1. Over the range of dextran solutions that we used (1–45% by mass), viscosity spanned nearly 5 orders of magnitude, providing a large range of experimental viscosities with Newtonian flow characteristics (i.e., negligible dependence of viscosity on shear-rate).

Measuring Locomotory Gait.

To quantify the crawling gait, worms were placed on 2 mm thick layers of 2% agarose in NGM buffer. To quantify the swimming gait in NGM buffer or in viscous fluids, worms were washed in NGM buffer and transferred to 0.1–0.2 ml fluid droplets in chambers composed of two glass slides separated by approximately 0.150 mm using coverslips. To prevent worms from adhering to glass surfaces when using pure NGM buffer, 0.1% (w/w) bovine serum albumen (BSA) was added to the solution.

We recorded image sequences of worms using either an inverted Nikon microscope under 2X–4X magnification with dark field illumination or a custom-built microscope using a zoom lens and dark field illumination provided by a ring of red LEDs. Image sequences were recorded on a computer at 30 Hz with a CCD camera (Imaging Source) using IC Capture software (Imaging Source).

Image analysis was performed using MATLAB (Mathworks) (Fig. S1). Briefly, image sequences were identified in which the worm performed consistent forward movement without reversals or turns. In these sequences, each image was background-subtracted, filtered by a disk-shaped smoothing filter with diameter equal to one fifth the worm diameter, then thresholded to give a binary image. The anterior and posterior ends of the worm were identified as the points of maximum convex curvature on the anterior and posterior halves of the boundary of the thresholded image. A centerline extending from the head to the tail of the worm was calculated such that the centerline was equidistant to nearest boundary points along the two sides of the worm boundary. A least-squares cubic smoothing spline fit to the centerline was then calculated. Curvature was calculated as the derivative with respect to the body coordinate of the unit vector tangent to the centerline.

The speed of the undulatory wave, in the reference frame of the worm body, was calculated using least-square linear fits to the zero crossings of curvature over the central 80% of the body length. Because the slope of positive-derivative zero crossings could slightly differ from the slope of negative-derivative zero crossings, an equal number of the two were used to calculate wave speed in each image sequence (Fig. S1). Undulatory frequency was calculated by dividing the number of cycles by the elapsed time during the image sequence. Undulatory wavelength was calculated as the ratio between speed and frequency.

To quantify the angle of attack that defines propulsive thrust, we computed the tangent angles along the worm centerline as a function of body coordinate and time. To eliminate the effect of slow changes in worm orientation that could occur over several cycles, we filtered the tangent angles using a temporal low-pass filter with time scale equal to the worm undulatory period, producing a slow-offset-subtracted angle. The average angle of attack, as well as 〈 sin²θ_a〉, were calculated using the slow-offset-subtracted angles, averaged over body coordinate over an integral number of undulations.

Measuring the Internal Viscoelasticity of the Worm Body.

To estimate the internal elasticity and viscosity of the worm body, we used a method similar to that of Sauvage (6). A glass capillary pipette was drawn over a flame, broken, and flame polished to narrow the opening to a diameter of about 20 μm. An adult N2 worm was washed in NGM buffer and its tail was partly drawn into the pipette by vacuum. The pipette holding the worm was attached to a culture dish containing viscous dextran solutions (1–25 mPa·s), such that the live worm was held about 2–3 mm above the bottom of the dish with its undulations in the plane of observation. The worm was monitored using darkfield illumination with a 4X objective on an inverted microscope. We used a glass pipette with a finely drawn hooked tip to bend the body to the ventral or dorsal side and then release it (Movie S5). The rapid relaxation of the worm body to its original position was recorded at 5,000 frames per second using a high-speed video camera (Phantom V9, Vision Research).

The exponential component of the time course of relaxation can be related to the coefficients of internal elasticity and viscosity of the worm body. With no active muscle torque, the passive relaxation of the body is described by:

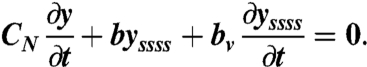[12]

A stationary bend is described by:

[13]

Solving for a(t), we arrive at

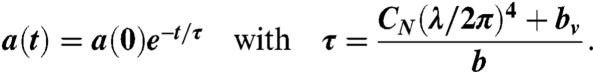[14]

When the body is allowed to relax, the response is dominated by the mode with lowest spatial frequency. In the case of a viscoelastic rod with one free end and one fixed end, the wavelength of this mode is λ = 4L_f, where L_f is the length of the free portion of the worm (which ranged from 0.72 mm to 0.90 mm in our experiments). Thus, the exponential time constant for relaxation is:

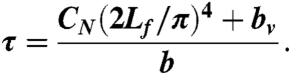[15]

The coefficient of viscous drag for transverse movement of a slender body with length Lf and diameter d in a solution with viscosity η is (18):

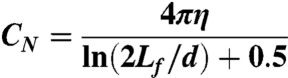[16]

where d ≈ 0.060 mm is the diameter of the worm. We thus find C_N≈3.3η. Taken together, these equations support an affine dependence of the exponential time constant of relaxation with external viscosity:

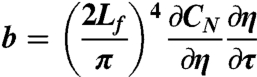[17]

[18]

To determine the elastic constant b, we estimated dη/dτ by using a linear fit to the data for the exponential time constant (scaled by 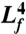) versus external viscosity (Fig. 4). We obtained the values b = 9.5 × 10^-14 Nm³ and b_v < 5.0 × 10^-16 Nm³ s. The latter represents an upper bound because the confidence interval of the y-intercept of the linear fit included zero. In any case, forces due to internal elasticity are at least 100 times larger than forces due to internal viscosity during locomotion.

Measuring the Coefficient of External Viscous Drag.

In our behavioral assays, each worm exhibited undulatory locomotion between two horizontal glass plates separated by 0.150 mm. Viscous coupling between the undulating worm and the nearby glass surfaces could alter the coefficients of viscous drag (C_N). To quantify the correction to these coefficients in our imaging chambers, we measured the sedimentation speeds of anesthetized worms in a buffer containing NGM + 0.1% BSA + 25 mM sodium azide. We placed worms in two types of chambers: (i) vertically oriented thin chambers, identical to those used in our experiments and (ii) a bulk liquid chamber comprised of a 2.5 cm × 2.5 cm × 4 cm transparent plastic container. Using a CCD camera, zoom lens, and tracking software, we measured the average sedimentation speeds of worms falling in the transverse direction (oriented within 10° of the horizontal). We found that worms sedimented with an average speed of 0.66 ± 0.04 mm/s (mean ± SD, N = 10) in bulk fluid and 0.068 ± 0.007 mm/s (mean ± SD, N = 10) in the thin chamber. Thus, the coefficient of viscous drag to transverse movement is approximately 9.7 times larger in the thin chamber compared with bulk fluid of the same viscosity. Note that such a correction was unnecessary when we measured the internal viscoelasticity of the worm, because, in those experiments, the worm was held at least 2 mm from any surfaces of the chamber.

Justification of Eq. 5.

Consider a segment of body. During locomotion its velocity can be written:

[19]

where t is the unit vector tangent to the segment, e_x is the unit vector in the direction of motion, v_und the velocity of the propagating undulation, cos(θ) = t·e_x and v_s = v_und - v is the slippage velocity. Then in the approximation where hydrodynamics interactions between segments are neglected, the viscous force on the fluid reads:

[20]

where n is the unit vector orthogonal to t. Using Eq. 19 in Eq. 20, and projecting the later on the direction e_x, one obtains:

[21]

Averaging Eq. 21 along the body leads to Eq. 5.